The Forward and Inverse Kinematics of a Delta Robot

Hugo Hadfield, Lai Wei, Joan Lasenby
University Of Cambridge,
Signal Processing and Communications Laboratory
Speaker: Hugo Hadfield
Geometry of a Delta Robot
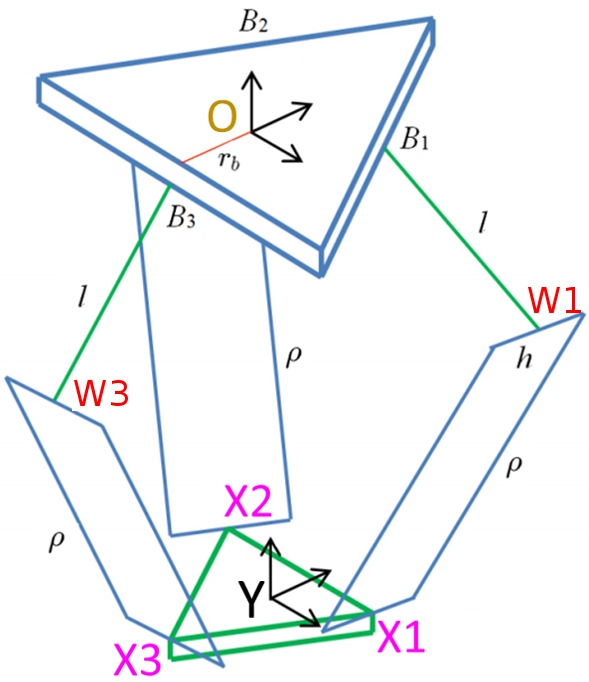

Image source: AEMK Systems

Inverse Kinematics
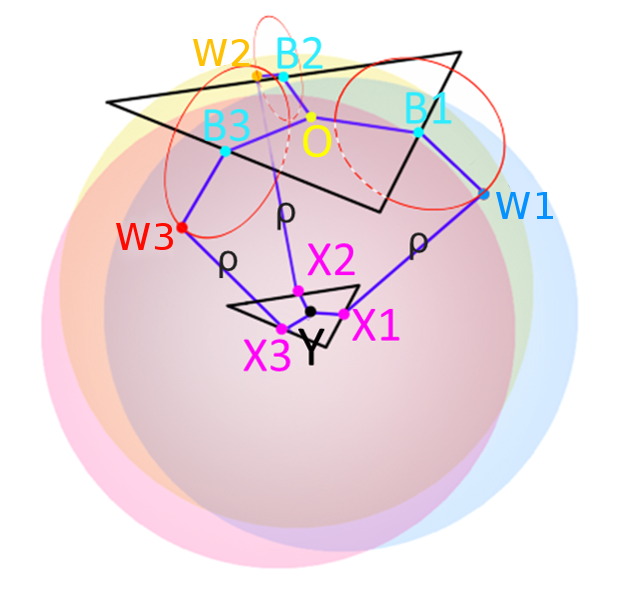
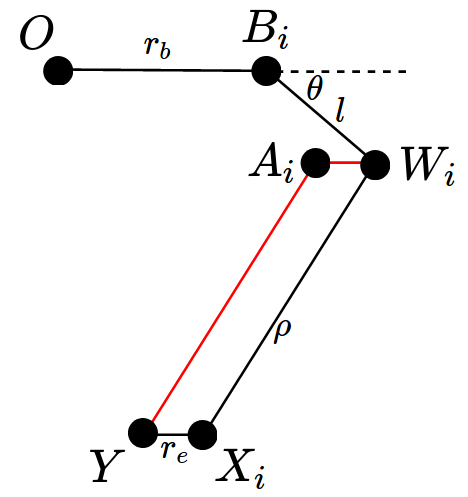

Inverse Kinematics

Forward Kinematics
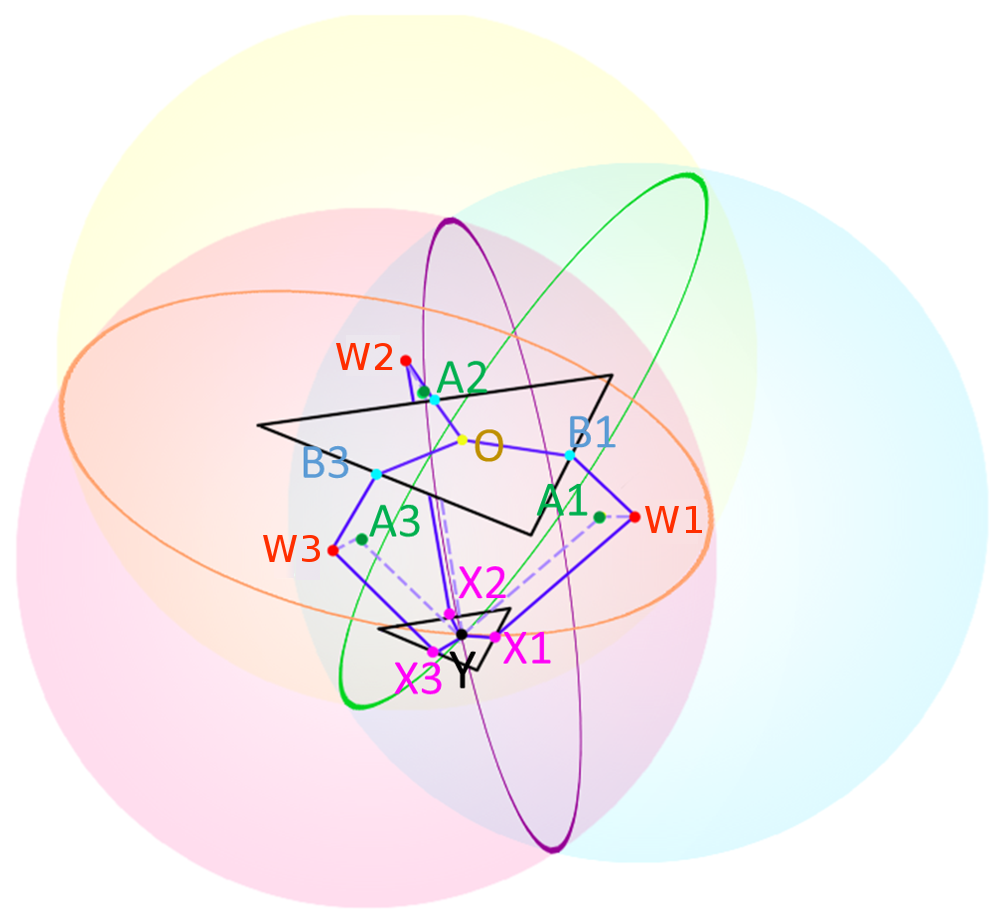


Forward Kinematics

Derivatives for the Jacobians
- In order to calculate the jacobians we will need some derivatives, let's put together a little collection:
- Derivative of a CGA point with respect to a parameter of the 3D point
- Derivative of the intersection of a circle and a sphere with respect to a parameter of the sphere centre
- Derivative of the intersection of three spheres to make a point pair
- Derivative of the extraction of the end points from a point pair
- Derivative of a 3D point with respect to parameters of its conformal equivalent

Derivative of a CGA point with respect to a parameter of the 3D point
- The 3D point \(x_i\) can then be represented as the CGA point \(X_i\):
X_i = \frac{1}{2}x_i^2n_\infty + x_i + n_0
\frac{\partial X_i}{\partial \alpha} = \left( \frac{\partial x_i}{ \partial \alpha}\cdot x_i \right)n_\infty + \frac{\partial x_i}{\partial \alpha}
- We can then take the derivative of the CGA point with respect to a parameter of the 3DGA point, \(\alpha\) :

Derivative of the intersection of a circle and a sphere with respect to a parameter of the sphere centre
- Consider the form of the dual CGA sphere:
\newcommand{\la}{\langle}
\newcommand{\ra}{\rangle}
\newcommand{\nn}{\nonumber}
\newcommand{\ninf}{n_{\infty}}
\newcommand{\einf}{e_{\infty}}
\newcommand{\no}{n_{0}}
\newcommand{\eo}{e_{0}}
\newcommand{\wdg}{\wedge}
\newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} }
\pdiff{T}{\alpha} = \left(\pdiff{\Sigma^*}{\alpha}\wedge C^*\right)^*
\newcommand{\la}{\langle}
\newcommand{\ra}{\rangle}
\newcommand{\nn}{\nonumber}
\newcommand{\ninf}{n_{\infty}}
\newcommand{\einf}{e_{\infty}}
\newcommand{\no}{n_{0}}
\newcommand{\eo}{e_{0}}
\newcommand{\wdg}{\wedge}
\newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} }
\Sigma^* = X - \frac{1}{2}\rho^2\ninf
\newcommand{\la}{\langle}
\newcommand{\ra}{\rangle}
\newcommand{\nn}{\nonumber}
\newcommand{\ninf}{n_{\infty}}
\newcommand{\einf}{e_{\infty}}
\newcommand{\no}{n_{0}}
\newcommand{\eo}{e_{0}}
\newcommand{\wdg}{\wedge}
\newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} }
\pdiff{\Sigma^*}{\alpha} = \pdiff{X}{\alpha}
- Take derivatives with respect to a parameter \(\alpha\) of the centre of the sphere:
- Finally consider the meet of the sphere and a fixed circle C, giving a point pair T:
\newcommand{\la}{\langle}
\newcommand{\ra}{\rangle}
\newcommand{\nn}{\nonumber}
\newcommand{\ninf}{n_{\infty}}
\newcommand{\einf}{e_{\infty}}
\newcommand{\no}{n_{0}}
\newcommand{\eo}{e_{0}}
\newcommand{\wdg}{\wedge}
\newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} }
T = \left(\Sigma^* \wedge C^* \right)^*

Derivative of the intersection of three spheres to make a point pair
- The point pair at the intersection of three spheres is given by:
T = (\Sigma_1\vee \Sigma_2 \vee \Sigma_3) \equiv (\Sigma_1^*\wedge \Sigma_2^*\wedge \Sigma_3^*)^*
\newcommand{\la}{\langle}
\newcommand{\ra}{\rangle}
\newcommand{\nn}{\nonumber}
\newcommand{\ninf}{n_{\infty}}
\newcommand{\einf}{e_{\infty}}
\newcommand{\no}{n_{0}}
\newcommand{\eo}{e_{0}}
\newcommand{\wdg}{\wedge}
\newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} }
\pdiff{T}{\theta_1} = \left(\pdiff{\Sigma_1^*}{\theta_1}\wedge \Sigma_2^*\wedge \Sigma_3^*\right)^*
, \hspace{0.1cm}
\pdiff{T}{\theta_2} = \left( \Sigma_1^*\wedge \pdiff{\Sigma_2^*}{\theta_2}\wedge \Sigma_3^*\right)^*
\\
\pdiff{T}{\theta_3} = \left(\Sigma_1^* \wedge \Sigma_2^*\wedge \pdiff{\Sigma_3^*}{\theta_3}\right)^*
- And so the derivatives of the point pair with respect to a parameter of each sphere individually is:
\newcommand{\la}{\langle}
\newcommand{\ra}{\rangle}
\newcommand{\nn}{\nonumber}
\newcommand{\ninf}{n_{\infty}}
\newcommand{\einf}{e_{\infty}}
\newcommand{\no}{n_{0}}
\newcommand{\eo}{e_{0}}
\newcommand{\wdg}{\wedge}
\newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} }
\pdiff{T}{\theta_i} = (-1)^{i-1}\left(\pdiff{\Sigma_i^*}{\theta_i}\wedge C^*\right)^*
, \hspace{0.1cm} \text{where} \,\,\, C^* = \bigwedge_{j \in {1,2,3} \,\,\, j\ne i}\Sigma_j^*
- This can also be written as:

Derivative of the extraction of the end points from a point pair
- To extract the end points of a point pair T we will follow the method given in [CovApproach]. First construct a projector:
\newcommand{\la}{\langle}
\newcommand{\ra}{\rangle}
\newcommand{\nn}{\nonumber}
\newcommand{\ninf}{n_{\infty}}
\newcommand{\einf}{e_{\infty}}
\newcommand{\no}{n_{0}}
\newcommand{\eo}{e_{0}}
\newcommand{\wdg}{\wedge}
\newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} }
P = \frac{1}{2}\left(1 + \frac{T}{\sqrt{T^2}}\right)
, \hspace{0.2cm}
\pdiff{P}{\alpha} = \frac{1}{2T^2}\left(\sqrt{T^2}\pdiff{T}{\alpha} - T\frac{\pdiff{T}{\alpha}\cdot T}{\sqrt{T^2}}\right)
\newcommand{\la}{\langle}
\newcommand{\ra}{\rangle}
\newcommand{\nn}{\nonumber}
\newcommand{\ninf}{n_{\infty}}
\newcommand{\einf}{e_{\infty}}
\newcommand{\no}{n_{0}}
\newcommand{\eo}{e_{0}}
\newcommand{\wdg}{\wedge}
\newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} }
Y = -\tilde{P}(T\cdot n_\infty)P
\newcommand{\la}{\langle}
\newcommand{\ra}{\rangle}
\newcommand{\nn}{\nonumber}
\newcommand{\ninf}{n_{\infty}}
\newcommand{\einf}{e_{\infty}}
\newcommand{\no}{n_{0}}
\newcommand{\eo}{e_{0}}
\newcommand{\wdg}{\wedge}
\newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} }
\pdiff{Y}{\alpha} = -\pdiff{\tilde{P}}{\alpha}(T\cdot n_\infty)P -\tilde{P}\left(\pdiff{T}{\alpha}\cdot n_\infty\right)P -\tilde{P}(T\cdot n_\infty)\pdiff{P}{\alpha}
- Then use it to project out a point:

Derivative of a 3D point with respect to parameters of its conformal equivalent
- To map back from a conformal point to a standard point we need to normalise by \(Y\cdot n_\infty\)
\newcommand{\la}{\langle}
\newcommand{\ra}{\rangle}
\newcommand{\nn}{\nonumber}
\newcommand{\ninf}{n_{\infty}}
\newcommand{\einf}{e_{\infty}}
\newcommand{\no}{n_{0}}
\newcommand{\eo}{e_{0}}
\newcommand{\wdg}{\wedge}
\newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} }
y = \frac{-\sum_{j=1}^{j=3}(Y\cdot e_j)e_j}{Y\cdot n_\infty}
\newcommand{\la}{\langle}
\newcommand{\ra}{\rangle}
\newcommand{\nn}{\nonumber}
\newcommand{\ninf}{n_{\infty}}
\newcommand{\einf}{e_{\infty}}
\newcommand{\no}{n_{0}}
\newcommand{\eo}{e_{0}}
\newcommand{\wdg}{\wedge}
\newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} }
\pdiff{y}{\theta_i} = \frac{ -\sum_{j=1}^{j=3}\left(\pdiff{Y}{\theta_i}\cdot e_{j}\right)e_j (Y\cdot\ninf) + \sum_{j=1}^{j=3}\left(Y\cdot e_{j}\right)e_j (\pdiff{Y}{\theta_i}\cdot\ninf) }{ (Y\cdot\ninf)^2 }
- And so we can calculate our final derivative:

Forward Kinematic Jacobian

Inverse Kinematic Jacobian Horizontal

Inverse Kinematic Jacobian Vertical

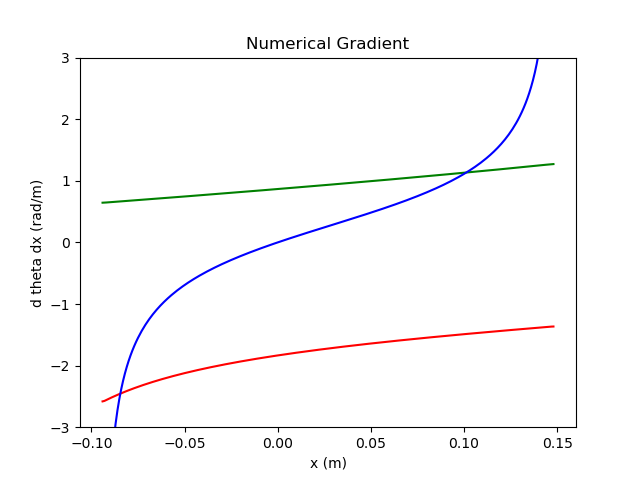
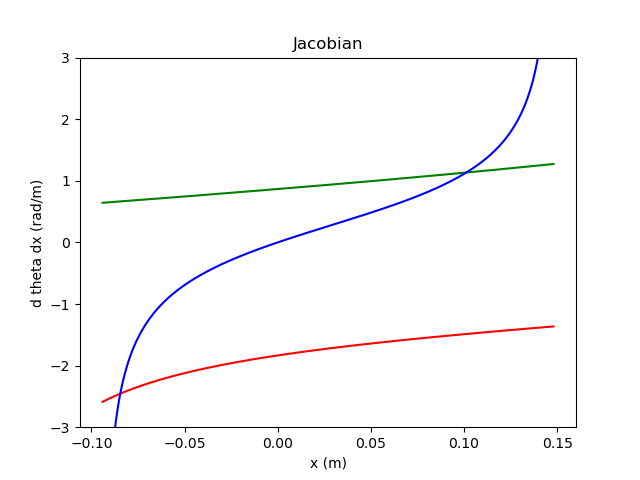
Verification and Visualisation of the Robot in Clifford Python
- We have implemented all of these derivatives in Clifford Python and tested them vs central differences with visualisation via pyganja

Designing Practical Controllers for the Delta Robot
- To design practical controllers for real robots we need to do some kind of dynamic modelling
- We also need a mechanism for modelling environmental disturbances
- We would like someone else to write the physics code - not the point of this paper
- We would like easy visualisation of everything in real time
Game engines tick all the boxes

Setting up Unity3D as a Simulation Environment

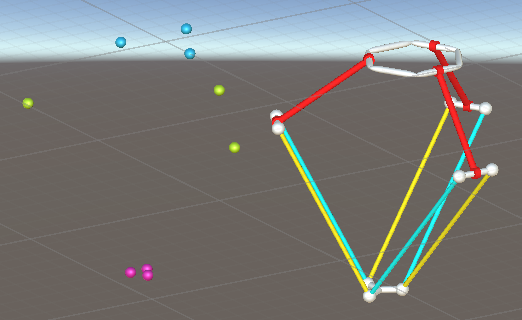
- Unity3D is programmed in C#
- Generated a C# library with ganja.js
- Fleshed out library to integrate with Unity3D
- Built a physical model of the robot
- Attached the CGA controller to it

Testing CGA based Controllers on Simulated Robots in Unity3D

Testing CGA based Controllers on Simulated Robots in Unity3D

Future Work
- Constructing a dynamic model of the delta robot within our GA framework will let us use more interesting controller designs and test physical design parameters
- We plan to connect our simulated robot and controller to a real Delta robot via ROS
- We plan to improve the Unity3D C# (C)GA library to allow fast iteration of robot/games/graphics related applied research

Conclusions
- (C)GA can provide a very useful framework for describing the kinematics of parallel robots
- Putting together a "data book" of derivatives of common operations in (C)GA would be very useful to practitioners trying to use GA in practice/in industry (boring but comprehensive is good?)
- There already exists a wide range of modern GA software packages of high quality but integration with game engines is very useful and hence desirable
