Quaternion Operations

Hugo Hadfield

hh409.user.srcf.net

Quaternion Multiplication

q_1 = w_1 + x_1\textbf{i} + y_1\textbf{j} + z_1\textbf{k}

q_2 = w_2 + x_2\textbf{i} + y_2\textbf{j} + z_2\textbf{k}

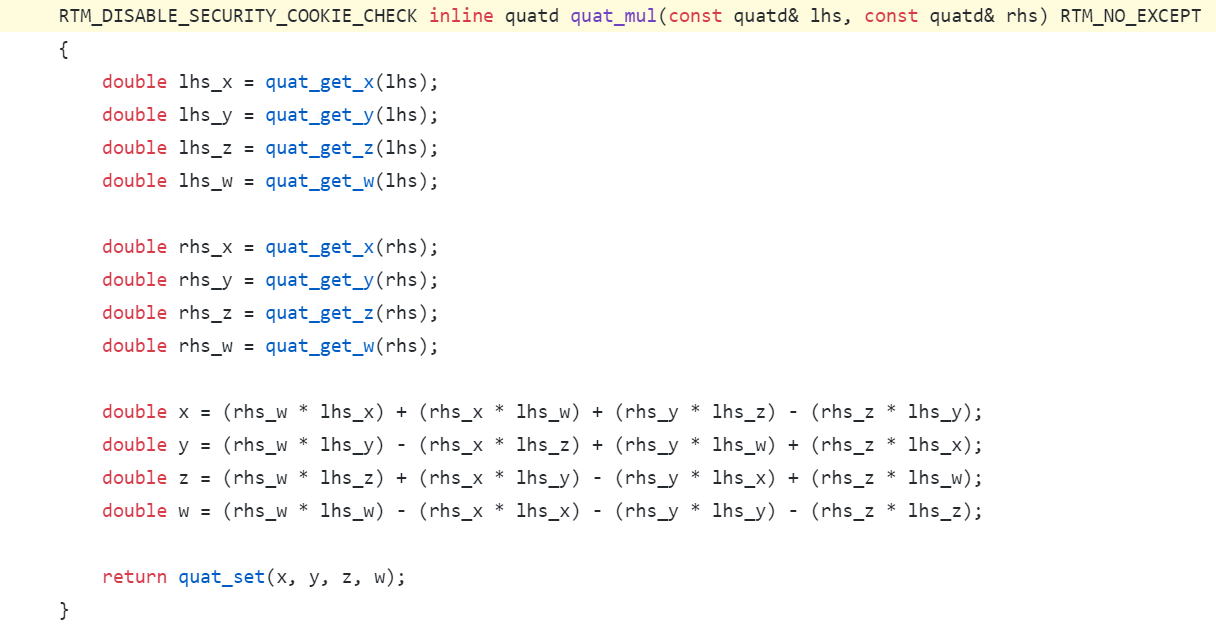
\textbf{ij = -ji = k, \,\, kj = -jk = i, \,\, ki = -ik = j}\\ \textbf{i}^2 = \textbf{j}^2 = \textbf{k}^2 = \textbf{ijk} = -1 \\\\ \\ q_1q_2 = (w_1 + x_1\textbf{i} + y_1\textbf{j} + z_1\textbf{k})(w_2 + x_2\textbf{i} + y_2\textbf{j} + z_2\textbf{k})\\ % = w_1w_2 + x_1w_2i + y_1w_2j + z_1w_2k + \\ % w_1x_2i + x_1x_2ii + y_1x_2ji + z_1x_2ki + \\ % w_1y_2j + x_1y_2ij + y_1y_2jj + z_1y_2kj + \\ % w_1z_2k + x_1z_2ik + y_1z_2jk + z_1z_2kk \\ % \\ = (w_1w_2 - x_1x_2 - y_1y_2 - z_1z_2) + \\ (x_1w_2 + w_1x_2 - z_1y_2 + y_1z_2)\textbf{i} \\ (y_1w_2 + w_1y_2 - x_1z_2 + z_1x_2)\textbf{j} \\ (z_1w_2 + w_1z_2 - y_1x_2 + x_1y_2)\textbf{k}\\

void mul(Quat4d & q1, Quat4d & q2, Quat4d & q3) {
    q3.w = q1.w * q2.w - q1.x * q2.x - q1.y * q2.y - q1.z * q2.z;
    q3.x = q1.x * q2.w + q1.w * q2.x - q1.z * q2.y + q1.y * q2.z;
    q3.y = q1.y * q2.w + q1.w * q2.y - q1.x * q2.z + q1.z * q2.x;
    q3.z = q1.z * q2.w + q1.w * q2.z - q1.y * q2.x + q1.x * q2.y;
}

GLM Real Code

GLM library implementation

RTM Real Code

RTM library implementation

Rotation by Quaternions

q_1 = w_1 + x_1\textbf{i} + y_1\textbf{j} + z_1\textbf{k}

\tilde{q_1} = w_1 - x_1\textbf{i} - y_1\textbf{j} - z_1\textbf{k}

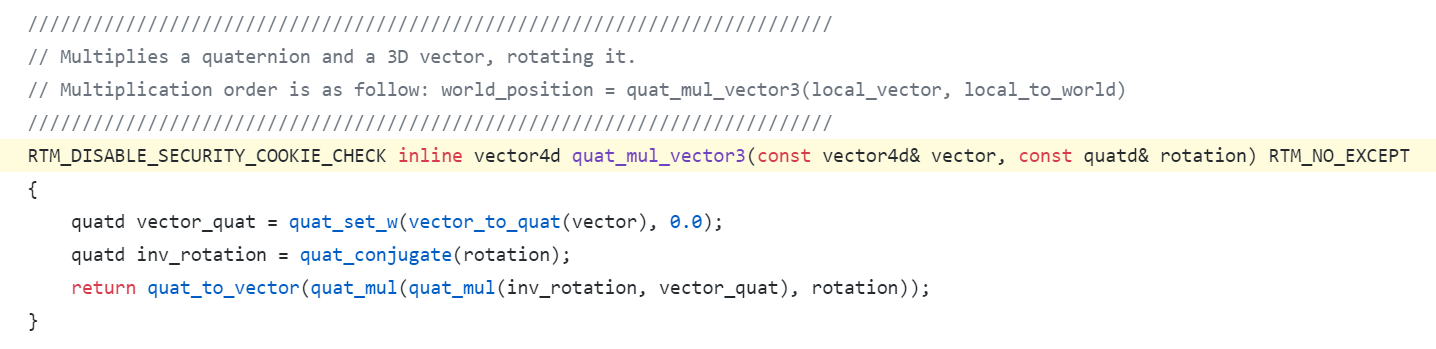
v' = q_1v\tilde{q_1} = q_1(x_v\textbf{i} + y_v\textbf{j} + z_v\textbf{k})\tilde{q_1}\\

void mul(Point3D & v, Quat4d & q2, Quat4d & qout) {
    qout.w = -v.x * q2.x - v.y * q2.y - v.z * q2.z;
    qout.x = v.x * q2.w - v.z * q2.y + v.y * q2.z;
    qout.y = v.y * q2.w - v.x * q2.z + v.z * q2.x;
    qout.z = v.z * q2.w - v.y * q2.x + v.x * q2.y;
}

void rotate(Quat4d & q1, Point3D & v, Point3D & vout) {
    w2 = -v.x * q2.x - v.y * q2.y - v.z * q2.z;
    x2 = -v.x * q2.w + v.z * q2.y - v.y * q2.z;
    y2 = -v.y * q2.w + v.x * q2.z - v.z * q2.x;
    z2 = -v.z * q2.w + v.y * q2.x - v.x * q2.y;
    vout.x = q1.x * w2 + q1.w * x2 - q1.z * y2 + q1.y * z2;
    vout.y = q1.y * w2 + q1.w * y2 - q1.x * z2 + q1.z * x2;
    vout.z = q1.z * w2 + q1.w * z2 - q1.y * x2 + q1.x * y2;
}

GLM Real Code

GLM library implementation

Uses an equivalent formulation but with cross products

RTM Real Code

RTM library implementation

SLERP

q_1 = w_1 + x_1\textbf{i} + y_1\textbf{j} + z_1\textbf{k}

q_2 = w_2 + x_2\textbf{i} + y_2\textbf{j} + z_2\textbf{k}

q_\alpha = \frac{\sin\left((1 - \alpha)\Omega\right)}{\sin{\Omega}}q_1 + \frac{\sin(\alpha\Omega)}{\sin(\Omega)}q_2