Applications of Geometric Algebra in Mathematical Engineering
Hugo Hadfield
Calculating the rotor between conformal objects
- This chapter introduces the concept of mirror objects, projectors and finding the rotor that takes one object to another
- Here is the first time we give an expression for the mirror object in terms of the addition of two object blades
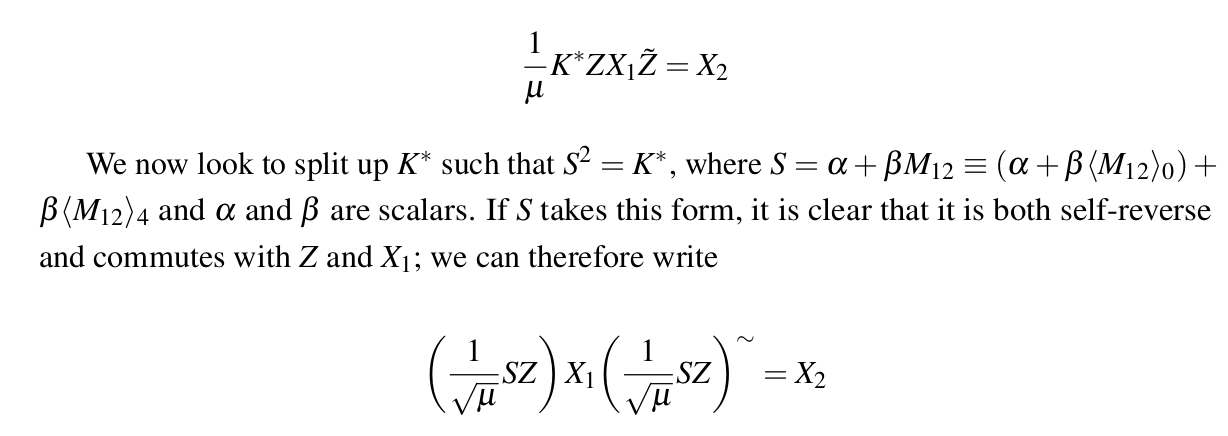
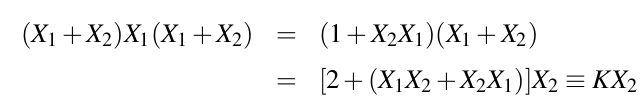
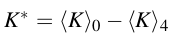
Direct linear interpolation of geometric objects in conformal geometric algebra
- Here we explore in detail the properties of the blade reprojection and linear interpolant objects
- This is the first time we touch on screw theory, although in a very limited way, in the context of the interpolation of lines
- Finally we look at some basic examples of applications
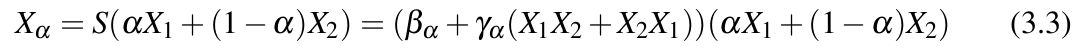
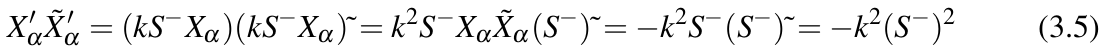
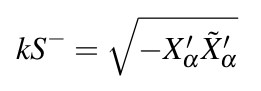
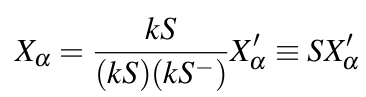
Exploring Novel Surface Representations via an Experimental Ray-Tracer in CGA
- In this chapter we describe higher order interpolations between objects and how surfaces made of these objects would interact with rays of light
- We then build a basic ray-tracer that can image a range of different objects and show how we can do texture mapping for these objects
- https://hugohadfield.github.io/tube_vis/
REFORM: Rotor Estimation From Object Resampling and Matching
- In this chapter we make use of the rotor between objects that we described in Chapter 2 to construct cost functions between objects that we can use as an optimisation target for finding unknown transformations between noisy objects in an ICP+Ransac like scheme
- We then also leverage the rotor between objects to design fast heuristic algorithms to solve the same problem
Screw Theory in Geometric Algebra for
Constrained Rigid Body Dynamics
- This chapter is about statics, dynamics, and screw theory
- First we describe forces and moments as lines and compare and contrast this force and moment representation with other examples from the literature
- Then we work through how the operators of algebraic Screw Theory embed into GA
- We then do dynamics, showing how the inertia tensor maps into CGA and PGA and how to represent non-axis-aligned inertia tensors
- We show how to impose constraints on our dynamics via traditional virtual power techniques and then via novel multivector pinning
- Finally we show how integration could be done in the bivector domain with a range of lie algebra mappings
The Kinematics of Multi-body Systems in
Geometric Algebra
- This chapter is about multi-body systems: joints, articulated robots etc.
- We describe how to use the richness of CGA to model the various kinematic joints commonly used in robotic mechanisms. Through a mechanism of shared geometry and invariant bilinear operations.
- We show how to form a collection of joint constraints into a matrix and use this matrix to solve articulated body problems in robotics
- We compare and contrast this screw theory based constraint matrix approach vs a direct calculation for the forward and inverse kinematics of the delta robot
Conclusions
- We added blades together and it was, in general, a really good idea!
- We showed how to use interpolated objects in a range of applications in graphics, vision and robotics
- We described how Screw Theory embeds into CGA and PGA
- We showed how to do statics, kinematics and constrained dynamics in CGA and PGA
- We derived the kinematic equations for several mappings from se3 to SE3
- We showed how to model the kinematics of jointed robots in CGA and PGA using a screw theory inspired method