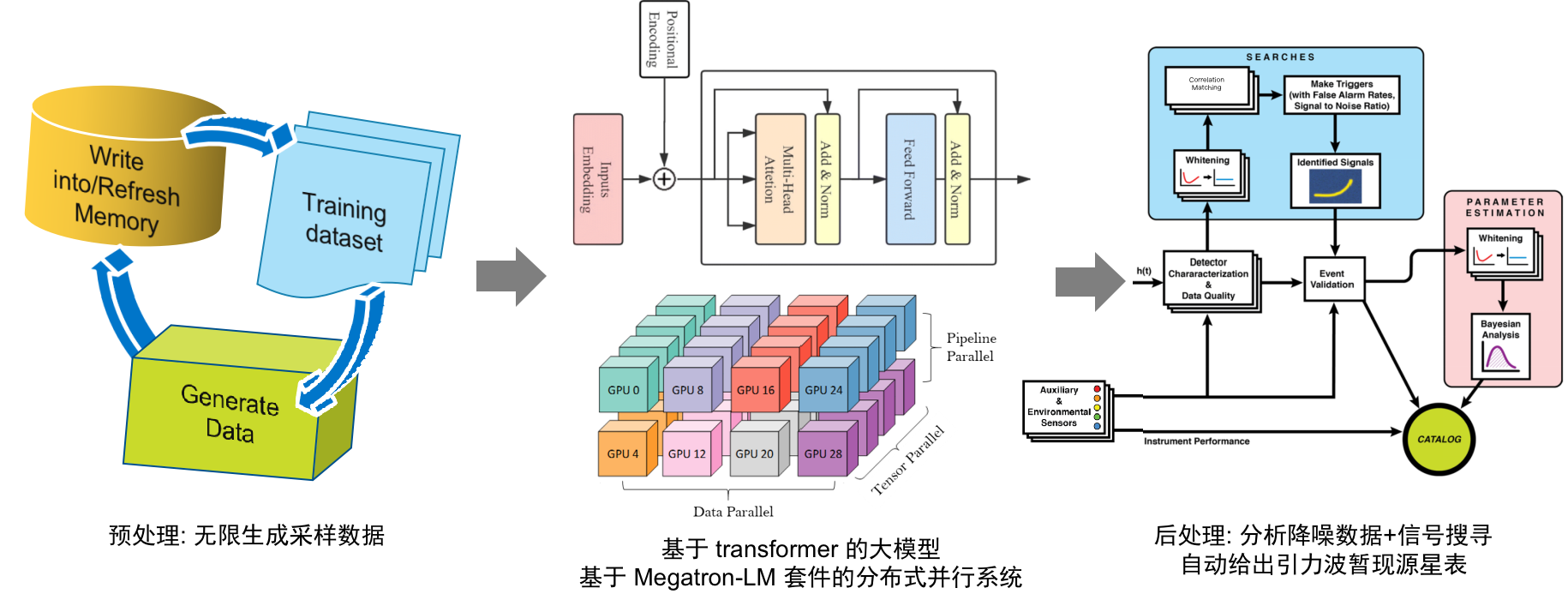
4 July, 10:15-10:30, GWAC 2024, Jingzhou, Hubei, China
WaveFormer: Transformer-based Denoising Method for Gravitational-wave Data
He Wang (王赫)
hewang@ucas.ac.cn
University of Chinese Academy of Sciences (UCAS)
On behalf of the LIGO-VIRGO-KAGRA collaborations



based on He Wang et al 2024 Mach. Learn.: Sci. Technol. 5 015046 (arxiv: 2212.14283)
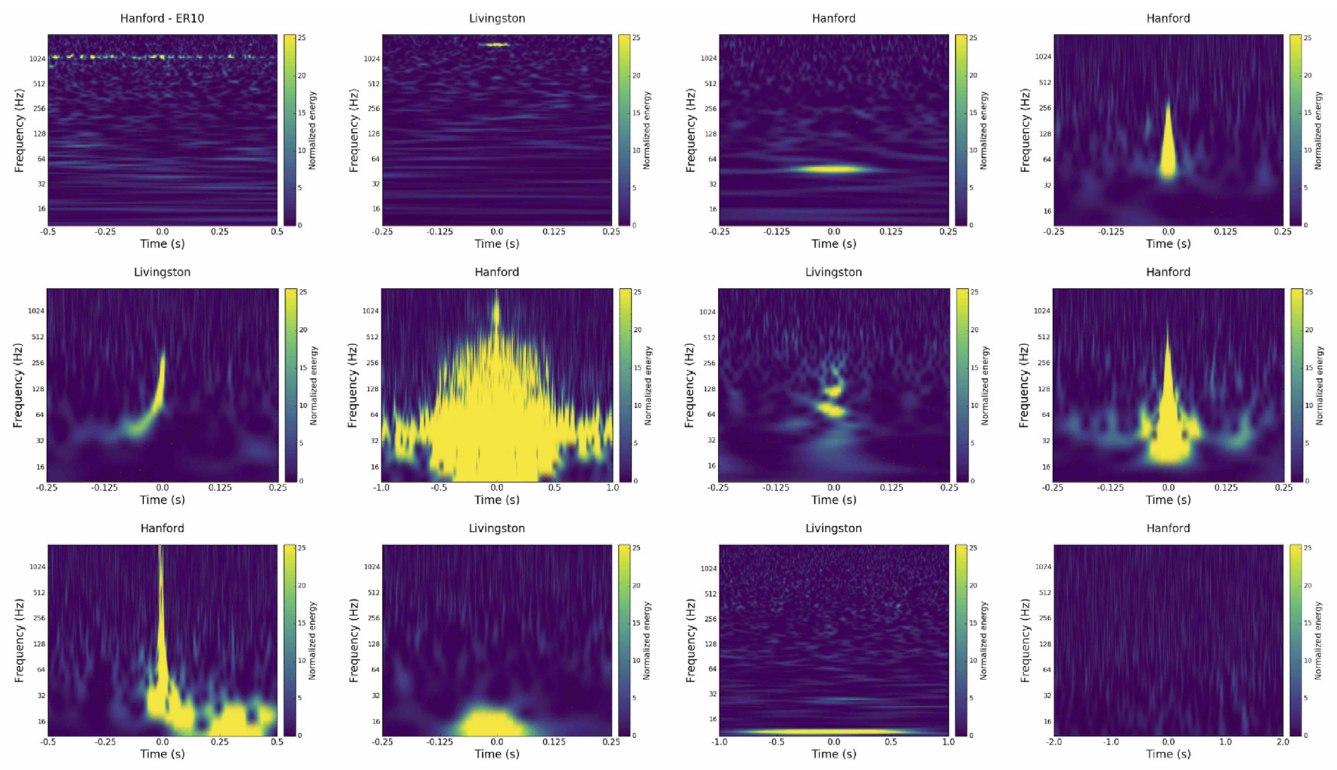
1400Ripples Air Compressor Blip
Extremely Loud Helix Koi Fish
Various types of Glitch
Background

-
The improvement of data quality is a very complex issue, with data from over 20,000 sensor channels determining the quality of the gravitational wave science data channel.
-
Reducing non-Gaussian short-duration pulse interference (Glitches) in gravitational wave data will help reduce the false alarm rate of gravitational wave signals.
-
Removing Glitches from gravitational wave detection data is a multi-classification problem.
- Traditional machine learning algorithms Powell J, et al. CQG, 2015
- Deep learning algorithms Zevin, M, et al. C
Ormiston R, et al. PRR, 2020
-
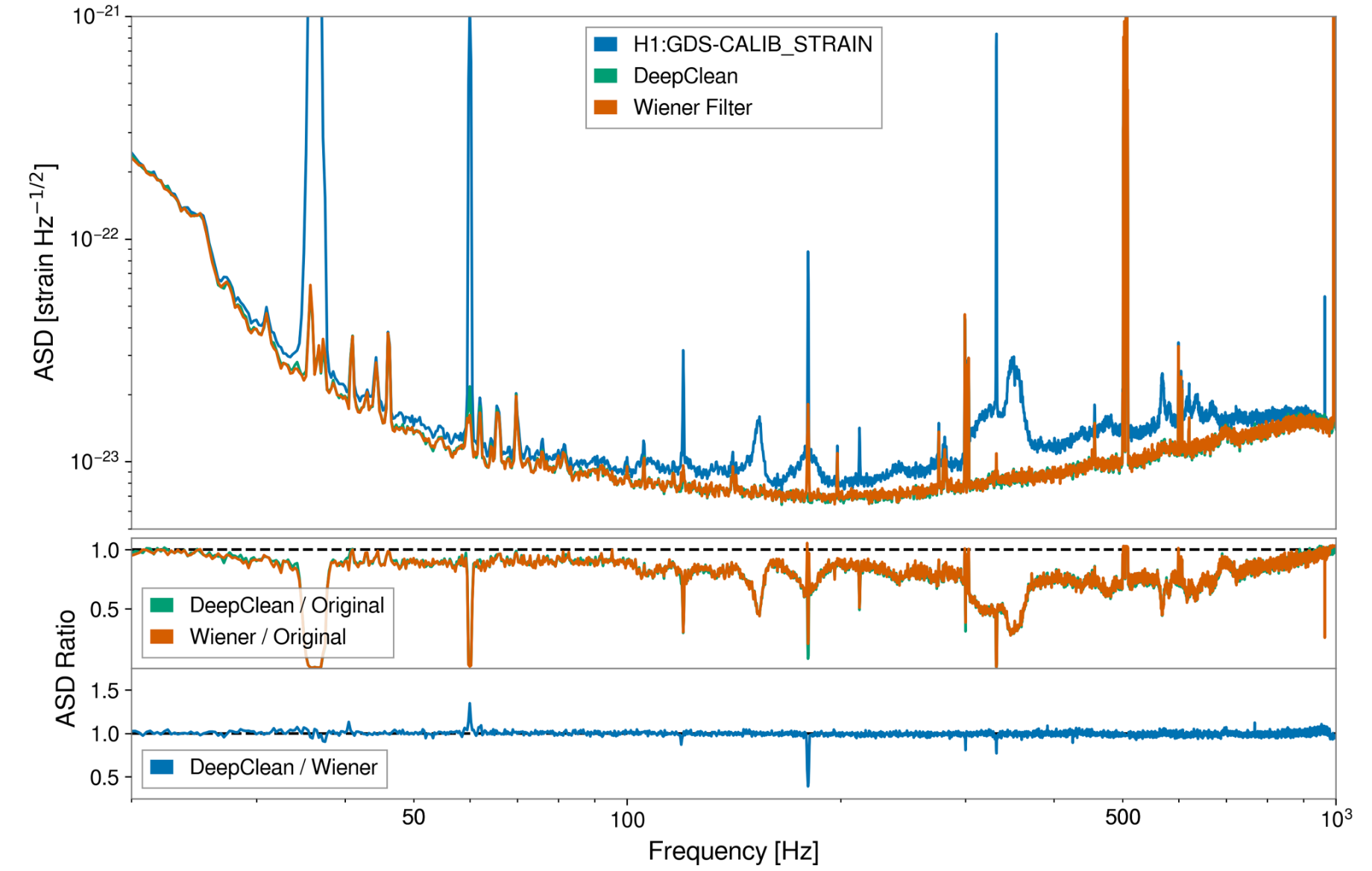
DeepClean: One-dimensional Convolutional Neural Network which takes a specified set of witness channels and subsequently outputs the predicted noise in strain.
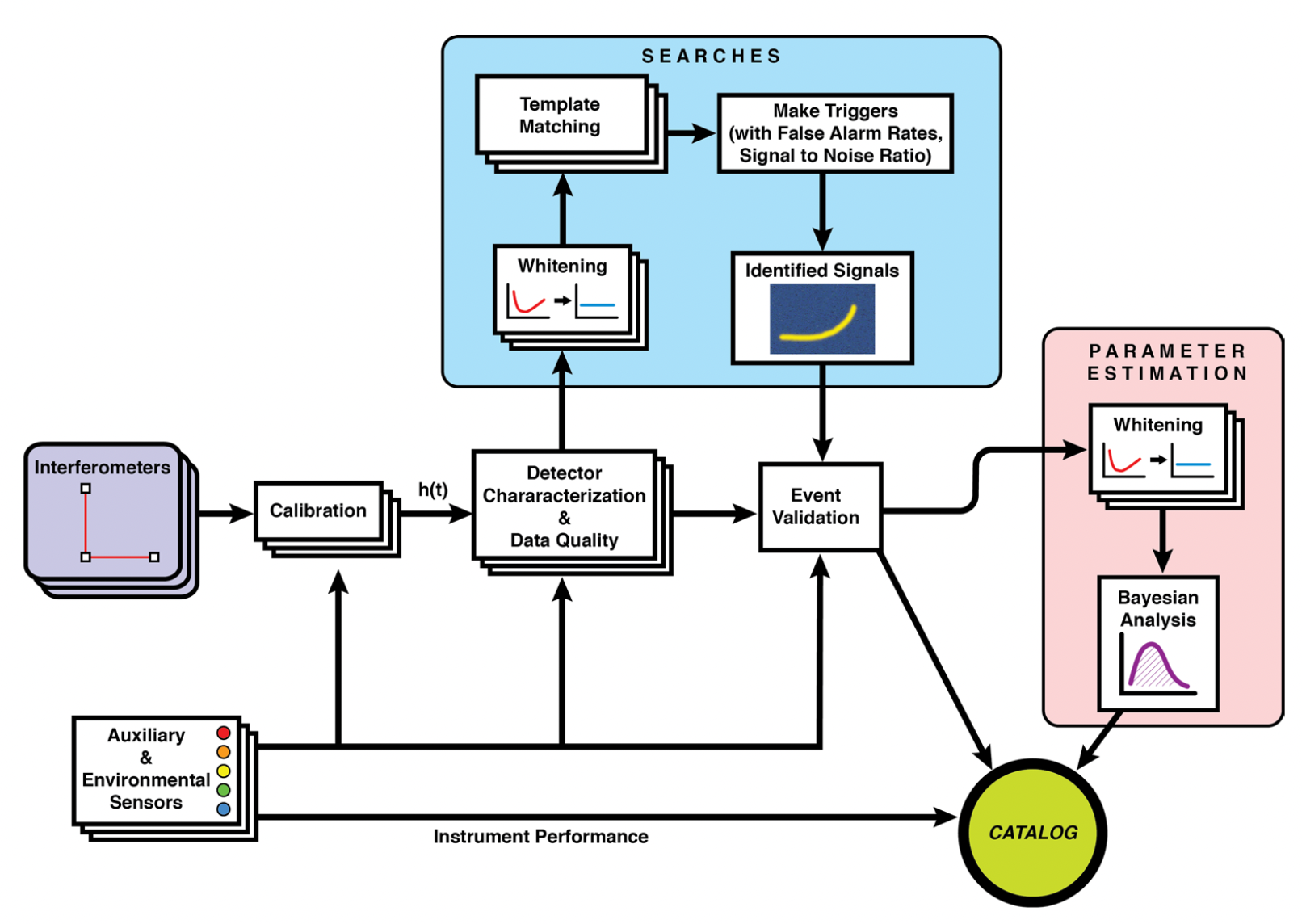
IGWN data processing
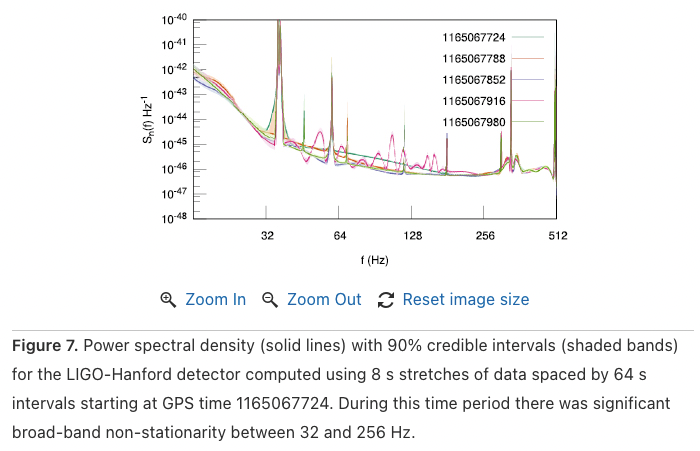
Non-stationary
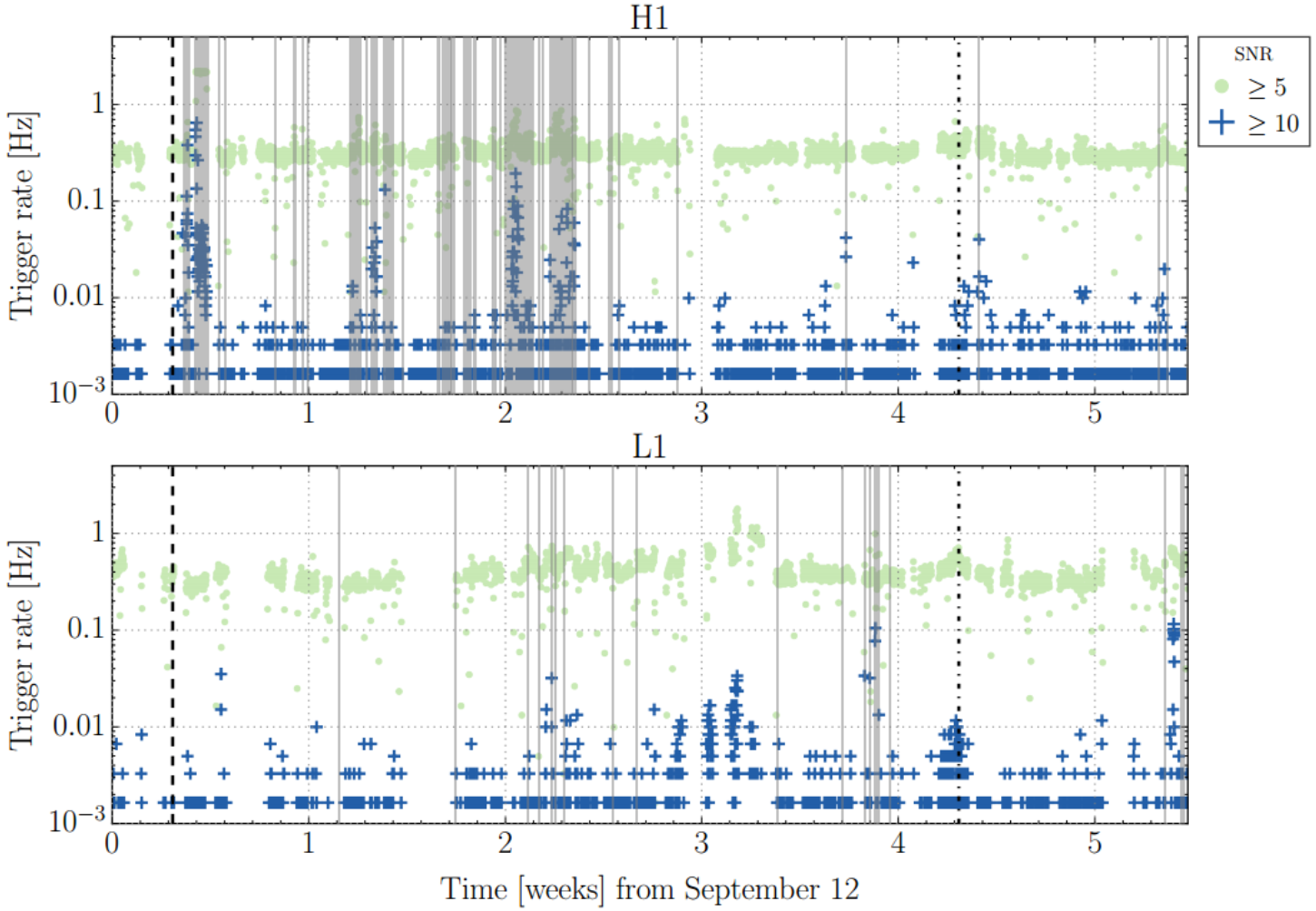
Non-Gaussianity
Background
Related Works
Model Structure
Precessing & Train
Effect on Noise
Effect on BBH signals
Credit: Marco Cavaglià
Related Works

-
Extraction and denoising GW signals using deep learning:
- Both Wei et al. [PLB 2020] and Chatterjee et al. [PRD 2021] have shown that considering phase overlaps yields excellent results.
-
Detecting and denoising GW signals using deep learning:
- Both Bacon et al. [2205.13513] and Murali et al. [PRD 2023] could recover the phase of original GW signal with certain cycles but failed to recover the complete evaluation in amplitude scale.
Chatterjee C, Wen L, et al. PRD 2021
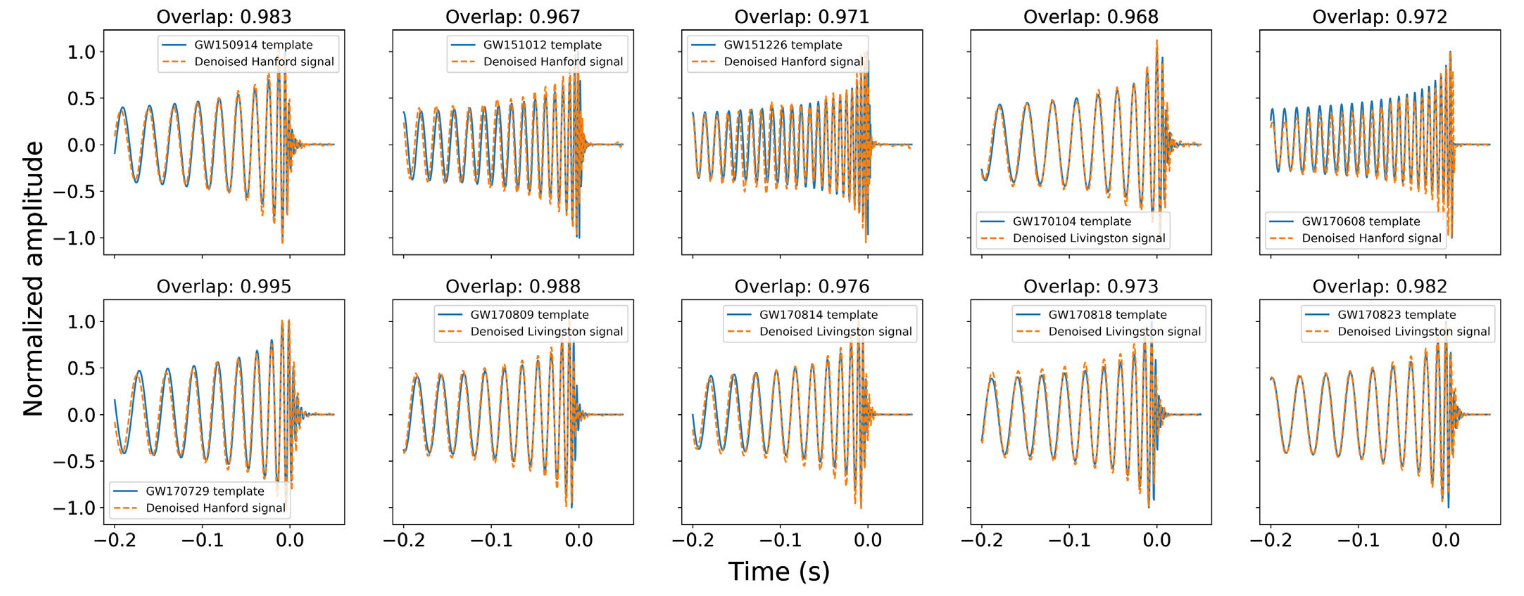
Wei W and Huerta E A. PLB 2020
Bacon P. et al. arXiv: 2205.13513
GW170823

Murali C & Lumley D. PRD 2023
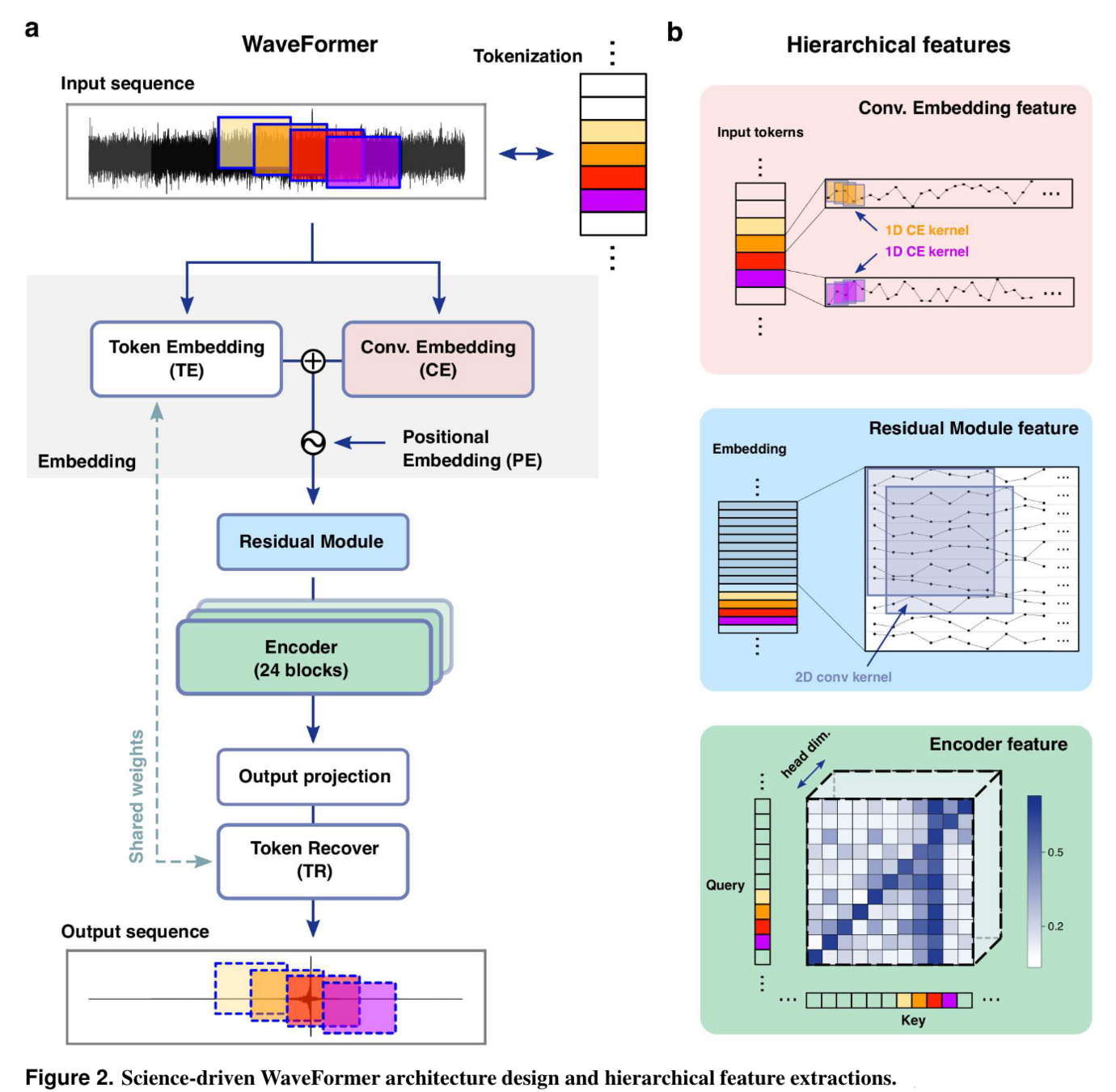
Network Architecture

- The WaveFormer, a billion-scale transformer-based model, excels in suppressing realistic noise and recovering injections or GW events, thereby significantly improving data quality.
- In its application, it treats each overlapping time-domain data subsequence as an individual token, akin to tokenization in natural language processing (NLP).




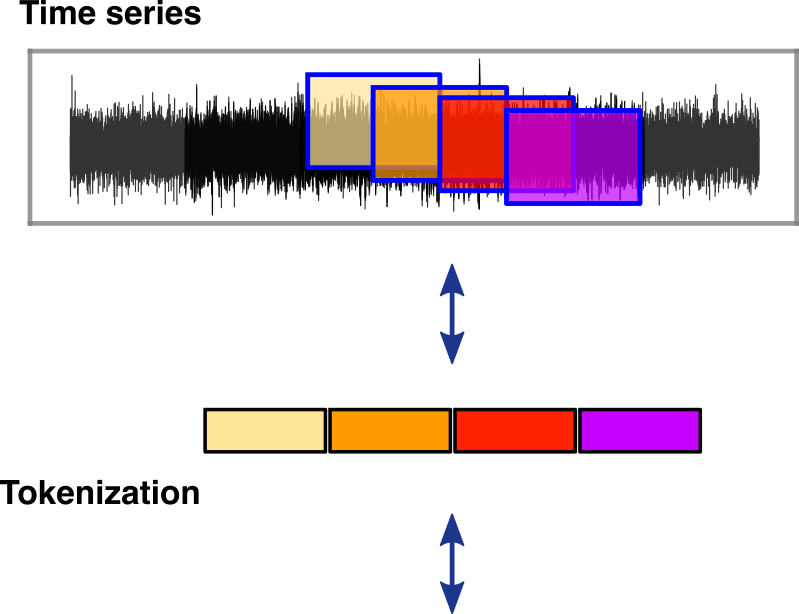
["This", "is", "a", "sample"]
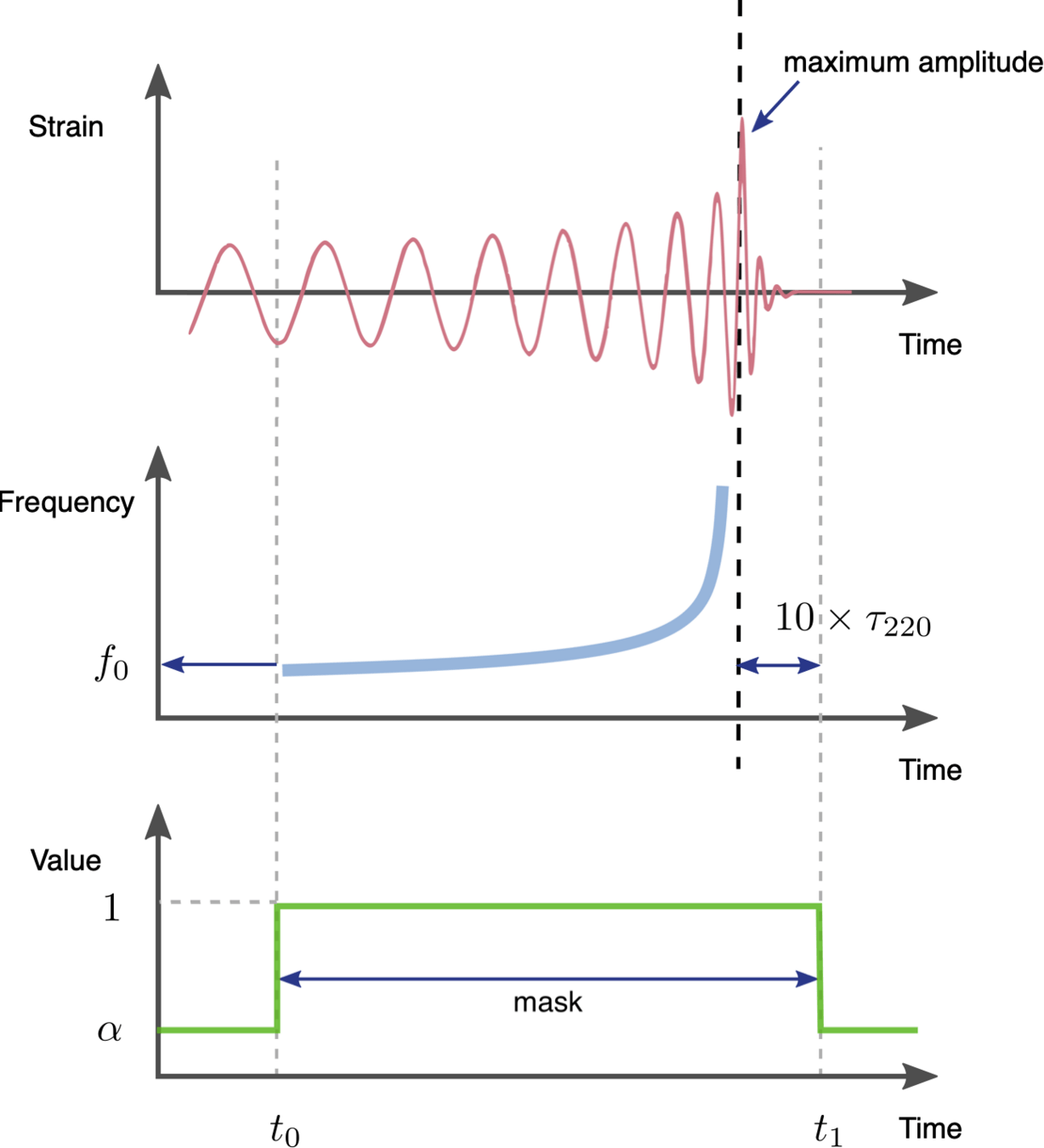
Data Preprocessing and Training Strategy

Strain
Whiten
Normalized
∼\(10^{−19}\)
∼\(10^{2}\)
∼\(10^{0}\)
32 s
32 s
merger
\(t_c\) (around GW150914)
(Cal network SNR)
Band-pass: [20, 2048] Hz
Patching (tokenized) with size 0.125 s and overlap 50%
[1, 128, 256]
(Standard normalization)
dynamic masking
[1, 16512]
[1, 128, 256]
(PSD\(_i\) from noise)
Band-pass: [20, 2048] Hz
WaveFormer
MSE-Loss\(_i\)
\(std\)
[1, 128, 256]
Noise\(_i\):
Signal\(_i\):
Input\(_i\):
Label\(_i\):
Output\(_i\):
8.0625 s
8.0625 s
Given �=ℎ+�d=h+n, we can normalize �d as follows:
-
Implementations:
- PSD sampling from real noise.
- input size: 8.0625 sec
- fs = 2048Hz
- Band-pass: 20~2048Hz
- Masked loss




1. d = h + n, 推导到 train/sampling 的递推式中
2. 数据 complex 化,表示为 A exp(i*phase) 或其他
3. loss x 2: 回归 amp (i.e. 包络线)
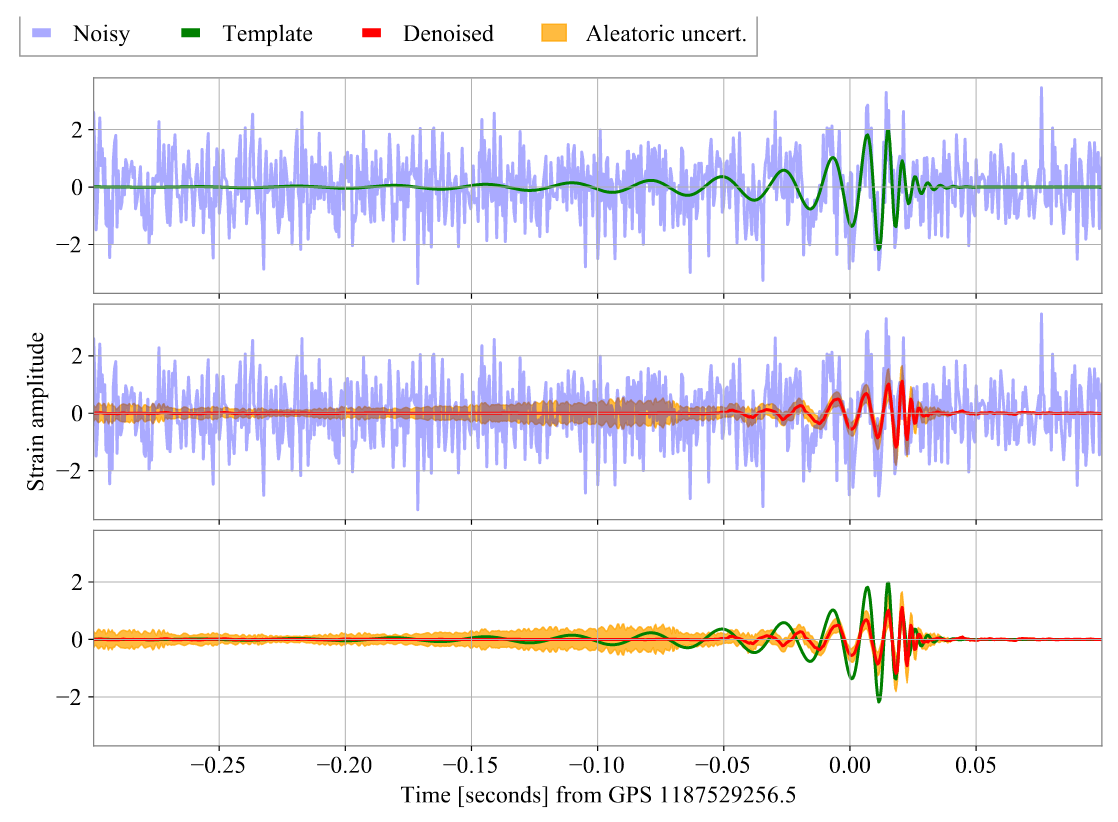
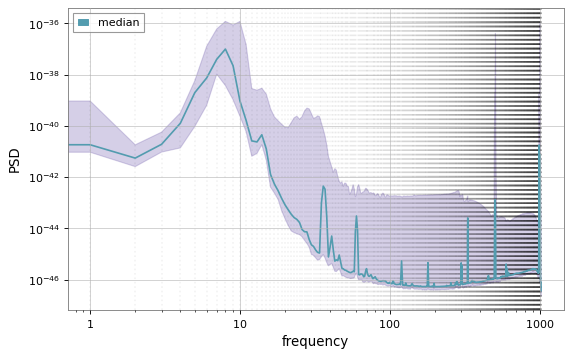
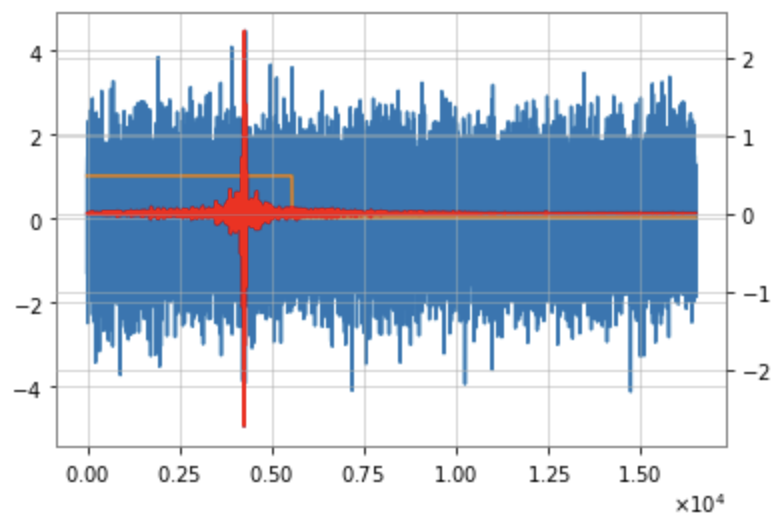
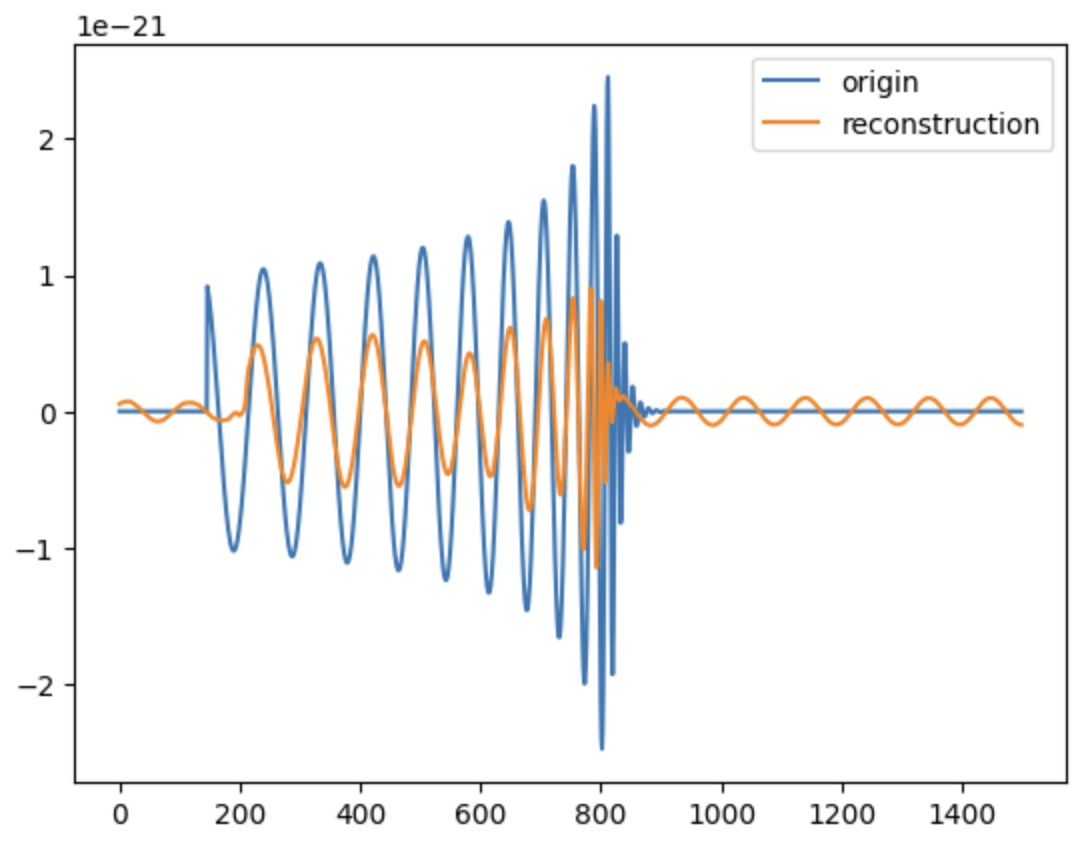
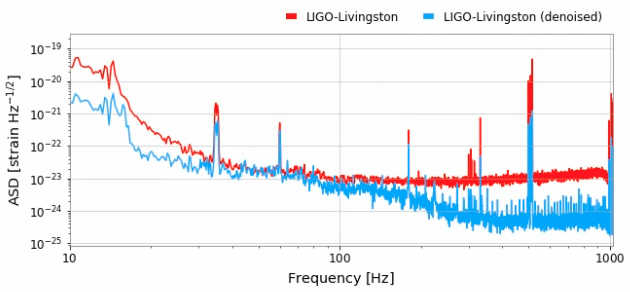
Effect on Realistic Noise

- Noise level percentile amplitude is significantly reduced, by approximately two orders.
- Further ASD analysis shows that WaveFormer effectively eliminates both narrowband and broadband spectral information, substantially lowering frequency contributions.
- Using the Gravity Spy database for glitches with SNR > 10 and confidence > 0.95, results show significant suppression of glitches in real advanced LIGO-Virgo noise.
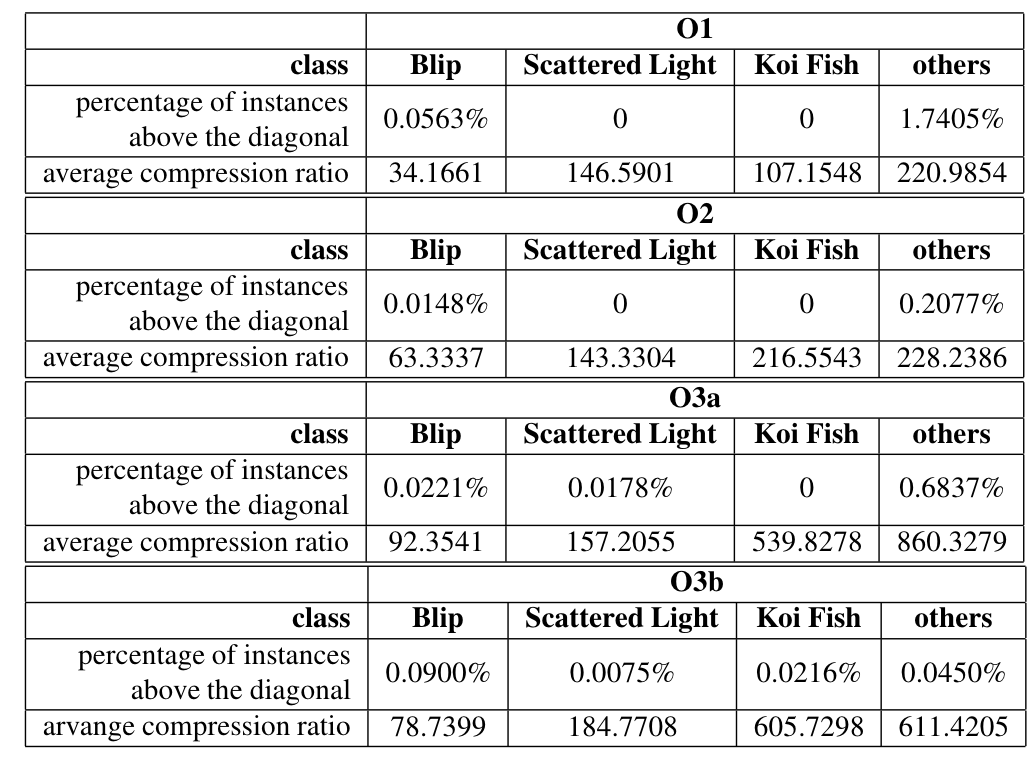
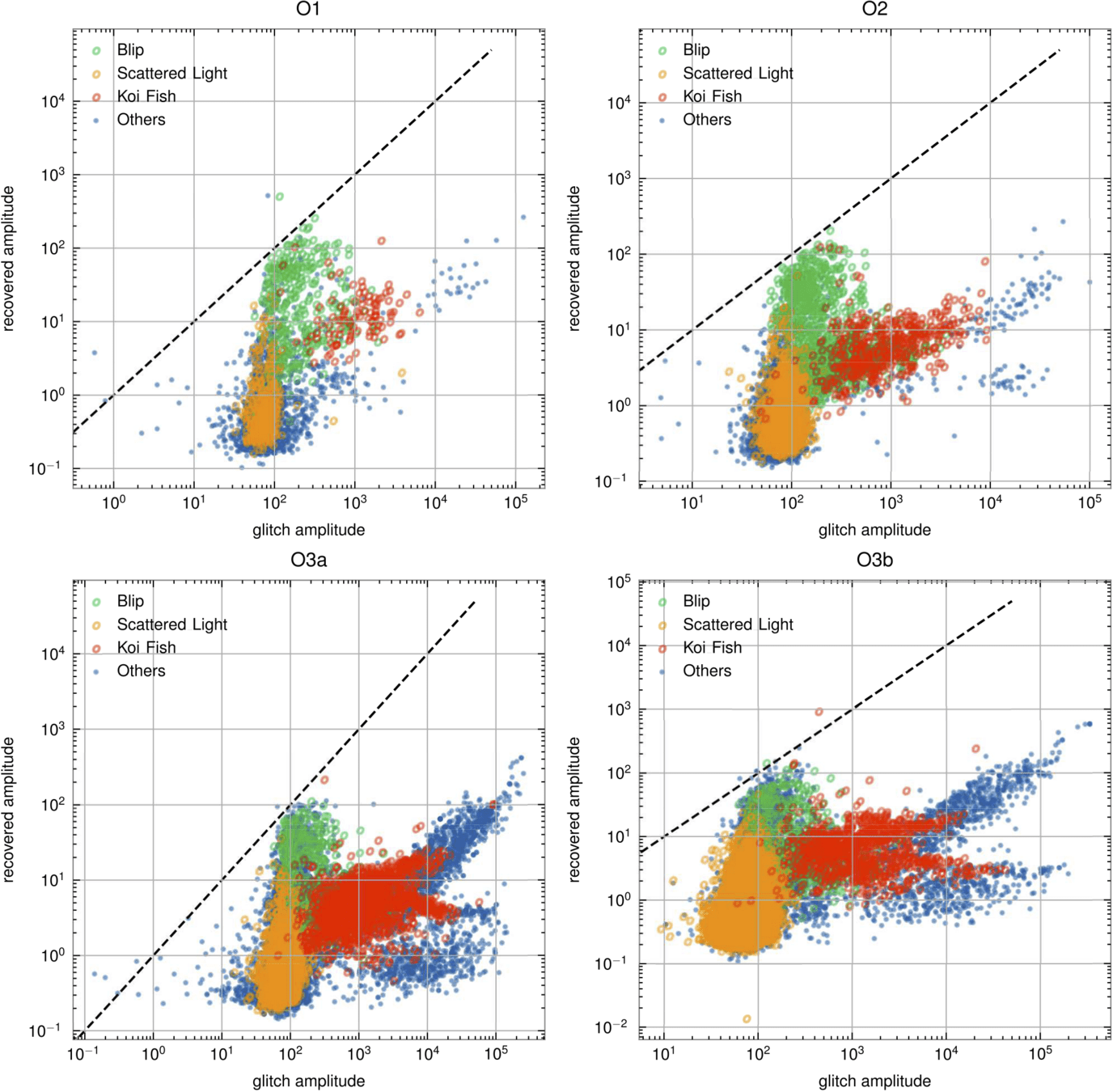
(Bottom panels: results of glitches)
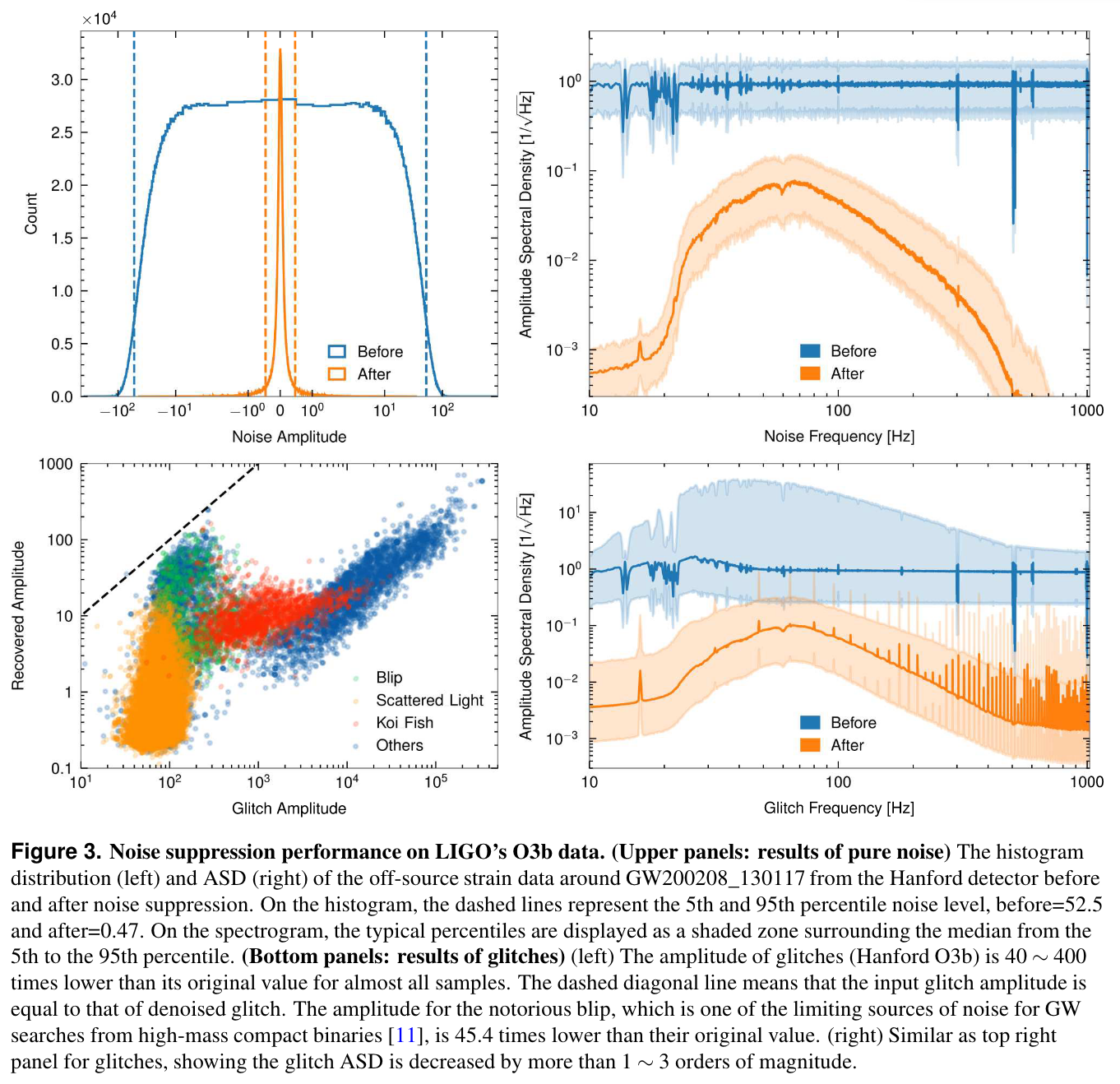

(Upper panels: results of pure noise)
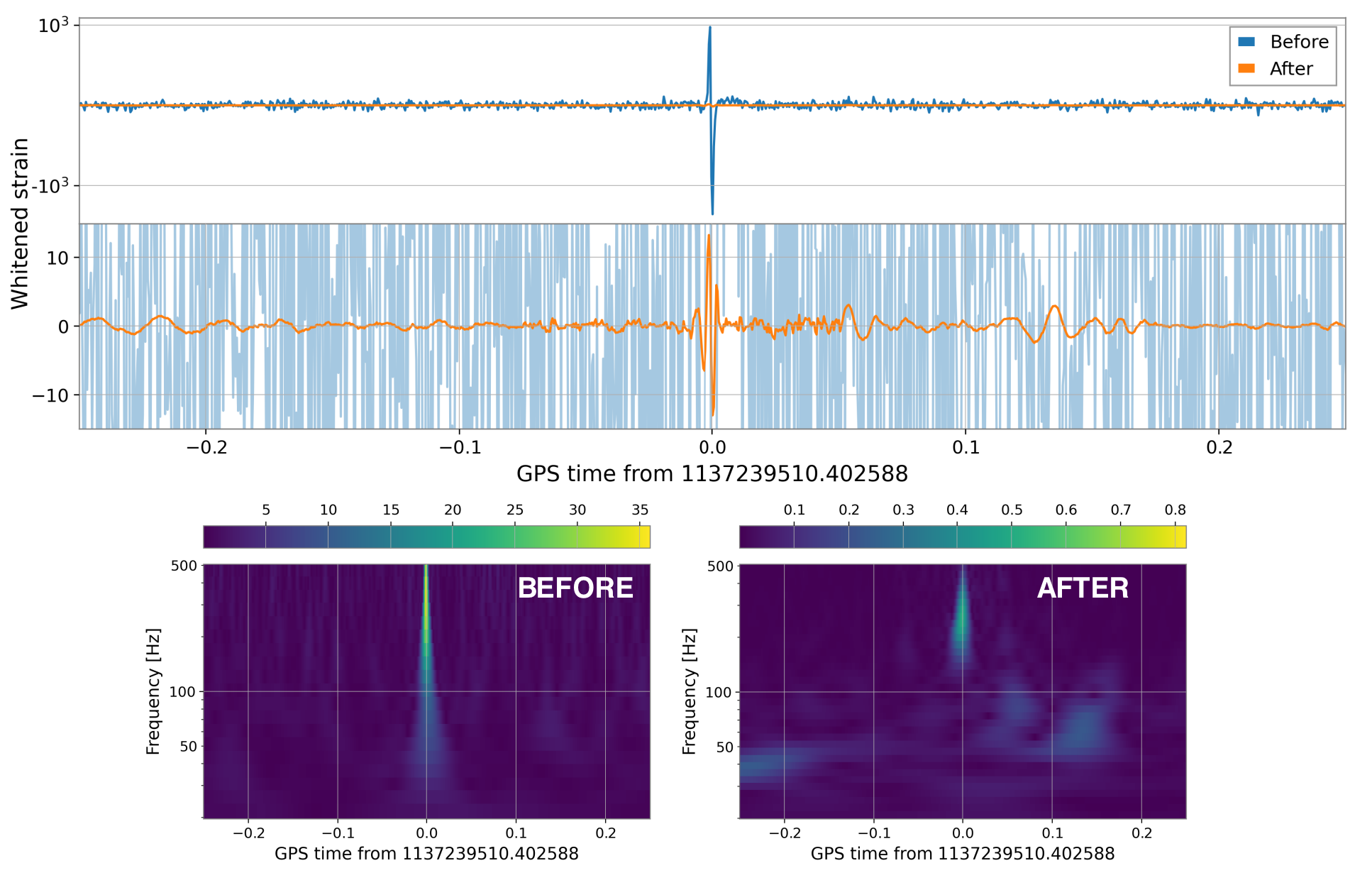
Time-series and spectrogram example of blip.

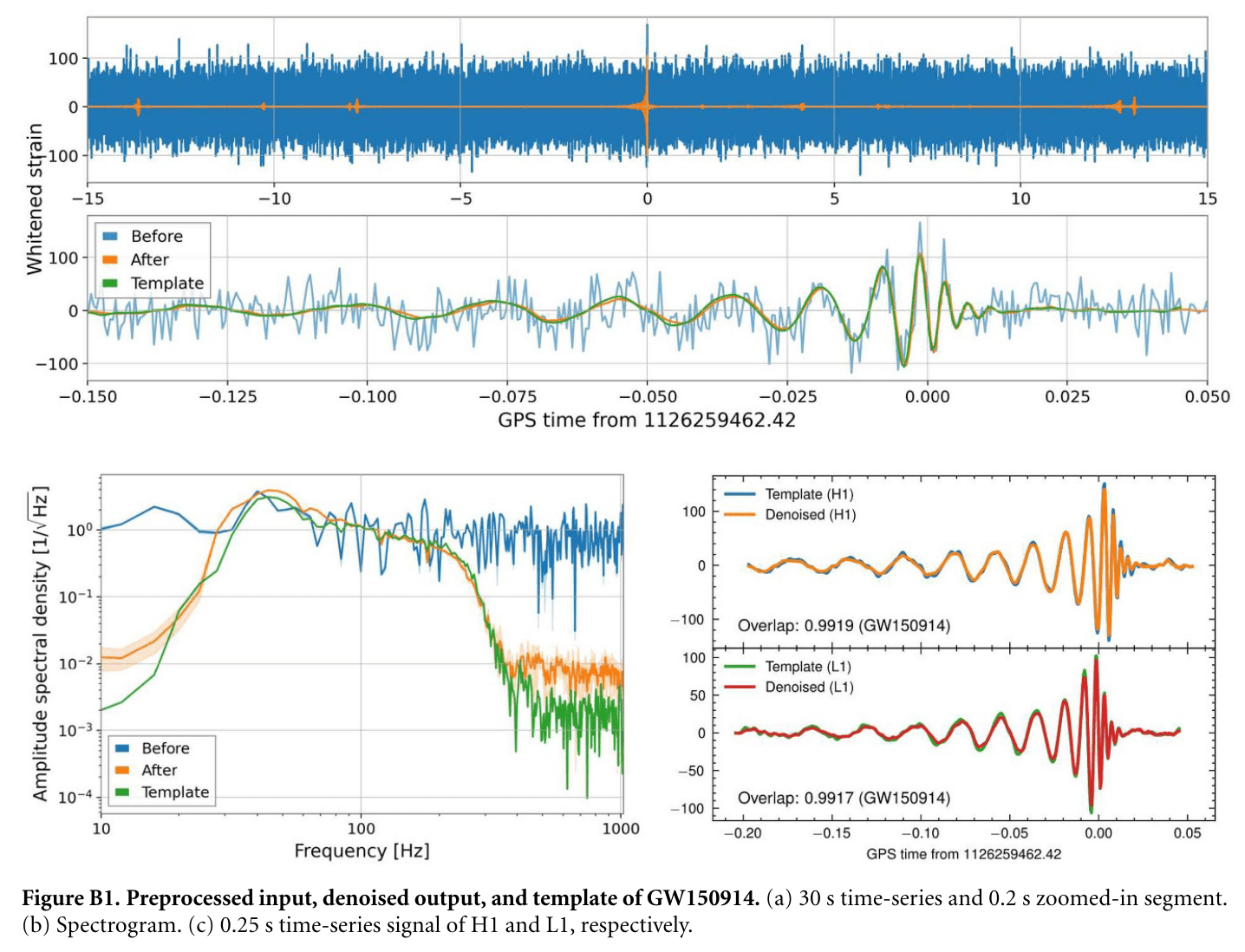
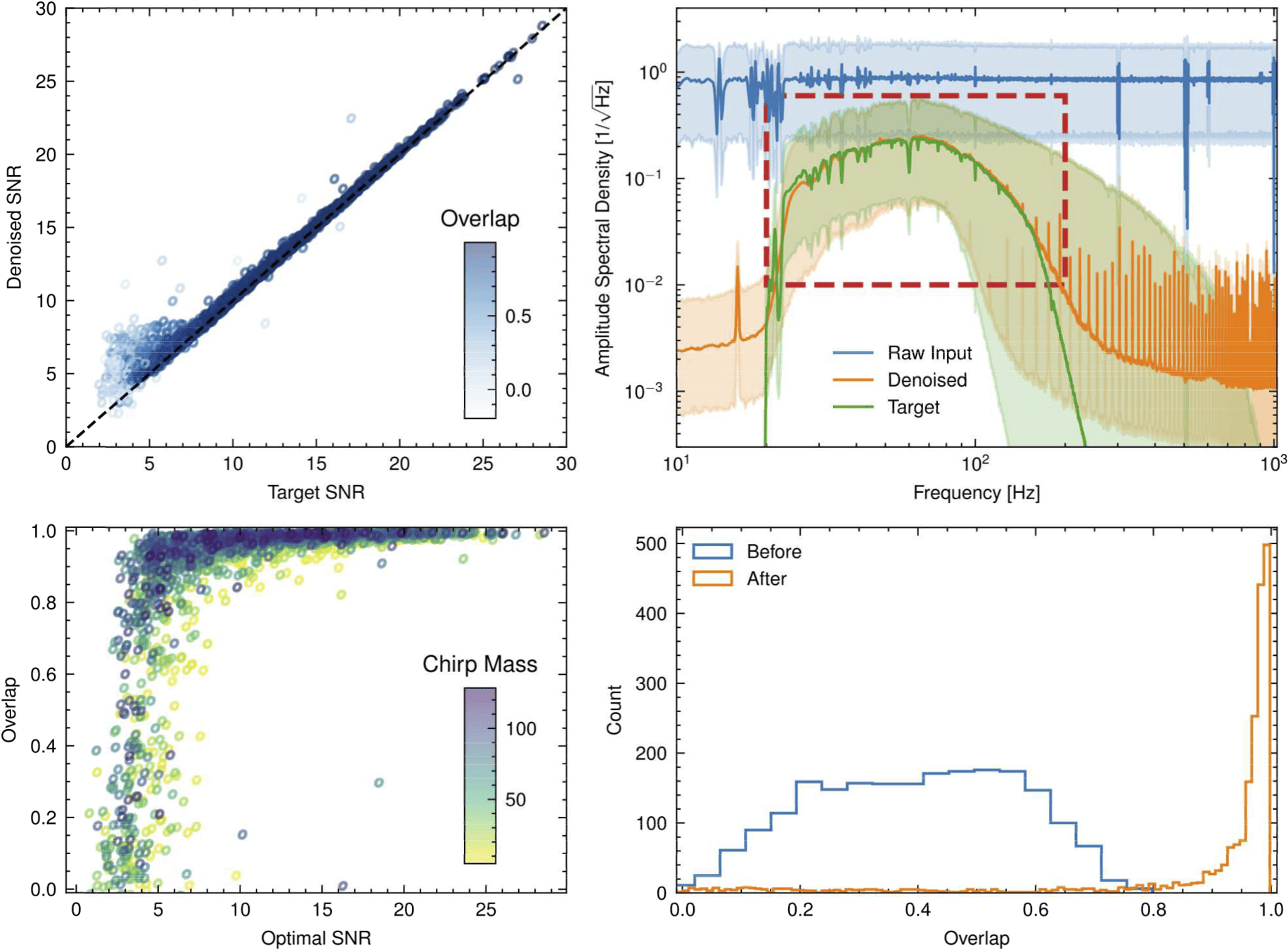
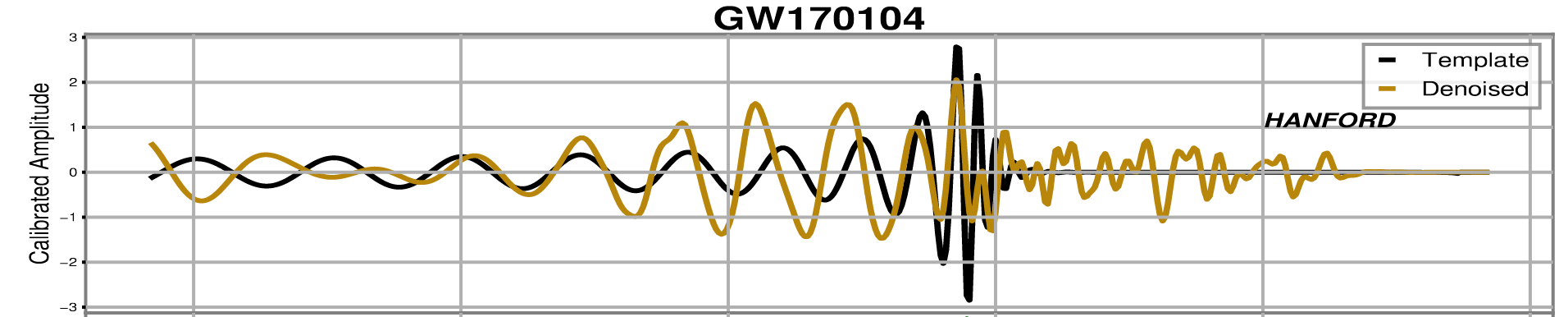
Recovery of Binary Black Holes

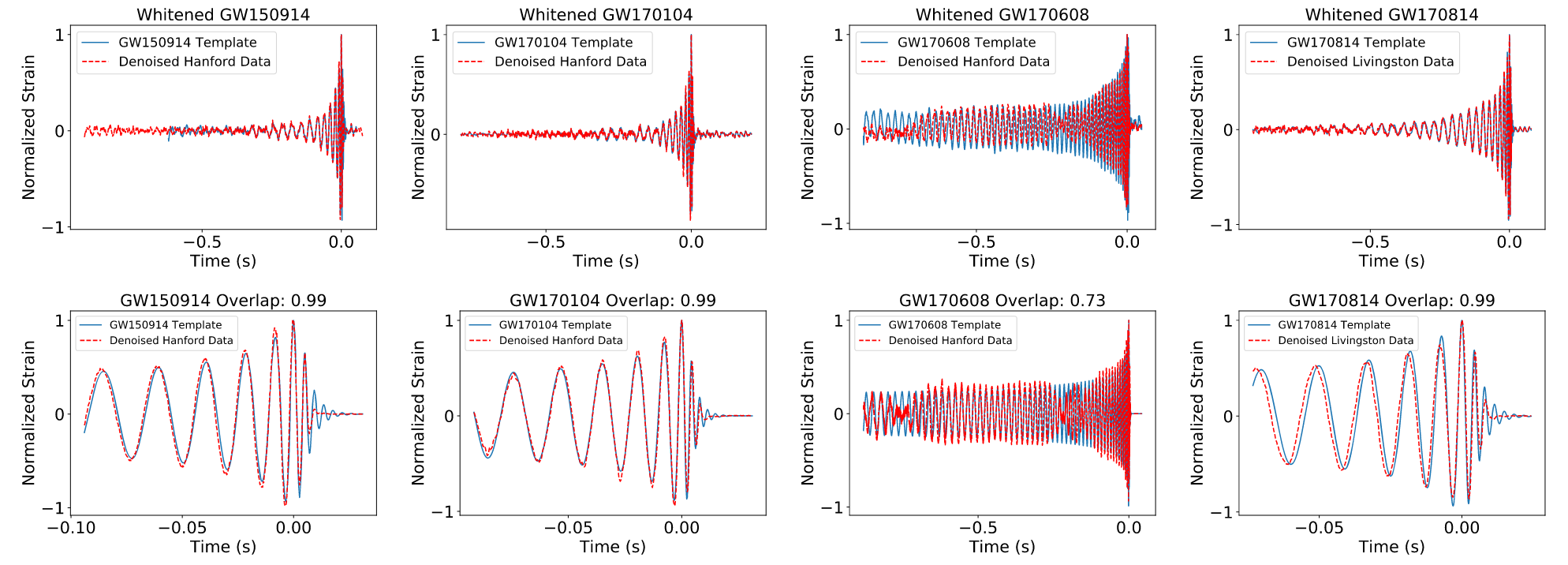
- Overlap and matched-filtering signal-to-noise are calculated to represent phase and amplitude recovery performance.
- Among the intermediate frequency range (20–200 Hz) that covers rich BBH signal information, the ASD distribution of denoised waveform is evidently consistent with that of target signal.
(Upper panels: Signal amplitude recovery performance

(Bottom panels: Signal phase recovery performance)
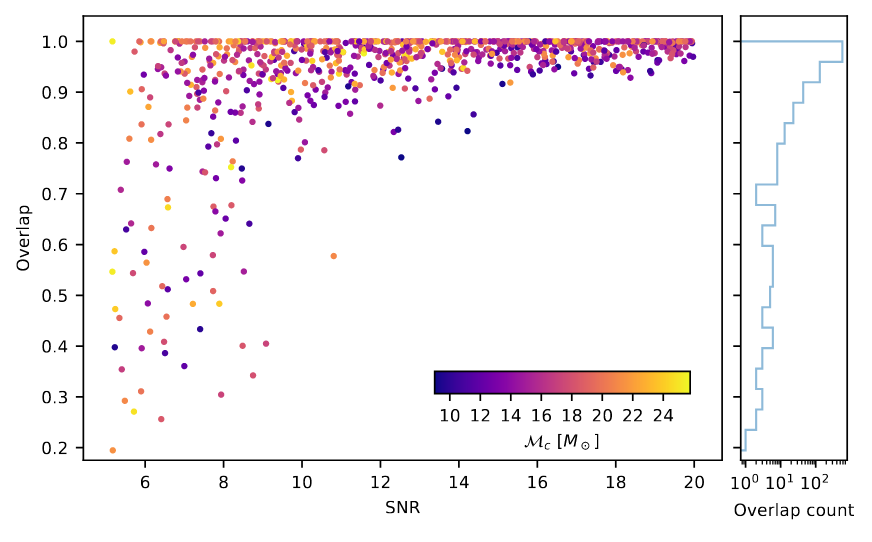
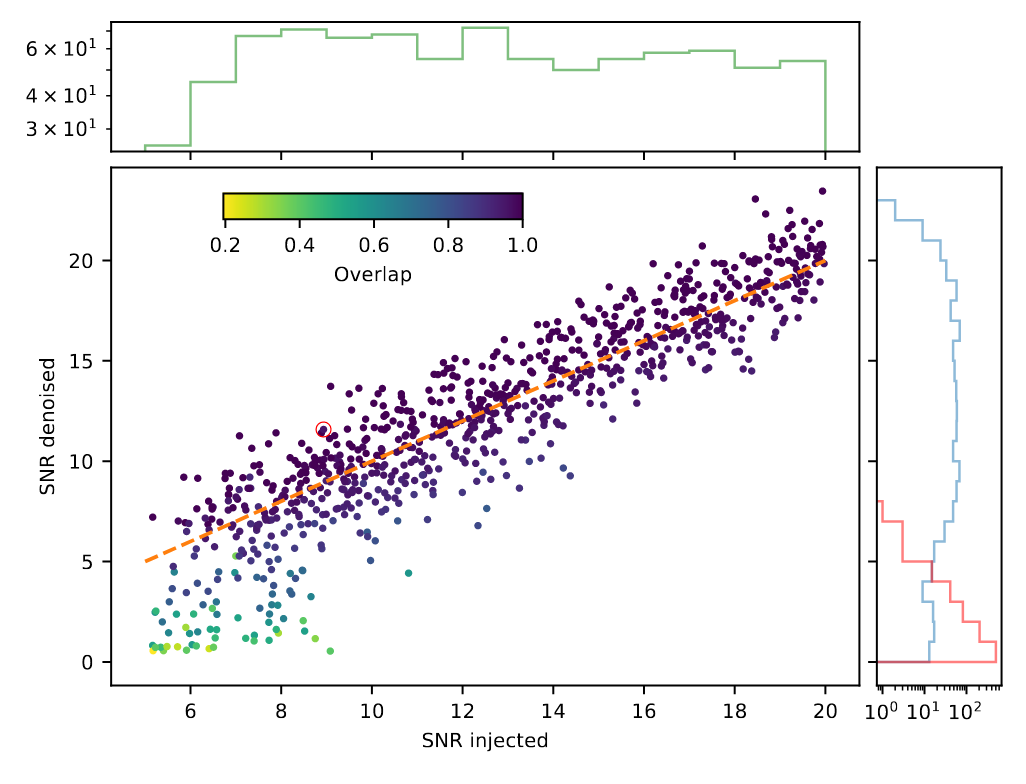
Bacon P. et al. arXiv: 2205.13513
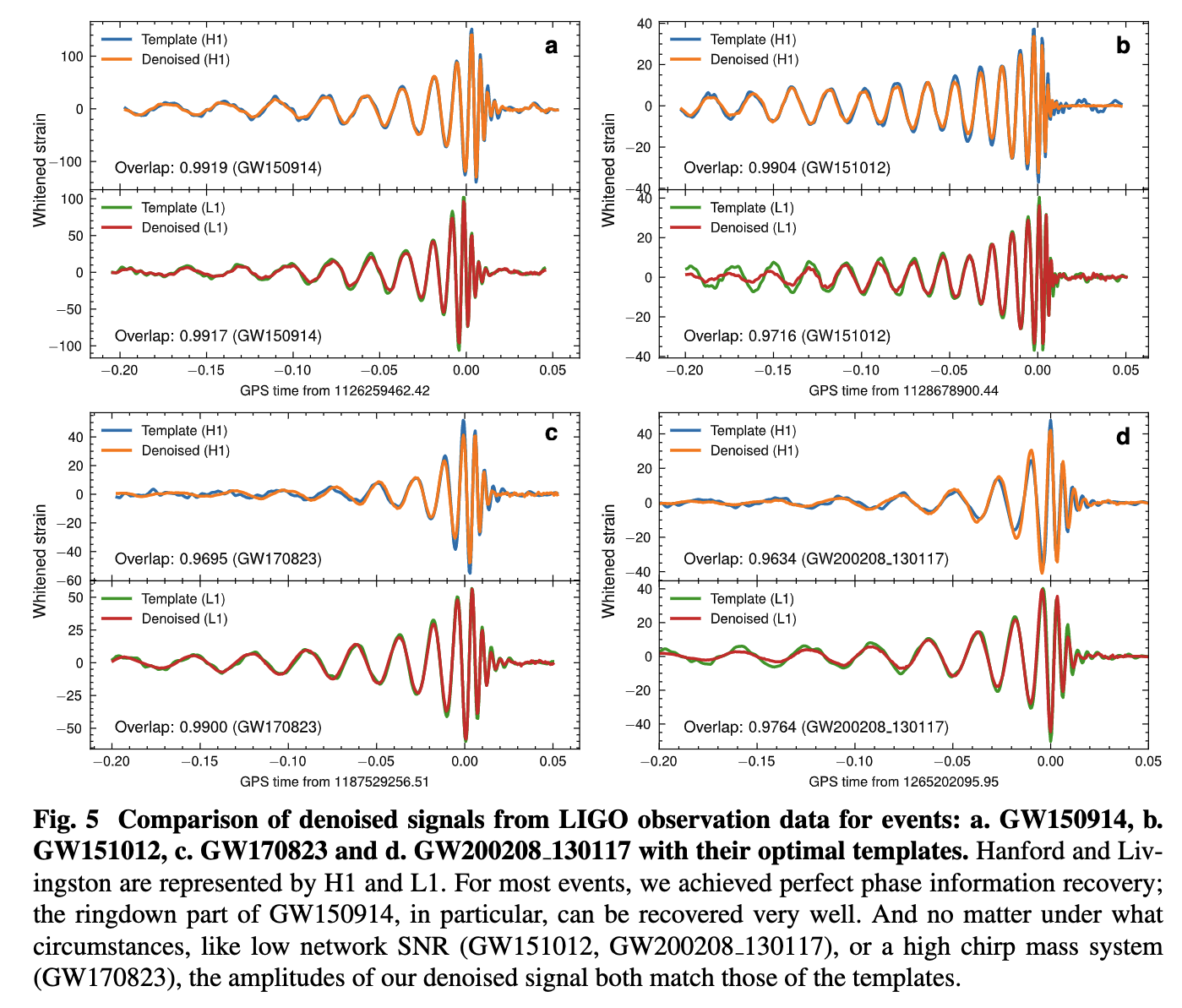

- These results show that our denoising algorithm outperformed others by capturing the characteristic chirping morphology of BBH evolution, and can denoise signals in realistic detection scenarios without affecting signal characteristics such as phase and amplitude.
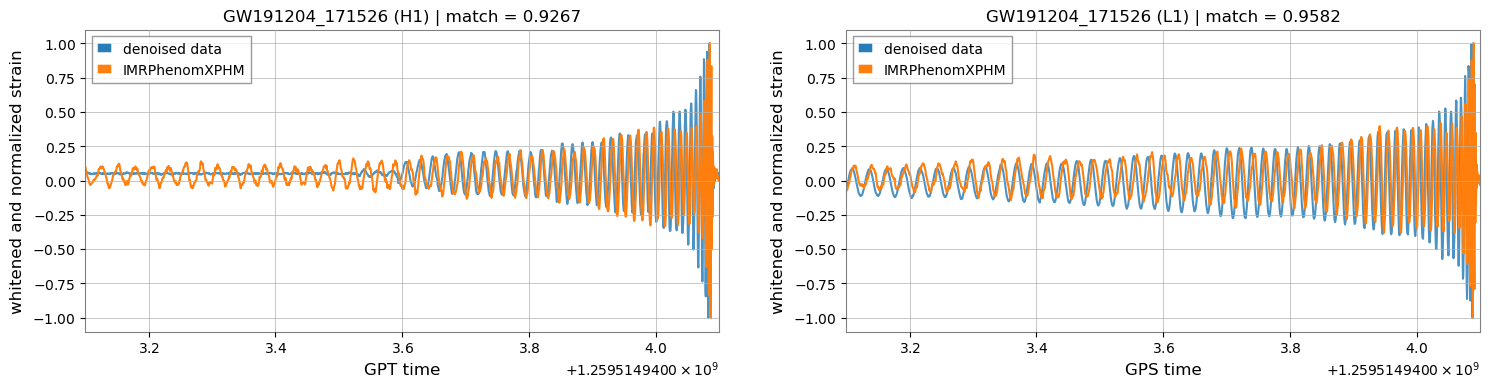
- For the event GW191204_171526, classified as either an NSBH or a low-mass BBH candidate in GWTC-3, the overlap with IMRPhenomXPHM achieved 0.93 and 0.95 on H1 and L1, respectively, which are marked improvements over those achieved by BayesWave and cWB (with overlaps between 0.82–0.86).
GW191204_171526
Recovery of Binary Black Holes
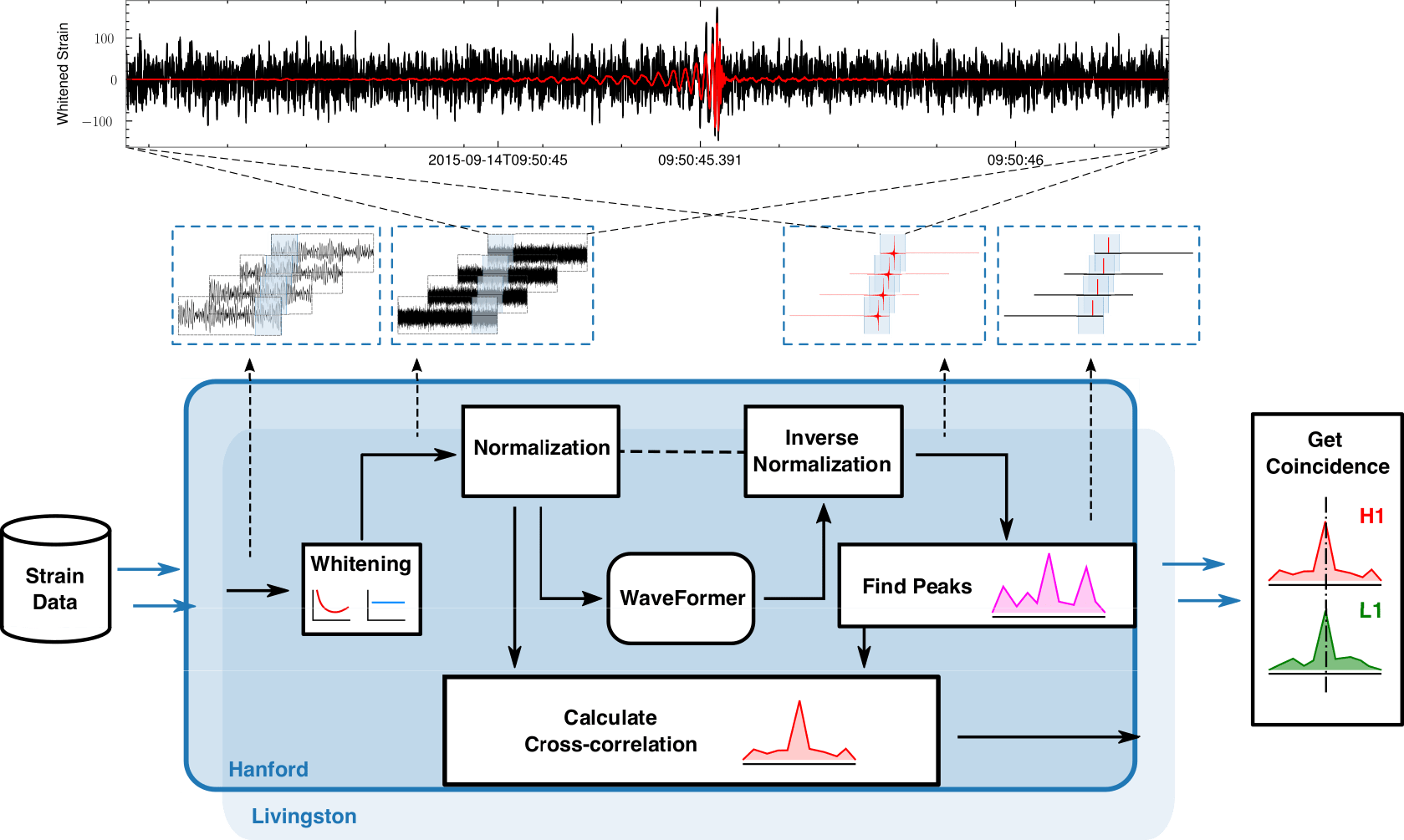
Search Strategy Overview

-
Firstly, we obtain the denoised output by utilizing Waveformer. Then, triggers are defined and identified by three steps including,
-
Find Peaks. Locate triggers on a single detector by finding its maximum all local-maximum (0.2s away from neighboring maximum/local-maximum).
-
-
An search algorithm for GW require that: [cite: 2010.07244]
-
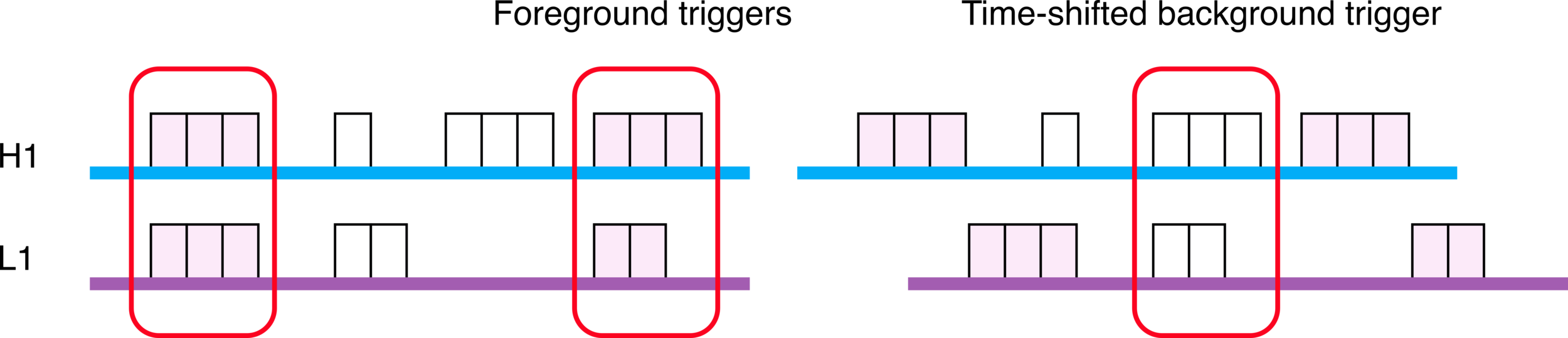
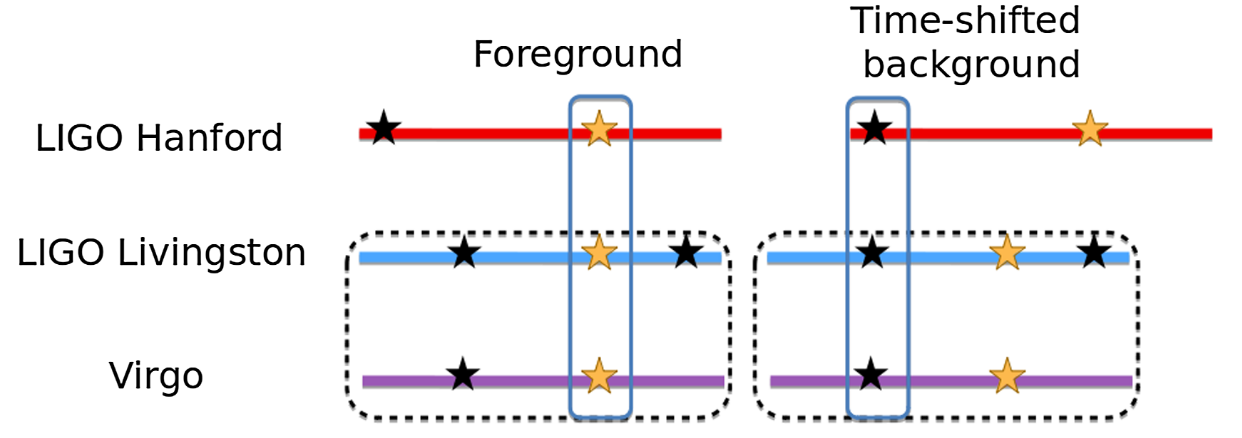
the same signal is seen in the detectors; (the same signal is seen by time-shifting in single detector)
-
the same waveform must be present both detectors;
-
and the signal’s time of arrival must be consistent with the GW travel time between the observatories.
-
Search Strategy Overview

-
Firstly, we obtain the denoised output by utilizing Waveformer. Then, triggers are defined and identified by three steps including,
-
Find Peaks. Locate triggers on a single detector by finding its maximum all local-maximum (0.2s away from neighboring maximum/local-maximum).
-
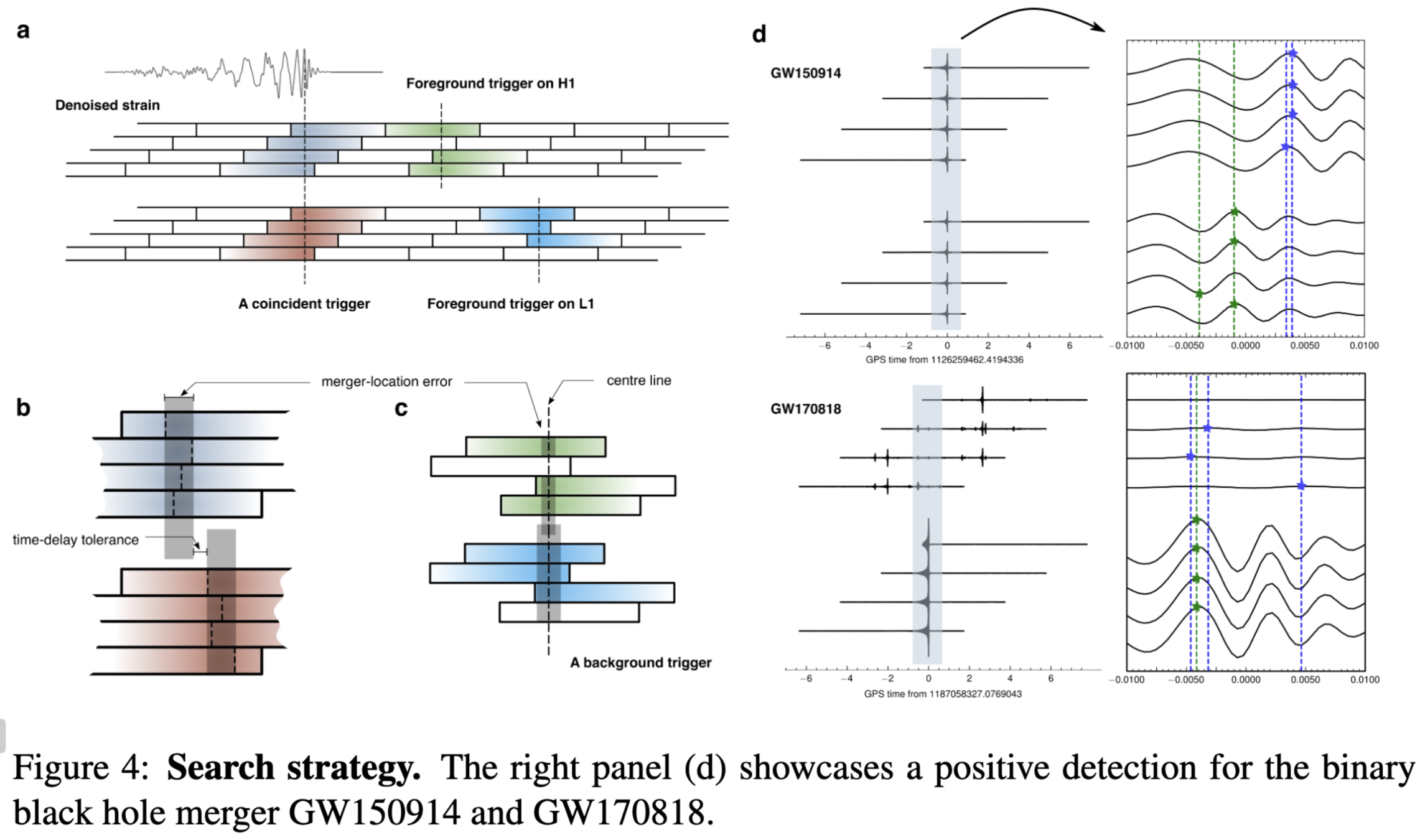
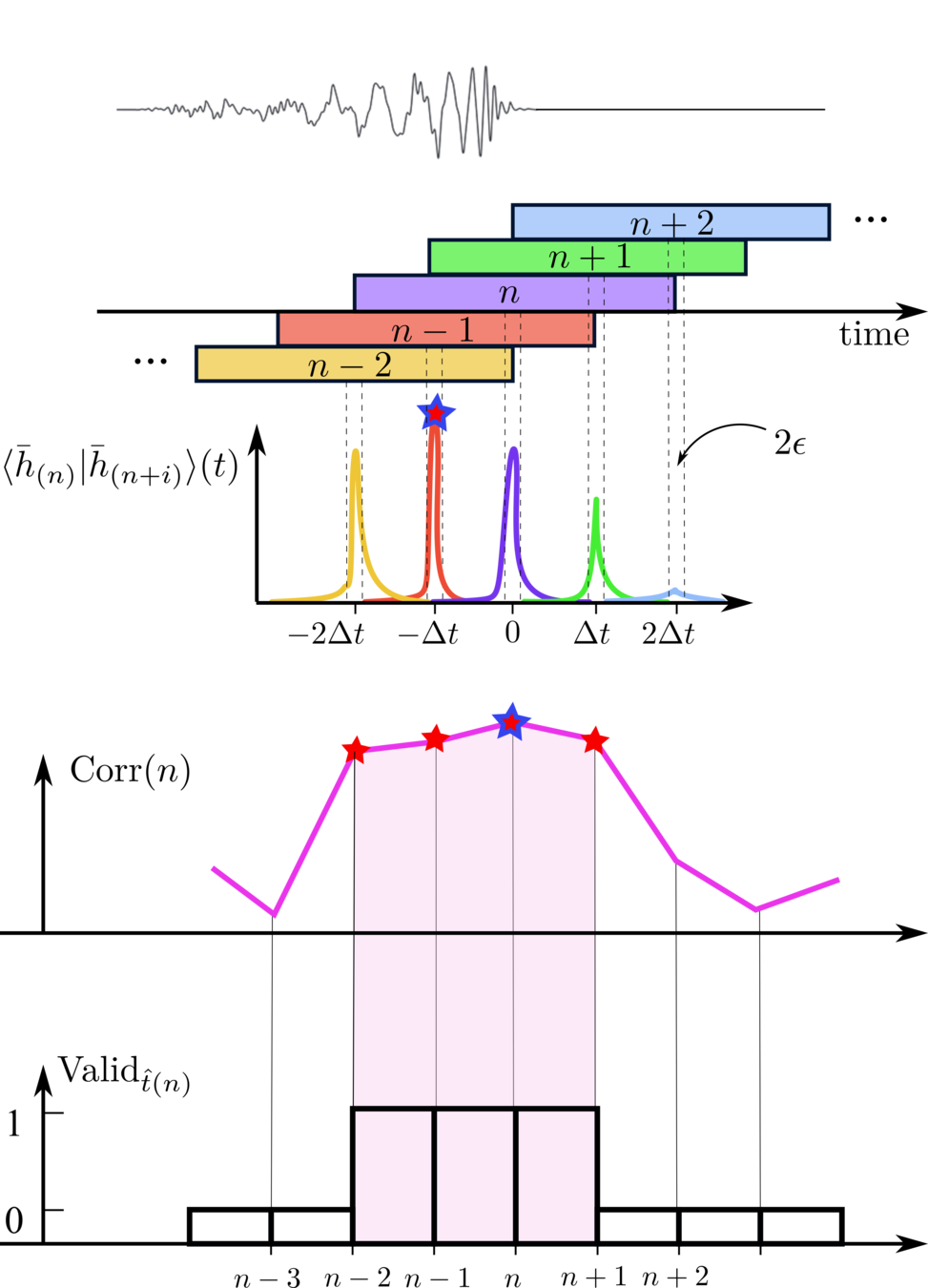
By constraining triggers that exist on both two detectors, we get VALID triggers. (consist 3~4 segments)
-
Search Strategy Overview

-
Firstly, we obtain the denoised output by utilizing Waveformer. Then, triggers are defined and identified by three steps including,
-
Find Peaks. Locate triggers on a single detector by finding its maximum all local-maximum (0.2s away from neighboring maximum/local-maximum).
-
By constraining triggers that exist on both two detectors, we get VALID triggers. (consist 3~4 segments)
-
Calculate the correlation of the to-be-evaluated trigger across channels or within a single channel, between its noisy and corresponding denoised segments, as well as between denoised segments themselves.
-


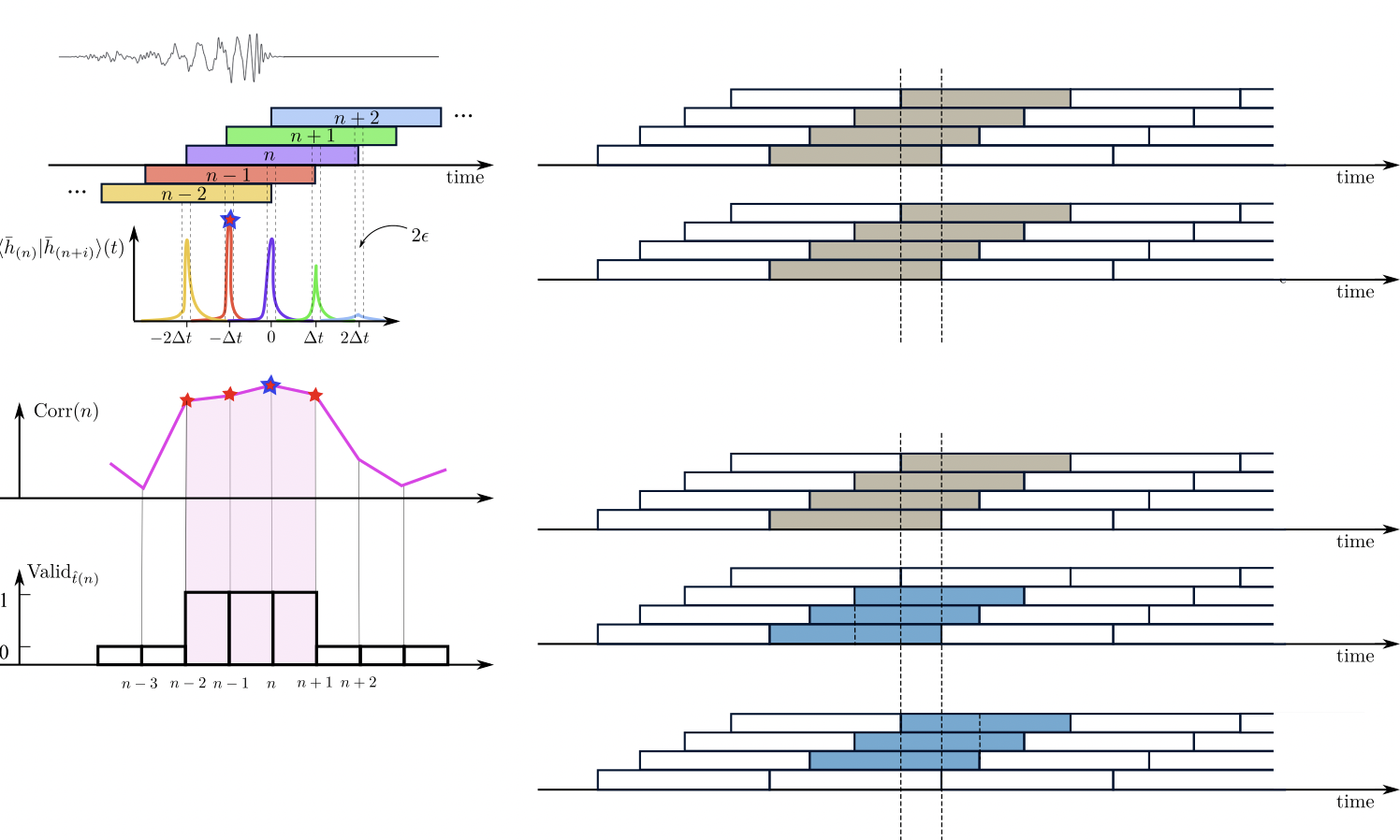
noisy input segments

denoised output segments
\(\bar{H}\)
\(\bar{L}\)
\({H}\)
\({L}\)
Inverse FAR calculation


-
Firstly, we obtain the denoised output by utilizing Waveformer. Then, triggers are defined and identified by three steps including,
-
Find Peaks. Locate triggers on a single detector by finding its maximum all local-maximum (0.2s away from neighboring maximum/local-maximum).
-
By constraining triggers that exist on both two detectors, we get VALID triggers. (consist 3~4 segments)
-
Calculate the correlation of the to-be-evaluated trigger across channels or within a single channel, between its noisy and corresponding denoised segments, as well as between denoised segments themselves.
-
- Through time shift, background analysis is done on other triggers around the target trigger. (time-shift interval 0.1 sec)
- Finally, by counting the number of false alarm trigger pairs, we obtain the IFAR value of the target trigger, which represents the reported or candidate BBH event in this experiment.
OURs
(PyCBC) Davies, et al. PRD 2020
Significance Estimates

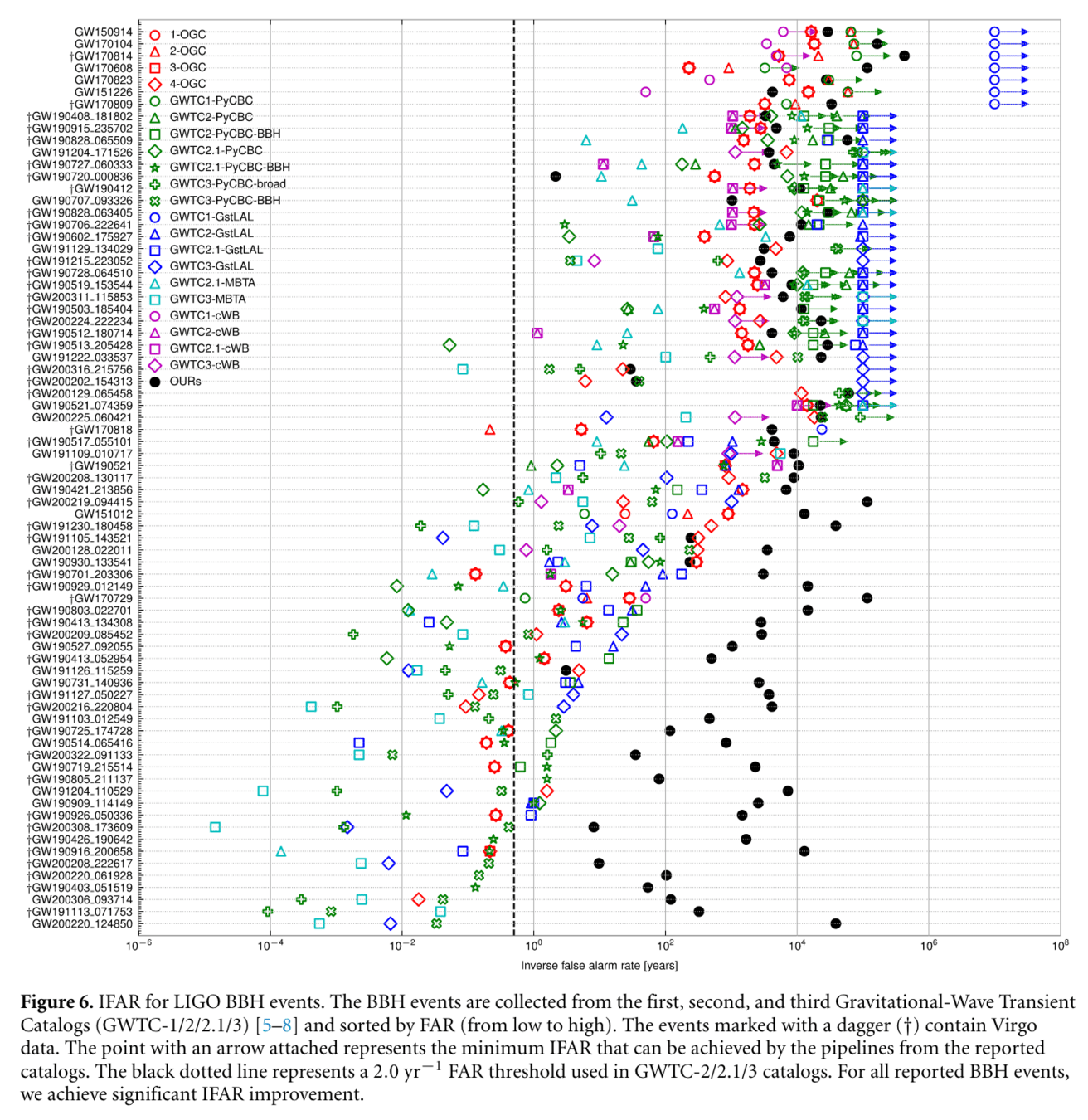
-
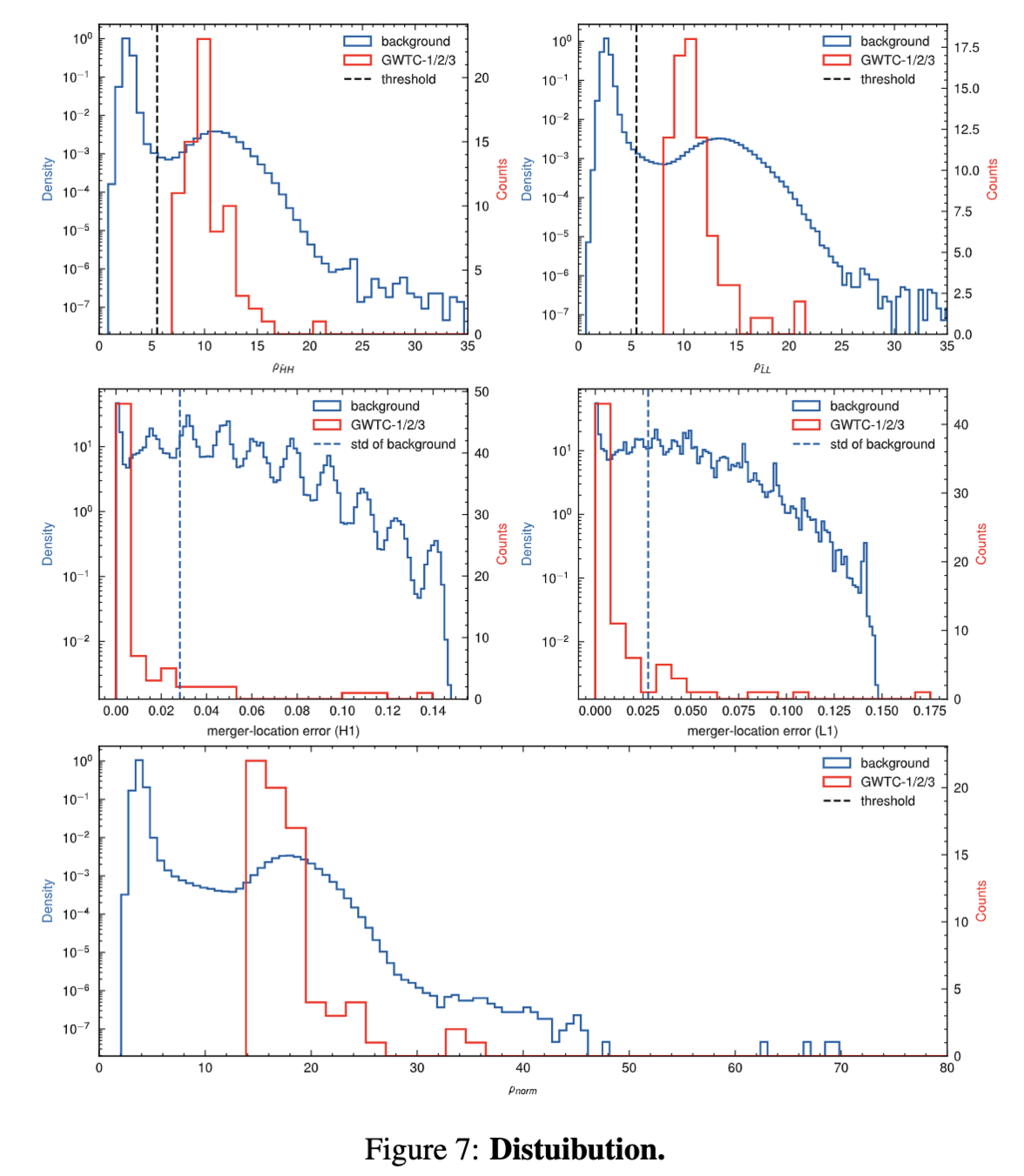
Assessed denoising workflow performance by comparing with GWTC-1, GWTC-2, GWTC2.1, and GWTC-3 catalogs and associated data releases.
-
Noted significant divergence in IFAR distribution between our results and those from GWTC and OGC catalogs.
-
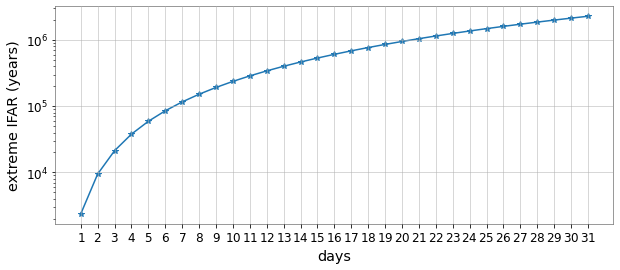
Achieved significant IFAR improvement across all 75 reported BBH events, indicating effective suppression of loud terrestrial noise.
-
Example: For low SNR (\(10.8_{-0.4}^{+0.3}\)) event GW200208_130117, obtained an IFAR of 8916 years, surpassing maximum IFAR of <4000 years in other catalogs.
-
-
Variability in IFAR improvement linked to the original data's noise nature, including its non-Gaussian, non-stationary characteristics, and different signal recognition strategies by pipelines.
-
IFAR performance significantly depends on the reduction of non-Gaussian noise near each event.
-
Events with substantial IFAR improvement had misleading non-Gaussian noise effectively eliminated.
-
Events where IFAR underperforms retained non-Gaussian characteristics, possibly due to WaveFormer's inherent systematic errors.
-
Summary & Discussion

- Developed an AI-based workflow with WaveFormer, combining convolutional neural network and transformer for effective GW noise suppression and hierarchical feature extraction across a wide frequency range.
- Achieved significant noise suppression and signal recovery performance improvements, including state-of-the-art results on real observational data and BBH events, leading to dramatic data quality improvement and significant IFAR enhancement on 75 reported BBH events.

Text
-
Challenges in Model Interpretability
- The black-box nature of AI models complicates interpretability, challenging the comparison of AI-generated detection statistics with traditional matched filtering chi-square distributions.
- Convincing the scientific community of the pipeline's validity and the statistical significance of new discoveries remains difficult despite the model's ability to identify potential gravitational wave signals.
OURs
LVK. PRD (2016). arXiv:1602.03839
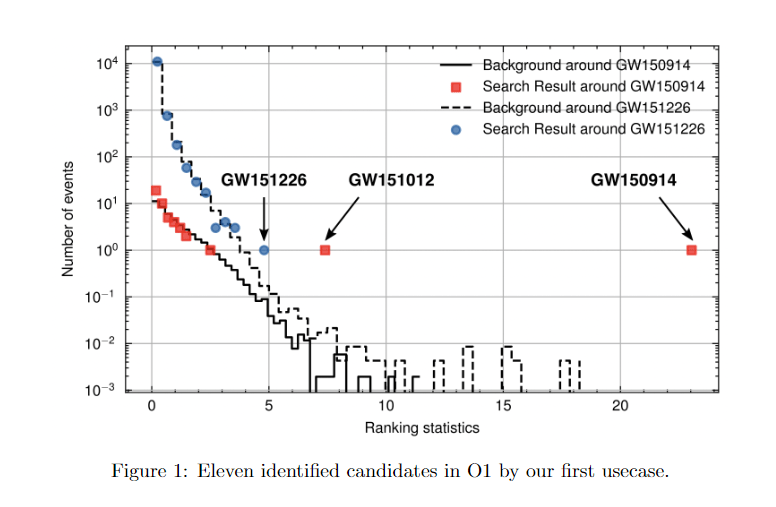
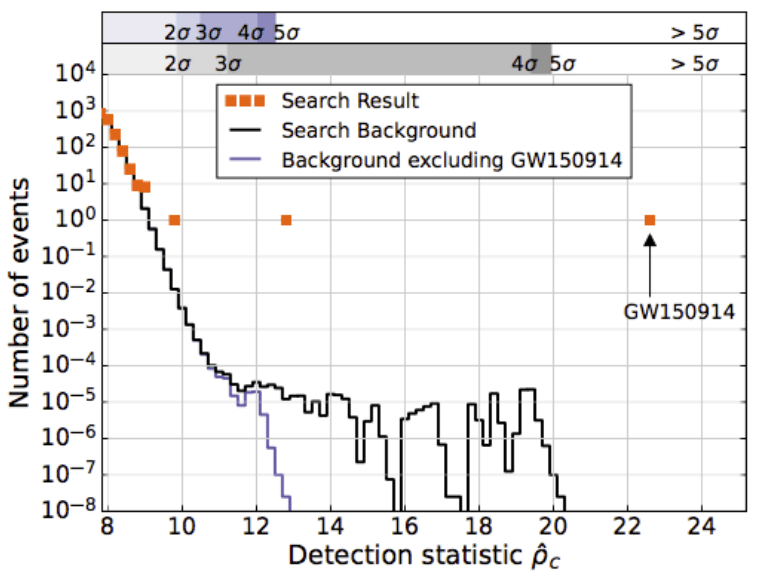
GW151226
GW151012
Summary

- Developed an AI-based workflow with WaveFormer, combining convolutional neural network and transformer for effective GW noise suppression and hierarchical feature extraction across a wide frequency range.
- Achieved significant noise suppression and signal recovery performance improvements, including state-of-the-art results on real observational data and BBH events, leading to dramatic data quality improvement and significant IFAR enhancement on 75 reported BBH events.

Text
Text

GW151226
GW151012
LVK. arXiv:1602.03839

He Wang, et al. MLST. 5, 1 (2024): 015046.
-
Challenges in Model Interpretability
- The black-box nature of AI models complicates interpretability, challenging the comparison of AI-generated detection statistics with traditional matched filtering chi-square distributions.
- Convincing the scientific community of the pipeline's validity and the statistical significance of new discoveries remains difficult despite the model's ability to identify potential gravitational wave signals.
-
Future Directions
- Construct a comprehensive GW signal search pipeline for BBH/BNS/NSBH events.
- Explore the use of ensemble learning and other statistical methods to enhance the interpretability of the AI detection pipeline and address issues related to its validity.
Ongoing Research & Future Goals

A Python Toolbox for Gravitational Wave Astronomy: GWToolkit
- This toolbox, powered by Ray/JAX, supports both CPU and GPU. It is specifically designed for machine learning applications in gravitational wave astronomy, providing efficient and scalable tools for data analysis and model training.
Can AI identify new GW events from LIGO data?
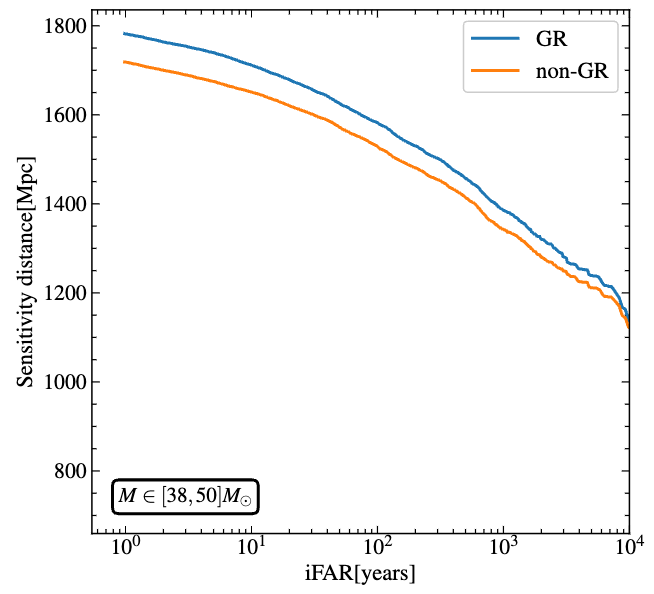
- Exploring the potential of AI to detect new gravitational wave events from LIGO data.
- Could these signals indicate phenomena beyond General Relativity (bGR) or do they exhibit eccentricity?
Mitigating bias in AI-Driven GW data analysis
- How can we address the issue of strong or unacceptable biases that occur when outputs from AI models are used jointly or in combination to measure properties of a population, sub-population, or ensemble?
(also addressed by 2405.18095)
Text

Text
Text
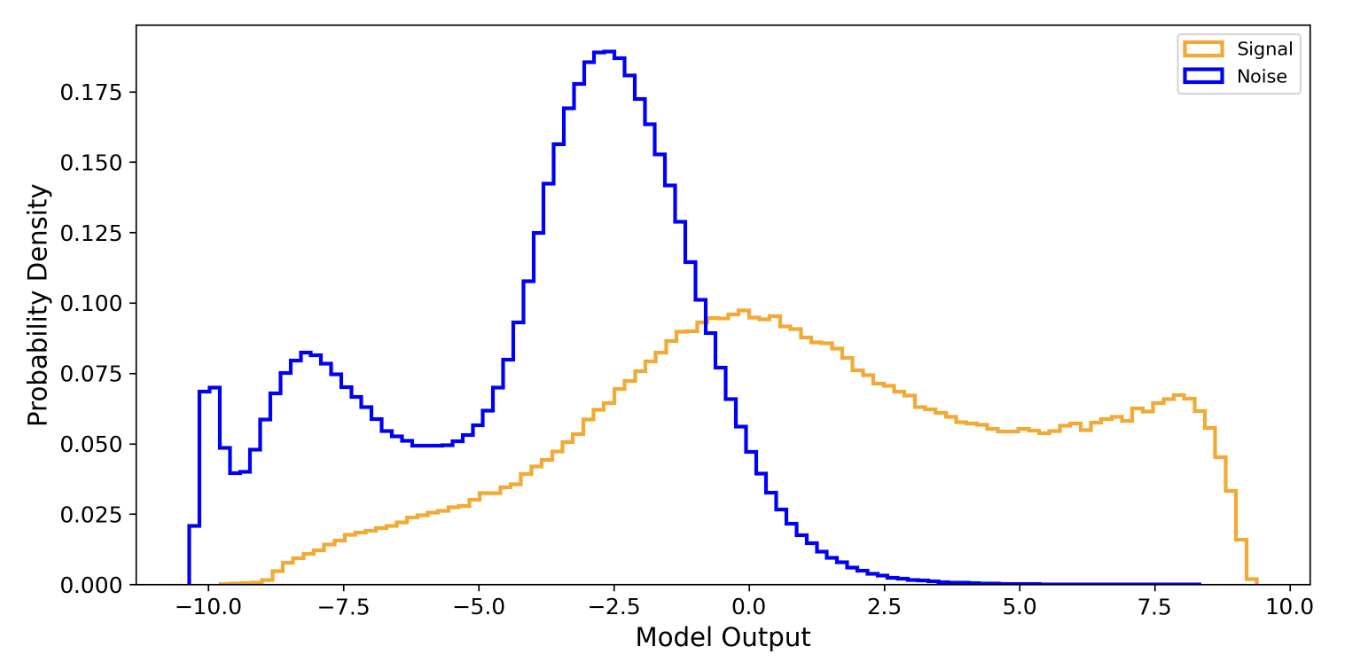
Alfaidi & Messerger. arXiv:2402.04589
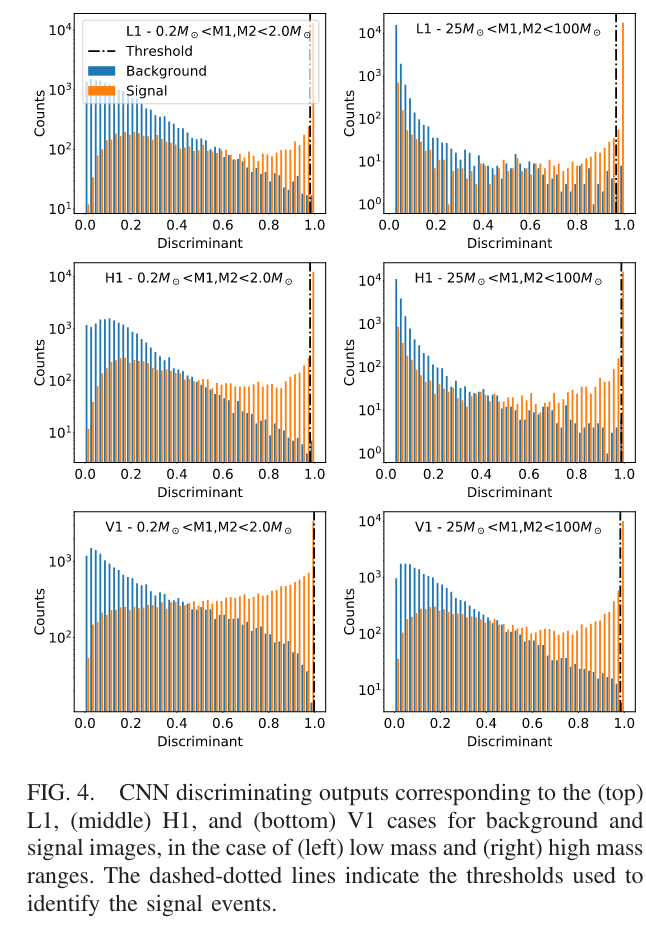
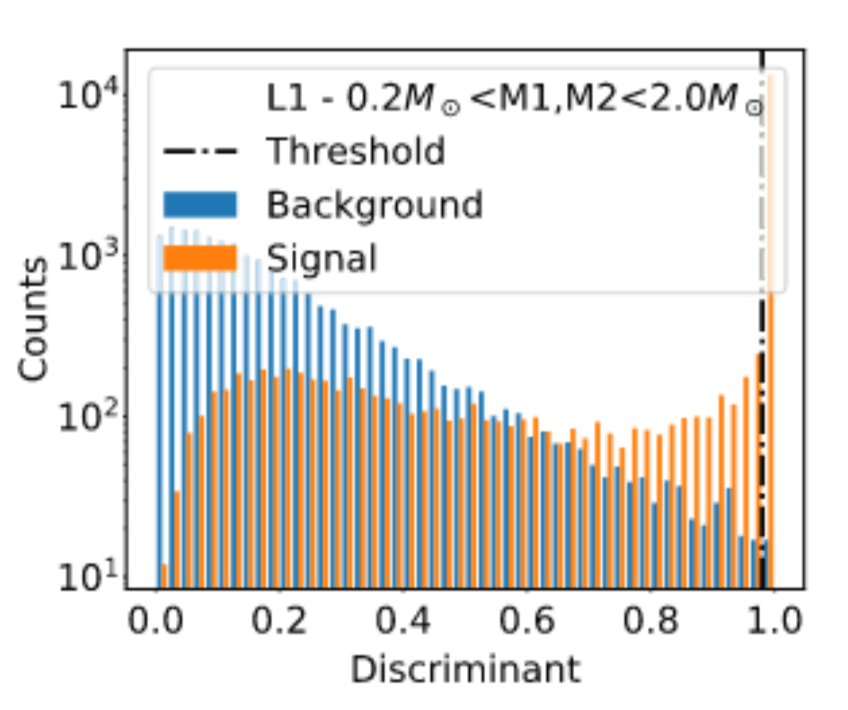
Menéndez-Vázquez A, et al. PRD 2021
"Draft in Progress"
Ongoing Research & Future Goals

A Python Toolbox for Gravitational Wave Astronomy: GWToolkit
- This toolbox, powered by Ray/JAX, supports both CPU and GPU. It is specifically designed for machine learning applications in gravitational wave astronomy, providing efficient and scalable tools for data analysis and model training.
Can AI identify new GW events from LIGO data?
- Exploring the potential of AI to detect new gravitational wave events from LIGO data.
- Could these signals indicate phenomena beyond General Relativity (bGR)?
Mitigating bias in AI-Driven GW data analysis
- How can we address the issue of strong or unacceptable biases that occur when outputs from AI models are used jointly or in combination to measure properties of a population, sub-population, or ensemble?
(also addressed by 2405.18095)
Text


Text
Text

Alfaidi & Messerger. arXiv:2402.04589

Menéndez-Vázquez A, et al. PRD 2021
Yu-Xin Wang, et al. "Draft in Progress"
for _ in range(num_of_audiences):
print('Thank you for your attention! 🙏')This slide: https://slides.com/iphysresearch/2024june_gwac