中国物理学会引力与相对论天体物理分会“2023年学术年会”

2023.04.23 11:10-11:30 | 中国·重庆

Clearing the Path to Discovery: Detecting and Denoising Gravitational Waves with Deep Learning

王赫

hewang@ucas.ac.cn

中国科学院大学 · 国际理论物理中心（亚太地区）

Reference:

  • PRD 107.2 (2023): 023021
  • PRD 107.6 (2023): 063029
  • PLB (2023): 137904.
  • arXiv:2212.14283
  • Gravitational Wave Astronomy
  • Gravitational Wave Detection
    • MFCNN
    • MLGWSC1
  • Gravitational Wave Observational Data Denoising
    • WaveFormer
  • Outlook
    • LLM / ChatGPT
    • GWToolkit
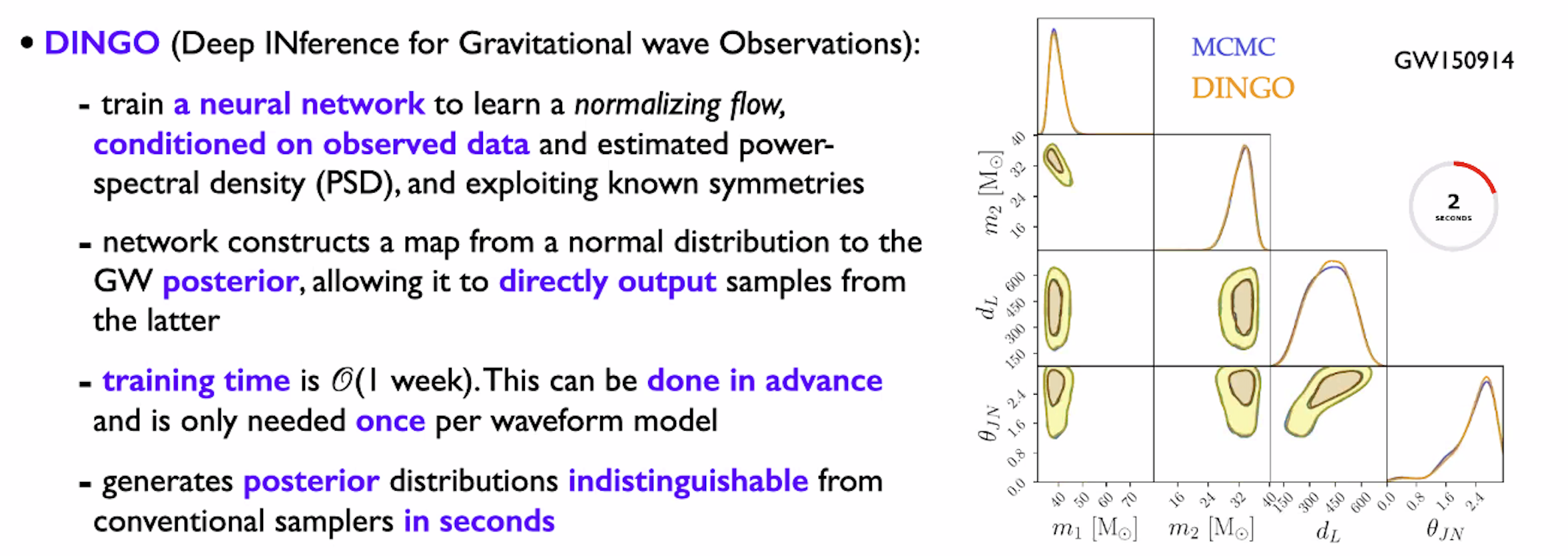
    • PE (DINGO)

Content

Gravitational Wave Astronomy

  • Fundamental physics
    • Existence of gravitational waves
    • To put constraints on the properties of gravitons
  • Astrophysics
    • Refine our understanding of stellar evolution
    • and the behavior of matter under extreme conditions.
  • Cosmology
    • The measurement of the Hubble constant
    • Dark energy

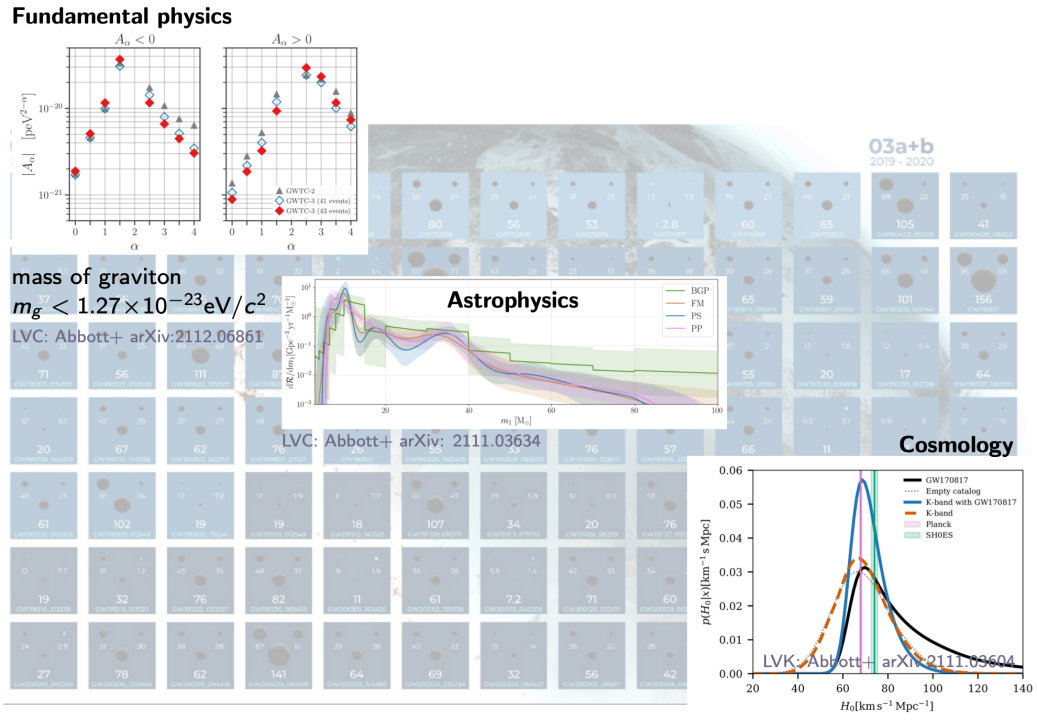
GWTC-3

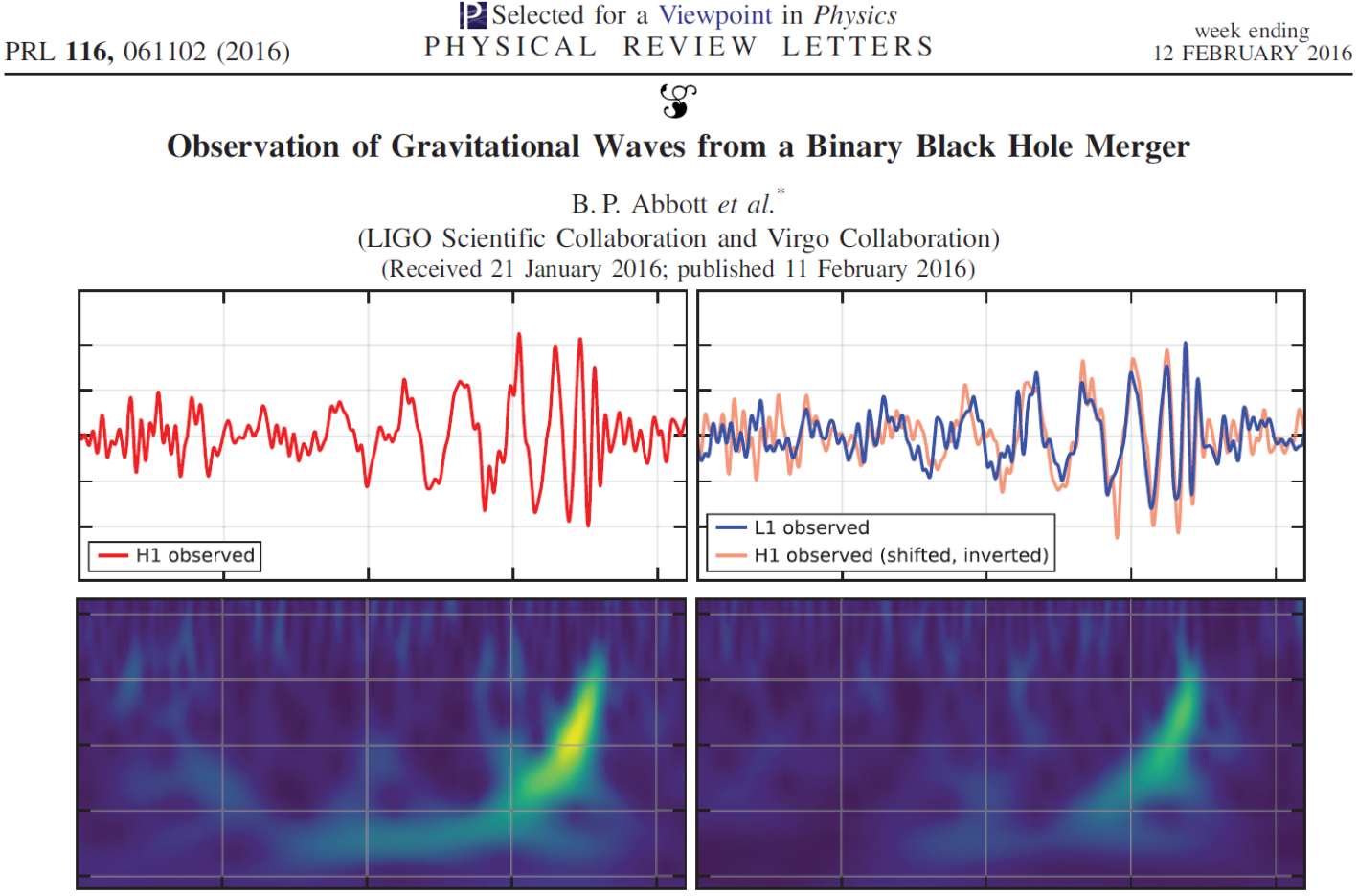
The First GW Event: GW150914

  • Detecting gravitational waves require a mix of FIVE key ingredients:
    1. good detector technology
    2. good waveform predictions
    3. good data analysis methodology and technology
    4. coincident observations in several independent detectors
    5. coincident observations in electromagnetic astronomy

—— Bernard F. Schutz

​​DOI:10.1063/1.1629411 

AI for Gravitational Wave

  • AI for Science \(\rightarrow\) AI for GW
  • Artificial Intelligence (AI) has great potential to revolutionize gravitational wave astronomy by improving data analysis, modeling, and detector development.

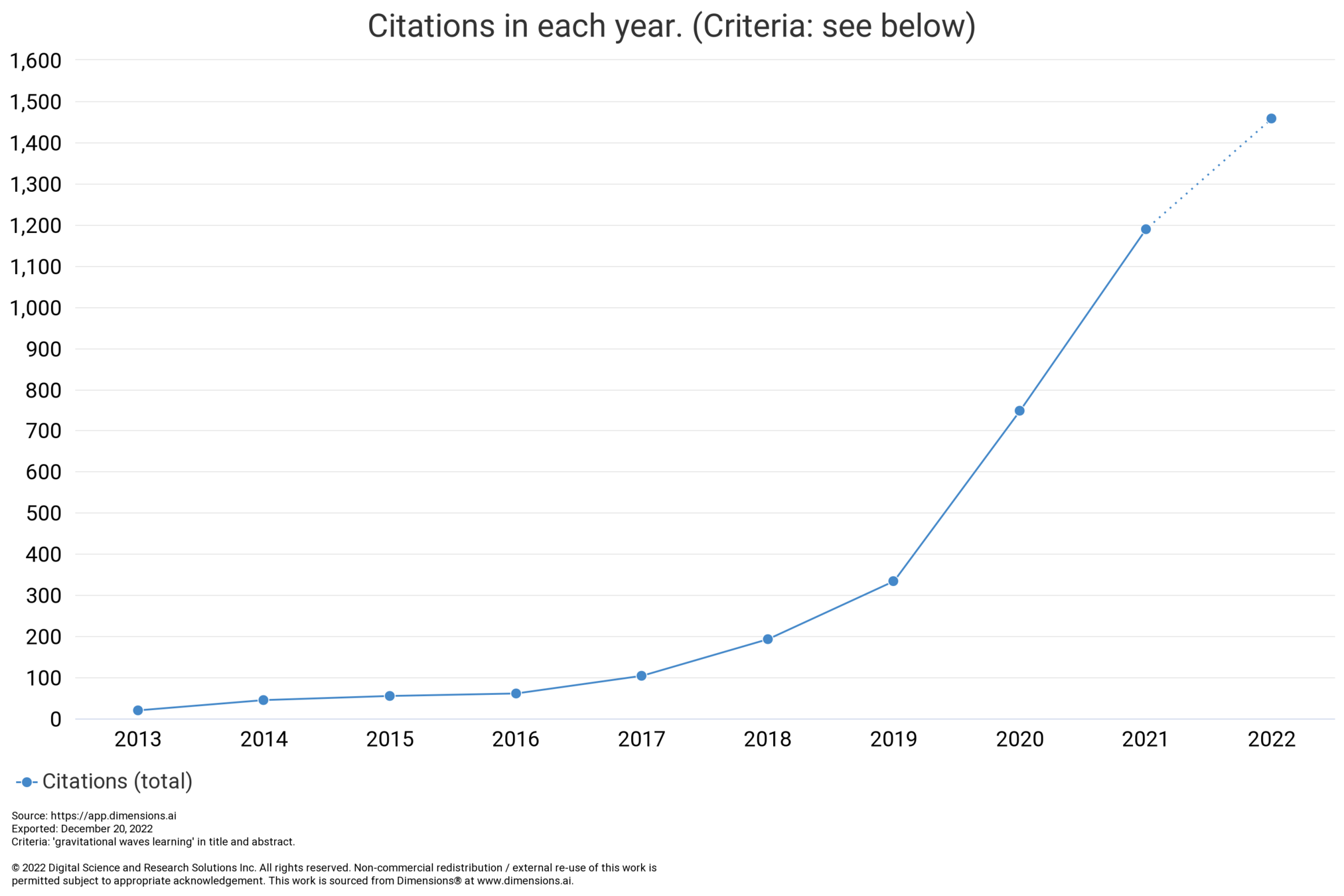
AI for Gravitational Wave

  • GW Data characteristics:

    • ​Noise: non-Gaussian and non-stationary

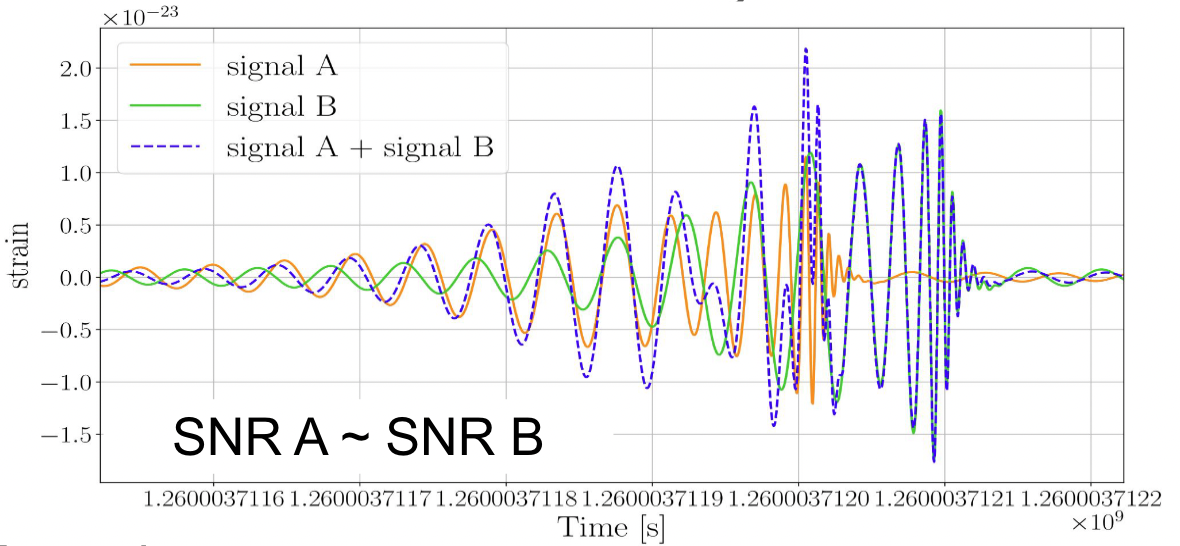
    • Signal: A low signal-to-noise ratio (SNR) which is typically about 1/100 of the noise amplitude (-60 dB)

Data quality improvement

Credit: Marco Cavaglià 

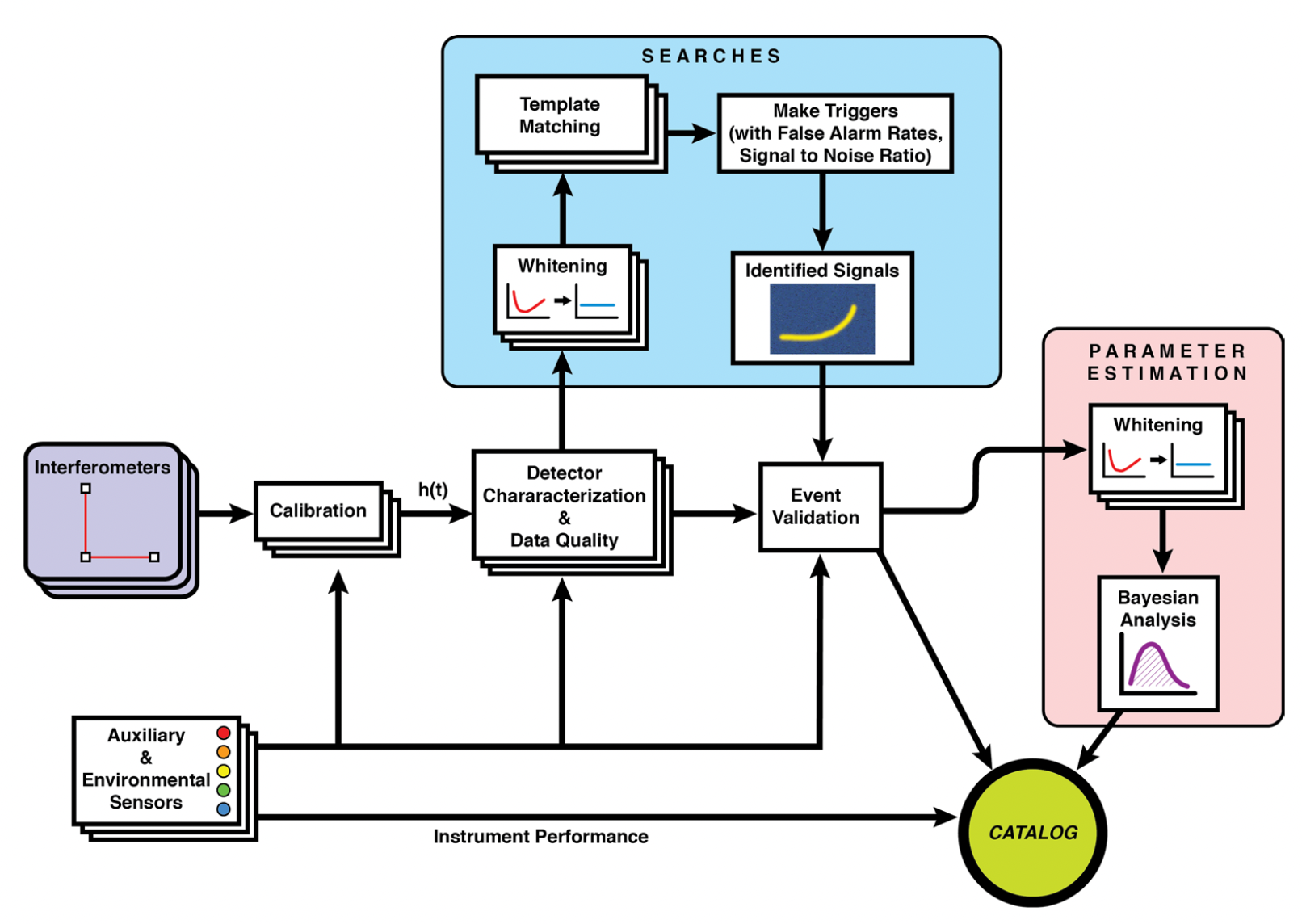
LIGO-Virgo data processing

GW waveform modeling

GW searches

Astrophsical interpretation of GW sources

CQG. 37 (2020) 055002

Gravitational Wave Detection

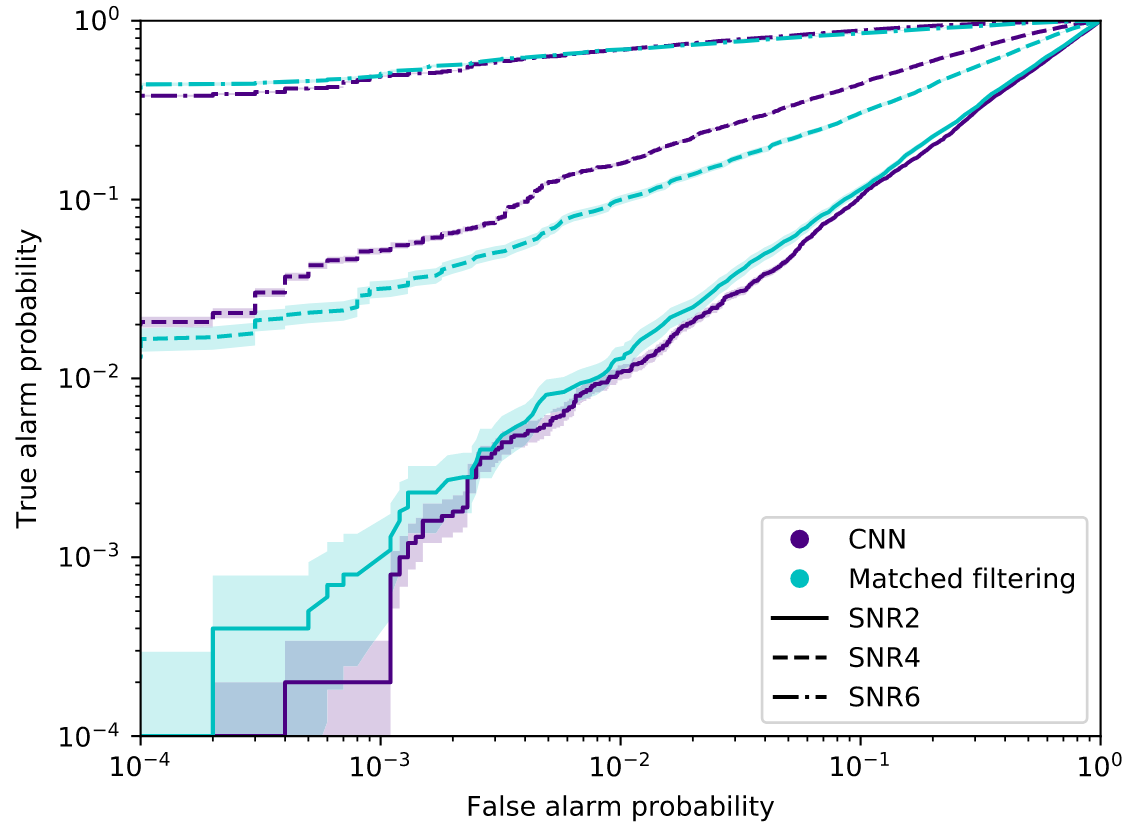
PRL, 2018, 120(14): 141103.

  • Matched filtering techniques (匹配滤波方法)

    • In Gaussian and stationary noise environments, the optimal linear algorithm for extracting weak signals

  • Convolutional neural networks (CNN) can achieve comparable performance to MF, and outperform them in terms of execution speed (with GPU support).

  • ... under Gaussian stationary noise.

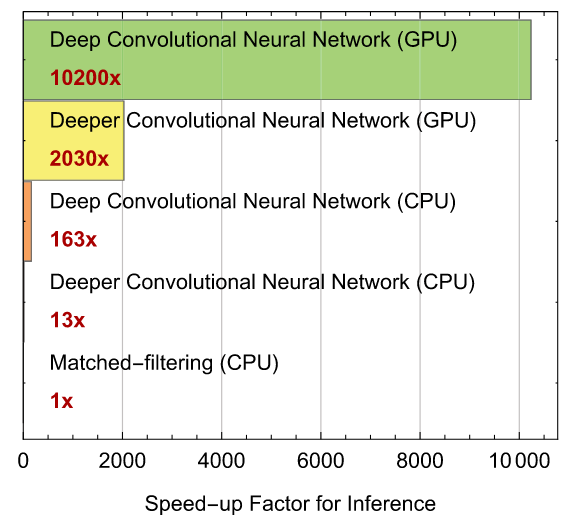
PRD, 2018, 97(4): 044039. ​​​​​​​

  • GW Data characteristics:

    • ​Noise: non-Gaussian and non-stationary

    • Signal: A low signal-to-noise ratio (SNR) which is typically about 1/100 of the noise amplitude (-60 dB)

Gravitational Wave Detection

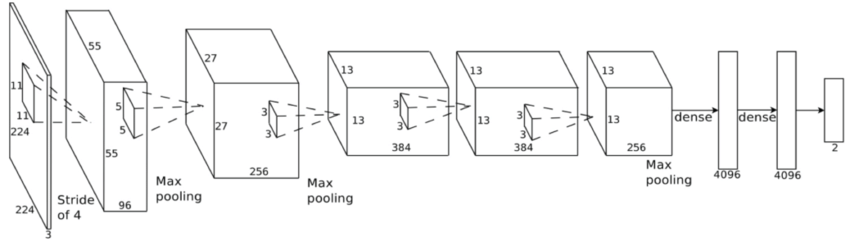
Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012)

Convolutional Neural Network (ConvNet or CNN)

  • Test the CNN model on real LIGO recordings and GW events, the output is very bad 😰

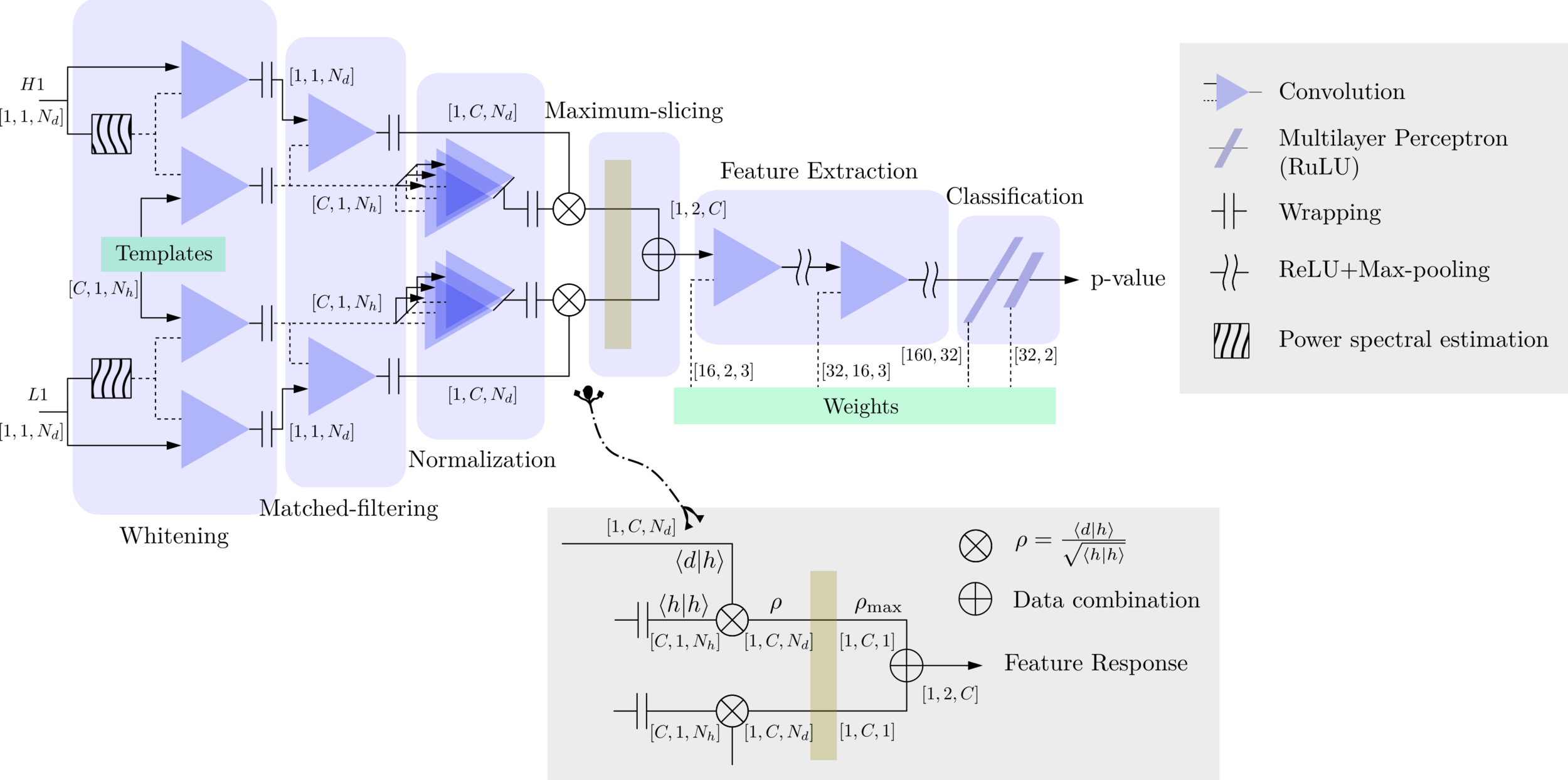
Matched-filtering Convolutional Neural Network (MFCNN)

GW150914

GW151012

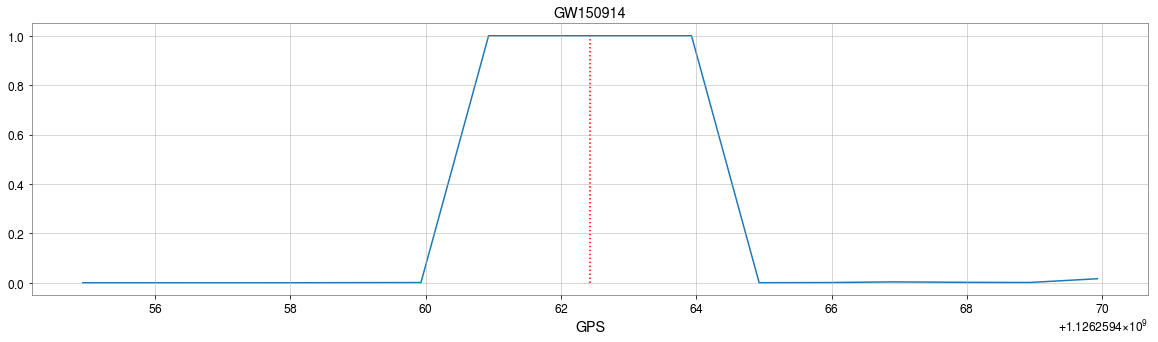
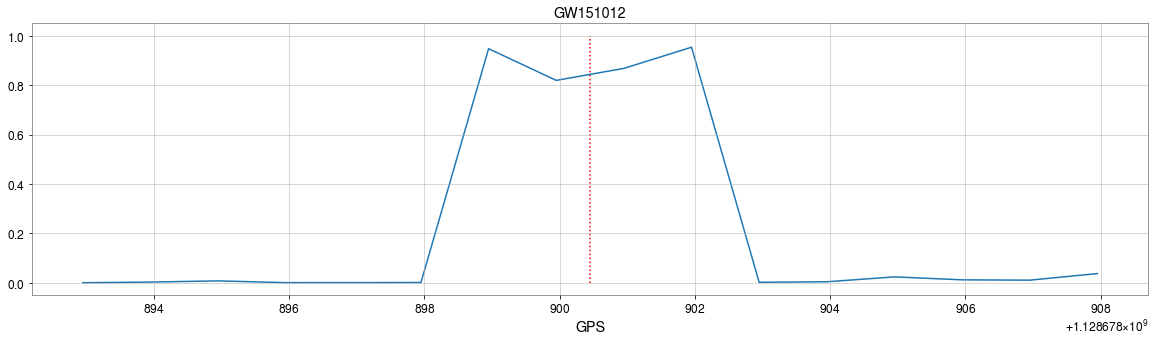
MFCNN
MFCNN

GPS time

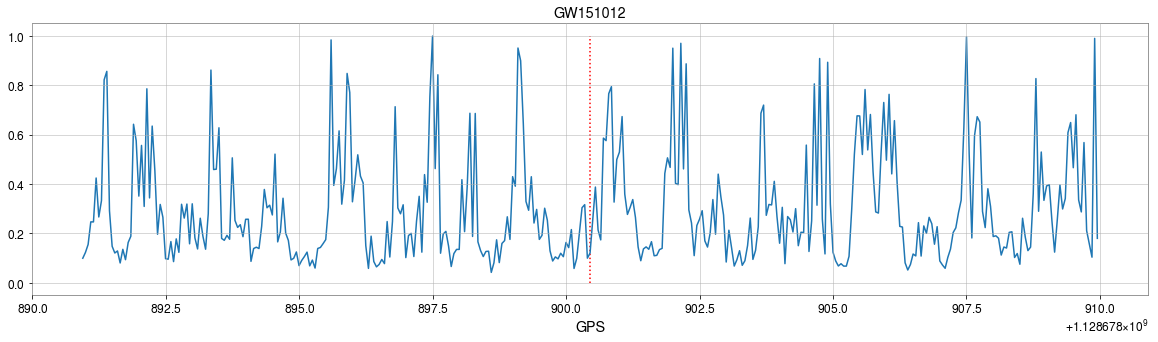
GW150914

GW151012

GPS time

Wang H, et al. PRD (2020)

Gravitational Wave Detection

  • 改进并开发神经网络模型，以适应真实的引力波观测数据的任务
  • 匹配滤波算法当中的波形模板 \(\rightarrow\) 卷积层中的卷积核权重参数
  • Matched-filtering layer (匹配滤波感知层)
  • 可以准确探测到 GWTC-1 中的 11 个真实引力波事件，甚至包括 GW170817
  • 可以直接应用于空间引力波数据场景，探测 MBHBs
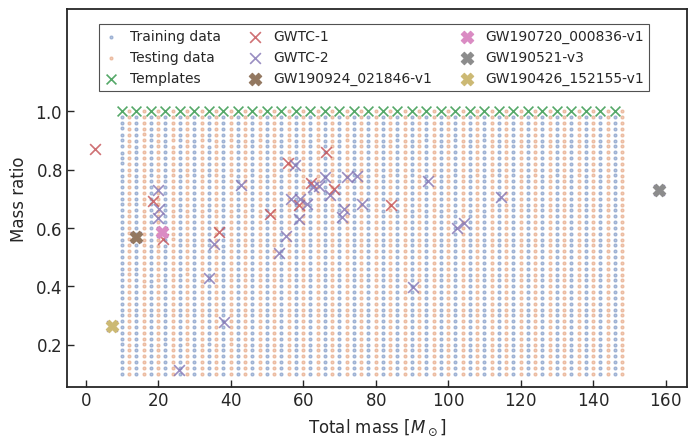
GW170817
GW190412
GW190814

mass distribution

Ruan WH, Wang H, et al. PLB (2023)

Matched-filtering Convolutional Neural Network (MFCNN)

Wang H, et al. PRD (2020)

Gravitational Wave Detection

  • 改进并开发神经网络模型，以适应真实的引力波观测数据的任务
  • 匹配滤波算法当中的波形模板 \(\rightarrow\) 卷积层中的卷积核权重参数
  • Matched-filtering layer (匹配滤波感知层)
  • “神经网络化”的探测统计量 (匹配滤波信噪比)

Frequency domain

\langle h|h \rangle = 4\int^\infty_0\frac{\tilde{h}(f)\tilde{h}^*(f)}{S_n(f)}df
\langle d|h \rangle (t) = 4\int^\infty_0\frac{\tilde{d}(f)\tilde{h}^*(f)}{S_n(f)}e^{2\pi ift}df

(whitening)

Time domain

(normalizing)

(matched-filtering)

\langle h|h \rangle \sim [\bar{h}(t) \ast \bar{h}(-t)]|_{t=0}
\langle d|h \rangle (t) \sim \,\bar{d}(t)\ast\bar{h}(-t)

where \(S_n(|f|)\) is the one-sided average PSD of \(d(t)\)

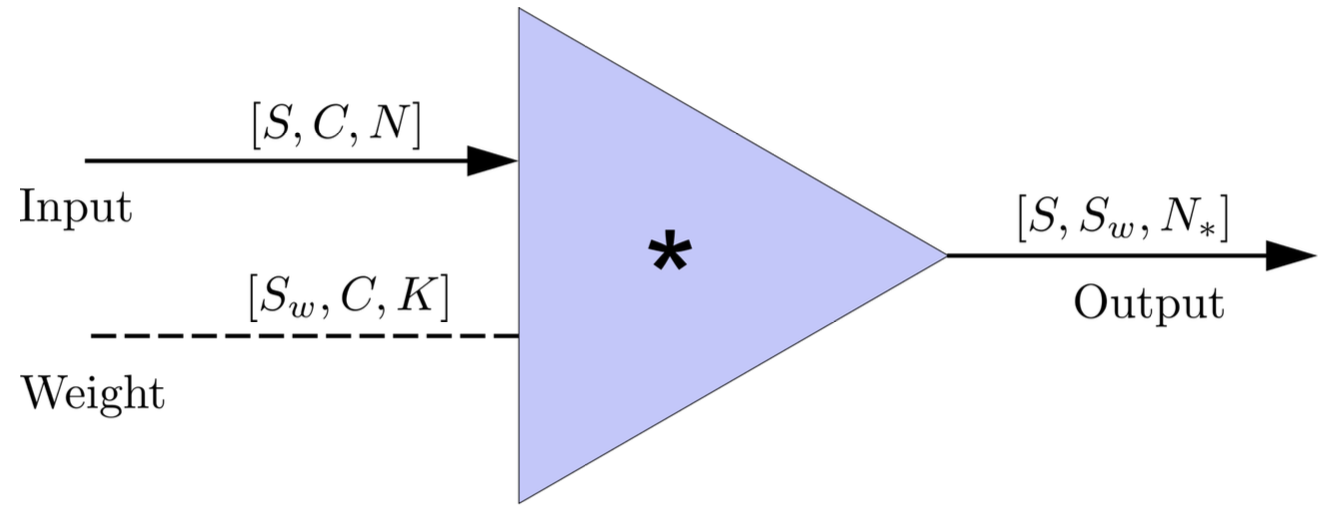
\bar{S_n}(t)=\int^{+\infty}_{-\infty}S_n^{-1/2}(f)e^{2\pi ift}df
\left\{\begin{matrix} \bar{d}(t) = d(t) * \bar{S}_n(t) \\ \bar{h}(t) = h(t) * \bar{S}_n(t) \end{matrix}\right.

In the 1-D convolution (\(*\)), given input data with shape [batch size, channel, length] :

（A schematic illustration for a unit of convolution layer)

\int\tilde{x}_1(f) \cdot \tilde{x}_2(f) e^{2\pi ift}df= x_1(t)*x_2(t)
x_1(t)*x_2^*(-t) = x_1(t)\star x_2(t)
\int\tilde{x}_1(f) \cdot \tilde{x}^*_2(f) e^{2\pi ift}df= x_1(t)\star x_2(t)

Matched-filtering Convolutional Neural Network (MFCNN)

Wang H, et al. PRD (2020)

Gravitational Wave Detection

  • 改进并开发神经网络模型，以适应真实的引力波观测数据的任务
  • 匹配滤波算法当中的波形模板 \(\rightarrow\) 卷积层中的卷积核权重参数
  • Matched-filtering layer (匹配滤波感知层)
  • “神经网络化”的探测统计量 (匹配滤波信噪比)
  • Insight: 引力波信号处理 \(\rightarrow\) 智能引力波信号处理

Matched-filtering Convolutional Neural Network (MFCNN)

Wang H, et al. PRD (2020)

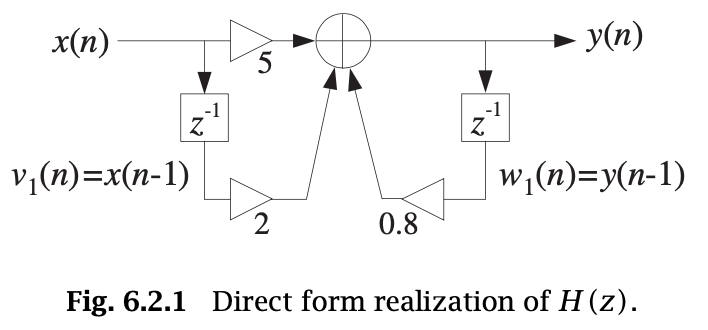
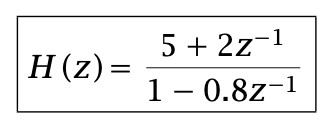
An example of transfer function:

CNN

RNN

Gravitational Wave Detection

  • 改进并开发神经网络模型，以适应真实的引力波观测数据的任务
  • 匹配滤波算法当中的波形模板 \(\rightarrow\) 卷积层中的卷积核权重参数
  • Matched-filtering layer (匹配滤波感知层)
  • “神经网络化”的探测统计量 (匹配滤波信噪比)
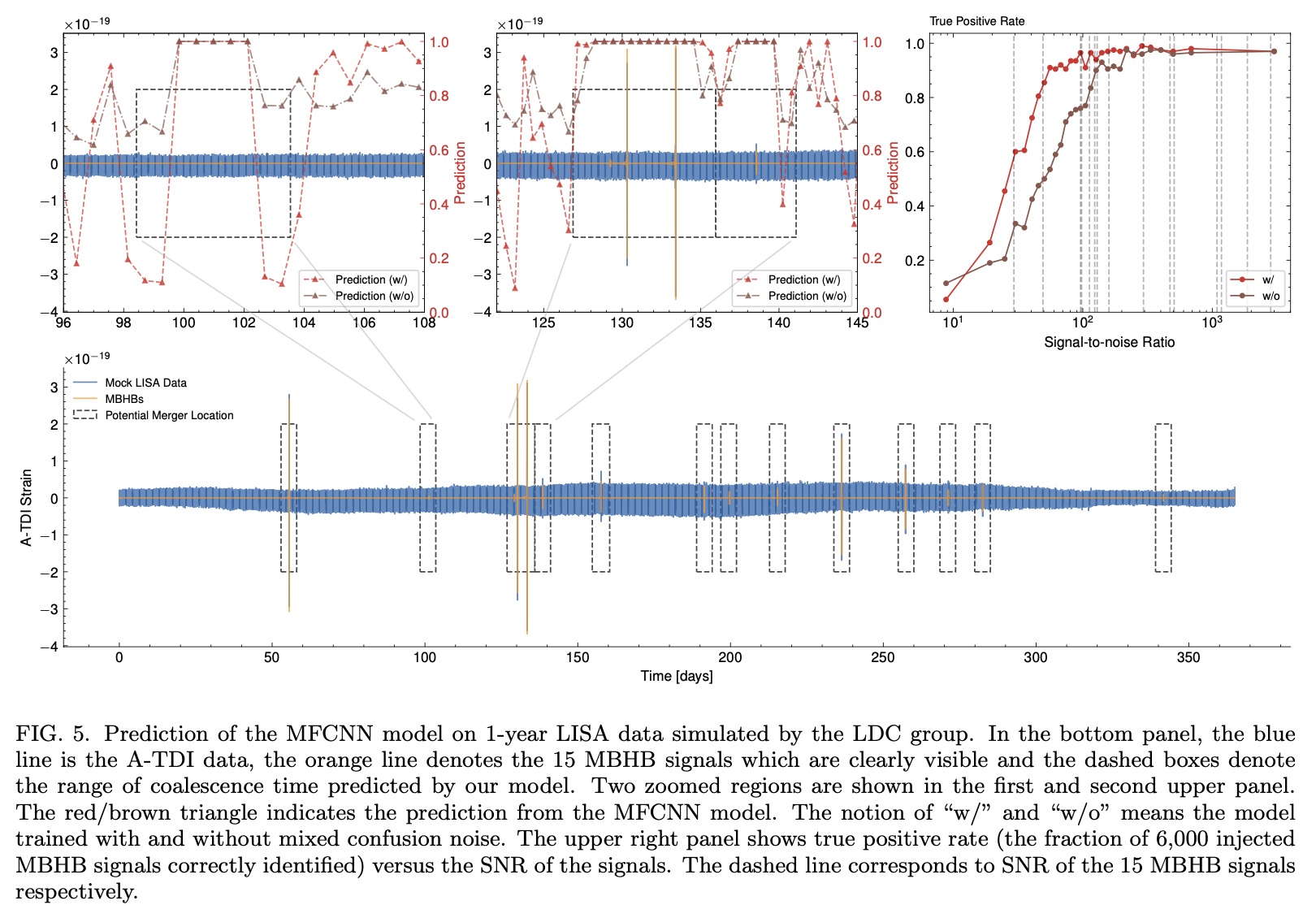
  • The first machine learning gravitational wave signal search challenge (MLGWSC1) https://github.com/gwastro/ml-mock-data-challenge-1

H1

L1

search scope

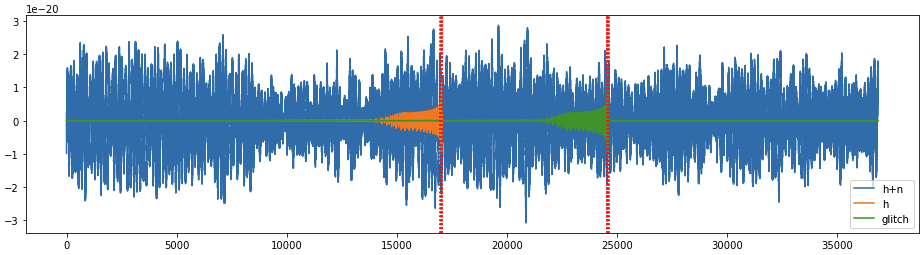
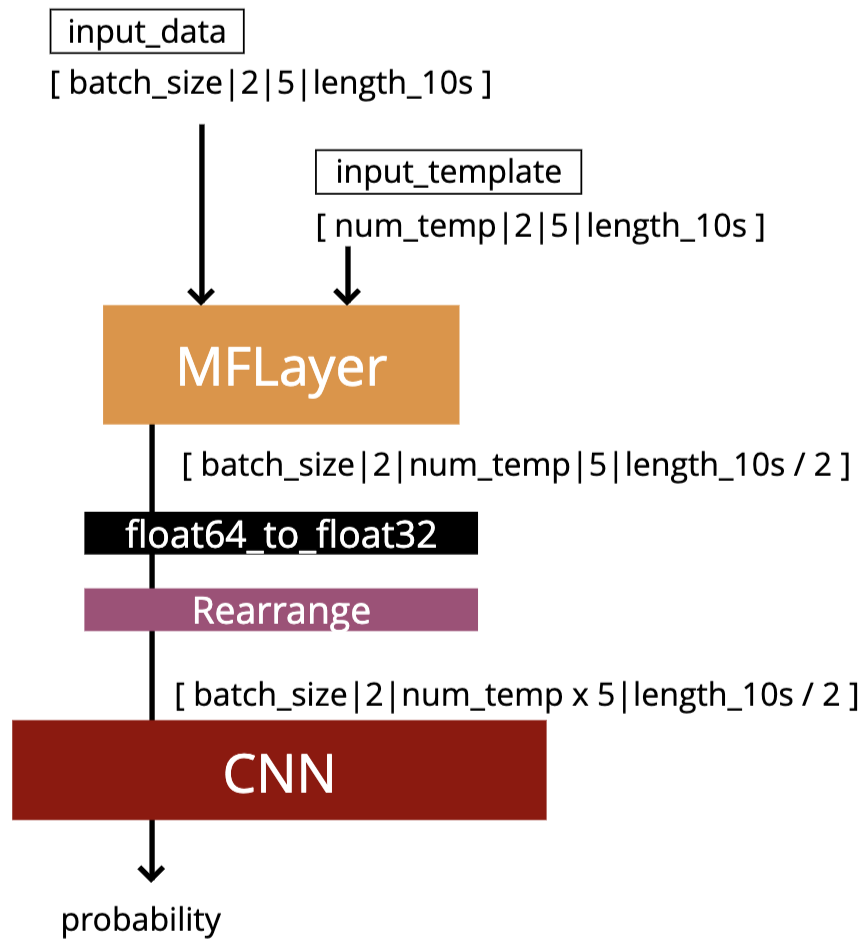
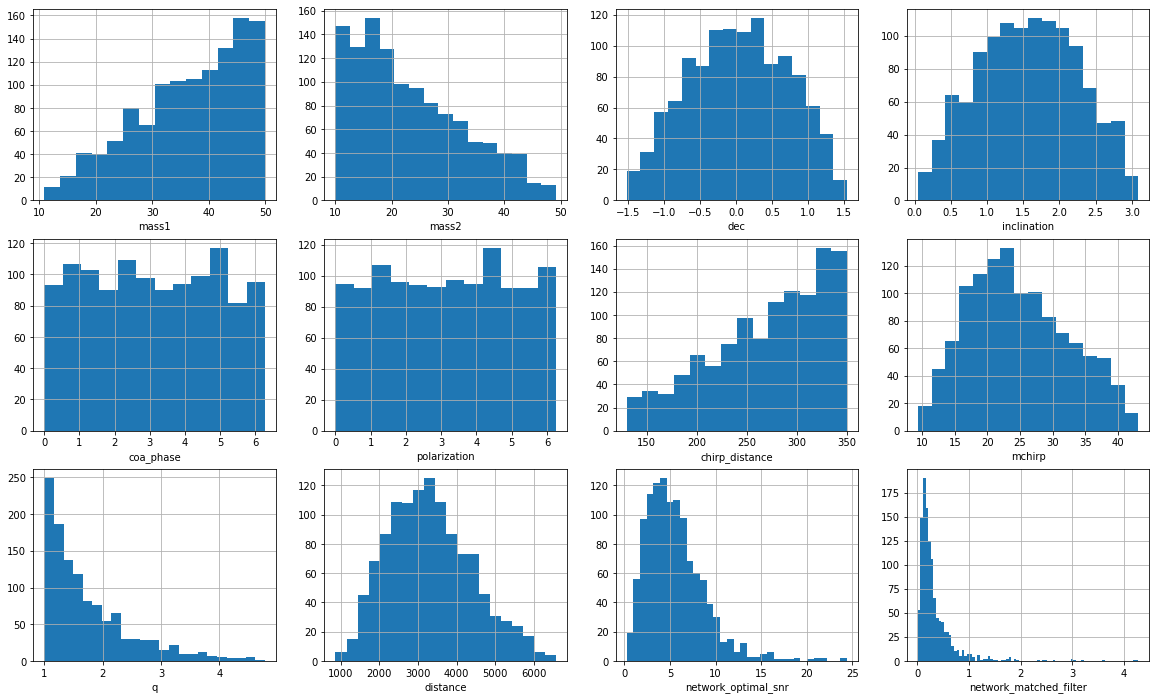
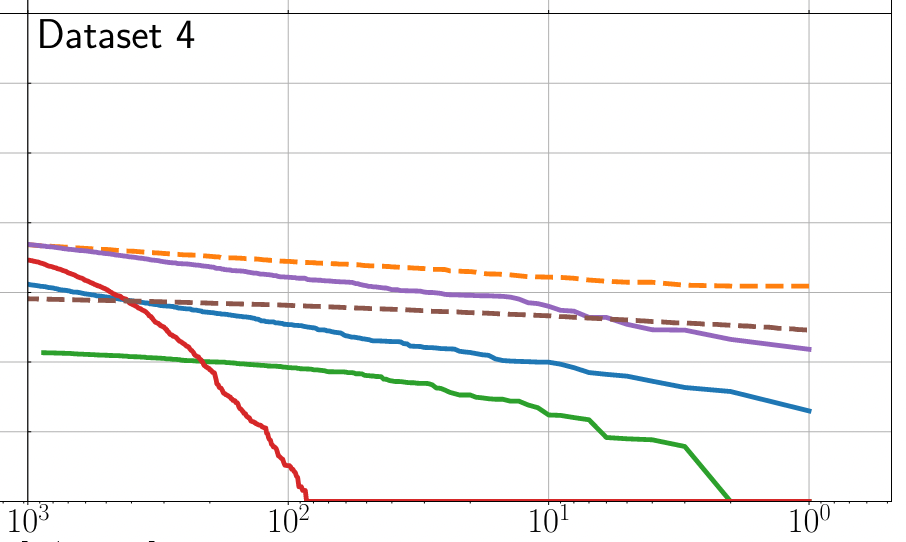
(MFCNN group) Wang H, et al. PRD (2023)

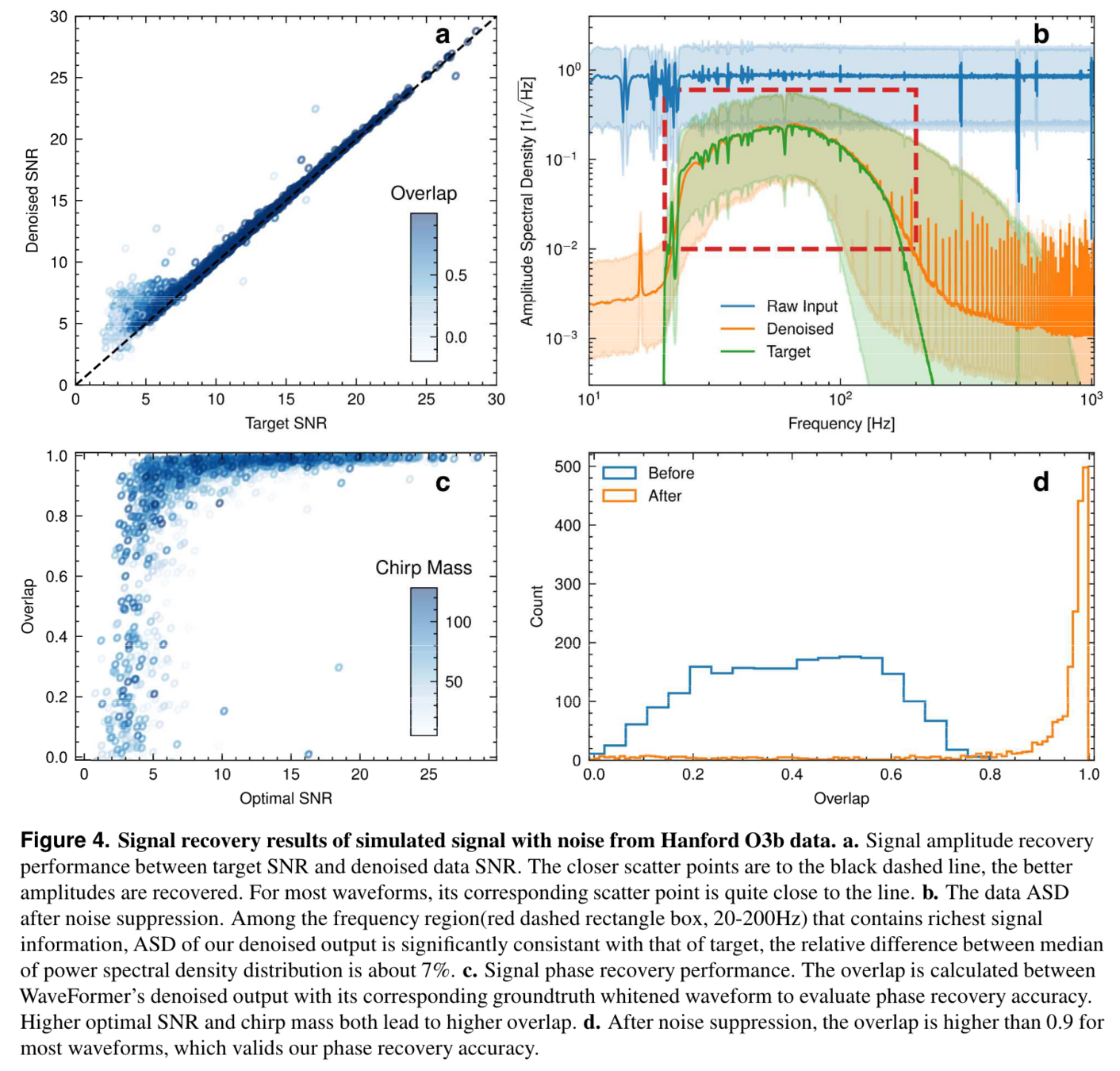
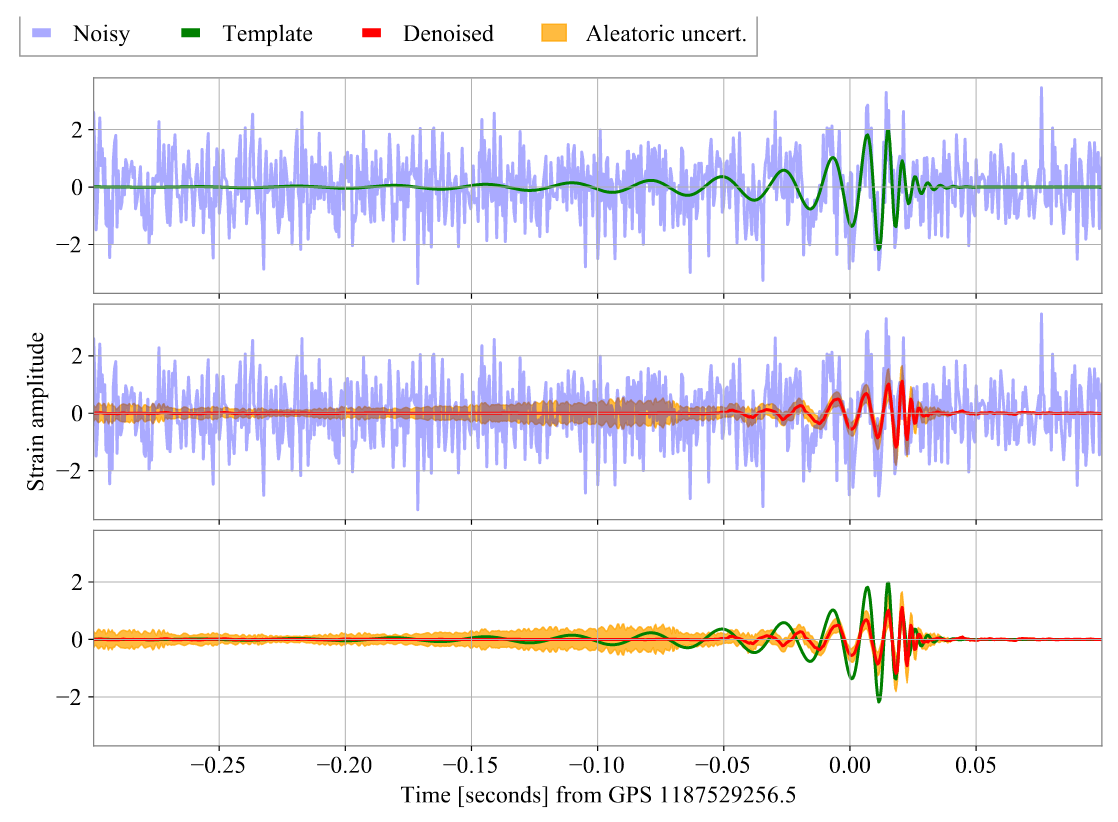
Gravitational Wave Observational Data Denoising

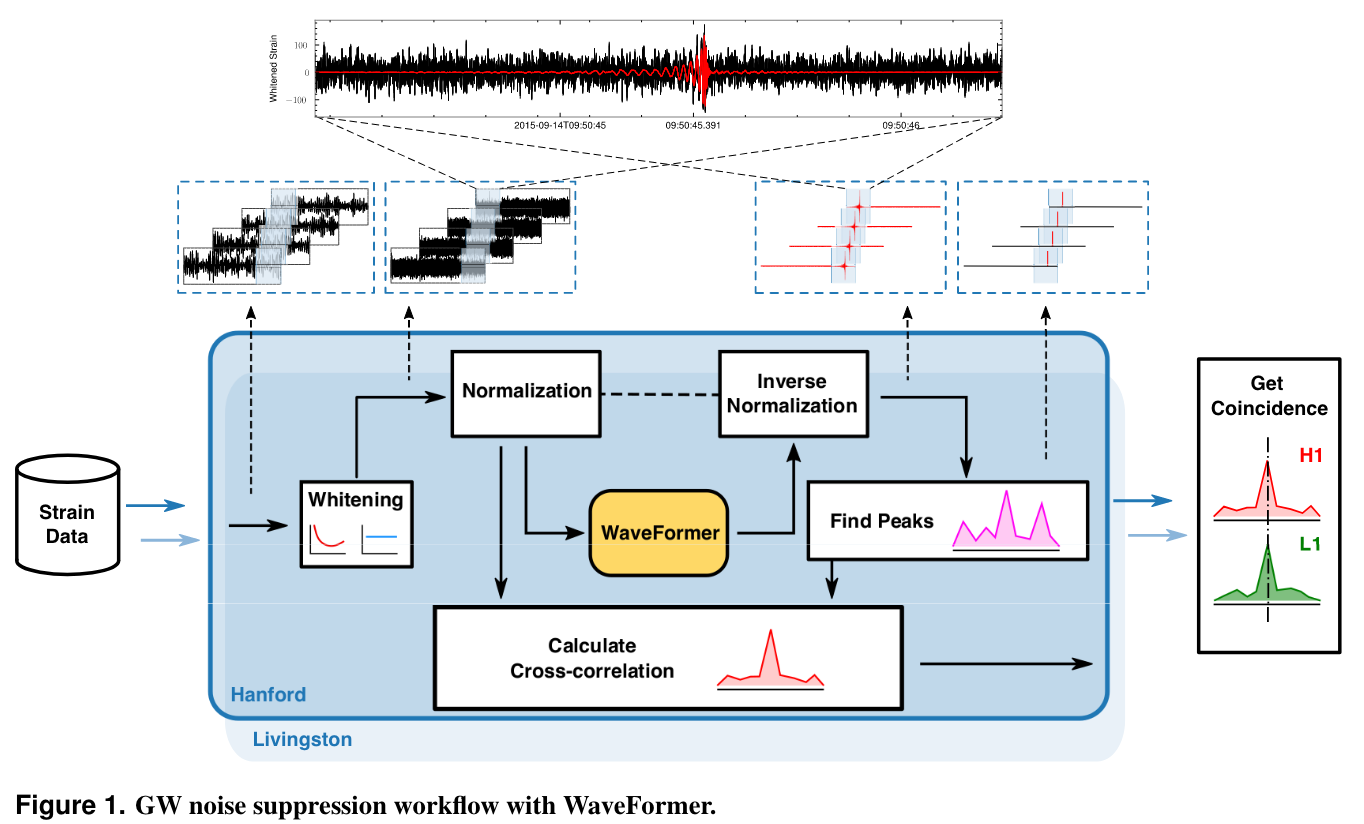
  • Billion-scale transformer-based model (WaveFormer)
    • Suppression on realistic noise, and
    • Recovery of injections / GW events
  • ​Application:
    • Data quality improvement

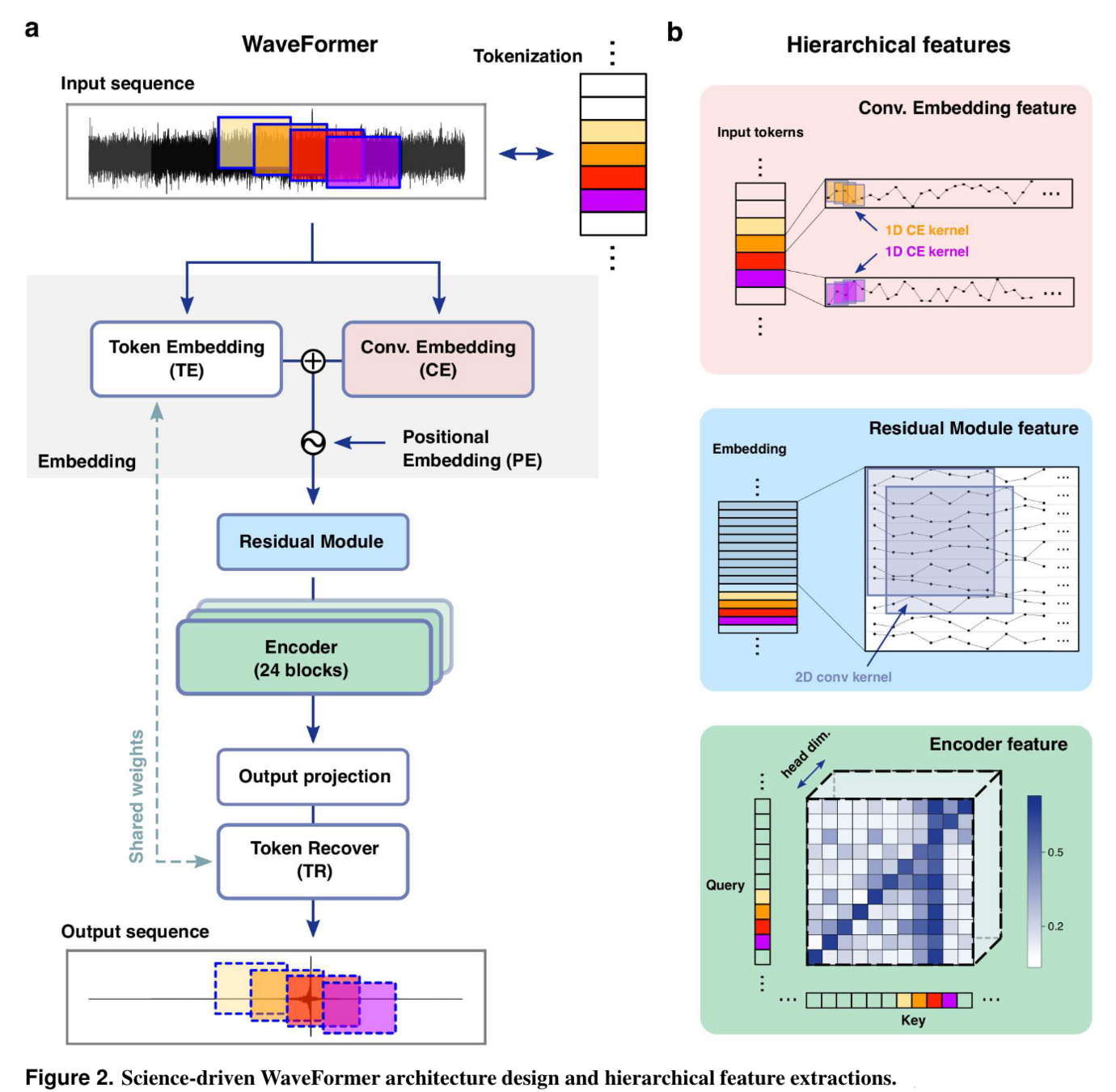
arXiv:2212.14283, DOI: 10.21203/rs.3.rs-2452860/v1

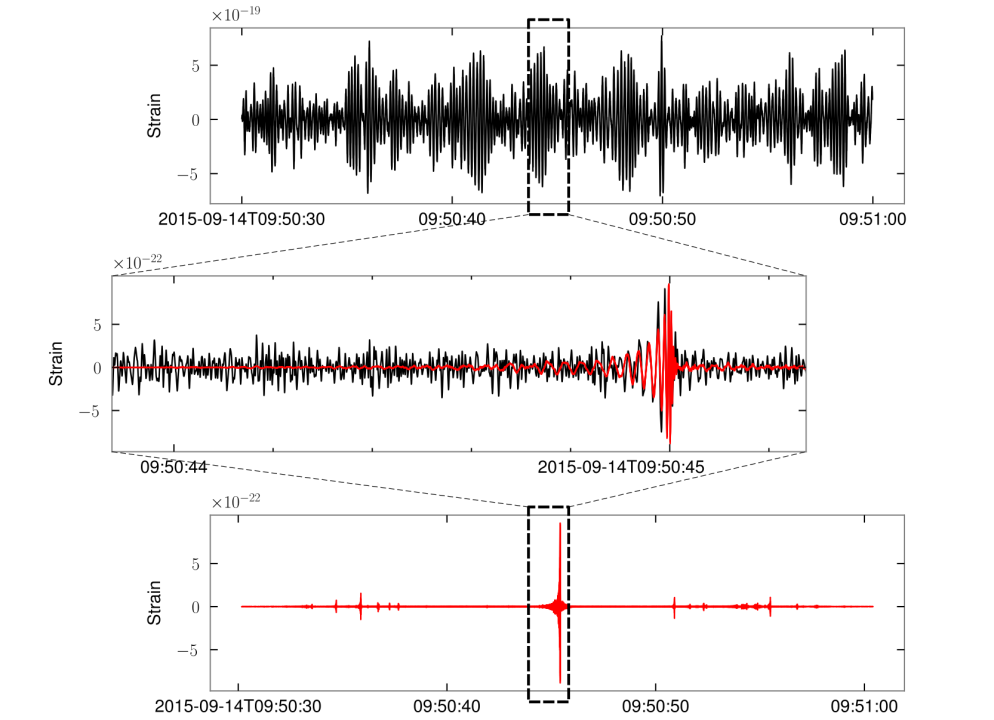
BEFORE

AFTER

Gravitational Wave Observational Data Denoising

  • Billion-scale transformer-based model (WaveFormer)
    • Suppression on realistic noise, and
    • Recovery of injections / GW events
  • ​Application:
    • Data quality improvement

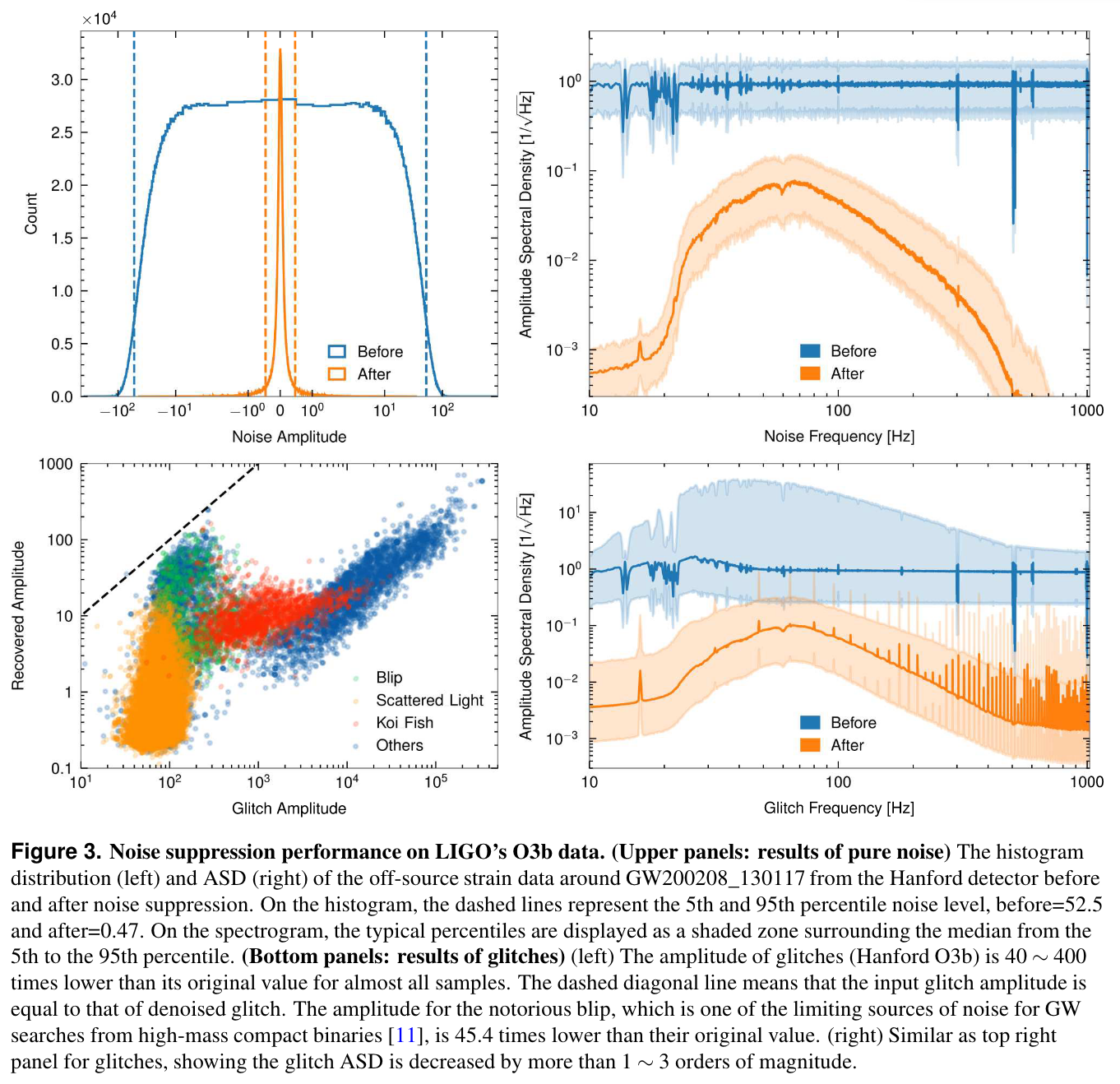
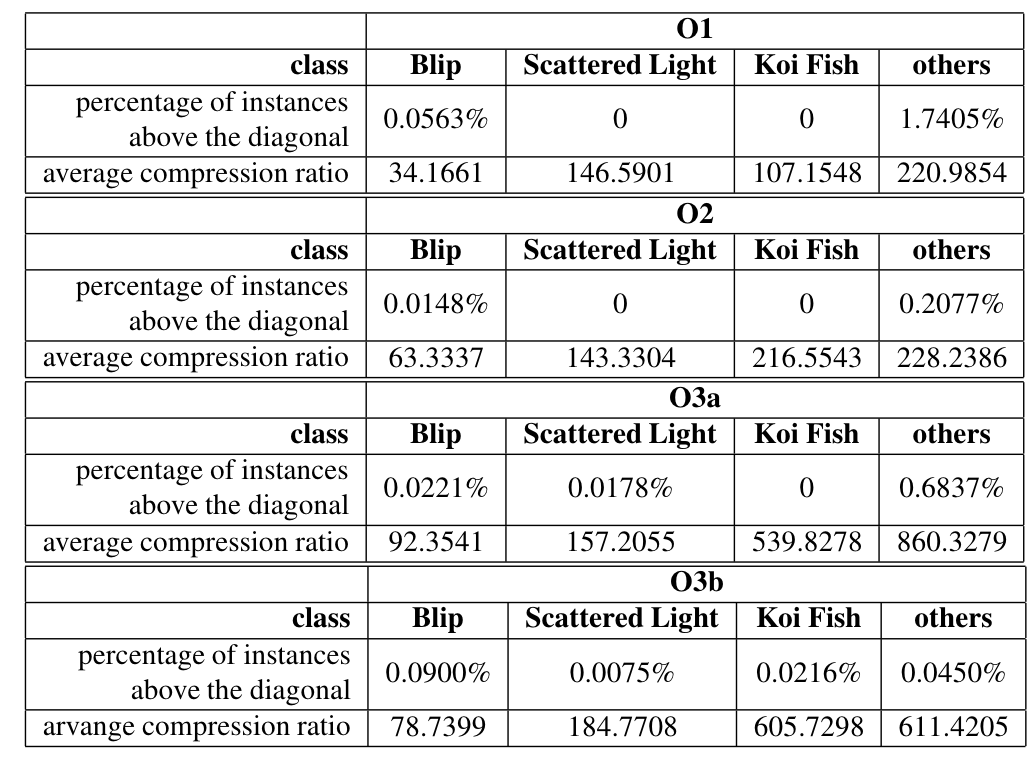
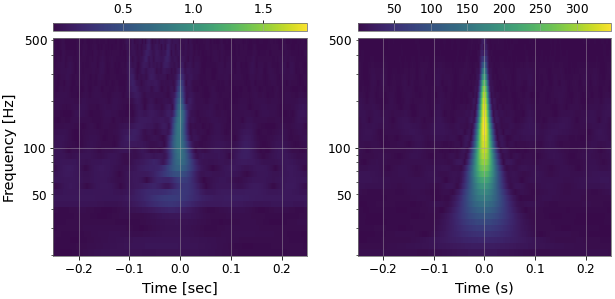
BEFORE

AFTER

Gravitational Wave Observational Data Denoising

  • Billion-scale transformer-based model (WaveFormer)
    • Suppression on realistic noise, and
    • Recovery of injections / GW events
  • ​Application:
    • Data quality improvement

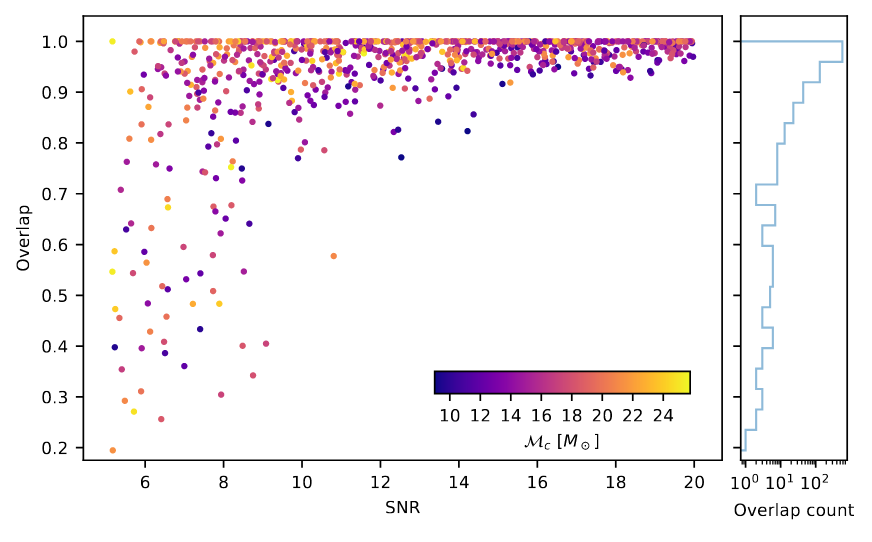
Bacon P. et al.  arXiv: 2205.13513

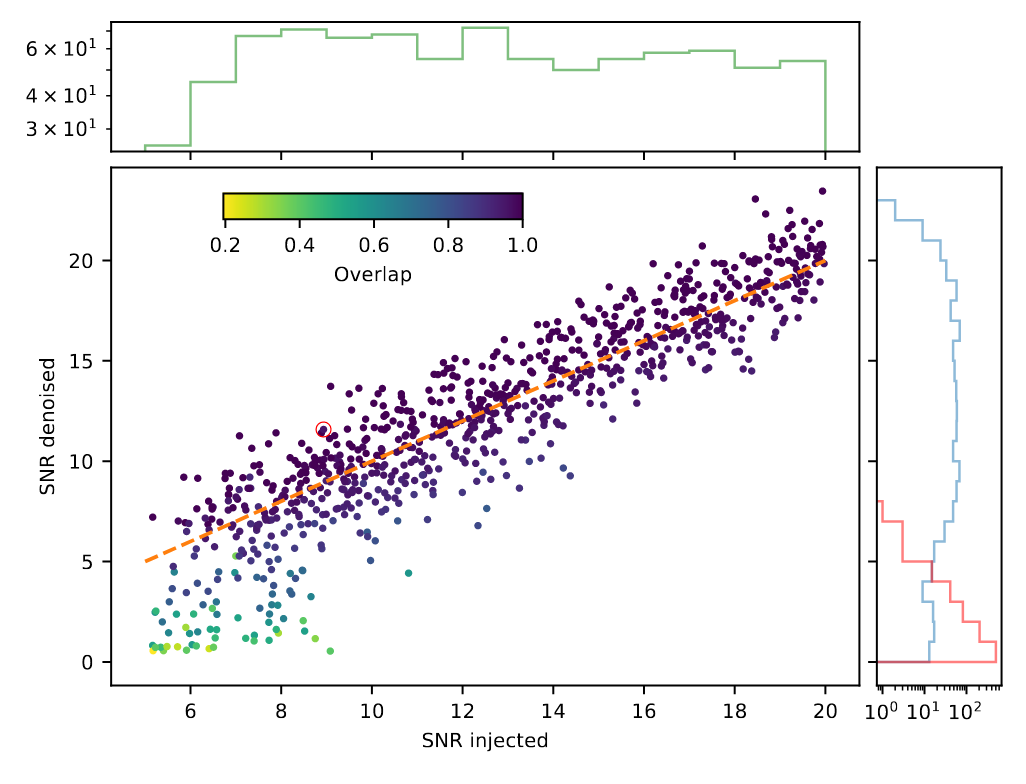
Gravitational Wave Observational Data Denoising

  • Billion-scale transformer-based model (WaveFormer)
    • Suppression on realistic noise, and
    • Recovery of injections / GW events
  • ​Application:
    • Data quality improvement

Bacon P. et al.  arXiv: 2205.13513

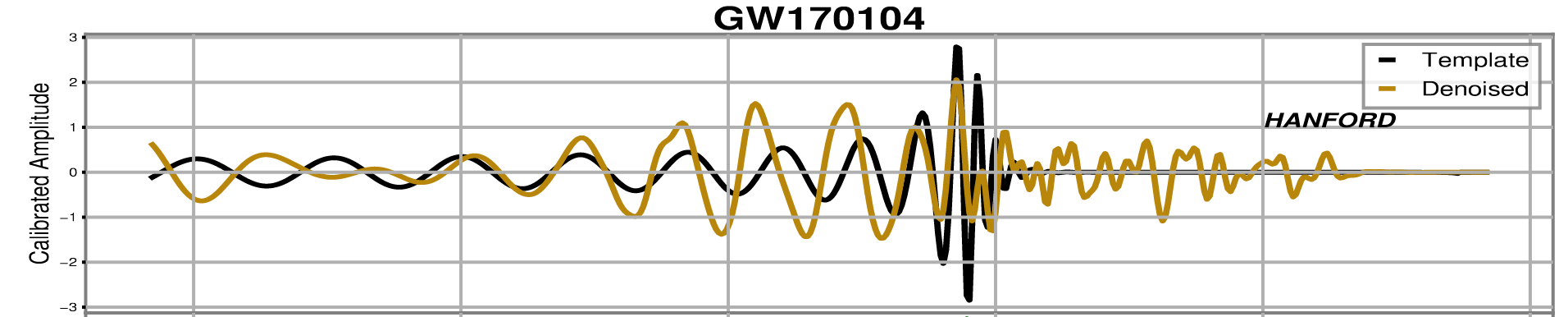
Murali C & Lumley D. arXiv: 2210.01718

Wei W and Huerta E A. PLB 2020

Chatterjee C, Wen L, et al. PRD 2021

arXiv:2212.14283, DOI: 10.21203/rs.3.rs-2452860/v1

GW170823

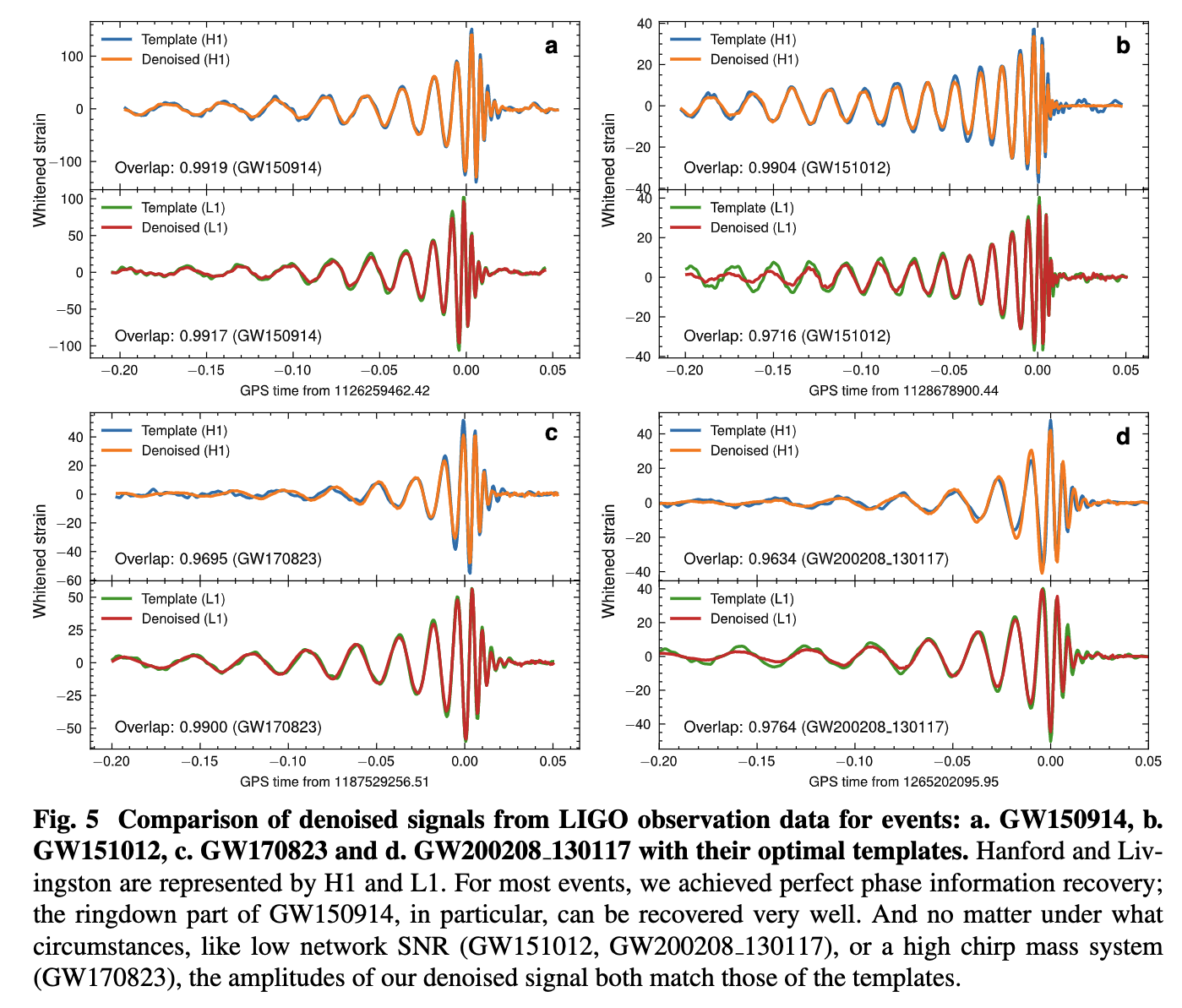
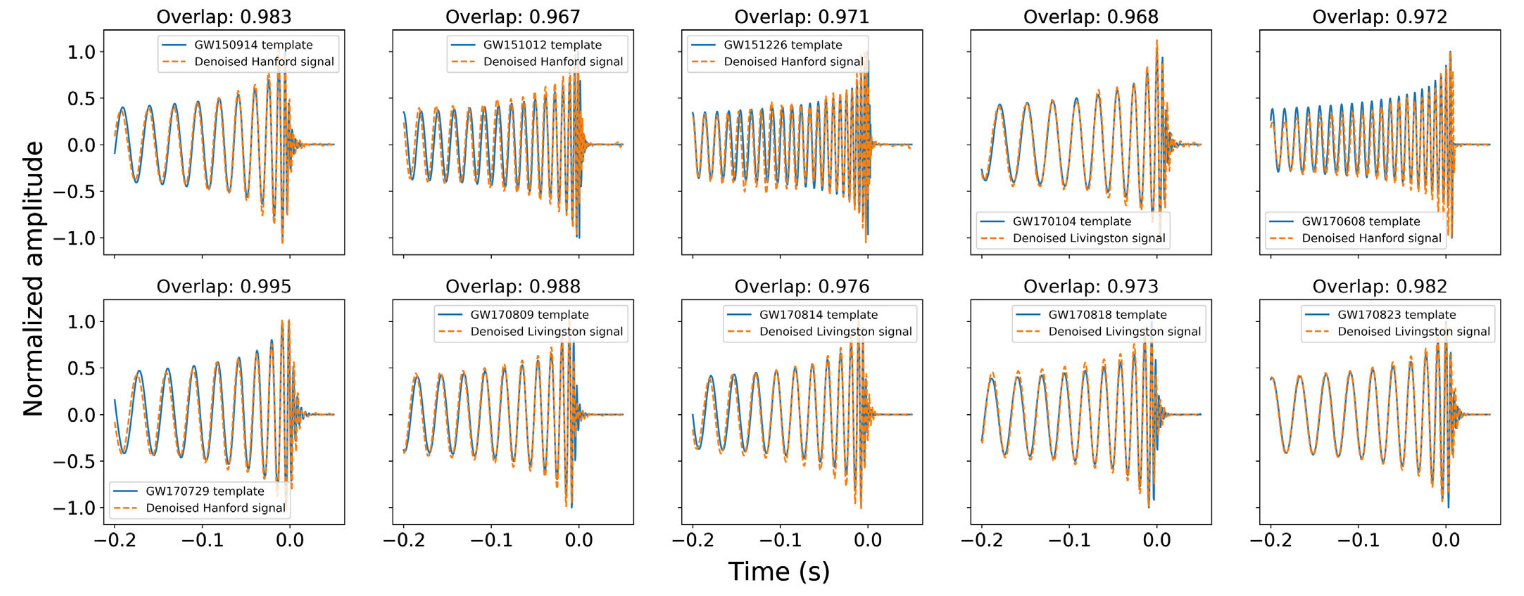
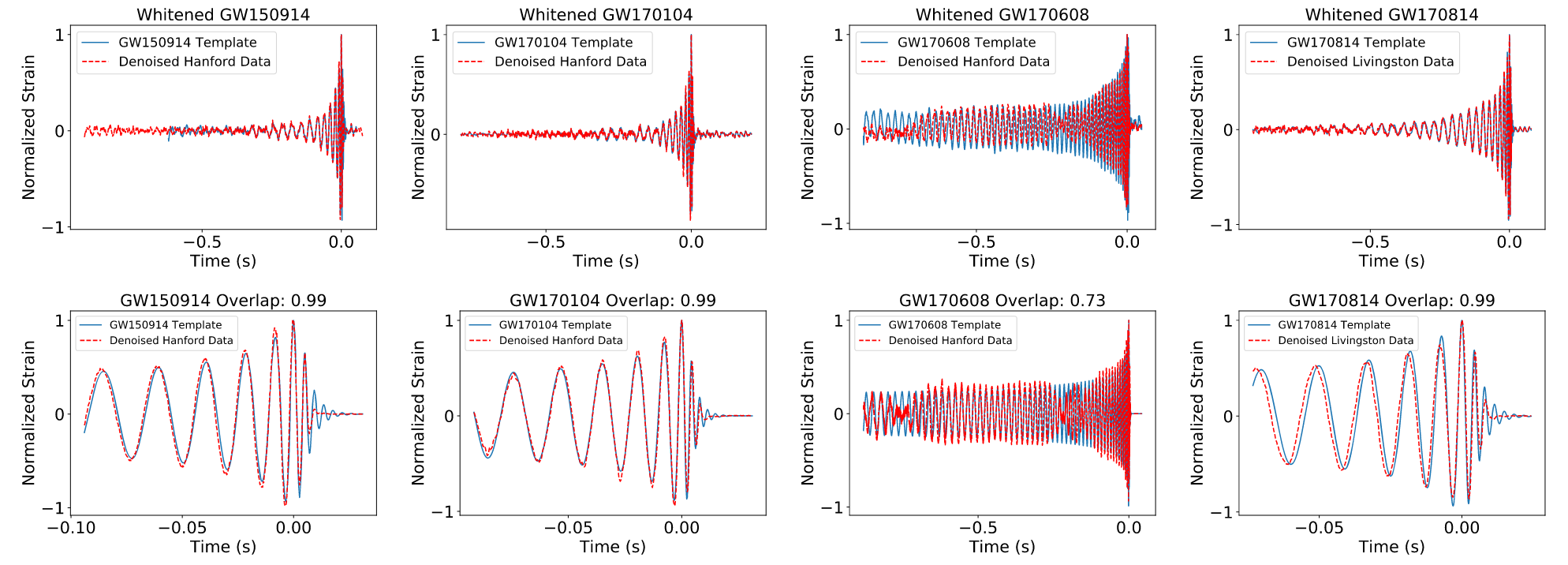
Gravitational Wave Observational Data Denoising

  • Billion-scale transformer-based model (WaveFormer)
    • Suppression on realistic noise, and
    • Recovery of injections / GW events
    ​Application:
    • Data quality improvement

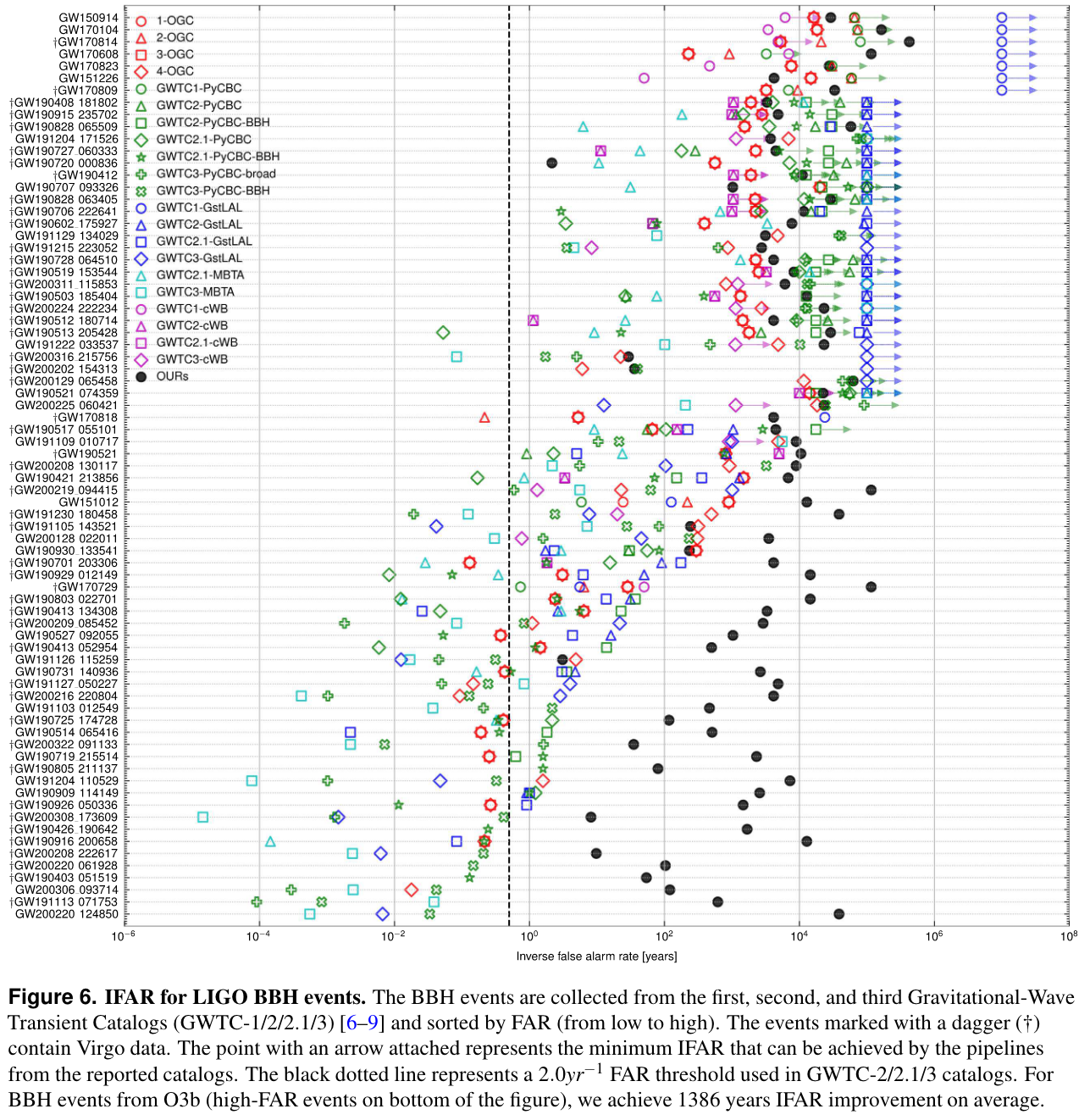
arXiv:2212.14283, DOI: 10.21203/rs.3.rs-2452860/v1

Outlook

  • Large Language Model (LLM) for GW data analysis.

WaveFormer

Transformer: 750x / 2yrs

Outlook

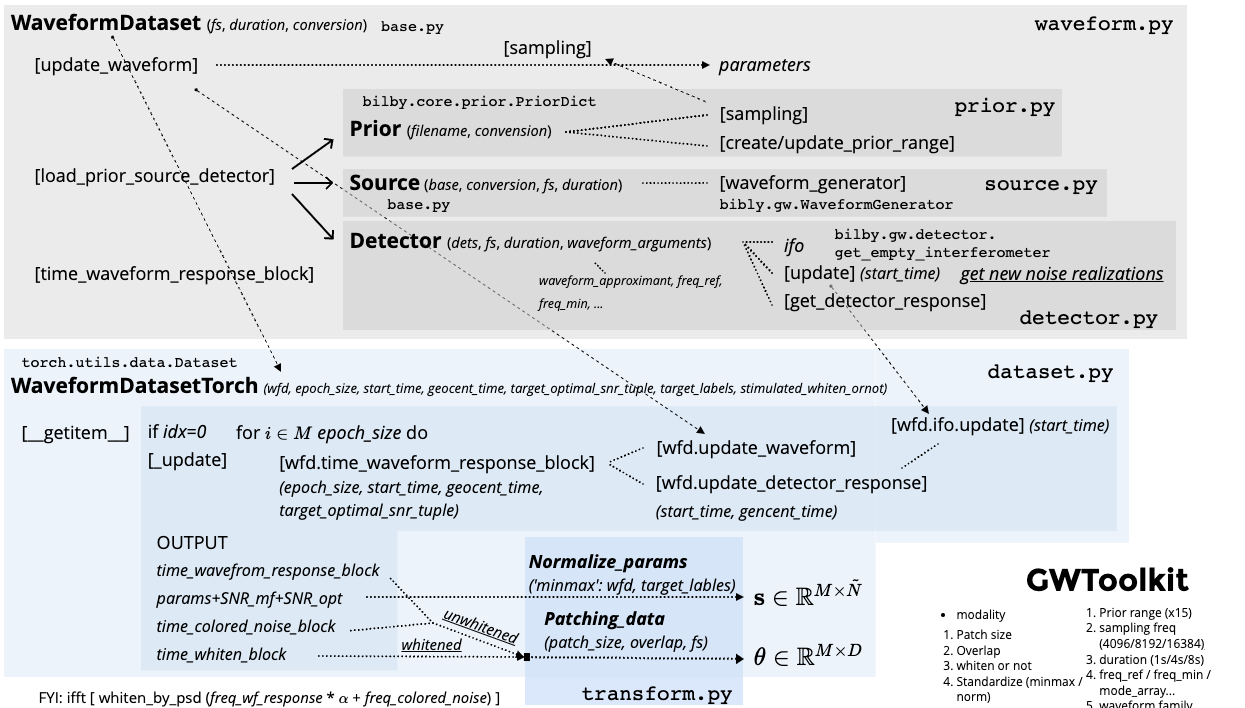
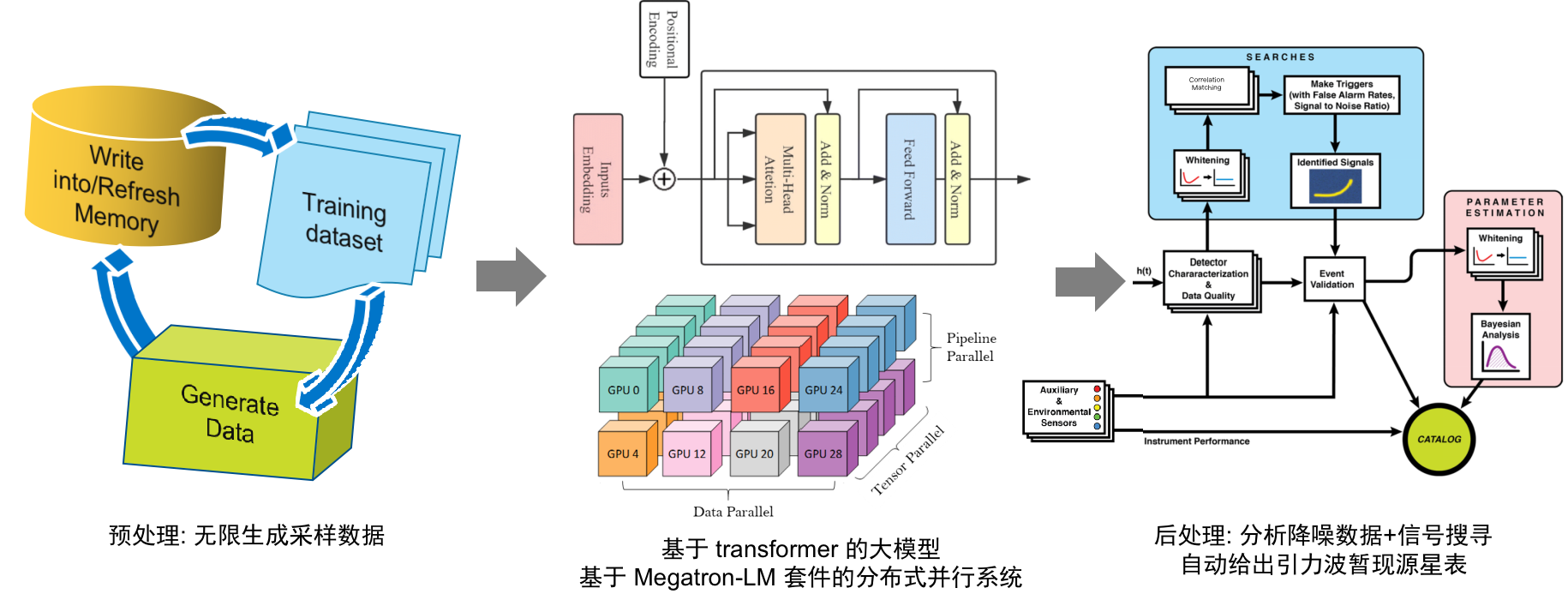
  • Large Language Model (LLM) for GW data analysis.
  • Software development: GWToolkit powered by Ray.

Outlook

  • Large Language Model (LLM) for GW data analysis.
  • Software development: GWToolkit powered by Ray.
  • Parameter estimation: "Curse of Dimensionality"
    • Multi-source events (overlapping signals / combining inference)

Recent Updates to Rapid PE

  • Pathak et al. (2210.02706). Rapid reconstruction of compact binary sources using meshfree approximation
  • Wofford et al. (2210.07912). Improving performance for GW PE with an efficient and highly-parallelized algorithm
  • Islam et al. (2210.16278). Factorized PE for Real-Time GW Inference
  • Digman & Cornish. (2212.04600). PE for Stellar-Origin Black Hole Mergers In LISA
  • Yelikar et al. (2301.01337). Low-latency PE enabled by a Gaussian likelihood approximation for RIFT
  • Wong et al. (2302.05333). Fast GW PE without compromises
  • Tiwari et al. (2303.01463). VARAHA: A Fast Non-Markovian sampler for estimating GW posteriors
  • Karnesis et al. (2303.02164). Eryn : A multi-purpose sampler for Bayesian inference
  • Fairhurst et al. (2304.03731). Fast inference of binary merger properties using the information encoded in the GW signal
  • ...

PRD 99, 124044 (2019)

Combining inferences from multiple sources

arXiv: 2211.01304

for _ in range(num_of_audiences):
    print('Thank you for your attention! 🙏')

This slide: https://slides.com/iphysresearch/gr2023

Outlook

  • Large Language Model (LLM) for GW data analysis.
  • Software development: GWToolkit powered by Ray.
  • Parameter estimation: "Curse of Dimensionality"
    • Multi-source events (overlapping signals / combining inference)

Recent Updates to Rapid PE

  • Pathak et al. (2210.02706). Rapid reconstruction of compact binary sources using meshfree approximation
  • Wofford et al. (2210.07912). Improving performance for GW PE with an efficient and highly-parallelized algorithm
  • Islam et al. (2210.16278). Factorized PE for Real-Time GW Inference
  • Digman & Cornish. (2212.04600). PE for Stellar-Origin Black Hole Mergers In LISA
  • Yelikar et al. (2301.01337). Low-latency PE enabled by a Gaussian likelihood approximation for RIFT
  • Wong et al. (2302.05333). Fast GW PE without compromises
  • Tiwari et al. (2303.01463). VARAHA: A Fast Non-Markovian sampler for estimating GW posteriors
  • Karnesis et al. (2303.02164). Eryn : A multi-purpose sampler for Bayesian inference
  • Fairhurst et al. (2304.03731). Fast inference of binary merger properties using the information encoded in the GW signal
  • ...

PRD 99, 124044 (2019)

Combining inferences from multiple sources

arXiv: 2211.01304

©Floor Broekgaarden (repo)

Gravitational Wave Astronomy

  • Looking towards the future of gravitational wave astronomy: O4 and beyond

LIGO-G2300554

AI for Gravitational Wave

  • 2016年，AlphaGo 第一版发表在了 Nature 杂志上

  • 2021年，AI预测蛋白质结构登上 Science、Nature 年度技术突破，潜力无穷

  • 2022年，DeepMind团队通过游戏训练AI发现矩阵乘法算法问题​

  • 《达摩院2022十大科技趋势》将 AI for Science 列为重要趋势

    • “人工智能成为科学家的新生产工具，催生科研新范式”

  • AI for Science：为科学带来了模型与数据双驱动的新的研究范式

    • AI + 数学、AI + 化学、AI + 医药、AI + 物理、AI + 天文 ...

AlphaGo 围棋机器人

AlphaTensor 发现矩阵算法

AlphaFold 蛋白质结构预测

Gravitational Wave Observational Data Denoising

  • 数据质量的提升是一个非常复杂的问题，超过 20 万个传感器通道的数据会决定引力波科学数据通道的质量

  • 降低引力波数据中非高斯的短时脉冲波干扰 (Glitch)，会有助于减少引力波信号误报率

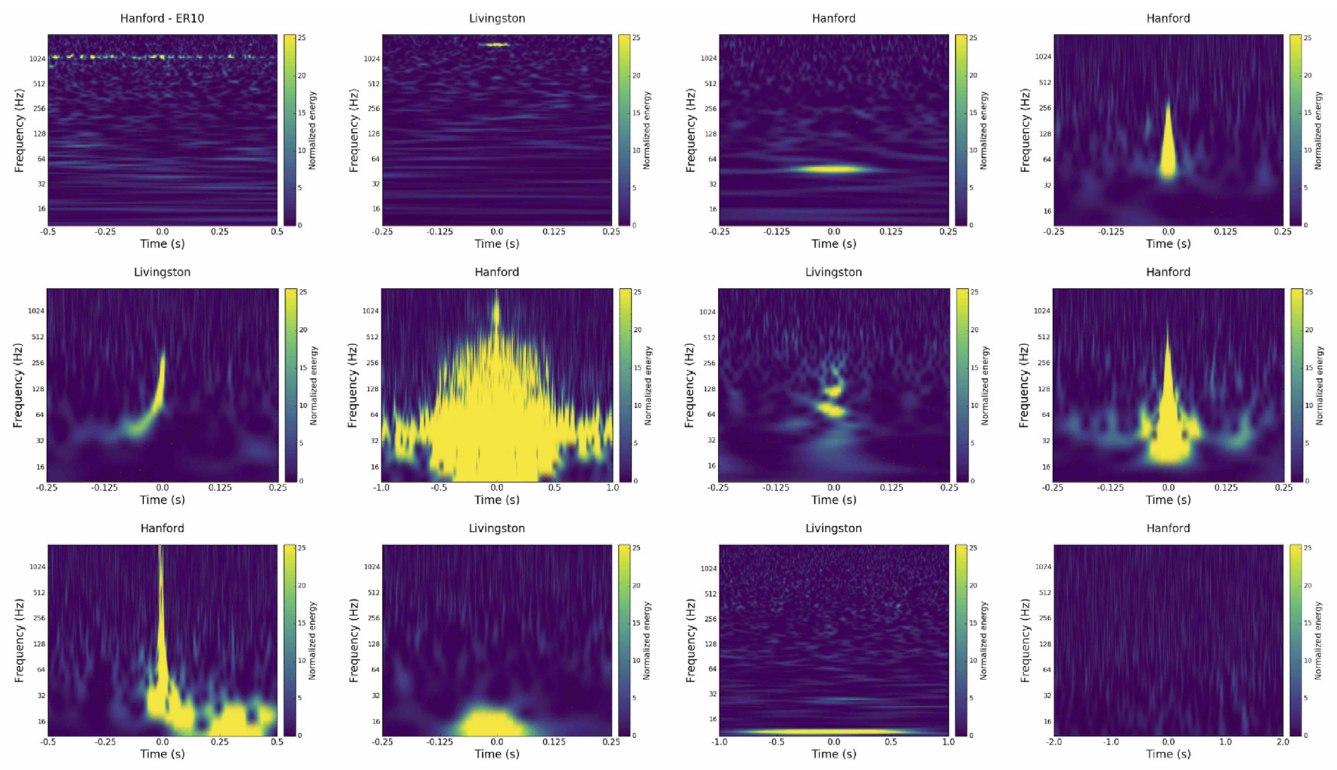
  • 引力波探测数据中去除 Glitch，是一个多分类问题

    • 传统机器学习算法​ ​Powell J, et al. CQG, 2015
    • 深度学习算法 Zevin, M, et al. CQG, 2017; Razzano M, Cuoco E. CQG, 2018; Ormiston R, et al. PRR, 2020
  • ​与其消除数据的非高斯性，何不直接把信号重构出来？这有助于发现理论预言之外的引力波信号！

    Extremely Loud                                  Helix                                          Koi Fish

Glitch cases

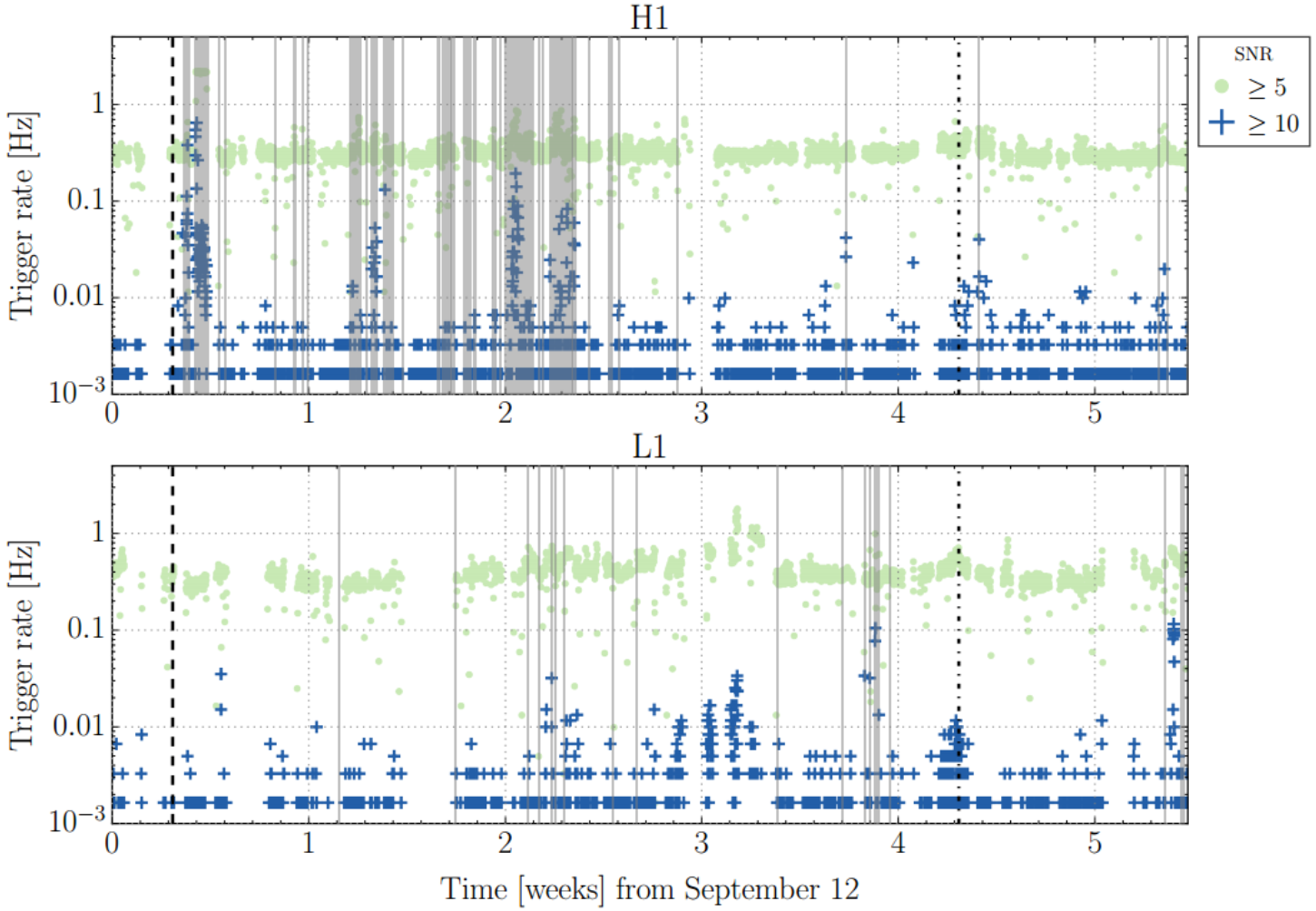
non-Gaussianess

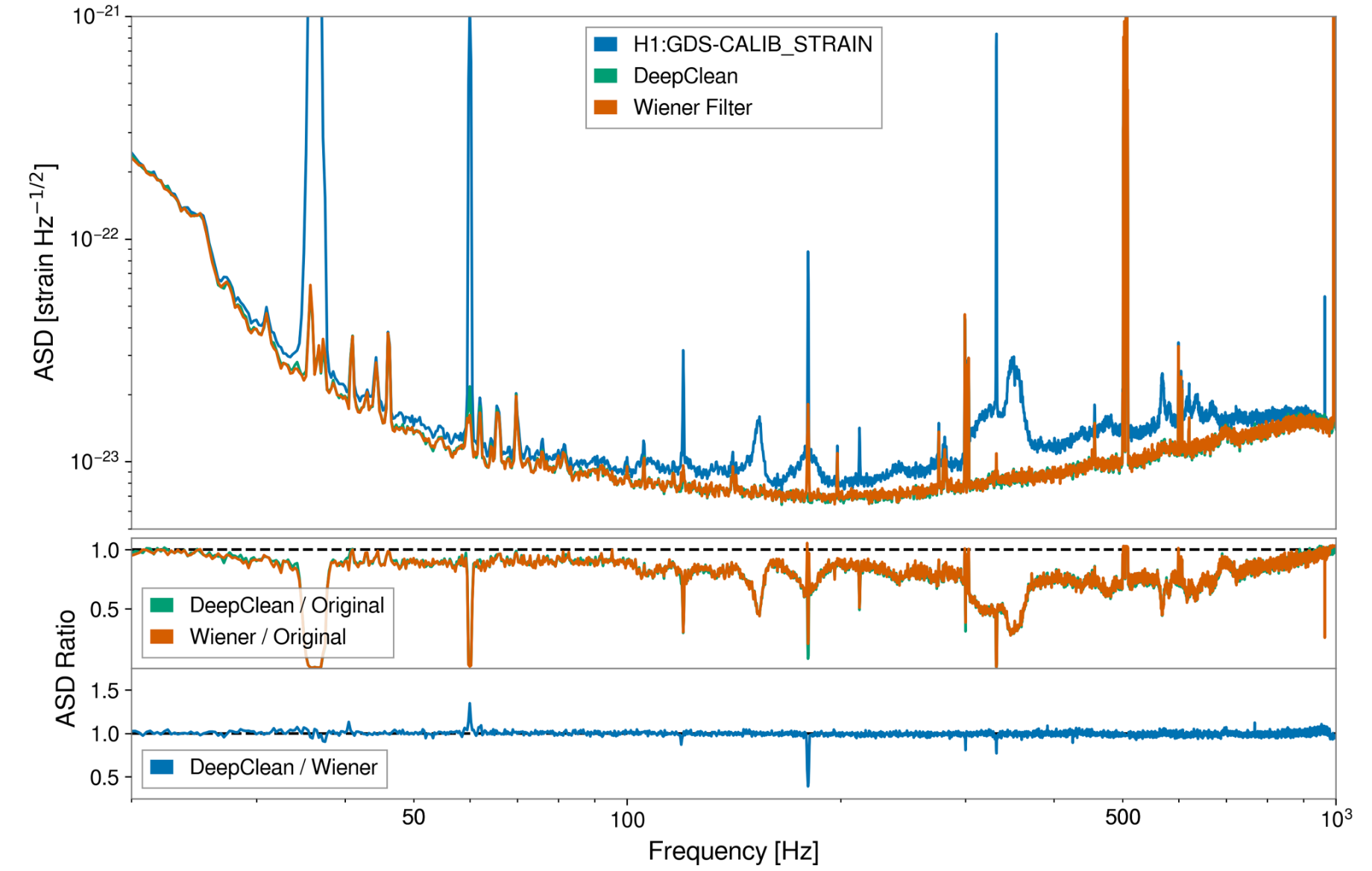
Ormiston R, et al. PRR, 2020