Deep Learning Networks & Gravitational Wave Signal Recognization

He Wang (王赫)  

[hewang@mail.bnu.edu.cn]

Department of Physics, Beijing Normal University

In collaboration with Zhou-Jian Cao

July 16th, 2019

Topological data analysis and deep learning: theory and signal applications - Part 4      ICIAM 2019

Outline

  • Introduction
    • Background
    • Related works
  • ConvNet Model
    • Our past attempts
  • ​ MF-ConvNet Model
    • Motivation
    • Matched-filtering in time domain
    • Matched-filtering ConvNet (MF-CNN)
  • Experiments & Results
    • Dataset & Training details
    • Recovering GW Events
    • Population property on O1
  • Summary

Introduction

  • Problems
    • Current matched filtering techniques are computationally expensive.
    • Non-Gaussian noise limits the optimality of searches.
    • Un-modelled signals?

A trigger generator \(\rightarrow\) Efficiency+ Completeness + Informative

Background

  • Solution:
    • Machine learning (deep learning)
    • ...

Introduction

  • Existing CNN-based approaches:
    • Daniel George & E. A. Huerta (2018)
    • Hunter Gabbard et al. (2018)
    • X. Li et al. (2018)
    • Timothy D. Gebhard et al. (2019)
 

Related works

Introduction

  • Our main contributions:
    • A brand new CNN-based architecture (MF-CNN)
    • Efficient training process (no bandpass, etc.)
    • Effective search methodology (4~5 days on O1)
    • Fully recognized and predicted precisely (<1s) for all GW events in O1/O2

ConvNet Model

  • Our past attempts

Past attempts on stimulated noise

  • The Influence of hyperparameters?

Convolutional neural network (ConvNet or CNN)

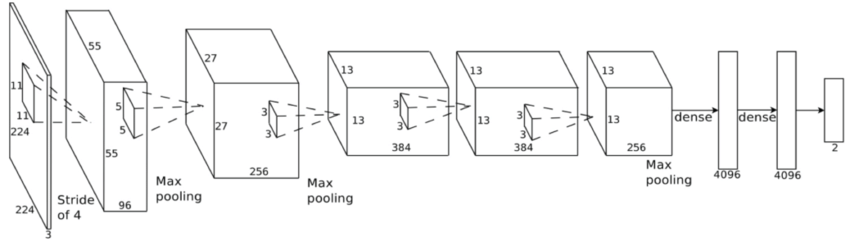
Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012)

ConvNet Model

  • The Influence of hyperparameters?

Feature extraction

Merge part

  • A glimpse of model Interpretability and Visualization

Convolutional neural network (ConvNet or CNN)

Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012)

Classification

Visualization for the high-dimensional feature maps of learned network in layers for bi-class using t-SNE.

Past attempts on stimulated noise

ConvNet Model

  • The Influence of hyperparameters?

Marginal!

Feature extraction

Convolutional neural network (ConvNet or CNN)

Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012)

Classification

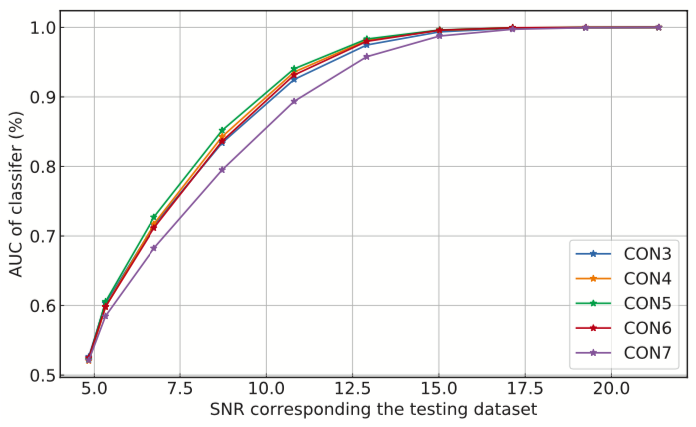
Effect of the number of the convolutional layers on signal recognizing accuracy.

Past attempts on stimulated noise

ConvNet Model

  • The Influence of hyperparameters?

Feature extraction

Convolutional neural network (ConvNet or CNN)

Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012)

Classification

Marginal!

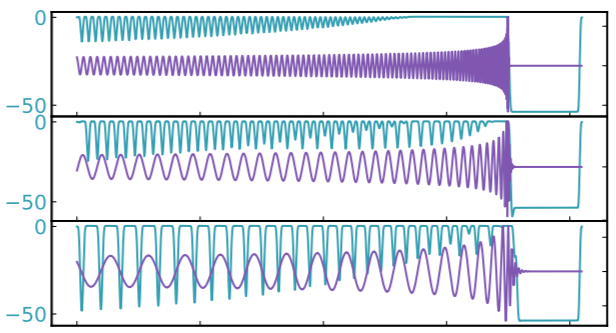
Visualization of the top activation on average at the \(n\)th layer projected back to time domain using the deconvolutional network approach

  • A glimpse of model Interpretability using Visualizing

Past attempts on stimulated noise

ConvNet Model

  • The Influence of hyperparameters?

Feature extraction

Peak of GW

Convolutional neural network (ConvNet or CNN)

Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012)

Classification

Marginal!

Occlusion Sensitivity

  • A glimpse of model Interpretability using Visualizing

Past attempts on stimulated noise

ConvNet Model

  • The Influence of hyperparameters?

Feature extraction

Convolutional neural network (ConvNet or CNN)

Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012)

A specific design of the architecture is needed.

 [as Timothy D. Gebhard et al. (2019)]

Classification

Marginal!

  • However, when on real noises from LIGO, this approach does not work that well. (too sensitive + hard to find the events)

Peak of GW

  • A glimpse of model Interpretability using Visualizing

Past attempts on stimulated noise

ConvNet Model

MF-ConvNet Model

  • Motivation

  • Matched-filtering in time domain

  • Matched-filtering ConvNet

(In preprint)

Motivation

Matched-filtering (cross-correlation with the templates) can be regarded as a convolutional layer with a set of predefined kernels.

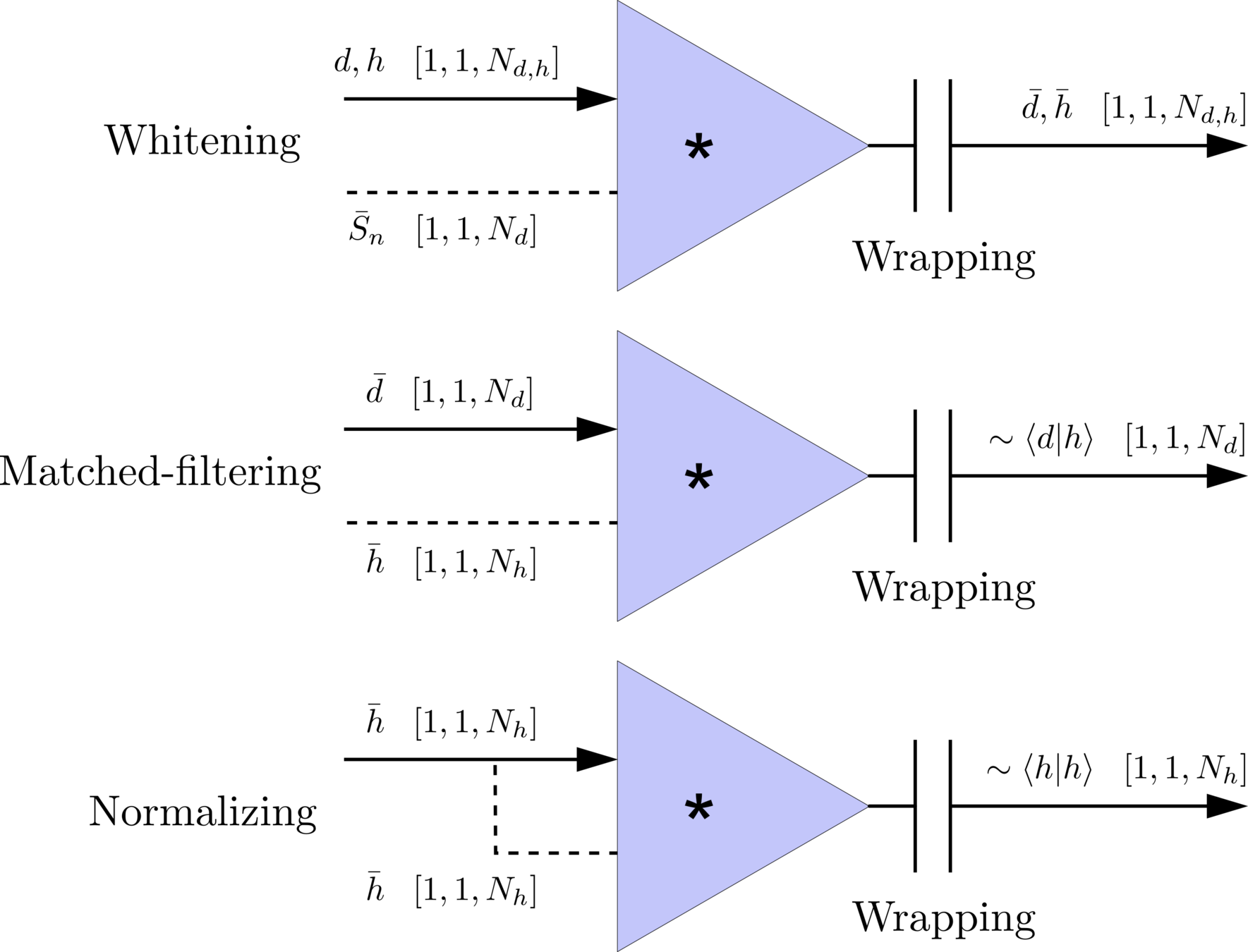
MF-ConvNet Model

Matched-filtering (cross-correlation with the templates) can be regarded as a convolutional layer with a set of predefined kernels.

Is it matched-filtering?

Motivation

MF-ConvNet Model

The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):

\rho^2(t)\equiv\frac{1}{\langle h|h \rangle}|\langle d|h \rangle(t)|^2
\langle d|h \rangle (t) = 4\int^\infty_0\frac{\tilde{d}(f)\tilde{h}^*(f)}{S_n(f)}e^{2\pi ift}df

Matched-filtering in time domain

Frequency domain

MF-ConvNet Model

\langle h|h \rangle = 4\int^\infty_0\frac{\tilde{h}(f)\tilde{h}^*(f)}{S_n(f)}df
\left\{\begin{matrix} \bar{d}(t) = d(t) * \bar{S}_n(t) \\ \bar{h}(t) = h(t) * \bar{S}_n(t) \end{matrix}\right.
\bar{S_n}(t)=\int^{+\infty}_{-\infty}S_n^{-1/2}(f)e^{2\pi ift}df
\langle d|h \rangle (t) \sim \,\bar{d}(t)\ast\bar{h}(-t)
\langle h|h \rangle \sim [\bar{h}(t) \ast \bar{h}(-t)]|_{t=0}
\rho^2(t)\equiv\frac{1}{\langle h|h \rangle}|\langle d|h \rangle(t)|^2
\langle d|h \rangle (t) = 4\int^\infty_0\frac{\tilde{d}(f)\tilde{h}^*(f)}{S_n(f)}e^{2\pi ift}df
\langle h|h \rangle = 4\int^\infty_0\frac{\tilde{h}(f)\tilde{h}^*(f)}{S_n(f)}df

(matched-filtering)

(normalizing)

Frequency domain

Time domain

where

(whitening)

\(S_n(|f|)\) is the one-sided average PSD of \(d(t)\)

Matched-filtering in time domain

MF-ConvNet Model

The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):

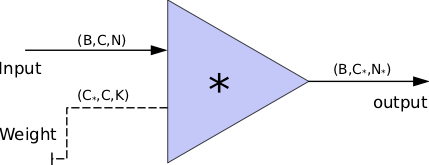
\rho^2(t)\equiv\frac{1}{\langle h|h \rangle}|\langle d|h \rangle(t)|^2
output[n, i, :] = \sum^{channel}_{j=0} input[n,j,:] \ast weight[i,j,:]

In the 1-D convolution (\(*\)), given input data with shape [batch size, channel, length] :

FYI:       \(N_\ast = \lfloor(N-K+2P)/S\rfloor+1\)

\bar{S_n}(t)=\int^{+\infty}_{-\infty}S_n^{-1/2}(f)e^{2\pi ift}df

Time domain

\left\{\begin{matrix} \bar{d}(t) = d(t) * \bar{S}_n(t) \\ \bar{h}(t) = h(t) * \bar{S}_n(t) \end{matrix}\right.
\langle d|h \rangle (t) \sim \,\bar{d}(t)\ast\bar{h}(-t)
\langle h|h \rangle \sim [\bar{h}(t) \ast \bar{h}(-t)]|_{t=0}

(matched-filtering)

(normalizing)

where

(whitening)

Matched-filtering in time domain

MF-ConvNet Model

The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):

\(S_n(|f|)\) is the one-sided average PSD of \(d(t)\)

（A schematic illustration for a unit of convolution layer)

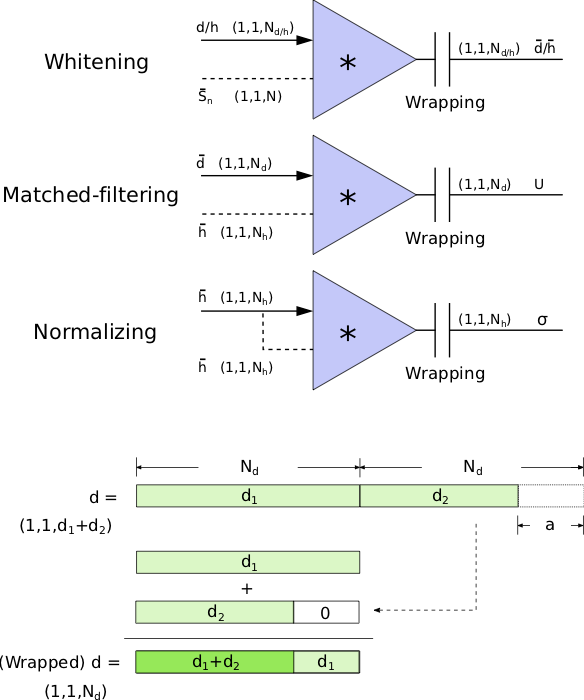
\rho^2(t)\equiv\frac{1}{\langle h|h \rangle}|\langle d|h \rangle(t)|^2
\bar{S_n}(t)=\int^{+\infty}_{-\infty}S_n^{-1/2}(f)e^{2\pi ift}df

Time domain

\left\{\begin{matrix} \bar{d}(t) = d(t) * \bar{S}_n(t) \\ \bar{h}(t) = h(t) * \bar{S}_n(t) \end{matrix}\right.
\langle d|h \rangle (t) \sim \,\bar{d}(t)\ast\bar{h}(-t)
\langle h|h \rangle \sim [\bar{h}(t) \ast \bar{h}(-t)]|_{t=0}

(matched-filtering)

(normalizing)

where

(whitening)

Matched-filtering in time domain

MF-ConvNet Model

The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):

\(S_n(|f|)\) is the one-sided average PSD of \(d(t)\)

Wrapping (like the pooling layer)

Architechture

\rho[1,C,N] = \frac{U[1,C,N]}{\sqrt{\sigma[1,C,0]\cdot fs}}
\rho_m[1,C,1] = \max{\rho[1,C,N]}

\(\bar{S_n}(t)\)

MF-ConvNet Model

\rho[1,C,N] = \frac{U[1,C,N]}{\sqrt{\sigma[1,C,0]\cdot fs}}
\rho_m[1,C,1] = \max{\rho[1,C,N]}
C_0 = \mathop{\arg\max}_{C}\rho[1,C,N] \,,\\ N_0 = \mathop{\arg\max}_{N} U[1,C_0,N]

\(\bar{S_n}(t)\)

In the meanwhile, we can obtain the optimal time \(N_0\) (relative to the input) of feature response of matching by recording the location of the maxima value corresponding to the optimal template \(C_0\)

Architechture

MF-ConvNet Model

Experiments & Results

  • Dataset & Templates
  • Training Strategy
  • Search methodology
  • Recovering GW Events
  • Population property on O1

Experiments & Results

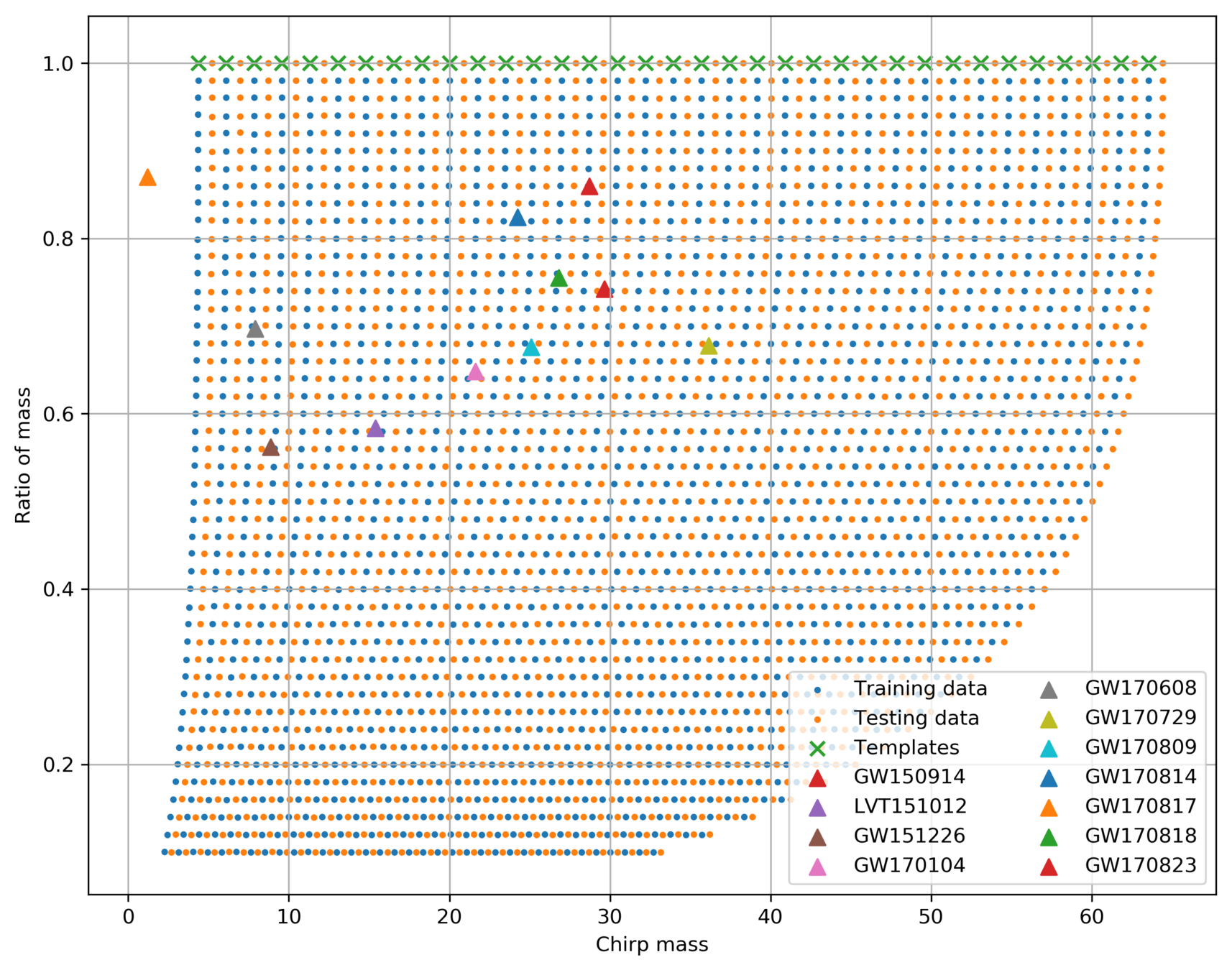
Dataset & Templates

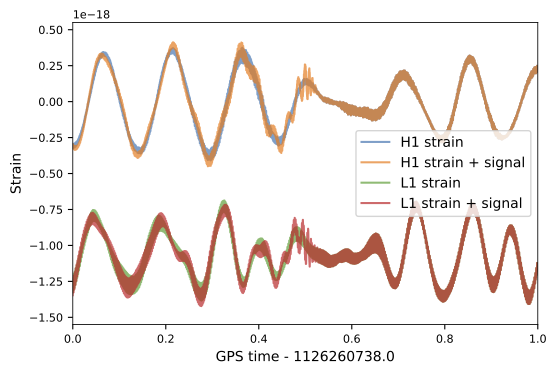
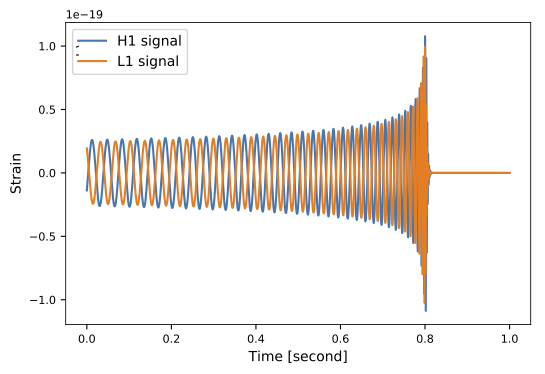
template waveform (train/test)
Number 35 1610
Length (s) 1 5
equal mass
  • We use SEOBNRE model [Cao et al. (2017)] to generate waveform, we only consider circular, spinless binary black holes.

FYI: sampling rate = 4096Hz

(In preprint)

  • The background noises for training/testing are sampled from a closed set (33*4096s) in the first observation run (O1) in the absence of the segments (4096s) containing the first 3 GW events.

62.50M⊙ + 57.50M⊙ (\(\rho_{amp}=0.5\))

Experiments & Results

Dataset & Templates

(In preprint)

template waveform (train/test)
Number 35 1610
Length (s) 1 5
equal mass
  • We use SEOBNRE model [Cao et al. (2017)] to generate waveform, we only consider circular, spinless binary black holes.
  • The background noises for training/testing are sampled from a closed set (33*4096s) in the first observation run (O1) in the absence of the segments (4096s) containing the first 3 GW events.

FYI: sampling rate = 4096Hz

Training Strategy

\rho_{amp} = \frac{\max_t h}{\sqrt{\sigma_{noise}}}
  • Tukey window for both data and templates before input the network.
  • Xavier initialization [X Glorot & Y Bengio (2010)]
  • Binary softmax cross-entropy loss
  • Optimizer: Adam [Diederik P. Kingma & Jimmy Ba (2014)]
  • Learning rate: 0.003
  • Batch size: 16 x 4
  • Curriculum learning: decreasing the signal data with SNR \(\rho_{amp}\) distributed at 1, 0.1, 0.03 and 0.02.
  • GPUs: 4 NVIDIA GeForce GTX 1080Ti
  • MXNet: A Scalable Deep Learning Framework

Probability

(sigmoid function)

Experiments & Results

(In preprint)

Search methodology

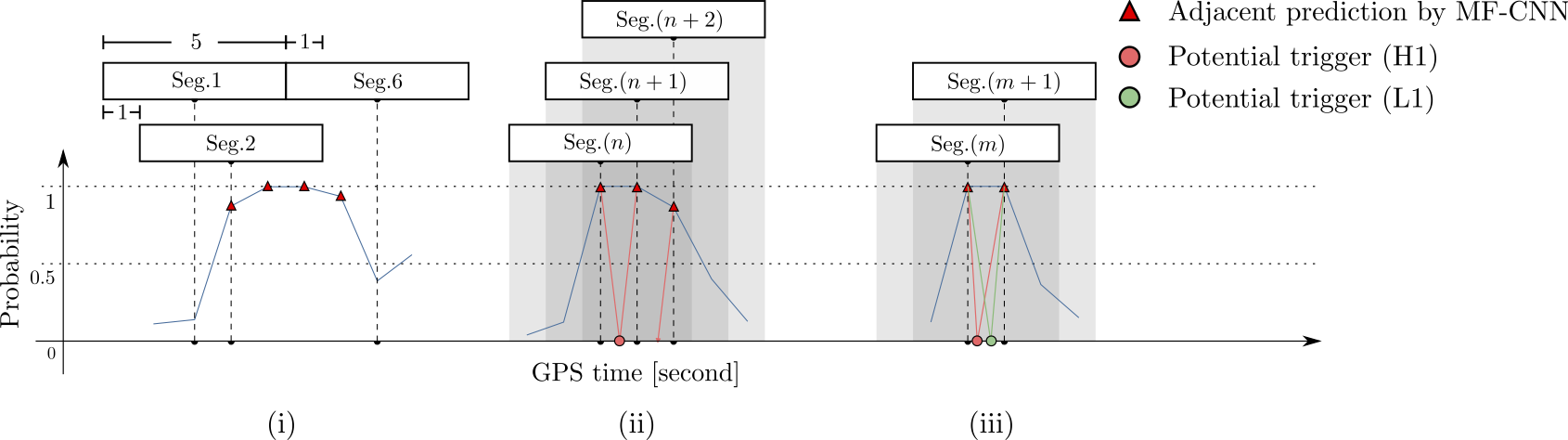
Experiments & Results

(In preprint)

  • Every 5 seconds segment as input of our MF-CNN with a step size of 1 second.
  • In the ideal case, with a GW signal hiding in somewhere, there should be 5 adjacent prediction for it with respect to a threshold.

Experiments & Results

(In preprint)

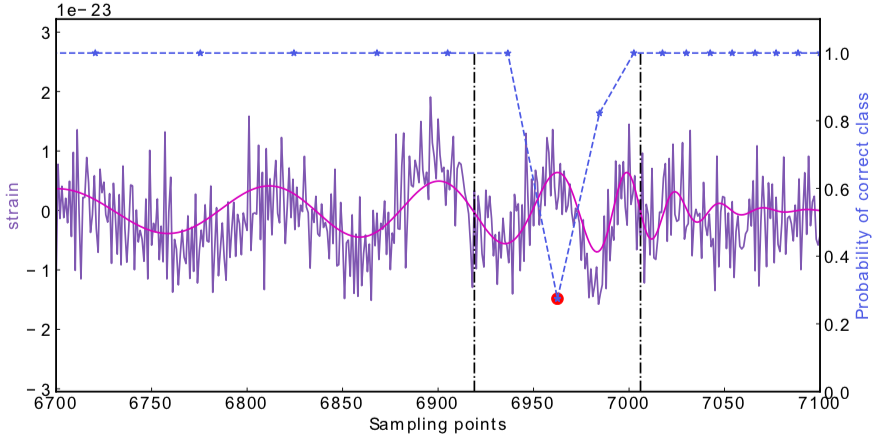
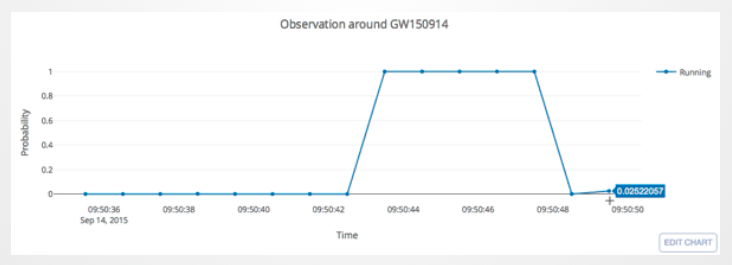
  • Recovering three GW events in O1

Experiments & Results

(In preprint)

  • Recovering three GW events in O1

Experiments & Results

(In preprint)

  • Recovering all GW events in O2

Experiments & Results

(In preprint)

  • Recovering all GW events in O2

Experiments & Results

(In progress)

Population property on O1

  • Sensitivity estimation
    • Background: using time-slides on the closed set from real LIGO recordings
    • Injection: random simulated waveform

Detection ratio

Experiments & Results

Population property on O1

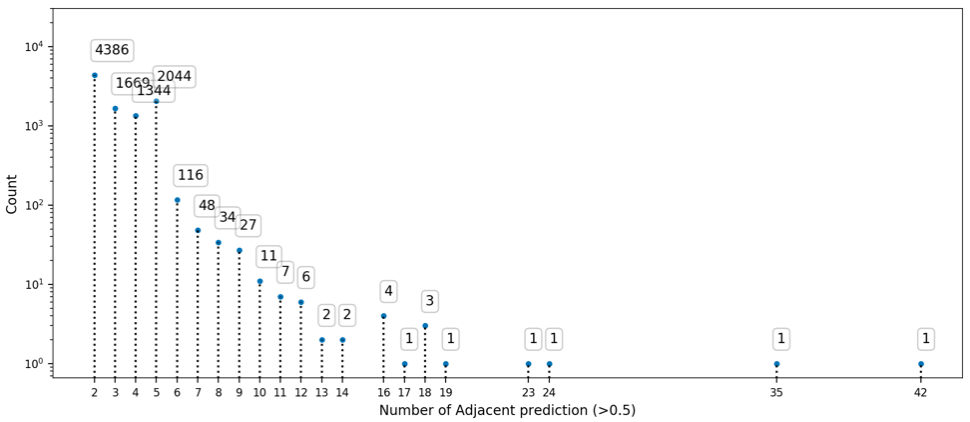
(In progress)

  • Statistical significance on O1
    • Count a group of adjacent predictions as one "trigger block"
    • For pure background (non-Gaussian), monotone trend should be observed.

Experiments & Results

Population property on O1

(In progress)

  • Statistical significance on O1

Experiments & Results

Population property on O1

(In progress)

  • Statistical significance on O1

Interesting!

Summary

  • Some benefits from MF-CNN architechure

    • Simple configuration for GW data generation

    • Almost no data pre-processing

    • Works on non-stationary background
    • Fast, high acc. on all the events

    • Easy parallel deployments, multiple detectors can be benefit a lot from this design

    • More templates / smaller steps for searching can improve further
    • Rethinking the deep learning neural networks?

Summary

Thank you for your attention!

  • Some benefits from MF-CNN architechure

    • Simple configuration for GW data generation

    • Almost no data pre-processing

    • Works on non-stationary background
    • Fast, high acc. on all the events

    • Easy parallel deployments, multiple detectors can be benefit a lot from this design

    • More templates / smaller steps for searching can improve further
    • Rethinking the deep learning neural networks?