Building a deep neural network
&
How could we use it as a density estimator
Based on :
[1] My tech post, "A neural network wasn't built in a day" (一段关于神经网络的故事) (2017)
[2] 1903.01998, 1909.06296, 2002.07656, 2008.03312; PRL(2020) 124 041102
Journal Club - Oct 20, 2020
Content
- What is a Neural Network (NN) anyway?
- One neural
- One layer of neural
- Basic types of neural network in academic papers
- A concise summary of current GW ML parameter estimation studies
- MAP, CVAE, Flow
- GSN (optional)
- What is a Neural Network (NN) anyway?
Objective:
- Input a sample to a function (our NN).
- Then evaluate how is it "close" to the truth (also called label)
- Eg:

Yes or No
A number
A sequence
- What is a Neural Network (NN) anyway?
What's happend in a neural?(一个神经元的本事)
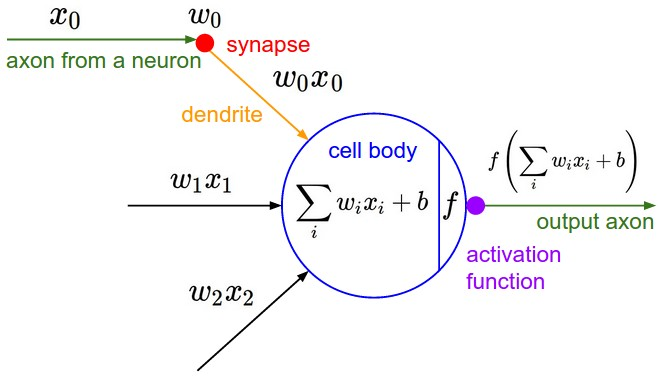
- Initialize a weight vector and a bias scalar randomly in one neural.
- Input a sample, then it gives us an output.
Objective:
- Input a sample to a function (our NN).
- Then evaluate how is it "close" to the truth (also called label)
"score"
"your performance"
"one judge"
- What is a Neural Network (NN) anyway?
What's happend in a neural?(一个神经元的本事)

- Initialize a weight vector and a bias vector randomly in one neural.
- Input some samples, then it gives us some outputs.
"a bunch guys' show"
Objective:
- Input a sample to a function (our NN).
- Then evaluate how is it "close" to the truth (also called label)
"scores"
"one judge"
- What is a Neural Network (NN) anyway?
What's happend in a neural?(一个神经元的本事)

- Initialize a weight vector and a bias vector randomly in one neural.
- Input some samples, then it gives us some outputs.
ReLU
Objective:
- Input a sample to a function (our NN).
- Then evaluate how is it "close" to the truth (also called label)
"a bunch guys' show"
"one judge"
"scores"
- What is a Neural Network (NN) anyway?
Generalize to one layer of neural(层状的神经元)
- Initialize a weight matrix and a bias scalar randomly in one layer.
- Input one sample, then it gives us an output.
Objective:
- Input a sample to a function (our NN).
- Then evaluate how is it "close" to the truth (also called label)
"score"
"10 judges"
"your performance"
- What is a Neural Network (NN) anyway?
Generalize to one layer of neural(层状的神经元)
- Initialize a weight matrix and a bias scalar randomly in one layer.
- Input one sample, then it gives us an output.
Objective:
- Input a sample to a function (our NN).
- Then evaluate how is it "close" to the truth (also called label)

"10 judges"
"scores"
"a bunch guys' show"
- What is a Neural Network (NN) anyway?
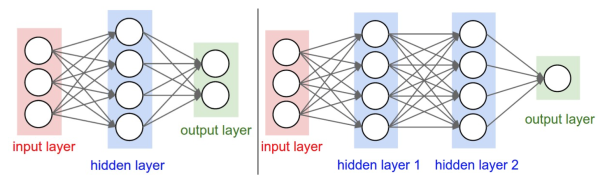
Fully-connected neural layers(全连接的神经元层)
Objective:
- Input a sample to a function (our NN).
- Then evaluate how is it "close" to the truth (also called label)

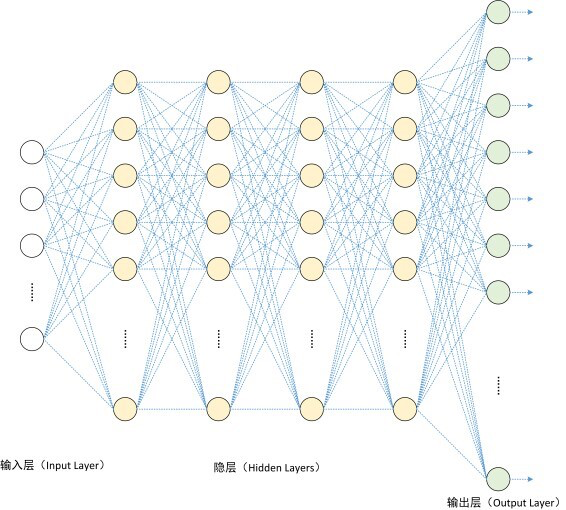
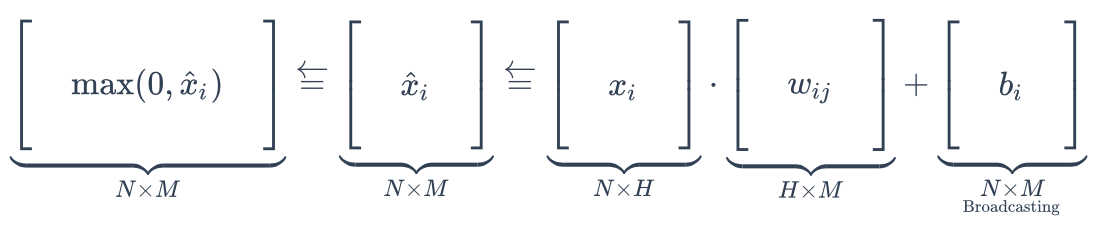
In each layer:
input
output
num of neurals in this layer
Draw how one sample data flows
- For a fully-connected neural network, only the number of weight columns in each layer is the hyper-parameter we need to fix first.
- Only one word for the evaluation... (no more slices)
- Loss/cost/error func.
- Gradient descent / backward propagation algorithm
And how the shape of data changs.
- What is a Neural Network (NN) anyway?
Objective:
- Input a sample to a function (our NN).
- Then evaluate how is it "close" to the truth (also called label)
Convolution is a specialized kind of linear operation.(卷积层是全连接层的一种特例)
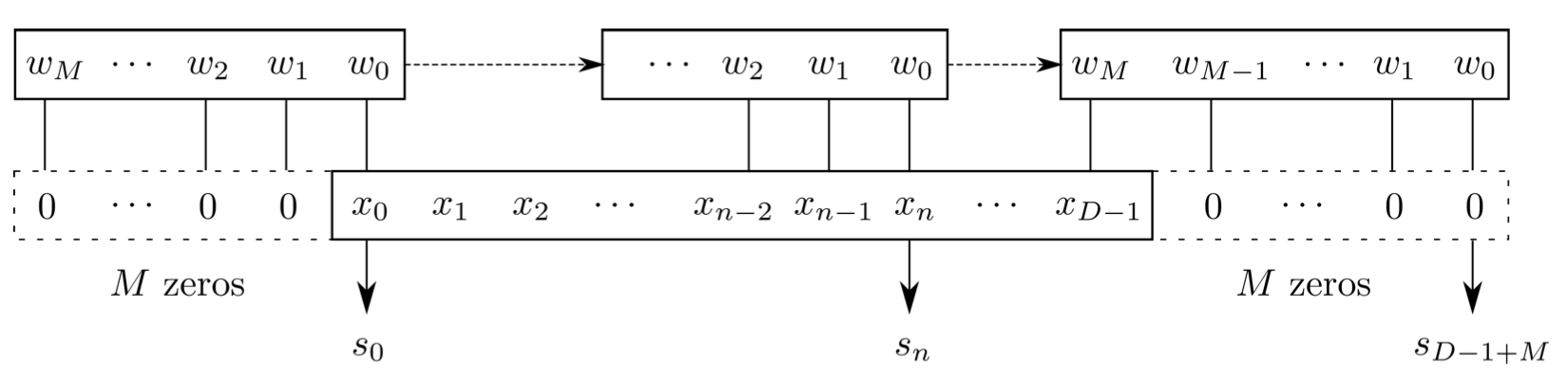
- Flip-and-slide Form
- Matrix Form :
- Integral Form
- Discrete Form
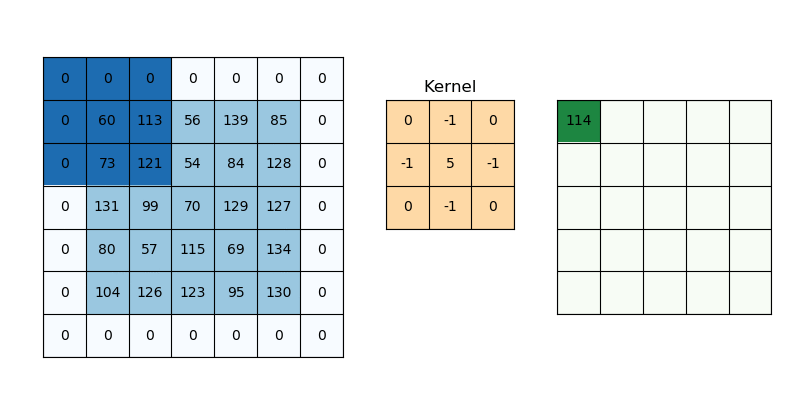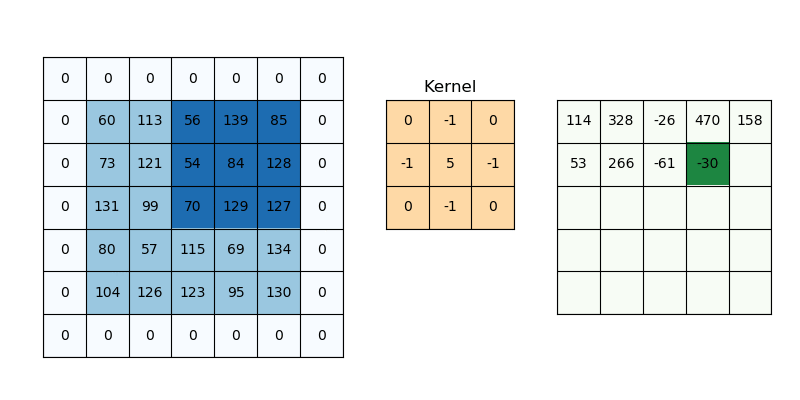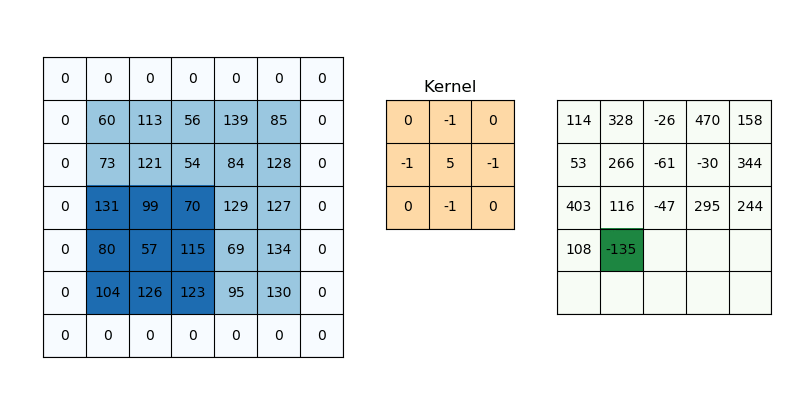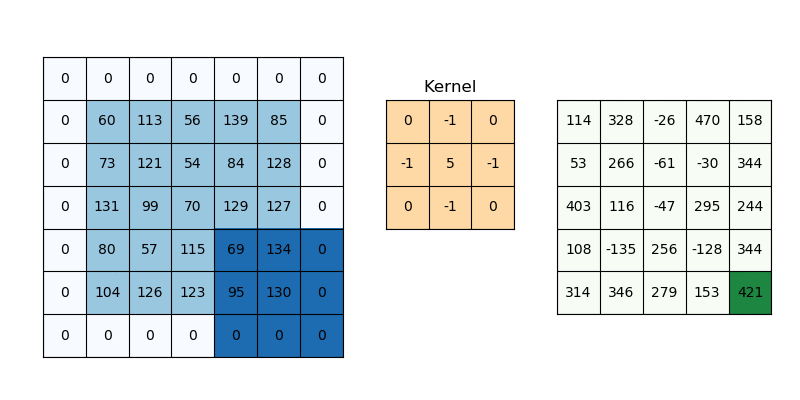
- 参数共享 parameter sharing
- 稀疏交互 sparse interactions
- What is a Neural Network (NN) anyway?
Objective:
- Input a sample to a function (our NN).
- Then evaluate how is it "close" to the truth (also called label)
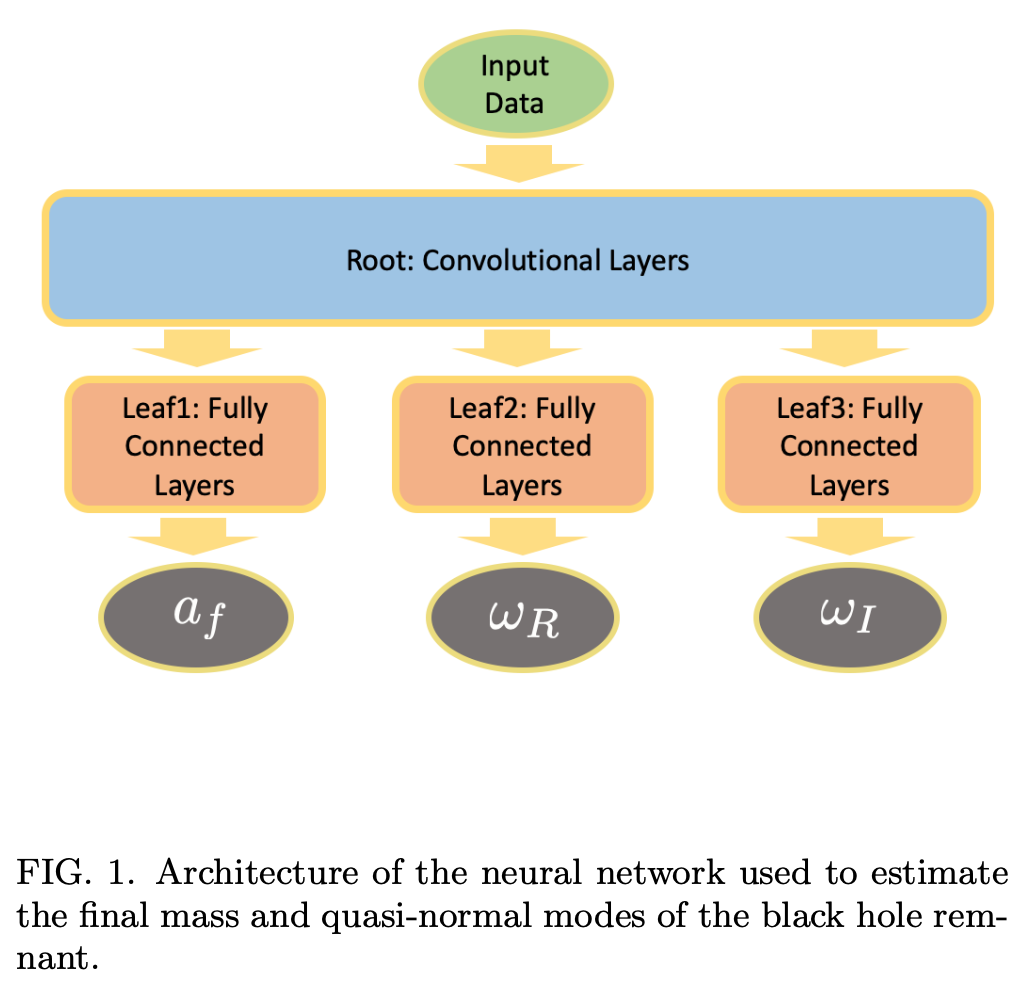
Neural networks in academic papers.(GW文献中的神经网络)
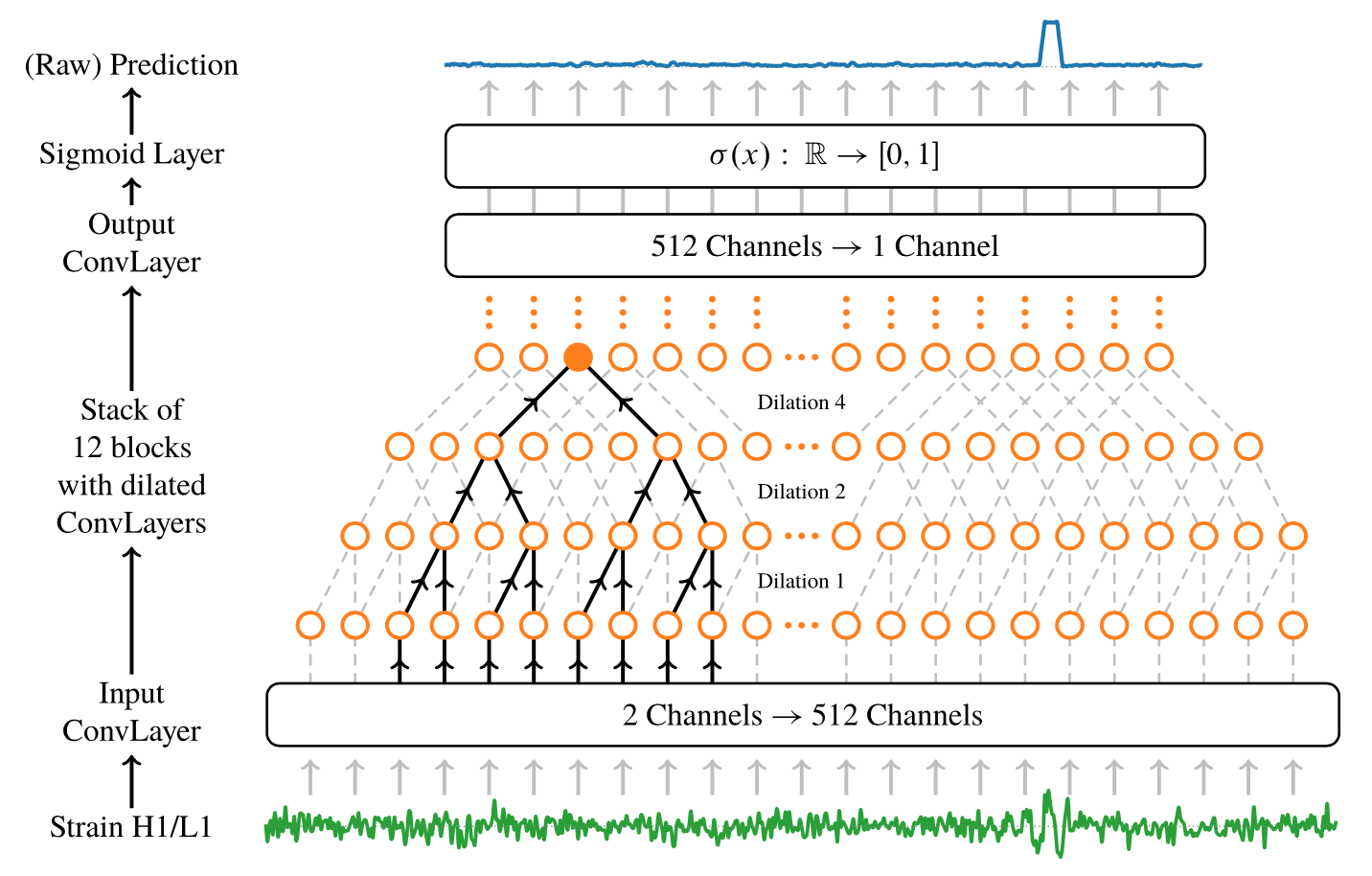
PRD. 100, 063015 (2019)
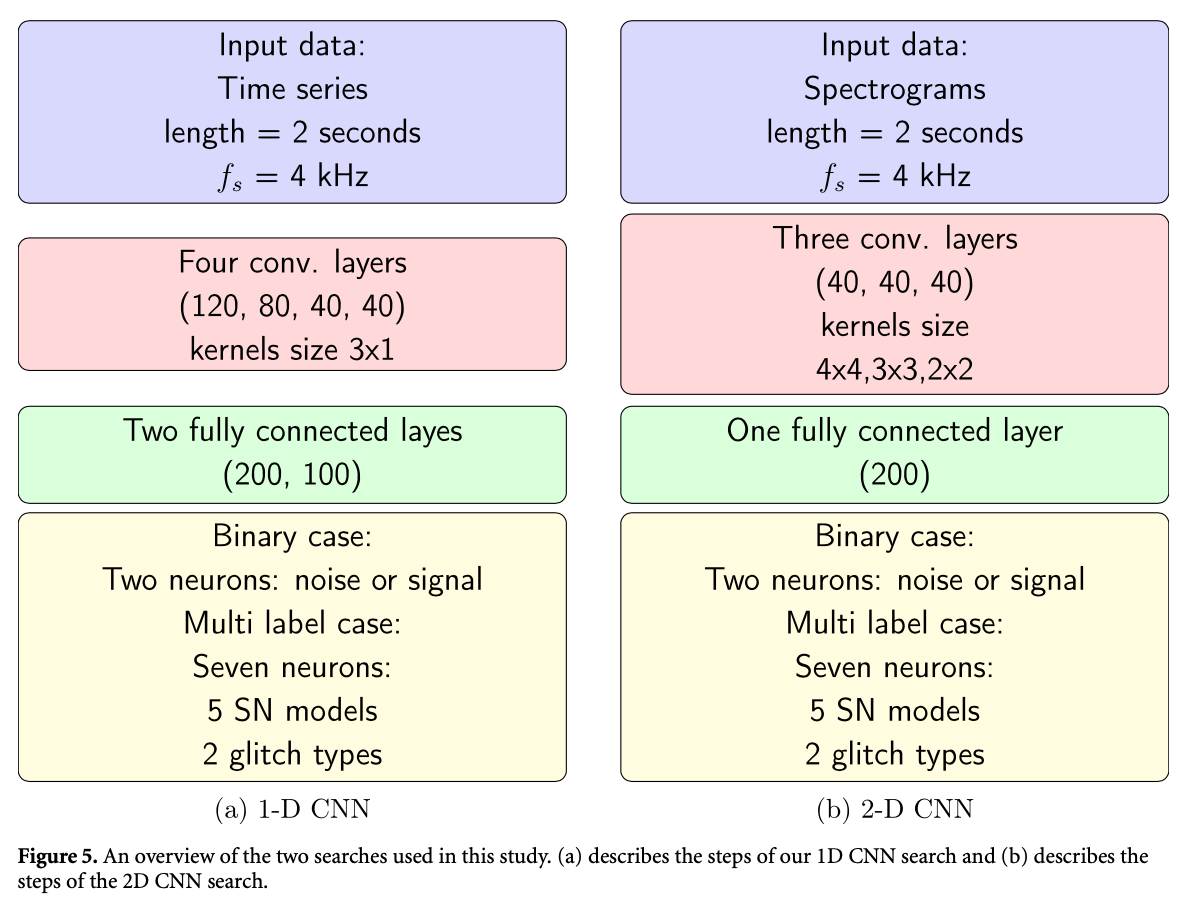
Mach. Learn.: Sci. Technol. 1 025014 (2020)
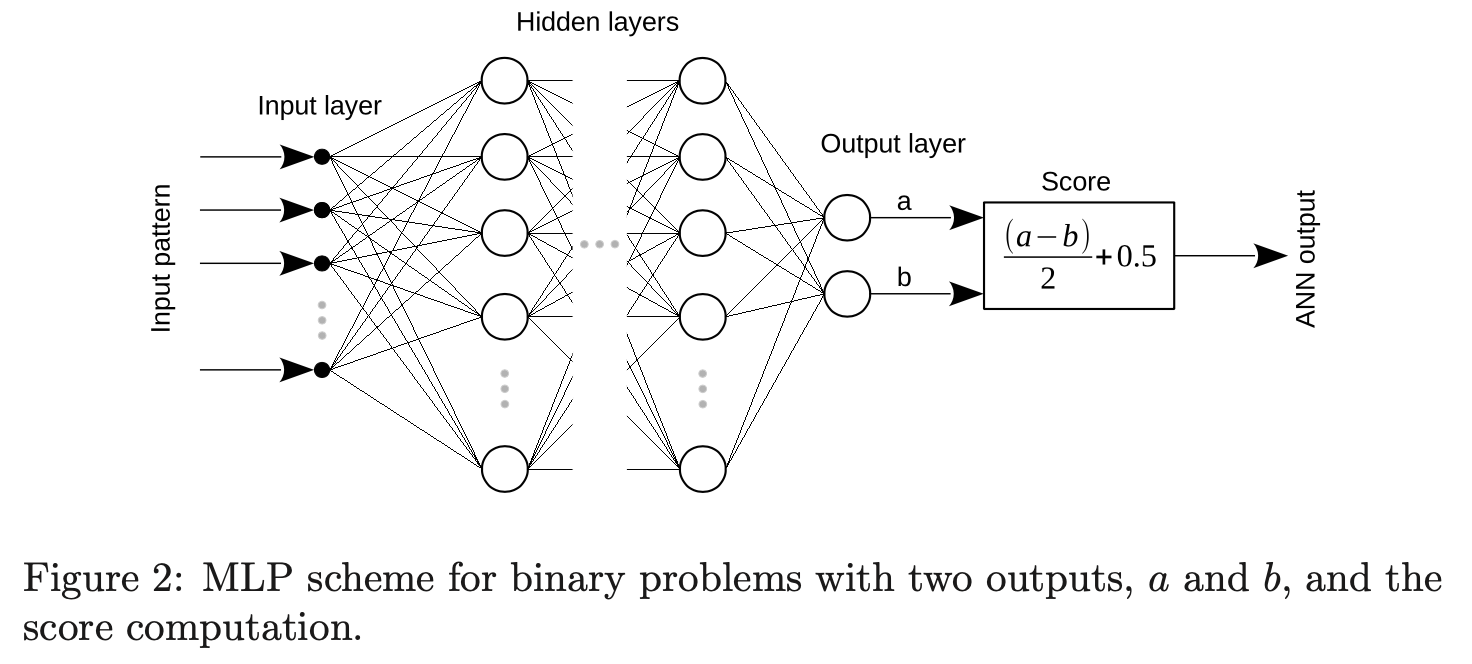
2003.09995
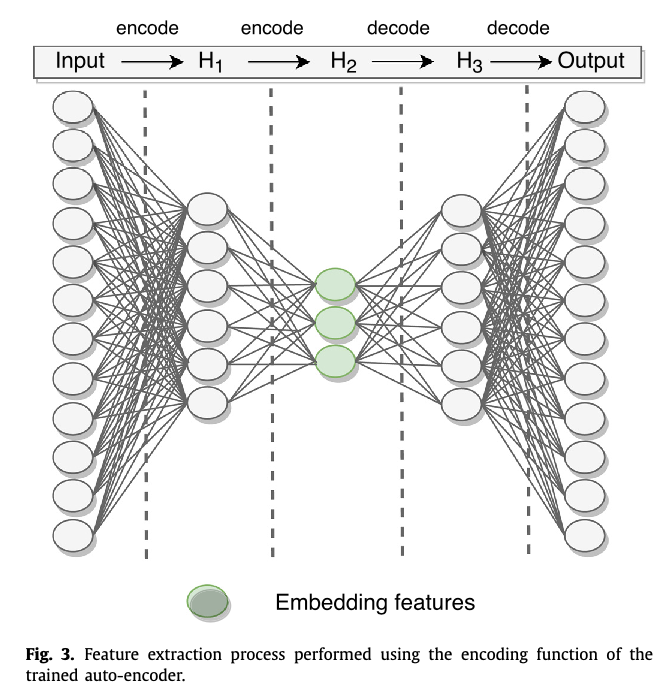
Expert Systems With Applications 151 (2020) 113378
"All of the current GW ML parameter estimation studies are still at the proof-of-principle stage" [2005.03745]
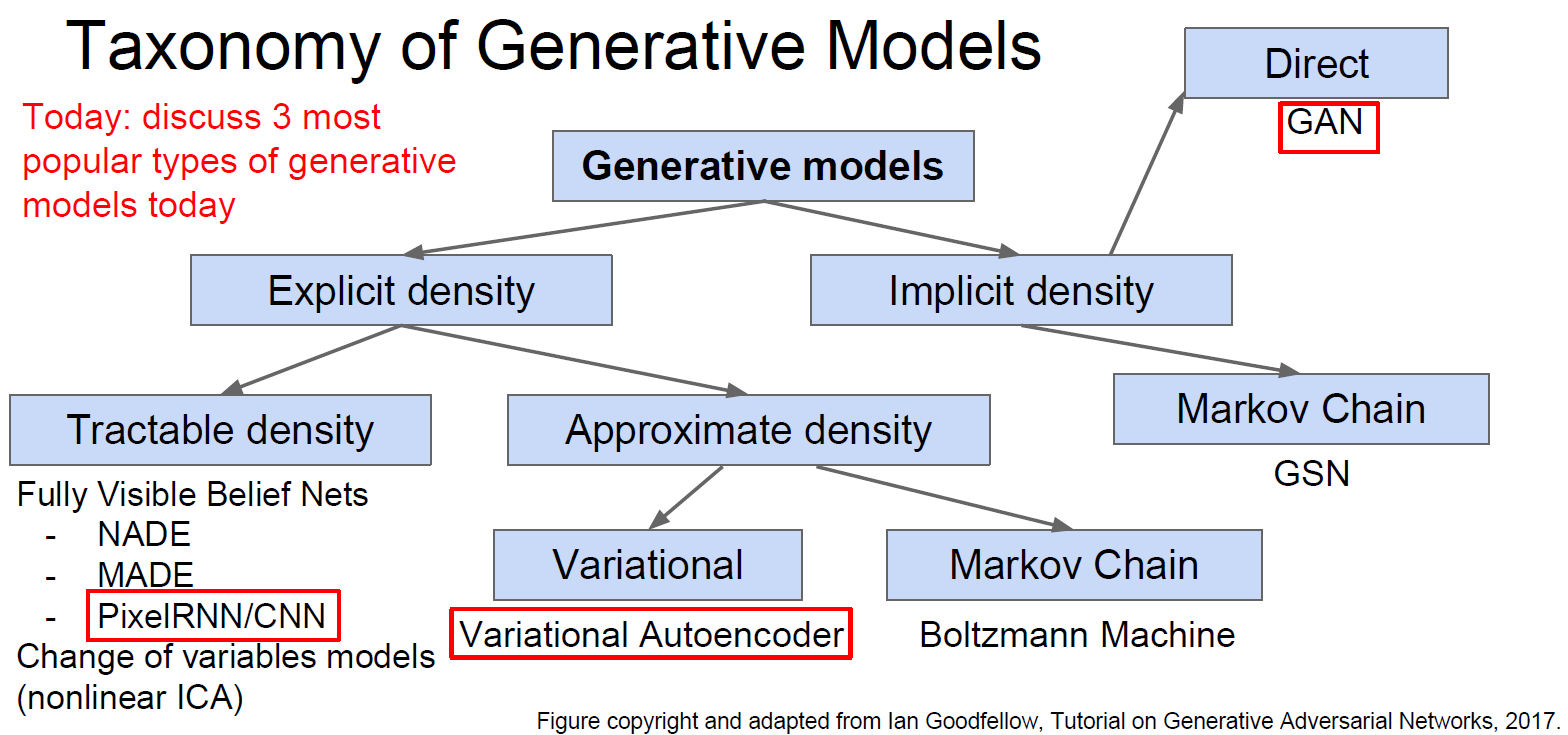
- A concise summary of current GW ML parameter estimation studies
Real-time regression
- Huerta's Group [PRD, 2018, 97, 044039], [PLB, 2018, 778, 64-70], [1903.01998], [2004.09524]
- Fan et al. [SCPMA, 62, 969512 (2019)]
- Carrillo et al. [GRG, 2016, 48, 141], [IJMP, 2017, D27, 1850043]
- Santos et al. [2003.09995]
- *Li et al. [2003.13928] (Bayes neural networks)
Explicit posteriors density
- Chua et al. [PRL, 2020, 124, 041102]
- produce Bayesian posteriors using neural networks.
- Gabbard et al. [1909.06296] (CVAE)
- produce samples from the posterior.
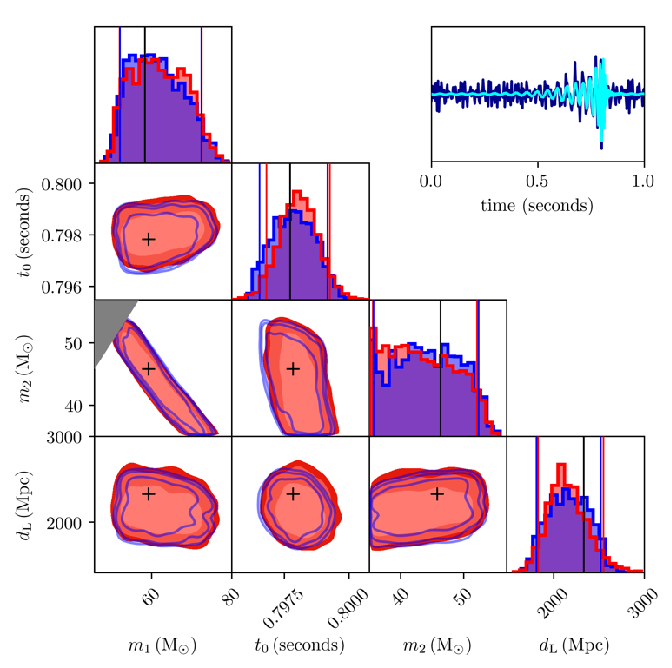
- 256Hz, 1-sec, 4-D, simulated noise
- Strong agreement between Bilby and the CVAE.
- Yamamoto & Tanaka [2002.12095] (CVAE)
- QNM frequencies estimations
- Green et al. [2002.07656, 2008.03312] (MAF, CVAE+,Flow-based)
- optimal results for now
Suppose we have a posterior distribution \(p_{true}(x|y)\). (\(y\) is the GW data, \(x\) is the corresponding parameters)
- The aim is to train a neural network to give an approximation \(p(x|y)\) to \(p_{true}(x|y)\).
- Take the expectation value (over \(y\)) of the cross-entropy (KL divergence) between the two distributions as the loss function:
fixed; costly sampling required
fixed; costly sampling required
Bayes' theorem
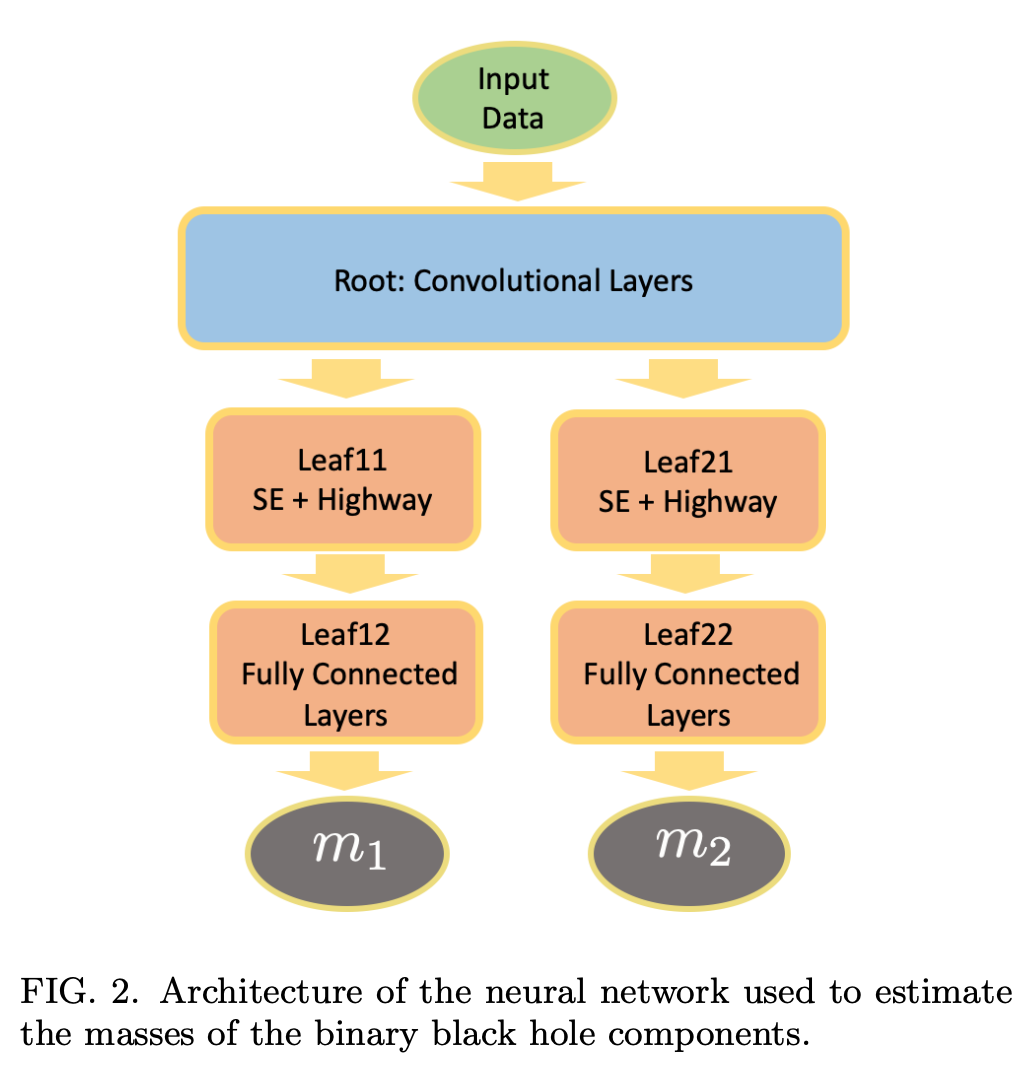
Chua et al. [PRL, 2020, 124, 041102] assume a multivariate normal distribution with weights:
NN
Suppose we have a posterior distribution \(p_{true}(x|y)\). (\(y\) is the GW data, \(x\) is the corresponding parameters)
- The aim is to train a neural network to give an approximation \(p(x|y)\) to \(p_{true}(x|y)\).
- Take the expectation value (over \(y\)) of the cross-entropy (KL divergence) between the two distributions as the loss function:
fixed; costly sampling required
Bayes' theorem
Chua et al. [PRL, 2020, 124, 041102] assume a multivariate normal distribution with weights:
Gabbard et al. [1909.06296] (CVAE)
NN
NN
NN
NN
Suppose we have a posterior distribution \(p_{true}(x|y)\). (\(y\) is the GW data, \(x\) is the corresponding parameters)
- The aim is to train a neural network to give an approximation \(p(x|y)\) to \(p_{true}(x|y)\).
- Take the expectation value (over \(y\)) of the cross-entropy (KL divergence) between the two distributions as the loss function:
fixed; costly sampling required
Bayes' theorem
Chua et al. [PRL, 2020, 124, 041102] assume a multivariate normal distribution with weights:
NN
Gabbard et al. [1909.06296] (CVAE)
NN
NN
NN
Green et al. [2002.07656] (MAF, CVAE+)
Suppose we have a posterior distribution \(p_{true}(x|y)\). (\(y\) is the GW data, \(x\) is the corresponding parameters)
- The aim is to train a neural network to give an approximation \(p(x|y)\) to \(p_{true}(x|y)\).
- Take the expectation value (over \(y\)) of the cross-entropy (KL divergence) between the two distributions as the loss function:
CVAE (Train)
\(Y\) (·, 256)
\(X\) (·, 5)
KL
E2
E1
\(X'\) (·, 5)
D
(2, 8)
FYI: if dims of latent space is 2, i.e.
sample \(z\) from \(\mathcal{N}\left(\vec{\mu}, \boldsymbol{\Sigma}^{2}\right)\)
\(Y\) (·, 256)
(1, 8)
Training set: \(N=10^6\)
batchsize = 512
(·, 8)
\([(\mu_{m_1}, \sigma_{m_1}), ...]\)
\(X_1\)
\(X_2\)
\(X_n\)
latent space
strain
params
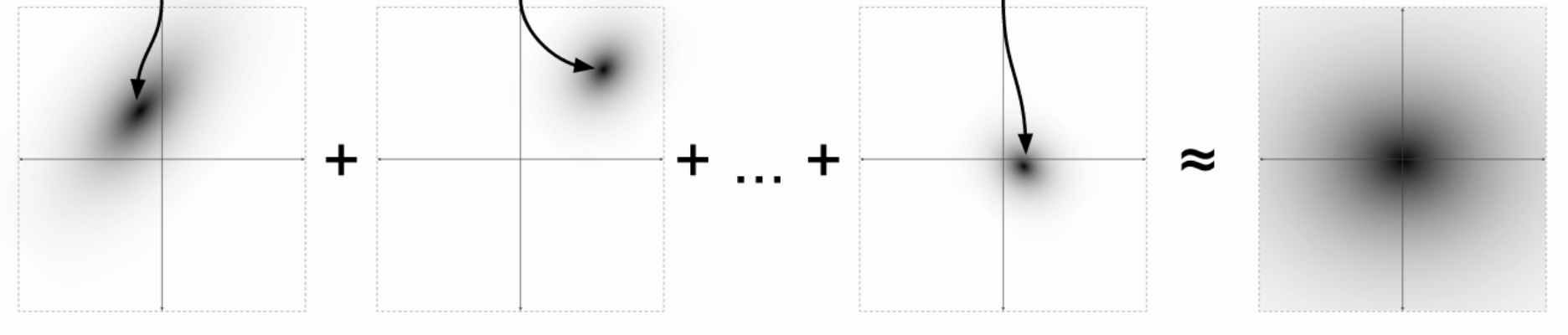
- The key is to notice that any distribution in \(d\) dimensions can be generated by taking a set of \(d\) variables that are normally distributed and mapping them through a sufficiently complicated function .
CVAE: conditional variational autoencoder
\(Y\) (·, 256)
\(X\) (·, 5)
KL
E2
E1
\(X'\) (·, 5)
D
(2, 8)
FYI: if dims of latent space is 2, i.e.
sample \(z\) from \(\mathcal{N}\left(\vec{\mu}, \boldsymbol{\Sigma}^{2}\right)\)
\(Y\) (·, 256)
(1, 8)
Training set: \(N=10^6\)
batchsize = 512
(·, 8)
\([(\mu_{m_1}, \sigma_{m_1}), ...]\)

\(X_1\)
\(X_2\)
\(X_n\)
latent space
strain
params
P
P
Q
- The key is to notice that any distribution in \(d\) dimensions can be generated by taking a set of \(d\) variables that are normally distributed and mapping them through a sufficiently complicated function .
CVAE (Train)
Objective: maximise \(L_{ELBO}\) (与数据点 X 相关联的变分下界)
ELBO: Evidence Lower Bound
CVAE: conditional variational autoencoder
FYI: if dims of latent space is 2, i.e.

\(X_1\)
\(X_2\)
\(X_n\)
latent space
- The key is to notice that any distribution in \(d\) dimensions can be generated by taking a set of \(d\) variables that are normally distributed and mapping them through a sufficiently complicated function .
CVAE (Test)
\(Y\) (·, 256)
E1
\(X'\) (·, 5)
D
sample \(z\) from \(\mathcal{N}\left(\vec{\mu}, \boldsymbol{\Sigma}^{2}\right)\)
\(Y\) (·, 256)
(1, 8)
Training set: \(N=10^6\)
batchsize = 512
(·, 8)
\([(\mu_{m_1}, \sigma_{m_1}), ...]\)
strain
P
(2, 8)
P
Objective: maximise \(L_{ELBO}\) (与数据点 X 相关联的变分下界)
ELBO: Evidence Lower Bound
CVAE: conditional variational autoencoder
\(Y\) (·, 256)
\(X\) (·, 5)
KL
E2
E1
\(X'\) (·, 5)
D
(2, 8)
sample \(z\) from \(\mathcal{N}\left(\vec{\mu}, \boldsymbol{\Sigma}^{2}\right)\)
\(Y\) (·, 256)
(1, 8)
Training set: \(N=10^6\)
batchsize = 512
(·, 8)
\([(\mu_{m_1}, \sigma_{m_1}), ...]\)
strain
params
Objective: maximise \(L_{ELBO}\) (与数据点 X 相关联的变分下界)
P
P
Q
CVAE
Drawbacks:
- KL divergence
- \(L_{ELBO}\)
Mystery:
- How could it still work that well?
(for simple case only)
The final slice. 💪
ELBO: Evidence Lower Bound
CVAE: conditional variational autoencoder