Gravitational-wave Signal Recognition of LIGO Data by Deep Learning

He Wang (王赫)

Institute of Theoretical Physics, CAS

Beijing Normal University

on behalf of the KAGRA collaboration

7th KAGRA International Workshop , 15:45-16:05 Asia/Taipei on December 19\(^\text{th}\), 2020

Based on DOI: 10.1103/physrevd.101.104003

hewang@mail.bnu.edu.cn / hewang@itp.ac.cn

Collaborators:

Zhoujian Cao (BNU)

Shichao Wu (BNU)

Xiaolin Liu (BNU)

Jian-Yang Zhu (BNU)

Content

  • Introduction
  • Challenge & Opportunity
  • Matched-filtering Convolutional Neural Network (MFCNN)
  • Configuration & Search Strategy
  • Results: GW events in O1/O2 & GWTC-2
  • Summary & Lesson Learned

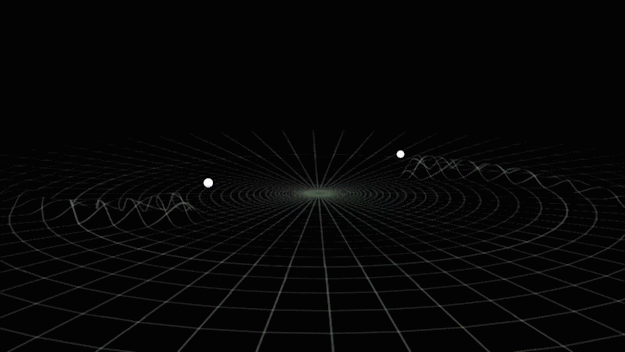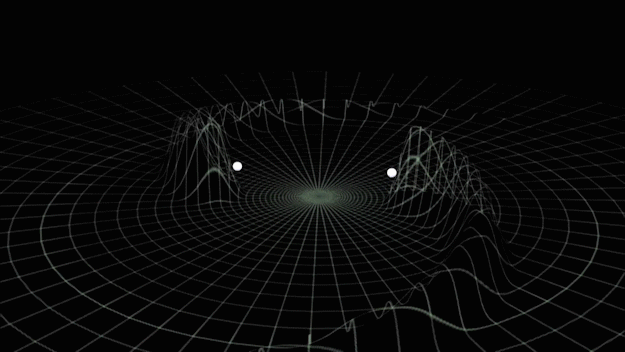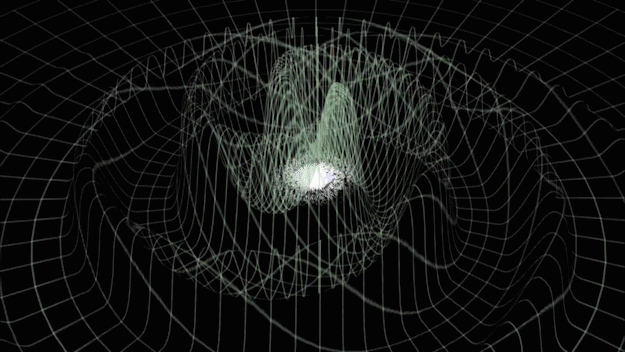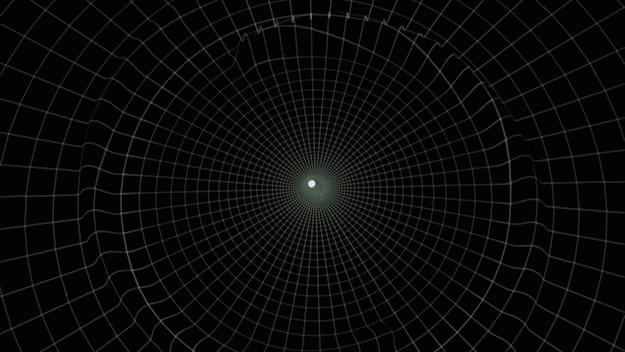
Gravitational-wave Astronomy

  • Advanced LIGO observing since 2015 (two detectors in US), joined by Virgo (Italy) in 2017 and KAGRA (Japan) in Japan in 2020.
  • Best GW hunter in the range 10Hz-10kHz.

Credit: Science Burrito

  • 100 years from Einstein's prediction to the first LIGO-Virgo detection (GW150914) announcement in 2016.
  • General relativity: "Spacetime tells matter how to move, and matter tells spacetime how to curve."
  • Time-varying quadrupolar mass distributions lead to propagating ripples in spacetime: GWs.

LIGO Hanford (H1)

KAGRA

LIGO Livingston (L1)

Noise power spectral density (one-sided)

  • Matched-filtering Technique:
    • It is an optimal linear filter for weak signals buried in the Gaussian and stationary noise \(n(t)\).
    • Works by correlating a known signal model \(h(t)\) (template) with the data.
    • Starting with data: \(d(t) = h(t) + n(t)\).
    • Defining the matched-filtering SNR \(\rho(t)\):

 

 

            where

  • The 4-D search parameter space in the first observation run covered by a template bank to circular binaries for which the spin of the systems is aligned (or antialigned) with the orbital angular momentum of the binary.
  • ~250,000 template waveforms are used for O1 (computationally expansive).

Phys.Rev.X 6 (2016) 4, 041015

The template that best matches GW150914 event

\langle h|h \rangle = 4\int^\infty_0\frac{\tilde{h}(f)\tilde{h}^*(f)}{S_n(f)}df
\langle d|h \rangle (t) = 4\int^\infty_0\frac{\tilde{d}(f)\tilde{h}^*(f)}{S_n(f)}e^{2\pi ift}df
\rho^2(t)\equiv\frac{1}{\langle h|h \rangle}|\langle d|h \rangle(t)|^2

Challenges in GW Data Analysis

Opportunities in GW Data Analysis

 

Proof-of-principle studies

Production search studies

Milestones

More related works, see Survey4GWML (https://iphysresearch.github.io/Survey4GWML/)

  • When machine & deep learning meets GW astronomy:
    • Covering more parameter-space (Interpolation)
    • Automatic generalization to new sources (Extrapolation)

    • Resilience to real non-Gaussian noise  (Robustness)

    • Acceleration of existing pipelines (Speed, <0.1ms)

 
 

Phys.Rev.Lett 120 (2019) 14, 141103

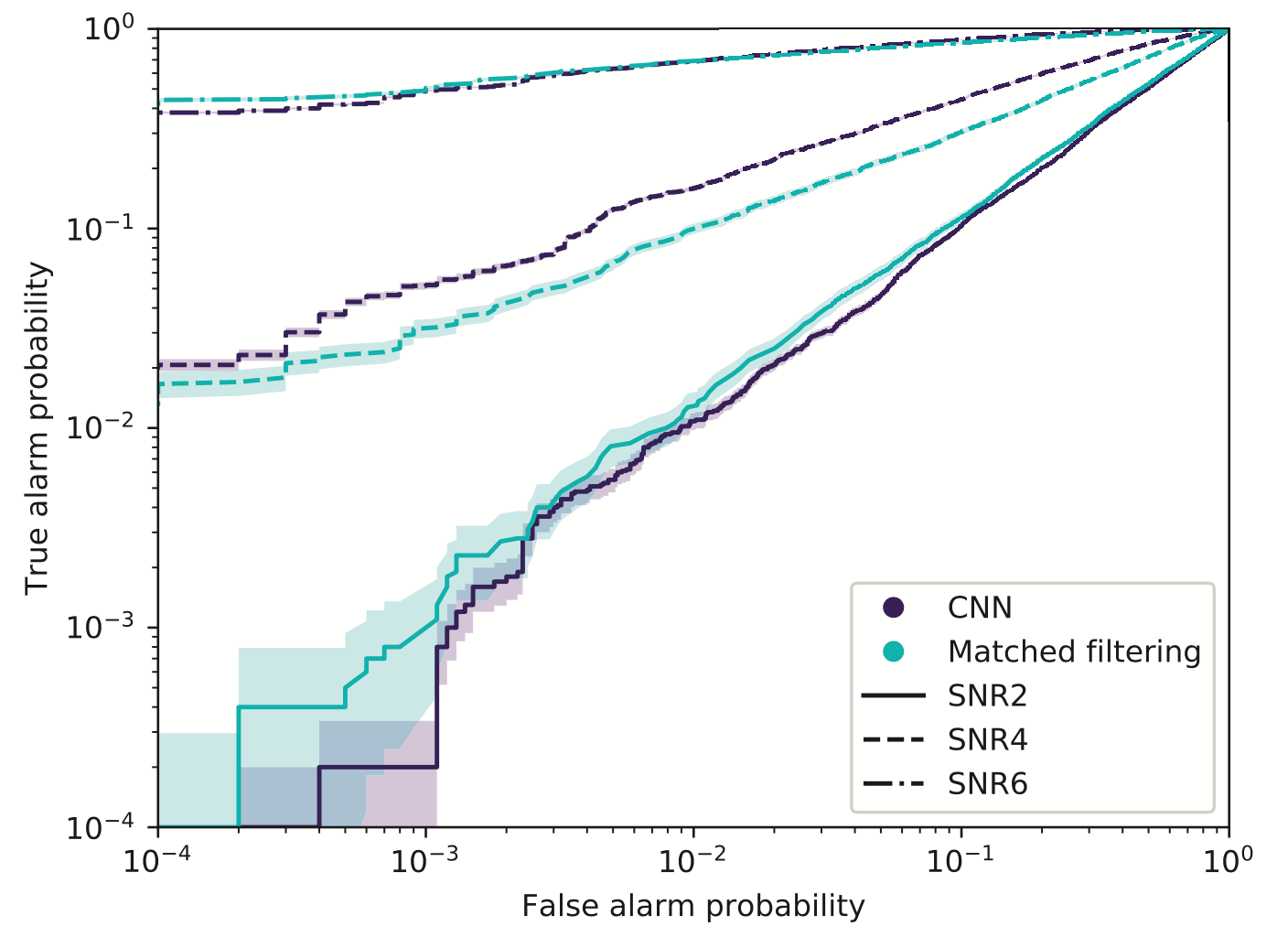
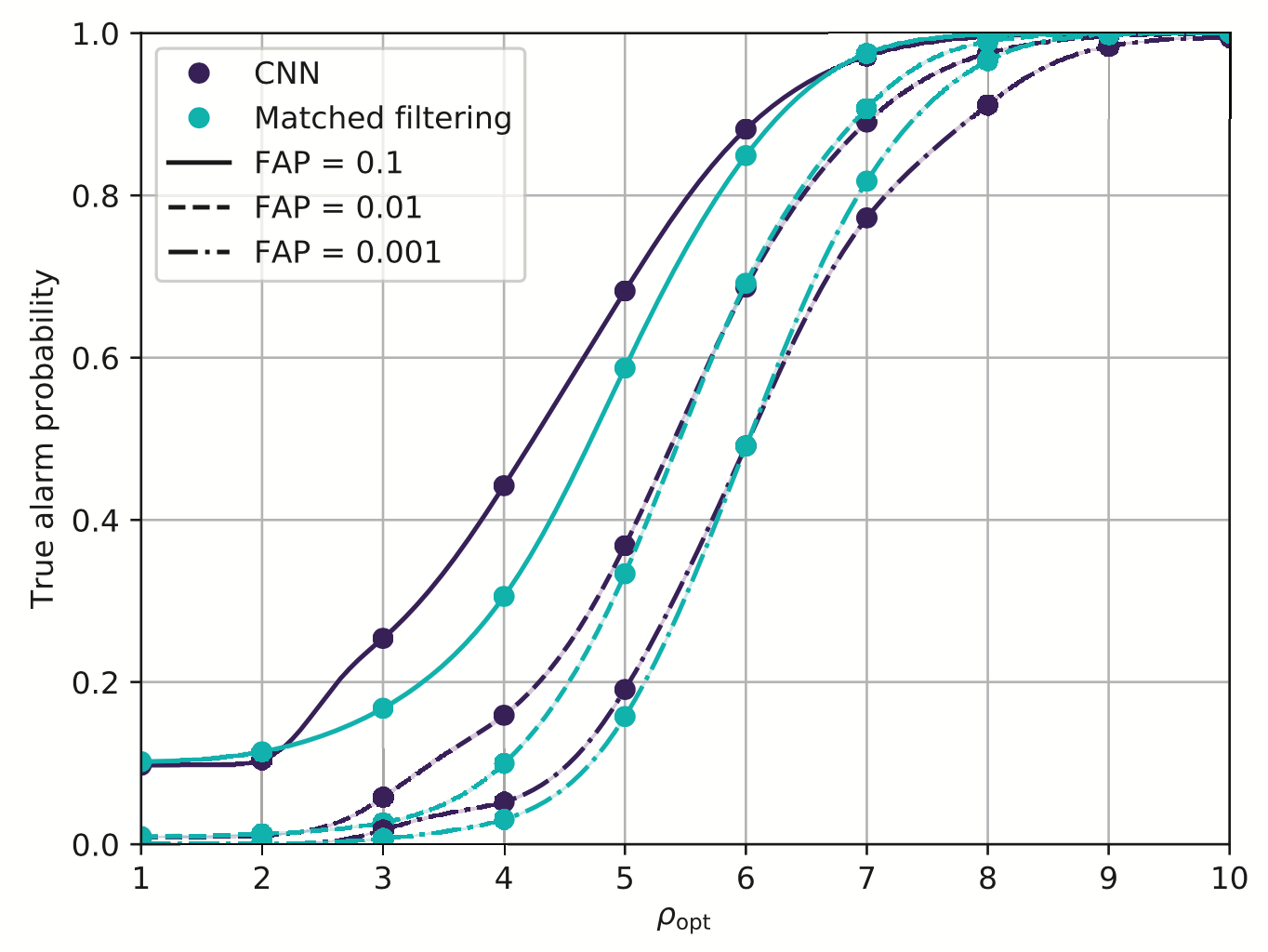
Stimulated background noises

  • CNNs structure performs as well as the standard matched filter method in extracting BBH signals under non-ideal conditions.

Attempts on Real LIGO Noise

Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012)

Classification

Feature extraction

  • CNNs always works pretty good on stimulated noises.
  • However, when on real noises from LIGO, this approach does not work that well.
  • It's too sensitive against the background + hard to find GW events)

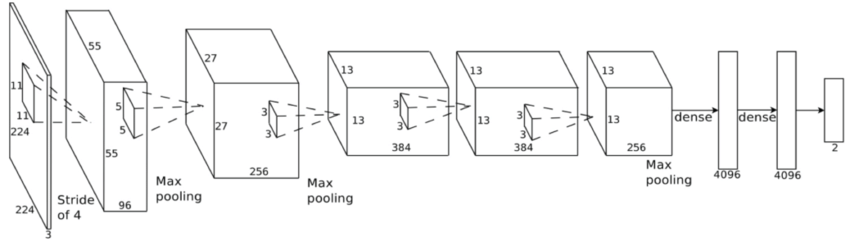
Convolutional Neural Network (ConvNet or CNN)

A specific design of the architecture is needed.

 [as Timothy D. Gebhard et al. (2019)]

A specific design of the architecture is needed.

 [as Timothy D. Gebhard et al. (2019)]

Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012)

Classification

Feature extraction

Convolutional Neural Network (ConvNet or CNN)

  • CNNs always works pretty good on stimulated noises.
  • However, when on real noises from LIGO, this approach does not work that well.
  • It's too sensitive against the background + hard to find GW events)
 MFCNN
 MFCNN
 MFCNN

Attempts on Real LIGO Noise

Motivation

  • With the closely related concepts between the templates and kernels , we attempt to address a question of:

Matched-filtering (cross-correlation with the templates) can be regarded as a convolutional layer with a set of predefined kernels.

>> Is it matched-filtering ?
>> Wait, It can be matched-filtering!
  • In practice, we use matched filters as an essential component of feature extraction in the first part of the CNN for GW detection.

Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012)

Classification

Feature extraction

Convolutional Neural Network (ConvNet or CNN)

Matched-filtering CNNs (MFCNN)

Frequency domain

\langle h|h \rangle = 4\int^\infty_0\frac{\tilde{h}(f)\tilde{h}^*(f)}{S_n(f)}df
\langle d|h \rangle (t) = 4\int^\infty_0\frac{\tilde{d}(f)\tilde{h}^*(f)}{S_n(f)}e^{2\pi ift}df
\rho^2(t)\equiv\frac{1}{\langle h|h \rangle}|\langle d|h \rangle(t)|^2
\int\tilde{x}_1(f) \cdot \tilde{x}_2(f) e^{2\pi ift}df= x_1(t)*x_2(t)
\int\tilde{x}_1(f) \cdot \tilde{x}^*_2(f) e^{2\pi ift}df= x_1(t)\star x_2(t)
  • Transform matched-filtering method from frequency domain to time domain.
  • The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):
x_1(t)*x_2^*(-t) = x_1(t)\star x_2(t)

Matched-filtering CNNs (MFCNN)

\(S_n(|f|)\) is the one-sided average PSD of \(d(t)\)

(whitening)

where

Time domain

Frequency domain

(normalizing)

(matched-filtering)

\langle h|h \rangle = 4\int^\infty_0\frac{\tilde{h}(f)\tilde{h}^*(f)}{S_n(f)}df
\langle d|h \rangle (t) = 4\int^\infty_0\frac{\tilde{d}(f)\tilde{h}^*(f)}{S_n(f)}e^{2\pi ift}df
\rho^2(t)\equiv\frac{1}{\langle h|h \rangle}|\langle d|h \rangle(t)|^2
\langle h|h \rangle \sim [\bar{h}(t) \ast \bar{h}(-t)]|_{t=0}
\langle d|h \rangle (t) \sim \,\bar{d}(t)\ast\bar{h}(-t)
\bar{S_n}(t)=\int^{+\infty}_{-\infty}S_n^{-1/2}(f)e^{2\pi ift}df
\left\{\begin{matrix} \bar{d}(t) = d(t) * \bar{S}_n(t) \\ \bar{h}(t) = h(t) * \bar{S}_n(t) \end{matrix}\right.
\int\tilde{x}_1(f) \cdot \tilde{x}_2(f) e^{2\pi ift}df= x_1(t)*x_2(t)
\int\tilde{x}_1(f) \cdot \tilde{x}^*_2(f) e^{2\pi ift}df= x_1(t)\star x_2(t)
  • Transform matched-filtering method from frequency domain to time domain.
  • The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):
x_1(t)*x_2^*(-t) = x_1(t)\star x_2(t)

Matched-filtering CNNs (MFCNN)

\(S_n(|f|)\) is the one-sided average PSD of \(d(t)\)

(whitening)

where

Time domain

Frequency domain

(normalizing)

(matched-filtering)

\langle h|h \rangle = 4\int^\infty_0\frac{\tilde{h}(f)\tilde{h}^*(f)}{S_n(f)}df
\langle d|h \rangle (t) = 4\int^\infty_0\frac{\tilde{d}(f)\tilde{h}^*(f)}{S_n(f)}e^{2\pi ift}df
\rho^2(t)\equiv\frac{1}{\langle h|h \rangle}|\langle d|h \rangle(t)|^2
\langle h|h \rangle \sim [\bar{h}(t) \ast \bar{h}(-t)]|_{t=0}
\langle d|h \rangle (t) \sim \,\bar{d}(t)\ast\bar{h}(-t)
\bar{S_n}(t)=\int^{+\infty}_{-\infty}S_n^{-1/2}(f)e^{2\pi ift}df
\left\{\begin{matrix} \bar{d}(t) = d(t) * \bar{S}_n(t) \\ \bar{h}(t) = h(t) * \bar{S}_n(t) \end{matrix}\right.
\int\tilde{x}_1(f) \cdot \tilde{x}_2(f) e^{2\pi ift}df= x_1(t)*x_2(t)
x_1(t)*x_2^*(-t) = x_1(t)\star x_2(t)
\int\tilde{x}_1(f) \cdot \tilde{x}^*_2(f) e^{2\pi ift}df= x_1(t)\star x_2(t)
  • Transform matched-filtering method from frequency domain to time domain.
  • The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):
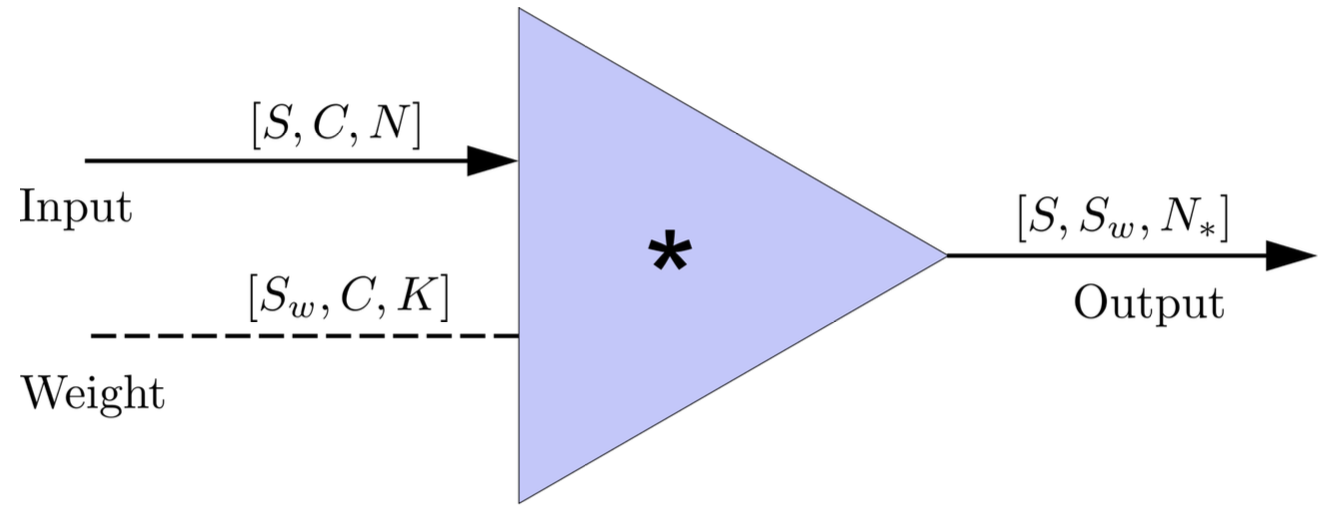
  • In the 1-D convolution (\(*\)) on Apache MXNet, given input data with shape [batch size, channel, length] :
output[n, i, :] = \sum^{channel}_{j=0} input[n,j,:] \ast weight[i,j,:]

FYI:       \(N_\ast = \lfloor(N-K+2P)/S\rfloor+1\)

（A schematic illustration for a unit of convolution layer)

Deep Learning Framework

Matched-filtering CNNs (MFCNN)

\(S_n(|f|)\) is the one-sided average PSD of \(d(t)\)

(whitening)

where

Time domain

Frequency domain

(normalizing)

(matched-filtering)

\langle h|h \rangle = 4\int^\infty_0\frac{\tilde{h}(f)\tilde{h}^*(f)}{S_n(f)}df
\langle d|h \rangle (t) = 4\int^\infty_0\frac{\tilde{d}(f)\tilde{h}^*(f)}{S_n(f)}e^{2\pi ift}df
\rho^2(t)\equiv\frac{1}{\langle h|h \rangle}|\langle d|h \rangle(t)|^2
\langle h|h \rangle \sim [\bar{h}(t) \ast \bar{h}(-t)]|_{t=0}
\langle d|h \rangle (t) \sim \,\bar{d}(t)\ast\bar{h}(-t)
\bar{S_n}(t)=\int^{+\infty}_{-\infty}S_n^{-1/2}(f)e^{2\pi ift}df
\left\{\begin{matrix} \bar{d}(t) = d(t) * \bar{S}_n(t) \\ \bar{h}(t) = h(t) * \bar{S}_n(t) \end{matrix}\right.
\int\tilde{x}_1(f) \cdot \tilde{x}_2(f) e^{2\pi ift}df= x_1(t)*x_2(t)
\int\tilde{x}_1(f) \cdot \tilde{x}^*_2(f) e^{2\pi ift}df= x_1(t)\star x_2(t)
  • Transform matched-filtering method from frequency domain to time domain.
  • The square of matched-filtering SNR for a given data \(d(t) = n(t)+h(t)\):

Deep Learning Framework

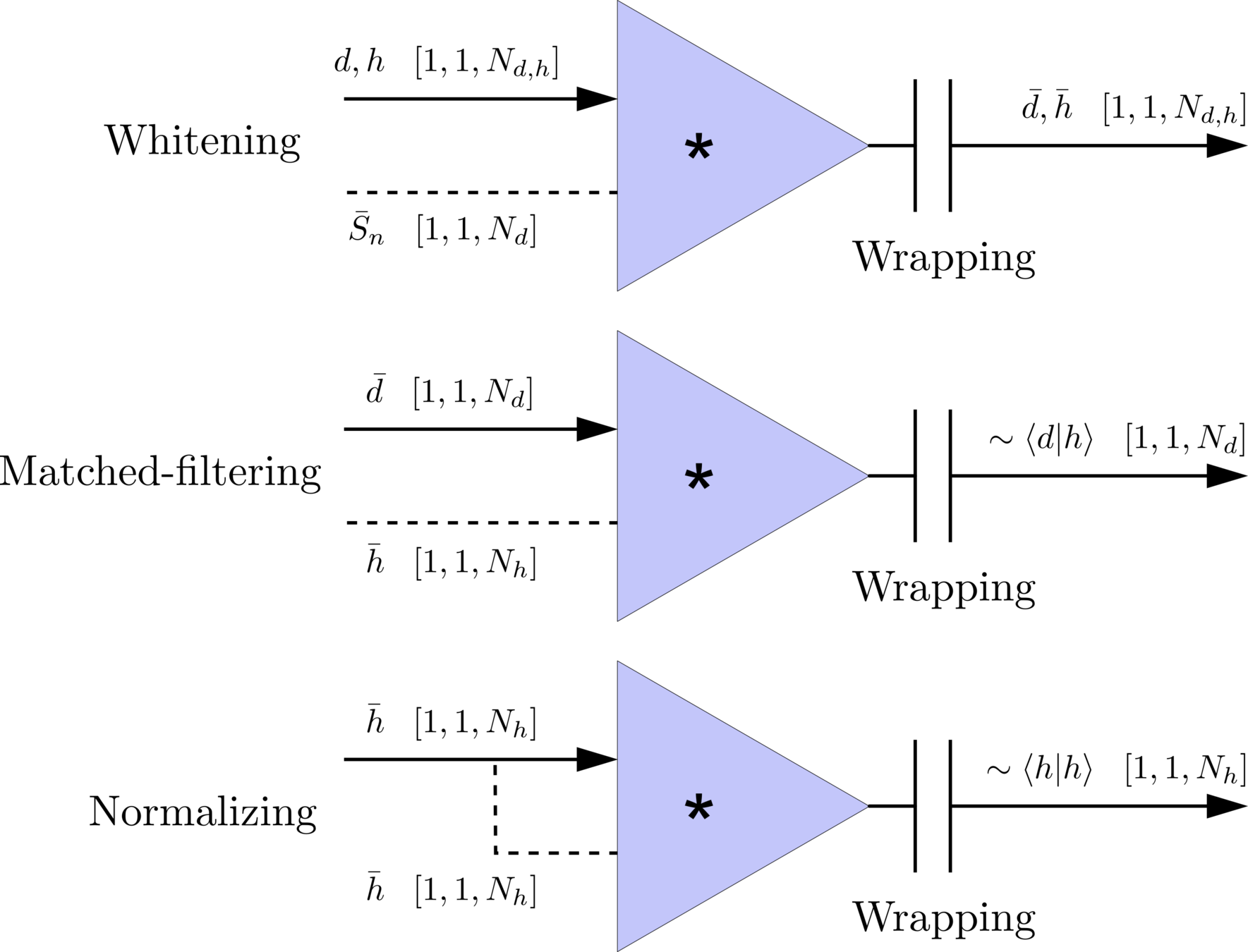
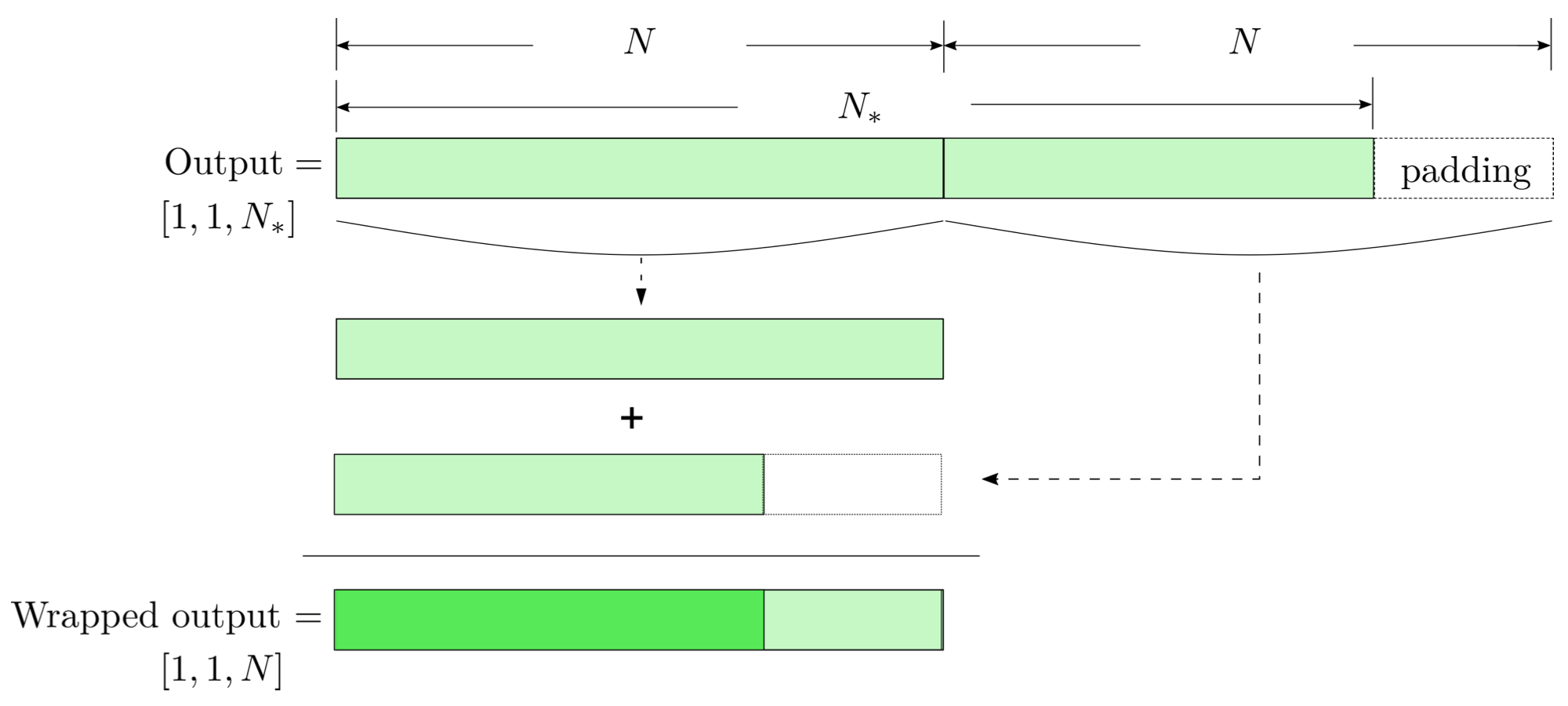
modulo-N circular convolution

x_1(t)*x_2^*(-t) = x_1(t)\star x_2(t)

Matched-filtering CNNs (MFCNN)

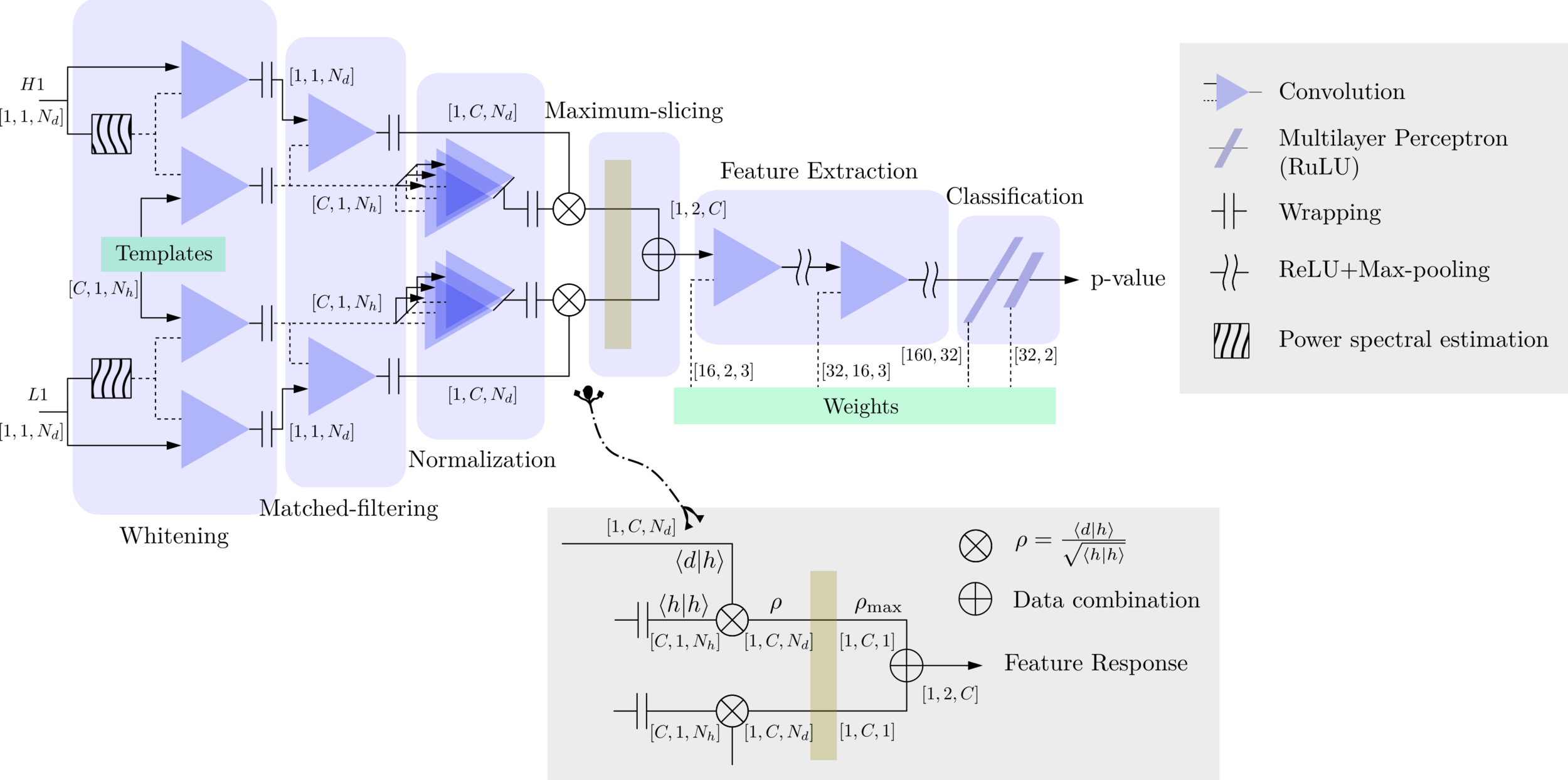
  • The structure of MFCNN:

Input

Output

Matched-filtering CNNs (MFCNN)

  • The structure of MFCNN:

Input

Output

C_0 = \mathop{\arg\max}_{C}\rho[1,C,N] \,,\\ N_0 = \mathop{\arg\max}_{N} \,\langle d \mid h\rangle[1,C_0,N]
  • In the meanwhile, we can obtain the optimal time \(N_0\) (relative to the input) of feature response of matching by recording the location of the maxima value corresponding to the optimal template \(C_0\).

Matched-filtering CNNs (MFCNN)

  • The structure of MFCNN:

Input

Output

C_0 = \mathop{\arg\max}_{C}\rho[1,C,N] \,,\\ N_0 = \mathop{\arg\max}_{N} \,\langle d \mid h\rangle[1,C_0,N]
  • In the meanwhile, we can obtain the optimal time \(N_0\) (relative to the input) of feature response of matching by recording the location of the maxima value corresponding to the optimal template \(C_0\).
import mxnet as mx
from mxnet import nd, gluon
from loguru import logger

def MFCNN(fs, T, C, ctx, template_block, margin, learning_rate=0.003):
    logger.success('Loading MFCNN network!')
    net = gluon.nn.Sequential()         
    with net.name_scope():
        net.add(MatchedFilteringLayer(mod=fs*T, fs=fs,
                                      template_H1=template_block[:,:1],
                                      template_L1=template_block[:,-1:]))
        net.add(CutHybridLayer(margin = margin))
        net.add(Conv2D(channels=16, kernel_size=(1, 3), activation='relu'))
        net.add(MaxPool2D(pool_size=(1, 4), strides=2))
        net.add(Conv2D(channels=32, kernel_size=(1, 3), activation='relu'))    
        net.add(MaxPool2D(pool_size=(1, 4), strides=2))
        net.add(Flatten())
        net.add(Dense(32))
        net.add(Activation('relu'))
        net.add(Dense(2))
	# Initialize parameters of all layers
    net.initialize(mx.init.Xavier(magnitude=2.24), ctx=ctx, force_reinit=True)
    return net

The available codes: https://gist.github.com/iphysresearch/a00009c1eede565090dbd29b18ae982c

1 sec duration
35 templates used

Training Configuration and Search Methodology

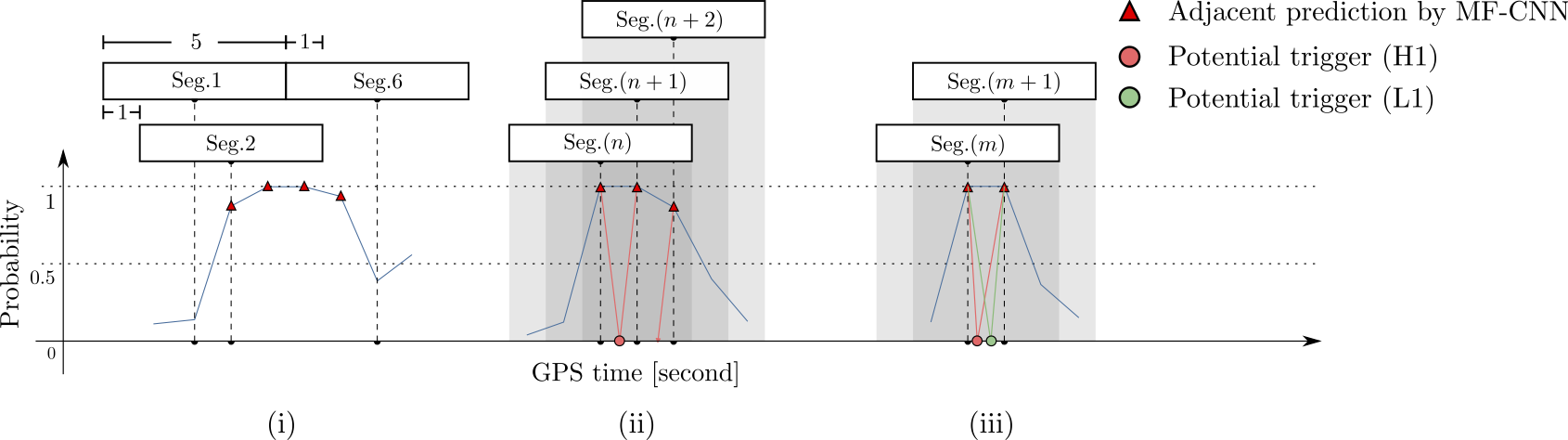
  • Every 5 seconds segment as input of our MF-CNN with a step size of 1 second.
  • The model can scan the whole range of the input segment and output a probability score.
  • In the ideal case, with a GW signal hiding in somewhere, there should be 5 adjacent predictions for it with respect to a threshold.

FYI: sampling rate = 4096Hz

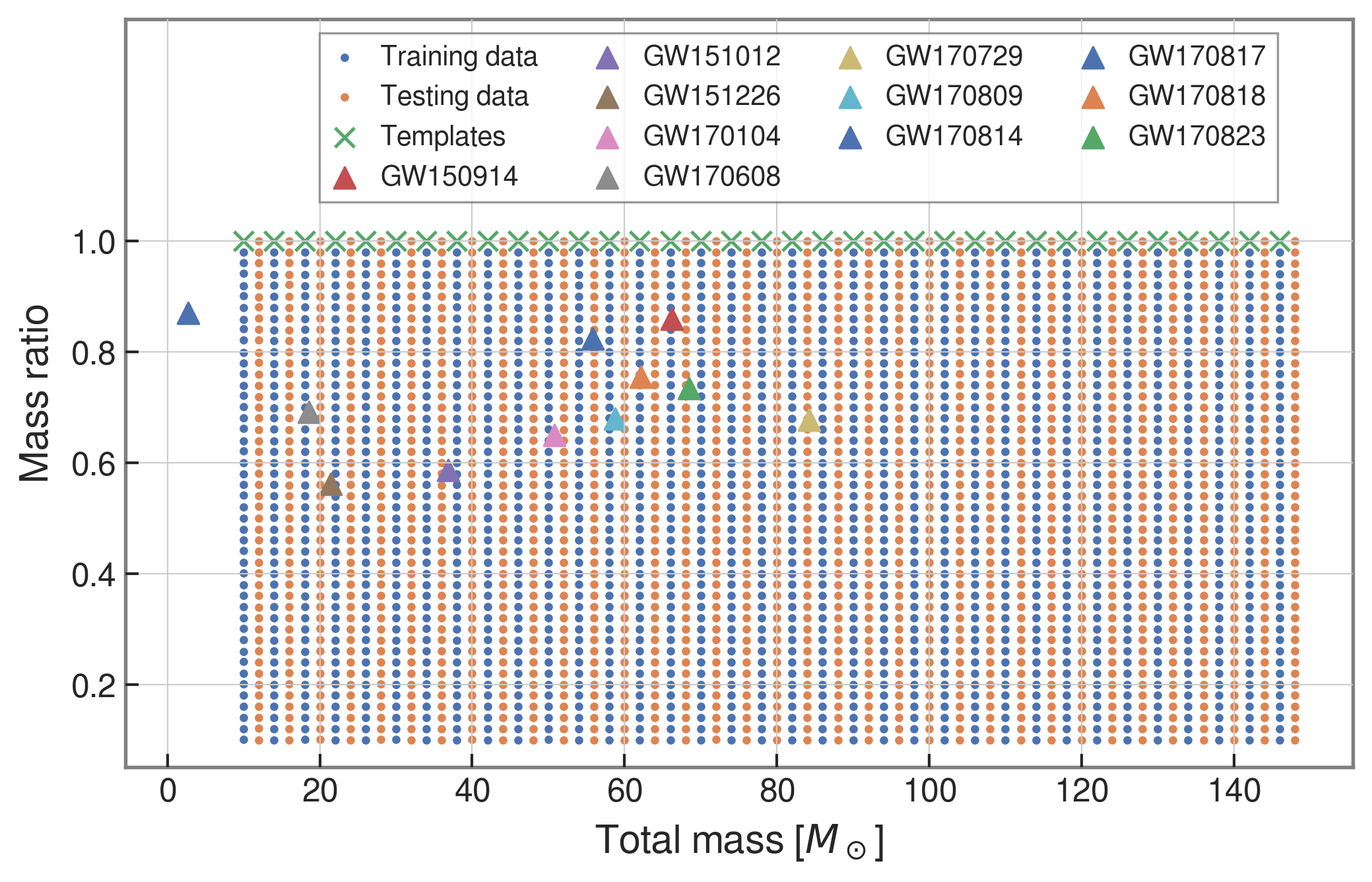
  • We use SEOBNRE model [Cao et al. (2017), Liu et al. (2020)] to generate waveform, we only consider circular, spinless binary black holes.
  • The background noises for training/testing are sampled from a small closed set (33*4096s) in the first observation run (O1) in the absence of the segments (4096s) containing the first 3 GW events.
templates waveforms (train/test)
Number 35 1610
Length (sec) 1 5
equal mass

Training Configuration and Search Methodology

  • We use SEOBNRE model [Cao et al. (2017), Liu et al. (2020)] to generate waveform, we only consider circular, spinless binary black holes.
  • The background noises for training/testing are sampled from a small closed set (33*4096s) in the first observation run (O1) in the absence of the segments (4096s) containing the first 3 GW events.
  • Every 5 seconds segment as input of our MF-CNN with a step size of 1 second.
  • The model can scan the whole range of the input segment and output a probability score.
  • In the ideal case, with a GW signal hiding in somewhere, there should be 5 adjacent predictions for it with respect to a threshold.

FYI: sampling rate = 4096Hz

templates waveforms (train/test)
Number 35 1610
Length (sec) 1 5
equal mass

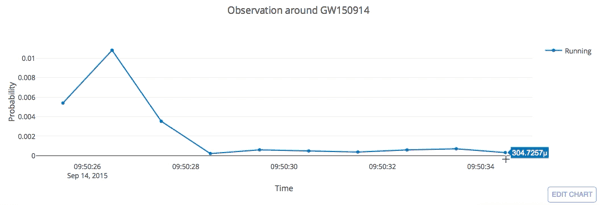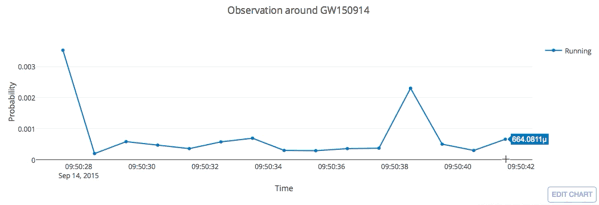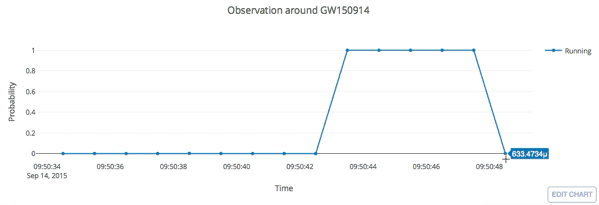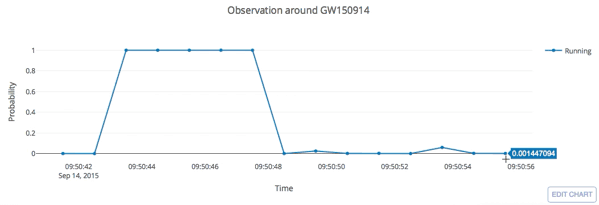
input

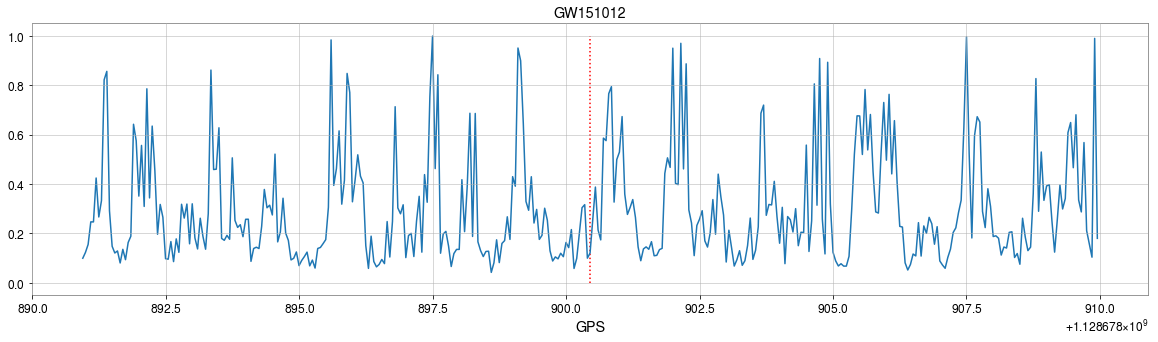
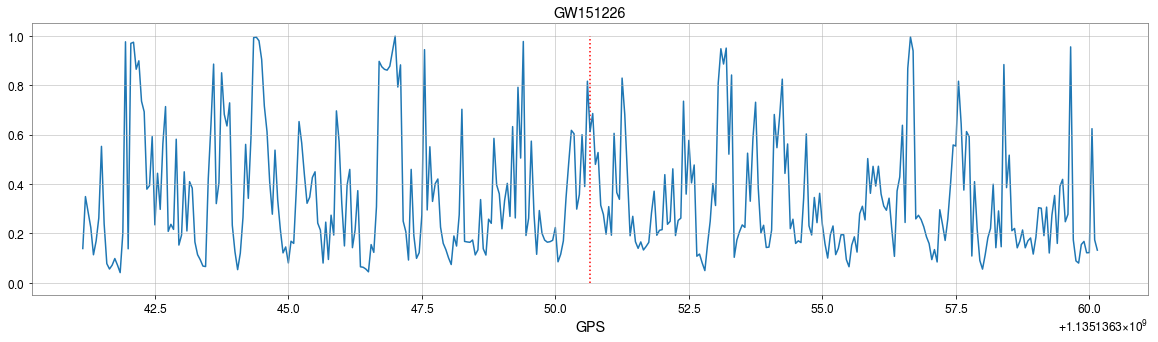
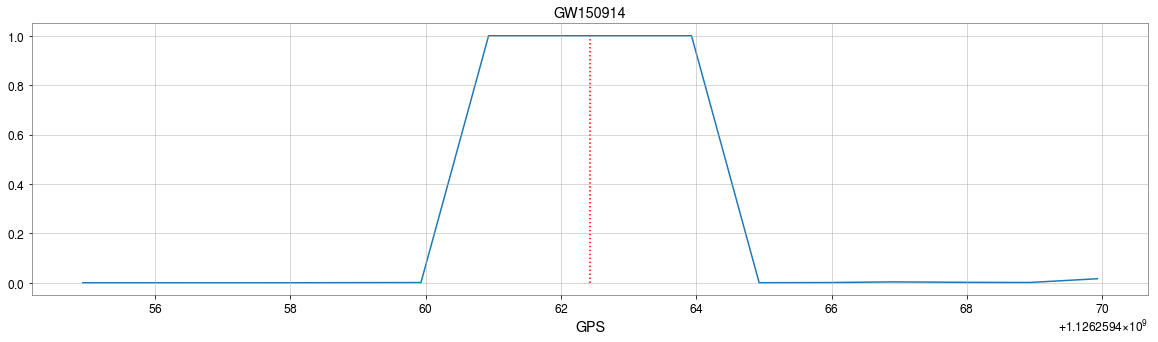
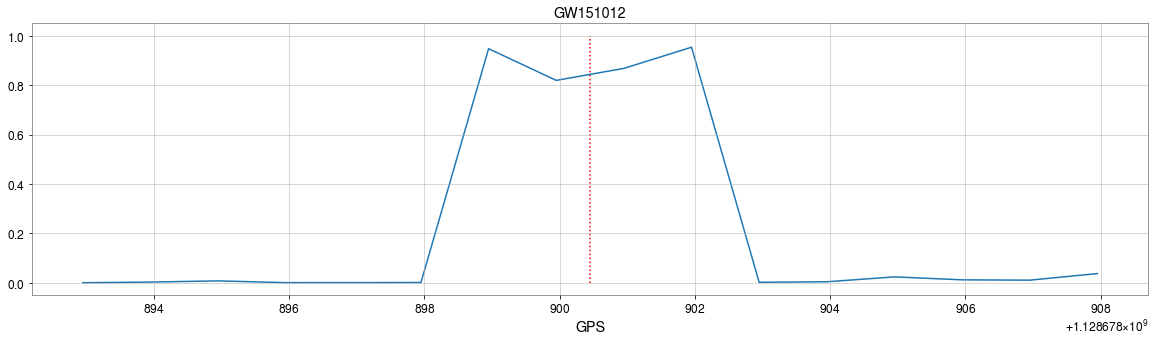
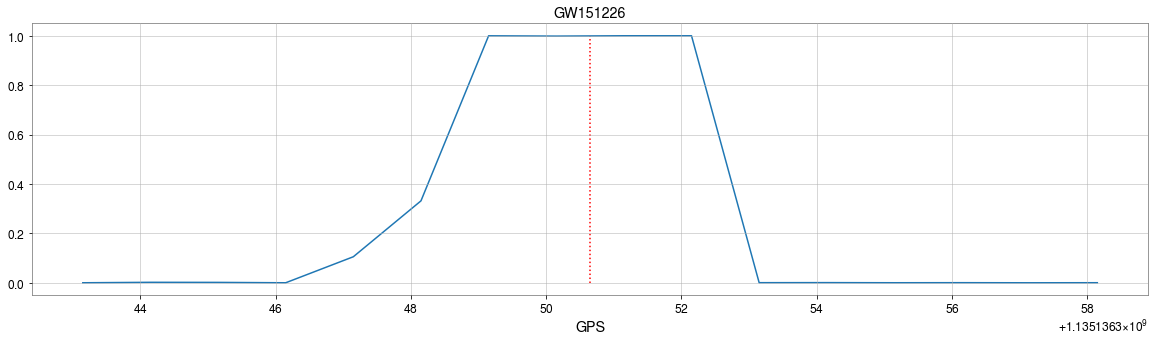
Result: GW events in O1/O2 & GWTC-2

  • Recovering the three GW events in O1.
  • Recovering all GW events in O2, even including GW170817 event.

Result: GW events in O1/O2 & GWTC-2

  • Recovering the three GW events in O1.
  • Recovering all GW events in O2, even including GW170817 event.

Result: GW events in O1/O2 & GWTC-2

  • Recovering the three GW events in O1.
  • Recovering all GW events in O2, even including GW170817 event.
  • (Some results on statistical significance on O1 data &​ glitches identification have skipped here)

 

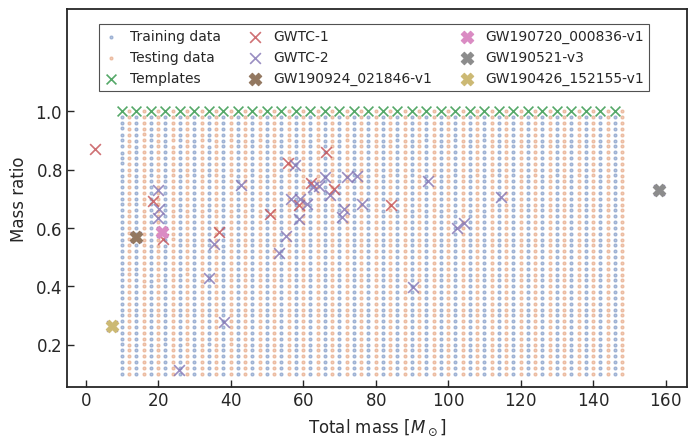
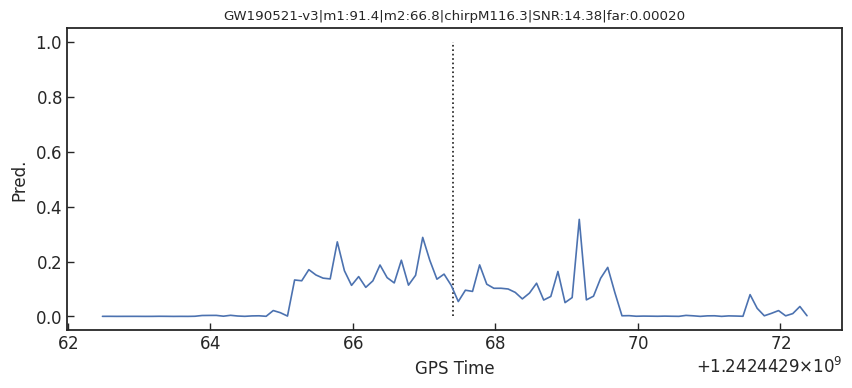
  • Consider 33 events (with H1 detector data) in O3a (39 events in total), 4 of them are misclassified. 
GW170817
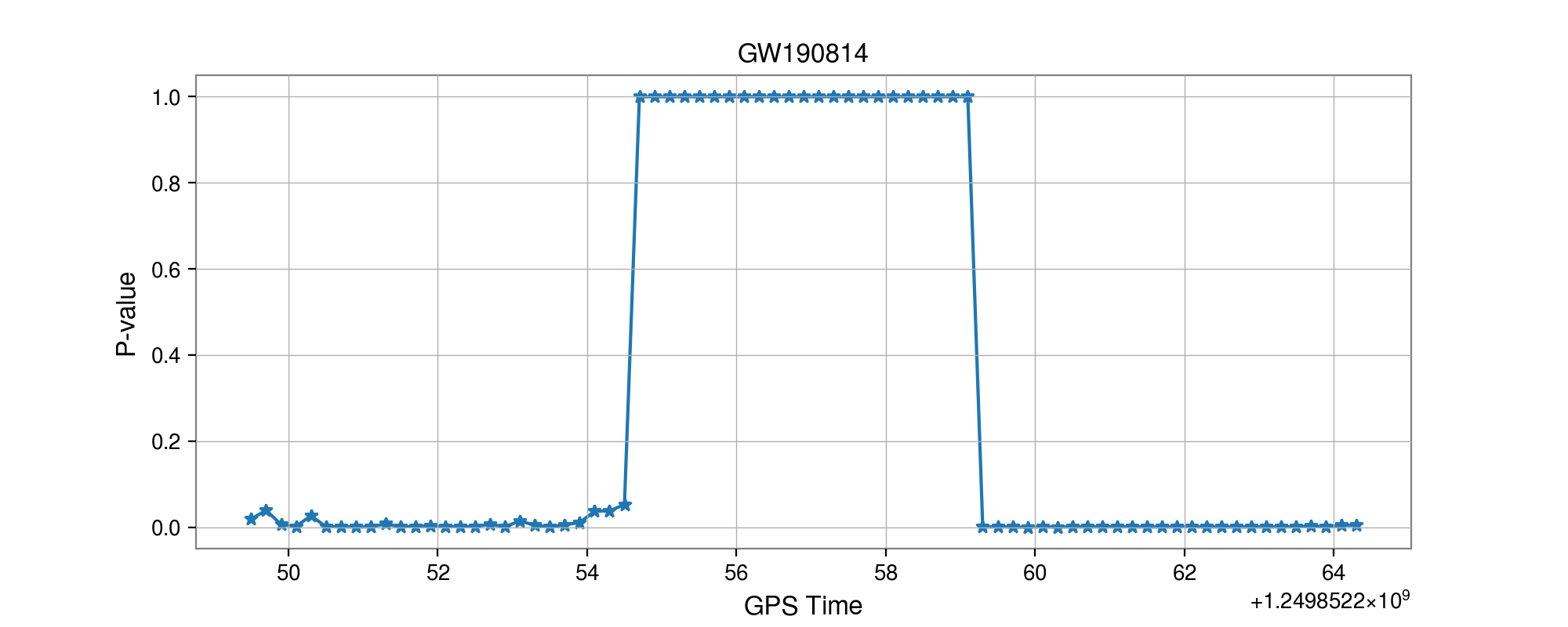
GW190814
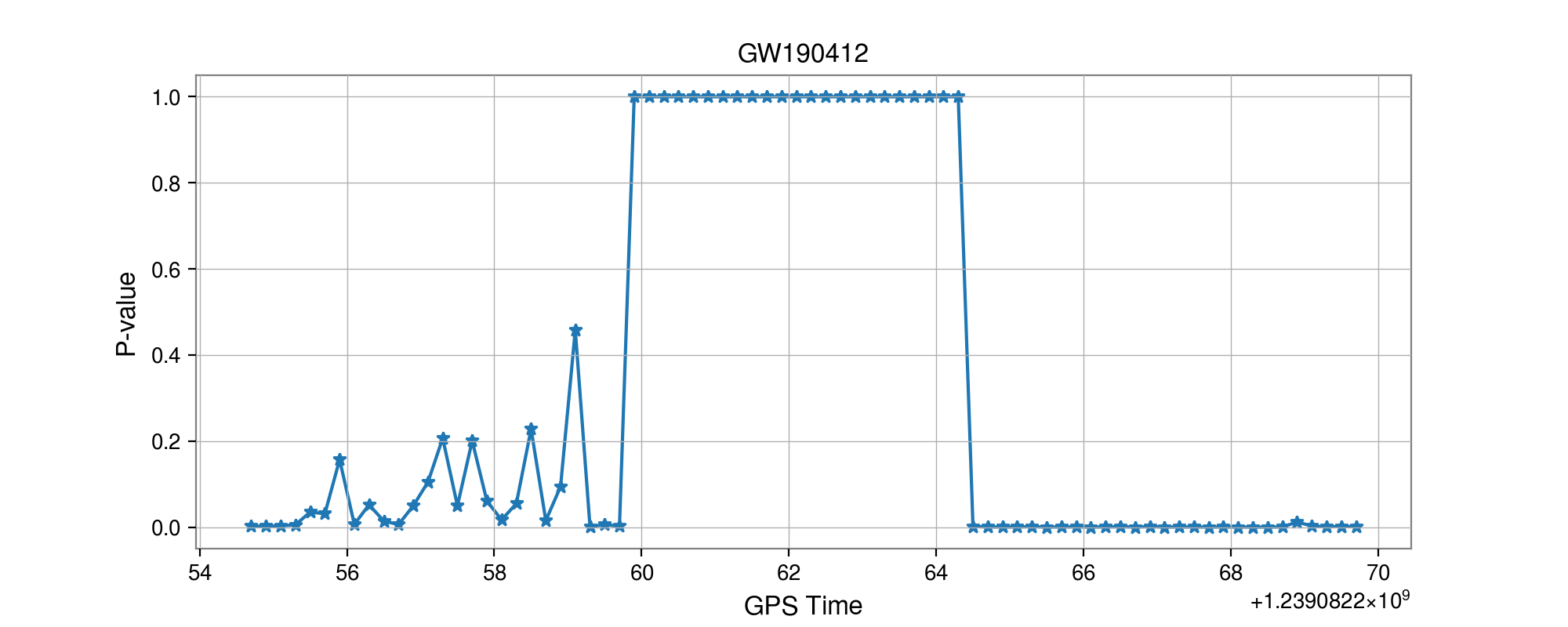
GW190412
  • Selected:

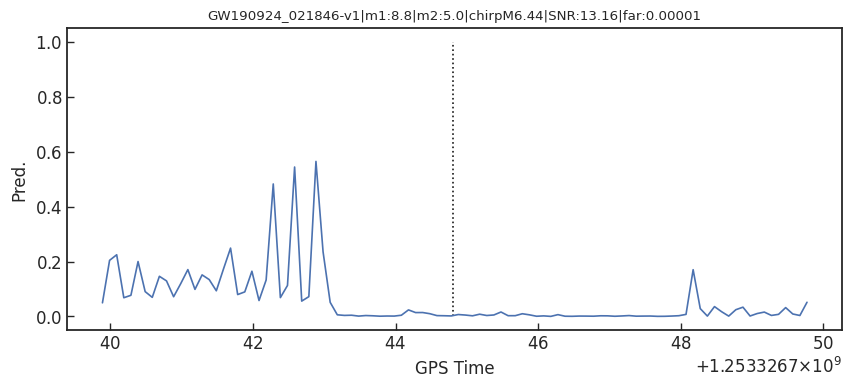
Summary & Lesson Learned

  • Some benefits from MFCNN architecture for GW detection:
    • Simple configuration for GW data generation and almost no data pre-processing.
    • It works on a non-stationary background.
    • Easy parallel deployments, multiple detectors can benefit a lot from this design.
    • Efficient searching with a fixed window.
  • Recovering all GW events in GWTC-1 and 29 of 33 GW events in GWTC-2 (39 events in total).
  • We realized that:
    • GW templates can be used as likely known features for signal recognition.
    • Generalization of both matched-filtering and neural networks.
    • Linear filters (i.e. matched-filtering) in signal processing can be rewritten as neural layers (i.e. CNNs).

Summary & Lesson Learned

  • The output of neural network (Softmax function) is not an optimal and reasonable detection statistic.
    • "The negative log-likelihood cost function always strongly penalizes the most active incorrect prediction."
      And the correctly classified examples will contribute little to the overall training cost.
      —— I. Goodfellow, Y. Bengio, A. Courville. Deep Learning.
    • Need more efforts to think about how to model a reliable, reasonable and trusted algorithm to recognize GW signal.

 

  • With optimal linear matched-filtering method, is there exist an optimal way to search weak signals by non-linear filter in real LIGO recordings?
    • Based on deep Learning technique, more efforts focus on building a non-linear neural network outperforming matched-filtering techniques.
    • or based on signal processing theory, is it possible to propose a better and effective non-linear filtering method, inspired by deep learning?

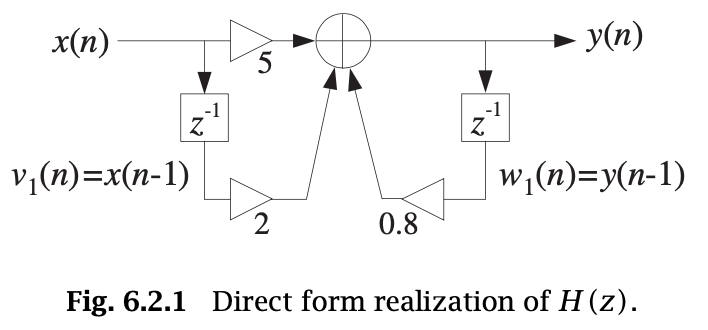
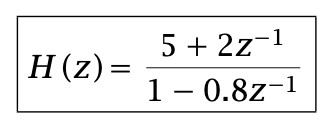
An example of transfer function:

CNN

RNN

Softmax function:

Score

Pred.

Summary & Lesson Learned

  • The output of neural network (Softmax function) is not an optimal and reasonable detection statistic.
    • "The negative log-likelihood cost function always strongly penalizes the most active incorrect prediction."
      And the correctly classified examples will contribute little to the overall training cost.
      —— I. Goodfellow, Y. Bengio, A. Courville. Deep Learning.
    • Need more efforts to think about how to model a reliable, reasonable and trusted algorithm to recognize GW signal.

 

  • With optimal linear matched-filtering method, is there exist an optimal way to search weak signals by non-linear filter in real LIGO recordings?
    • Based on deep Learning technique, more efforts focus on building a non-linear neural network outperforming matched-filtering techniques.
    • or based on signal processing theory, is it possible to propose a better and effective non-linear filtering method, inspired by deep learning?

This slide: https://slides.com/iphysresearch/kiw7

for _ in range(num_of_audiences):
    print('Thank you for your attention! 🙏')

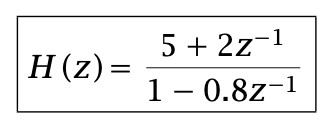
A example of Transfer function:

Softmax function:

Pred.