Particle Swarm Optimization From Scratch Using Python

Particle Swarm Optimization (PSO)

This slide: https://slides.com/iphysresearch/pso

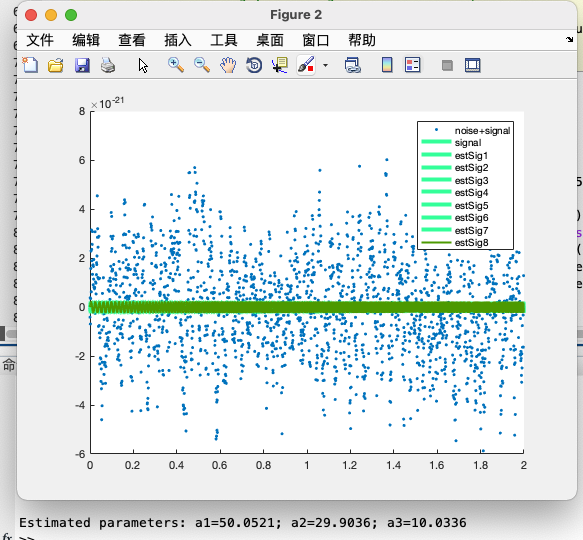
Particle Swarm Optimization (PSO)

Code: https://github.com/iphysresearch/PSO_python_demo

This slide: https://slides.com/iphysresearch/pso

function innProd = innerprodpsd(xVec,yVec,sampFreq,psdVals)
%P = INNERPRODPSD(X,Y,Fs,Sn)
%Calculates the inner product of vectors X and Y for the case of Gaussian
%stationary noise having a specified power spectral density. Sn is a vector
%containing PSD values at the positive frequencies in the DFT of X
%and Y. The sampling frequency of X and Y is Fs.

%Soumya D. Mohanty, Mar 2019

nSamples = length(xVec);
if length(yVec) ~= nSamples
    error('Vectors must be of the same length');
end
kNyq = floor(nSamples/2)+1;
if length(psdVals) ~= kNyq
    error('PSD values must be specified at positive DFT frequencies');
end

fftX = fft(xVec);
fftY = fft(yVec);
%We take care of even or odd number of samples when replicating PSD values
%for negative frequencies
negFStrt = 1-mod(nSamples,2);
psdVec4Norm = [psdVals,psdVals((kNyq-negFStrt):-1:2)];

dataLen = sampFreq*nSamples;

innProd = (1/dataLen)*(fftX./psdVec4Norm)*fftY';
innProd = real(innProd);

def innerprodpsd(xVec,yVec,sampFreq,psdVals):
    """
    P = INNERPRODPSD(X,Y,Fs,Sn)
    Calculates the inner product of vectors X and Y for the case of Gaussian
    stationary noise having a specified power spectral density. Sn is a vector
    containing PSD values at the positive frequencies in the DFT of X
    and Y. The sampling frequency of X and Y is Fs.

    Soumya D. Mohanty, Mar 2019

    He Wang
    Mar 2021: Adapted for python
    """
    
    nSamples = len(xVec)
    assert len(yVec) == nSamples, 'Vectors must be of the same length'
    kNyq = np.floor(nSamples/2)+1
    assert len(psdVals) == kNyq, 'PSD values must be specified at positive DFT frequencies'
    
    # Why 'scipy.fftpack.fft'? 
    # See: https://iphysresearch.github.io/blog/post/signal_processing/fft/#efficiency-of-the-algorithms
    fftX = fft(xVec)
    fftY = fft(yVec)
    #We take care of even or odd number of samples when replicating PSD values
    #for negative frequencies
    negFStrt = 1 - np.mod(nSamples, 2)
    psdVec4Norm = np.concatenate((psdVals, psdVals[(kNyq.astype('int')-negFStrt)-1:0:-1]))
    
    dataLen = sampFreq * nSamples
    innProd = np.sum((1/dataLen) * (fftX / psdVec4Norm)*fftY.conj())
    innProd = np.real(innProd)
    return innProd

MATLAB

Python

Particle Swarm Optimization (PSO)

Code: https://github.com/iphysresearch/PSO_python_demo

This slide: https://slides.com/iphysresearch/pso

# Python
from scipy.signal import firwin2, firwin

f1 = firwin(30+1, (30/256), pass_zero='lowpass',)
f2 = firwin(30+1, [(30/256), 50/256], pass_zero='bandpass',)
f2 = firwin(30+1, (30/256), pass_zero='highpass',)

ff = firwin2(150+1, [0.0, 0.5, 1.0], [1.0, 1.0, 0.0])

# MATLAB

f1 = fir1( 30, 30/2/(256/2), 'low' )
f2 = fir1( 30, [(30)/2/(256/2),(50)/2/(256/2)], 'bandpass' )
f3 = fir1( 30, 30/2/(256/2), 'high' )

ff = fir2(150,[0.0, 0.5, 1.0], [1.0, 1.0, 0.0])

partCoord

partVel

partPbest

partLocalBest

-1

x\sim U(0,1)

v\sim -x+U(0,1)

partFitPbest

partFitCurr

partFitLbest

partInertia

\infty

0.9

partFlagFitEval

partFitEvals

gbestVal

gbestLoc

bestFitness

\infty

```
partCoord: Particle location
```
```
partVel: Particle velocity 
```
```
partPbest: Particle pbest
```
```
partFitPbest: Fitness value at pbest
```

partFitCurr: Fitness value at current iteration

partFitLbest: Fitness value at local best location

```
partInertia: Inertia weight
```

partLocalBest: Particles local best location

partFlagFitEval: Flag whether fitness should be computed or not

partFitEvals: Number of fitness evaluations

gbestVal: Best value found by the swarm over its history

gbestLoc: Location of the best value found by the swarm over its history

bestFitness: Best value found by the swarm at the current iteration

Initialization

popsize = 40

Number of PSO particles

pop

Step.0: Specify information about each particle stored as a row of a matrix ('pop').

Fitness

Location

partCoord

partVel

partPbest

partLocalBest

k th

-1

x\sim U(0,1)

v\sim -x+U(0,1)

partFitPbest

partFitCurr

partFitLbest

partInertia

\infty

partFlagFitEval

partFitEvals

gbestVal

gbestLoc

bestFitness

\infty

Start PSO iterations

fitfuncHandle

(glrtqcsig4pso)

Step.1: for each particle, update partFitCurr / partFitEvals / partFitPbest / partPbest.

Output from your fitness function

Escape from special boundary condition

\vdots

partFitCurr

for each particle

\vdots

partPbest

partCoord

popsize = 40

Number of PSO particles

partFitCurr

partFitPbest

partCoord

\text{ if}\,\,\,\,\,<\,\,\,\,\,,

partFitLbest

pop

0.9

if partFlagFitEval

partFitEvals += 1

partFitEvals += 0

For each particle, record the best location and fitness value over its history.
(记录个人历史最好成绩)

Fitness

Location

partCoord

partVel

partPbest

partLocalBest

k' th

-1

x\sim U(0,1)

v\sim -x+U(0,1)

x_\text{best}

partFitPbest

partFitCurr

partFitLbest

partInertia

\text{float}

\infty

\text{float}

partFlagFitEval

partFitEvals

gbestVal

gbestLoc

bestFitness

\infty

fitfuncHandle

(glrtqcsig4pso)

Step.2: for all particles, update gbestLoc / gbestVal.

Output from your fitness function

find the global minimum

\text{ if}\,\,\,\,\,<\,\,\,\,\,,

gbestVal

gbestLoc

\infty

+=1

partCoord

popsize = 40

Number of PSO particles

partFitCurr

partCoord

pop

0.9

0,1

Start PSO iterations

For all particles, record the best location and fitness value over their history.
(记录全局历史最好成绩)

Fitness

Location

partCoord

partVel

partPbest

partLocalBest

k th

popsize = 40

Number of PSO particles

-1

x\sim U(0,1)

v\sim -x+U(0,1)

partFitLbest

partInertia

\infty

partFlagFitEval

partFitEvals

0,1

gbestVal

gbestLoc

bestFitness

\infty

fitfuncHandle

(glrtqcsig4pso)

Step.3: for local neighborhood of each particle, update partFitLbest / partLocalBest.

Output from your fitness function

find the local minimum

(0,1)

\vdots

x_\text{best}

partFitPbest

partFitCurr

\text{float}

partLocalBest

partCoord

nbrhdSz \(\le\) 3

Number of particles in a ring topology neighborhood.

partFitLbest

partFitCurr

\text{ if}\,\,\,\,\,>\,\,\,\,\,,

partCoord

\vdots

pop

0.9

Eg:
For particle 1, its local neighborhood is: [5 1 2]
For particle 2, its local neighborhood is: [1 2 3]
For particle 3, its local neighborhood is: [2 3 4]
For particle 4, its local neighborhood is: [3 4 5]
For particle 5, its local neighborhood is: [4 5 1]

Start PSO iterations

For each particle, record the best location and fitness value of its local neighborhood.
(记录局部历史最好成绩)

Fitness

Location

pop

partCoord

partVel

partPbest

partLocalBest

k th

popsize = 40

Number of PSO particles

-1

x\sim U(0,1)

v\sim -x+U(0,1)

partFitLbest

partInertia

\text{float}

partFlagFitEval

partFitEvals

0\text{ or }1

gbestVal

gbestLoc

bestFitness

\infty

Step.4: for each particle (update velocity), update partVel / partFitCurr / partFlagFitEval.

(0,1)

\vdots

x_\text{best}

partFitPbest

partFitCurr

\text{float}

0.9 \rightarrow 0.2

0,1

partInertia \(\times\) partVel + \(c_1\) \(\times\) \(\chi_1\) \(\times\) ( partPbest - partCoord ) + \(c_2\) \(\times\) \(\chi_2\) \(\times\) ( partLocalBest - partCoord )

c_1 = 2; \chi_1\sim U(0,1)

NEW partVel

c_2 = 2; \chi_2\sim U(0,1)

partCoord +

NEW partVel

NEW partCoord

Start PSO iterations

For each particle, record the difference (velocity) in current iteration, update its coordinate.
(记录位置偏移量，更新各自的位置)

Fitness

Location

pop

partCoord

partVel

partPbest

partLocalBest

k th

popsize = 40

Number of PSO particles

-1

x\sim U(0,1)

v\sim -x+U(0,1)

partFitLbest

partInertia

\text{float}

partFlagFitEval

partFitEvals

0\text{ or }1

gbestVal

gbestLoc

bestFitness

\infty

Step.4: for each particle (update velocity), update partVel / partFitCurr / partFlagFitEval.

(0,1)

\vdots

x_\text{best}

partFitPbest

partFitCurr

\text{float}

0.9 \rightarrow 0.2

0,1

partInertia \(\times\) partVel + \(c_1\) \(\times\) \(\chi_1\) \(\times\) ( partPbest - partCoord ) + \(c_2\) \(\times\) \(\chi_2\) \(\times\) ( partLocalBest - partCoord )

c_1 = 2; \chi_1\sim U(0,1)

NEW partVel

c_2 = 2; \chi_2\sim U(0,1)

partCoord +

NEW partVel

NEW partCoord

Start PSO iterations

For each particle, record the difference (velocity) in current iteration, update its coordinate.
(记录位置偏移量，更新各自的位置)

Fitness

Location

Step.0

Step.1

Step.2

Step.3

Step.4

maxStep = 2000

Number of iterations for termination

nRuns = 8

Number of independent PSO runs

First run of PSO

Fitness

Location

"Particle Swarm Optimization Visually Explained":

https://towardsdatascience.com/particle-swarm-optimization-visually-explained-46289eeb2e14

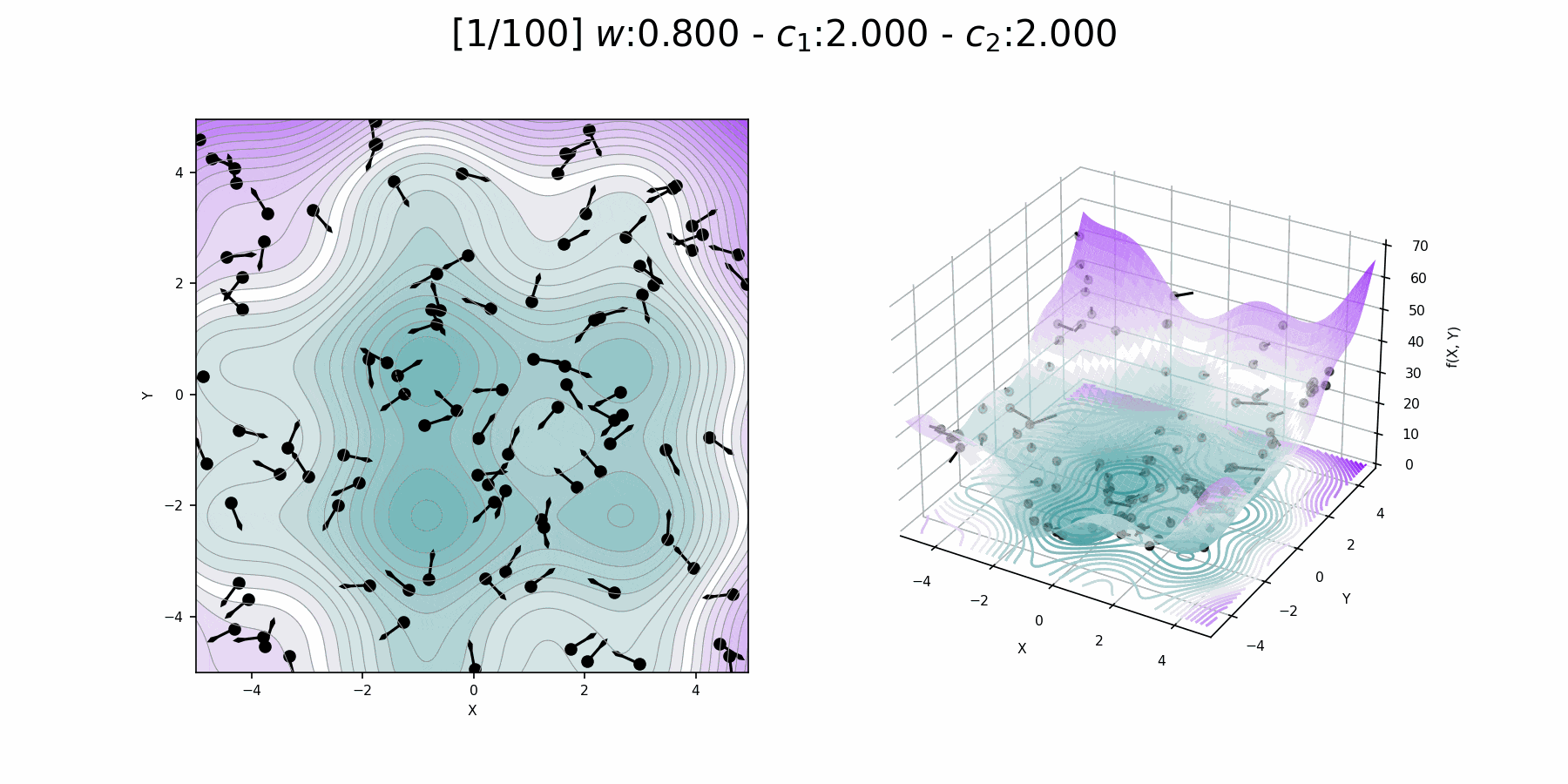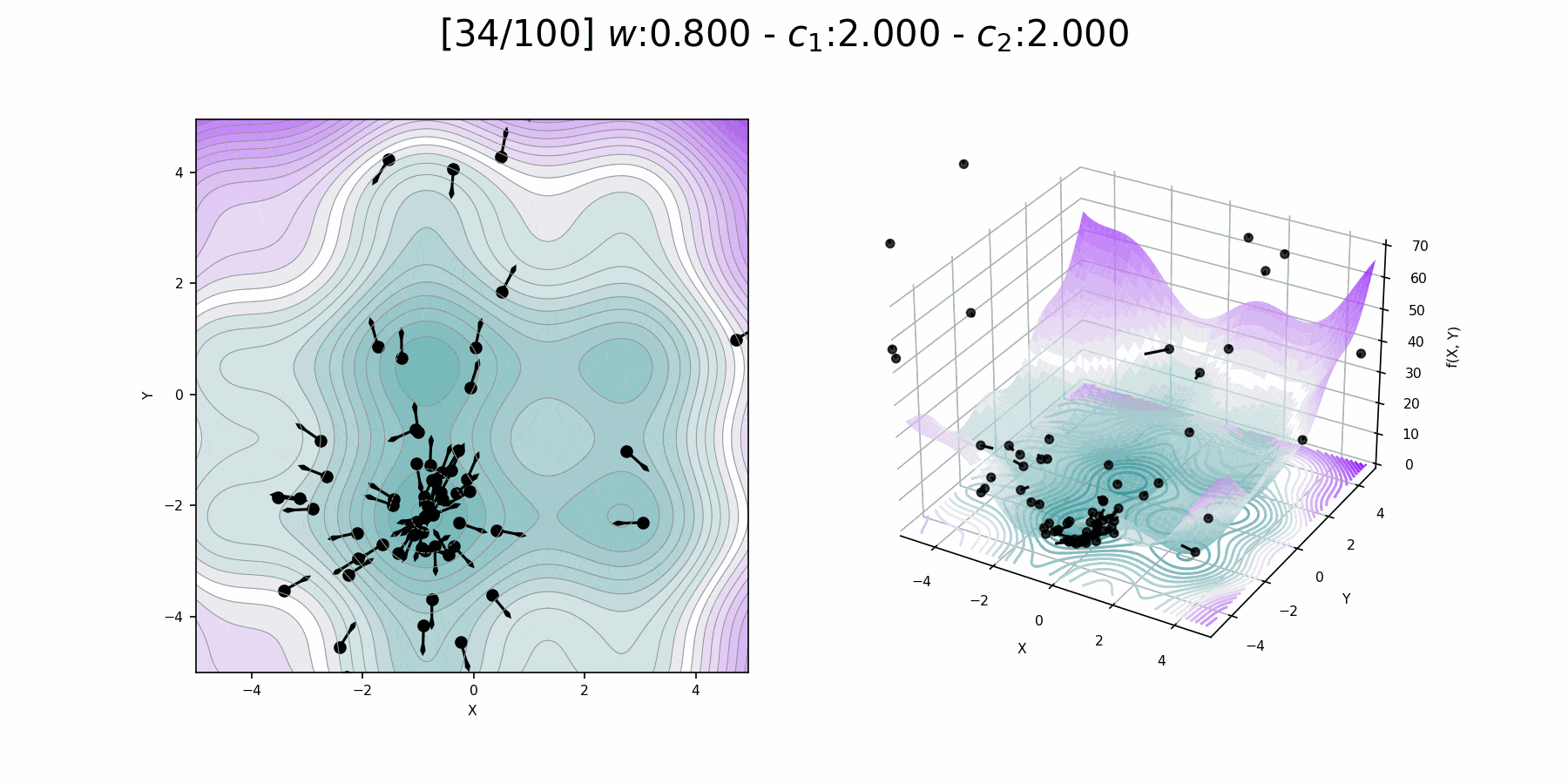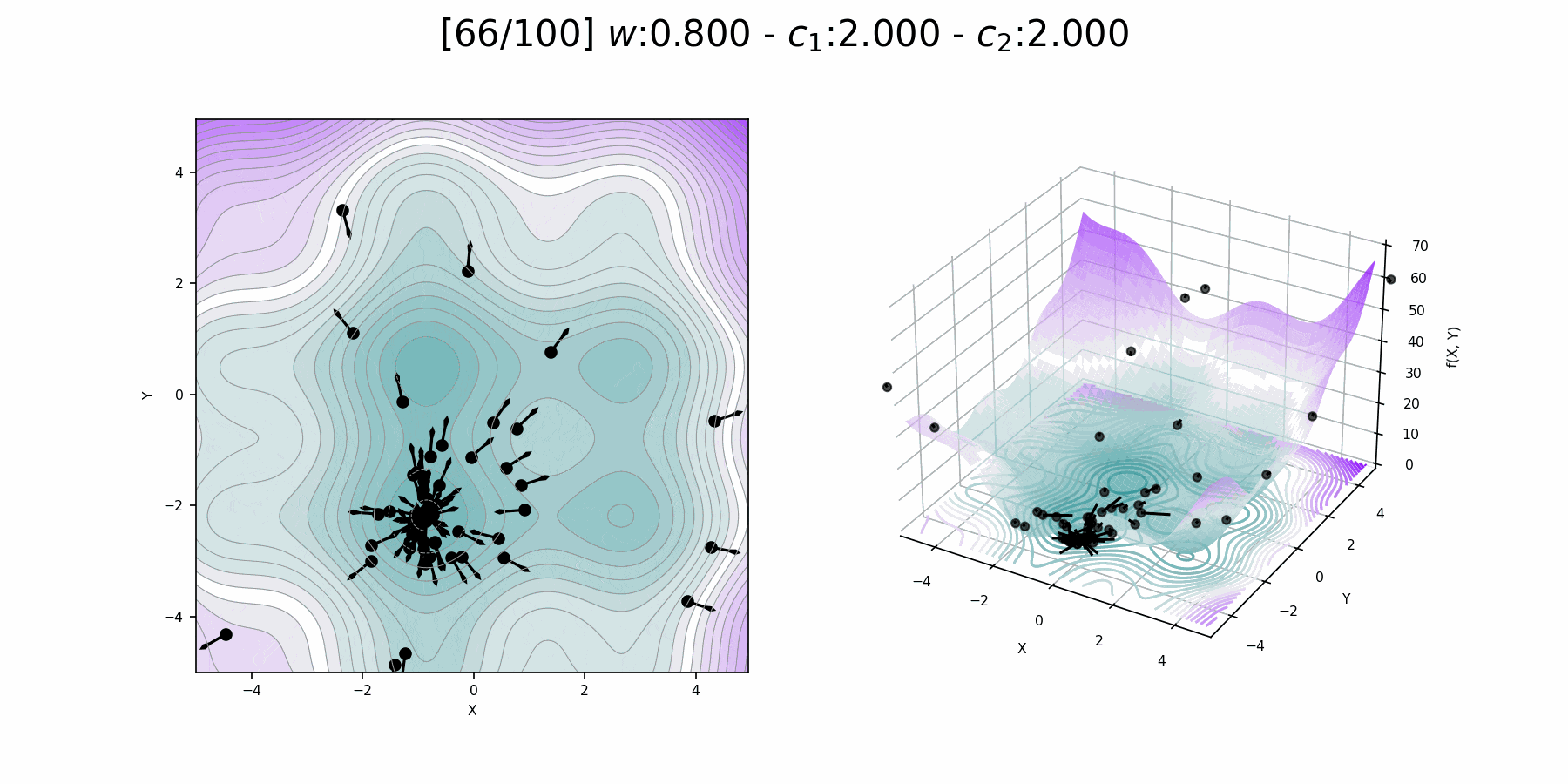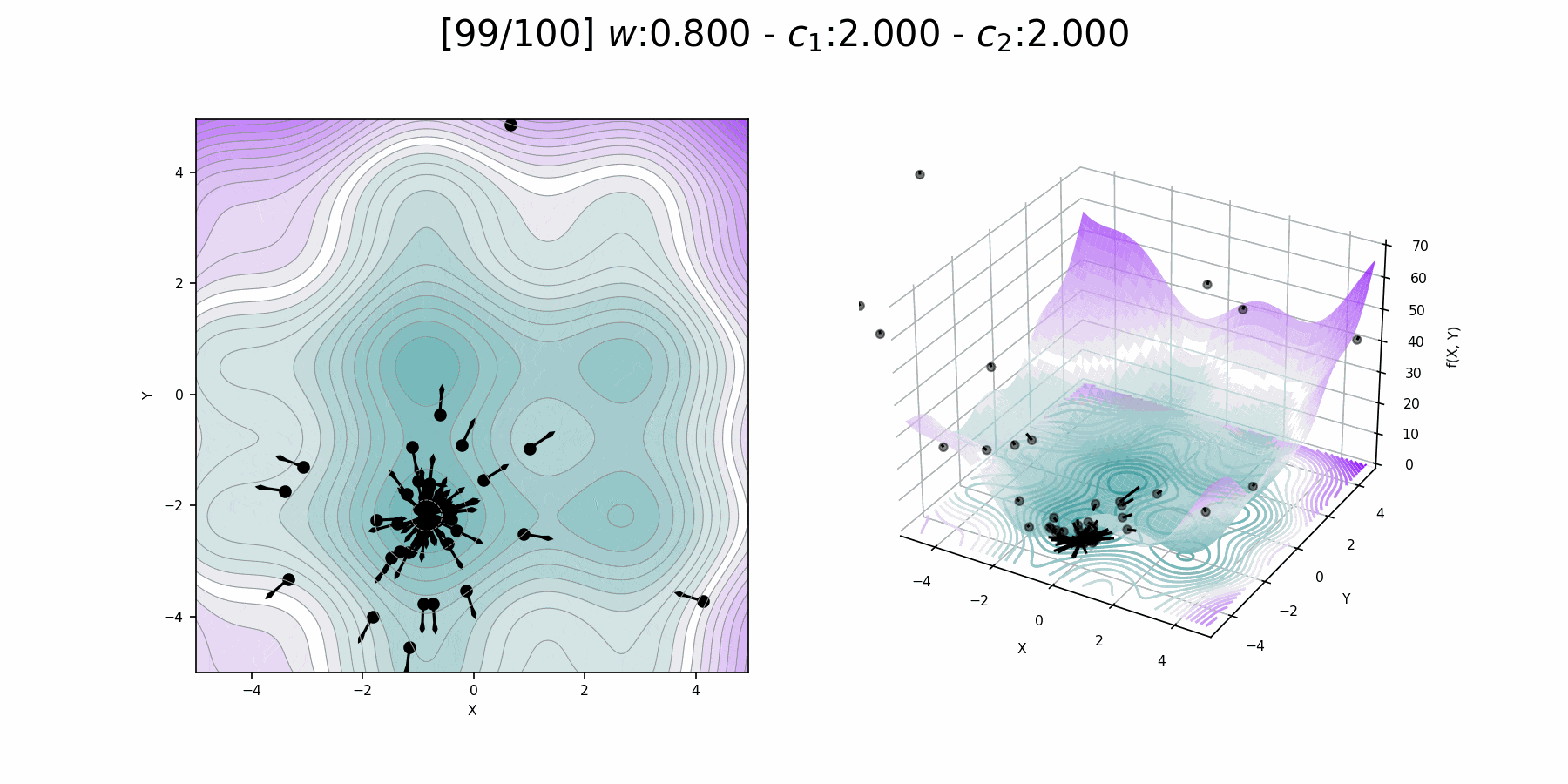
Inertia weight comparison

Fitness

Location

"Particle Swarm Optimization Visually Explained":

https://towardsdatascience.com/particle-swarm-optimization-visually-explained-46289eeb2e14

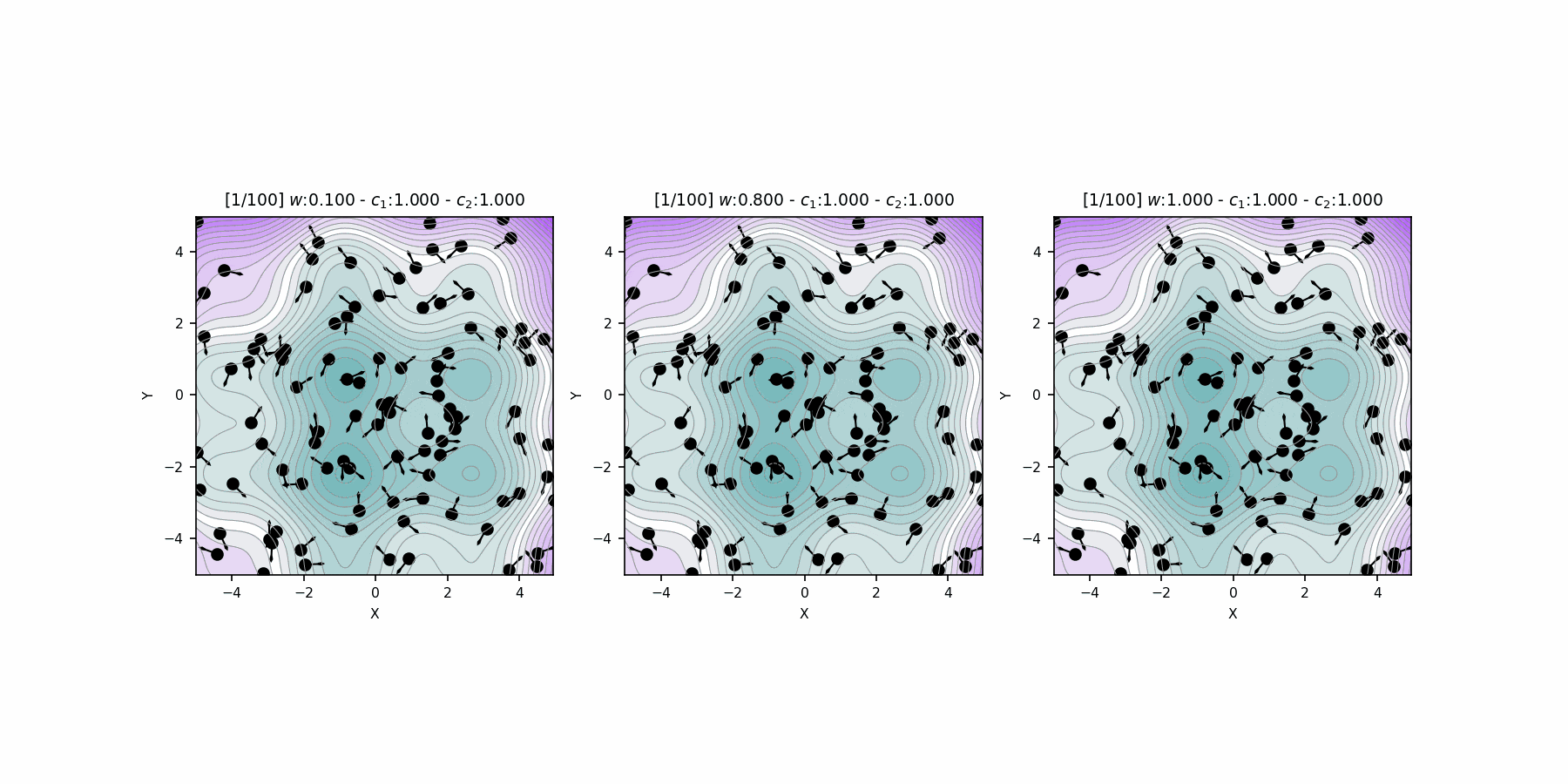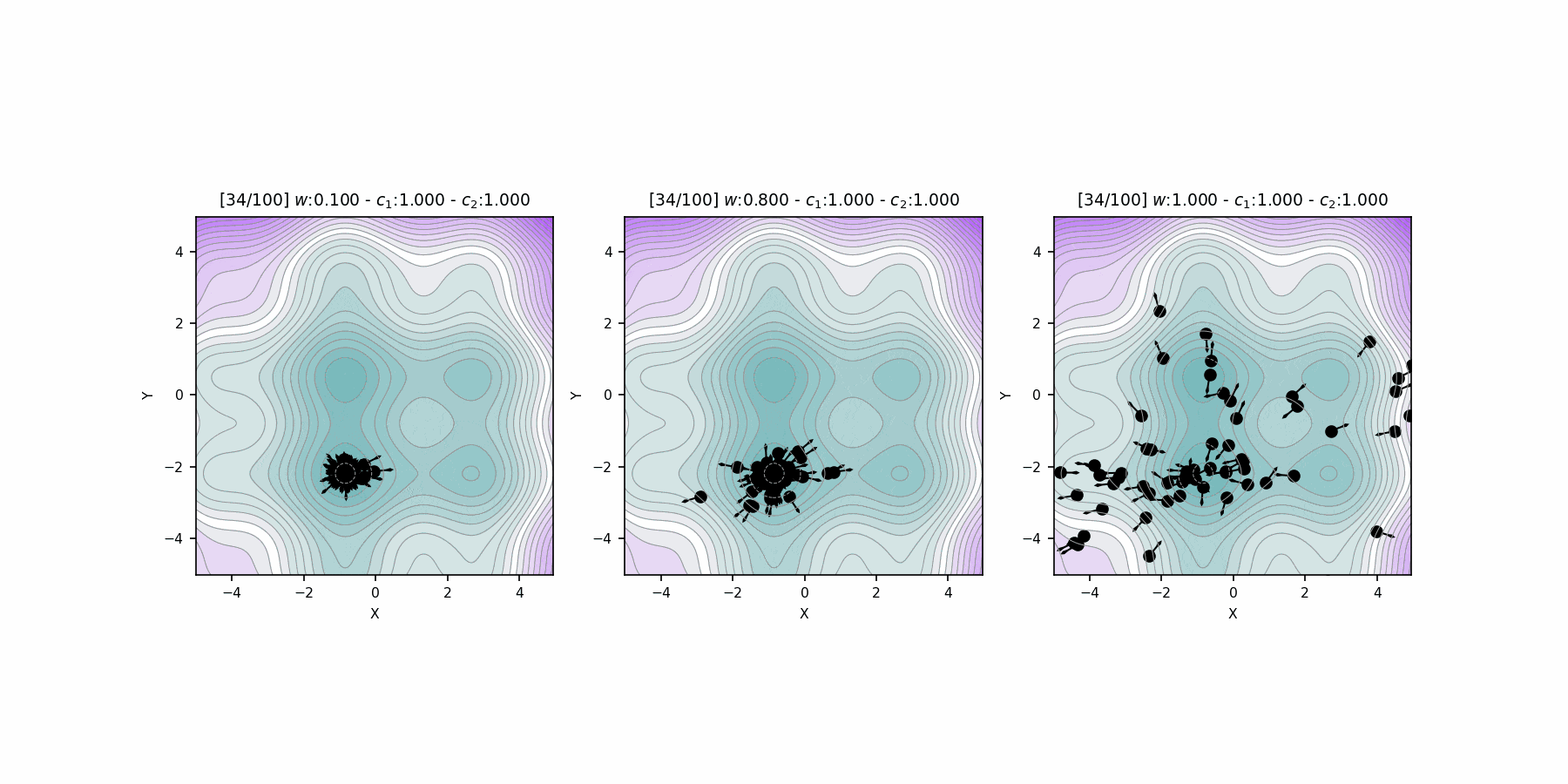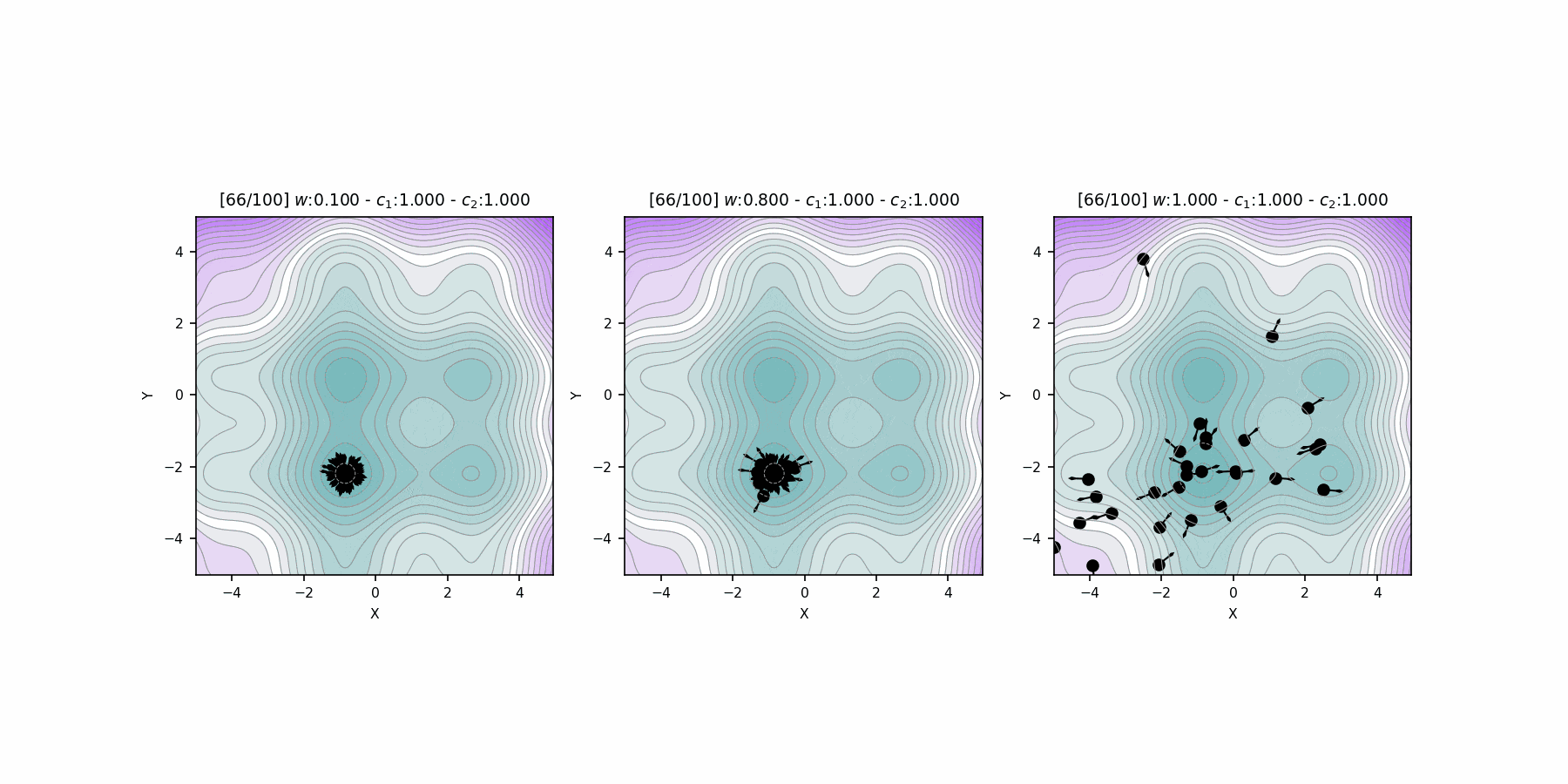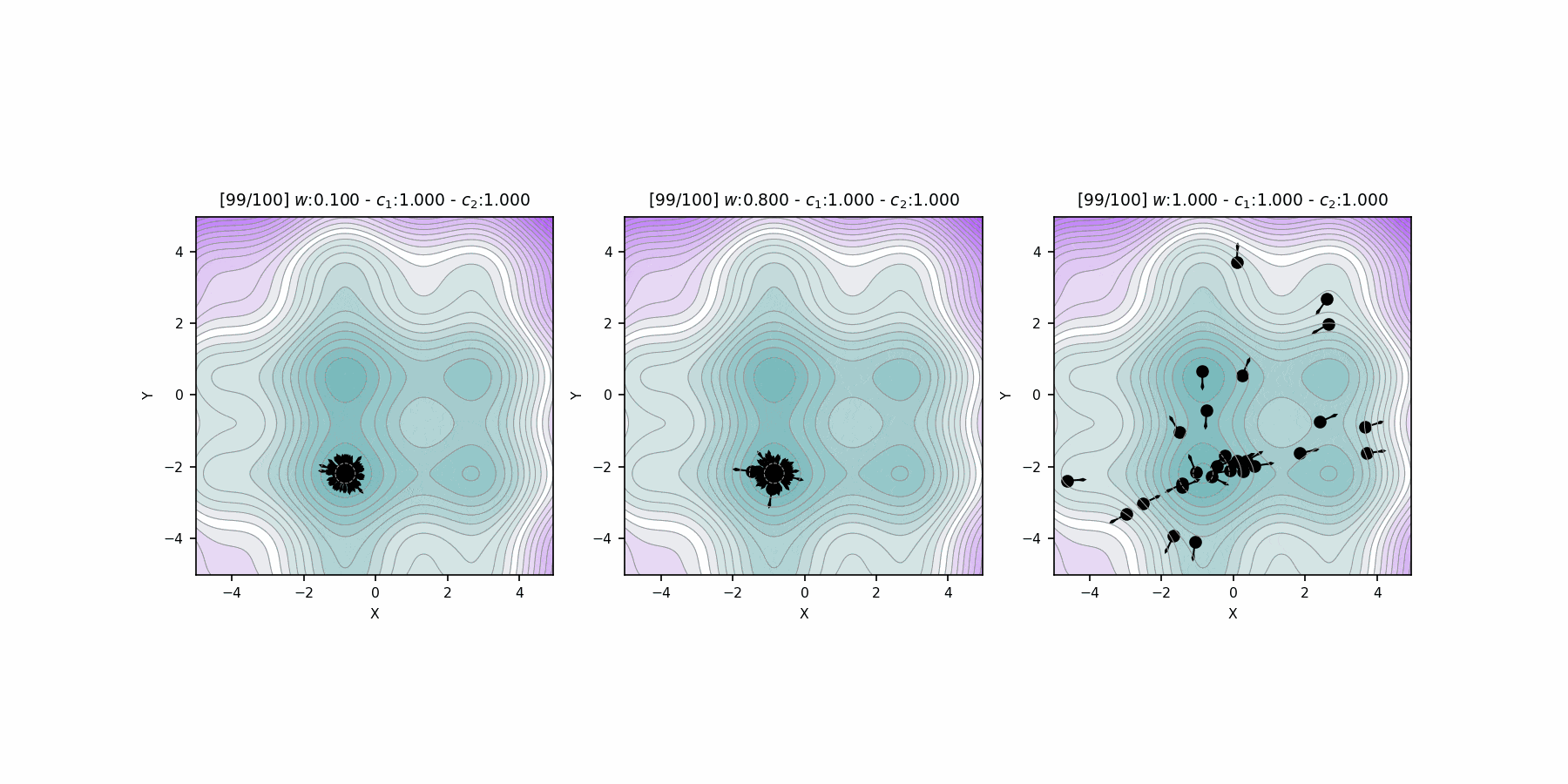
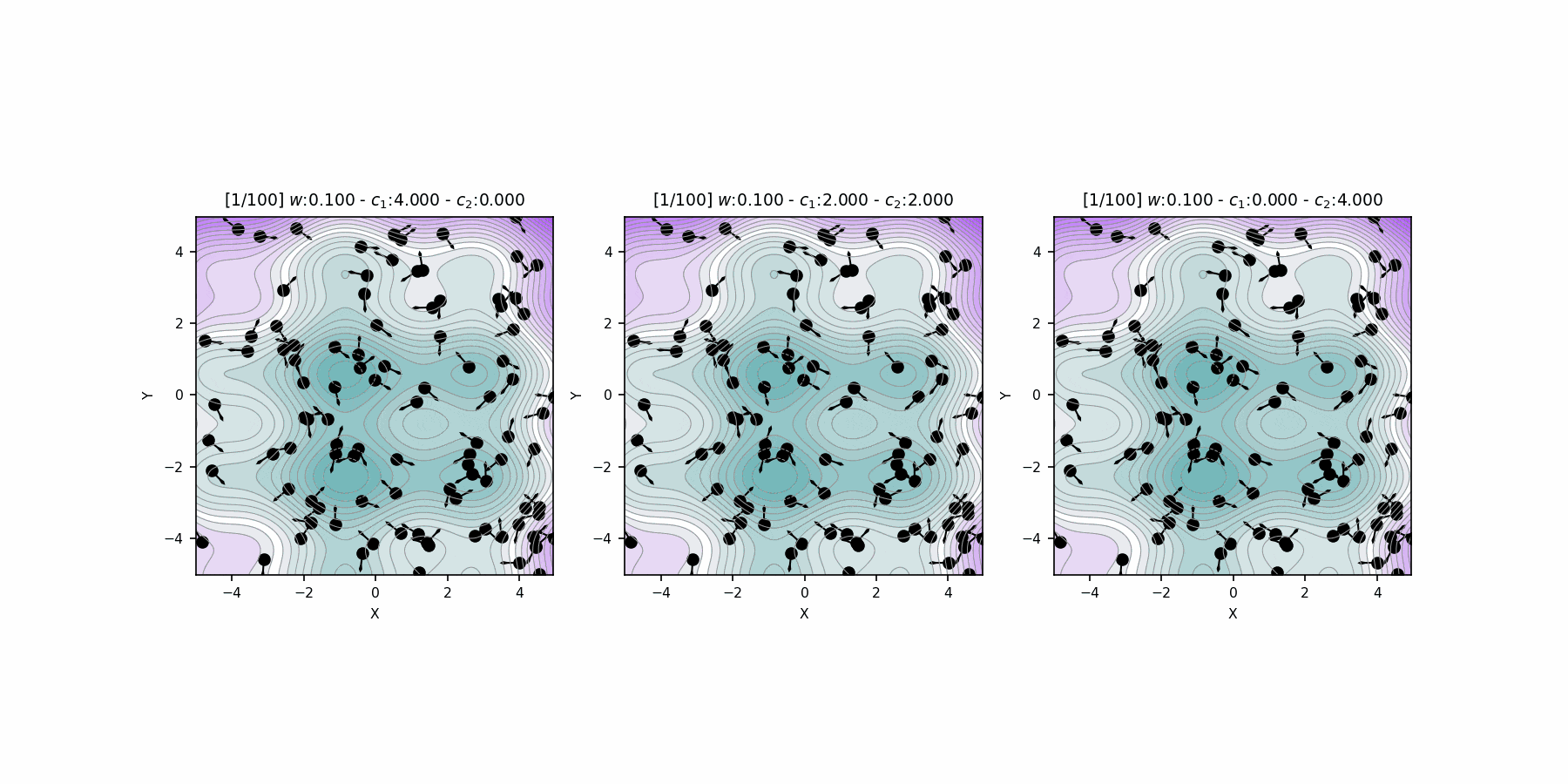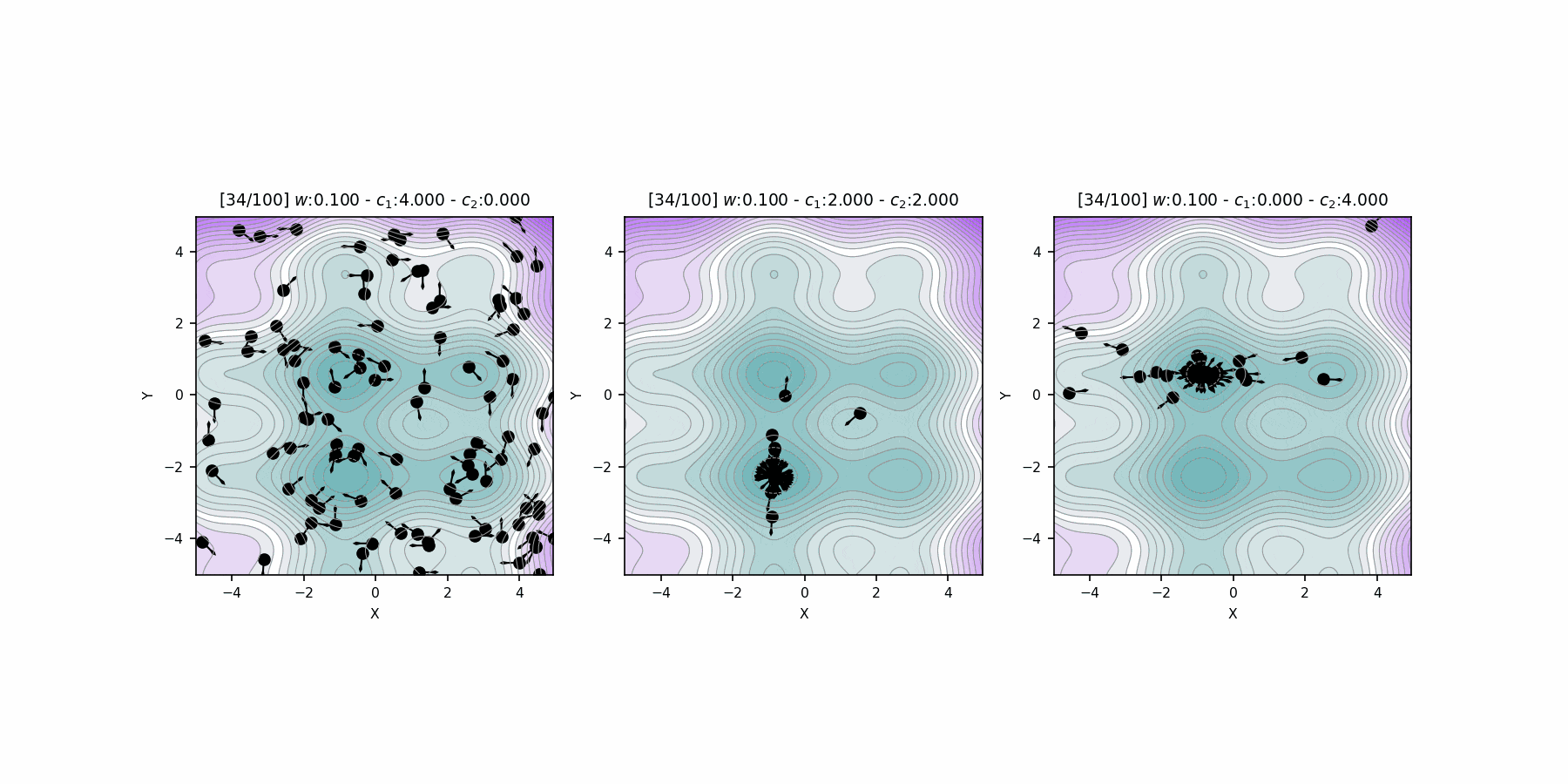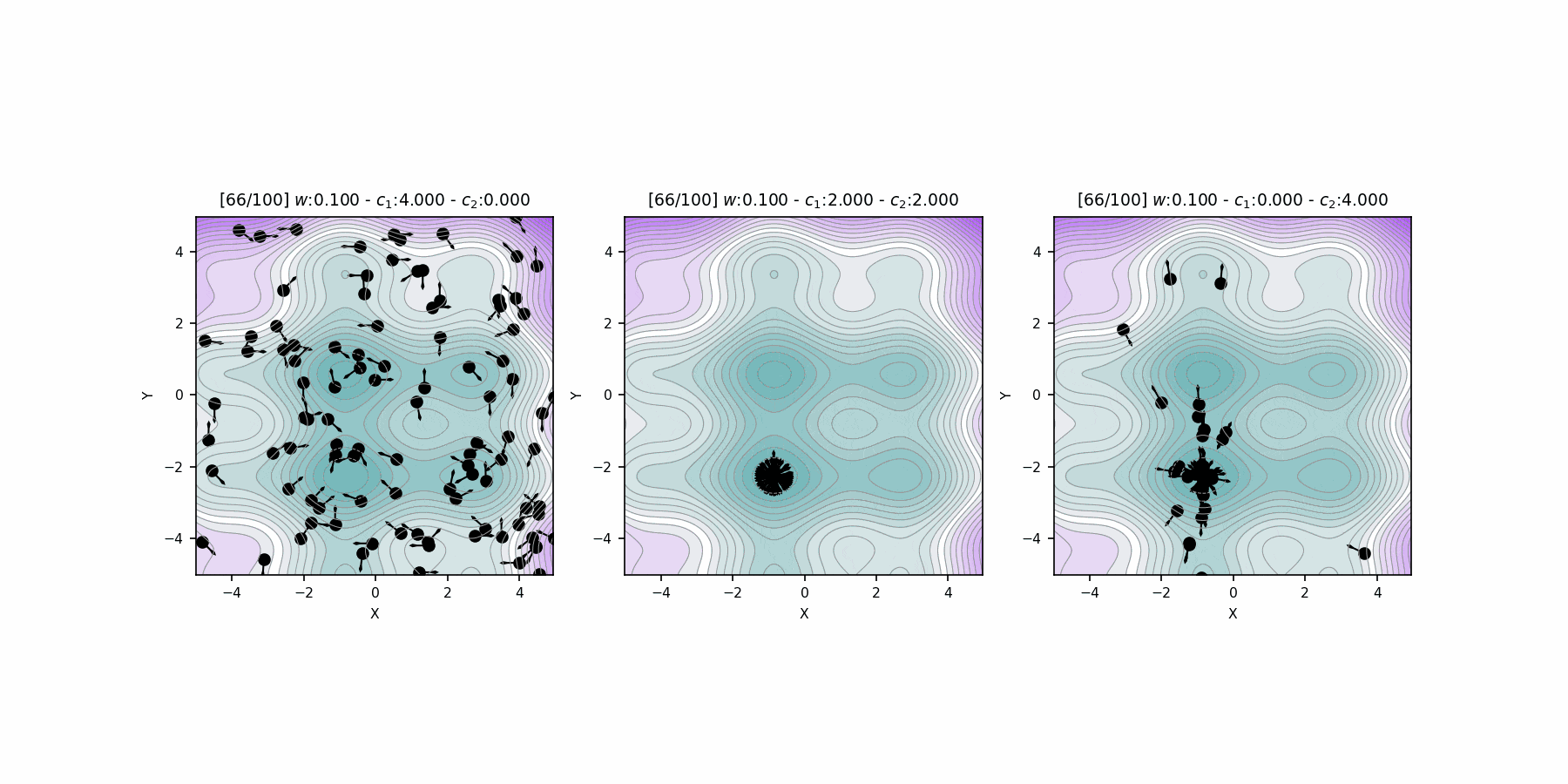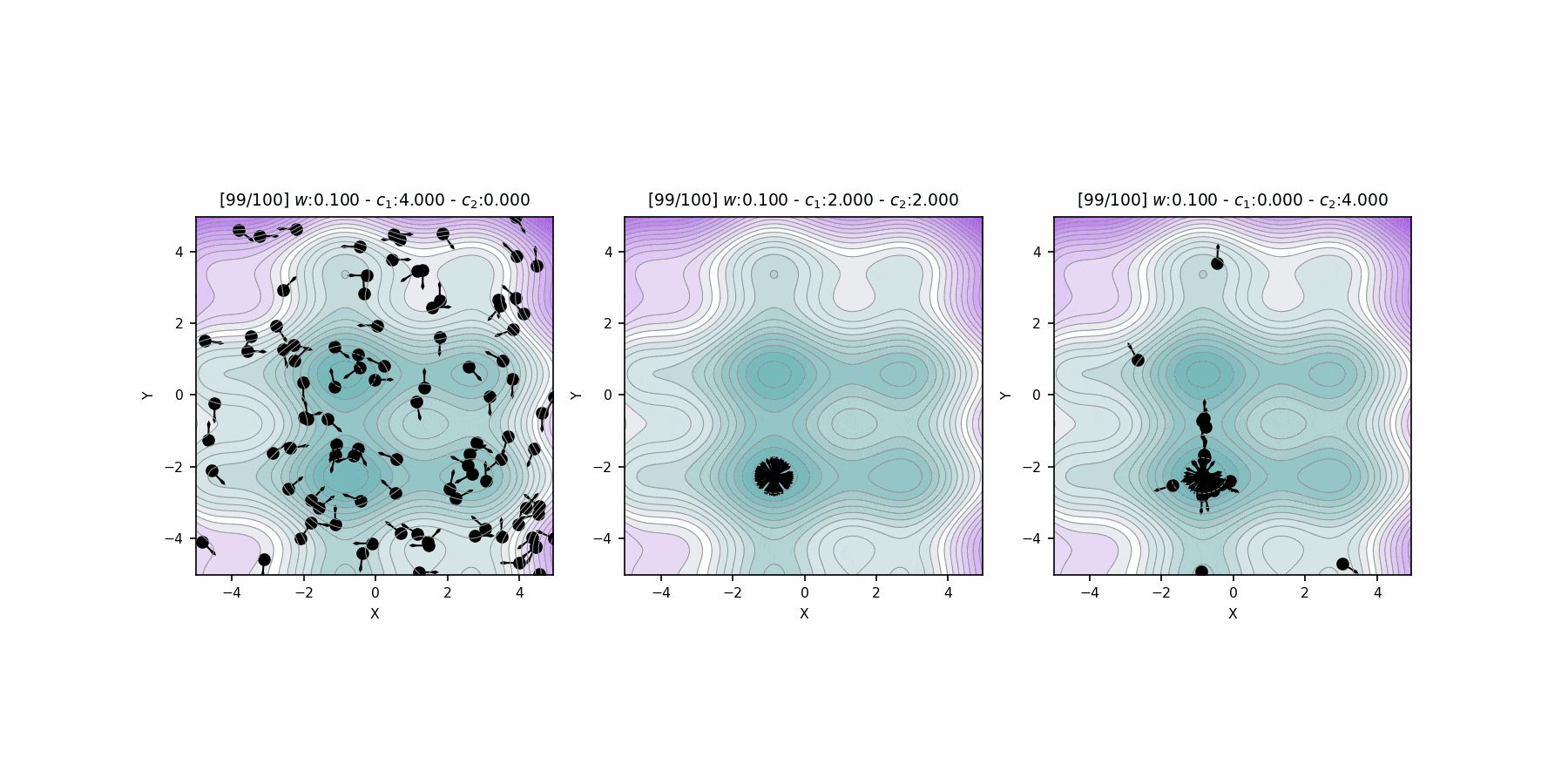
Hyperparameter \(c_1\), \(c_2\) comparison

Fitness

Location

"Particle Swarm Optimization Visually Explained":

https://towardsdatascience.com/particle-swarm-optimization-visually-explained-46289eeb2e14

for _ in range(num_of_audiences):
    print('Thank you for your attention! 🙏')