Characterization of Characteristics
— by BDMOW
Contents
Characteristic
Substructure or partitions that do not change under automorphisms.
1.
Category Actions
Categories acting is more intuitive than groups acting.
2.
Characteristic = biaction homomorphisms.
A complete description of characteristic without involving isomorphisms.
3.
Meet the Team
Josh
Maglione

Brooksbank,
Pete
Heiko
Dietrich
Eamonn
O'Brien
James
Wilson
Thanks
-
DFG grant VO 1248/4-1 & DFG-GRK 2297
-
Marsden Fund of New Zealand UOA 107
-
Simons Foundation #636189
-
USA NSF 2319370
Characteristic
Characteristic
Substructure or partitions that do not change under automorphisms.
1.
Category Actions
Categories acting is more intuitive than groups acting.
2.
Characteristic = biaction homomorphisms.
A complete description of characteristic without involving isomorphisms.
3.

Characteristic
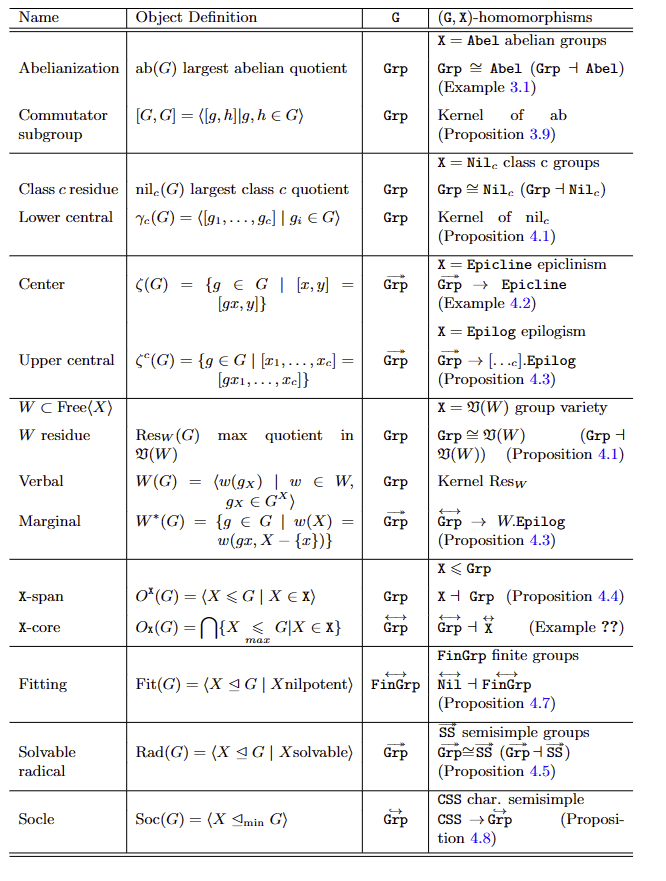
\(H\leq G\) where for every automorphism \(\varphi:G\to G\), \(\varphi(H)=H\).

Characteristic
\(H\leq G\) where for every automorphism \(\varphi:G\to G\), \(\varphi(H)=H\).
Contents
Characteristic
Substructure or partitions that do not change under automorphisms.
1.
Category Actions
Categories acting is more intuitive than groups acting.
2.
Characteristic = biaction homomorphisms.
A complete description of characteristic without involving isomorphisms.
3.
Concept
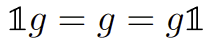
Abstract Category
\(g(hk)=(gh)k\) when defined &
A partial associative multiplication with 1s.
\[\begin{array}{|c|ccc|} \hline * & e & h & f\\ \hline e & e & \bot & \bot \\ h & h & \bot & \bot \\ f & \bot & h & f \\ \hline\end{array}\]

Functions
Functions \(x\mapsto M\)
- Evaluate \(M[x:=a]\): replace \(x\) with \(a\).
- Rewrite: convert new string by stated equal symbols.

Typed Functions
Some Functions \(x\mapsto M\) obey inference \[\frac{a:A}{M[x:=a] : B}\]
Write \(f:A\to B\)
\(Y^?=Y\sqcup\{\bot\}\). Partial function means \(f:X\to Y^?\).
Partial Equality: \(y\asymp y'\) means if \(y,y'\in Y\) then \(y=y'\).
\(G\) is an abstract category if it has a binary partial operation such that
\[\begin{aligned} g\cdot (h\cdot k) & \asymp (g\cdot h)\cdot k\\ 1_G \cdot g&=\{g\}\\ g\cdot 1_G&=\{g\}\end{aligned}\]
A mix of groupoid and monoid.
Note \(1_G\) is all the identities.
Abstract Category
Laws
- \(s(x)=t(y)\) if, and only if, \(xy\in C\)
- \(s(t(x))=t(x)\) & \(t(s(x))=s(x)\)
- \(s(xy)=s(s(x)y)\) & \(t(xy)=t(xt(y))\)
- \(xy, yz\in C\) then \(x(yz)=(xy)z\)
- \(xs(x)=x=t(x)x\)
Theory
- \(s(s(x))=s(x)\) & \(t(t(x))=t(x)\)\[\begin{aligned}Pf.\qquad s(s(x)) & = s(t(s(x))) \\ &=t(s(x))=s(x)\quad \Box \end{aligned}\]
- \(s(xy)=s(y)\) & \(t(xy)=t(x)\)\[\begin{aligned}Pf.\qquad s(xy) & = s(s(x)y)\\ &=s(t(y)y)=s(y)\qquad \Box\end{aligned}\]
- \(xy,yz\in C \Rightarrow x(yz),(xy)z\in C\)\[\begin{aligned}Pf.\qquad (s(x)&=t(y)) \wedge(s(y)=t(z)) \\ & \Rightarrow t(yz)=t(y)=s(x)\,\Box\end{aligned}\]
\(P\vdash \)
\(\vdash P\)
A change in notation
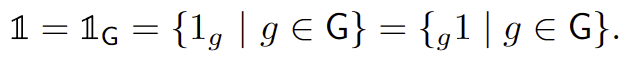
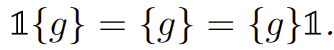
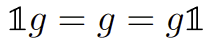
Fact
Abuse of Notation
\(1_g:=s(g)\) & \({_g 1}:=t(g)\)
Notation
\(G\) is an abstract category, \(X\) a type/class, a \(G\)-act is a partial function \(\cdot :G\times X\to X^?\) where
\[\begin{aligned} g\cdot (h\cdot x) & \asymp (gh)\cdot x\\ 1_G \cdot x&=\{x\}\end{aligned}\]
Much like a monoid act mixed with a groupoid act.
Category Action
\(G,H\) abstract categories, \(f:G\to H\) homomorphism (functor) of abstract categories. Then define
\[\cdot :G\times H\to H\qquad g\cdot h := f(g)h.\]
Category Action by Functor
Fact. \(_G H\) is a cat-act and furthermore, a \((G,H)\)-biact in that
\[(g\cdot h)h'=g\cdot (hh')\]
Assume pure vanilla then all \(_G H_H\) induced by homomorphism \(f:G\to H\).
Theorem. \(G\) and \(H\) are abstract categories acting purly vanilla on each other and
\[\begin{aligned}\mathcal{M}&:{_G H_H}\to {_G H_H}\\ \mathcal{M}(g\cdot xh)& =g\mathcal{M}(x)\cdot h\end{aligned}\]
then \(\epsilon=\mathcal{M}(1_H)\) is a counit.
\((G,H)\)-homomorphisms a source of counitals
Corollary. If \(I:G\hookrightarrow Grp\) and \(\mathcal{M}:{_G H_H}\to {_G G_H}\) then \[\iota=I\epsilon=I\mathcal{M}(1_H)\] is a counital. In particular it determines invariant substructure.
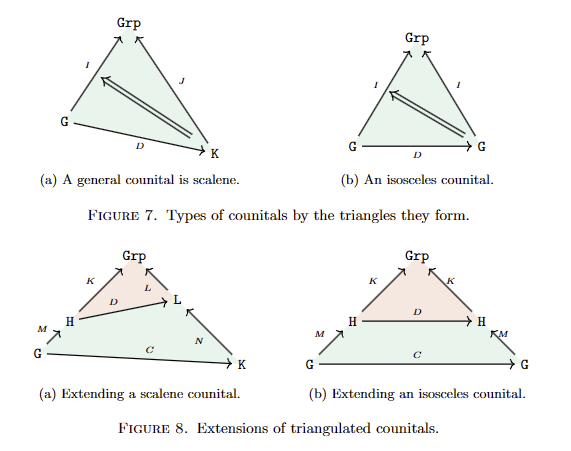
The converse
Extension Theorem.
\(G\leq H\leq Grp\) with \(G\) full in \(H\) then every counital on \(G\) extends to one on \(H\).
1.
Isoscoles counitals extend to internal
2.
Internal counitals are counits of a (G,H)-homomorphism.
3.
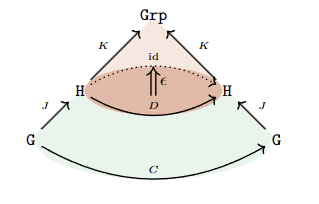
Categorificaiton of Characteristic
- \(G\) a group. \(H\) a characterisitic subgroup is equivalent to a counital \(C:Aut(G)\to Core(Grp)\).
- Extend isosceles counital to \(D:Core(Grp)\to Core(Grp)\) using extension theorem.
- Extends \(D\) to internal counital \(I\epsilon\).
- Apply homomorphism chacacterization of counits.
\((G,H)\)-homomorphisms ONLY source of counitals