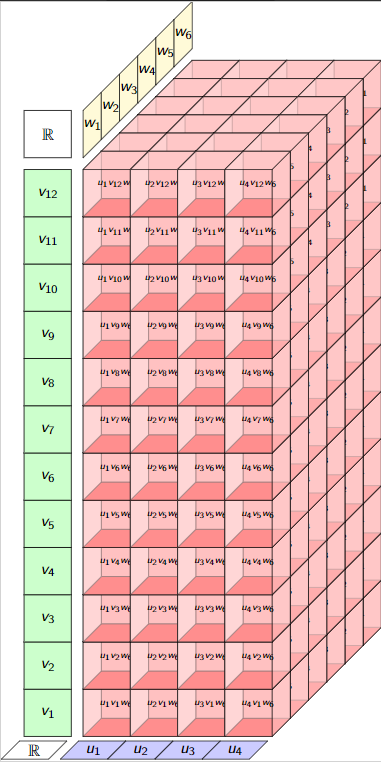
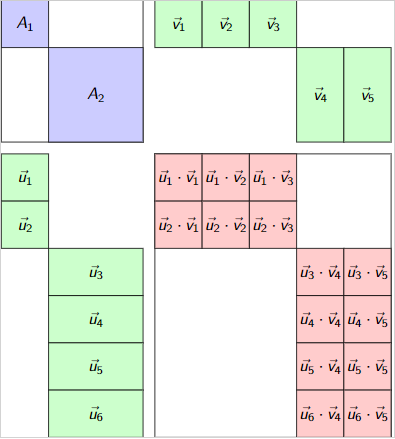
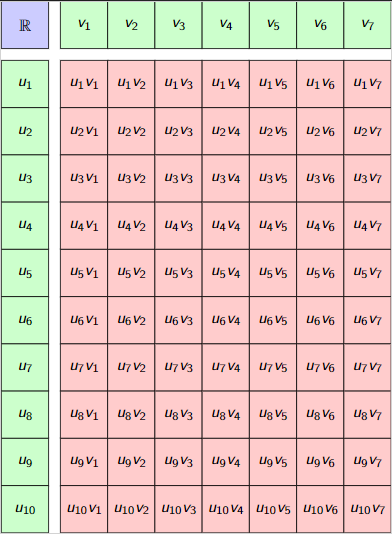
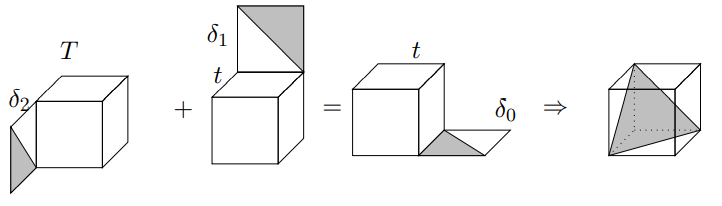
Denser Tensor Spaces
2021 James B. Wilson, Colorado State University

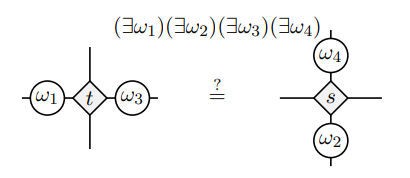

Major credit is owed to...


Uriya First
U. Haifa
Joshua Maglione,
Bielefeld
Peter Brooksbank
Bucknell
- The National Science Foundation Grant DMS-1620454
- The Simons Foundation support for Magma CAS
- National Secturity Agency Grants Mathematical Sciences Program
- U. Colorado Dept. Computer Science
- Colorado State U. Dept. Mathematics

Three Goals of This Talk
- Cluster non-zeros in a tensor.
- Compare two tensors up to basis change
- Make the algorithms for the above feasible.
Can we agree on "tensors"?
(I hope!)
Are all of these tensors?

Don't be a joke
If you don't use linear combinations on some axis of your data...
then its not actually a tensor, sorry.
"What is a vector?"
"An element of a vector space."
\(U_0\oslash U_1=\{f:U_1\to U_0\mid f(u+\lambda v)=f(u)+\lambda f(v)\}\)
\(U_0,U_1,\ldots\) are vector spaces (or modules).
Linear maps:
\(U_0\oslash U_1\oslash U_2 := \{f:U_2\to U_0\oslash U_1 \mid f(u+\lambda v)=f(u)+\lambda f(v)\}\)
Bi-Linear maps:
\(U_0\oslash \cdots U_{k-1}\oslash U_k:=(U_0\oslash\cdots\oslash U_{k-1})\oslash U_k\)
\(k\)-multi-linear maps:
"What is a tensor?"
"An element of a tensor space."
\(U_0,U_1,\ldots\) are vector spaces (or modules).
\(U_0\oslash \cdots U_{k-1}\oslash U_k:=(U_0\oslash\cdots\oslash U_{k-1})\oslash U_k\)
\(k\)-multi-linear maps:
Defn. A Tensor Space \(T\) is a vector space an a linear map \[\langle \cdot|:T\to U_0\oslash\cdots\oslash U_k\]
Tensors are elements of tensor spaces.
\(T=\mathbb{M}_{2\times 3}(\mathbb{R})\) is a tensor space in at least 3 ways!
\[\langle \cdot |:T\mapsto \mathbb{R}^2\oslash \mathbb{R}^3\]
\[\langle M|u\rangle := Mu\]
\[|\cdot \rangle:T\mapsto \mathbb{R}^3\oslash \mathbb{R}^2\]
\[\langle v| M\rangle := v^{\dagger}M\]
\[|\cdot|:T\mapsto \mathbb{R}\oslash\mathbb{R}^2\oslash \mathbb{R}^3\]
\[\langle v| M|u\rangle := v^{\dagger}Mu\]
Matrix as linear map on right.
Matrix as linear map on left.
Matrix as bilinear form.
This abstraction does wonders for creating a fluid tensor software package.
Operating on Tensors
Tier I

low-brow: reindex,
high-brow: affine transforms of polytopes
Evaluation
Contractions
Layout data so nothing moves!
Logically equivalent circuits
Fight eager evaluation
Tier II

=
(Data) Acting on Tensors as arrays
(Lin. Alg.) Acting on tensors as functions
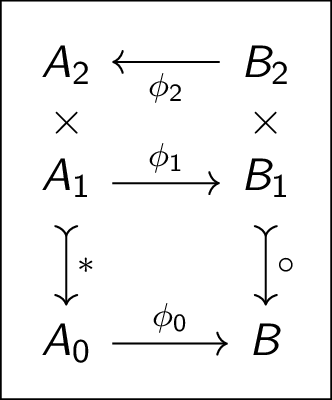
(Physics/Algebra) Acting on Tensors as Operads/Networks
Tier II key: Iterate
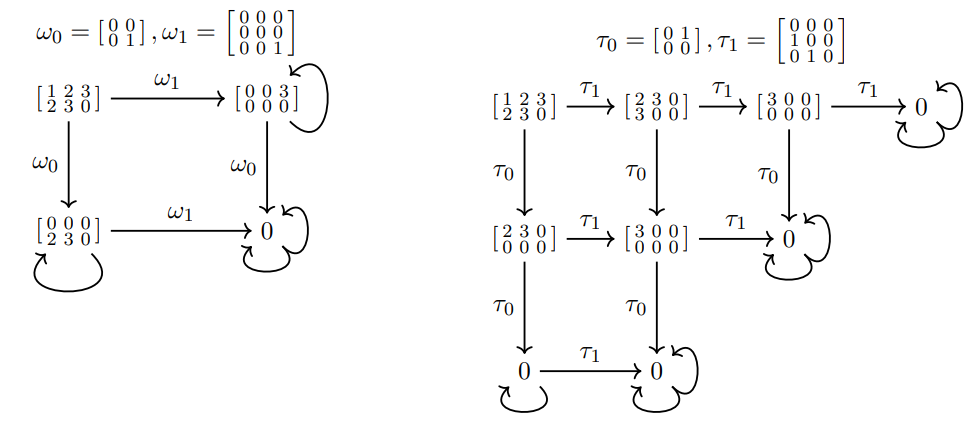
Generalizes Characteristic polynomial to ideals
\[I(t,\omega)=(x^2-x, y^2-y, xy)\qquad I(t,\tau)=(x^2, y^3,xy-y^2)\]
Multi-spectrum Rule = \(\langle t| p(\omega) =0\)
Thm FMW-Connection. \(S\) set of tensors, \(P\subset \mathbb{R}[X]\), \(\Omega\subset \prod_a \mathbb{M}_{d_a}(\mathbb{R})\)
\[T(P,\Omega)=\{t\mid P\textnormal{ in multi-spec } t\text{ at } \Omega\}\]
\[I(S,\Omega)=\{p\mid p\textnormal{ in multi-spec } S\text{ at } \Omega\}\]
\[Z(S,P)=\{\omega \mid P\textnormal{ in multi-spec } S\text{ at } \omega\}\]
Then \[S\subset T(P,\Omega)\Leftrightarrow P\subset I(S,\Omega) \Leftrightarrow \Omega\subset Z(S,P)\]
Thm FMW-Construction.
These are each polynomial time computable.
Multi-spectrum Rule = \(\langle t| p(\omega) =0\)
Tier III
Functors on tensors, e.g. \((U_0\oslash\cdots \oslash U_K)\to (U_i\otimes\cdots\otimes U_k\to U_0\oslash\cdots\oslash U_{i-1})\)

Save yourself time if you program these functors and avoid boiler plate later
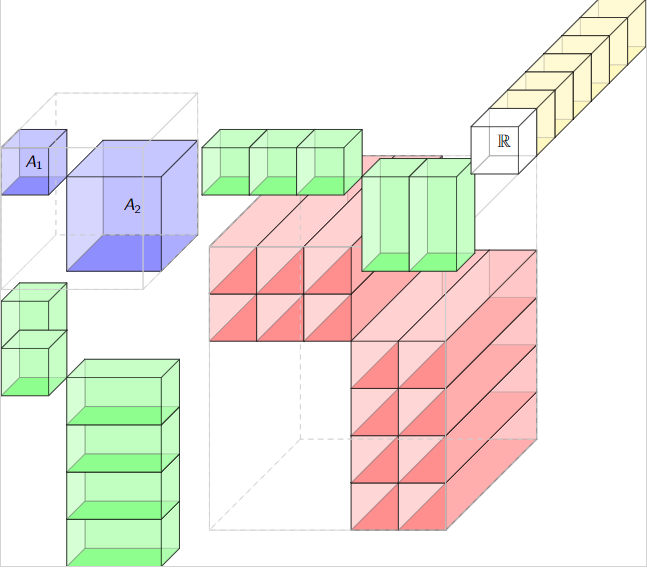
How to shrink a tensor space
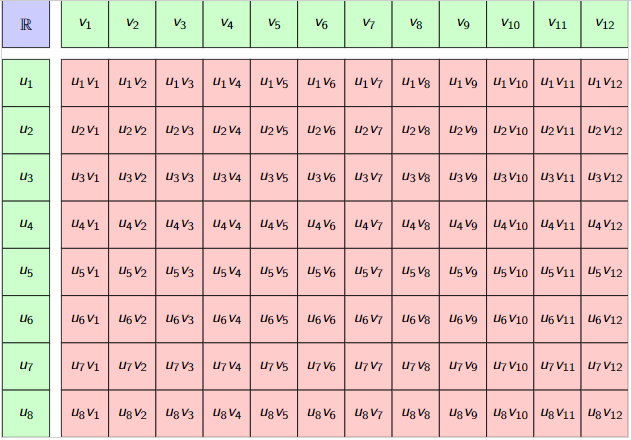
Red is the space we search/work within.

Add some algebra \(A\) in the form of \(U\otimes_A V\)
The bigger the algebra the better.
Rule of thumb
\[\dim (U\otimes_A V)\approx \frac{\dim U\dim V}{\dim A}\]
Some effort now in working with the algebra & modules, yet you can at least prove and plan for that.

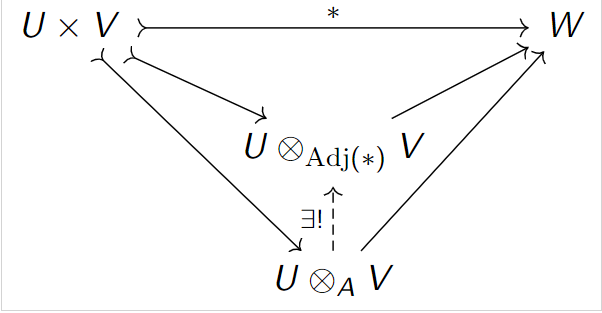
Adjoint-Tensor Theorem
- Given: 2-tensors \(S\subset \mathbb{M}_{a\times b}(\mathbb{R})\)
- Want: Algebra to shrink space around \(S\)
Theorem Brooksbank-W. (2012) \[\mathrm{Adj}(S)=\{(F,G)\in \mathbb{M}_a(\mathbb{R})\times \mathbb{M}_b(\mathbb{R})\mid (\forall T\in S)(FT=TG^t)\}\] is an optimal choice and unique up to isomorphism.
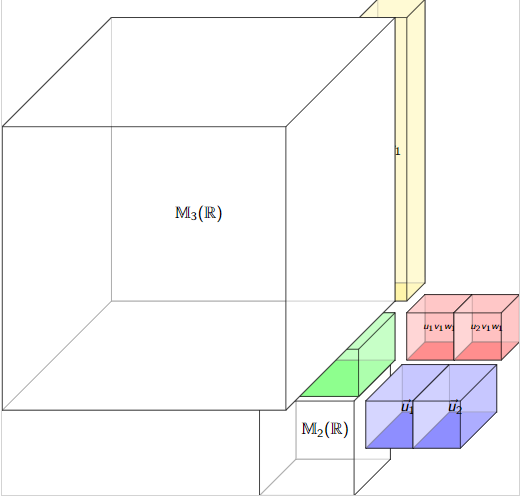
How not to shrink a tensor space

\(\mathbb{R}^4\otimes_{\mathbb{R}}\mathbb{R}^{12}\otimes_{\mathbb{R}}\mathbb{R}^{6}\)
\(\mathbb{R}^4\otimes_{\mathbb{M}_2(\mathbb{R})}\mathbb{R}^{12}\otimes_{\mathbb{M}_3(\mathbb{R})}\mathbb{R}^{6}\)
\(\cong\mathbb{R}^2\otimes_{\mathbb{R}}\mathbb{R}^{2}\otimes_{\mathbb{R}}\mathbb{R}^{2}\)


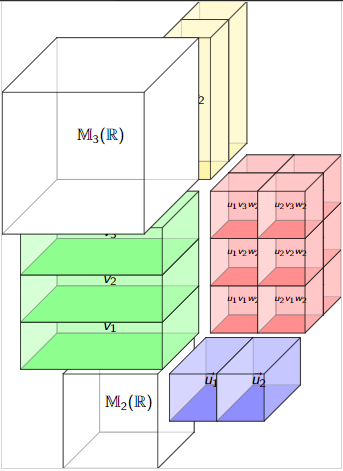
\(\mathbb{R}^4\otimes_{\mathbb{M}_4(\mathbb{R})}\mathbb{R}^{12}\otimes_{\mathbb{M}_3(\mathbb{R})}\mathbb{R}^{6}\)
\(\cong\mathbb{R}\otimes_{\mathbb{R}}\mathbb{R}\otimes_{\mathbb{R}}\mathbb{R}^{2}\)
\(\mathbb{R}^4\otimes_{\mathbb{M}_2(\mathbb{R})}\mathbb{R}^{12}\otimes_{\mathbb{M}_6(\mathbb{R})}\mathbb{R}^{6}\)
\(\cong\mathbb{R}^2\otimes_{\mathbb{R}}\mathbb{R}\otimes_{\mathbb{R}}\mathbb{R}\)
Adjoint-tensor methods in valence \(>2\)
- \(S\subset U_1\otimes\cdots\otimes U_v\) get \(\binom{v}{2}\) generalized adjoints i.e. \[\mathrm{Adj}(S)_{ij}\subset \mathbb{M}_{d_i}(\mathbb{R})\times \mathbb{M}_{d_j}(\mathbb{R})\]
- But the product only has \(v-1\) spots to hang them...\[U_1\otimes_{A_{12}}U_2\otimes_{A_{23}}U_3\otimes\cdots\otimes_{A_{(v-1)v}} U_v.\]
- We can permute...but rather arbitrary.
Things I wonder about....
Why can't we just act on one side?
E.g. \(U\otimes_A V\) needs \(U_A, {_A V}\). Worse, \(U\otimes_A V\otimes_B W\) needs \({_A V_B}\) a "bi-module".
Why do we tolerate "natural" isomorphisms \[U\otimes (V\otimes W)\cong (U\otimes V)\otimes W\]
If its natural, can't we just write these down as equal?!
A new tensor product


Whitney Tensor Product
A Different Tensor Product
New Tensor product:
\(\Omega\subset \mathbb{M}_{d_1}(\mathbb{R})\times\cdots \times \mathbb{M}_{d_k}(\mathbb{R})\); \(P\subset \mathbb{R}[x_1,\ldots,x_k]\)
\[\Xi(P,\Omega)=\left\langle \sum_e \lambda_e \omega_1^{e_1}\otimes\cdots\otimes \omega_k^{e_k} ~\middle|~\sum_e\lambda_e X^e\in P, \omega\in \Omega\right\rangle\]
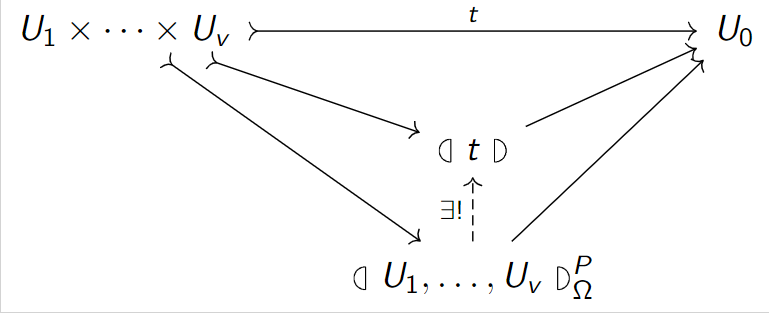
\[(]U_1,\ldots,U_k[)_{\Omega}^P := (U_1\otimes \cdots \otimes U_k)/\Xi(P,\omega)\]
Then we have:
\[(]\cdots[):U_1\times\cdots\times U_k\hookrightarrow (]U_1,\ldots,U_k[)_{\Omega}^P\]
defined by
\[(]u_1,\ldots,u_k[) := u_1\otimes\cdots\otimes u_k+\Xi(P,\Omega)\]
Condensing Whitney Tensor Products
Condensing our alternative
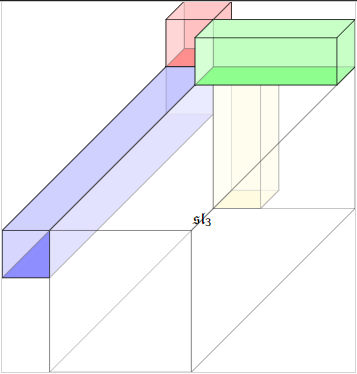
One corner to contract makes each axis independent.
(No bimodules, no "associative" rules)
\[(]\cdots[):U_1\times\cdots\times U_k\hookrightarrow (]U_1,\ldots,U_k[)_{\Omega}^P\]
is the universal tensor such that every \(\omega\in \Omega\) has \(P\) in its multi-spectrum.
Intuition....force the spectrum
Consequence:
- If \(P\) is homogeneous linear (so zero's are some affine subspace)
- Then it is contained in a hyperplane.
- Generically all hyperplanes are equal up to the torus action!
- Maybe there is a universally smallest product....?
Derivation-Densor Theorem
- Given: tensors \(t\in \mathbb{R}^{d_1}\otimes \cdots \otimes \mathbb{R}^{d_v}\)
- Want: Algebra to shrink space around \(t\)
Theorem First-Maglione-W. \(\mathrm{Der}(t)\) is all \((\delta_i)_i\in \prod\mathbb{M}_{d_i}(\mathbb{R})\) satisfying \[0=\langle t|\delta_1u_1,\ldots,u_n\rangle+\cdots+\langle t|u_1,\ldots,\delta_v u_v\rangle\] is an optimal choice and unique up to isomorphism.
Lie algebras are required
Theorem First-Maglione-W. If \(P=(\Lambda X)\), \(\Lambda\in \mathbb{M}_{r\times k}\) is full rank and if \[Z(t,P)=\{\omega\mid P\textnormal{ in the multi-spec } t\}\]
is an algebra, then it is a Lie algebra in at least \[k-2r\] coordinates.
\(U\otimes_A V\) for \(A\) associative is a fluke, it is the r=1 case when k=2.
Lie algebras are a good thing
- No bimodule condition as Lie is skew-commutative.
- Unlike square matrix rings, a fixed simple Lie algebra can act faithfully and irreducibly on unbounded dimensions.
- Hence compression like this exists even with just 3-dimensional derivations!

Orthogonalizing data
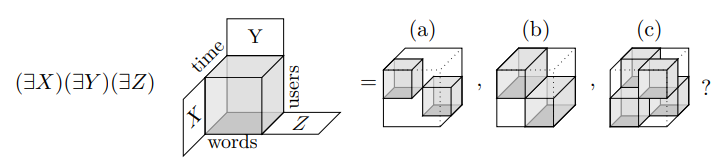
Problem posed in:
Acar, Camtepe, and Yener, Collective Sampling and Analysis of High Order Tensors for Chatroom Communications, Proc. 4th IEEE Int. Conf.Intel. and Sec. Info., 2006, pp. 213–224
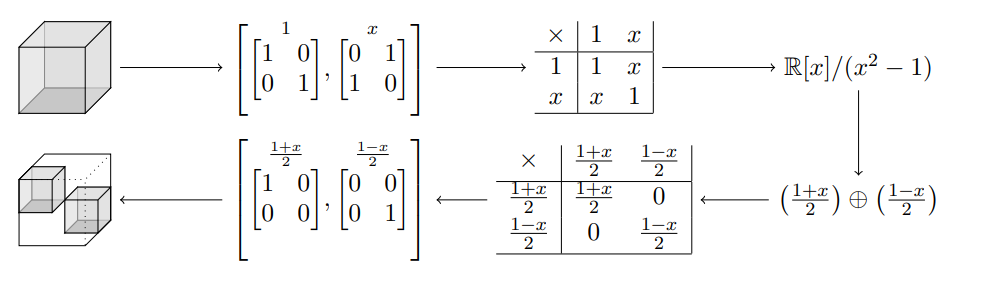
Orthogonalizing a tensor is an algebra problem.
Reality
The algebra is never there,
never that nice,
not even associative.
No algebra? Make one by enrichment!
Its decompositions do the job.
\(t\in \mathbb{R}^{10}\otimes \mathbb{R}^7\)
\(\mathrm{Adj}(t)\cong \mathbb{R}\oplus \mathbb{M}_2(\mathbb{R})\) \[\begin{aligned} t & \in \mathbb{R}^{10}\otimes_{\mathrm{Adj}(t)}\mathbb{R}^7 \\ & \cong (\mathbb{R}^{10}\otimes_{\mathbb{R}\oplus 0}\mathbb{R}^7)\oplus (\mathbb{R}^{10}\otimes_{0\oplus \mathbb{M}_2(\mathbb{R})}\mathbb{R}^7) \\ & = (\mathbb{R}^2\otimes \mathbb{R}^3)\oplus (\mathbb{R}^4\otimes\mathbb{R}^2)\end{aligned}\]

\[U\otimes_{A_1\oplus A_2}V\otimes W\cong (U_1\otimes_{A_1} V_1\otimes W)\oplus(U_2\oplus_{A_2}V_2\otimes W)\]
Orthogonalizes in higher valence
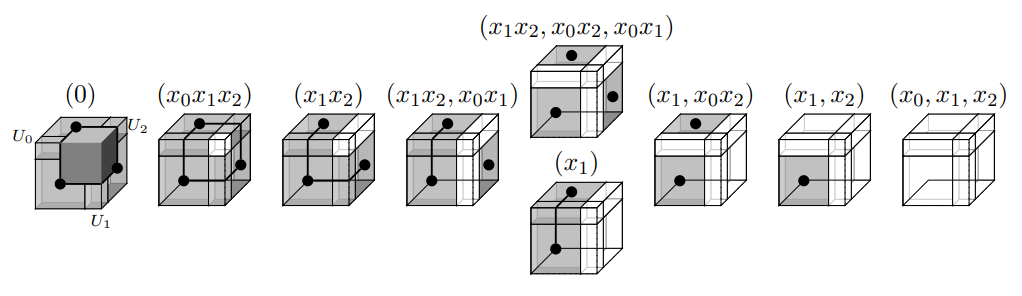
Did we get all decomposition types?
Thm. (FMW-Singular)
- Singularities types are in bijection with simplicial complexes \(\Delta\).
- The multi-spectrum of operators supported on singularities contain the Stanely-Reisner ideal \((X^e\mid \mathrm{supp}(e)\notin \Delta)\)
Valence 2
Valence 3
Theory & Practice
Parker-Norton 1975 MeatAxe: polynomial time algorithm for \[XTX^{-1}=T_1\oplus \cdots \oplus T_{\ell}.\]
Performance: Dense 1/2 million dimensions in an hour, on desktop.
W. 2008: Proved uniqueness and polytime-algorithms for \[\begin{aligned} XTX^{\dagger} & = T_1\perp\cdots\perp T_{\ell}\\ XTY & =T_1\oplus \cdots\oplus T_{\ell}\end{aligned}\]
Generalizations being explored now.
Pros.
- Exact solution, no missing outliers, no need to train AI.
- Comes with uniqueness theorems (Jordan-Holder, Krull-Schmidt)
- Polynomial-time, in fact nearly linear time.
Cons.
- The algebra is tough (non-associative, hard modules) (...solution...hire algebraist...)
- Implementations are in Computer Algebra Systems (with increased funding this will change)
- Noise model is unexplored (Statisticians I've asked are more optimistic than me...hmm.)
Structure in Networks
Data credit to Frank W. Marrs III
Los Alamos National Labs
Further Fact of spectra:
If derivation and nilpotent then...
How to apply?
- Compute Der,
- Use Lie theory algorithms to locate such \(\delta\)
- change coordinates to make data structured.
Actor Pair Exchange Conditions
Partners
Action/Reaction
Benafactor
Between pairs, 6 total (3 pictured)
\(\vdots\)
Actor Pair Exchange on 7 actors

Tensor:
- Rows/Columns are pairs (a,b)
- each slice of tensor is a exchange pattern.
- Very combinatorial but 10,584 params.
- Calls for spectural "graph theory" but on hypergraphs
Actor Pair Exchange on 7 actors
Tensor:
- Algebras identify 2 outliers
- Cluster data into 4 layers (ideals) \(\Rightarrow\) breakup into 4 iterations
- Reduced to 250 parameters.

Entanglement Classes
Verstraete, Dehaene, De Moor, Verschelde, Four qubits can be entangled in nine different ways, Phys. Rev. A 65 (2002)
D. and B. Williamson,Mari¨en, Matrix product operators for symmetry-protected topological phases: Gauging and edge theories, Phys. Rev. B 94 (2016)

Quantum Particles modeled as vectors in \(\mathbb{C}^d\)
Entangled Particles as in \(\mathbb{C}^{d_1}\otimes\cdots \otimes \mathbb{C}^{d_k}\)
Visualize as n-gon.
Objective: What is the large-scale physics of a many body quantum material?
Comes down to symmetries of then tensors.
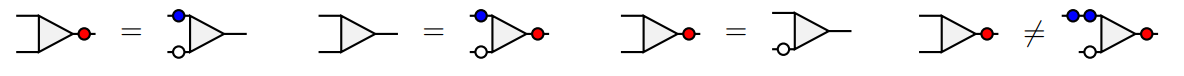
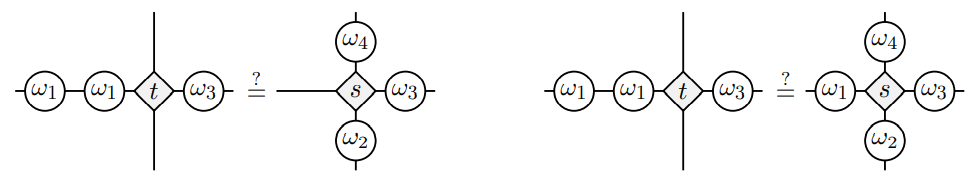
Valence 4?
What qualifies as a symmetry of a tensor? Not just anything...surprisingly combinatorial...
Valance 3
Yes
No.
Thm FMW-Groupoid.
\[Z(t,p)^{\times}=\{\omega\mid p \textnormal{ in multi-spec } t\}\] is a group in some tensor category if, and only if, \[p=X^g(X^e-X^f)\] where \(e,f\) have disjoint support and are \(\{0,1\}\) valued.
Solution: chase the algebraic geometry of the spectra.... it turns out to be toric and thus combinatorial!
QuickSylver
Solving \((\forall i)(XA_i+B_iY=C_i)\) in nearly linear time
Derivations require Solving
\((\forall i)(XA_i+B_iY=C_i)\) and variations.
Naive:
Solving \((\forall i)(XA_i+B_iY=C_i)\) is linear in \(d^2\) variables so \(O(d^{2\omega})\subset O(d^6)\) work.
Good enough in theory, but hard to fit in memory and unrealistic at scale.
Bartels-Stewart Type Solution for\[XA+BY=C\]
- Choose \(E\) and \(F\) low rank matrices with pseudo-inverses \(E^*,F^*\).
- Solve \[E(XA)F+E(BY)F=ECF\] which has lower dimension.
- Pullback solution using \(E^*,F^*\).
Yields \(O(d^{\omega})\) time algorithms, \(\omega\leq 3\)
Tensor Bartels-Stewart Solving\[(\forall i)(XA_i+B_iY=C_i)?\]
- Choose \([E]\) and \([F]\) low rank tensors with pseudo-inverses \([E]^*,[F]^*\).
- Solve \[[E](X[A])[F]+[E]([B]Y)[F]=[E]C[F]\] which has lower dimension.
- OVERLAPS DESTROY EACH OTHER'S WORK

\[\delta_A^{12}(u\otimes v\otimes w)=u\otimes v\otimes w-u_1\sum_{\ell=2} e_{\ell}\otimes e_{\ell}A v\otimes w\]
Prop. \(\delta_A^{12}\circ \delta_B^{13}=\delta_B^{13}\circ \delta_A^{12}\)
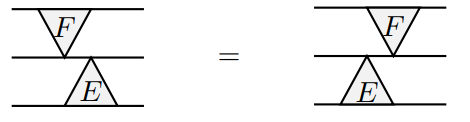
\(E=\delta_B^{13}\) and \(F=\delta_A^{12}\)
Face Elimination: a tensor solution
Tensor Bartels-Stewart Solving\[(\forall i)(XA_i+B_iY=C_i)?\]
- Choose \([E]\) and \([F]\) low rank tensors with pseudo-inverses \([E]^*,[F]^*\).
- Solve \[[E](X[A])[F]+[E]([B]Y)[F]=[E]C[F]\] which has lower dimension.
- OVERLAPS SLIDE PAST EACH OTHER


Thm Collery-Maglione-W.
QuickSylver solves simultaneous generalized Sylvester equations in time \(O(d^{3})\) (for 3-tensors).
Thank You!
Want details?
Several related videos/software/resources at
https://thetensor.space/
A recently updated version of some of the main results at
https://www.math.colostate.edu/~jwilson/papers/Densor-Final-arxiv.pdf