=
=
— James B. Wilson, CSU
Story problems
Isomorphism
3-Cats & \(\cong\)-strats

Privacy
Brenda the Bank manager knows the privacy laws.
If a client leaves the bank, their data leaves with them, like they where never there!
Privacy Law
db = ... // bank database
db2 = add(db,x) // Operation adds client
db3 = remove(db2,x) // Operation removes client
d == db3 // Leave no Trace.\(d\boxplus x\)
\(d\boxminus x\)
\(d = (d \boxplus x)\boxminus x\)
Algebra of the program
Other Laws of the Program
x == find(add(db,x),x)\(x=(d\boxplus x)\cap x\)
add(db,x) == add(add(db,x),x)\(d\boxplus x=(d\boxplus x)\boxplus x\)
Adding works
Adding happens once
None == find(remove(db,x),x)\(\emptyset=(d\boxminus x)\cap x\)
Removing works
add(add(db,x),y) == add(add(db,y),x)\((d\boxplus x)\boxplus y=(d\boxplus y)\boxplus x\)
Adding commutes
The "Algebra of the API"
Used to design software and test it.
IT Planning
Alarmed by ransomware the IT department make snapshots of all database transactions to be restore everything identically after an attack.

More operators, more laws
transactions(db)+1 == transactions(add(db,x))
transactions(db)+1 == transactions(remove(db,x))
\(\#(d)+1 = \#(d\boxplus x)\)
\(\#(d)+1=\#(d\boxminus x)\)
Log Transactions Laws
\[\#(d) = \#( (d\boxplus x)\boxminus x) = \#(d\boxplus x)+1=\#(d)+2\]
\[0=2\]
Elementary Abstract Algebra Solves This.
But it might go by too fast to be noticed...
Free Algebra \(F\langle X\rangle\)
- \[\begin{aligned} F\langle X\rangle & = \emptyset\\ & \mid (d:F\langle X\rangle)\boxplus (x:X)\\ & \mid (d:F\langle X\rangle)\boxminus (x:X)\\ \end{aligned}\] E.g. \((\emptyset \boxplus x)\boxminus y):F\langle x,y\rangle\)
- Laws \(R\): equations you want to be true, e.g. \[d=(d\boxplus x)\boxminus x\].
- Test: Quotient \[F\langle X\rangle/\langle R\rangle\] is nontrivial.
- Church-Rosser, Todd-Coxeter, Schreier-Sims, Tait-Martin-Lof, ....
Consistency testing
by algebra
- Free algebra \(F\langle X\rangle\): the algebra of all formulas using variables \(X\) and the given operations. E.g. polynomials, words in groups, \((d\boxplus x)\boxminus x)\), &c.
- Laws \(R\): equations you want to be true, e.g. \(d=(d\boxplus x)\boxminus x\).
- Test: Show \[F\langle X\rangle/\langle R\rangle\] is nontrivial.
- Church-Rosser, Todd-Coxeter, Schreier-Sims, Tait-Martin-Lof, ....
Algebraist
Consistency is a
solved problem. Use GAP4
Programmer
- Which VS code Linter checks this?
- Is this what Rust is doing?
- I watched Wadler at \(\lambda\)-con and he lost me at "aliens and C++".
Not solved...
Algebra rewriting is "solved" on homogeneous algebra, e.g.
\[*:A\times A\to A\]
Most applications are heterogeneous, e.g.
\[*:A\times B\to C\]
Operads overshot the generality end up with topology questions not algebra.
Fix the problem
Disagree about equality.

Equals is different things to different people.
- Bank manager: databases are equal if have the same clients.
- IT manager: databases are equal if one is a backup of the other.
Equality you begin with
E.g. IT/Software company
Coarser equality e.g. bank manager
Equivalence Relations
A solution
IT keeps two notions of equal.
- \(d=f\) for interchangeable databases.
- \(d\equiv f\) for equal client data.
Manager axioms are true under \(\equiv\) only.
Implement \(\equiv\) by a function \[\pi:DBSnaps\to DB\qquad \pi(d,actions)=d\] that makes technical IT data private to management system.
Circle back to reality
More disagree about equality.

Equals is different things to the same people.
- Bank manager: databases are equal if have the same clients.
- IT manager: databases are equal if one is a backup of the other.
- Bank manager: storing multiple copies of the same thing is not as cheap as storing fewer!
Equality you begin with
E.g. IT/Software company
Refined equality, e.g. power company
Coarser equality e.g. bank manager
Equivalence Relations
What?
Story problems
Isomorphism
3-Cats & \(\cong\)-strats
How to refine equality
- Admit you have a problem. \[S=T\Longleftrightarrow S\subset T \vee T\subset S\] is not a open to interpretation. Set theory is not capable of performing interesting equality.
- Appeal to a higher power...
- Higher Inductive Types
- Higher Categories (next talk)
Leibniz
\[x=y\Longleftrightarrow (\forall P)(P(x)\Leftrightarrow P(y))\]
Coarser equality
looks at fixed \(P_i\)
Liebniz:
only \[x=x\]
Equivalence Relations are removing properties
Refine is to add properties
Ex. Manger's database
\[\begin{aligned} DB[X] & = 0:DB \\ & \mid (d:DB)\boxplus (x:X)\\ & \mid (d:DB)\boxminus (x:X)\\ & / \text{refl}(d): (d=_{DB}d)\\ & / \text{priv}(x): (d=_{DB} (d\boxplus x)\boxminus x)\\ & / duplicate(d):(d=_{BD} copy(d))\end{aligned}\]
Ex. IT's database
\[\begin{aligned} DB[X] & = 0:DB \\ & \mid (d:DB)\boxplus (x:X)\\ & \mid (d:DB)\boxminus (x:X)\\ & / \text{refl}(d): (d=_{DB}d)\\ & / duplicate(d):(d=_{BD} copy(d))\end{aligned}\]
Ex. Full database
\[\begin{aligned} DB[X] & = 0:DB \\ & \mid (d:DB)\boxplus (x:X)\\ & \mid (d:DB)\boxminus (x:X)\\ & / \text{refl}(d): (d=_{DB}d)\end{aligned}\]
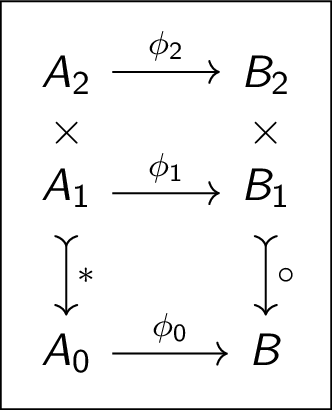
Story problems
Isomorphism
3-Cats & \(\cong\)-strats
Testing =
So equals is not absolute but variable.
New problem:
- Given level \(i\)
- Want level \(j\)
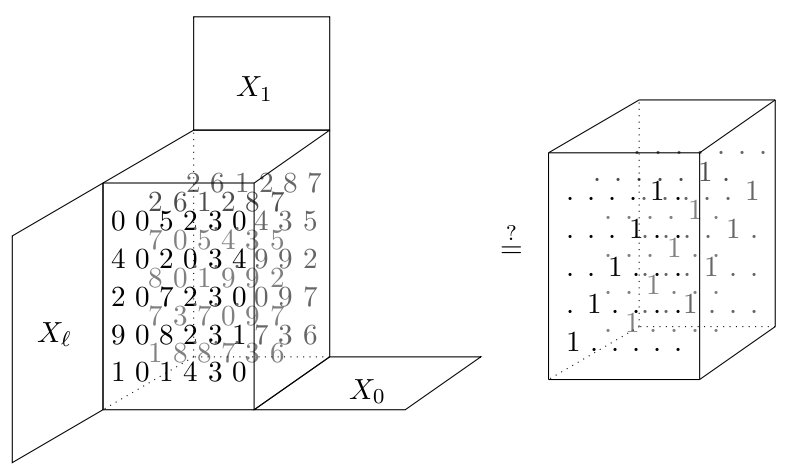
Basic equality refinement

Less basic equality test

Less basic equality test

Non-basic equality test
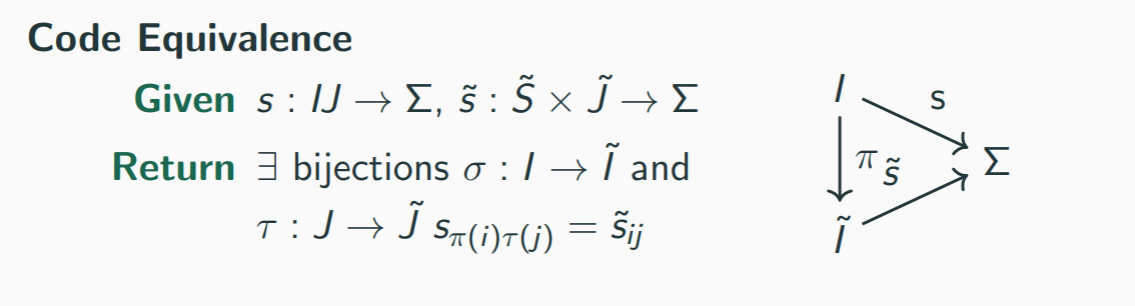
Breakit up
When frontal assualt fails, go the other direction!
1. Relax equality until it is easy.
2. Do the successive refinement with groupoid isomorphism.

Next...Cats acting on cats
