Euclid: Classical Geometry

Ingredients: Rock, paper, scissors

Hamilton: Paper=Vector Space

Cauchy: Rock + scissors = Norm, Inner product;

In fact, you can use the scissors as your straight-edge if you want, i.e. Inner product gets you a norm.

Classified at this point

\(\langle|\rangle:M\times M\rightarrowtail \mathcal{O}\) where \[\langle u|v\rangle =\bar{u}^tDv^d\]

• Orthogonal: \(\mathcal{O}\) field \(K\), identity involution, \(M=K^d\), \(D\) diagonal, determinant square class defines the geometry.*
• Unitary: \(\mathcal{O}=\left(\frac{\alpha}{K}\right)\) involution swaps roots (note may be split), \(D=I_d\).
• Symplectic:\(\mathcal{O}=\left(\frac{\alpha,\beta}{K}\right)\), adjugate involution, \(M=(\mathcal{O}e)^{d}\) if split \(e^2=e\not\in \{0,1\}\); else \(M=\mathcal{O}^d\), \(D=I_d\).
• Exceptional:\(\mathcal{O}=\left(\frac{\alpha,\beta}{K}\right)\), \(M=\mathcal{O}^{1,3}\), octonion/Albert involution, \(D=I_d\).

*If \(2K=0\) then orthogonal uses norm not product.

The Kronecher Challenge

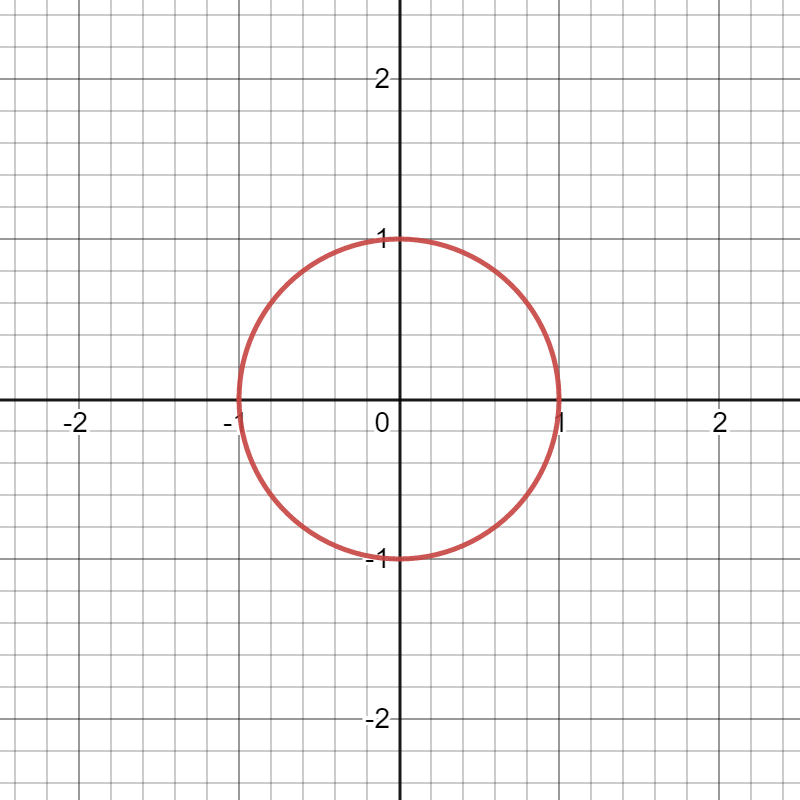
Start with Euclidean inner product

Unit circle Drawn

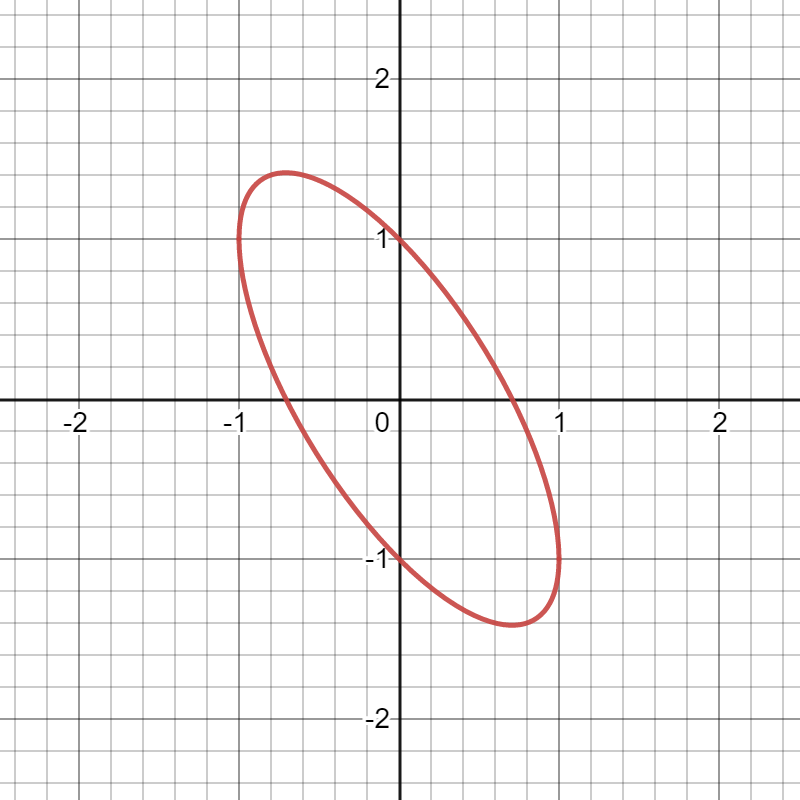
Fix some other

inner product

Unit circle Drawn

...Gram-Schmidt should not be done in public...

Unit circle Drawn

• Start with \(e_1, e_2\)
• \(u_1=e_1\)
• Replace \(u_2=e_2-\frac{\langle e_2|u_1\rangle}{\langle u_1|u_1\rangle}u_1=\begin{bmatrix} -\frac{1}{2} \\ 1 \end{bmatrix}\)

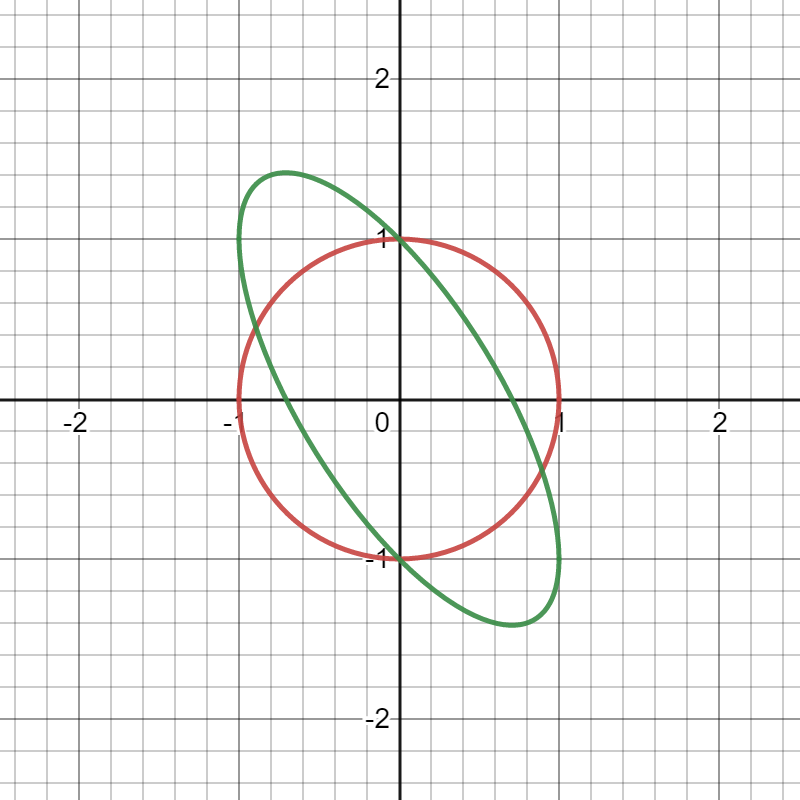
Now Find a Simultaneous

orthonormal basis for both!

Unit circles Drawn

...Gram-Schmidt should not be done in public...

Unit circle Drawn

• Start with \(e_1, e_2\)
• Normalize \(e_1\) as \(u=\frac{e_1}{\sqrt{\langle e_1|e_1\rangle}}=\begin{bmatrix} \frac{\sqrt{2}}{2}\\ 0 \end{bmatrix}\)
• Replace \(u_2=e_2-\frac{\langle e_2|u_1\rangle}{\langle u_1|u_1\rangle}u_1=\begin{bmatrix} -\frac{1}{2} \\ 1 \end{bmatrix}\)
• Norm. \(u_2=\frac{u_2}{\sqrt{\langle u_2|u_2\rangle}}=\begin{bmatrix} -\sqrt{2}/2\\\sqrt{2}\end{bmatrix}\)

The Problem

•  ONE INNER PRODUCT: BE GREEDY.  Every nonzero vector \(v\) is orthogonal to a hyperplane \(H=v^{\bot}\), recurse.
• TWO INNER PRODUCTS:
  • \(v\) is perpendicular to \(H_1=v^{\bot(1)}\) and \(H_2=v^{\bot(2)}\).
  • Only get an simultaneous ortho. basis if \(H_1=H_2\).
• Generically \(H_1\cap H_2\) has codimension 2, so not equal.
• Greed fails. You must know where to start.

Some Consequences

Theorem. Ivanyos-Qiao

For \(p\neq 2\) average case class 2 \(p\)-group isomorphism is in polytime.

Theorem. Ivanyos-Qiao

For \(2K=K\) breaks the Patarin post-quantum cypher.

Theorem. Li-Qiao

For \(2K=K\) solve isometry in polytime.

Theorems...Li-Qiao, Li, Qiao, et. al.

Complexity of tensor graph analogs.

Theorems. Grochow-Qiao

Group isomorphism by extension in polytime; tensor isomorphism, complixity classes, etc.

Brooksbank-Maglione-O'Brien-W.

Theorem. Lewis-W.

For \(p\neq 2\) isomorphism of quotients of Heisenberg groups in polytime.

Find characteristic subgroups, isomorphism test, invariants.

Algorithm. Brooksbank-W.

For \(p\neq 2\) adjoint-tensor isomorphism test.

Theorem. W.

The optimal bound on Gowers profiles is \(\log n-2\).

Theorem. Brooksbank-Maglione-W.

Isomorphism testing genus 2 is polytime.

Theorem. Kassabov-Tybursky-W.

Subgroup lattices of simple groups are as diverse as possible.

Defn. W.

\(\alpha\)-Filter refinement.

\(\alpha\)-filters in polytime.

Theorem. Brooksbank-Li-Qiao-W.

A Weisefeller-Lehman for groups

Theorems.  Maglione

Proof Sketch \(2K=K\)

Outline

• \(\mathrm{Isom}(\Phi) = \mathrm{Adj}(\Phi)^{\#}\)
• Taft: \(2K=K\) implies \((A,*) = (S,*)\ltimes (J(A),*)\)
• Albert: \((S,*)=(S_1,*_1)\oplus \cdots\oplus (S_{\ell},*_{\ell})\) *-simples
• Weil: \((S_i,*_i)\cong \mathrm{Adj}(\phi_i:V_i\times V_i\rightarrowtail L_i)\)
• Step I. Find ways to detect all this.
• Step II. write down \(\bot_i\)-bases of \(V_i\).
• Step III. Write down Steinberg generators.
• Step IV. Glue along diagonal.
• Step V. Magic power series \(z+\sqrt{1+z^2}\) a basis of \(\mathrm{Alt}\cap J(A)\)

Further Consequence

Precise structure formula \(\forall \Phi,\exists \tau_1,\ldots,\tau_{\ell}\) where \[\begin{aligned} \mathrm{Isom}(\Phi)&=(\mathrm{Isom}(\tau_1)\times\cdots\times \mathrm{Isom}(\tau_{\ell}))\ltimes O_p\\ O_p & = \{z+\sqrt{1+z^2}\mid \exists n.(z^n=0)\wedge(z^*=-z)\}.\end{aligned}\]

Informally: Neo-classical geometry decomposes into a series of classical geometries.

Why not \(2K=0\)?

\(2K=K\)

• Uni-triangular Isometries \[\{z+\sqrt{1+z^2}\mid \exists n.(z^n=0), z^*=-z\}\]
• Taft decomposition \[(A,*)=(S,*)\ltimes J(A)\]
• \((\mathbb{M}_d(K),*)=\mathrm{Sym}\oplus \mathrm{Alt}\)
• \(\mathrm{Isom}(\phi)=\mathrm{Adj}(\phi)^{\#}\)

\(2K=0\)

• \(z+\sqrt{1+z^2}\) divides by 0.
• \(\exists (A,*)\) where \(J(A)\) does not split.
• \(\mathrm{Alt}\leq \mathrm{Sym}\)
• Orthogonal groups are not unitary for ring involutions.

So what is new?

\(z+\sqrt{1+z^2}\) asks too much

• Use a semi-standard induction through linear layers
• Actually you discover along the way that this induction has infinitely many cut-downs, no power series can exist.

Almost always Taft decompositions exist for subalgebras that contain \(A^{\#}\)

In non-orthogonal type this happens and the invariant is to commute with a derivation (1-cocycle).

How do show this? Assume so, write down what it would require, call all failures "exceptional".

The exceptional case

Over \(L=K[t]/(t^2)\) in \(\mathbb{M}_{2m}(L)\) make

No Taft splitting.

Isometries of \((A,*)/(J(A),*)\) do not lift.

Those that lift are

\[S^{\diamond}=\{s\in S\mid s^*s\equiv 1\mod{J(A)}, \exist m.((s+m)^*(s+m)=1)\}\]

These are quadratic equations, no hope to solve.

Reconfigure

After some algebra

\[\exists m.(\delta(s)= sm+ms)\]

\[S^{\diamond}=\{s\in S\mid sm\bar{s}=m\}\]

Still quadratic, but concentrates on a single defect, \(m\).

Freshman's Dream

If \(pK=0\) then \((a+b)^p=a^p+b^p\).

If \(2K=0\) then for all \(M\in \mathrm{Sym}\),

\[(A+B)M(A+B)^*\equiv AMA^*+BMB^*\pmod{\mathrm{Alt}}\]

Professor's Dream

Fix involution \(M\mapsto M^*\) on \(\mathbb{M}_d(K)\), 

\[\mathrm{Sym}=\{X\mid X^*=X\}\qquad \mathrm{Alt}=\{X\mid X^*=-X,\textnormal{0 diag}\}\]

Corollary. The isometries that lift are

\[\begin{aligned}S^{\diamond} & = \{s\mid \bar{s}s=1, sm\bar{s}=m\}\\ & = \{s\mid \bar{s}s=1, s\cdot m=m\}\\ & =\mathrm{Stab}_{\mathrm{Isom}(\phi)}(M)\end{aligned}\]

This is a known group: a max parabolic in an orthogonal group.  You just write it down!