Our Quantum Future through the Algebratrics Lens
CC-BY 2021 James B. Wilson, Colorado State University, Mathematics
https://slides.com/jameswilson-3/quantumfuture/live
Steps
- Learn key experiments
- Navigate Philosophy
- Learn notation
- Spot the Math Problems
- Handle the Hype
- Hot poker/Black-body Radiation \(\Rightarrow\) Energy scales discretely by Planck's Constant \(\hbar\) \[E=n\hbar \nu\qquad n\in \mathbb{N}\]
Experiments that made us Quantum
We can see Temperature
- Black---Grey \(\Rightarrow\) Cold to warm
- Red----Yellow \(\Rightarrow\) hot
- Blue----White \(\Rightarrow\) blazing hot
- "White Hot" \(\Rightarrow\) ...illusion that could have altered history


Touch and say ouch!
Touch and loose finger
Two Theories Collide
- Light
- Newton: light spectra
- Hertz: spectra=frequency
- Heat
- Boltzman: Temperature is smoothed out statistic of total energy, i.e. motion of particles.
Ultraviolet Catastrophe
- Boltzman + Hertz \(\Rightarrow\) all colors equally welcome....and leads to infinite energy.
-
Max Planck: one color at each temperature, i.e.: energy \(E\) proportional to frequency \(\nu\) \[E=\hbar \nu\]
- Boltzman \(\exp{E/T}\) terms become Planck's \[\exp(\hbar \nu/T)\]
- But only matches observation when \(\nu\) is an integer...the first quantization.
- \(\hbar\approx 6.62\times 10^{-34}\) is Planck Constant.
Could have been missed...
(Newton) White = blend of all colors
So "white hot" supports Boltzman theory of heat.
Eventually we learned human vision at extremes is grey scale (rods not cones).
...science is not inevitable
- Hot poker \(\Rightarrow\) Energy scales discretely by Planck's Constant \(\hbar\) \[E=n\hbar \nu\qquad n\in \mathbb{N}\]
- Photo-electric Effect \(\Rightarrow\) Einstein: light is quantized with energy \[E=\hbar \nu\]
Experiments that made us Quantum
Photo-electric effect
Shine a light on metal at right frequency \(\nu\),
Electrons scatter instantly,
No "warm up", non-continuous effect.
Einstein. Argues light is discrete particles (later called "photons") having energy exactly Planck's formula \[E=\hbar \nu\]
- Hot poker \(\Rightarrow\) Energy scales discretely by Planck's Constant \(\hbar\) \(E=n\hbar \nu\qquad n\in \mathbb{N}\).
- Photo-electric Effect \(\Rightarrow\) Einstein: light is quantized with energy \(E=\hbar \nu\).
- Two slits \(\Rightarrow\) Particle-wave "duality" (duplex?) & Heisenberg Uncertainty Principal \[\Delta x\Delta p\geq \hbar/4\pi.\]
Experiments that made us Quantum
Light is a Particle.
I can hear sound (wave) around trees
Can't see (particle) around trees.
...Newton and others
Light is a wave.
Prism spreads light by slowing its speed so frequencies split,
Just like waves in water.
...Huygens and others
Young's 2-slit experiment. Eventually proved both are correct.
Maxwell extended to all electromagnetism
Jubobroff, CC BY-SA 3.0 , via Wikimedia Commons
Note that "observer" is an apparatuses, not a human
Heisenberg's Uncertainty .
\[\Delta (position)\cdot \Delta(momentum) \geq \frac{\hbar}{4\pi}\]
(\(\Delta\) standard dev. in measurement)
the \(4\pi\) is unit specific.
Particle-wave "duality" is intuitive justification
- Hot poker \(\Rightarrow\) Energy scales discretely by Planck's Constant \(\hbar\) \(E=n\hbar \nu\qquad n\in \mathbb{N}\).
- Photo-electric Effect \(\Rightarrow\) Einstein: light is quantized with energy \(E=\hbar \nu\).
- Two slits \(\Rightarrow\) Particle-wave "duality" & Heisenberg Uncertainty Principal \(\Delta x\Delta p\geq \hbar/4\pi\).
- Spectral Lines \(\Rightarrow\) Bohr's Electron Shells & Dirac-Pauli Spin
Experiments that made us Quantum
- Hot poker \(\Rightarrow\) Energy scales discretely by Planck's Constant \(\hbar\) \(E=n\hbar \nu\qquad n\in \mathbb{N}\).
- Photo-electric Effect \(\Rightarrow\) Einstein: light is quantized with energy \(E=\hbar \nu\).
- Two slits \(\Rightarrow\) Particle-wave "duality" & Heisenberg Uncertainty Principal \(\Delta x\Delta p\geq \hbar/4\pi\).
- Spectral Lines \(\Rightarrow\) Bohr's Electron Shells & Dirac-Pauli Spin
- Bell Tests \(\Rightarrow\) Einstein-Padolsky-Rosen paradox & Entanglement
Experiments that made us Quantum
Philosophy
Interpretations
- Copenhagen: states are waves that collapse to a particle when measured.
- Pilot Wave: particles are surfing on waves, sometimes you watch the wave, sometimes the surfer
- Many Worlds: all possibilities happen, but in parallel worlds
- Bayesianism: measurement merely updates our probabilities to better match new evidence.
Interpretations of Measurement
- Copenhagen: states are waves that collapse(undefined/Circular argument) to a particle when measured.
- Pilot Wave: particles are surfing on waves, sometimes you watch the wave, sometimes the surfer (incomplete/how does entanglement propogate to surfer instantly?).
- Many Worlds: all possibilities happen, but in parallel worlds(untestable/Argumentum ad Mysteriam).
- Bayesianism: measurement merely updates our(anthropic) probabilities to better match new evidence.
Notation & Vocabulary
Books say Dirac Notation
``Bra-t''\[\langle t|=\begin{bmatrix} \bar{t}_1 & \cdots & \bar{t}_n\end{bmatrix}\]
``ket-u'' \[|u\rangle = \begin{bmatrix} u_1\\ \vdots \\ u_n\end{bmatrix}\]
``bracket-t-u''
\[\langle t|u\rangle=t^{\dagger} u \in \mathbb{C}\]
Generalize to infinite dimensional Hilbert spaces \(\mathcal{H}\) where \(\langle t|\) becomes an integral (Riesz Representation Theorem).
\(\langle t|\) vs. \(|t\rangle\) all taste,
I like rows, they use typed text space better.
Reality
\[\langle +-+| = \frac{\sqrt{2}}{2} (\langle 010|+\langle 101|)\]
\[H^{\otimes 4}|0000\rangle = |x\rangle\]
\[QFT(|x\rangle) =\frac{1}{\sqrt{2^n}}\bigotimes_{i=1}^n\left(|0\rangle+e^{x_i 2^{-i+1}\pi i}|1\rangle\right)\]
Extend Dirac Notation
What is a vector?
....element of a vector space.
What is a tensor?
What is a tensor?
....element of a tensor space.
\[U_R=R^X/\mathrm{Span}_R S=\mathrm{Pres}_R\langle X|S\rangle\]
\[{_R V}=R^Y/\mathrm{Span}_R T=\mathrm{Pres}_R\langle Y|T\rangle\]
\[U\otimes_R V = R^{X\times Y}/(R^X\otimes T+S\otimes R^Y)\]
\[\begin{aligned} \otimes :R^X\times & R^Y\to R^{X\times Y}\\ (u\otimes v)_{xy}& =u_x v_y\end{aligned}\]
I.e.\[u\otimes v=\begin{bmatrix}u_1\\ \vdots \\ u_{m}\end{bmatrix}\begin{bmatrix} v_1 & \cdots & v_n\end{bmatrix} = \begin{bmatrix} u_1 v_1 & \cdots & u_1 v_n\\ \vdots & & \vdots \\ u_m v_1 & \cdots & u_m v_n\end{bmatrix}\]
- Linear form \(\langle t|:U_1\to \mathbb{C}\) so evaluate \(|u_1\rangle\) as \[\langle t|u_1\rangle\]
- Bi-linear form \(\langle t|:U_2\to (U_1\to \mathbb{C})\) so evaluate \(|u_2\rangle\) as \[\langle t|u_2\rangle:U_1\to \mathbb{C}\] then on \(|u_1\rangle\) to get \[\langle t|u_2,u_1\rangle=\langle t|u_2\rangle|u_1\rangle\in \mathbb{C}\]
- Tri-linear...\[\langle t|:U_3\times U_2\times U_1\to \mathbb{C}\]
- \(\ldots\)
How to imagine tensors with high valence?
Look at data!
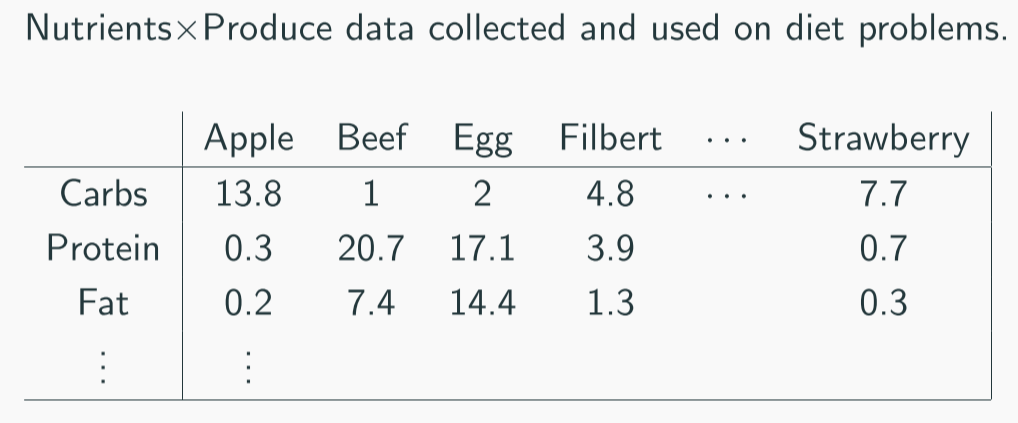
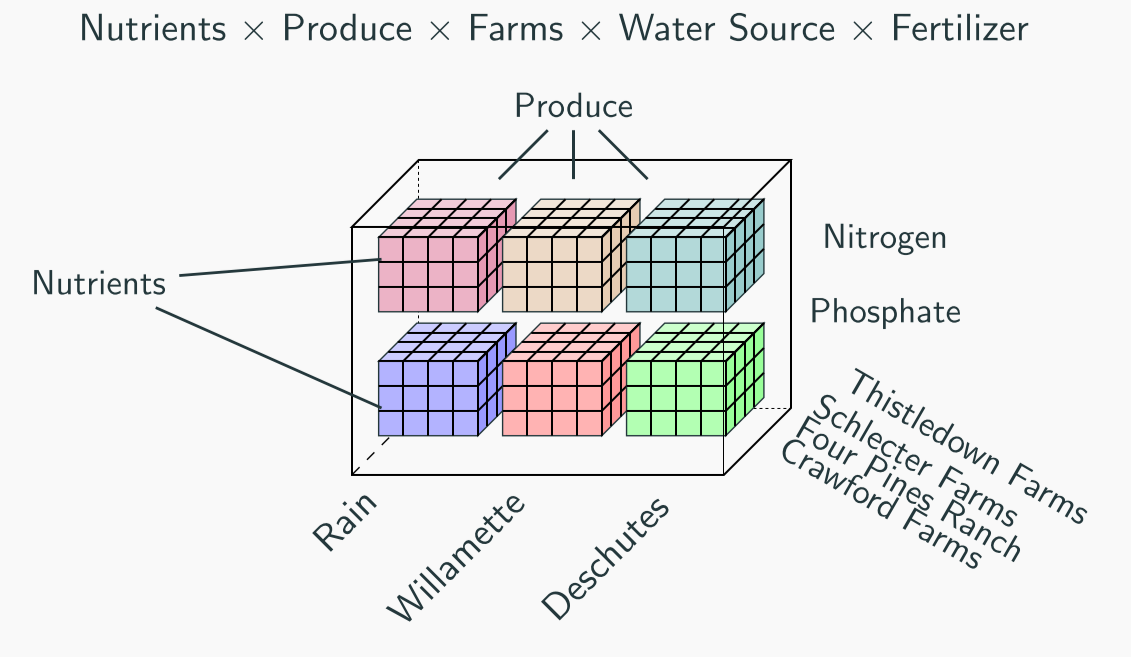
How to imagine tensors with high valence?
Look at data!
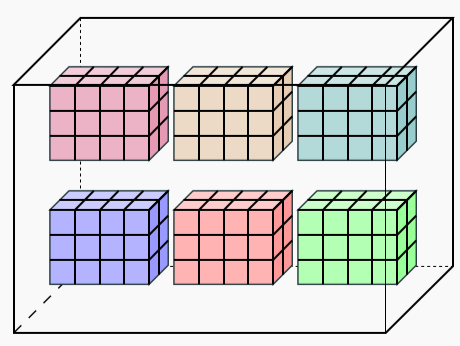
5-valent tensor
Tensor Networks
(Operads)
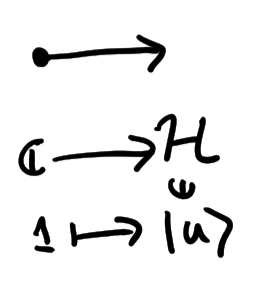
Make a vector...
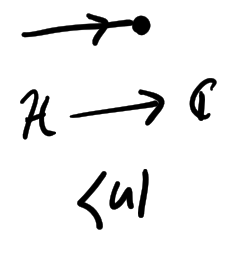
Measure a vector...
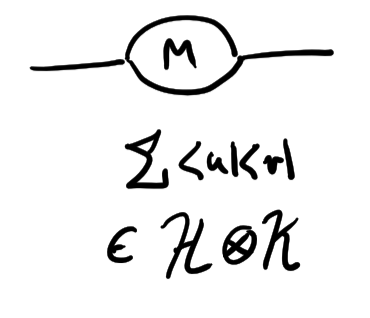
Make a 2-tensor...
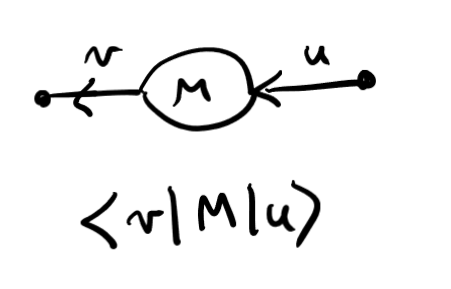
Use a 2-tensor

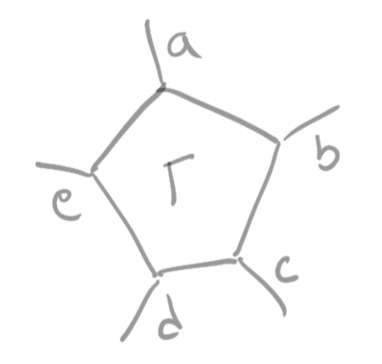
\[\Gamma_{abcde}\in \mathbb{C}\]
Extend Dirac Notation
Defn. A tensor space \(T\) is a vector space (module) with a linear map \[\langle \cdot |:T\to (V_1\otimes\cdots \otimes V_{\ell})^*\] \(t\in T\) is a tensor, \(V_a\) axes (or modes, or legs), and \(V_1,\ldots,V_{\ell}\) the (reference) frame.
\(\langle \cdot|\) interprets \(t\in T\) as multi-linear.
What is a tensor?
....element of a tensor space.
Let \(T=\mathbb{C}\hat{0}\oplus \mathbb{C}\hat{1}\), i.e. 2-dimensions with a silly basis \(\{\hat{0},\hat{1}\}\).
\(\langle \cdot |:\mathbb{C}^2\to (\mathbb{C}^2)^*\) will be simply \[\langle \alpha\hat{0}+\beta\hat{1}|u\rangle =\alpha u_1+\beta u_2.\]
So \(\langle \hat{0}|=[1,0]\) and \(\langle \hat{1}|=[0,1]\).
\(\langle t|\) interprets \(t\) as multi-linear
Now delete the hats!
So \(\langle 0|=[1,0]\) and \(\langle 1|=[0,1]\).
Let \(A=\mathbb{C}^{2}=\mathbb{C}\langle 0|\oplus \mathbb{C}\langle 1|\) and \(B=\mathbb{C}^{3}=\mathbb{C}\langle 0|\oplus \mathbb{C}\langle 1|\oplus \mathbb{C}\langle 2|\).
Let \[\langle ab|:=\langle a|\langle b|=\langle a|\otimes \langle b|\in (A\otimes B)^*\]
E.g. \(\langle 01|=\langle 0|\langle 1|=\begin{bmatrix} 1\\0 \end{bmatrix}\begin{bmatrix}0 & 1& 0 \end{bmatrix}=\begin{bmatrix} 0 & 1 & 0\\ 0 & 0 & 0 \end{bmatrix}\in (\mathbb{C}^2\otimes \mathbb{C}^3)^*\)
\(\langle t|\) interprets \(t\) as multi-linear
\(\langle 00|=E_{11},\langle 01|=E_{12},\langle 02|=E_{13}, \langle 10|=E_{21}, \langle 11|=E_{22},\langle 12|=E_{23}\)
\(\langle 0|,\ldots\langle m|\) usually just a basis, but common to write \[x=x_n 2^n+\cdots+x_0 2^0\qquad x_i\in \{0,1\}\] and so \[\langle x|=\langle x_n| \cdots \langle x_0|\in (\mathbb{C}^2)^{\otimes n}\] hence integer data written in binary "bits", only quantum so "qu-bits"
E.g. \(\langle 01|=\langle 0|\langle 1|=\begin{bmatrix} 1\\0 \end{bmatrix}\begin{bmatrix}0 & 1& 0 \end{bmatrix}=\begin{bmatrix} 0 & 1 & 0\\ 0 & 0 & 0 \end{bmatrix}\in (\mathbb{C}^2\otimes \mathbb{C}^3)^*\)
\(\langle t|\) interprets \(t\) as multi-linear
QUIZ
Explain \[\langle \uparrow\uparrow|-i\langle \downarrow\downarrow|\]
- Need a vector space with basis \(\{\uparrow,\downarrow\}\) so \(\mathbb{C}^2\) will do.
- Need two copies, so \(\mathbb{C}^2\otimes \mathbb{C}^2\), i.e. \((2\times 2)\) complex matrices.
- \[\langle \uparrow\uparrow|-i\langle\downarrow \downarrow|=\begin{bmatrix}1 & 0 \\ 0 & 0 \end{bmatrix}-i\begin{bmatrix}0 & 0 \\ 0 & 1\end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -i\end{bmatrix}\]
Quantum Future
- Quantum Computer
- Quantum Materials
- Quantum Information
Emerging Math Problems
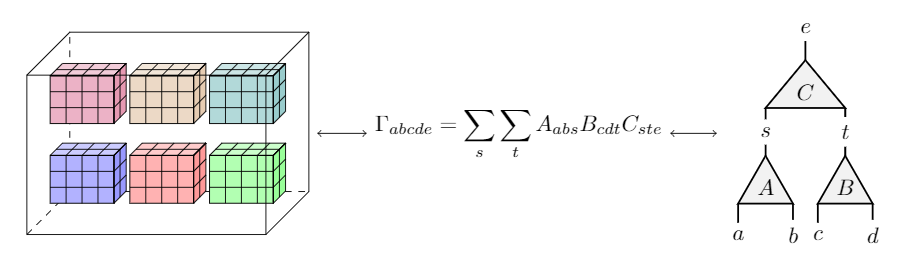
Tensor is a grid of numbers.
Numbers can be results of formulas ("tensor contraction")
Structure of formulas \(\Leftrightarrow\) Structure of Entanglement of many bodies
Question I
-
Find tensor network decompositions
-
Explain relations between equivalent decompositions
-
Classify, at least on small scales.
Math is graph theory & algebra & topology.
Quantum materials
- Classical Chemistry:
- Given atoms,
- find & bend the rules for bonding.
- Combinatorics: matching problems: \(H\) wants an electron, \(OH\) has more than it wants\(\Rightarrow\) \(H_2 )\))
- Topology: molecule shape prevents easy bonding
- Algebra: crystal symmetry, degrees of freedom forced by representation theory.
Quantum materials
- Classical Chemistry:
- Given atoms,
- find & bend the rules for bonding.
- combinatorics, topology, algebra
- Quantum Materials:
- Given particles
- find & bend the rules for entanglement.
- Algebraic
- Isomorphism invariants (ranks, SVD, eigen, derivations, adjoints...)
- Gauge symmetries
- Combinatorial: networks
- Perturbative, Annealing, Neural Nets,...

Tensor network of quantum entanglements in a quantum material.
Material interacts with environment on boundary (red dots).
The boundary (edge) physics is about the symmetries of individuals.
Question 2
-
Explain the boundary physics of quantum materials ("edge theory")
Math is isomorphism testing of tensors and graphs.

Notice the Noise (Green). It somehow only locally obstructed symmetry.
Graphical properties of the network explain how to adjust edge theories under noise.
Question 2'
-
Explain the boundary physics of quantum materials ("edge theory") under noise
Very strange that something as precise as graph theory, not analysis, handles noise model....
Understanding Quantum Hype
Recent "breakthroughs"
- Factoring
- Ramsey Numbers
- Quantum
SupremacyAdvantage - Time Crystal
Factoring
- Biggest RSA type factorization: 830-bits \(2^{830}\), RSA of today is 2040-bits so about \(2^{1200}\) TIMES HARDER
- Biggest Quantum factorization
- NONE!
- But kinda 15, 21
- Needs a lot of qubits more than we have in the world to run fault-tolerant error-corrected
- DWAVE is adiabatic, not circuit based, better for modeling quantum behavior not quantum computing
Ramsey Number
- Adiabatic solution reproduced signals "near" expected values of known Ramsey numbers, and signals for others unknown....but no way to test.
Quantum Advantage
- Context:
- Google buys UC Santa Barbara quantum computing lab.
- Newly minted Google Q Team invents a problem: "Can Quantum Computer generate probabilities of random quantum operations faster than a classical computer?"
- Asked and answered: yes. Gets a lot of press.
- Reaction within CS...
- is this a well-posed question?
- assume a classical computer has to analyze a quantum computer, not a head-to-head fight
Time Crystals
- Context:
- Einstein: time-space unified.
- Wilczek: crystals are symmetries in space...maybe there are symmetries in time?
- Synthesized quantum states in Google's quantum computer seem to have achieved this.
- Synthesized quantum experiments are what Feynman wanted quantum computer to do...it seems they might do that!
Understanding Quantum Hype, II
Reality
- Eventually quantum computers threaten security, so change the locks now
- Quantum computing has changed how we model computation --- much more attention to low-level efficiency useful in everyday computing
- Making quantum materials will let us make quantum who knows what.