Is a constant function ever the identity?
2021 James B. Wilson, Colorado State University
The brief story of trouble with substitution and why we need λ-calculus .
λ
Variables often treated as blanks to be filled. f(x)=x+5
becomes
...which becomes
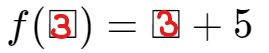
In time the boxes are imaginary and substitution is immediate
f(3)=3+5
f(□)=□+5
Two simple functions emerge.
First are constant functions: f(x)g(y)h(u)=5=π=cat
There are too many constant functions to name. So we capture them all with a c Kc(x)=c
Two simple functions emerge.
Second are the identity functions: f(x)g(y)h(u)=x=y=u
Though distinct in symbols, we find no difference when we substitute.
So we equate all these in a unified concept, a single identity function I(x)=x
Two simple functions emerge, and then provoke a protest.
Constant functions Kc(x)=c and the identity function I(x)=x should coexist in peace.
So what laws of substitution take control in a function such as Kx(x)=x?
Is this constant and never changing?
Or is it the identity---always reflecting the changes of the input?
Substitutions needs rules, but...
Making rules will impose limits and concern.
- Will banning some substitutions lead to loosing power, like recursion?
- Will the rules be consistent or lead to their own paradoxes?
- If the rules be consistent, will they be easy to follow?
- Will some substitutions never end?
Alonzo Church give us the answers in the form of his λ-calculus.
It was soon seen as equivalent to Turing's notion of computation.
In their honors today we teach
- The Turing Machine as the universal computer, and
- λ-calculus as the universal programming language.