From Spins to Society: Modeling Collective Social Behavior with Statistical Physics

From Spins to Society:

Modeling Collective Social Behavior

with Statistical Physics

Jan Korbel

Slides available at: slides.com/jankorbel

Personal web: jankorbel.eu

Motivation

Modeling the social systems is typically a very complicated and complex task

Many different approaches are used to model social systems - agent-based models, for example

One way of modeling the social systems is to use the methods of statistical physics to describe the social behavior

The application of statistical physics methods in social systems gave rise to a new field - sociophysics

Most of the sociophysics models are based on simplifying assumptions.
- These assumptions allow us to use the methods of statistical physics and (at least qualitatively) study the macroscopic behavior of social systems.
The main aim of sociophysics, therefore, is different from the application of statistical physics in natural systems
- In natural systems, we ideally want to fully understand the phenomena that can be observed in the system
- This is typically possible since natural systems have many symmetries
- Social systems, on the other hand, are more complex, and therefore, complete understanding is almost impossible

Initial Remark

Some pioneering models

Voter model - agents influence each other to change their opinions

Sznajd model - model is based on a concept of social validation

Axelrod model - describes the cultural dissemination

Bounded confidence models- Individuals adjust their opinions if they are sufficiently close

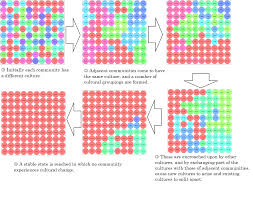
Main driving mechanisms

Homophily

Dyadic relation between opinions of pairs
"Birds of a feather flock together"
People tend to like other peers with similar opinions
McPherson, Smith-Lovin and Cook (2001). Annual Review of Sociology. 27: 415–444.

Social balance

Triadic relation between friendly and inimical relations
"friend of my friend is my friend, enemy of my enemy is my friend"
People tend to prefer balanced triangle relationships
Heider (1946). The Journal of Psychology. 21: 107–112.

Main driving mechanisms

Physical interpretation

We now discuss how these mechanisms can be translated into statistical physics models
We model the individuals as particles and their opinions as (binary) spins
The social models then correspond to various Ising-type models

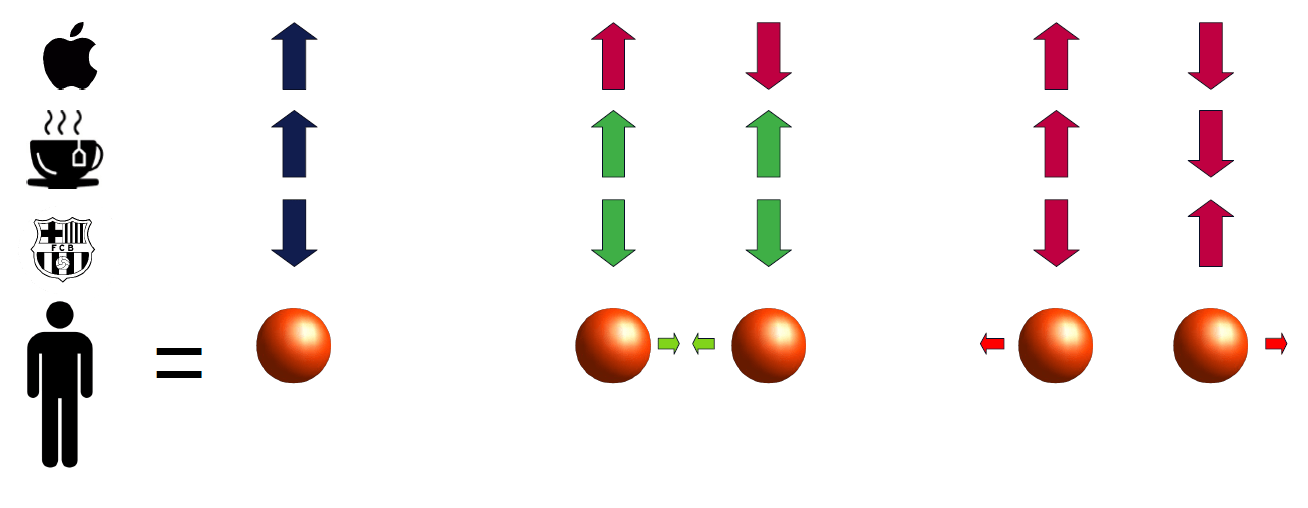
Social Hamiltonian

In statistical physics, the main quantity is the Hamiltonian, which quantifies the energy of the system
The system tends to reach the minimal energy state
Here, the social Hamiltonian plays the role of social stress
Similarly to physics, individuals tend to minimize their social stress as much as possible
We define the opinion vector of individual $i$ as $$s_i= \{s_i^1,\dots,s_i^G\} \in \{-1,+1\}^G$$
We also define the relations between individuals as $$A_{ij} \in \{-1,0,1\}$$ for inimical, non-existent, and friendly relations, respectively
In some situations we only consider friendly or none relations

Social Hamiltonian for homophily

Let us first consider that $A_{ij} \in \{0,1\}$
For homophily, the Hamiltonian can be written as $$H(s_i) = - J \sum_{ij} A_{ij} s_i \cdot s_j$$ where $s_i \cdot s_j := \frac{1}{G} \sum_{k=1}^G s_i^k s_j^k$ measures the similarity between opinion vectors $s_i$ and $s_j$
This corresponds to the Ising model with multiple layers of spins, each corresponding to one opinion type

Social Hamiltonian for social balance

In this case, the social balance is solely about relations
Therefore, it is independent of the opinions
Assuming the adjacency matrix $A_{ij} \in \{-1,0,1\}$
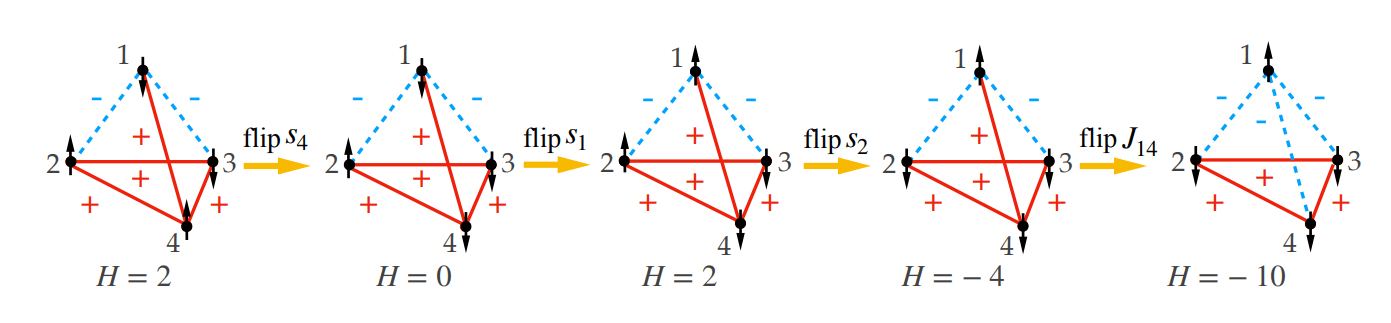
The social balance Hamiltonian can be defined as $$H(A_{ij}) = - J\sum_{ijk} A_{ij} A_{jk} A_{ki}$$
The cubic term $A_{ij} A_{jk} A_{ik}$ is equal to:
- +1, if the triangle is balanced
- - 1, if the triangle is unbalanced
- 0, if the triangle is not closed
This corresponds to the Baxter-Wu model on the links

Combining homophily and social balance

Both phenomena have been extensively studied separately
By combining both terms, we obtain the Hamiltonian describing both homophily and social balance $$H(s_i,A_{ij})= - \sum_{ij} A_{ij} s_i \cdot s_j - g \sum_{ijk} A_{ij}A_{jk}A_{ki}$$
In this model, both opinions and relations co-evolve together
It was first introduced in

[1] J. R. Soc. Interface. (2020) 1720200752

Social fragmentation

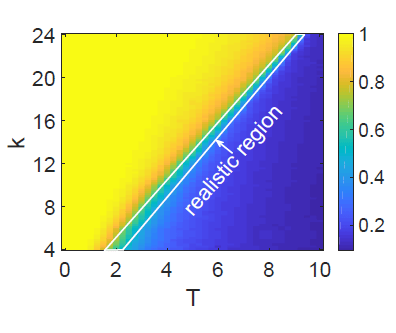
The system exhibits a phase transition between balanced and unbalanced state
We define $f = \frac{n_{+}-n_{-}}{n_{+}+n_{-}}$ where $n_\pm$ is the number of (un)balanced triangles
We observe the transition from a fragmented to a polarized society which depends on the network degree $k$

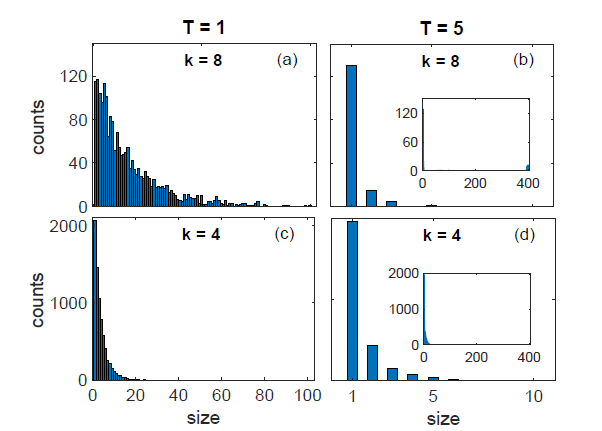
The main issue with this model is that it does not relax to the global minimum but often gets stuck in a local minimum
This is known as a rough energy landscape
Furthermore, it is unrealistic that individuals would update their opinions and have in mind whether these changes result in a shift in balanced triangles into unbalanced
Therefore, a more realistic approach is to assume that individuals can update their opinions by not anticipating the change in the triadic balance for all possible triangles

Rough energy landscape

Local Hamiltonian approach

[2] Sci. Rep. (2021) 11, 17188

We generalize the Hamiltonian model to consider an agent-based model, where the agents try to optimize their individual social stress
A social stress of an individual $i$ can be written as $$H^i(s_{i}) = - \sum_{j \in \mathcal{N}_i} A_{ij} s_i s_j - \sum_{j,k \in \mathcal{Q}_i} A_{ij} A_{jk} A_{ki}$$
Here, the relation between two individuals is determined as $A_{ij} = \mathrm{sign}(s_i \cdot s_j)$, so friendly we the two individuals have more common than different opinions and vice versa
$\mathcal{N}_i$ is the neighborhood of $i$
$\mathcal{Q}_i$ is a fraction of triangles that contain $i$

Monte Carlo update with limited rationality

The evolution is given by the following algorithm:
1. Initialize opinion vectors
2. Update
  - Pick a node at random
  - Pick a fraction of triangles $q_i=\mathcal{Q}_i/N ^\Delta_i$ at random
  - Try to flip one opinion at random
  - Accept the flip with probability $ \min\{1,e^{-\beta \Delta H^i}\}$
3. Repeat until the system converges
By taking into account a fraction of triangles, the agents can be irrational and increase the total social stress

Sample step

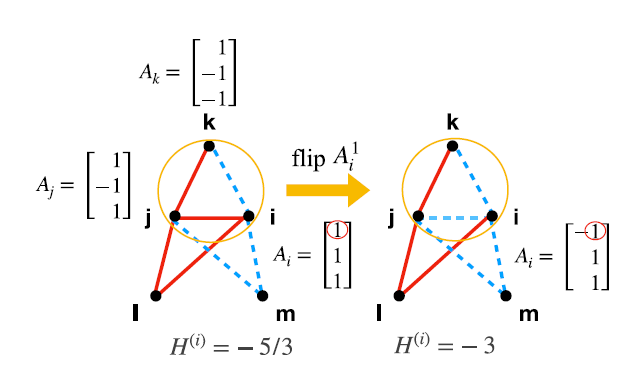
Here the flip is accepted even if it decreases number of balanced triangles

Phase diagram

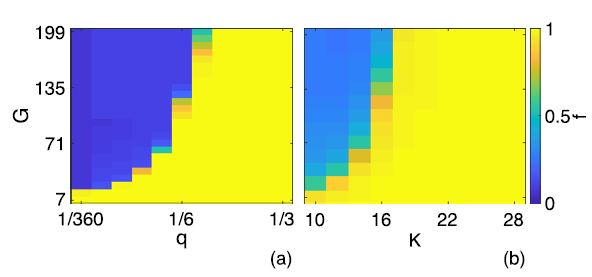
For large enough $q$ and degree $k$ the system reachs stationary, balanced, and fragmented state

Is social balance an emergent phenomenon?

[3] PNAS (2022) 119 (6) e2121103119

In many real-world social systems, the tendency to create balanced triangles has been verified
However, it is questionable whether the individuals can follow all possible triangles to adjust their opinions
Particularly, this is not realistic on social networks where individuals have hundreds (or thousands) of friends
So the question is whether the social balance is not just an emergent statistical phenomenon that arises as a consequence of dyadic interactions

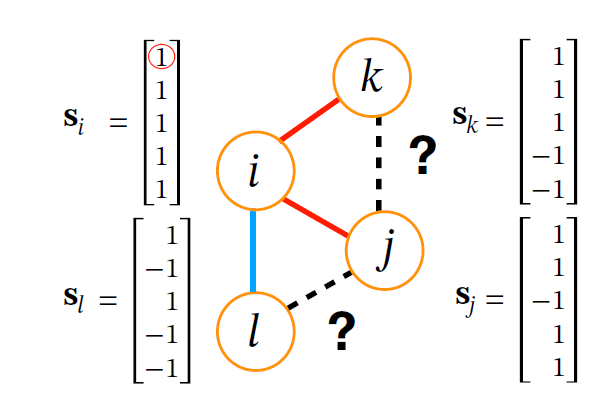
Is social balance in homophily framework

Individual $i$ does not know the relations between other individuals, just to his/her neighbors
The key aspect is that social balance takes both positive and negative links into account

Local Hamiltonian of social systems

We consider that individuals do not care about social balance
However, they do care about their friends as well as their enemies
Therefore, the individual social stress can be expressed as $$H^i(s) = - \alpha \sum_{j: A_{ij}=1}s_i \cdot s_j + (1-\alpha) \sum_{j: A_{ij}=-1} s_i \cdot s_j$$
The links are determined from $A_{ij}= \mathrm{sign}(s_i \cdot s_j)$
The first term describes homophily with friends
The second term describes heterophily with enemies
The parameter $\alpha$ weights the importance of friendship versus inimical relations

Phase diagram

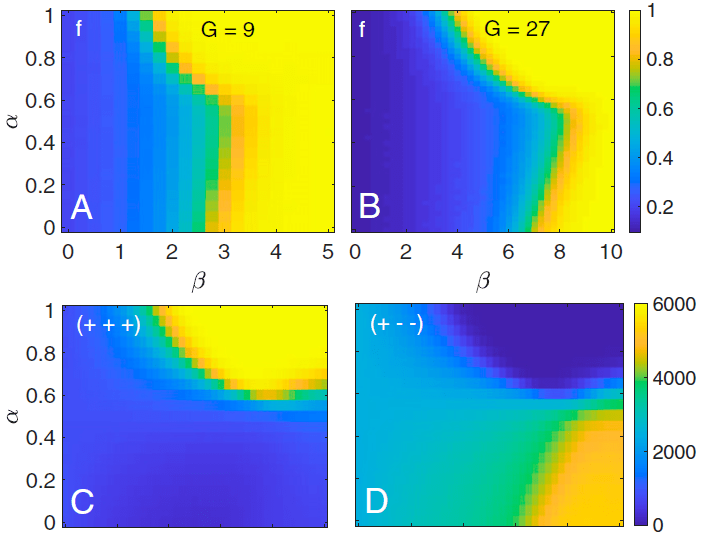
Yellow region - the system is balance (triangles are balanced) - difference between (+ + +) and (+ - - )

Application to PARDUS online game

Pardus is an online multiplayer game where the players have to cooperate or attack each other to progress
In the dataset, we can measure the complete network topology as well as if the relation is friendly or hostile

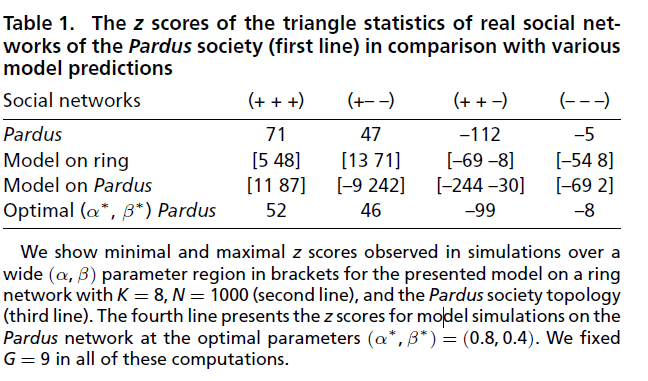
Empirical validation in the social experiment

[4] npj Complexity 2 (2025) 1

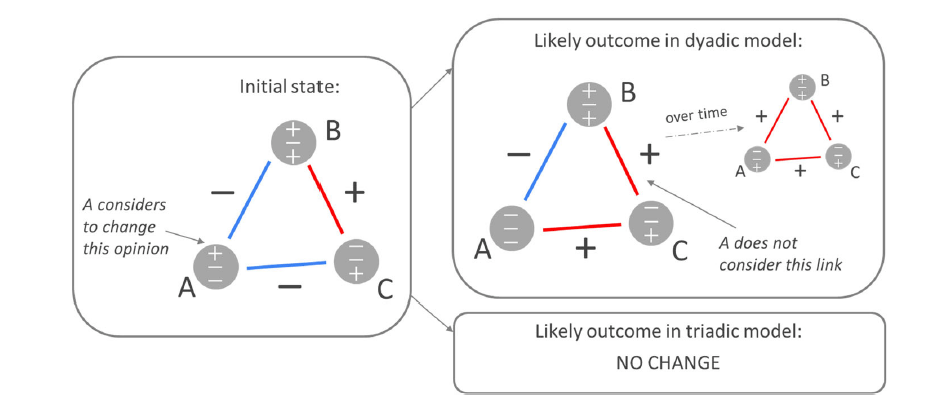
In a recent study, a team around Mirta Galesic and Henrik Olsson showed the validity of this model in a real-life experiment
In the longitudinal group experiment with 480 interacting participants, the authors find that
triadic social balance can be achieved even if people pay attention only to dyadic relationships

Application to to group-size distribution

[5] Phys. Rev. Lett. 130 (2023) 057401

Hamiltonian of a group $\mathcal{G}$

$H(\mathbf{s}_{i_1},\dots,\mathbf{s}_{i_k}) = \textcolor{red}{\underbrace{- \phi \, \frac{J}{2} \sum_{ij \in \mathcal{G}} A_{ij} \mathbf{s}_i \cdot \mathbf{s}_j}_{intra-group \ social \ stress}} \textcolor{blue}{ + \underbrace{(1-\phi) \frac{J}{2} \sum_{i \in \mathcal{G}, j \notin \mathcal{G}} A_{ij} \mathbf{s}_{i} \cdot \mathbf{s}_j}_{inter-group \ social \ stress}} - \underbrace{h \sum_{i \in \mathcal{G}} \mathbf{s}_i \cdot \mathbf{w}}_{external \ field}$

Group 1

Group 2

friends

enemies

To derive the equilibrium distribution, we extend entropy to systems with emergent structures (molecules, social groups...)

Entropy for structure-forming systems

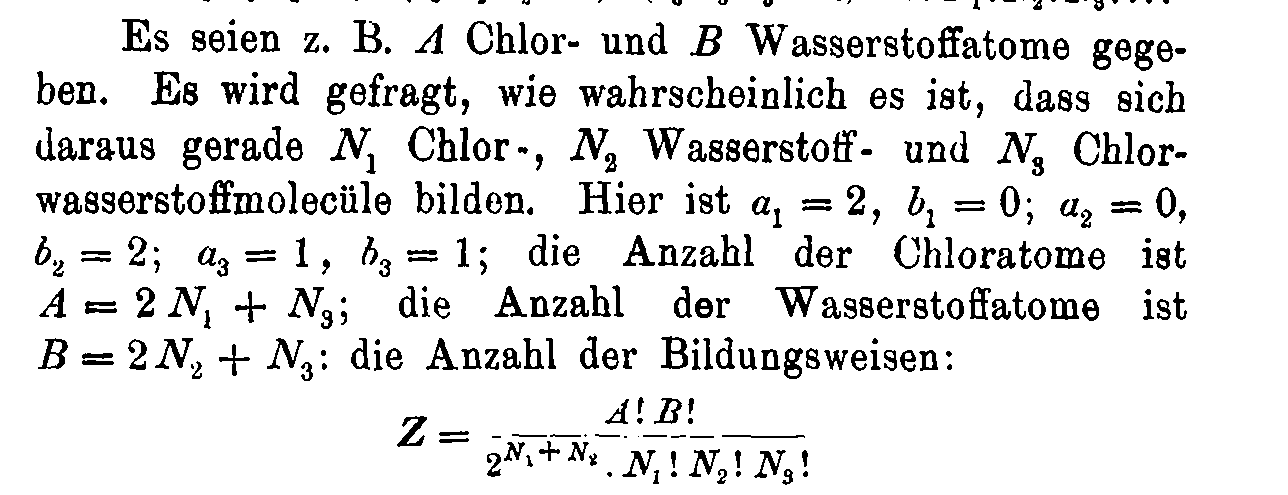
$W(n_i^{(j)}) = \frac{n!}{\prod_{ij} n_i^{(j)}! \color{red}(j!)^{n_i^{(j)}}}$

$$\mathcal{S} = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{red}- 1}) {\color{red}- \sum_{ij} \wp_i^{(j)}\log \frac{j!}{n^{j-1}}}$$

$ S = k \cdot \log W$

[6] Nat. Comm. 12 (2021) 1127

MaxEnt distribution

To calculate the MaxEnt distribution, we maximize the entropy w.r.t. to
- normalization $\sum_{ij} j \wp_{i}^{(j)}=1$
- average energy $\sum_{ij} \wp_{i}^{(j)} \epsilon_{i}^{(j)} = E$
Equilibrium distribution: $$\hat{\wp}_i^{(j)} = \frac{n^{j-1}}{j!} \exp(-\alpha j - \beta \epsilon_i^{(j)})$$
Normalization: we solve the equation $\sum_{ij} j \wp_i^{(j)} = \sum_{ij} \frac{n^{j-1}}{(j-1)!} e^{-{\color{red} \alpha} j - \beta \epsilon_i^{(j)}} = 1$ for ${\color{red} \alpha}$

Model approximations

Configuration model: We do not know the full network but just a degree distribution.
- The probability of observing a link between $i$ and $j$ is proportional to $k_i k_j$
Mean-field approximation: We use the mean-field approximation of the Hamiltonian
These two approximations lead to the set of self-consistency equations:

$$m^{(k)} = k \sum_{q^{(k)} q^{(k,l)}} P(q^{(k)}) P(q^{(k,l)}) \tanh(\beta H^{(k)}(m^{(l)},q^{(k)},q^{(k,l)})) $$

where $q^{(k)}$ is the intra-group degree, $q^{(k,l)}$ is the inter-group degree and $P$ is the degree distribution

Results for zero intra-group degree

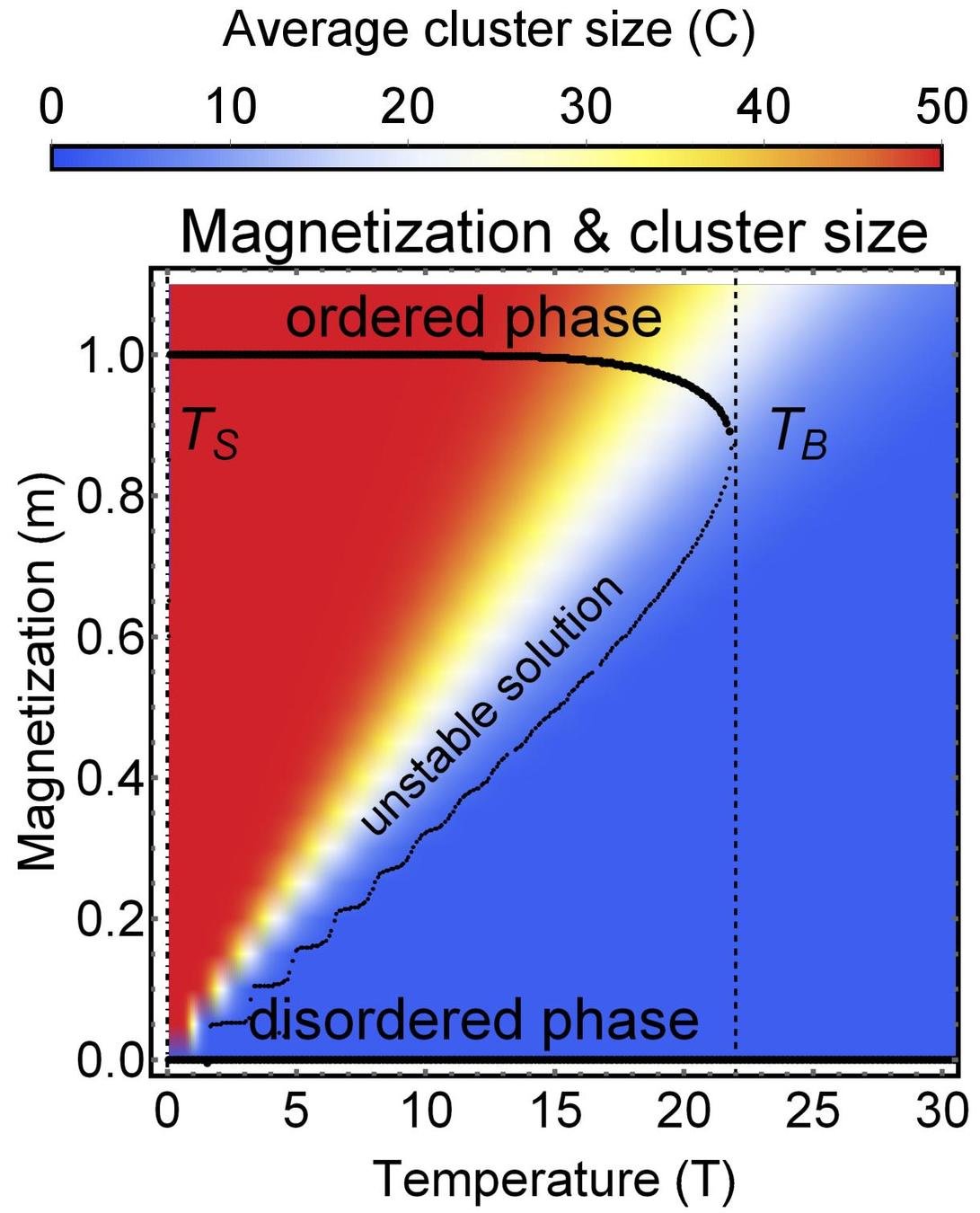
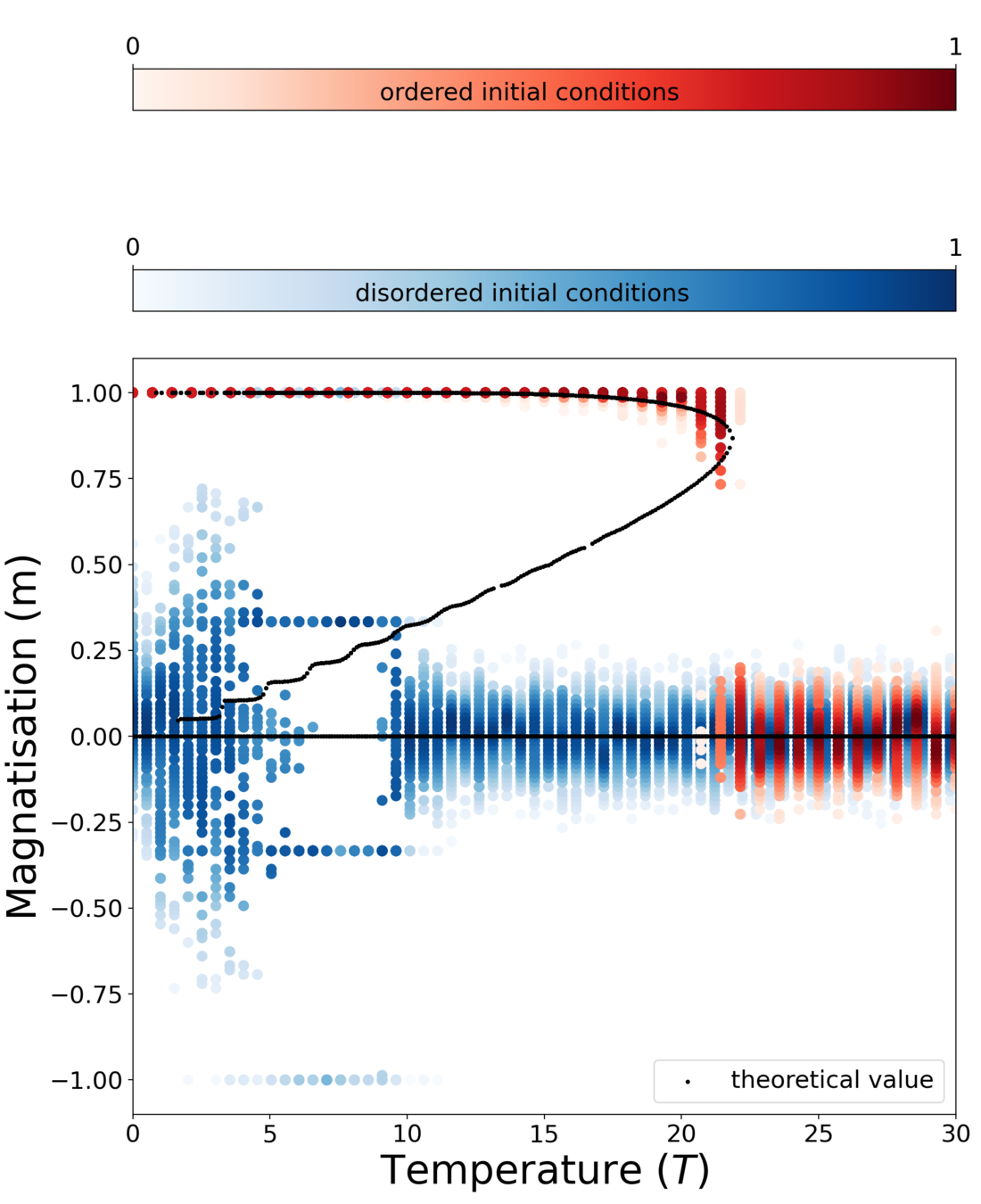
Theory

MC simulation

Pardus group size distribution

Social polarization

[7] to be submitted soon

Currently, we are investigating how the increase in network connectivity affects polarization
With the advent of social networks, the average number of connections increased
We also observe the increase in polarization with the advent of social networks
Can these two phenomena be explained by the model?

Social polarization

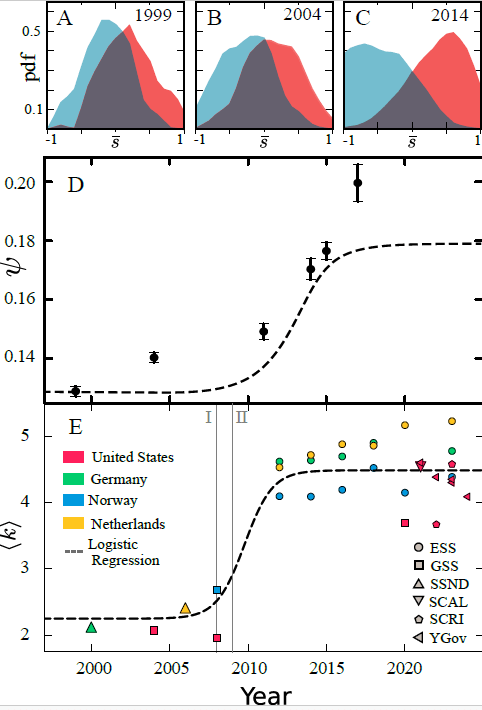
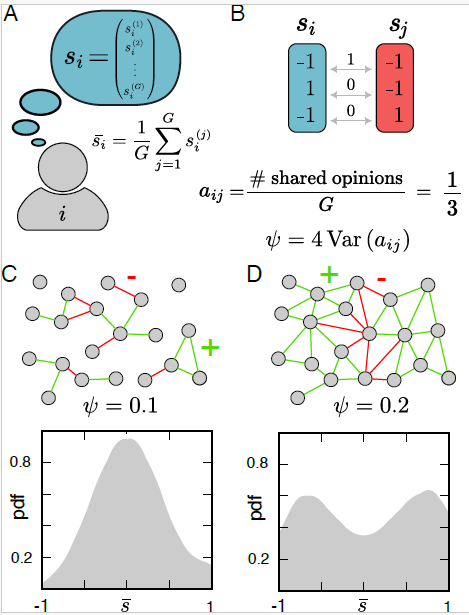
Phase transition in polarization

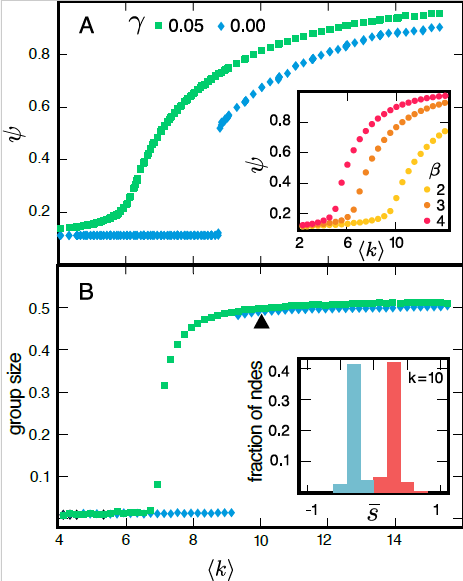
Future work

[8] Nat. Commun. 16 (2025) 2628

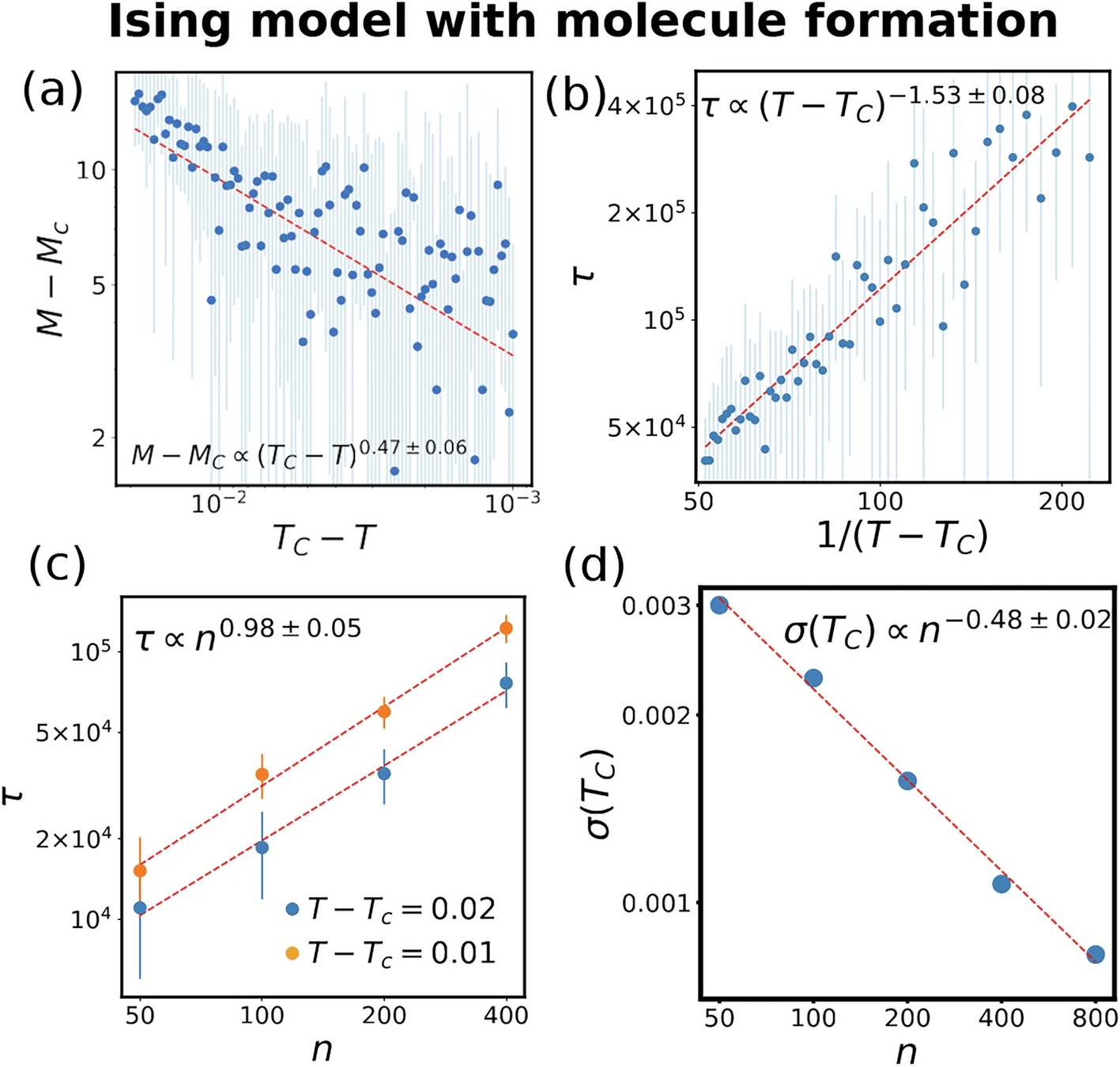
Recently, we have shown that for a special class of phase transitions that are both first-order (jump) and second-order (criticality), which is called mixed-order transition
The system exhibits a long plateau at a metastable state before it jumps to another phase

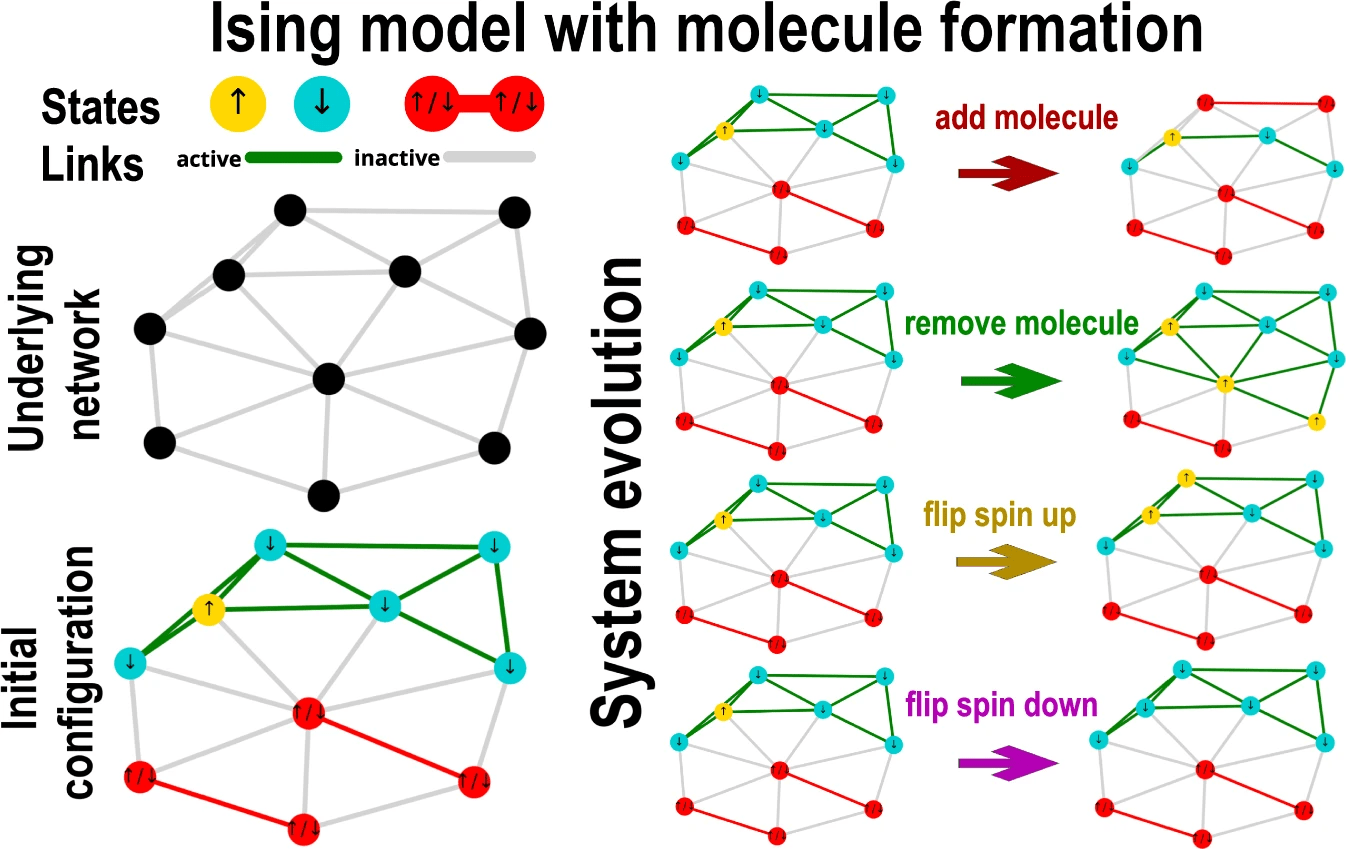
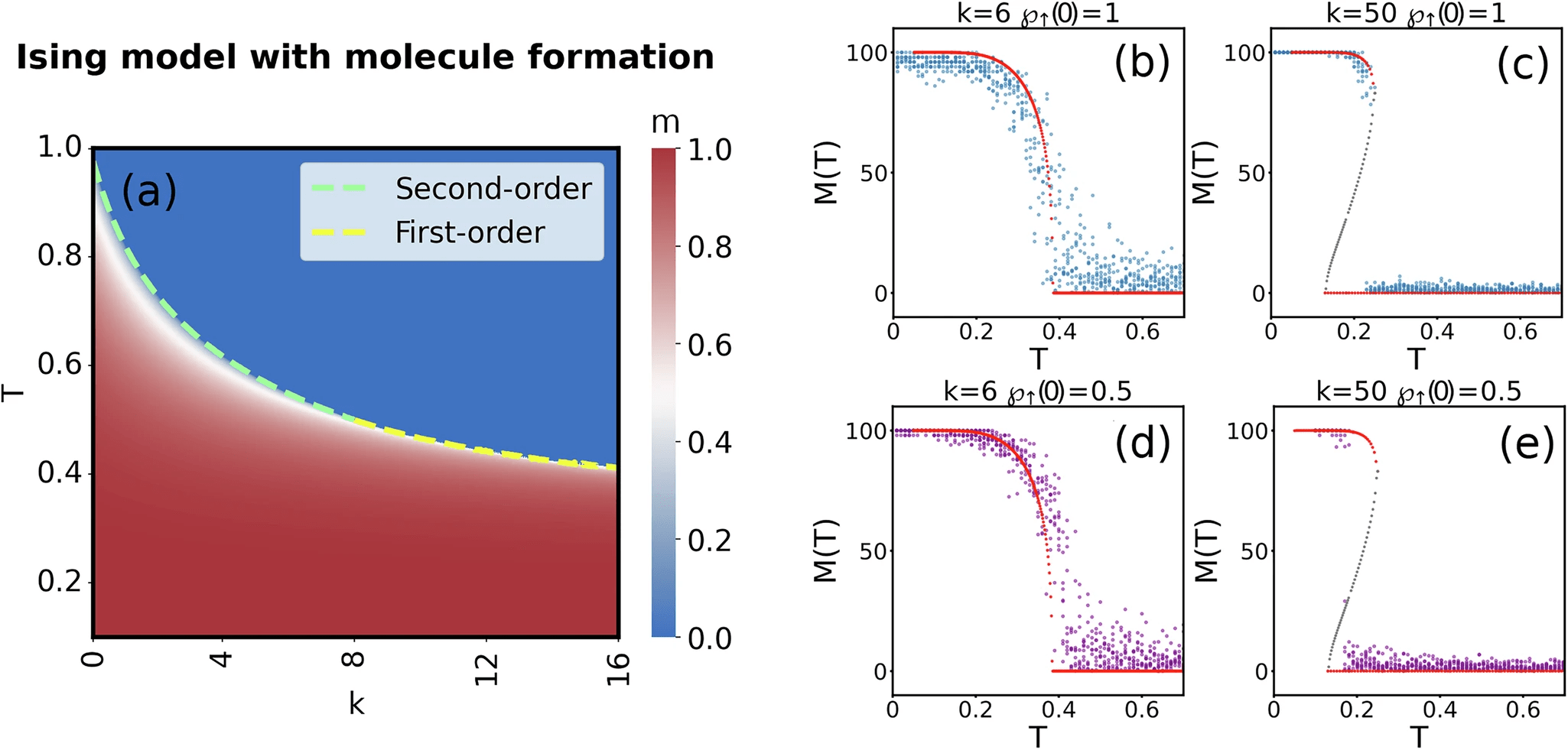
Future work

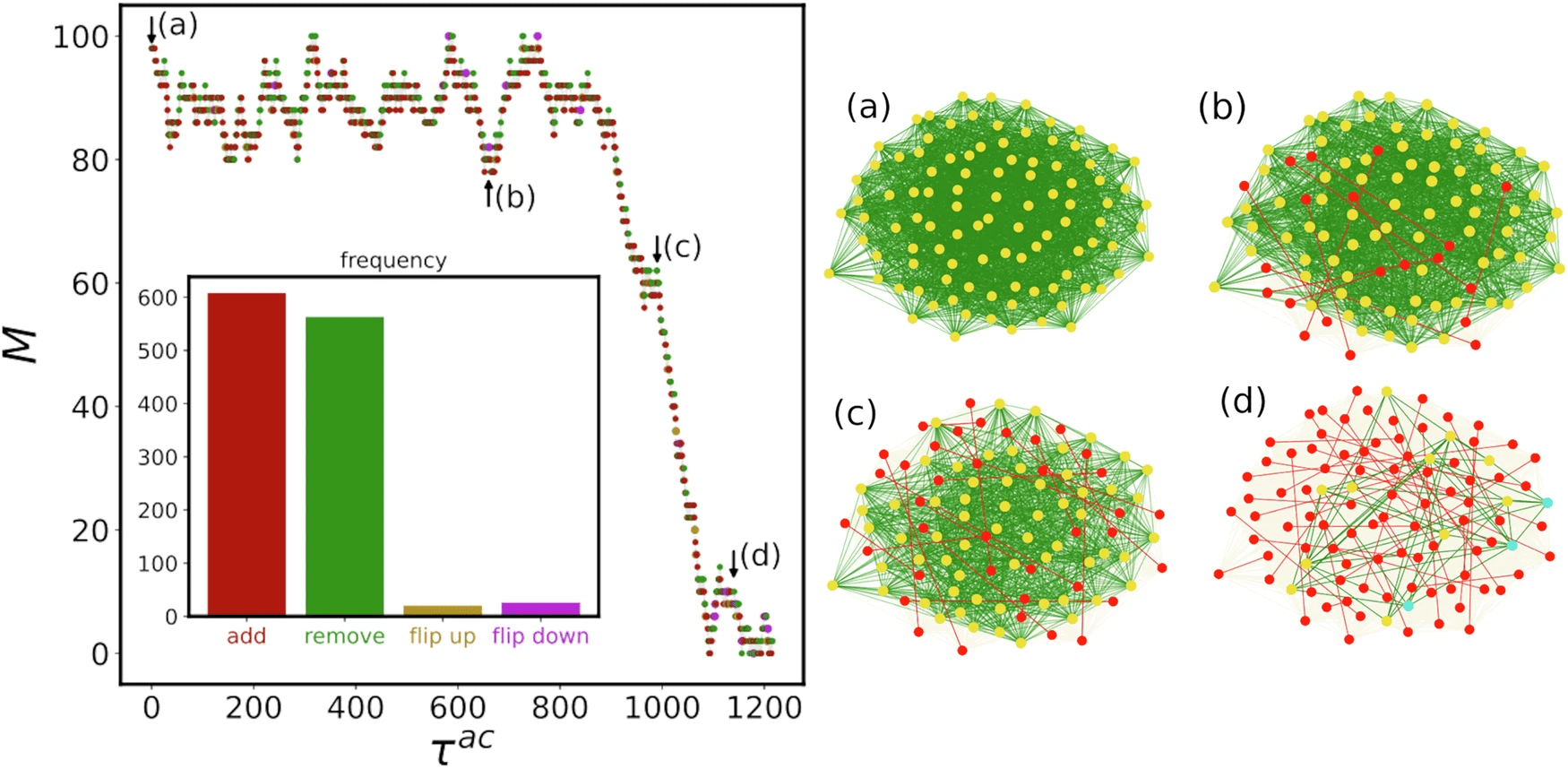
This behavior is typical for systems with long-range interactions, like social systems
Mixed-order transitions correspond to sudden jumps that cannot be easily predicted
Is it the case of of real social systems?

In collaboration with:

csh.ac.at

Stefan Thurner

Rudolf Hanel

Tuan Pham Minh

Simon Lindner

Markus Hofer

Mirta Galesic

Henrik Olsson

Remah Dahdoul

csh.ac.at

References:

[1] T.P.M., Imre Kondor, R.H., S.T., Journal of Royal Society Interface (2020) 1720200752

[2] T.P.M., Andrew Alexander, J.K., R.H., S.T., Scientific Reports 11 (2021) 17188

[3] T.P.M., J.K. R.H., S.T., PNAS 119 (6) (2022) e2121103119

[4] M.G., H.O., T.P.M., Johannes Sorger, S.T., npj Complexity 2 (2025) 1

[5] J.K., S.L., T.P.M., R.H., S.T. Physical Review Letters 130 (2023) 057401

[6] J.K., S.L., R.H., S.T., Nature Communications 12 (2021) 1127

[7] M.H., J.K., S.T., to be submitted

[8] J.K., Shlomo Havlin, S.T., Nature Communications 16 (2025) 2628