Thermodynamics of structure-forming systems
Jan Korbel

Slides available at: slides.com/jankorbel
Personal web: jankorbel.eu
JETC 2025, Belgrade


Structure-forming systems
- Many real-world systems form structures:
- molecules of atoms
- clusters of colloidal particles
- (bio)polymers or micelles
- social groups
- The main characteristic is that the number of structures (e.g., molecules) is not conserved, while the number of entities (e.g., particles) is conserved


Grand-canonical ensemble
- These systems are typically described by the grand-canonical ensemble with chemical potential(s) \(\mu_i\)
- The particle conservation is obeyed only on average by using the mass action law
- In chemistry, we are dealing with large systems
- What if the system consists of a small number of particles?
- But is it possible to describe the systems with the canonical ensemble?



Thermodynamics of structure-forming systems


Toy model - magnetic coin model
We consider a coin with two states: head and tail
The coins are magnetic and can stick together
How many states we get for N coins?
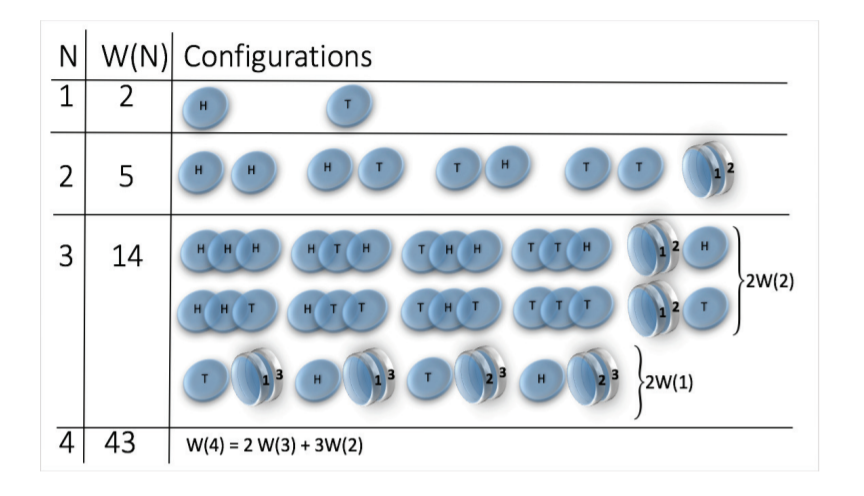
\(W(N) \sim N^N\)
(non-magnetic coins \(W(N) = 2^N\))



H. J. Jensen et al 2018 J. Phys. A: Math. Theor. 51 375002


Boltzmann's entropy
\(S = k_B \log W\)



Multiplicity of structure-forming systems
Boltzmann entropy formula: \(S(n_i) = k_B \log W(n_i)\)
where \(W\) is multiplicity
(number of microstates corresponding to a mesostate \(n_i\))
Microstate: state of each particle (if more particles are bound to a molecule, then state of each molecule)
Mesostate: how many particles and/or molecules are in given state
Example: magnetic coin model: 3 coins, magnetic
microstates mesostate multiplicity

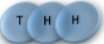
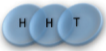

2 x 1x
1 x 1x
3
3





How to calculate a multiplicity?
- Consider a mesostate
- Make all permutations of particles
- Some microstates are overrepresented - calculate how many permutations belong to the same microstate
Examples
2 x 1x
1 x 1x









1 1 2 2 3 3
2 3 1 3 1 2
3 2 3 1 2 1
1 1 2 2 3 3
2 3 1 3 1 2
3 2 3 1 2 1



= (1,2,3) , (2,1,3)
= (1,3,2) , (3,1,2)
= (2,3,1) , (3,2,1)



= (1,2,3) , (1,3,2)
= (2,1,3) , (2,3,1)
= (3,1,2) , (3,2,1)


General formula for multiplicity
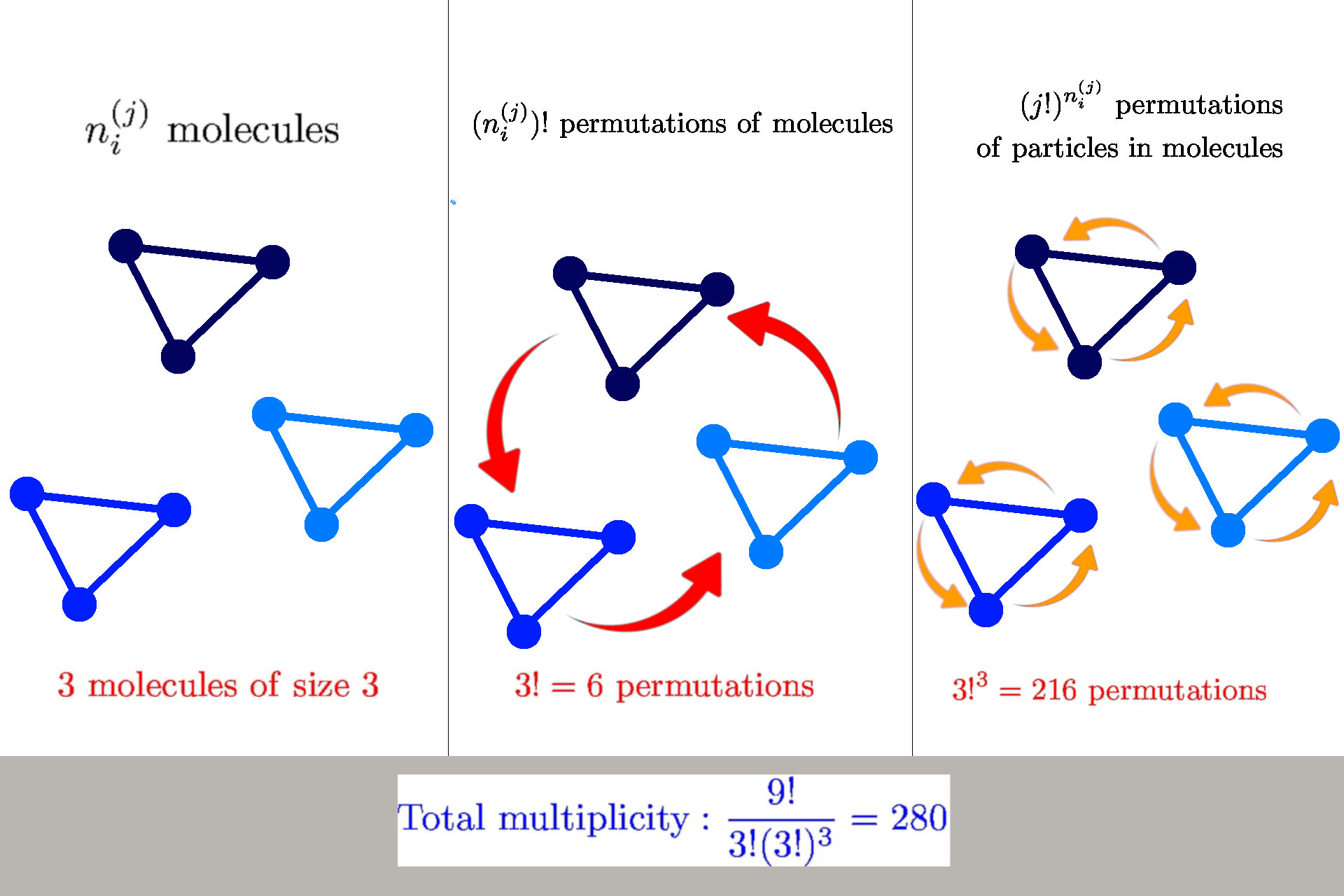
General formula: \(W(n_i^{(j)}) = \frac{n!}{\prod_{ij} n_i^{(j)}! {\color{red} (j!)^{n_i^{(j)}}}}\)
we have \(n_i^{(j)}\) molecules of size \(j\) in a state \(s_i^{(j)}\)



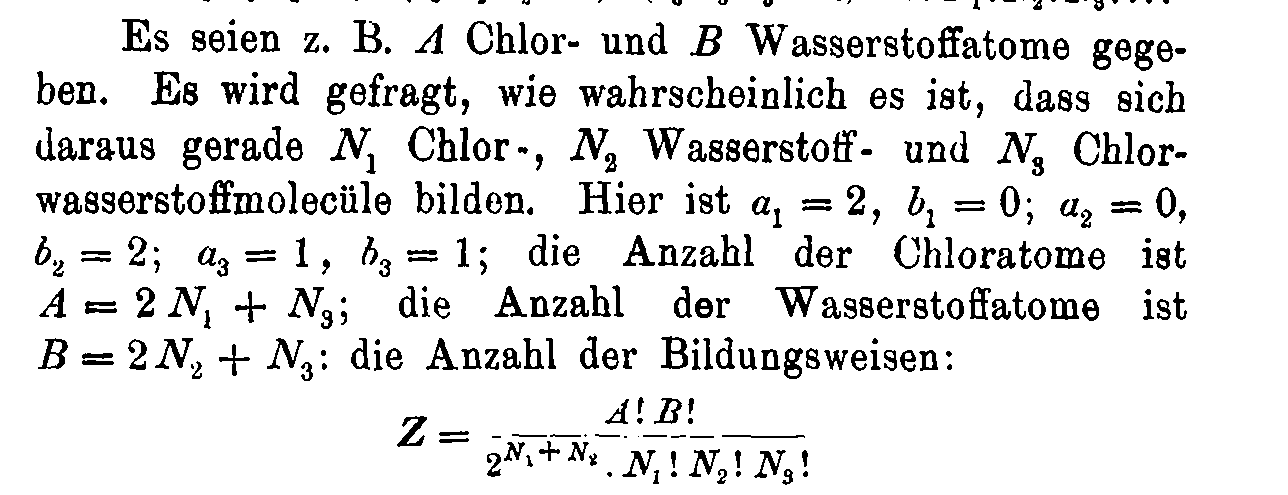
Boltzmann's 1884 paper


Entropy of structure-forming systems
Entropy from Boltzmann's formula using Stirling's approximation
$$ S = \log W \approx n \log n - \sum_{ij} \left(n_i^{(j)} \log n_i^{(j)} - n_i^{(j)} + {\color{red} n_i^{(j)} \log j!}\right)$$
Introduce "probabilities" \(\wp_i^{(j)} = n_i^{(j)}/n\)
$$\mathcal{S} = S/n = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{red}- 1}) {\color{red}- \sum_{ij} \wp_i^{(j)}\log \frac{j!}{n^{j-1}}}$$
Normalization: \( \sum_{ij} j \wp_i^{(j)} = 1\)
Finite interaction range: \(b\) boxes, concentration \({\color{blue} c} = n/b\)
$$\mathcal{S} = S/n = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{red}- 1}) {\color{red}- \sum_{ij} \wp_i^{(j)}\log \frac{j!}{{\color{blue}c^{j-1}}}}$$

Entropy of structure-forming systems
Axiomatic approaches:
- The entropy fulfills Shannon-Khinchin axioms 1,3,4, but does not fulfill axiom SK 2 (it is not maximized by uniform distribution)
- The entropy fulfills Lieb-Yngvason axioms (it is additive, and it is extensive for \(c=const\) )
- The entropy fulfills Shore-Johnson axioms 1,3,4, but does not fulfill axioms SJ 2 (permutation/coordinate invariance)
- The entropy fulfills Tempesta group-composability axiom but is not symmetric in its arguments
- The scaling exponents according to Hanel-Thurner axioms are \(c=0,d=1\), the same as for Shannon entropy
\( \Rightarrow\) The entropy satisfies all common axiomatic schemes but it is not symmetric in probabilities

$$\hat{\wp}_i^{(j)} = \frac{c^{j-1}}{j!} \exp(-\alpha j - \beta \epsilon_i^{(j)})$$
MaxEnt distribution
To find the MaxEnt distribution we define Lagrange functional
\(\mathcal{L}(\wp) = S(\wp) - \sum_{ij} j \wp_{i}^{(j)} - \beta \sum_{ij} \epsilon_i^{(j)} \wp_{i}^{(j)} \)
By maximizing \(\mathcal{L}\) we obtain the MaxEnt distribution
This looks almost like the Boltzmann distribution, but there are a few differences
\(\sum_{ij} j \wp_i^{(j)} = \sum_{ij} \frac{c^{j-1}}{(j-1)!} e^{-{\color{red} \alpha} j - \beta \epsilon_i^{(j)}} = 1\) for \({\color{red} \alpha}\)
Normalization is not obtained by calculating the partition function but by solving
which is a polynomial equation in \(e^{-\alpha}\) of order equal to the maximum size of the molecule

Free energy and cluster-size distribution
Consequently, the free energy can be calculated as
\( F = U - \beta^{-1} S = - \frac{\alpha}{\beta} {\color{red}- \frac{\mathcal{M}}{\beta}}\)
where \(\mathcal{M} = \sum_{ij} \wp_{i}^{(j)}\) is the number of molecules (per particle)
If we focus only on the group-size distribution, we define
\( \wp^{(j)} = \sum_i \wp_i^{(j)}=e^{-j\alpha} \mathcal{Z}_j\)
where \(\mathcal{Z}_j = \frac{c^{j-1}}{j!}\sum_i e^{-\beta \epsilon_i^{(j)}}\) is the partial partition function
We define the coarse-grained entropy
\(S_c(\wp) = - \sum_j \wp^{(j)} (\log \wp^{(j)}-1)\)
and partial free energy \(F_j = -\beta^{-1} \ln \mathcal{Z}_j\)
The coarse-grained distribution can be obtained by maximizing \(L_c(\wp) = S_c(\wp) - \beta \sum_j \wp_j F_j\)


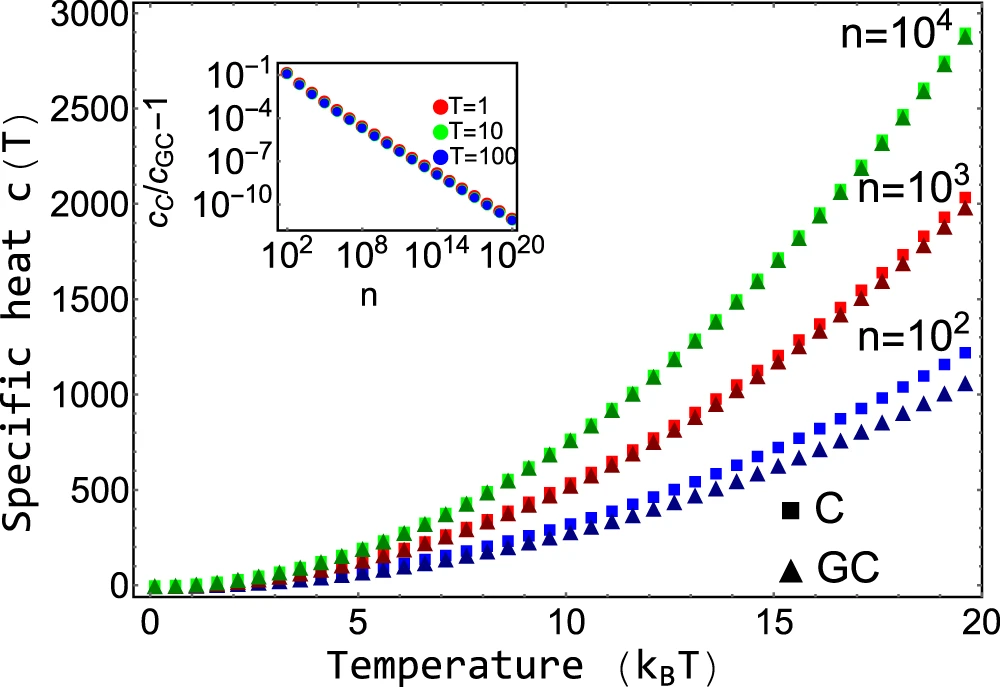
Comparison with grand-canonical ensemble


Stochastic thermodynamics of structure-forming systems
1. Linear Markov (= memoryless) with distribution \(\wp_i(t)\).
Its evolution is described by master equation
$$ \dot{\wp}^{(j)}_i(t) = \sum_{kl} [w_{ik}^{jl} \wp_{k}^{(l)}(t) - w_{ki}^{lj} \wp_i^{(j)}(t) ]$$
\(w_{ij}\) is transition rate. Normalization \(\sum_{ij} j \dot{\wp}_{i}^{(j)}(t) = 0 \)
2. Detailed balance
|
$$\frac{{w}_{ik}^{jl}}{{w}_{ki}^{lj}}= \frac{\hat{\wp}_i^{(j)}}{\hat{\wp}_{k}^{(l)}} = {\color{red}\frac{j!}{l!}{c}^{l-j}}\exp \left[{\color{red}\alpha (l-j)}+\beta \left({\epsilon }_{k}^{(l)}-{\epsilon }_{i}^{(j)}\right)\right]$$ |
Assumptions

Stochastic thermodynamics of structure-forming systems
Results
1. Second law of thermodynamics for non-equilibrium systems
|
$$\frac{{\rm{d}}{\mathcal{S}}}{{\rm{d}}t}={\dot{{\mathcal{S}}}}_{i}+\beta \dot{{\mathcal{Q}}}$$ where \(\dot{\mathcal{S}}_i \geq 0\) is entropy production flow and \(\dot{\mathcal{Q}}\) is the heat flow |
2. Detailed fluctuation theorem for structure-forming systems
$$\frac{P(\Delta \sigma)}{\tilde{P}(-\Delta \sigma)} = e^{\Delta \sigma}$$
where \(\Delta \sigma = \Delta s_i + {\color{red} \log j_0 - \log j_f}\)
\(\Delta s_i\) is the trajectory entropy production



Applications


Self-assembly of Janus particles
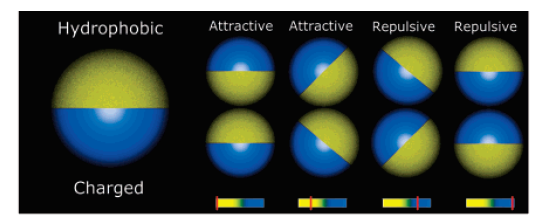
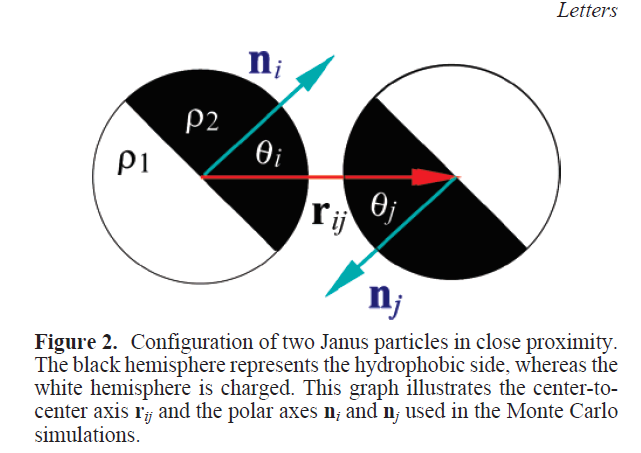



Kern-Frenkel model
Pair-wise potential: \(U^{KF}(r_{ij},n_i,n_j) = u(r_{ij}) \Omega(r_{ij},n_i,n_j) \)
Square-well interaction with hard sphere:
$$ u(r_{ij}) = \left\{ \begin{array}{rl} \infty, & r_{ij} \leq \sigma \\ - \epsilon, & \sigma < r_{ij} < \sigma + \Delta \\ 0, & r_{ij} > \sigma + \Delta. \end{array} \right.$$
\(\Omega\) decribes orientation of particles:
Particle coverage \(\chi = \sin^2(\theta/2) = \frac{1-\cos{\theta}}{2}\)
Polymers: \(\chi = 0.3\)
Janus particles: \(\chi = 0.5\)
Crystalic structures: \(\chi = 0.6\) (stable lamellar crystals)
$$\Omega(r_{ij},n_i,n_j) = \left\{\begin{array}{rl} -1 & \mathrm{if} \ r_{ij} \cdot n_i > \cos(\theta) \ \mathrm{and} \ r_{ij} \cdot n_j > \cos(\theta)\\ 0 & \mathrm{otherwise} \end{array} \right.$$


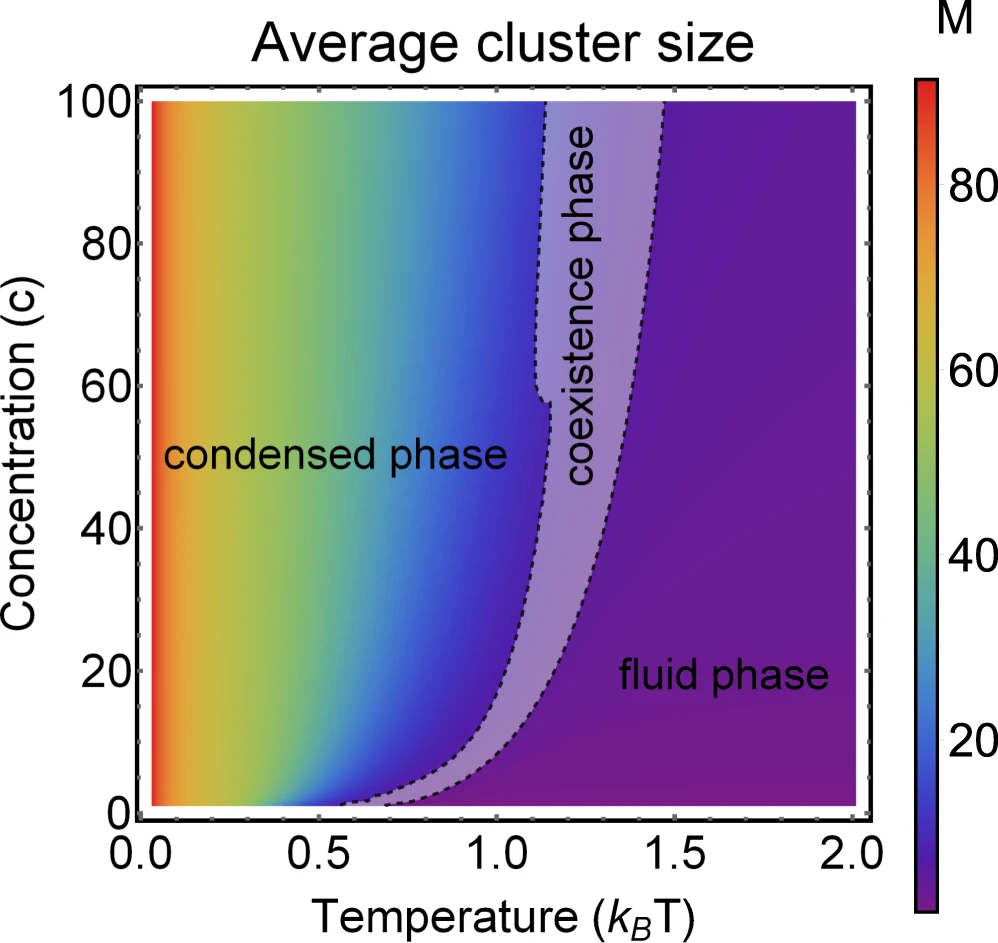
Phase diagram of Janus particles for average cluster size \(M\)
The phase diagram is in agreement with the known theory of self-assembly


Group formation in opinion dynamics model




Driving forces in opinion dynamics
- Many opinion dynamics systems follow two basic concepts:
- Homophily - people tend to be friends with peers with similar opinions
- Social balance - a friend of my friend is my friend, enemy of my friend is my enemy
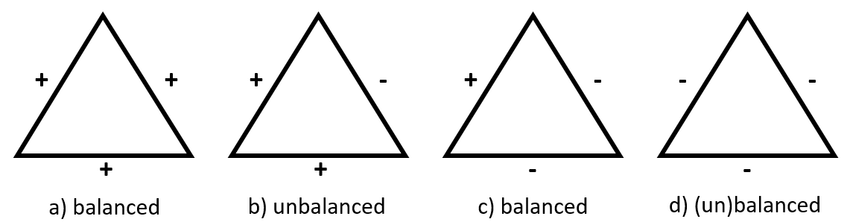
These two concepts can be related through the local Hamiltonian approach


- We introduce a local Hamiltonian (=local stress) based on homophily and show how it is related to social balance
- Each individual has \(G\) binary opinions, \(s_i \in \{-1,1\}^G\)
- If two connected individuals have more common opinions than different opinions, they become friends and vice versa \(J_{ij} = sign(s_i \cdot s_j)\)
- Both homophily and social balance can be incorporated by taking the following social Hamiltonian $$H(s_i) = -\alpha \sum_{i,j:\mathrm{friends} } s_i s_j + (1-\alpha) \sum_{i,j: \mathrm{enemies} } s_i s_j$$
Local Hamiltonian approach

Group formation based on homophily
Hamiltonian of a group \(\mathcal{G}\)
\(H(\mathbf{s}_{i_1},\dots,\mathbf{s}_{i_k}) = \underbrace{- \phi \, \frac{J}{2} \sum_{ij \in \mathcal{G}} A_{ij} \mathbf{s}_i \cdot \mathbf{s}_j}_{\textcolor{red}{intra-group \ social \ stress}}+ \underbrace{(1-\phi) \frac{J}{2} \sum_{i \in \mathcal{G}, j \notin \mathcal{G}} A_{ij} \mathbf{s}_{i} \cdot \mathbf{s}_j}_{\textcolor{aqua}{inter-group \ social \ stress}} \\ \qquad \qquad \qquad \qquad - \underbrace{h \sum_{i \in \mathcal{G}} \mathbf{s}_i \cdot \mathbf{w}}_{external \ field}\)
Group formation based on opinion= self-assembly of spin glass
Group 1
Group 2


Results for zero inter-group degree
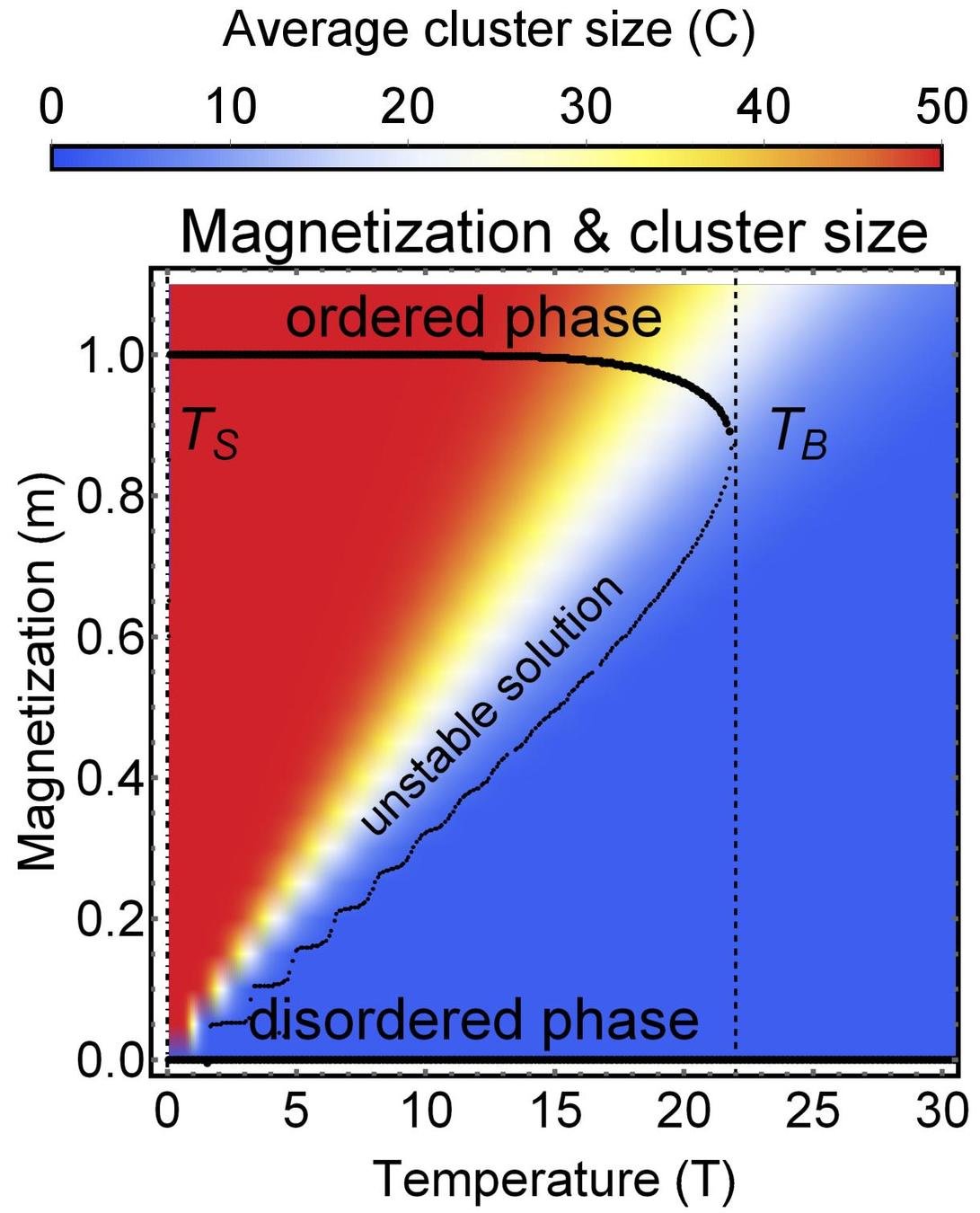
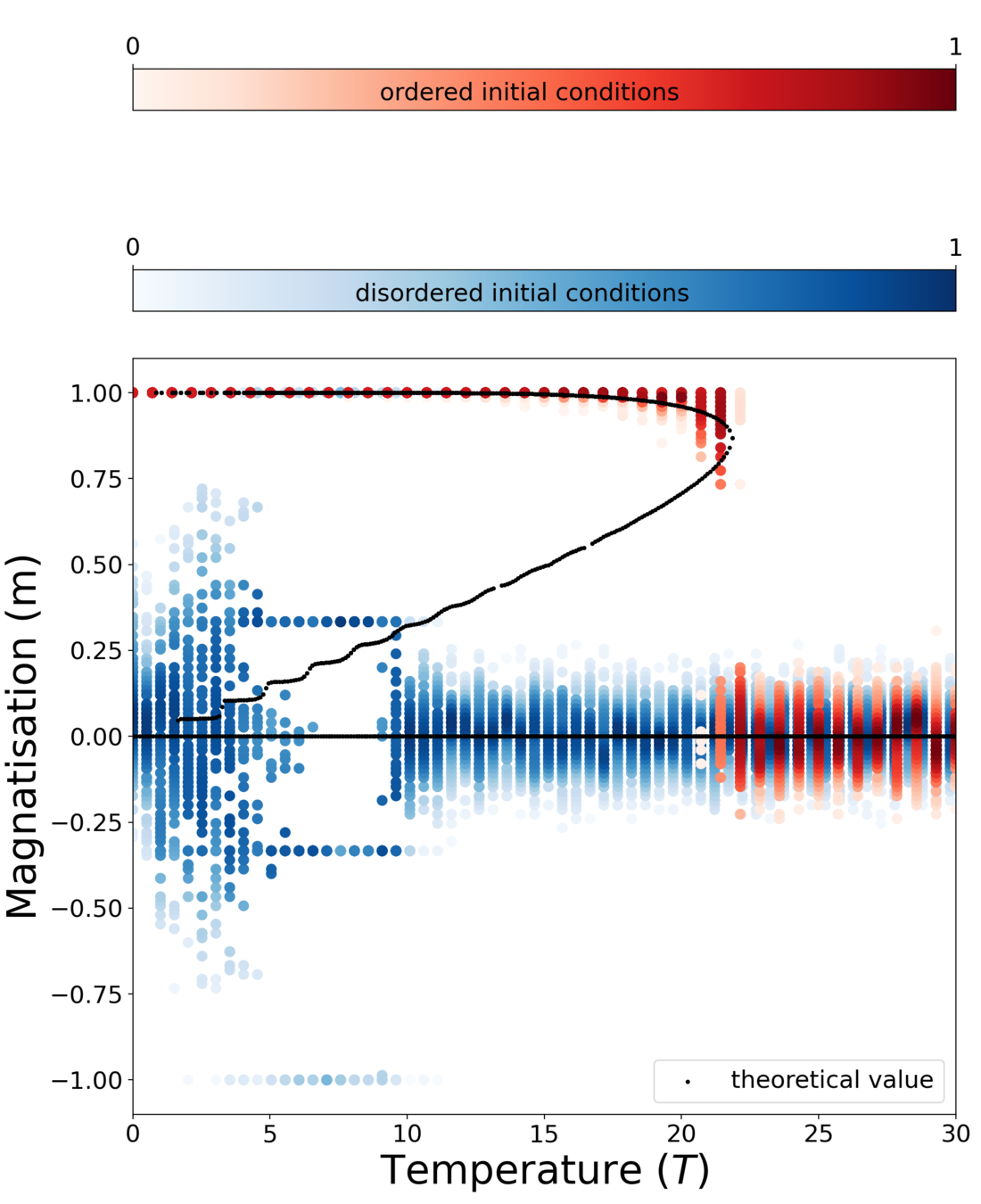
Theory
MC simulation



Application online multiplayer game PARDUS


Phase transitions in structure-forming systems



Ising model with molecule formation
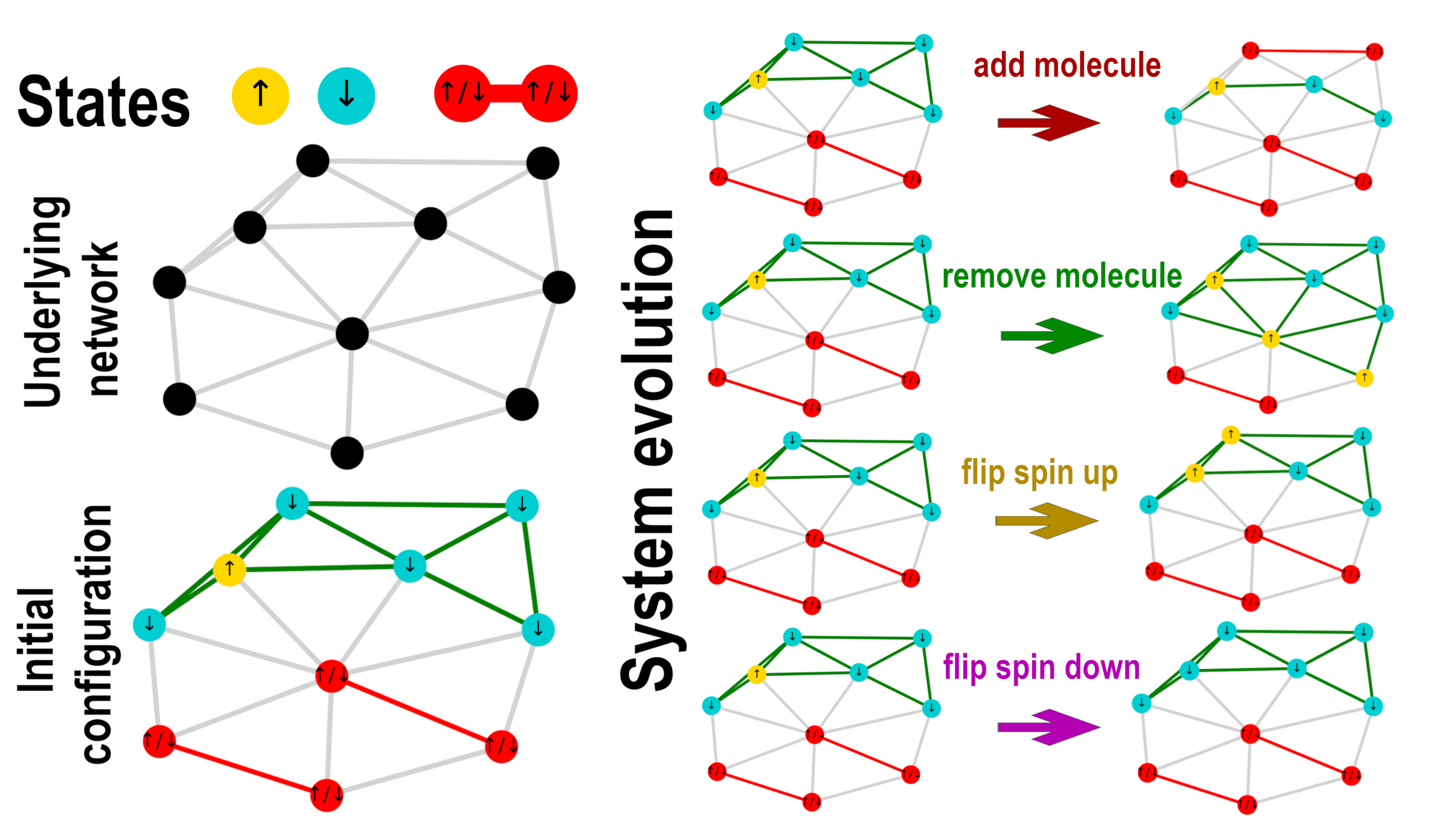


Multiplicity on a network
- We derive the multiplicity of a state \(\{n_\uparrow,n_\downarrow,n_\|\}\)
- The normalization is \(n_\uparrow+n_\downarrow+ 2 n_\| = n\)
- It can be derived as \(W(n_\uparrow,n_\downarrow,n_\|) = \Omega(n_\uparrow,n_\downarrow,n_\|) M(n_\|) \)
- Here, \(\Omega(n_\uparrow,n_\downarrow,n_\|) = \binom{n}{n_\uparrow \ n_\downarrow \ 2 n_\|}\) is the multinomial factor representing the number of divisions of \(n\) particles into the states of the system
- \(M(n_\|)\) represents the number of ways that \(2 n_\|\) particles can form \(n_\|\) molecules
- In fully-connected network, we know it is equal to $$M(n_\|) = \frac{(2 n_\|)!}{(n_\|)! 2^{n_\|}}$$


Multiplicity on random network
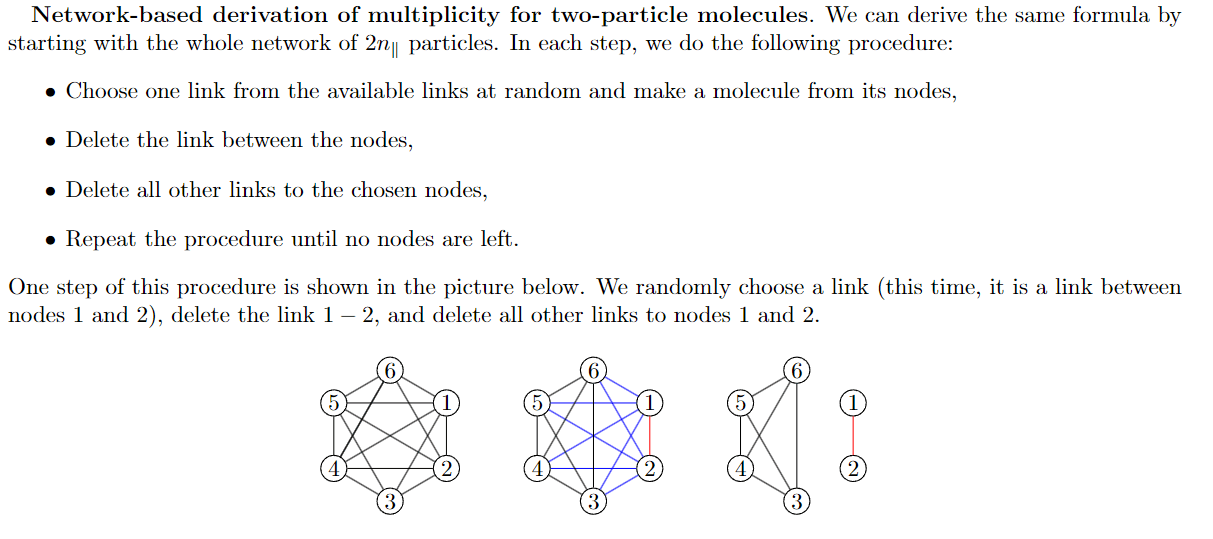
By using the procedure above, we can show that$$M(n_\|) = \frac{1}{(n_\|)!} \prod_{i=0}^{n_\|-1} L(2n_\|-2i)$$

- For each step, we can approximate the number of links by \(L = k/(2n)\) where \(k\) is the average degree
- By using this approximation, we end with
$$M(n_\|) = \frac{(2n_\|)!}{n_\|!} \left(\frac{k}{2(n-1)}\right)^{n_\|} $$
Entropy of Ising model with molecules
- Entropy can be expressed from \(S \equiv \log W = \log (\Omega M) \)
- It leads to $$S(\wp_\uparrow,\wp_\downarrow,\wp_\|) = - \wp_\uparrow (\log \wp_\uparrow - 1) - \wp_\downarrow (\log \wp_\downarrow - 1)$$ $$- \wp_\| (\log \wp_\| - 1)- \wp_\| \log \left(\frac{2(n-1)}{k n}\right) $$
- By solving the self-consistency equation, we observe the transition between second-order and first-order transtion

Phase diagram
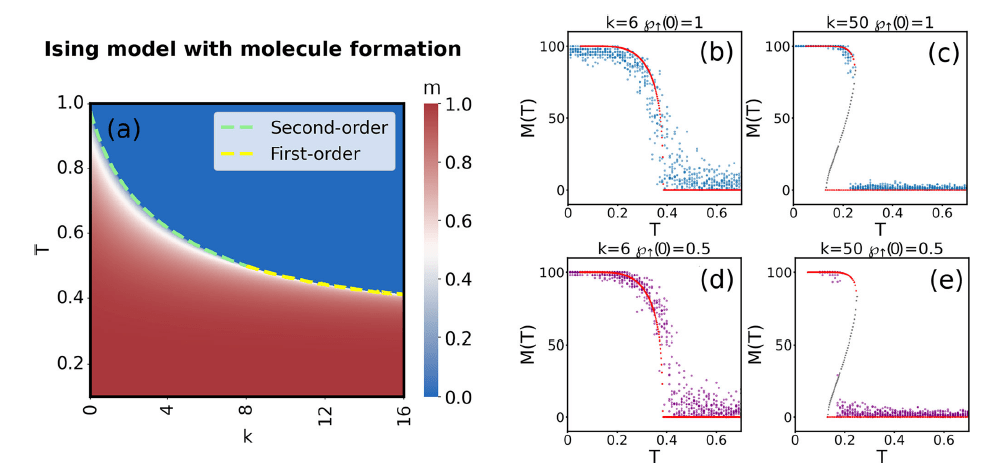
$$m = \frac{2 \left(- \cosh( \beta J m) + \sqrt{ \cosh^2(\beta J m) + k}\right)}{k} \sinh (\beta J m )$$


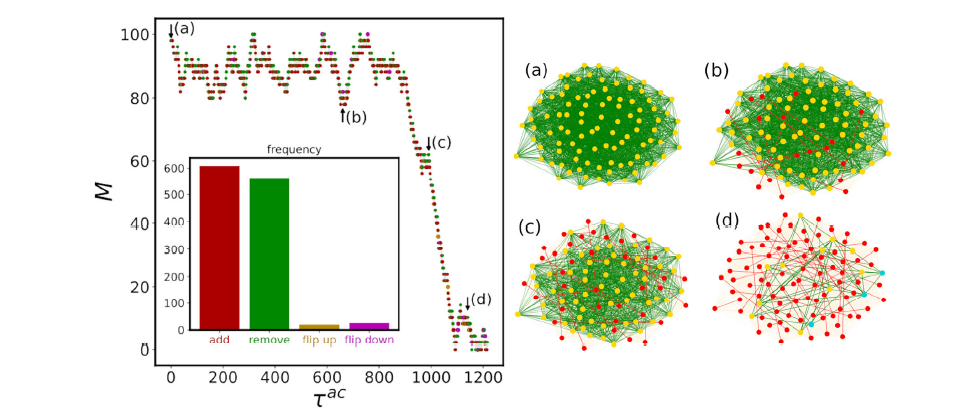
Microscopic origin of abrupt phase transition
csh.ac.at

Conclusions
- Many real-world systems form structures
- Their thermodynamics can be described in terms of the canonical ensemble
- We obtain entropy for structure-forming systems
- The results have applications in soft matter, sociophysics and critical phase transitions
csh.ac.at

In collaboration with:
Stefan Thurner
Rudolf Hanel
Tuan Pham Minh
Simon Lindner
Shlomo Havlin
Slides available at: slides.com/jankorbel
Personal web: jankorbel.eu