Why information theory
in complex systems?

introductory talk
Workshop "Information-theoretic Methods for Complexity Science" April 29-May 1, 2019, Vienna
"You should call it entropy, for two reasons: In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, nobody knows what entropy really is, so in a debate you will always have the advantage."
John von Neuman's reply to Claude Shannon's question how to name newly discovered measure of missing information
- What is the use of entropies for complex, driven and out-of-equilibrium systems and networks?
-
Can we classify complex systems using information theory?
- What are the necessary ingredients of such classification?
- Is this classification sufficient?
-
What must a thermodynamics of complex systems be able to do?
- What is the role of entropy in thermodynamics?
- What are the thermodynamic potentials for complex systems?
- Do we need Legendre structure?
-
How can we use information geometry in complex systems?
- Is it in the context of complex systems more than just a framework?
- Can we anticipate phase transitions in complex systems?
- Does information geometry help in classification of complex systems?
- Can it be used to appropriate dimension reduction of the data?
Main questions of the workshop
- We focus on the questions from the previous slide
- The workshop is very informal
- The program is only tentative
- No difference between talks and questions
- Everybody can ask/comment any time
- Coffee and lunch breaks are perfect for discussions
- Round table sessions
- We hope that the discussion will also continue after the WS
Please send the slides to jan.korbel@meduniwien.ac.at
after your talk, we will distribute it to everybody
How do we reach the answers?
Main topics
what we were/are interested in
Classification of statistical complex systems
- Many examples of complex system are statistical (stochastic) systems
- Statistical complex systems near the thermodynamic limit \(N \rightarrow \infty \) can be characterized by asymptotics of its sample space \(W(N)\)
- Asymptotic behavior can be described by scaling expansion
- Coefficients of scaling expansion correspond to scaling exponents
- Scaling exponents completely determine universality classes
- Corresponding extensive entropy can be also expressed in terms of its scaling exponents - generalization of (c,d)-entropy
Rescaling the sample space
- How the sample space changes when we rescale its size \( N \mapsto \lambda N \)?
- The ratio behaves like \(\frac{W(\lambda N)}{W(N)} \sim \lambda^{c_0} \) for \(N \rightarrow \infty\)
- the exponent can be extracted by \(\frac{d}{d\lambda}|_{\lambda=1}\): \(c_0 = \lim_{\rightarrow \infty} \frac{N W'(N)}{W(N)}\)
- For the leading term we have \(W(N) \sim N^{c_0}\).
- Is it only possible scaling? We have \( \frac{W(\lambda N)}{W(N)} \frac{N^{c_0}}{(\lambda N)^{c_0}} \sim 1 \)
- Let us use the other rescaling \( N \mapsto N^\lambda \)
- The we get that \(\frac{W(N^\lambda)}{W(N)} \frac{N^{c_0}}{N^{\lambda c_0}} \sim \lambda^{c_1}\)
- First correction is \(W(N) \sim N^{c_0} (\log N)^{c_1}\)
- It is the same scaling like for \((c,d)\)-entropy
- Can we go further?
-
We define the set of rescalings \(r_\lambda^{(n)}(x) := \exp^{(n)}(\lambda \log^{(n)}(x) \) )
- \( f^{(n)}(x) = \underbrace{f(f(\dots(f(x))\dots))}_{n \ times}\)
- \(r_\lambda^{(0)}(x) = \lambda x\), \(r_\lambda^{(1)}(x) = x^\lambda\), \(r_\lambda^{(2)}(x) = e^{\log(x)^\lambda} \), ...
- They form a group: \(r_\lambda^{(n)} \left(r_{\lambda'}^{(n)}\right) = r_{\lambda \lambda'}^{(n)} \), \( \left(r_\lambda^{(n)}\right)^{-1} = r_{1/\lambda}^{(n)} \), \(r_1^{(n)}(x) = x\)
-
We repeat the procedure: \(\frac{W(N^\lambda)}{W(N)} \frac{N^{c_0} (\log N)^{c_1} }{N^{\lambda c_0} (\log N^\lambda)^{c_1}} \sim 1\),
- We take \(N \mapsto r_\lambda^{(2)}(N)\)
- \(\frac{W(r_\lambda^{(2)}(N))}{W(N)} \frac{N^{c_0} (\log N)^{c_1} }{r_\lambda^{(2)}(N)^{c_0} (\log r_\lambda^{(2)}(N))^{c_1}} \sim \lambda^{c_2}\),
- Second correction is \(W(N) \sim N^{c_0} (\log N)^{c_1} (\log \log N)^{c_2}\)
Rescaling the sample space
Rescaling the sample space
- General correction is given by \( \frac{W(r_\lambda^{(k)}(N))}{W(N)} \prod_{j=0}^{k-1} \left(\frac{\log^{(j)} N}{\log^{(j)}(r_\lambda^{(k)}(N))}\right)^{c_j} \sim \lambda^{\bf c_k}\)
-
Possible issue: what if \(c_0 = +\infty\)? Then \(W(N)\) grows faster than any \(N^\alpha\)
- We replace \(W(N) \mapsto \log W(N)\)
- The leading order scaling is \(\frac{\log W(\lambda N)}{\log W(N)} \sim \lambda^{c_0} \) for \(N \rightarrow \infty\)
- So we have \(W(N) \sim \exp(N^{c_0})\)
- If this is not enough, we replace \(W(N) \mapsto \log^{(l)} W(N)\) so that we get finite \(c_0\)
- General expansion of \(W(N)\) is $$W(N) \sim \exp^{(l)} \left(N^{c_0}(\log N)^{c_1} (\log \log N)^{c_2} \dots\right) $$
J.K., R.H., S.T. New J. Phys. 20 (2018) 093007
Extensive entropy
- We can do the same procedure with entropy \(S(W)\)
- Leading order scaling: \( \frac{S(\lambda W)}{S(W)} \sim \lambda^{d_0}\)
-
First correction \( \frac{S(W^\lambda)}{S(W)} \frac{W^{d_0}}{W^{\lambda d_0}} \sim \lambda^{d_1}\)
- First two scalings correspond to \((c,d)\)-entropy for \(c= 1-d_0\) and \(d = d_1\)
- Scaling expansion of entropy $$S(W) \sim W^{d_0} (\log W)^{d_1} (\log \log W)^{d_2} \dots $$
-
Requirement of extensivity \(S(W(N)) \sim N\) determines the relation between \(c\) and \(d\) :
- \(d_l = 1/c_0\), \(d_{l+k} = - c_k/c_0\) for \(k = 1,2,\dots\)
| Process | S(W) | |||
|---|---|---|---|---|
| Random walk |
0 |
1 |
0 |
|
| Aging random walk |
0 |
2 |
0 |
|
| Magnetic coins * |
0 |
1 |
-1 |
|
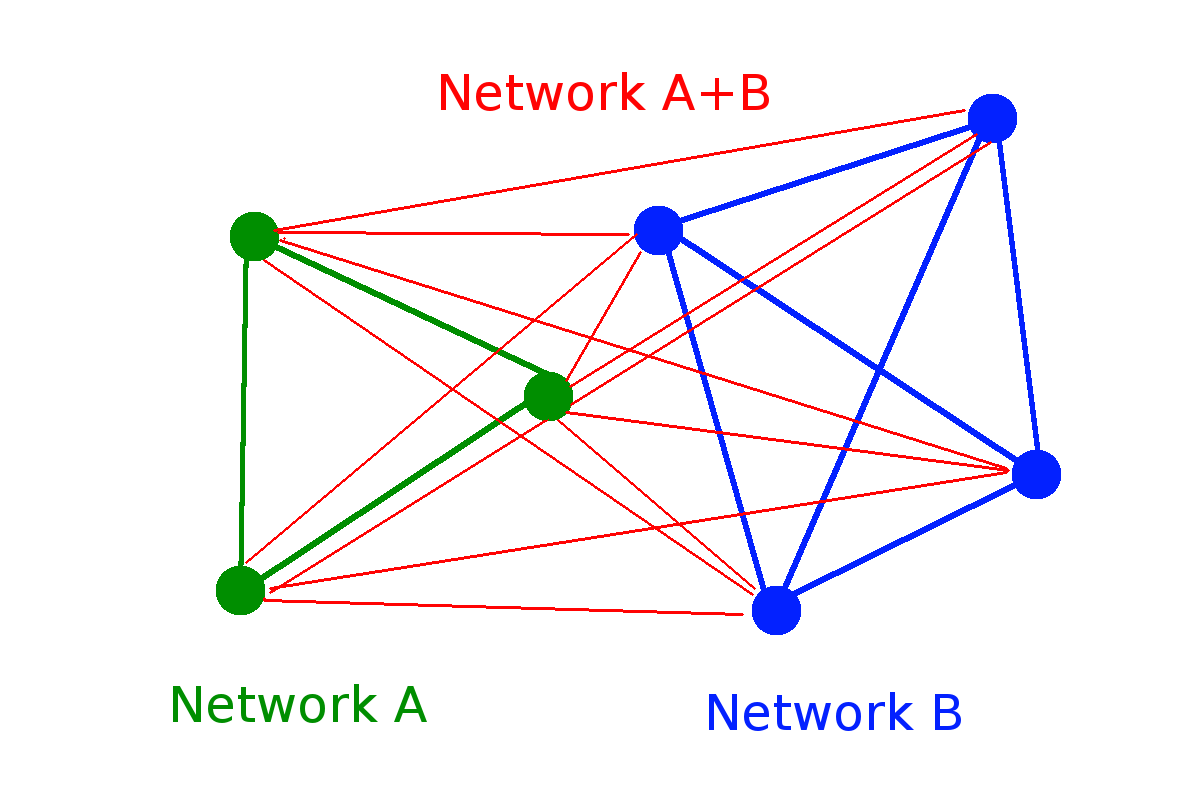
| Random network |
0 |
1/2 |
0 |
|
| Random walk cascade |
0 |
0 |
1 |
\( \log W\)
\( (\log W)^2\)
\( (\log W)^{1/2}\)
\( \log \log W\)
\(d_0\)
\(d_1\)
\(d_2\)
\( \log W/\log \log W\)
* H. Jensen et al. J. Phys. A: Math. Theor. 51 375002
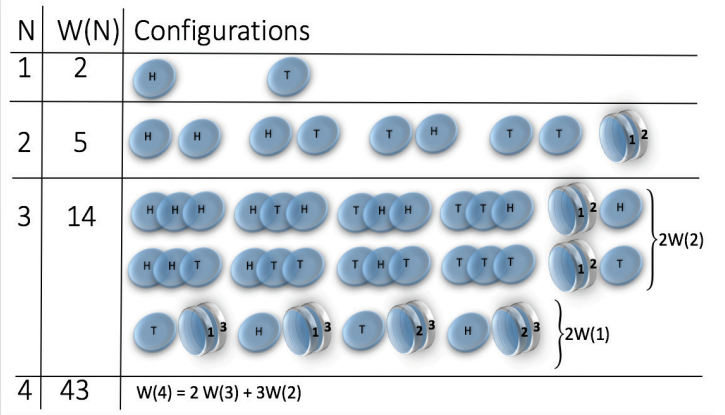
\( W(N) = 2^N\)
\(W(N) \approx 2^{\sqrt{N}/2} \sim 2^{N^{1/2}}\)
\( W(N) \approx N^{N/2} e^{2 \sqrt{N}} \sim e^{N \log N}\)
\(W(N) = 2^{\binom{N}{2}} \sim 2^{N^2}\)
\(W(N) = 2^{2^N}-1 \sim 2^{2^N}\)

Parameter space of \( (c,d) \) entropy
How does it change for one more scaling exponent?
R.H., S.T. EPL 93 (2011) 20006
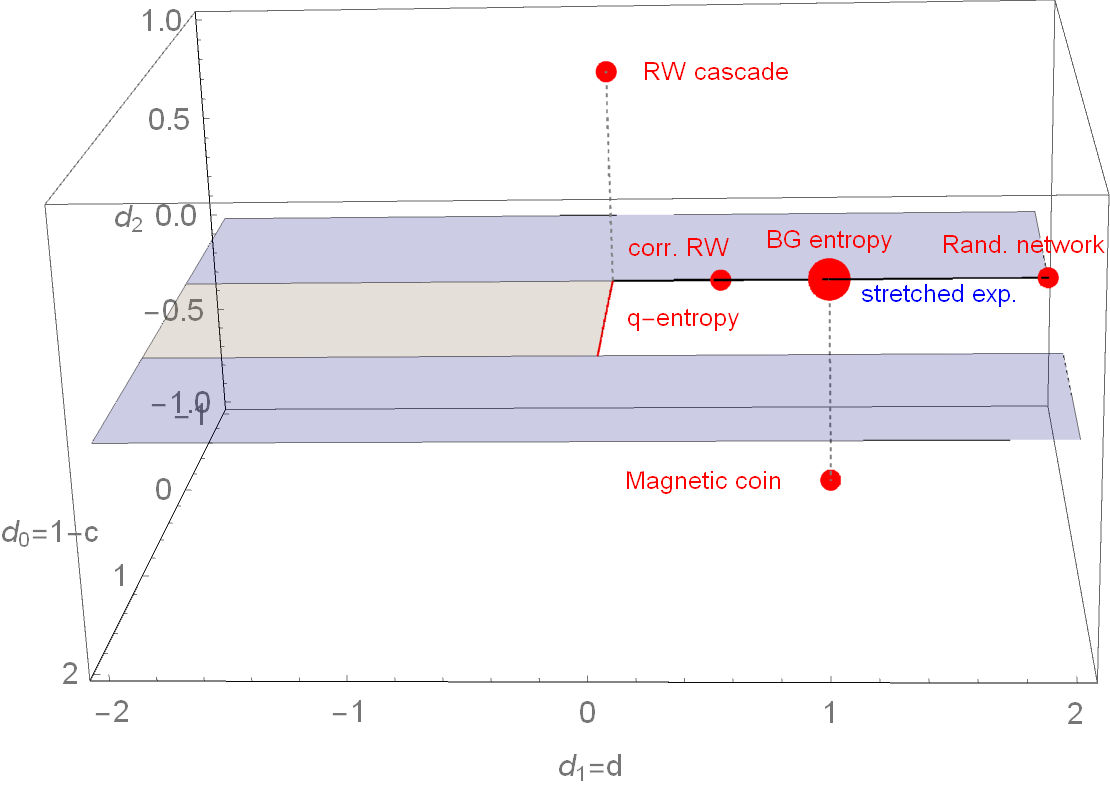
Parameter space of \( (d_0,d_1,d_2) \)-entropy
To fulfill SK axiom 2 (maximality): \(d_l > 0\), to fulfill SK axiom 3 (expandability): \(d_0 < 1\)
Entropy as a measure of information
- Until now, we were interested extensive entropy \(S_{EXT}(W(N)) \sim N \) motivated by thermodynamics
- There are other concepts of entropy, for example information rate of message \(x(N)\) is generally defined as $$S_{IT}(x(N)) = - \frac{1}{N} \log p(x_1,x_2,\dots,x_n) $$
- For Markov process we obtain $$\lim_{N \rightarrow \infty} -\sum_j p_j \sum_i p_{i|j} \log p_{i|j} = H(X_n|X_{n-1})$$
- Moreover, if \(p_{i|j} = p_i\) we obtain Shannon entropy \(H(X)\)
- This gets more complicated for history-dependent processes
Entropy in the statistical inference
- Entropy is closely related to the Maximum entropy principle
- What is the most probable histogram of a process \(X(N,\theta)\)?
- \(\theta\) - parameters, \(k\) histogram of \(X(N,\theta) \)
- \(P(k|\theta)\) is probability of finding a histogram
- Most probable histogram \(k^\star = \argmin_k P(k|\theta) \)
-
In many cases, the probability can be decomposed to $$P(k|\theta) = M(k) G(k|\theta)$$
- \(M(k)\) - multiplicity of histogram
- \(G(k|\theta)\) - probability of a microstate belong to \(k\)
-
$$\underbrace{\log P(k|\theta)}_{S_{rel}}= \underbrace{\log M(k)}_{S_{MEP}} + \underbrace{\log G(k|\theta)}_{S_{cross}} $$
- \(S_{rel}\) - relative entropy (divergence)
- \(S_{cross}\)- cross-entropy, depends on constraints given by \(\theta\)
Three faces of entropy for complex systems
S.T., B.C.-M., R.H. Phys. Rev. E 96 (2017) 093007
- There are at least three ways how to conceptualize entropy
- Information theoretic entropy $$S_{IT}(P) = - \frac{1}{N} \log p(x_1,x_2,\dots,x_n) $$
- Thermodynamic extensive entropy $$S_{EXT}(W(N)) \sim N$$
- Maximum entropy principle entropy $$ S_{MEP}(k) = \log M(k)$$
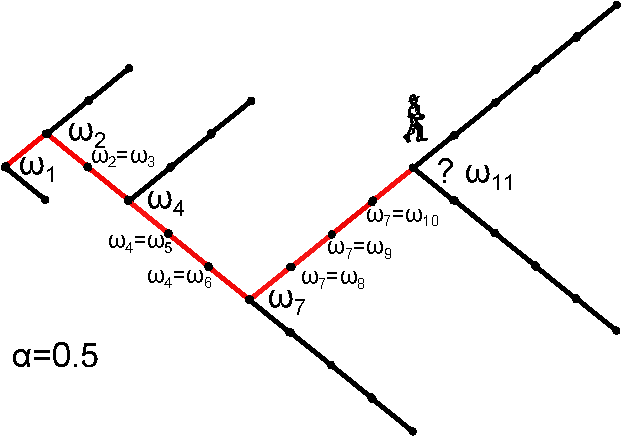
Example: Sample space reducing (SSR) processes


B.C.-M., R.H., S.T. PNAS 112(17) (2015) 5348
(more in the talk by Stefan Thurner)
-
SSR reduce its sample space over time
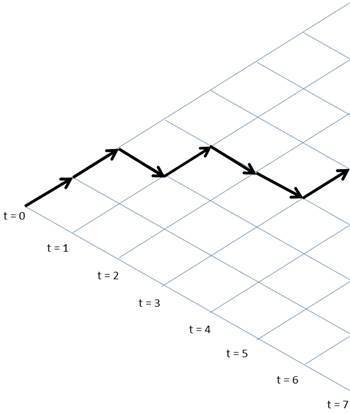
- toy example: a ball on a staircase
-
Irreversible, dissipative system
- the ball can only jump down
-
Driven system
- if the ball jumps all the way down, we put it again to the top of the staircase
-
Natural framework for power-laws
- visiting distribution - Zipf's law $$p(i) = i^{-1}$$
Three faces of entropy for SSR process
$$S_{IT}(P) \sim 1 +1/2 \log W $$
$$S_{EXT}(P) \sim H(P) $$
$$S_{MEP}(P) =- \sum_{k=2}^W \left[p_i \log\left(p_i/p_1\right) + (p_1-p_i) \log\left(1-p_i/p_1\right)\right]$$
S.T., B.C.-M., R.H. Phys. Rev. E 96 (2017) 093007
Thermodynamics of driven out-of-equilibrium systems
R.H., S.T. Entropy 20(11) (2018) 838

- We can calculate the three entropies also for more complicated SSR processes
- SSR with state-dependent driving
- \(P(k|\theta)\) can be still decomposed \( \Rightarrow S_{MEP} = \log M(k)\)
- What is the thermodynamics?
- For the free enegy \(F = -\alpha/\beta\) we get $$ U - S_{MEP}/\beta = F - W_D - Q_D$$
- Legendre structure remains preserved
- Interpretation of \(W_D\) and \(Q_D\) depends on particular system
Axiomatic definition of entropy - Shannon-Khinchin axioms
(more in several other talks)
Axiomatization from the Information theory point of view
- Continuity.—Entropy is a continuous function of the probability distribution only.
- Maximality.— Entropy is maximal for the uniform distribution.
- Expandability.— Adding an event with zero probability does not change the entropy.
- Additivity.— \(S(A \cup B) = S(A) + S(B|A)\) where \(S(B|A) = \sum_i p_i^A S(B|A=a_i)\)
There are many generalizations of 4th axiom:
- q-additivity: \(S(A \cup B) = S(A) \oplus_q S(B|A)\) \(S(B|A)= \sum_i \rho_i(q)^A S(B|A=a_i)\)
- Kolmogorov-Nagumo average: \(S(B|A)= f^{-1}(\sum_i \rho_i(q)^A f(S(B|A=a_i))\)
-
Group composability*: \(S(A \cup B) = \phi(S(A) ,S(B))\) for independent \(A\) and \(B\)
-
Asymptotic scaling: (c,d)-entropies
* P. Tempesta, Proc. R. Soc. A 472 (2016) 2195
- Axiomatization from the Maximum entropy principle point of view
- Principle of maximum entropy is an inference method and it should obey some statistical consistency requirements.
- Shore and Johnson set the consistency requirements:
- Uniqueness.—The result should be unique.
- Permutation invariance.—The permutation of states should not matter.
- Subset independence.—It should not matter whether one treats disjoint subsets of system states in terms of separate conditional distributions or in terms of the full distribution.
- System independence.—It should not matter whether one accounts for independent constraints related to disjoint subsystems separately in terms of marginal distributions or in terms of full-system constraints and joint distribution.
- Maximality.—In absence of any prior information the uniform distribution should be the solution.
Axiomatic definition of entropy - Shore-Johnson axioms
(more in the talk by Petr Jizba)
P.J., J.K. Phys. Rev. Lett. 122 (2019), 120601
Equivalency of SK and SJ axioms?
Are the axioms set by theory of information and statistical inference different or can we find some overlap?
Let us consider the 4th SK axiom
in the form equivalent to composability axiom by P. Tempesta:
4. \(S(A \cup B) = f[f^{-1}(S(A)) \cdot f^{-1}(S(B|A))]\)
\(S(B|A) = S(B)\) if B is independent of A.
Entropies fulfilling SK and SJ: $$S_q^f(P) = f\left[\left(\sum_i p_i^q\right)^{1/(1-q)}\right] = f\left[\exp_q\left( \sum_i p_i \log_q(1/p_i) \right)\right]$$
work in progress
Information geometry of complex systems
- What is the information metric \(g_{ij}(p)\) corresponding to generalized entropies?
- Can we use it to predict phase transitions in systems?
- The metric is connected to Entropy \(S(P)\) trough divergence
- Bregman divergence $$D(p||q) = S(p)-S(q) - \langle \nabla S(q),p-q\rangle $$
Example: information metric for (c,d)-entropies


\( g_{ij}(p) = \frac{\partial^2 D(p||q)}{\partial q_i \partial q_j}|_{p=q} \)
J.K., R.H., S.T. Entropy 21(2) (2019) 112
References
- J.K., R.H., S.T. Classification of complex systems by their sample-space scaling exponents, New J. Phys. 20 (2018) 093007
- H. Jensen, R. H. Pazuki, G. Pruessner, P. Tempesta, Statistical mechanics of exploding phase spaces: Ontic open systems, J. Phys. A: Math. Theor. 51 375002
- R.H., S.T. A comprehensive classification of complex statistical systems and an axiomatic derivation of their entropy and distribution functions, EPL 93 (2011) 20006
- S.T., B.C.-M., R.H. The three faces of entropy for complex systems - information, thermodynamics and the maxent principle, Phys. Rev. E 96 (2017) 093007
- B.C.-M., R.H., S.T. Understanding scaling through history-dependent processes with collapsing sample space, PNAS 112(17) (2015) 5348
- R.H., S.T. Maximum configuration principle for driven systems with arbitrary driving, Entropy 20(11) (2018) 838
- P. Tempesta, Formal groups and Z-entropies, Proc. R. Soc. A 472 (2016) 2195
- P.J., J.K. Maximum Entropy Principle in Statistical Inference: Case for Non-Shannonian Entropies, Phys. Rev. Lett. 122 (2019), 120601
- J.K., R.H., S.T. Information Geometric Duality of ϕ-Deformed Exponential Families, Entropy 21(2) (2019) 112