Homophily-Based Social Group Formation
in a Spin Glass Self-Assembly Framework




in collaboration with
Simon Lindner
Tuan Pham
Rudolf Hanel
Stefan Thurner
Journal Ref.: Phys. Rev. Lett. 130, 057401
Slides available at: www.slides.com/jankorbel
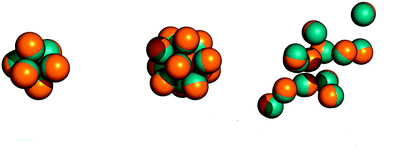
Graphical abstract
Self-assembly
Spin glasses
Social group formation
1. Thermodynamics of self-assembly

- Many systems form structures: molecules of atoms, clusters of colloidal particles, (bio)polymers, or even social groups
- We study the thermodynamics of structure-forming systems
- For small systems, we get a correction to Shannon entropy
- We apply the results to several physical systems
Motivation
Boltzmann's formula for entropy

\( S = k \cdot \log W\)
Typically, \(W = \frac{n!}{n_1!\dots n_j!}\)
Then \(S = - \sum_j p_j \log p_j\)
where \(p_j = n_j/n\)
Toy model - magnetic coin model
We consider a coin with two states: head and tail
The coins are magnetic and can stick together
How many states we get for N coins?
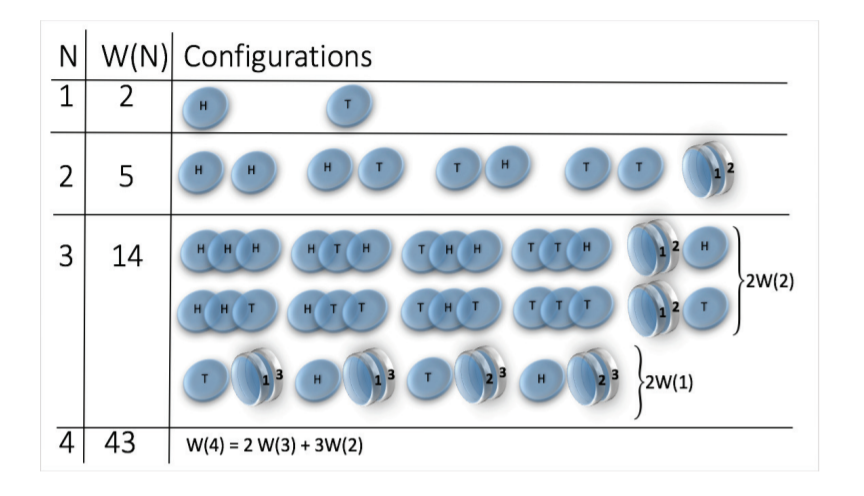
\(W(N) \sim N^N\)
(non-magnetic coins \(W(N) = 2^N\))



picture taken from: H. J. Jensen et al 2018 J. Phys. A: Math. Theor. 51 375002
Multiplicity and entropy
of structure-forming systems
Boltzmann entropy formula: \(S(n_i) = k_B \log W(n_i)\)
where \(W\) is multiplicity
(number of microstates corresponding to a mesostate \(n_i\))
Microstate: state of each particle; if more particles are bound to a molecule, then the state of each molecule
Mesostate: how many particles and/or molecules are in a given state
Example: magnetic coin model: 3 coins, magnetic
microstates mesostate multiplicity

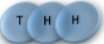
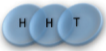

2 x 1x
1 x 1x
3
3




How to calculate a multiplicity?
- Consider a mesostate
- Make all permutations of particles
- Some microstates are overrepresented - calculate how many permutations belong to the same microstate
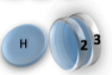
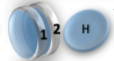
Examples
2 x 1x
1 x 1x










1 1 2 2 3 3
2 3 1 3 1 2
3 2 3 1 2 1
1 1 2 2 3 3
2 3 1 3 1 2
3 2 3 1 2 1



= (1,2,3) , (2,1,3)
= (1,3,2) , (3,1,2)
= (2,3,1) , (3,2,1)



= (1,2,3) , (1,3,2)
= (2,1,3) , (2,3,1)
= (3,1,2) , (3,2,1)
General formula for multiplicity
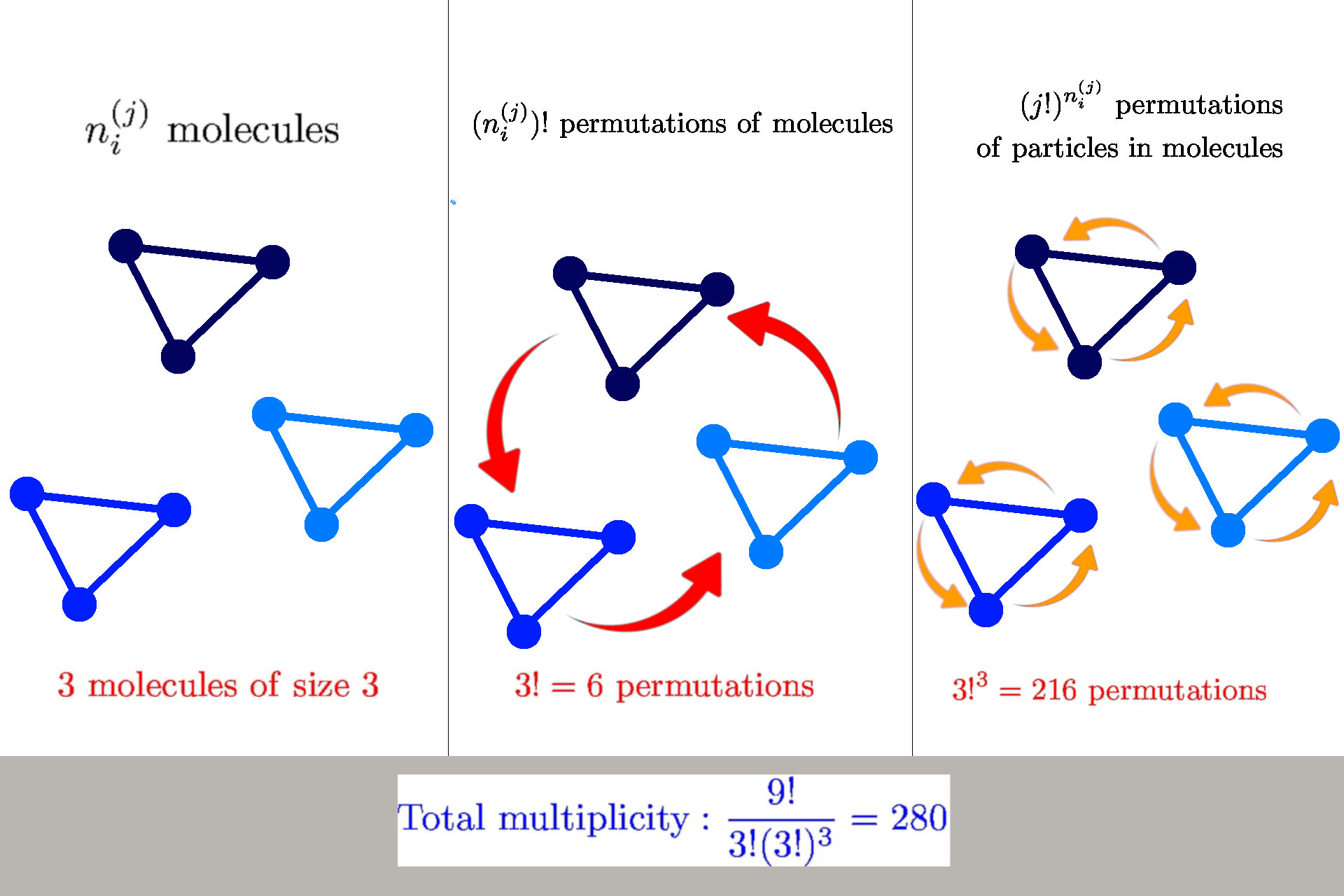
General formula: \(W(n_i^{(j)}) = \frac{n!}{\prod_{ij} n_i^{(j)}! {\color{red} (j!)^{n_i^{(j)}}}}\)
we have \(n_i^{(j)}\) molecules of size \(j\) in a state \(s_i^{(j)}\)

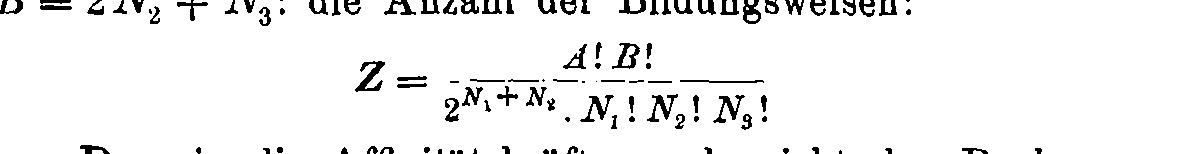
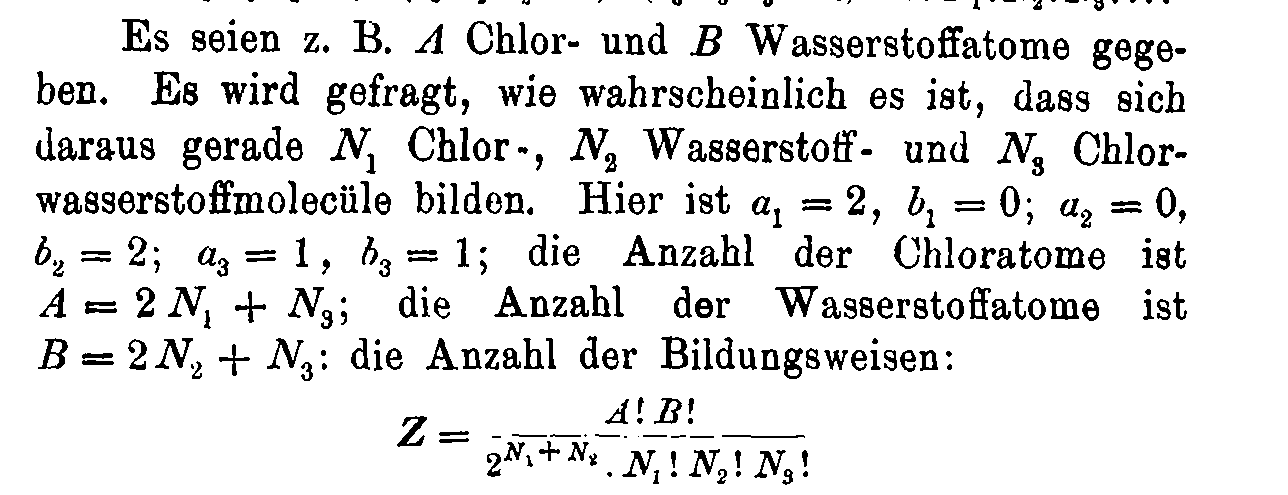
Boltzmann's 1884 paper
Entropy of structure-forming systems
$$ S = \log W \approx n \log n - \sum_{ij} \left(n_i^{(j)} \log n_i^{(j)} - n_i^{(j)} + {\color{red} n_i^{(j)} \log j!}\right)$$
Introduce "probabilities" \(\wp_i^{(j)} = n_i^{(j)}/n\)
$$\mathcal{S} = S/n = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{red}- 1}) {\color{red}- \sum_{ij} \wp_i^{(j)}\log \frac{j!}{n^{j-1}}}$$
Finite interaction range: concentration \(c = n/b\)
$$\mathcal{S} = S/n = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{red}- 1}) {\color{red}- \sum_{ij} \wp_i^{(j)}\log \frac{j!}{{\color{orange}c^{j-1}}}}$$
Equilibrium distribution:
$$\hat{\wp}_i^{(j)} = \frac{c^{j-1}}{j!} \exp(-\alpha j - \beta \epsilon_i^{(j)})$$
normalization by solving
\(\sum_{ij} j \wp_i^{(j)} = \sum_{ij} \frac{c^{j-1}}{(j-1)!} e^{-{\color{red} \alpha} j - \beta \epsilon_i^{(j)}} = 1\) for \({\color{red} \alpha}\)
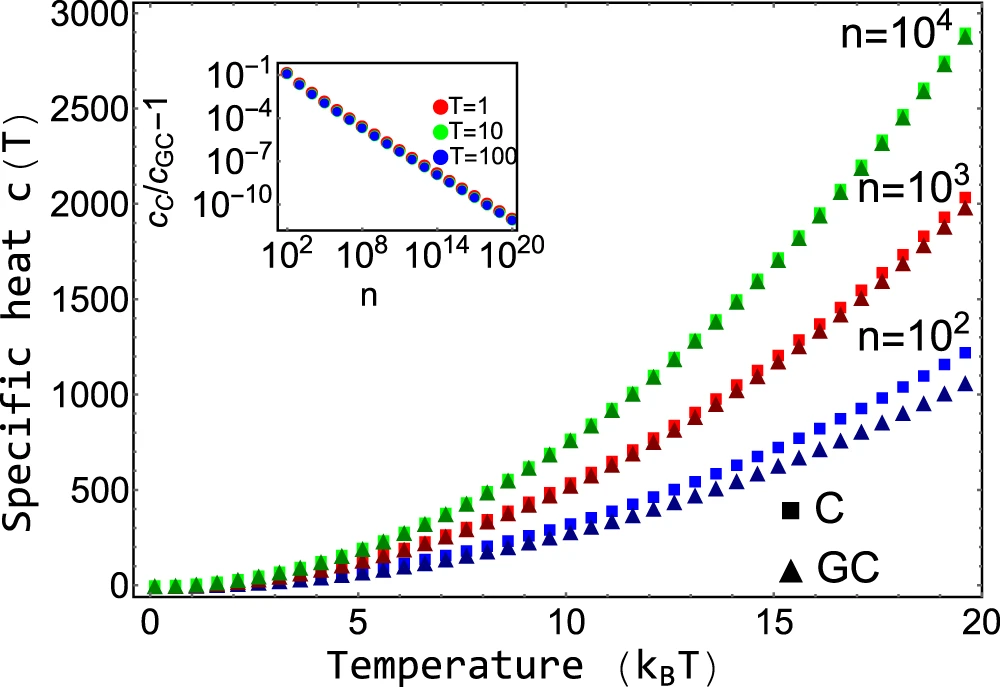
Comparison with Grand-canonical ensemble
Application: Self-assembly of Janus particles
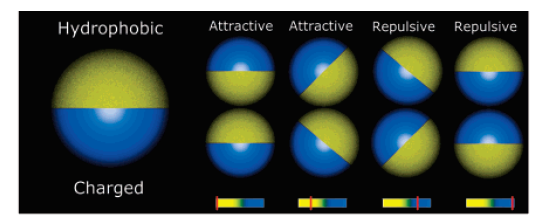
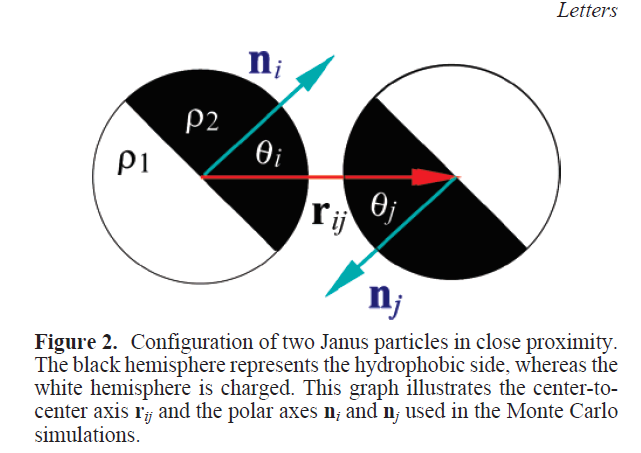

Kern-Frenkel model
Pair-wise potential: \(U^{KF}(r_{ij},n_i,n_j) = u(r_{ij}) \Omega(r_{ij},n_i,n_j) \)
Square-well interaction with hard sphere:
$$ u(r_{ij}) = \left\{ \begin{array}{rl} \infty, & r_{ij} \leq \sigma \\ - \epsilon, & \sigma < r_{ij} < \sigma + \Delta \\ 0, & r_{ij} > \sigma + \Delta. \end{array} \right.$$
\(\Omega\) decribes orientation of particles:
Particle coverage \(\chi = \sin^2(\theta/2) = \frac{1-\cos{\theta}}{2}\)
Polymers: \(\chi = 0.3\)
Janus particles: \(\chi = 0.5\)
Crystalic structures: \(\chi = 0.6\) (stable lamellar crystals)
$$\Omega(r_{ij},n_i,n_j) = \left\{\begin{array}{rl} -1 & \mathrm{if} \ r_{ij} \cdot n_i > \cos(\theta) \ \mathrm{and} \ r_{ij} \cdot n_j > \cos(\theta)\\ 0 & \mathrm{otherwise} \end{array} \right.$$
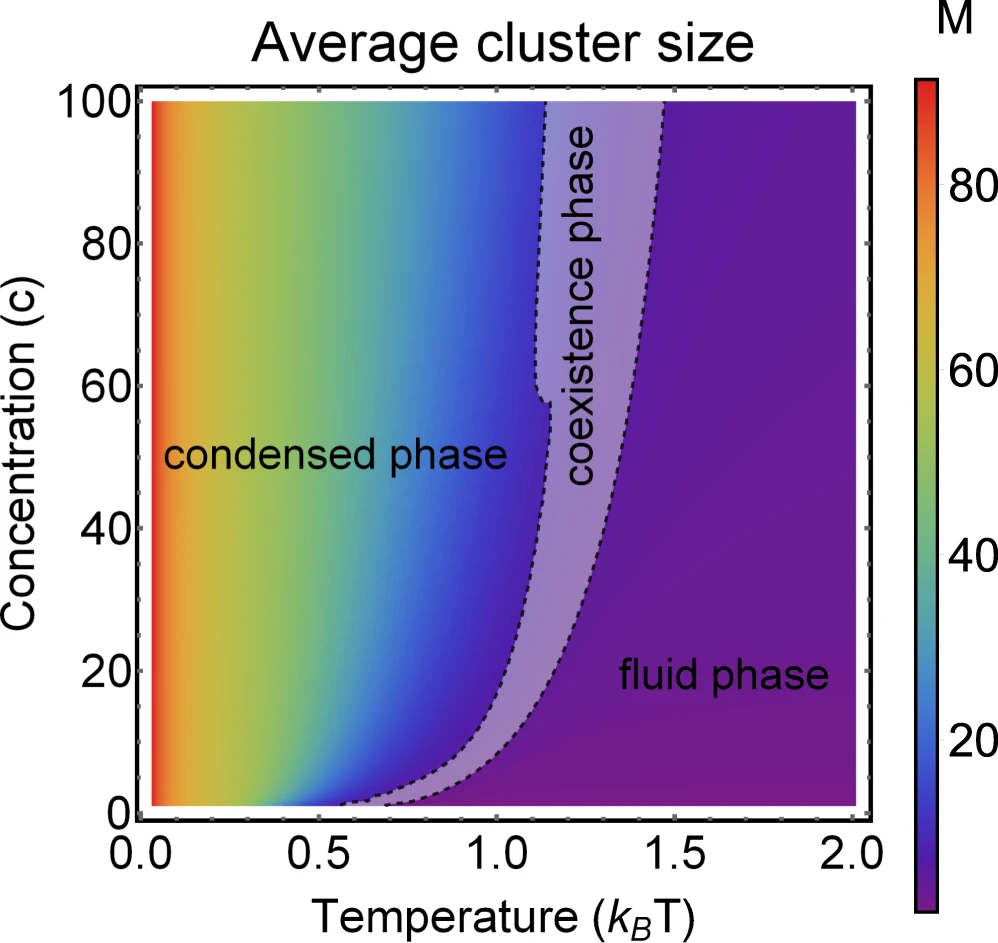
Phase diagram of Janus particles for average cluster size \(M\)
Application: Currie-Weiss model with molecules
(= fully connected Ising model with bound states)
$$ H(s_i) = - \frac{J}{n-1} \sum_{i \neq j, \ free} s_i s_j - h \sum_{j, \ free} s_j $$
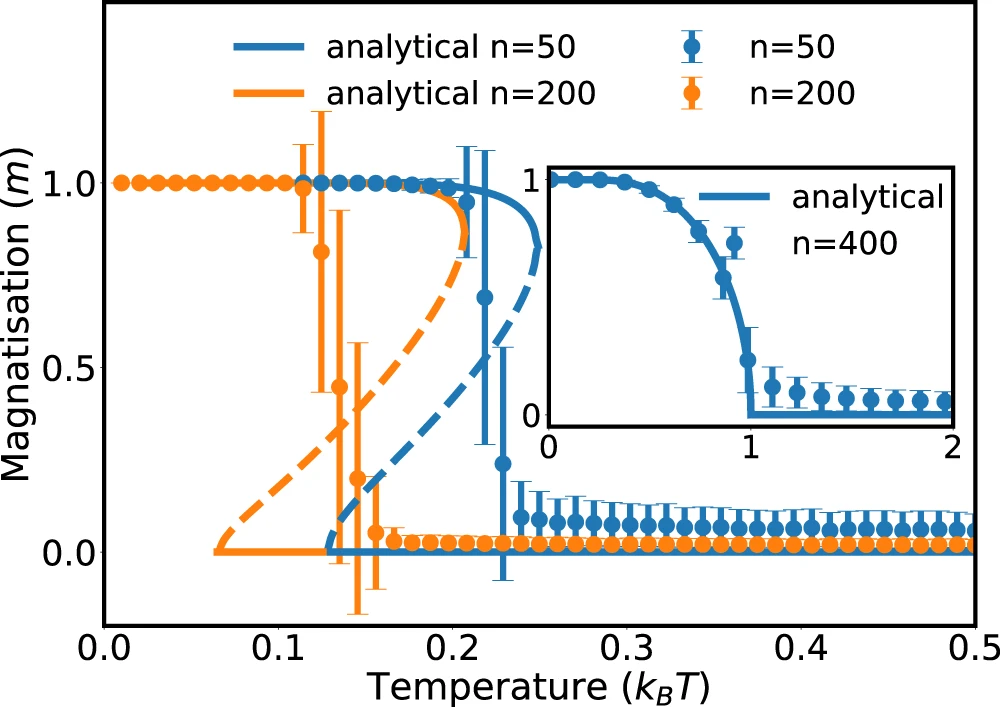
Application: Phase transitions in systems with several interactions

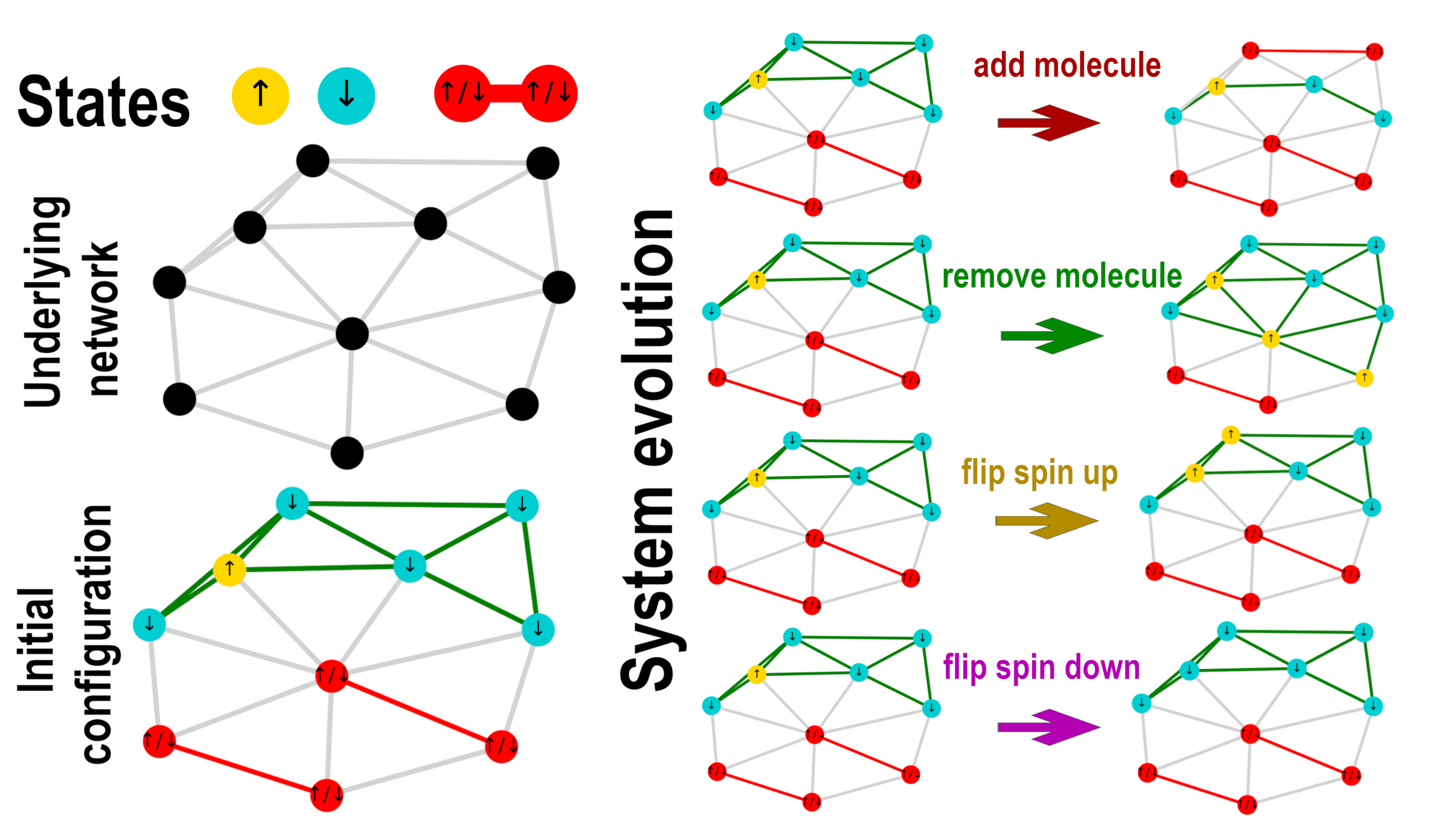
a fraction of particles \(q\) can form molecules
Phase diagram
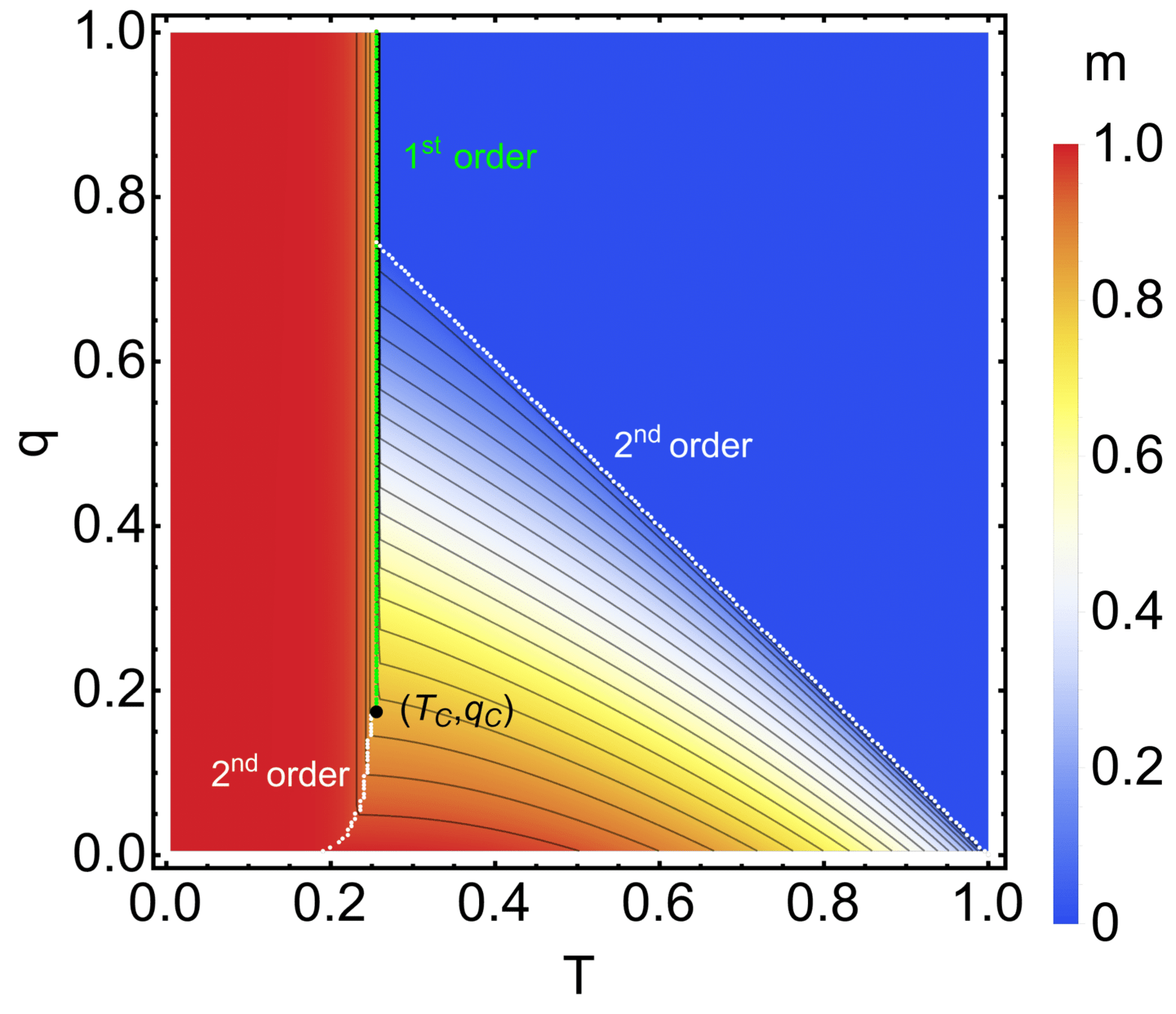
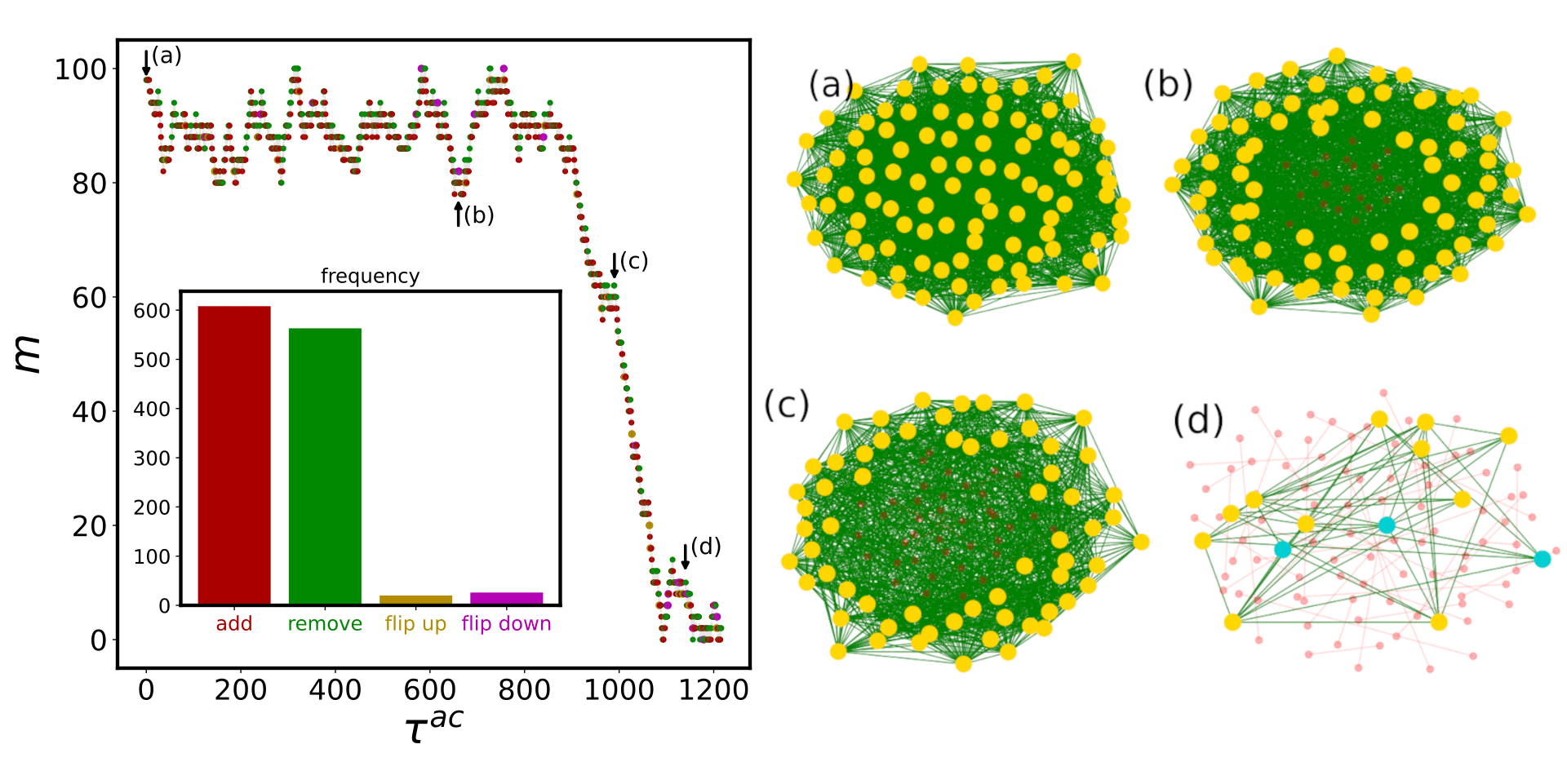
Microscopic origin

2. Spin glasses in opinion dynamics
Motivation
- Many opinion dynamics systems follow two basic concepts:
- Homophily - people tend to be friends with peers with similar opinions
- Social balance - a friend of my friend is my friend, enemy of my friend is my enemy
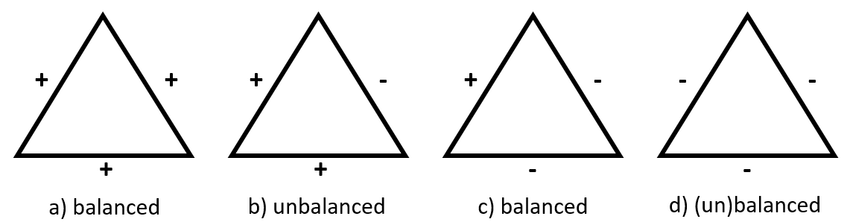
How are these two concepts related?
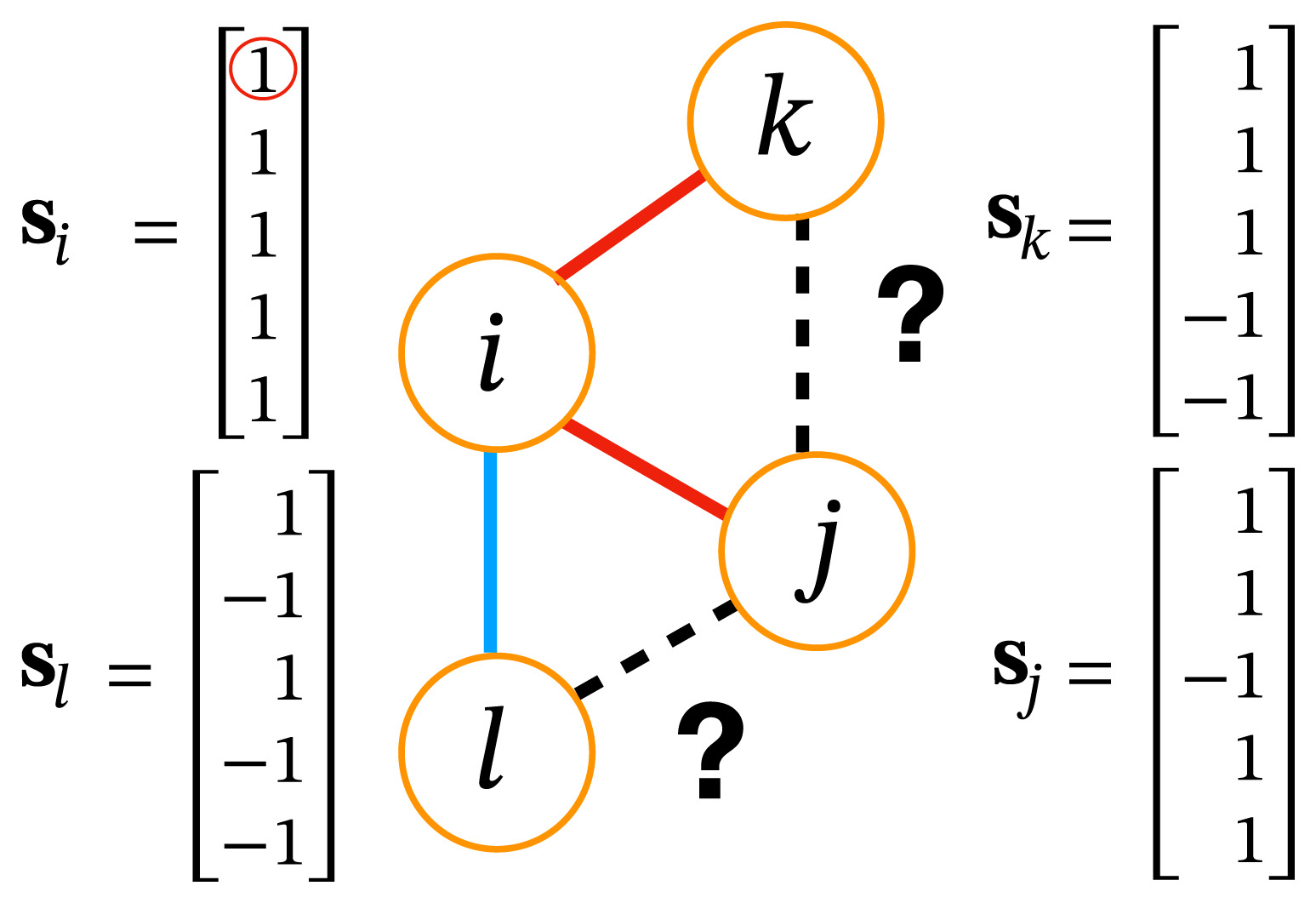
Friendship in large networks
In large networks, it is hard to know the relations among all our friends (a lot of information)
Local Hamiltonian approach
- We introduce a local Hamiltonian (=local stress) based on homophily and show how it is related to social balance
- Each individual has \(G\) binary opinions, \(s_i \in \{-1,1\}^G\)
- If two connected individuals have more common opinions than different opinions, they become friends and vice versa; \(J_{ij} = sign(s_i \cdot s_j)\)
- The local stress Hamiltonian is defined as $$H^{(i)} = -\frac{\alpha}{G} \sum_{j: J_{ij} =1} s_i \cdot s_j + \frac{1-\alpha}{G} \sum_{j: J_{ij} = -1} s_i \cdot s_j$$
- Parameter \(\alpha\) is the relative strength between friendship and enmity
- Individuals tend to minimize their local stress over time
- We define the following order parameters:
- Balance: \(f = \frac{n_{+}-n_{-}}{n_{+}+n_{-}}\) the relative difference of balanced and unbalanced triangles
- Average social stress: \(H = \sum_i H^{(i)}\)
- Similarity score: \(C = \frac{1}{NG} \sum_{i} \sum_{j: J_{ij}} \frac{s_i \cdot s_j}{N_i}\), where \(N_i\) is the number of friends of i
Order parameters
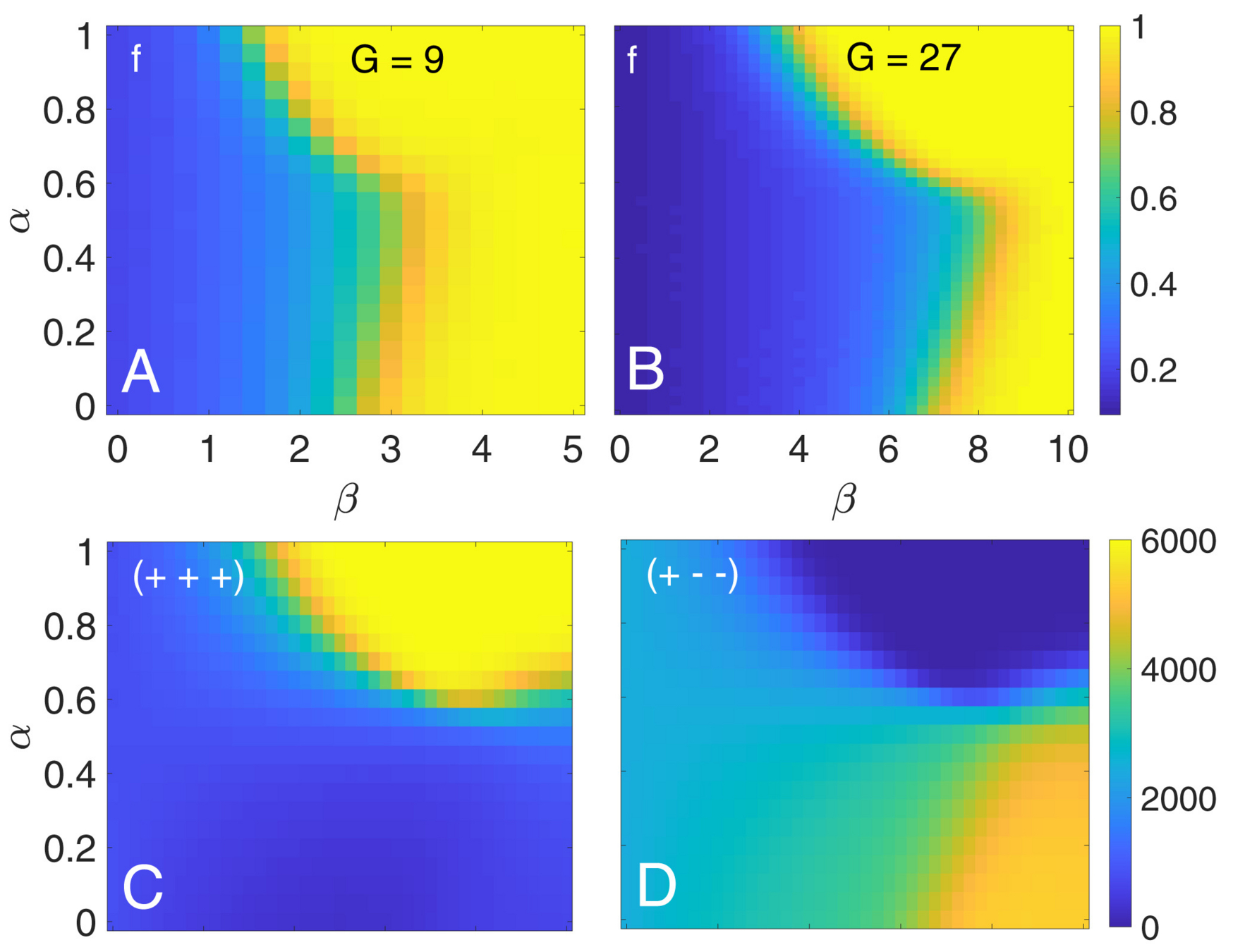
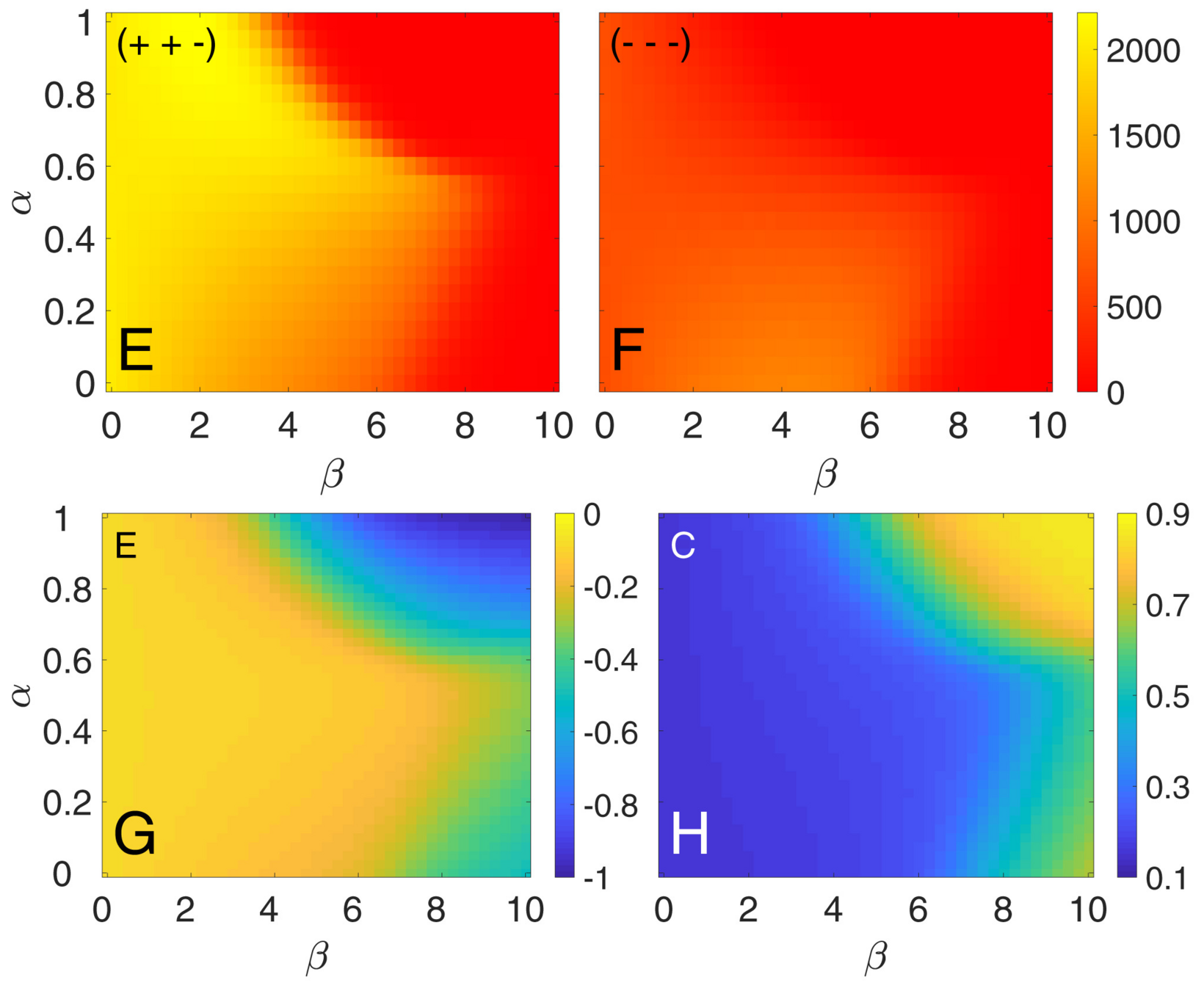
Phase diagrams
\(\beta\) represents "willingness to change",
the analog of inverse temperature
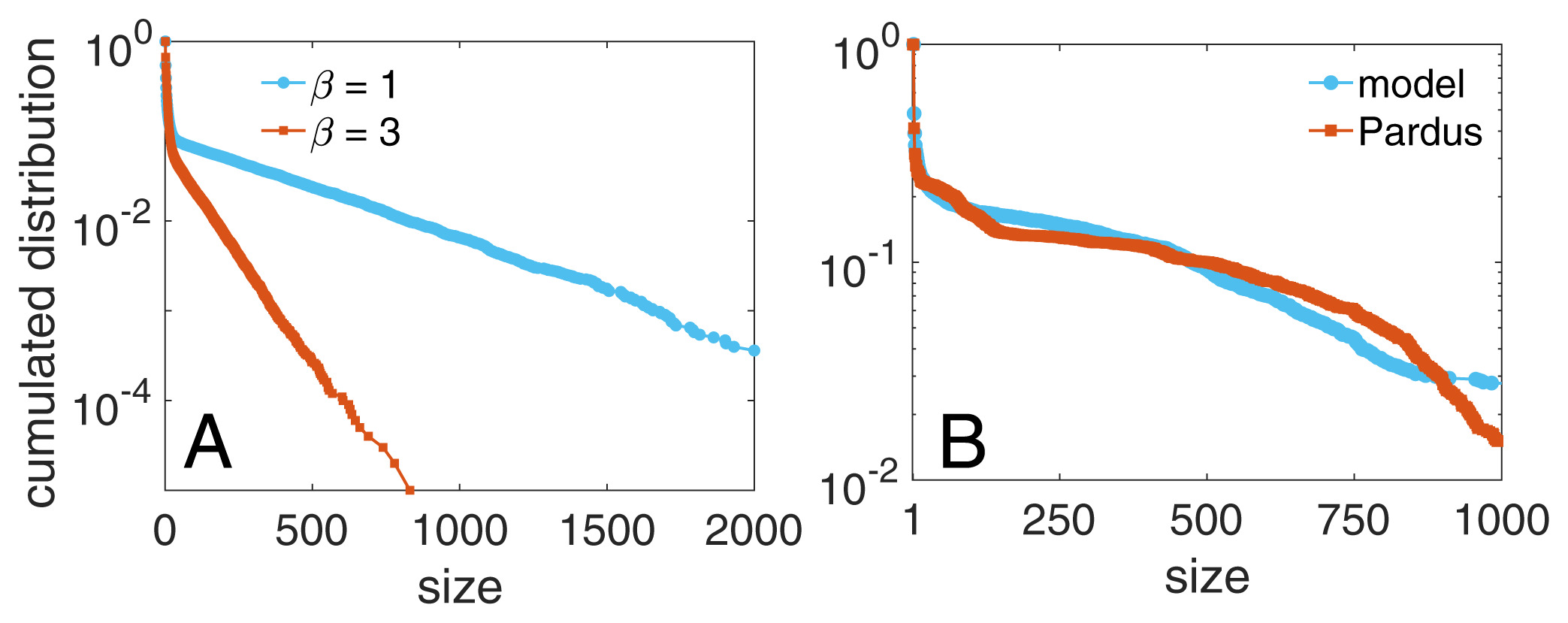
Group size distribution in Pardus
Pardus is an online multiplayer game where players have to interact with other peers
3. Social group formation


Dora Brücke-Teleky award
Motivation
- Main motivation: application of soft-matter self-assembly and condensed-matter spin glasses in a new framework of social group formation based on homophily
- We use the equilibrium distribution from (1) and the local Hamiltonian from (2) to obtain the group-size distribution and the phase diagram
- Again, we compare it with the real data of Pardus
Group formation based on homophily
Hamiltonian of a group \(\mathcal{G}\)
\(H(\mathbf{s}_{i_1},\dots,\mathbf{s}_{i_k}) = \underbrace{- \phi \, \frac{J}{2} \sum_{ij \in \mathcal{G}} A_{ij} \mathbf{s}_i \cdot \mathbf{s}_j}_{\textcolor{red}{intra-group \ social \ stress}}+ \underbrace{(1-\phi) \frac{J}{2} \sum_{i \in \mathcal{G}, j \notin \mathcal{G}} A_{ij} \mathbf{s}_{i} \cdot \mathbf{s}_j}_{\textcolor{blue}{inter-group \ social \ stress}} \\ \qquad \qquad \qquad \qquad - \underbrace{h \sum_{i \in \mathcal{G}} \mathbf{s}_i \cdot \mathbf{w}}_{external \ field}\)
Group formation based on opinion= self-assembly of spin glass
Group 1
Group 2
Approximations used in the model
1. Simulated annealing (configuration model)
- We do not know the full network, just a degree distribution. The probability of observing a link between \(i\) and \(j\) is proportional to the degree i.e., \(A_{ij} \propto k_i k_j\)
2. Mean-field approximation
- We replace the original Hamiltonian by the mean-field approximation, where \(m^{(k)} = \sum_{i \in group \ of \ size \ k} s_i\) is the average opinion vector of a group of size \(k\)
These two approximations lead to the set of self-consistency equations:
$$m^{(k)} = k \sum_{q^{(k)} q^{(k,l)}} P(q^{(k)}) P(q^{(k,l)}) \tanh(\beta H^{(k)}(m^{(l)},q^{(k)},q^{(k,l)})) $$
where \(q^{(k)}\) is the intra-group degree, \(q^{(k,l)}\) is the inter-group degree and \(P\) is the degree distribution
Results for zero inter-group degree
Theory
MC simulation
Dependence on external field

Application: PARDUS multiplayer online game
Summary and future research
- Based on physical models of self-assembly and spin glasses, we created a homophily-based social group formation model that requires only a few parameters, as average friendship degree
- The model has some limitations indeed:
- Lack of higher-order structures in the network (e.g., triangles)
- Lack of enmity relations within groups
- Opinions are considered to be independent (no belief system)
- Real social networks are typically multilayer (family x work x leisure)
- Influence of different opinions on different types of links
- All the limitations are suggestions for future work