Overview of the main Properties of Generalized Entropies

Jan Korbel

CSH Workshop

"Holographic and other Cosmologically Relevant Entropies"

20-22 January 2025

Slides available at: https://slides.com/jankorbel

Personal web: https://jankorbel.eu

Introduction

The main aim of the workshop is to study the relevance of entropy in cosmology
One part of this is to focus on using generalized entropies like:
- Rényi entropy $R_q = \frac{1}{1-q} \log \sum_i p_i^q$
- Tsallis entropy $S_q =\frac{1}{1-q} (\sum_i p_i^q -1) $
- Sharma-Mittal entropy $M_{Q,q} = \frac{1}{1-Q} ((\sum_i p_i^{q})^{\frac{1-Q}{1-q}} -1)$
- Tsallis-Cirto entropy $S_{q,\delta} = \sum_i p_i (\log_q 1/p_i)^\delta$
- Kaniadakis entropy $K_\kappa = \frac{1}{2 \kappa}\sum_i (p_i^{1+\kappa} - p_i^{1-\kappa})$
- and other
All these entropies are generalizations of Shannon entropy $H = -\sum_i p_i \log p_i$
This talk focuses on the properties of generalized entropies
We will go through some key aspects of entropy in thermodynamics, information theory and statistical inference

Introduction

Generalized entropies were introduced in statistical physics to describe systems where the Boltzmann-Gibbs statistics fail
The main applications of generalized entropies include:
- Non-extensive systems (e.g., long-range interactions)
- Non-ergodic systems (not all states are sampled equally)
- Non-exponential MaxEnt distributions
- Complex systems
The main applications of generalized entropies include:
- Plasmas, high-energy physics, and gravitational systems
- Quantum entanglement and decoherence
- Information theory and statistical inference
- Non-physical systems, e.g., biology, linguistics, finance

Information theory:

Shannon-Khinchin axioms

with Petr Jizba (CTU in Prague)

Axiomatization from the Information theory point of view

 Continuity.—Entropy is a continuous function of the probability distribution only.
Maximality.— Entropy is maximal for the uniform distribution.
Expandability.— Adding an event with zero probability does not change the entropy.
Additivity.— $H(A \cup B) = H(A) + H(B|A)$ where $H(B|A) = \sum_i p_i^A H(B|A=a_i)$

These four axioms lead to Shannon entropy $$ H(P) = - \sum_i p_i \log p_i $$
Many authors have considered generalizations of 4th Axiom
We show a natural generalization covering a wide class of entropies

Shannon-Khinchin axioms

Kolmogorov-Nagumo algebra

Let us considering a bijection $ f(x) $
We define addition, subtraction, multiplication, and division as follows $$x\oplus y = f(f^{-1}(x) + f^{-1}(y))$$ and similarly for other operations
In 1930, Andrey Kolmogorov and Mitio Nagumo independently introduced a generalization called f-mean for an arbitrary continuous and injective function

$$\langle X \rangle_f := f^{-1} \left(\frac{1}{n} \sum_i f(x_i)\right)$$

The basic property is that the mean is invariant to the transformation $f(x) \mapsto a f(x) + b$
The Hölder mean is obtained for $f(x) = x^p$

We now replace SK4 with the following axiom:

4. Composability: Entropy of a joined system $ A \cup B$ can be expressed as $S(A \cup B) = S(A|B) \otimes_f S(B)$, where $S(A|B)$ is conditional entropy satisfying consistency requirements I.), II.)

I.) For independent variables $A,B$, the joint entropy $S(A \cup B)$ should be composable from entropies $S(A)$ and $S(B)$, i.e., $S(A \cup B) = F(S(A),S(B))$

II.) Conditional entropy should be decomposable into entropies of conditional distributions, i.e., $S(B|A) = G\left( P_A, \{S(B|A=a_i)\}_{i=1}^m\right)$

Kolmogorov-Nagumo algebra

P.J. & J.K. Phys. Rev. E 101, 042126

Class of admissible entropies

Entropies fulfilling KN type of SK: $$S_q^f(P) = f\left[\left(\sum_i p_i^q\right)^{1/(1-q)}\right] = f\left[\exp_q\left( \sum_i p_i \log_q(1/p_i) \right)\right]$$
where
- $\exp_q(x) := \left(1 + (1-q) x\right)_+^{1/(1-q)}$
- $\log_q(x) := \frac{x_+^{1-q}-1}{1-q}$
- Here $ x_+$ denotes $\max\{x,0\}$
Notable examples
- $f(x) = \log(x)$ - Rényi entropy $R_q = \frac{1}{1-q} \log \sum_i p_i^q$
- $f(x) = \log_q(x)$ - Tsallis entropy $S_q = \frac{1}{1-q}(\sum_i p_i^q -1)$
- $f(x) = \log_Q(x)$ - Sharma-Mittal entropy $M_{Q,q} = \frac{1}{1-Q} ((\sum_i p_i^{q})^{\frac{1-Q}{1-q}} -1)$
Note that the entropy can be written as a KN mean

Statistical inference:

Shore-Johnson axioms

with Petr Jizba (CTU in Prague)

Shore-Johnson axioms

Axiomatization from the Maximum entropy principle point of view
Principle of maximum entropy is an inference method and it should obey some statistical consistency requirements.
Shore and Johnson set the consistency requirements:

 Uniqueness.—The result should be unique.
Permutation invariance.—The permutation of states should not matter.
Subset independence.—It should not matter whether one treats disjoint subsets of system states in terms of separate conditional distributions or in terms of the full distribution.
System independence.—It should not matter whether one accounts for independent constraints related to disjoint subsystems separately in terms of marginal distributions or in terms of full-system constraints and joint distribution.
Maximality.—In absence of any prior information the uniform distribution should be the solution.

P.J. & J.K. Phys. Rev. Lett. 122 (2019), 120601

Uffink class of entropies

Entropies fulfilling SJ axioms is the same as for SK axioms: $$S_q^f(P) = f\left[\left(\sum_i p_i^q\right)^{1/(1-q)}\right] = f\left[\exp_q\left( \sum_i p_i \log_q(1/p_i) \right)\right]$$

MaxEnt distribution: q-exponential

$$p_i = \frac{1}{Z_q} \exp_q\left(-\hat{\beta} \Delta E_i \right)$$
$$ Z_q = \sum_i \left[\exp_q\left(-\hat{\beta} \Delta E_i \right)\right]$$

$$\hat{\beta} = \frac{\beta}{q f'\left(Z_q\right) Z_q}$$

Conclusions: Uffink class of entropies can be used as a measure of information as well as for Maximum entropy principle

composition rule of $p_{ij} \propto \exp_q (-\beta (E_i + E_j)) $

$$\frac{1}{p_{ij} Z_q(P)} = \frac{1}{u_{i} Z_q(U)} \otimes_q \frac{1}{v_{j} Z_q(V)} $$

or in terms of escort distributions $P_{ij}(q) = p_{ij}^q/\sum_{ij} p_{ij}^q $

$$ \frac{P_{ij}(q)}{p_{ij}} = \frac{U_{i}(q)}{u_{i}}\ + \ \frac{V_{j}(q)}{v_{j}} - 1$$

Composition rule for

q-exponentials

Calibration invariance

of MaxEnt principle

Calibration invariance

of MaxEnt principle

The Principle of maximum entropy is used in physics and other fields, including statistical inference
In physics, it actually consists of two parts:
1. Finding a distribution (MaxEnt distribution) that maximizes entropy under given constraints
2. Plugging the distribution into the entropic functional and calculating physical quantities as thermodynamic potentials, temperature, or response coefficients (specific heat, compressibility, etc.).
Only 1.) + 2.) uniquely characterize the properties of a physical system
When MaxEnt is only used to obtain a distribution, there can be more combinations of entropy and constraints, yielding the same distribution

J.K. Entropy 23 (2021) 96

Calibration invariance

of MaxEnt principle

Typically, one can relate the Langrange multipliers to physical quantities
In the case of Shannon entropy with normal constraints, Langange functional is $$L(p) = - \sum_i p_i \log p_i - \alpha (\sum_i p_i - 1) - \beta (\sum_i p_i \epsilon_i - U)$$
- $\beta$ is the inverse temperature $\beta= \frac{1}{k_B T}$
- $\alpha$ is related to free energy $-\frac{\alpha}{\beta} = F$
Are these relations still conserved when the MaxEnt distribution is the same but entropy and/or constraints change?

Example: $f(S)$

Maximizing entropy $S$ leads to the same MaxEnt distribution as maximizing $f(S)$ where $f$ is an increasing function
The Lagrange fuction is $$L_f = f(S) - \alpha_f (\sum_i p_i -1) \beta_f (\sum_i p_i \epsilon_i-U)$$
By using the method of Lagrange multipliers, we get that
- $\beta_f = f'(S) \beta$
- $\alpha_f = f'(S) \alpha$
This transformation actually forms a group:
- if $g(x) = f_1(f_2(x))$ then $\beta_g = f_1'(f_2(S)) f_2'(S) \beta$
Examples:
- Rényi and Tsallis entropy $R_q = \frac{1}{1-q} \ln[1+(1-q)S_q]$
- Shannon entropy and entropy power $P(p) = \prod_i (1/p_i)^{p_i}$ the relation is $P = \exp(H)$

Thermodynamics of exponential KN averages

with Fernando Rosas (ICL London) and Pablo Morales (Araya, Japan)

Kolmogorov-Nagumo averages revisited

The arithmetic mean can be uniquely determined from the class of KN-means by the following two properties:

Homogeneity $\langle a X \rangle = a \langle X \rangle $
Translation invariance $ \langle X +c \rangle = \langle X \rangle +c$

Note that the Hölder means ($f(x)=x^p$) satisfy Property 1 but not property 2
What is the class of means that satisfies Property 2?

Exponential KN averages

The solution is given by the function $f(x) = (e^{\gamma x}-1)/\gamma$ and the inverse function is $f^{-1}(x) = \frac{1}{\gamma} \ln (1+\gamma x)$
This leads to the exponential KN mean$$ \langle X \rangle_\gamma = \frac{1}{\gamma} \ln \left(\sum_i \exp(\gamma x_i)\right) $$
We recover the arithmetic mean by $\gamma \rightarrow 0$
Note that one can relate $q$ and $\gamma$ as $\gamma = 1-q$
Property 2 is important for thermodynamics since the average energy $\langle E \rangle$ does not depend on the energy of the ground state
The additivity is preserved for independent variables

$$\langle X + Y \rangle_\gamma = \langle X \rangle_\gamma + \langle Y \rangle_\gamma \Leftrightarrow X \perp \!\!\! \perp Y$$

The general additivity formula is given as $$ \langle X + Y \rangle_\gamma = \langle X + \langle Y|X \rangle_\gamma\rangle_\gamma$$ where the conditional mean is given as $$ \langle X | Y \rangle_\gamma = \frac{1}{\gamma} \ln \left(\sum_i p_i \exp(\gamma \langle Y|X = x_i\rangle_\gamma ) \right) $$
The exponential KN mean is closely related to the cumulant generating function $$M_\gamma(X) = \ln \langle \exp(\gamma X)\rangle = \gamma \langle X \rangle_\gamma $$

Exponential KN averages

Rényi entropy as exponential KN average

Rényi entropy can be naturally obtained as the exponential KN average of the Hartley information $\ln 1/p_k$
We define the Rényi entropy as $$ R_\gamma(P) = \frac{1}{1-\gamma} \langle \ln 1/p_k \rangle_\gamma = \frac{1}{\gamma(1-\gamma)} \ln \sum_k p_k^{1-\gamma}$$
The role of the prefactor will be clear later, but one of the reasons is that the limit $\gamma \rightarrow 1$ is the well-defined Burg entropy $- \sum_k \ln p_k$
We also naturally obtain the conditional entropy $$ R_\gamma(X,Y) = R_\gamma(X) + R_\gamma(Y|X)$$

P.M., J.K. & F. E. R. New J. Phys 25 (2023) 073011

Equilibrium thermodynamics of Exponential KN Averages

Let us now consider thermodynamics, where all quantities are exponential KN averages
We consider that the system entropy is described by Rényi entropy
The internal energy is described as the KN average of the energy spectrum $\epsilon$ $$U_\gamma^\beta := \frac{1}{\beta} \langle \beta \epsilon \rangle_\gamma = \frac{1}{\beta \gamma} \ln \sum_i p_i \exp(\beta \gamma \epsilon_i)$$
The inverse temperature $\beta = \frac{1}{k_B T}$ ensures that the energy has correct units

MaxEnt distribution

Let us now calculate the MaxEnt distribution obtained from Rényi entropy with given internal energy $U^\beta_\gamma $
The Lagrange function is $$ \mathcal{L} = R_\gamma - \alpha_0 \sum_i p_i - \alpha_1 \frac{1}{\beta}\langle \beta \epsilon \rangle_\gamma$$
The MaxEnt distribution $\pi_i$ can be obtained from

$$ \frac{1}{\gamma} \frac{\pi_i^{-\gamma}}{\sum_k \pi_k^{1-\gamma}} - \alpha_0 - \frac{\alpha_1}{\beta \gamma} \frac{e^{\gamma \beta \epsilon_i}}{\sum_k \pi_k e^{\gamma \beta \epsilon_k}} = 0$$

By multiplying by $\pi_i$ and summing over $i$ we obtain $\alpha_0 = \frac{1-\alpha_1}{\gamma}$ and therefore $$\pi_i = \frac{\left(\sum_k \pi_k e^{\gamma \beta \epsilon_k}\right)^{1/\gamma}}{\left(\sum_k \pi_k^{1-\gamma}\right)^{1/\gamma}} \exp(-\beta \epsilon_i) = \frac{\exp(-\beta \epsilon_i)}{Z^\beta}$$

MaxEnt distribution

We obtained Boltzmann distribution from non-Shannonian entropy with non-arithmetic constraint
We immediately obtain that $$\ln \pi_i = - \beta(\epsilon_i - U_\gamma^\beta(\pi)) - (1-\gamma) R_\gamma(\pi)$$ which leads to $$\ln \sum_k e^{-\beta \epsilon_k} = (1-\gamma) R_\gamma - \beta U^\beta_\gamma = \Psi_\gamma - \gamma R_\gamma$$ where $\Psi_\gamma = R_\gamma - \beta U_\gamma^\beta$ is the Massieu function
The Helmholtz free energy can be expressed as $$F^\beta_\gamma(\pi) = U_\gamma^\beta(\pi)- \frac{1}{\beta} R_\gamma(\pi) = \frac{1}{(\gamma-1) \beta} \ln \sum_k e^{(\gamma-1)\beta \epsilon_k}.$$
Thus, although we get the same distribution as for the ordinary thermodynamics, the thermodynamic relations are different!

Thermodynamic interpretation

We calculate equilibrium Rényi entropy $$ \mathcal{R}_\gamma^\beta = \frac{1}{\gamma(1-\gamma)} \ln \sum_i \left(\frac{e^{-\beta \epsilon_i}}{Z^\beta}\right)^{1-\gamma} = \frac{1}{\gamma(1-\gamma)} \ln \sum_i e^{-(1-\gamma)\beta} - \frac{1}{\gamma} \ln Z^\beta $$
Thus we get that Rényi entropy of a Boltzmann distribution is $$\mathcal{R}_\gamma^\beta = -\frac{\beta}{\gamma} \left(\mathcal{F}^{(1-\gamma) \beta} - \mathcal{F}^{\beta}\right)$$
By defining $\beta' = (1-\gamma)\beta \quad \Rightarrow \quad \gamma = 1-\frac{\beta'}{\beta}$ we can express it as

$$ \mathcal{R}_\gamma^\beta = \beta^2 \, \frac{\mathcal{F}^{\beta'} - \mathcal{F}^\beta}{\beta'-\beta} $$

which is the $\beta$ rescaling of the free energy difference.

This can be interpreted as the maximum amount of work the system can perform by quenching the system from inverse temperature $\beta$ to inverse temperature $\beta'$.
This has been first discovered by John Baez.

By taking $\gamma \rightarrow 0$ we recover the relation between entropy and free energy $$\mathcal{S}^\beta = \beta^2 \left(\frac{\partial \mathcal{F}^\beta}{\partial \beta}\right)$$
As shown before, the free energy can be expressed as $$ \mathcal{F}_\gamma^\beta = \mathcal{F}^{(1-\gamma)\beta}$$ so it is clear that the temperature is rescaled from $\beta$ to $(1-\gamma)\beta$
Finally the internal energy can be expressed as $$ \mathcal{U}^\beta_\gamma = \frac{\beta' \mathcal{F}^{\beta'} - \beta \mathcal{F}^\beta}{\beta'-\beta} = - \frac{\Psi^{\beta'}-\Psi^\beta}{\beta'-\beta}$$
Again, by taking $\gamma \rightarrow 0$ we recover

$$ \mathcal{U}^\beta = - \left(\frac{\partial \Psi^\beta}{\partial \beta}\right)\, $$

Thermodynamic interpretation

Asymptotic scaling:

scaling expansion

with Rudolf Hanel and Stefan Thurner (both CSH)

Classification of statistical complex systems

Many examples of complex systems are statistical systems
Statistical systems near the thermodynamic limit $N \rightarrow \infty $ can be characterized by asymptotics of its sample space $W(N)$ - space of all possible configurations
Asymptotic behavior can be described by scaling expansion
- Coefficients of scaling expansion correspond to scaling exponents
- Scaling exponents completely determine universality classes
We can find corresponding extensive entropy
- generalization of (c,d)-entropy $^\star$

$^\star$ R.H., S.T. EPL 93 (2011) 20006

Rescaling the sample space

How does the sample space change when we rescale its size $ N \mapsto \lambda N $?
- The ratio behaves like $\frac{W(\lambda N)}{W(N)} \sim \lambda^{c_0} $ for $N \rightarrow \infty$
- the exponent $c_0$ can be extracted by $\frac{d}{d\lambda}|_{\lambda=1}$: $c_0 = \lim_{N \rightarrow \infty} \frac{N W'(N)}{W(N)}$
- For the leading term we have $W(N) \sim N^{c_0}$.
Is it only possible scaling? We have $ \frac{W(\lambda N)}{W(N)} \frac{N^{c_0}}{(\lambda N)^{c_0}} \sim 1 $
- Let us use the other rescaling $ N \mapsto N^\lambda $
- The we get that $\frac{W(N^\lambda)}{W(N)} \frac{N^{c_0}}{N^{\lambda c_0}} \sim \lambda^{c_1}$
- First correction is $W(N) \sim N^{c_0} (\log N)^{c_1}$
- It is the same scaling like for $(c,d)$-entropy
Can we go further?

We define the set of rescalings $r_\lambda^{(n)}(x) := \exp^{(n)}(\lambda \log^{(n)}(x) $ )
- $ f^{(n)}(x) = \underbrace{f(f(\dots(f(x))\dots))}_{n \ times}$
- $r_\lambda^{(0)}(x) = \lambda x$, $r_\lambda^{(1)}(x) = x^\lambda$, $r_\lambda^{(2)}(x) = e^{\log(x)^\lambda} $, $r_\lambda^{(-1)}(x) = x + \log \lambda$
- They form a group: $r_\lambda^{(n)} \left(r_{\lambda'}^{(n)}\right) = r_{\lambda \lambda'}^{(n)} $, $ \left(r_\lambda^{(n)}\right)^{-1} = r_{1/\lambda}^{(n)} $, $r_1^{(n)}(x) = x$
We repeat the procedure: $\frac{W(N^\lambda)}{W(N)} \frac{N^{c_0} (\log N)^{c_1} }{N^{\lambda c_0} (\log N^\lambda)^{c_1}} \sim 1$,
- We take $N \mapsto r_\lambda^{(2)}(N)$
- $\frac{W(r_\lambda^{(2)}(N))}{W(N)} \frac{N^{c_0} (\log N)^{c_1} }{r_\lambda^{(2)}(N)^{c_0} (\log r_\lambda^{(2)}(N))^{c_1}} \sim \lambda^{c_2}$,
- Second correction is $W(N) \sim N^{c_0} (\log N)^{c_1} (\log \log N)^{c_2}$

Rescaling the sample space

General correction is given by $ \frac{W(r_\lambda^{(k)}(N))}{W(N)} \prod_{j=0}^{k-1} \left(\frac{\log^{(j)} N}{\log^{(j)}(r_\lambda^{(k)}(N))}\right)^{c_j} \sim \lambda^{\bf c_k}$
Possible issue: what if $c_0 = +\infty$?
- Then $W(N)$ grows faster than any $N^\alpha$
  - We replace $W(N) \mapsto \log W(N)$
  - The leading order scaling is $\frac{\log W(\lambda N)}{\log W(N)} \sim \lambda^{c_0} $ for $N \rightarrow \infty$
  - So we have $W(N) \sim \exp(N^{c_0})$
If this is not enough, we replace $W(N) \mapsto \log^{(l)} W(N)$ so that we get finite $c_0$
General expansion of $W(N)$ is $$W(N) \sim \exp^{(l)} \left(N^{c_0}(\log N)^{c_1} (\log \log N)^{c_2} \dots\right) $$

J.K., R.H., S.T. New J. Phys. 20 (2018) 093007

Rescaling the sample space

$$W^{(l)}(N) \equiv \log^{(l+1)}(W(x)) = \sum_{j=0}^n c_j^{(l)} \log^{(j+1)}(N) + \mathcal{O} (\phi_n (N))$$

Scaling Expansion

Previous formula can be expressed in terms of Poincaré asymptotic expansion

Coefficients of the expansion are scaling exponents and can be calculated from:

$$ c^{(l)}_k = \lim_{N \rightarrow \infty} \log^{(k)}(N) \left( \log^{(k-1)} \left(\dots\left( \log N \left(\frac{N W'(N)}{\prod_{i=0}^l \log^{(i)}(W(N))}-c^{(l)}_0\right)-c^{(l)}_1\right) \dots\right) - c^{(l)}_k\right)$$

Extensive entropy

We can do the same procedure with entropy $S(W)$
Leading order scaling: $ \frac{S(\lambda W)}{S(W)} \sim \lambda^{d_0}$
First correction $ \frac{S(W^\lambda)}{S(W)} \frac{W^{d_0}}{W^{\lambda d_0}} \sim \lambda^{d_1}$
- First two scalings correspond to $(c,d)$-entropy for $c= 1-d_0$ and $d = d_1$
Scaling expansion of entropy $$S(W) \sim W^{d_0} (\log W)^{d_1} (\log \log W)^{d_2} \dots $$
Requirement of extensivity $S(W(N)) \sim N$ determines the relation between $c$ and $d$ :
- $d_l = 1/c_0$, $d_{l+k} = - c_k/c_0$ for $k = 1,2,\dots$

Process
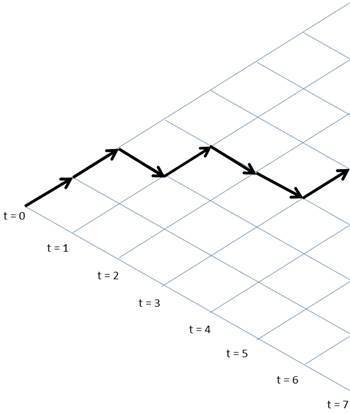
Random walk	1	0
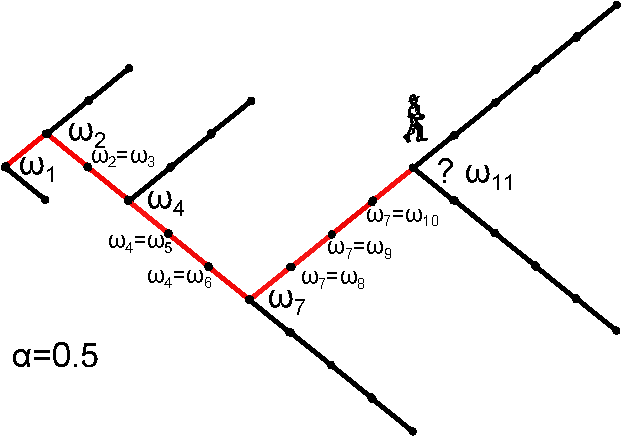
Aging random walk	2	0
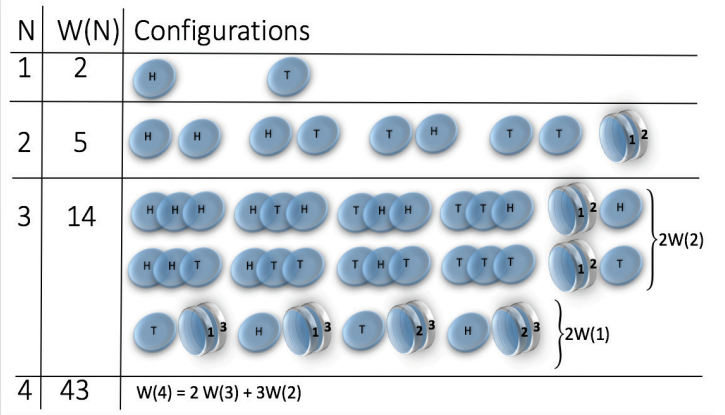
Magnetic coins *	1	-1
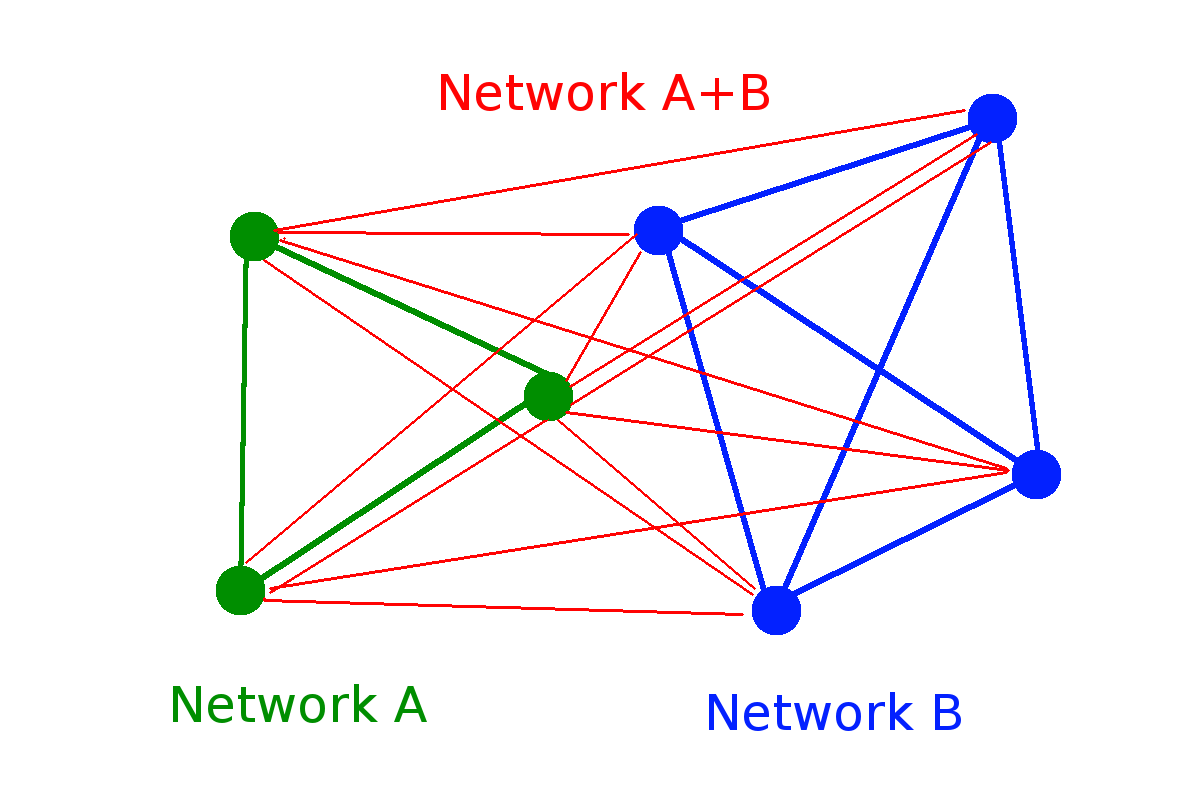
Random network	1/2	0
Random walk cascade	0	1

$ \log W$

$ (\log W)^2$

$ (\log W)^{1/2}$

$ \log \log W$

$d_0$

$d_1$

$d_2$

$ \log W/\log \log W$

* H. Jensen et al. J. Phys. A: Math. Theor. 51 375002

$ W(N) = 2^N$

$W(N) \approx 2^{\sqrt{N}/2} \sim 2^{N^{1/2}}$

$ W(N) \approx N^{N/2} e^{2 \sqrt{N}} \sim e^{N \log N}$

$W(N) = 2^{\binom{N}{2}} \sim 2^{N^2}$

$W(N) = 2^{2^N}-1 \sim 2^{2^N}$

Parameter space of $ (c,d) $ - entropy

How does it change for one more scaling exponent?

R.H., S.T. EPL 93 (2011) 20006

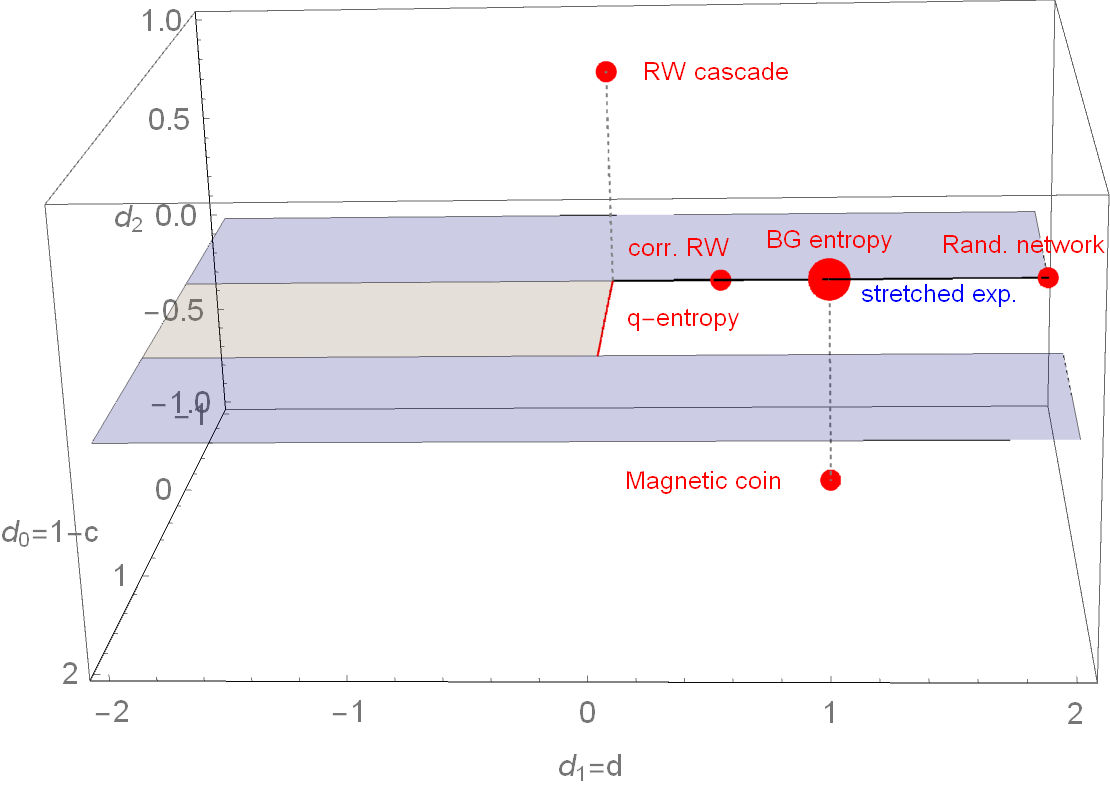
Parameter space of $ (d_0,d_1,d_2) $-entropy

To fulfill SK axiom 2 (maximality): $d_l > 0$, to fulfill SK axiom 3 (expandability): $d_0 < 1$