James L. Weaver
Developer Advocate

jweaver@pivotal.io
JavaFXpert.com

Dr. Johan Vos
Co-founder & CTO

johan.vos@gluonhq.com
gluonhq.com

@J ohanVos

Quantum Computing

Hacking into Nature's Computer

About Presenter James Weaver

Java Champion, JavaOne Rockstar, plays well with others, etc :-)

Author of several Java/JavaFX/RaspPi books

Developer Advocate & International Speaker for Pivotal

@JavaFXpert

Mission: "Transform how the world builds software"

@JavaFXpert

Mission: "Transform how the world builds software"

@JavaFXpert

About Presenter Dr. Johan Vos

Developer / Physicist / Writer / Speaker - Gluon

@JohanVos

About Gluon

@JohanVos

Gluon CloudLink

Concepts we'll address today

Introduction to quantum computing

Representing qubits

Axioms of quantum mechanics

Superposition principle
Measurement
Unitary evolution

Quantum computing algorithms

Quantum entanglement

More algorithms

Supplementary resources

@JavaFXpert

@JohanVos

Intro to Quantum Computing

@JavaFXpert

@JohanVos

from: wikipedia.org/wiki/Quantum_computing

History repeating itself

@JavaFXpert

@JohanVos

ENIAC computer circa 1947

IBM Research quantum computer circa 2017

massive hardware, limited bits, software infancy

Quantum computers make direct use of quantum-mechanical phenomena, such as superposition and entanglement, to perform operations on data.

Some QC proofs of concept

@JavaFXpert

@JohanVos

University of Sussex

Delft University of Technology

mini-universe in your garage

Don't try this at home, kids!

@JavaFXpert

@JohanVos

Why use a quantum computer?

Feasible on classical computers

Feasible on quantum computers

Solutions to problems

some problems may be solved exponentially faster

@JavaFXpert

@JohanVos

Transistors can't get much smaller

the quantum tunneling struggle is real

spectrum.ieee.org/semiconductors/devices/the-tunneling-transistor

Breaking RSA crypto

someday maybe, using Shor's algorithm

@JavaFXpert

@JohanVos

newscientist.com/article/mg22029445-100-my-quantum-algorithm-wont-break-the-internet-yet/

“If you start factoring 10-digit numbers then it’s going to start getting scary”

Dr. Peter Shor, 2013

Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer

Related paper published 25 Jan 1997 by Dr. Shor:

Note: Shor's algorithm was formulated in 1994

Quickly searching unsorted data

using Grover's algorithm

@JavaFXpert

@JohanVos

outlookindia.com/magazine/story/ring-o-stars/220719

"Programming a quantum computer is particularly interesting since there are multiple things happening in the same hardware simultaneously. One needs to think like both a theoretical physicist and a computer scientist."

Dr. Lov Grover, 2002

Quantum Mechanics helps in searching for a needle in a haystack

Related paper published 17 Jul 1997 by Dr. Grover:

Simulating nature

complex chemical reactions, for example

@JavaFXpert

@JohanVos

“Nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem, because it doesn't look so easy.”

Dr. Richard Feynman, 1981

en.wikipedia.org/wiki/Richard_Feynman

bigbangtheory.wikia.com/wiki/Richard_Feynman

@JavaFXpert

@JohanVos

Nature journal issued 14 September 2017

Leveraging quantum computing for chemistry

arxiv.org/abs/1710.07629

@JavaFXpert

@JohanVos

Quantum communication and cryptography

arxiv.org/abs/1707.00542

arxiv.org/abs/1707.00934

Concepts we'll address today

Introduction to quantum computing

Representing qubits

Axioms of quantum mechanics

Superposition principle
Measurement
Unitary evolution

Quantum computing algorithms

Quantum entanglement

More algorithms

Supplementary resources

@JavaFXpert

@JohanVos

Classical bits vs. qubits

@JavaFXpert

@JohanVos

two discrete states vs. infinite superpositions

from: The Future of Computing – Quantum & Qubits by Sam Sattel

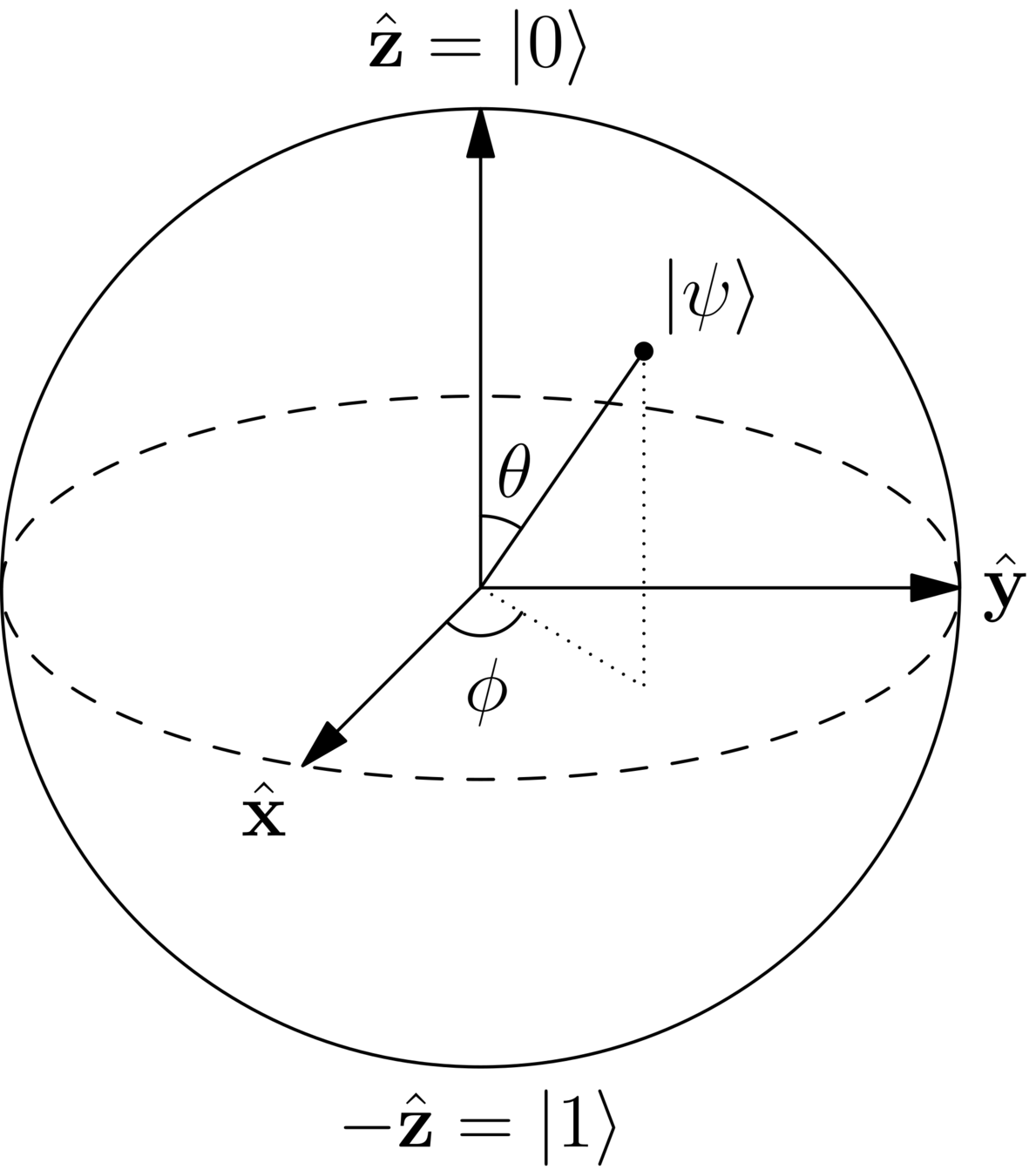
Qubit geometry

@JavaFXpert

@JohanVos

desmos.com/calculator/hjpqghdeat

Representing qubits

@JavaFXpert

@JohanVos

The Mathematics of Quantum Computers | PBS Infinite Series

ket notation, vectors, and geometrically

Hardware representation of qubits

@JavaFXpert

@JohanVos

Physical support	Type
Photon	Polarization	Horizontal	Vertical
Electrons	Spin	Up	Down
Superconductor	Charge	Uncharged	Charged

\vert0\rangle

\vert0\rangle

\vert1\rangle

\vert1\rangle

from wikipedia.org/wiki/Qubit

Superconducting qubits on a chip

@JavaFXpert

@JohanVos

Rigetti Computing

Concepts we'll address today

Introduction to quantum computing

Representing qubits

Axioms of quantum mechanics

Superposition principle
Measurement
Unitary evolution

Quantum computing algorithms

Quantum entanglement

More algorithms

Supplementary resources

@JavaFXpert

@JohanVos

Diagonally polarized photon

collapsing to a measurement basis state

@JavaFXpert

@JohanVos

From video: Some light quantum mechanics by 3Blue1Brown with MinutePhysics

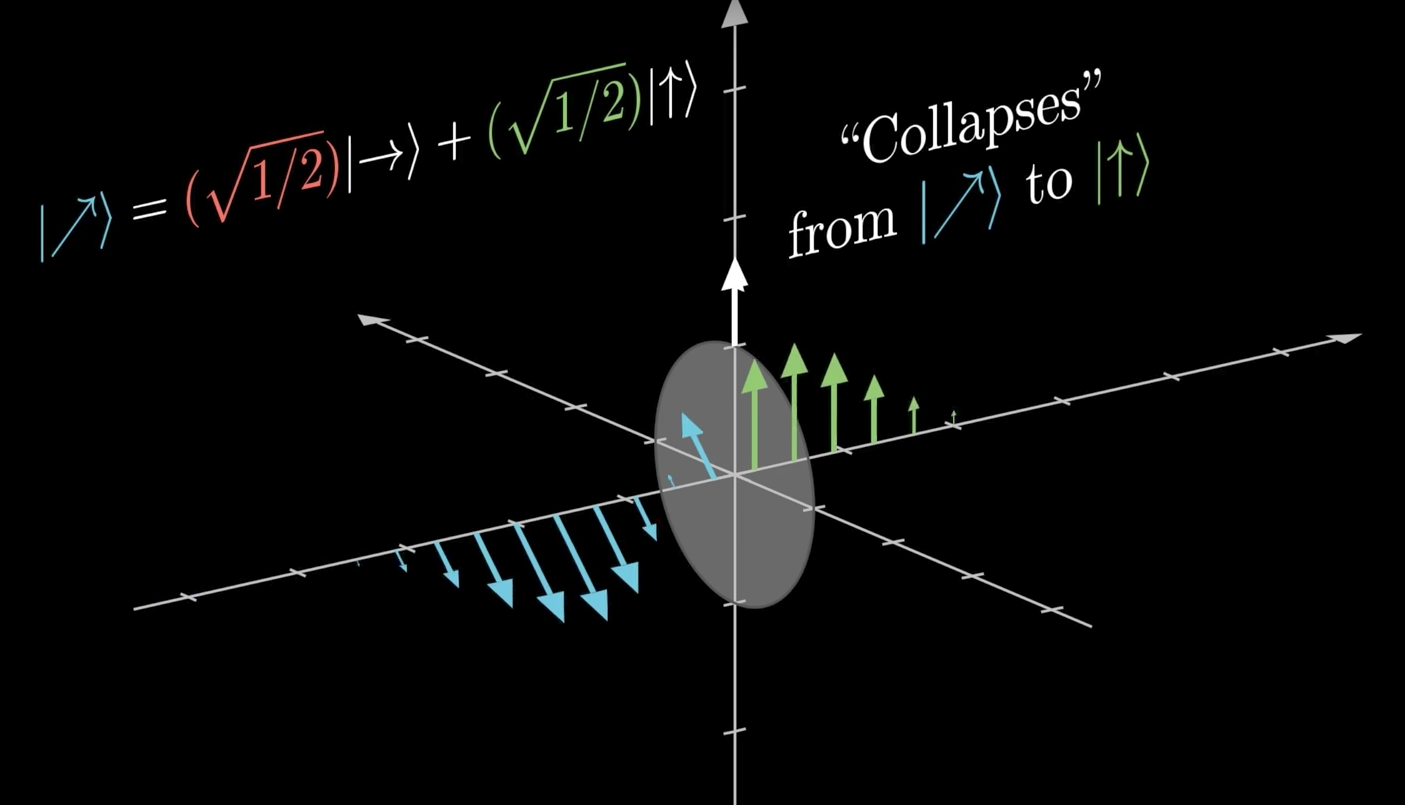
Measuring in the computational basis

@JavaFXpert

@JohanVos

Visualizing quantum measurement

Polarized lenses blocking light

@JavaFXpert

@JohanVos

From video: Some light quantum mechanics by 3Blue1Brown with MinutePhysics

Vertically polarized photon

won't pass through horizontally polarized filter

@JavaFXpert

@JohanVos

From video: Some light quantum mechanics by 3Blue1Brown with MinutePhysics

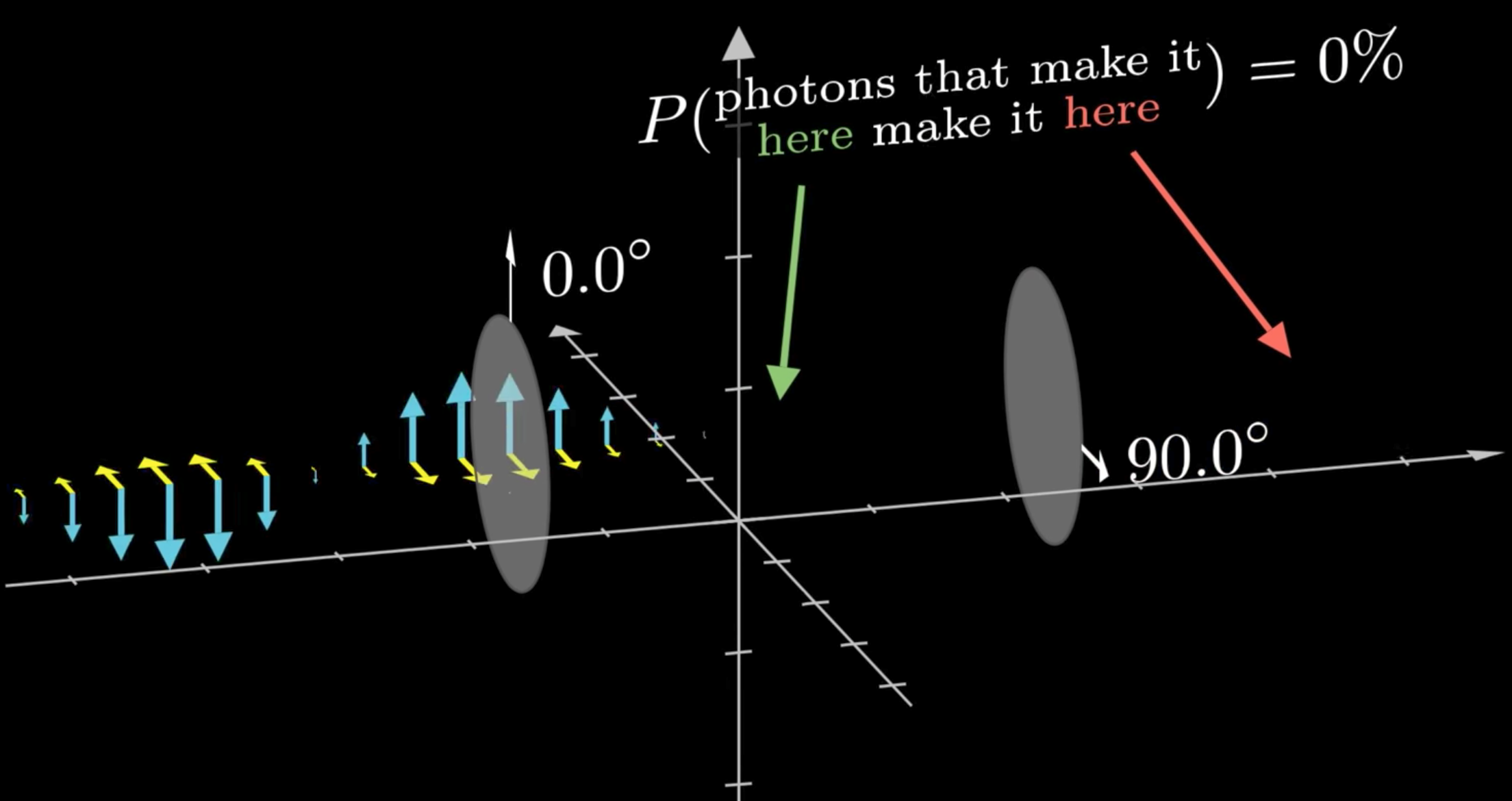
Superposition collapse

Why does adding a lens let more light through?

@JavaFXpert

@JohanVos

From video: Some light quantum mechanics by 3Blue1Brown with MinutePhysics

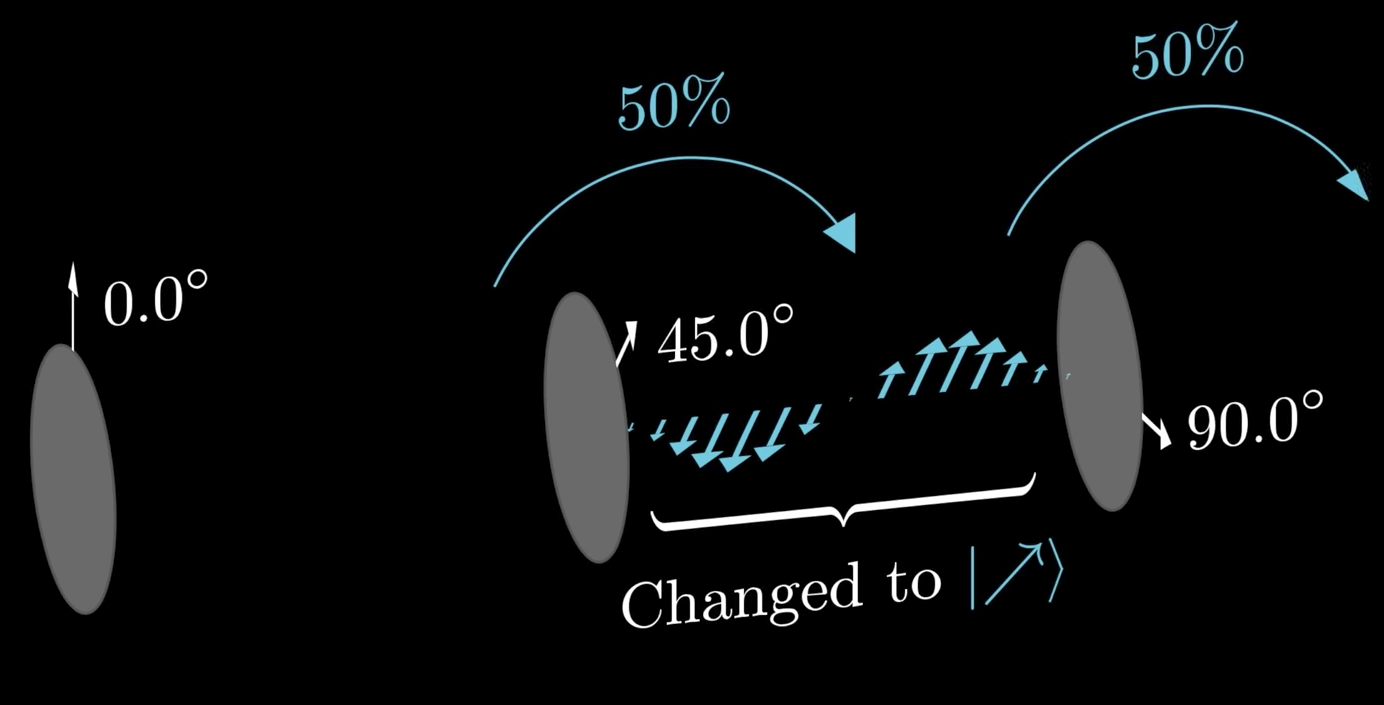
Measuring in an alternative basis

@JavaFXpert

@JohanVos

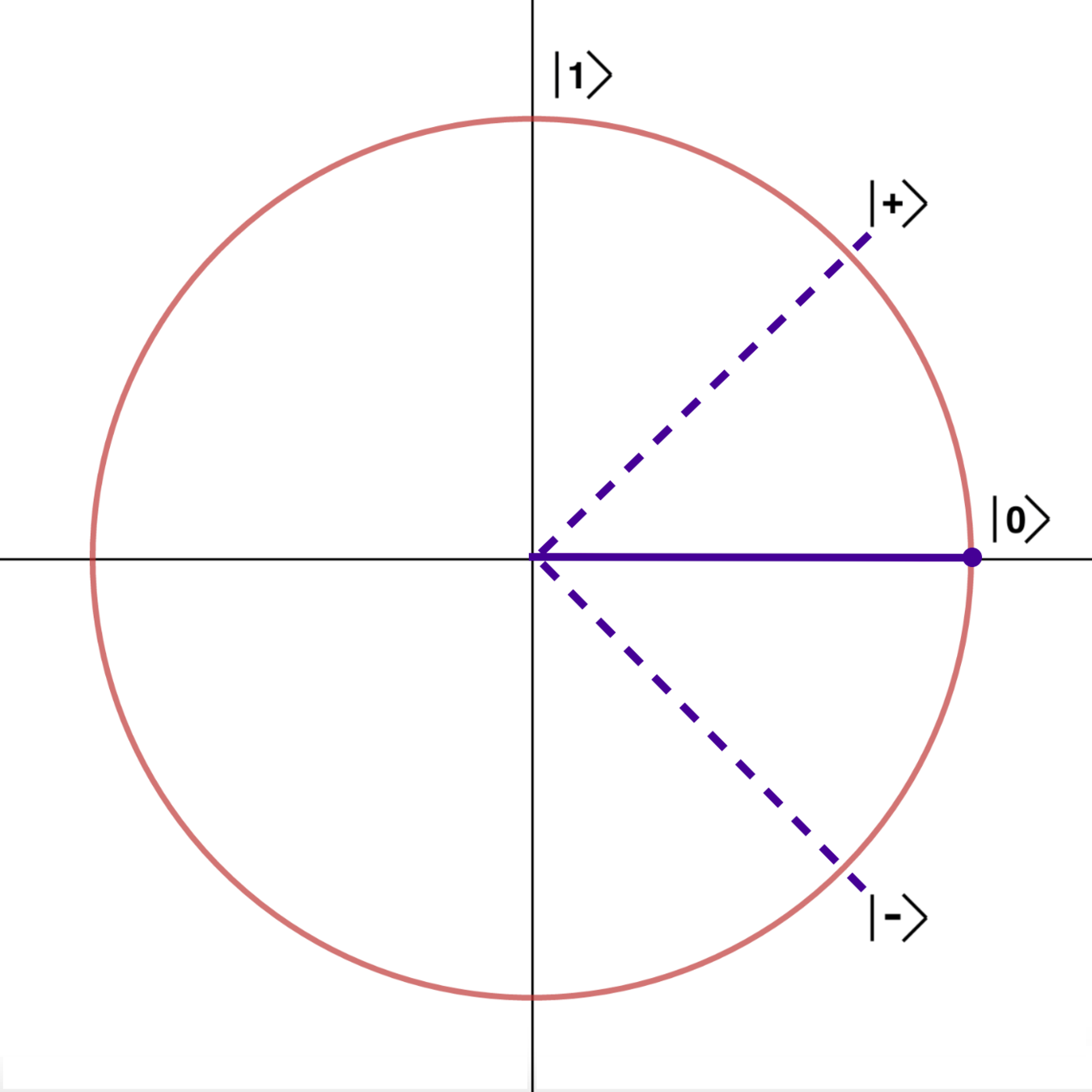
Orchestrating superpositions

Measuring in various basis states

@JavaFXpert

@JohanVos

From video: Some light quantum mechanics by 3Blue1Brown with MinutePhysics

Double-slit experiment

constructive and destructive interference

@JavaFXpert

Text

Wikimedia commons Two-Slit_Experiment_Light

Classic logic gates

@JavaFXpert

@JohanVos

a quick review for comparison to quantum gates

imgur.com/M59IOZQ

Some quantum gates

@JavaFXpert

@JohanVos

krishnakumarsekar/awesome-quantum-machine-learning

matrix operations model quantum mechanical behavior

More quantum gates

@JavaFXpert

@JohanVos

d.umn.edu/~vvanchur/2015PHYS4071/Chapter4.pdf

just going though a phase

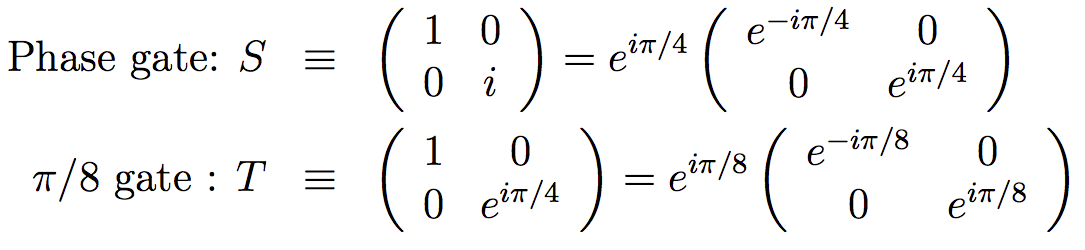
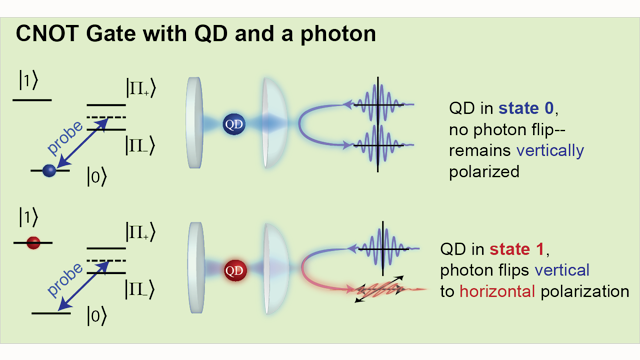
Quantum gate hardware

@JavaFXpert

@JohanVos

example using photons

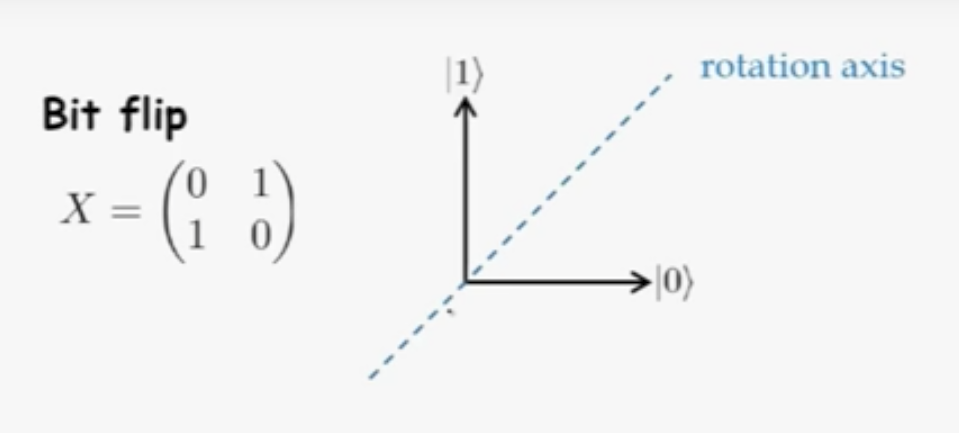
A quantum logic gate between a solid-state quantum bit and a photon

NOT / Pauli-X / Bit flip gate

@JavaFXpert

@JohanVos

from video: Single qubit gates - Umesh Vazirani

Pauli-Z / Phase flip gate

@JavaFXpert

@JohanVos

from video: Single qubit gates - Umesh Vazirani

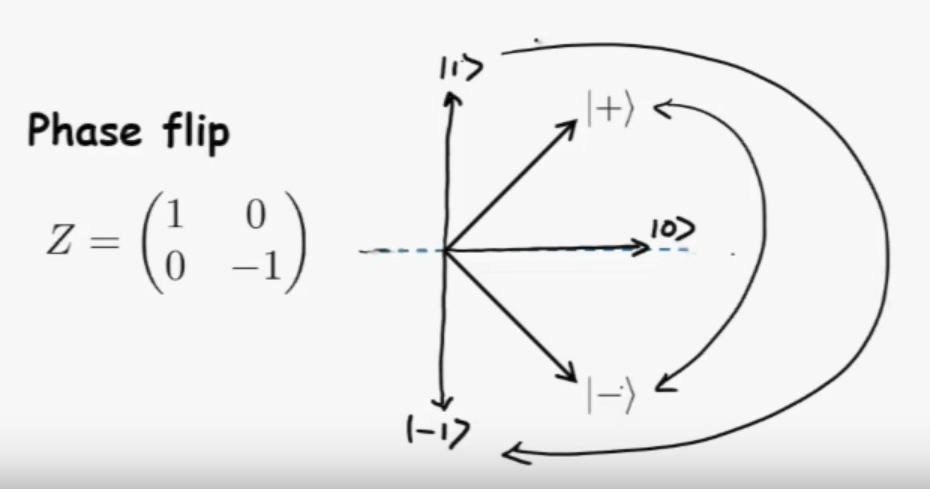
Hadamard gate

@JavaFXpert

@JohanVos

from video: Single qubit gates - Umesh Vazirani

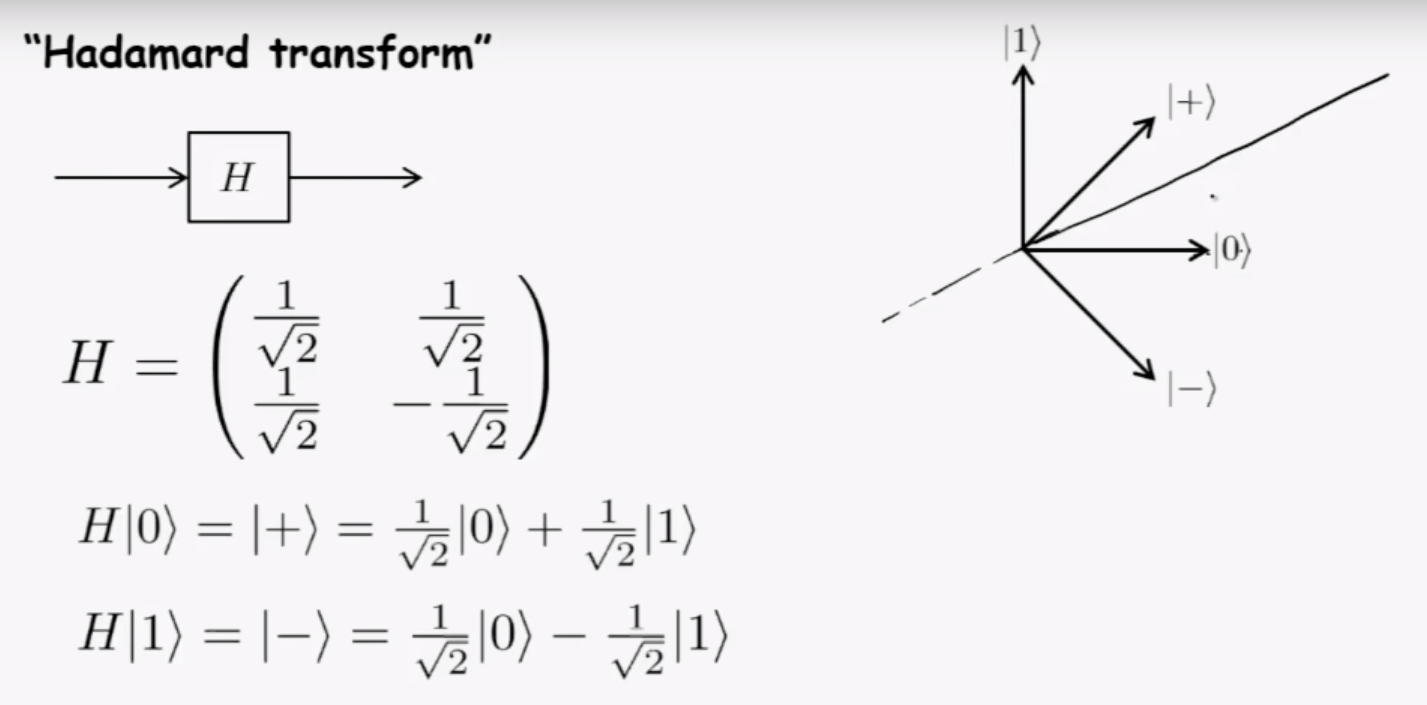
CNOT gate

@JavaFXpert

@JohanVos

from video: Two qubit gates and tensor products - Umesh Vazirani

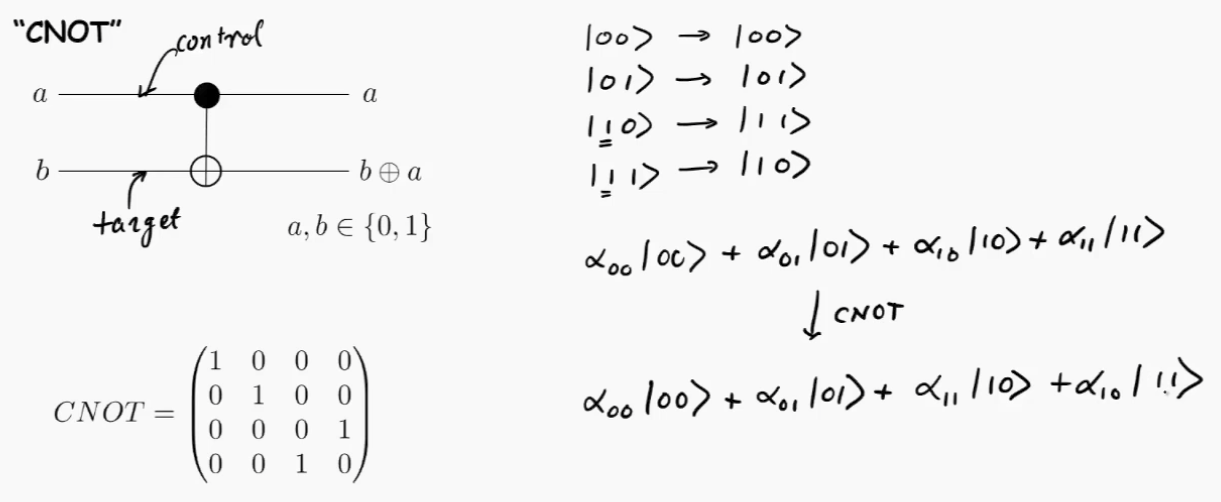
Strange?

@JavaFXpert

@JohanVos

Java-based quantum simulator

Exploring the quantum simulator

@JavaFXpert

@JohanVos

e.g. visualize states of multiple qubits: |00>

from Lecture 2: Overview of quantum information by John Watrous, University of Calgary

open in Quirk quantum circuit simulator

Exploring the quantum simulator

@JavaFXpert

@JohanVos

e.g. visualize states of multiple qubits: |01>

from Lecture 2: Overview of quantum information by John Watrous, University of Calgary

open in Quirk quantum circuit simulator

Simple quantum circuit

@JavaFXpert

@JohanVos

collapses to 8 random states with equal probability

open in Quirk quantum circuit simulator

Quantum superpositions

and observability

http://dilbert.com/strip/2012-04-17

@JavaFXpert

@JohanVos

Measuring qubits

@JavaFXpert

@JohanVos

The Mathematics of Quantum Computers | PBS Infinite Series

collapses to a basis state, discarding superposition

Measuring quantum state

@JavaFXpert

@JohanVos

a Java analogy

from an IndicThreads slide deck

Measuring quantum state

@JavaFXpert

@JohanVos

Hitchhiker's Guide to the Galaxy analogy

Deep Thought after 7.5 million years of calculation

Concepts we'll address today

Introduction to quantum computing

Representing qubits

Axioms of quantum mechanics

Superposition principle
Measurement
Unitary evolution

Quantum computing algorithms

Quantum entanglement

More algorithms

Supplementary resources

@JavaFXpert

@JohanVos

Deutsch's algorithm (1985)

Literally the Hello World of quantum algorithms

@JavaFXpert

Lecture 4: Quantum Teleportation; Deutsch’s Algorithm by John Watrous, University of Calgary

Deutsch's algorithm

Determine if function is constant or balanced

Input a	Constant f(a)	Constant f(a)	Balanced f(a)	Balanced f(a)
0	0	1	0	1
1	0	1	1	0

@JavaFXpert

Lecture 4: Quantum Teleportation; Deutsch’s Algorithm by John Watrous, University of Calgary

Deutsch's algorithm

How many queries of the oracle to solve?

Classical:

This oracle requires 2 queries classically

Quantum:

We create a superposition of inputs to the oracle for constructive/destructive interference.

@JavaFXpert

1

2

Querying the oracle classically

@JavaFXpert

\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}

\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}

\vert01\rangle

\vert01\rangle

\vert11\rangle

\vert11\rangle

example: f (0) = 0 and f (1) = 1 balanced

Quantum parallelism

what is it, really?

@JavaFXpert

Double-slit experiment

constructive and destructive interference

@JavaFXpert

Text

Wikimedia commons Two-Slit_Experiment_Light

Choreographing interference

to increase the chance of getting the right answer

@JavaFXpert

Text

Excerpts from “THE TALK” by Scott Aaronson and Zach Weinersmith

Querying the oracle quantumly

@JavaFXpert

\begin{bmatrix} +\frac{1}{2} & +\frac{1}{2} & +\frac{1}{2} & +\frac{1}{2} \\ +\frac{1}{2} & -\frac{1}{2} & +\frac{1}{2} & -\frac{1}{2} \\ +\frac{1}{2} & +\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ +\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & +\frac{1}{2} \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} +\frac{1}{2} \\ +\frac{1}{2} \\ -\frac{1}{2} \\ -\frac{1}{2} \end{bmatrix}

\begin{bmatrix} +\frac{1}{2} & +\frac{1}{2} & +\frac{1}{2} & +\frac{1}{2} \\ +\frac{1}{2} & -\frac{1}{2} & +\frac{1}{2} & -\frac{1}{2} \\ +\frac{1}{2} & +\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ +\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & +\frac{1}{2} \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} +\frac{1}{2} \\ +\frac{1}{2} \\ -\frac{1}{2} \\ -\frac{1}{2} \end{bmatrix}

example: f (0) = 0 and f (1) = 1 balanced

\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} +\frac{1}{2} \\ +\frac{1}{2} \\ -\frac{1}{2} \\ -\frac{1}{2} \end{bmatrix} = \begin{bmatrix} +\frac{1}{2} \\ -\frac{1}{2} \\ -\frac{1}{2} \\ +\frac{1}{2} \end{bmatrix}

\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} +\frac{1}{2} \\ +\frac{1}{2} \\ -\frac{1}{2} \\ -\frac{1}{2} \end{bmatrix} = \begin{bmatrix} +\frac{1}{2} \\ -\frac{1}{2} \\ -\frac{1}{2} \\ +\frac{1}{2} \end{bmatrix}

\begin{bmatrix} +\frac{1}{2} & +\frac{1}{2} & +\frac{1}{2} & +\frac{1}{2} \\ +\frac{1}{2} & -\frac{1}{2} & +\frac{1}{2} & -\frac{1}{2} \\ +\frac{1}{2} & +\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ +\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & +\frac{1}{2} \end{bmatrix} \cdot \begin{bmatrix} +\frac{1}{2} \\ -\frac{1}{2} \\ -\frac{1}{2} \\ +\frac{1}{2} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}