6o Congreso Internacional de Matemática Educativa
Ciudad de México, 31 Ago - 11 Sept


Juan Carlos Ponce Campuzano

jcponce.com



Juan Carlos Ponce Campuzano

jcponce.com



Juan Carlos Ponce Campuzano

jcponce.com

Diseño de applets interactivos y actividades para el aprendizaje y enseñanza de las matemáticas


Construcción De Cónicas Como Envolventes De Familias De Rectas:
Una Exploración Geométrica Y Dinámica Usando Geogebra
6o Congreso Internacional de Matemática Educativa
Ciudad de México, 31 Ago - 11 Sept
Juan Carlos Ponce Campuzano
jcponce.com

Contenido
- Cónicas y su estudio en nivel preparatoria.
- Construcción de cónicas como envolventes de líneas rectas usando GeoGebra.
- Propuestas didácticas con el uso de GeoGebra.
- GeoGebra Classroom
- Comentarios finales
1. Cónicas y su estudio en nivel preparatoria
Una sección cónica se le denomina la curva resultante de la intersección entre un cono y un plano.
1. Cónicas y su estudio en nivel preparatoria
Su estudio en la preparatoria se aborda usualmente como lugar geométrico y con su ecuación general:
Parábola
El lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco, y de una recta llamada directriz.
\((y-h)^2 = 2p(x-h)^2\), con centro \((h,k)\).
Lugar geométrico
Ecuación
1. Cónicas y su estudio en nivel preparatoria
Su estudio en la preparatoria se aborda usualmente como lugar geométrico y con su ecuación general:
Elipse
El lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es una constante positiva.
\(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\), con centro \((h,k)\).
Lugar geométrico
Ecuación
1. Cónicas y su estudio en nivel preparatoria
Su estudio en la preparatoria se aborda usualmente como lugar geométrico y con su ecuación genereal:
Hipérbola
El lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos, llamados focos, es constante y menor que la distancia entre los focos.
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\), con centro \((h,k)\).
Lugar geométrico
Ecuación
1. Cónicas y su estudio en nivel preparatoria
¿Es posible abordar las cónicas de otra forma?
2. Cónicas como envolventes de líneas rectas usando Geogebra
A partir de construcciones geométricas sencillas podemos generar
- Parábolas
- Ellipses
- Hipérbolas

Parábola
Considera un punto A, una recta y un punto D que se mueve sobre la recta dada. Traza las mediatrices de A y D.
2. Cónicas como envolventes de líneas rectas usando Geogebra
Elipse
Considera ahora un círculo, un punto C (adentro del círculo) y D que se mueva sobre la circunferencia. Traza las mediatrices del punto C y D.
2. Cónicas como envolventes de líneas rectas usando Geogebra
Hipérbola
Considera ahora un círculo, un punto C (afuera del círculo) y D que se mueva sobre la circunferencia. Traza las mediatrices del punto C y D.
2. Cónicas como envolventes de líneas rectas usando Geogebra
Elipse
2. Cónicas como envolventes de líneas rectas usando Geogebra

CE + EA = constante
AD = EA + ED
= EA + CE
Hipérbola
2. Cónicas como envolventes de líneas rectas usando Geogebra

EA - EC = constante
AD = EA - ED
= EA - EC
¿Cómo podemos aprovechar estas construcciones en el salón de clases?
2. Cónicas como envolventes de líneas rectas usando Geogebra
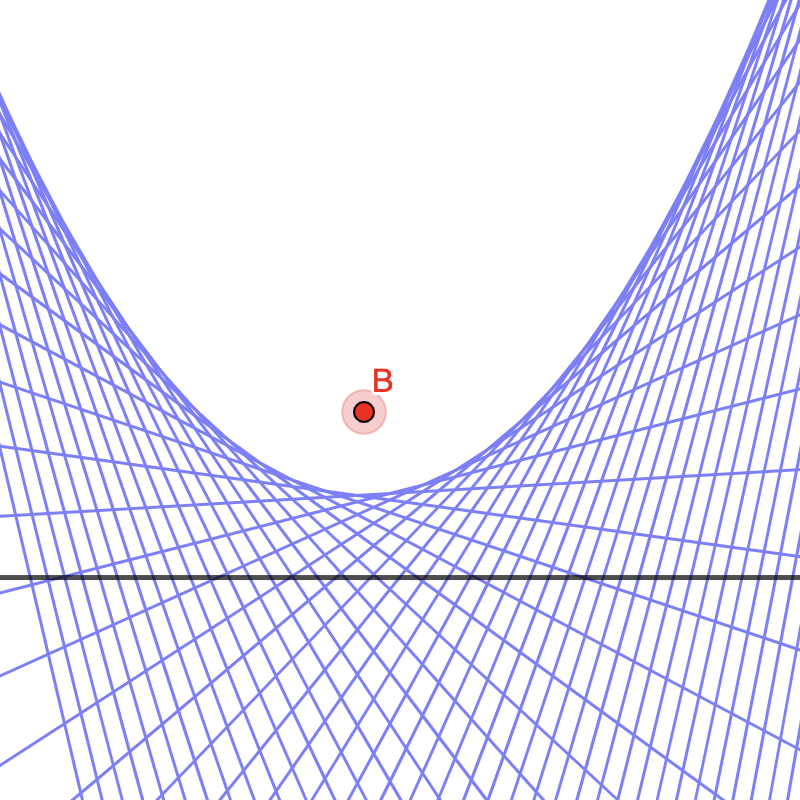
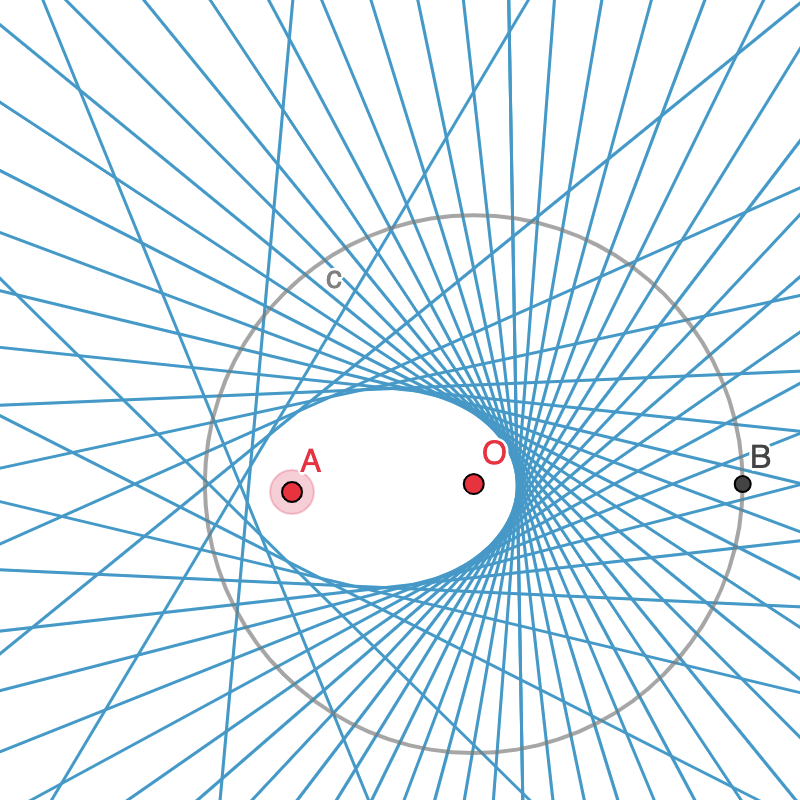

Tecnologías digitales tales como GeoGebra
3. Propuestas didácticas con el uso de GeoGebra
Actividad 1:
Dada una recta y un punto A que no esté sobre la recta, ¿cómo se puede trazar un círculo tangente a la recta que pase por el punto A?
¿Qué significa que una línea recta sea tangente a un círculo?
3. Propuestas didácticas con el uso de GeoGebra
¿Qué significa que una línea recta sea tangente a un círculo?
- Describe los casos que observas al mover el círculo.
- ¿Qué propiedad existe entre la tangente y el radio del círculo?
Exploración preliminar
3. Propuestas didácticas con el uso de GeoGebra
Actividad 1:
Dada una recta y un punto A que no esté sobre la recta, ¿cómo se puede trazar un círculo tangente a la recta que pase por el punto A?
3. Propuestas didácticas con el uso de GeoGebra
Actividad 2:
Dada una recta y un círculo con centro O arbitrarios, ¿cómo se puede trazar un círculo (o más) tangente a la recta y al círculo dados?
¿Qué significa que una dos círculos sean tangentes entre sí?
3. Propuestas didácticas con el uso de GeoGebra
¿Qué significa que una dos círculos sean tangentes entre sí?
Exploración preliminar
- Describe los casos que observas al mover el círculo.
- ¿Qué propiedad existe entre la tangente y los radios de los círculos?
3. Propuestas didácticas con el uso de GeoGebra
Actividad 2:
Dada una recta y un círculo con centro O arbitrarios, ¿cómo se puede trazar un círculo (o más) tangente a la recta y al círculo dados?
4. GeoGebra Classroom

¿Cómo podemos aprovechar las herramientas digitales para la educación remota?
4. GeoGebra Classroom
¿Qué es GeoGebra Classroom?
Es una plataforma virtual con la cual
podemos:
- asignar tareas interactivas y atractivas para estudiantes
- ver el progreso actualizado en vivo de los estudiantes que trabajan en una tarea específica
- hacer preguntas a toda la clase y ver todas las respuestas de los estudiantes al instante
- facilitar discusiones enriquecedoras e interactivas entre todos los estudiantes, grupos de estudiantes y de forma individual.
4. GeoGebra Classroom

¿Cómo funciona GeoGebra Classroom?
Comentarios Finales
-
Construcción de cónicas por medio de rectas
- Propuestas didácticas usando geometría dinámica: GeoGebra
- GeoGebra Classroom como una herramienta potencial para la educación remota
Comentarios Finales

Poderosa herramienta digital para
la enseñanza y el estudio de
las matemáticas forma dinámica,
desde nivel básico hasta nivel universitario.
Comentarios Finales
Es gratuita y cuenta con cientos de tutoriales y actividades pre diseñadas.
Comentarios Finales
Comunidad latinoamericana dedicada a la creación, curación y difusión de tutoriales y actividades para la enseñanza y aprendizaje de las matemáticas.
La belleza de las matemáticas solo se muestra a los seguidores más pacientes.
Maryam Mirzakhani