Open-source online tools to visualise and explore complex functions

with domain colouring 🌈

Juan Carlos Ponce Campuzano

 

  1. What is domain colouring?
  2. How can it be implemented in the computer?
  3. How can we use it to explore complex functions?
  4. Open-source online tools

 

Complex functions

f:\mathbb C \rightarrow \mathbb C

live in a 4-dimensional space

🤔

Methods to visualize complex functions

- Domain colouring

- Real and Imaginary components

- Analytic Landscapes

- Mappings

😃

Domain colouring

  1. Assign a colour to every point in the complex plane.
  2. Colour the domain of \(f\) by painting the location \(z\) with the colour determined by the value \(f(z)\).

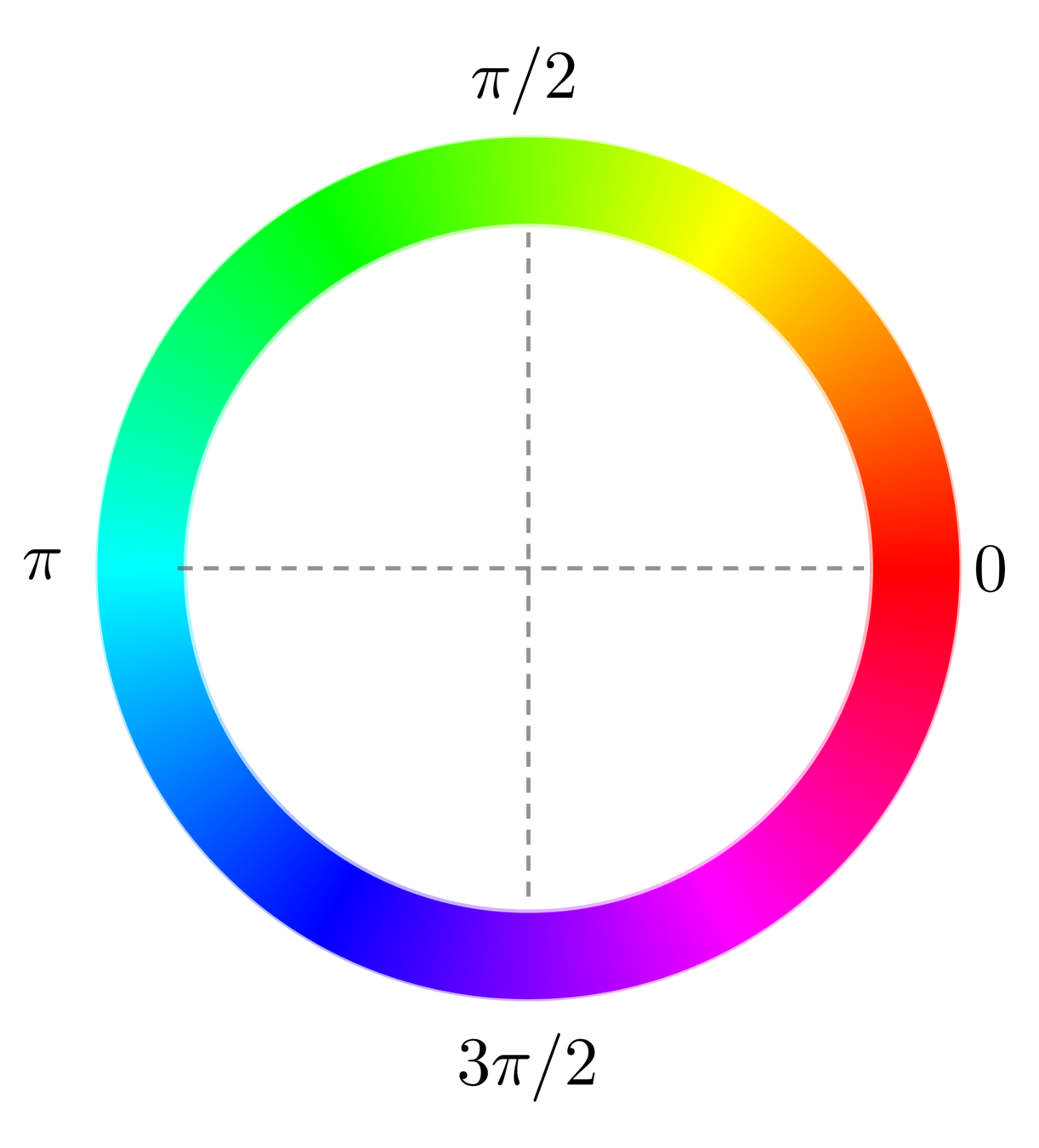
The colour wheel

  • H = Phase
  • S = 1
  • B = 1

Hue , Saturation & Brightness

(HSB) 

Implementation in the computer

- Phase portraits

- Enhanced Phase portraits

Domain colouring

Basic Examples

Phase portraits

Phase portrait

f(z)=z\\ [-2,2] \times [-2,2]

Phase portrait

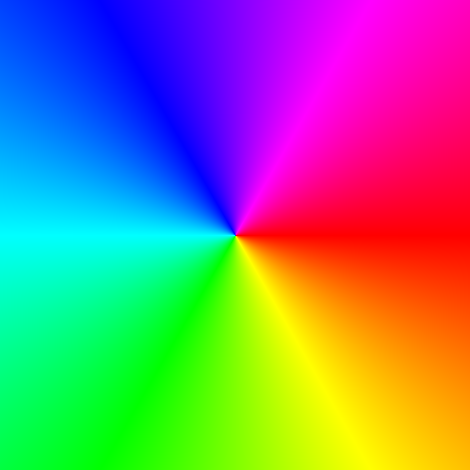
f(z)=\dfrac{1}{z}\\ [-2,2] \times [-2,2]

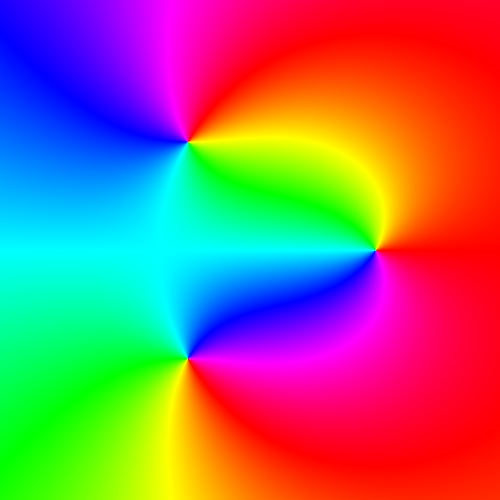
Phase portrait

f(z)=\dfrac{z-1}{z^2+z+1}\\ [-2,2] \times [-2,2]

Enhanced phase portraits

  • H = Phase
  • S = 1
  • B = \(\log\big|f\big|- \lfloor \log |f| \rfloor\)

Elias Wegert's work from 2012

=\text{Phase}-\lfloor \text{Phase} \rfloor

Enhanced phase portraits: Level curves

f(z)=z

Phase

Modulus

Enhanced phase portraits: Level curves

f(z)=z

Phase

Modulus

Combined

Enhanced phase portraits: Modulus

f(z)=z
f(z)=1/z

Enhanced phase portraits:

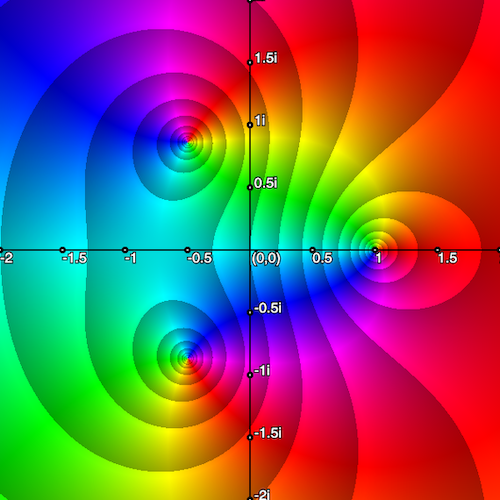
\(f(z)=\dfrac{z-1}{z^2+z+1}\)

www.dynamicmath.xyz/domain-coloring/

Online tools

Thank you!

Online resources:

https://www.dynamicmath.xyz/domain-coloring/

Contact:

j.ponce@uq.edu.au

Slides: reveal.js