Visualization of Complex Functions
Domain Coloring

\(\theta=\text{phase}\)
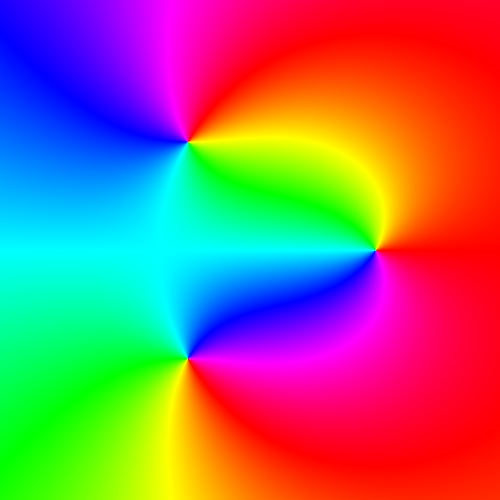
Complex functions are not easy to visualize
compared to functions of real variable:
\(\mathbb R=\) Set of real numbers
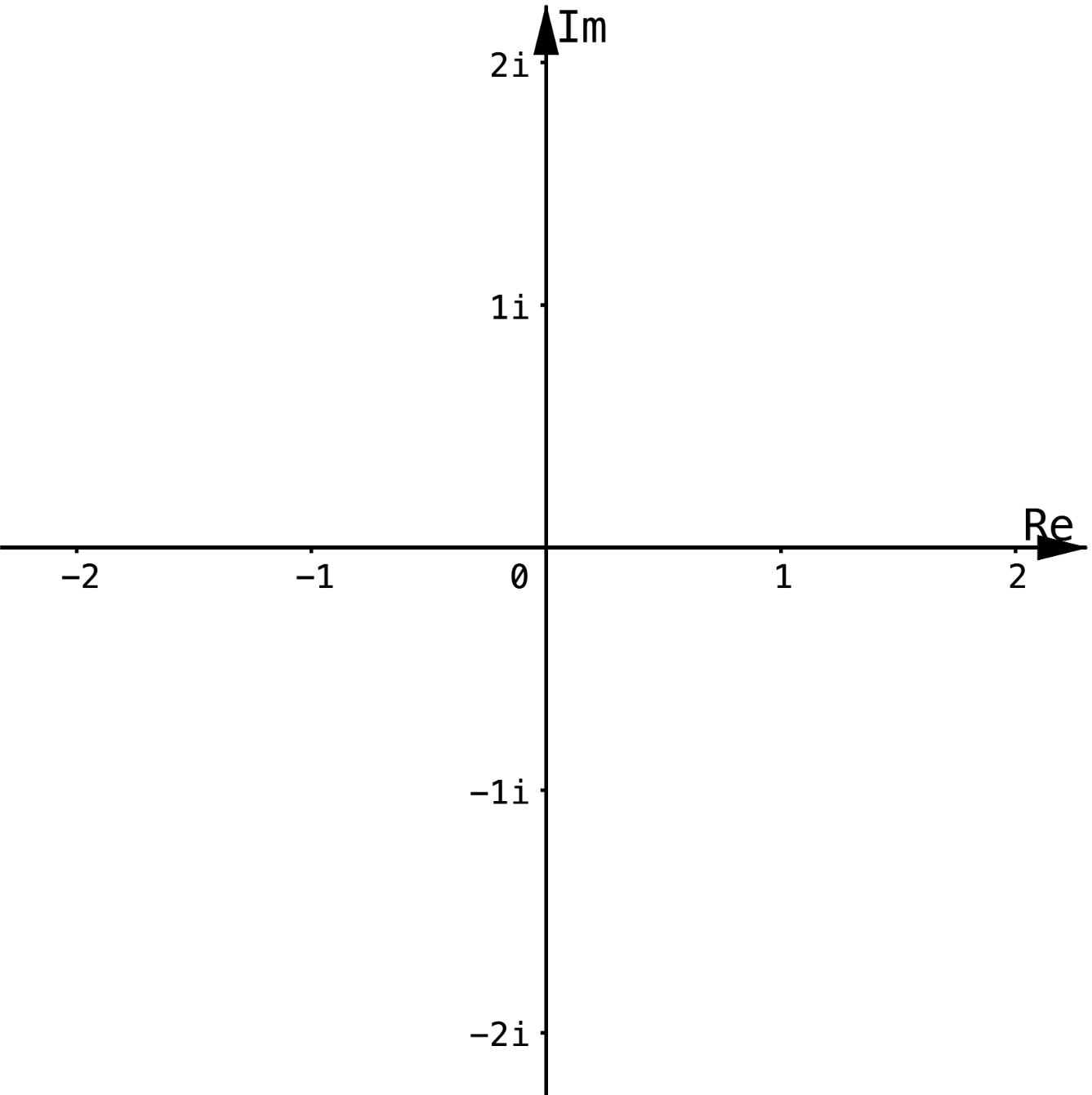
For \(z\in \mathbb C,\)
then \(z=x+iy.\)
Real
component
Imaginary
component
So the plot of a complex function \(f\) lives in a four-dimensional space.
The output \(\,f(z)\)
For \(z\in \mathbb C,\)
then \(z=x+iy.\)
real and imaginary components.
has also
\(=u+iv\)
\(\in \mathbb C\,\)
So the plot of a complex function \(f\) lives in a four-dimensional space.
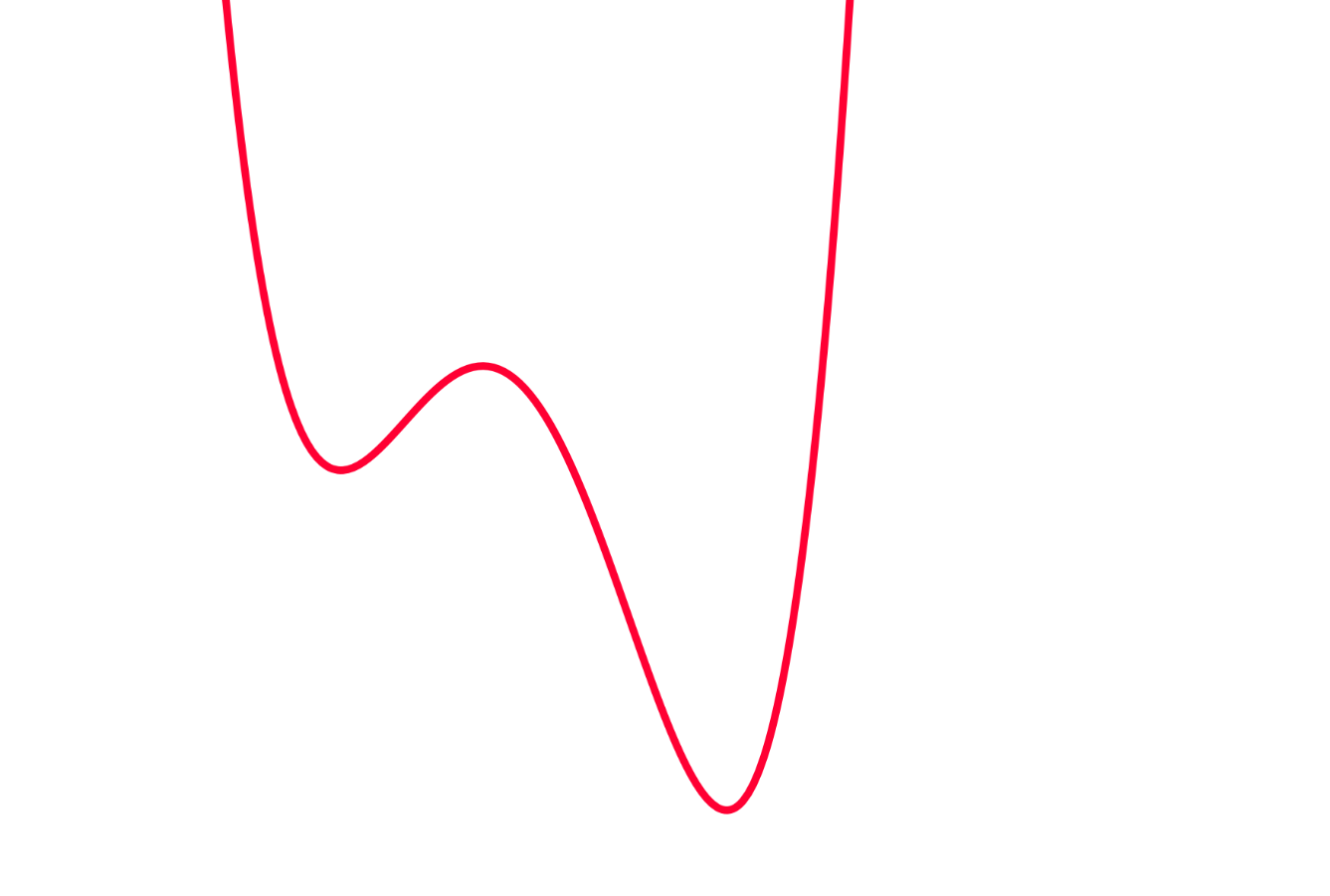
We can use what we know about plotting functions of real variables:
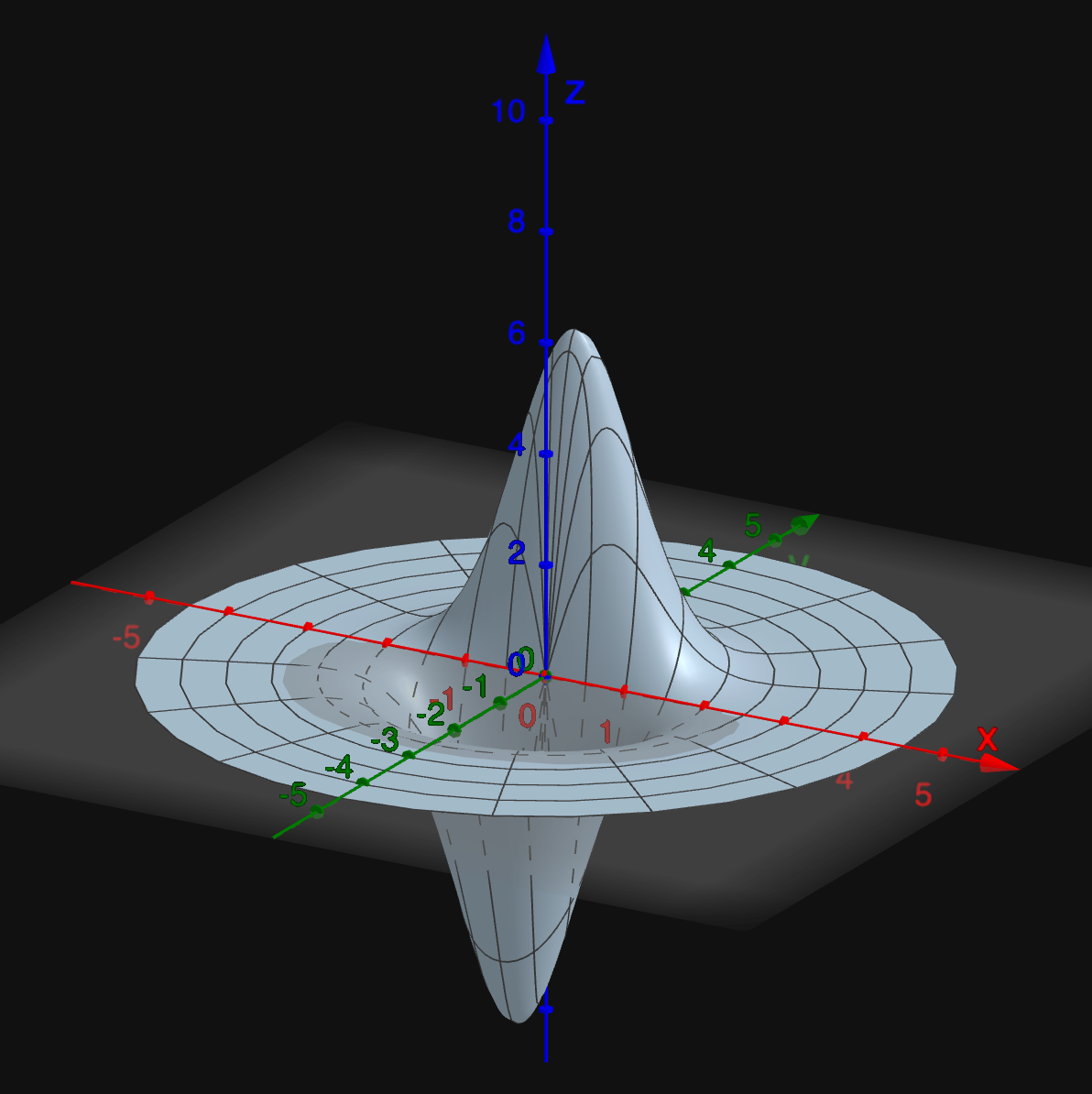
Good News!

Methods to visualize complex functions
Plotting Real and Imaginary components
-
Analytic landscapes
-
Mappings
-
Domain coloring
-
Methods to visualize complex functions
Plotting Real and Imaginary components
-
Analytic landscapes
-
Mappings
-
-
Domain coloring

What is domain coloring?
A technique for visualizing complex functions by assigning a color to each point of the complex plane.
Proposed by Frank Farris in the 90s as an alternative way to explore geometric properties of complex functions.
- Assign a color to every point in the complex plane.
- Color the domain of \(f\) by painting the location \(z\) with the color determined by the value \(f(z)\).
How does domain coloring work?
Color the domain of \(f\) by painting the location \(z\) with the color determined by the value \(f(z)\).
How does domain coloring work?
Color the domain of \(f\) by painting the location \(z\) with the color determined by the value \(f(z)\).
How does domain coloring work?
Color the domain of \(f\) by painting the location \(z\) with the color determined by the value \(f(z)\).

Hue
How does domain coloring work?
Color the domain of \(f\) by painting the location \(z\) with the color determined by the value \(f(z)\).

How does domain coloring work?
Color the domain of \(f\) by painting the location \(z\) with the color determined by the value \(f(z)\).

How does domain coloring work?

How does domain coloring work?
The identity function
Color represents
\(\theta=\text{phase of }z\)

Assign a color to every point in the complex plane.

Domain coloring

The identity function
Color represents
\(\theta=\text{phase of }z\)
Phase Portraits


Basic examples: Phase Portraits


Basic examples: Phase Portraits


Basic examples: Phase Portraits




Basic examples: Phase Portraits


Rational function
Basic examples: Phase Portraits


Note that \(f(1)=0.\)
\(z_0=1\) is a zero/root of \(f.\)
Also \(f\) is undefined at
\[z_1=\frac{-1+i\sqrt{3}}{2},\;z_2=\frac{-1-i\sqrt{3}}{2}.\]
\(z_1,z_2\;\) are poles of \(f.\)
Basic examples: Phase Portraits


To locate Zeros and Poles
we just need to look at where all
the colors meet!

Basic examples: Phase Portraits


it becomes difficult to determine which points are Zeros or Poles.

If we do not know the expression defining the function \(f,\)

Enhanced Phase Portraits



We can solve this issue by introducing the level curves of the modulus \(|f(z)|.\)
Enhanced Phase Portraits
Recall we used Hue \(\leftrightarrow\) Phase

\(0\)
\(\pi/2\)
\(\pi\)
\(3\pi/2\)
\(2\pi\)
Enhanced Phase Portraits
Recall we used Hue \(\rightarrow\) Phase


\(0\)
\(\pi/2\)
\(\pi\)
\(3\pi/2\)
\(0\)
\(\pi/2\)
\(\pi\)
\(3\pi/2\)
\(2\pi\)
The color wheel
Enhanced Phase Portraits
Recall we used Hue \(\rightarrow\) Phase

\(0\)
\(\pi/2\)
\(\pi\)
\(3\pi/2\)
The color wheel
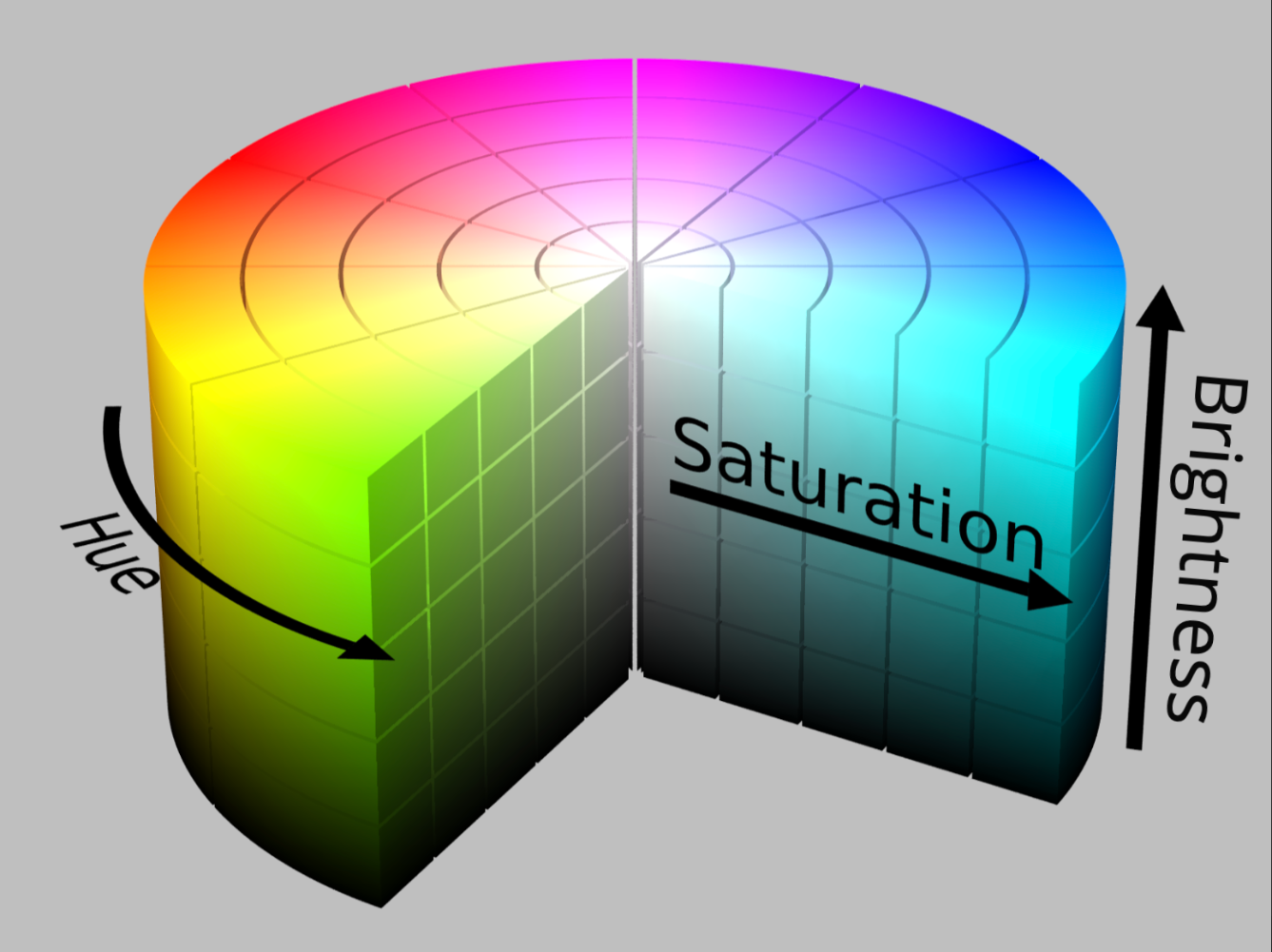
HSB scheme
- H = Phase
Hue
Enhanced Phase Portraits

, Saturation
- B = 1
HSB scheme
& Brightness
- S = 1
- H = Phase
Hue
Enhanced Phase Portraits
\(\log\big|f\big|- \lfloor \log |f| \rfloor\)

, Saturation
- S = 1
- B =
HSB scheme
& Brightness
Enhanced Phase Portraits
Plain
Level curves: modulus




Enhanced Phase Portraits

Level curves: Phase
Plain
B = \(\log\big|f\big|- \lfloor \log |f| \rfloor\)
B = \(\text{Phase}-\lfloor \text{Phase} \rfloor\)
Level curves: modulus


Enhanced Phase Portraits
Combine
B = \(\log\big|f\big|- \lfloor \log |f| \rfloor\)
B = \(\text{Phase}-\lfloor \text{Phase} \rfloor\)



Enhanced Phase Portraits


Level curves: Modulus
Zero at \(z_0=0\)
Pole at \(z_0=0\)
Lighter

Enhanced Phase Portraits


Level curves: Modulus
Zero at \(z_0=0\)
Pole at \(z_0=0\)
Darker

Enhanced Phase Portraits


Level curves: Modulus
Zero at \(z_0=0\)
Pole at \(z_0=0\)
Darker

Enhanced Phase Portraits


Level curves: Modulus
Zero at \(z_0=0\)
Pole at \(z_0=0\)
Lighter

Enhanced Phase Portraits
Plain

There are three points where to colors meet!
Enhanced Phase Portraits
Level curves: Modulus

This is a zero
These are poles

Enhanced Phase Portraits
Level curves: Modulus

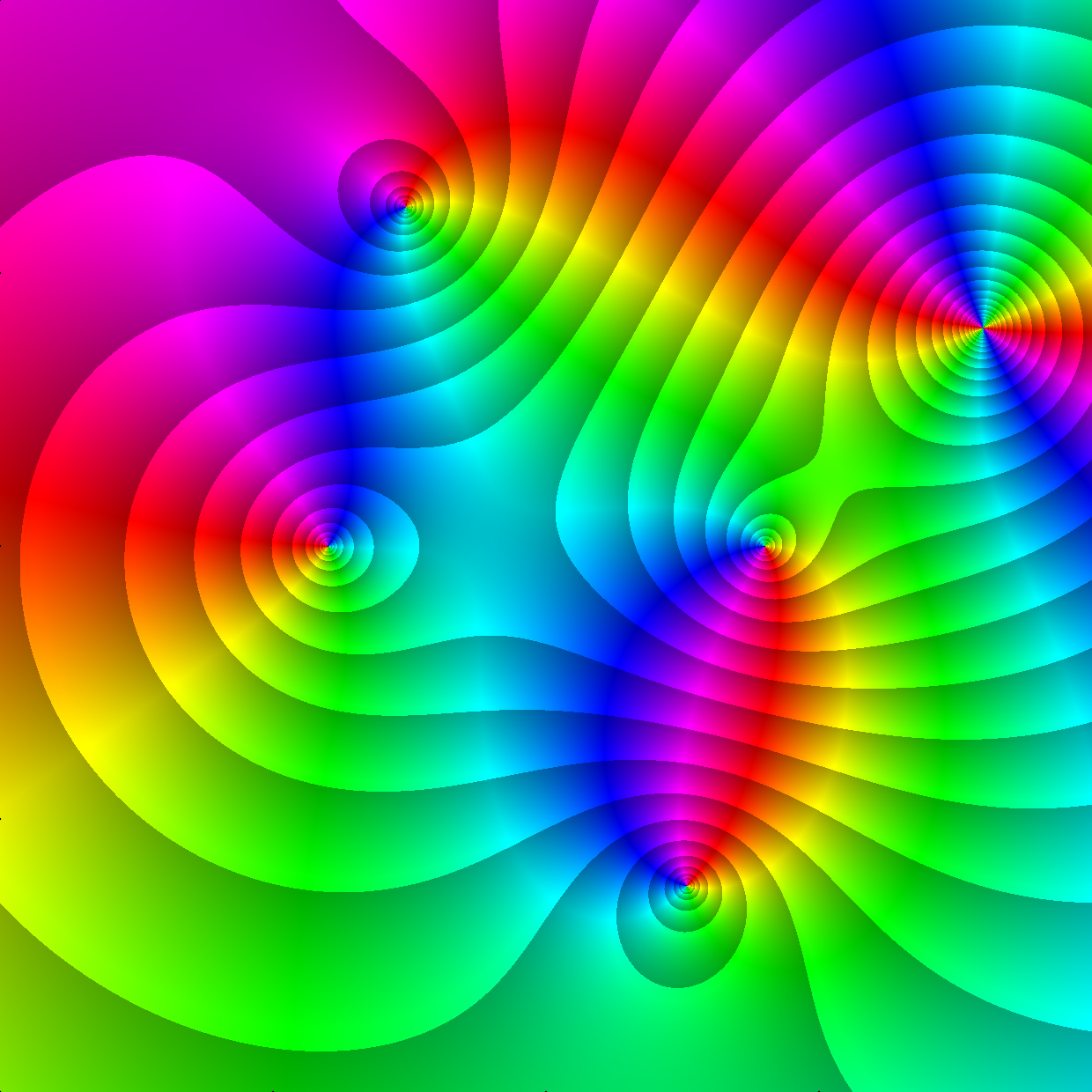
Enhanced Phase Portraits
Level curves: Modulus

Zeros

Enhanced Phase Portraits
Level curves: Modulus

Poles

Enhanced Phase Portraits
Level curves: Modulus


Enhanced Phase Portraits
Level curves: Modulus

3 zeros

Enhanced Phase Portraits
Level curves: Modulus

2 poles

Domain coloring
Visualizing
complex functions
- Zeros & Poles of functions
Enhanced Phase Portraits
- Multiplicity of zeros
- Classification of singularities
- The Fundamental Theorem of Algebra
- Roots of unity

and more...
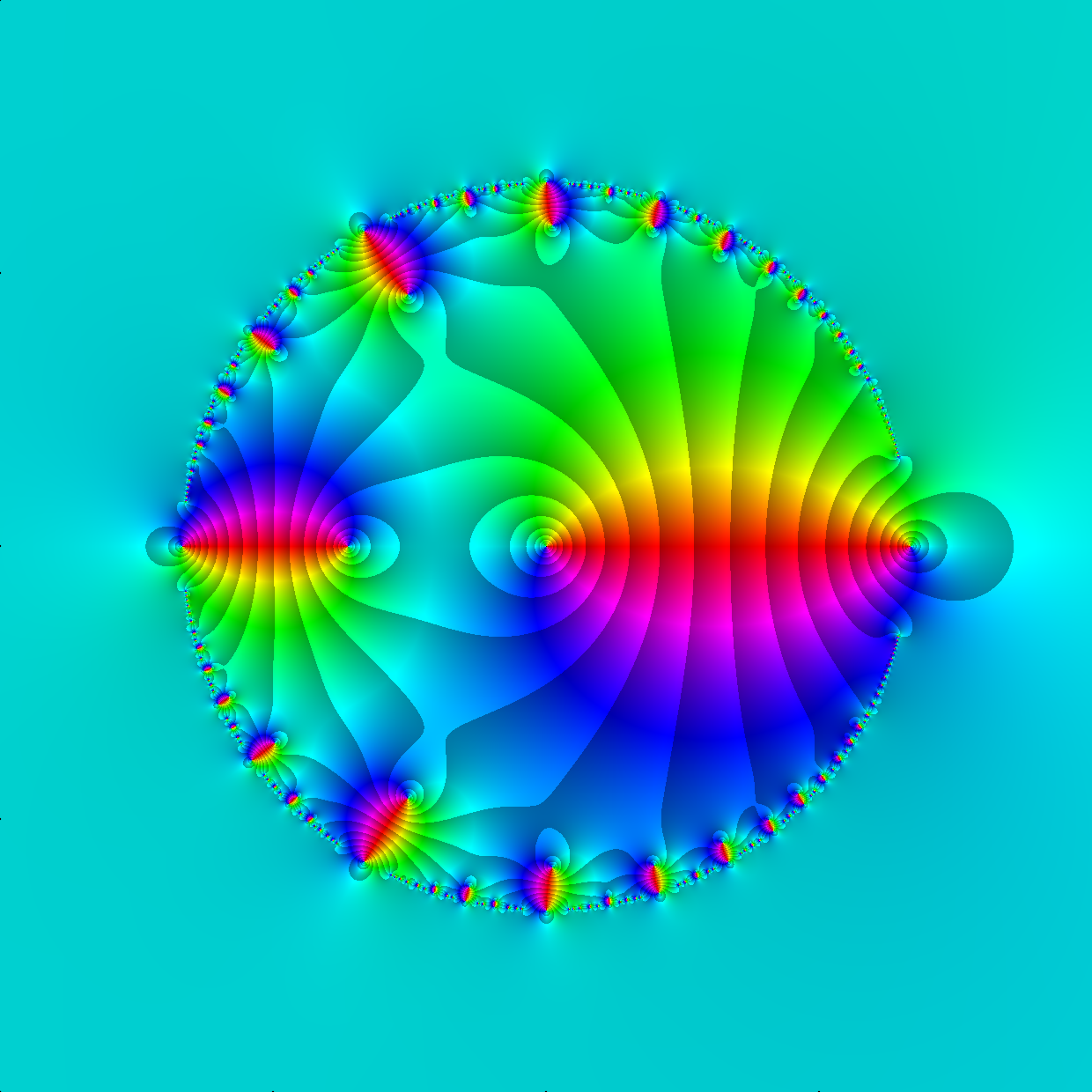

Endless possibilities!
Mathematical Art


\(f(z)=0.926(z+0.073857 z^5+0.0045458 z^9)\)
RGB

B&W

Discrete HSB

Mathematical Art
Other color schemes
Level curves of the real and imaginary components
Mathematical Art
Other color schemes
Hydrodynamics
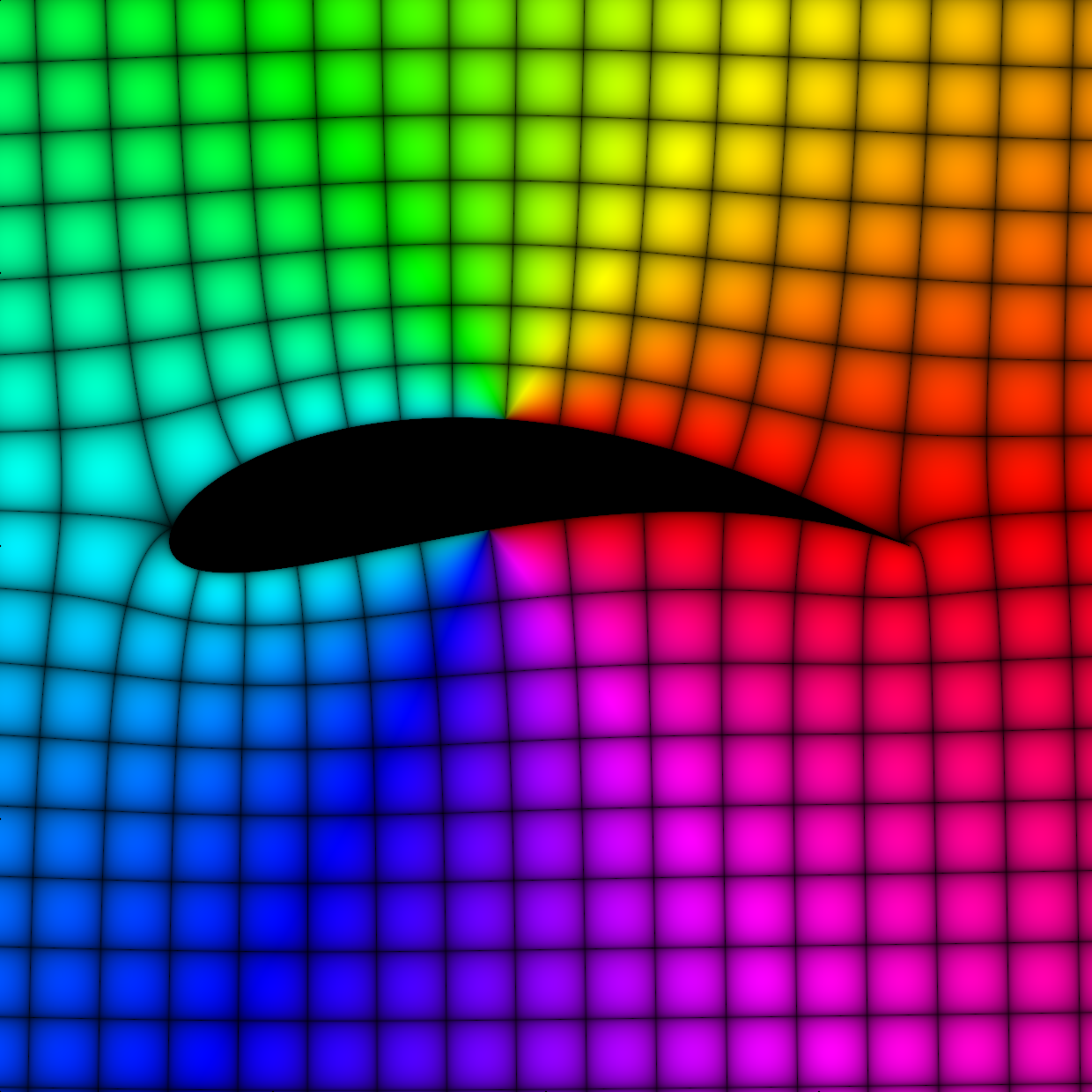
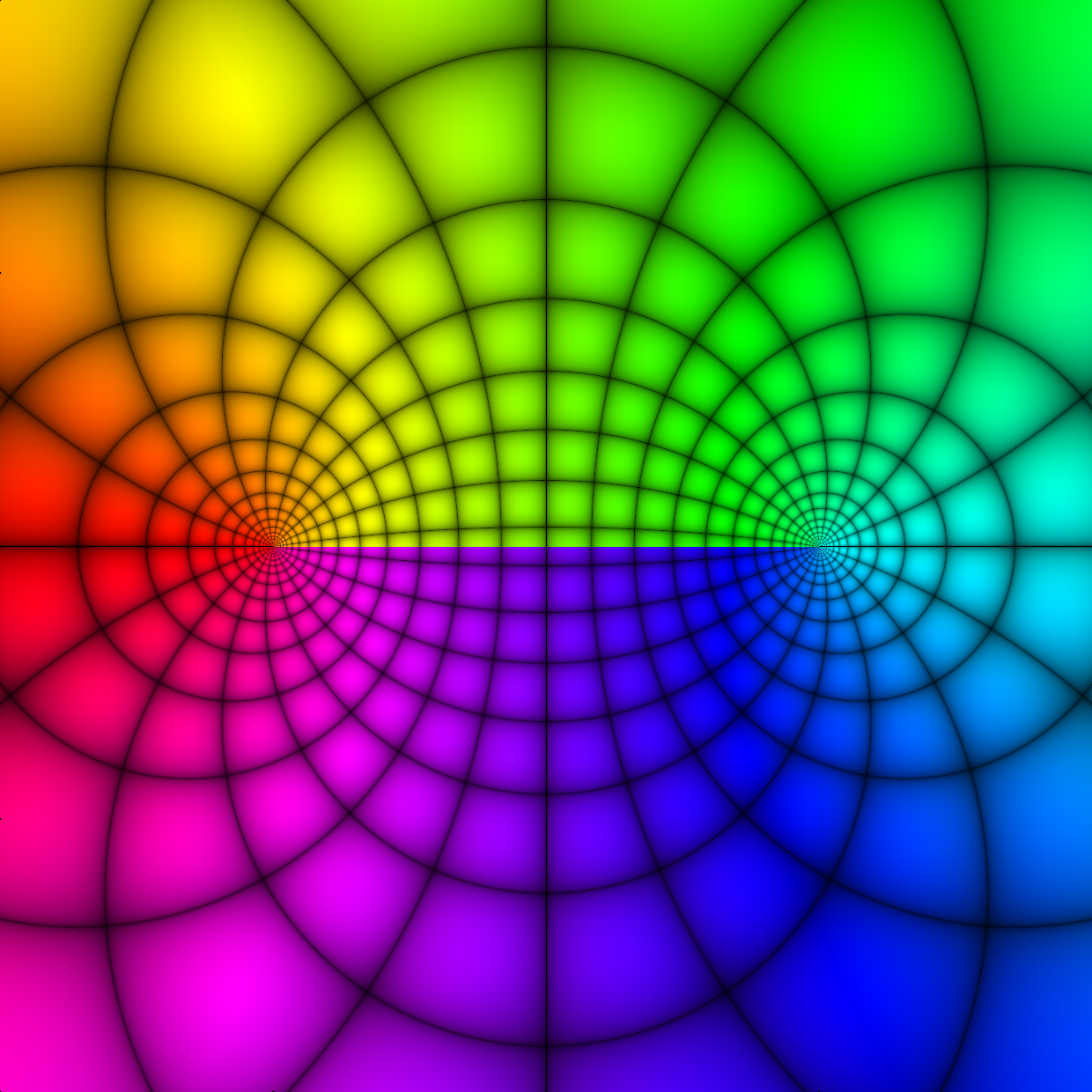
Electric potential
Online tools
www.dynamicmath.xyz
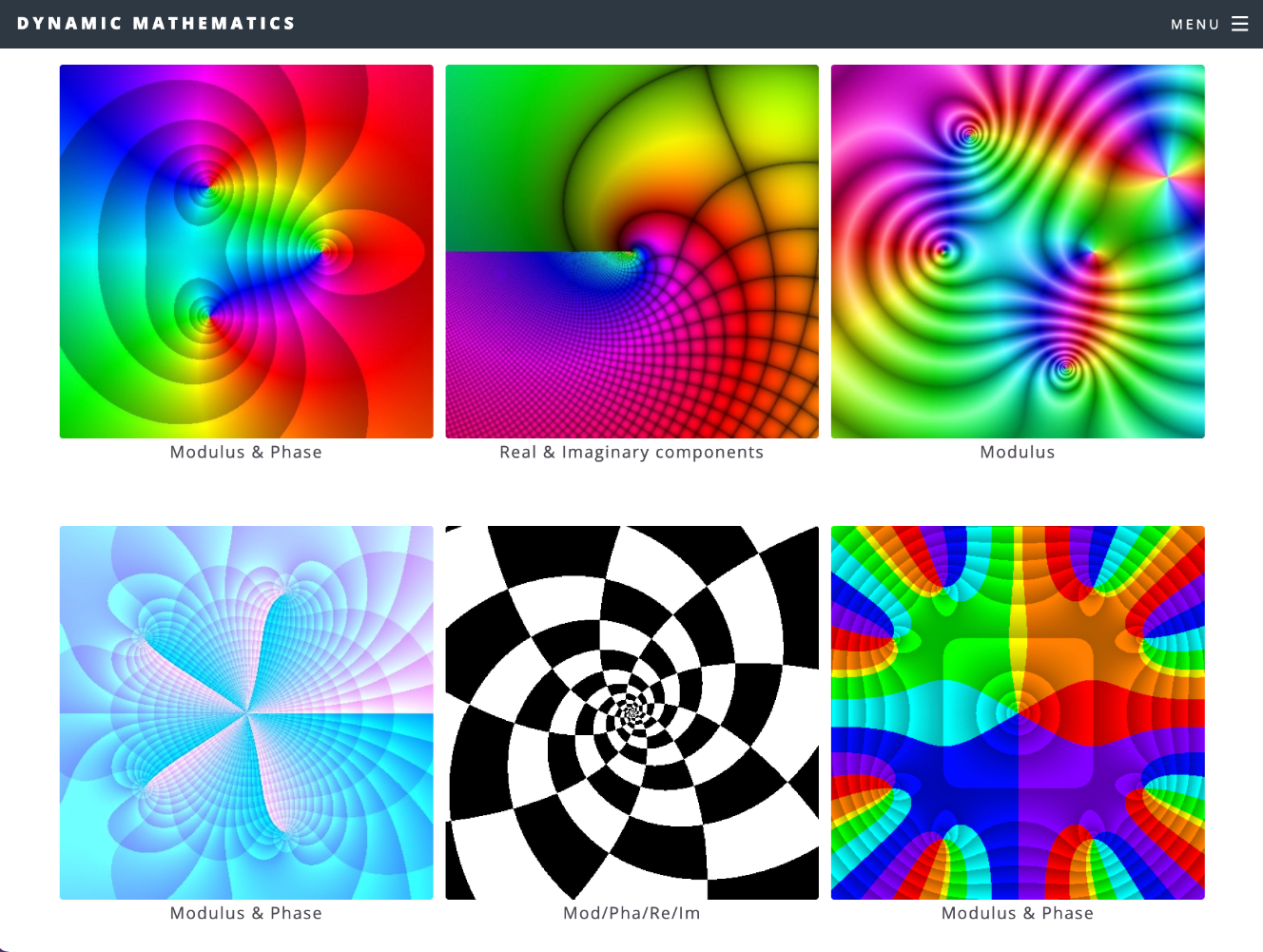


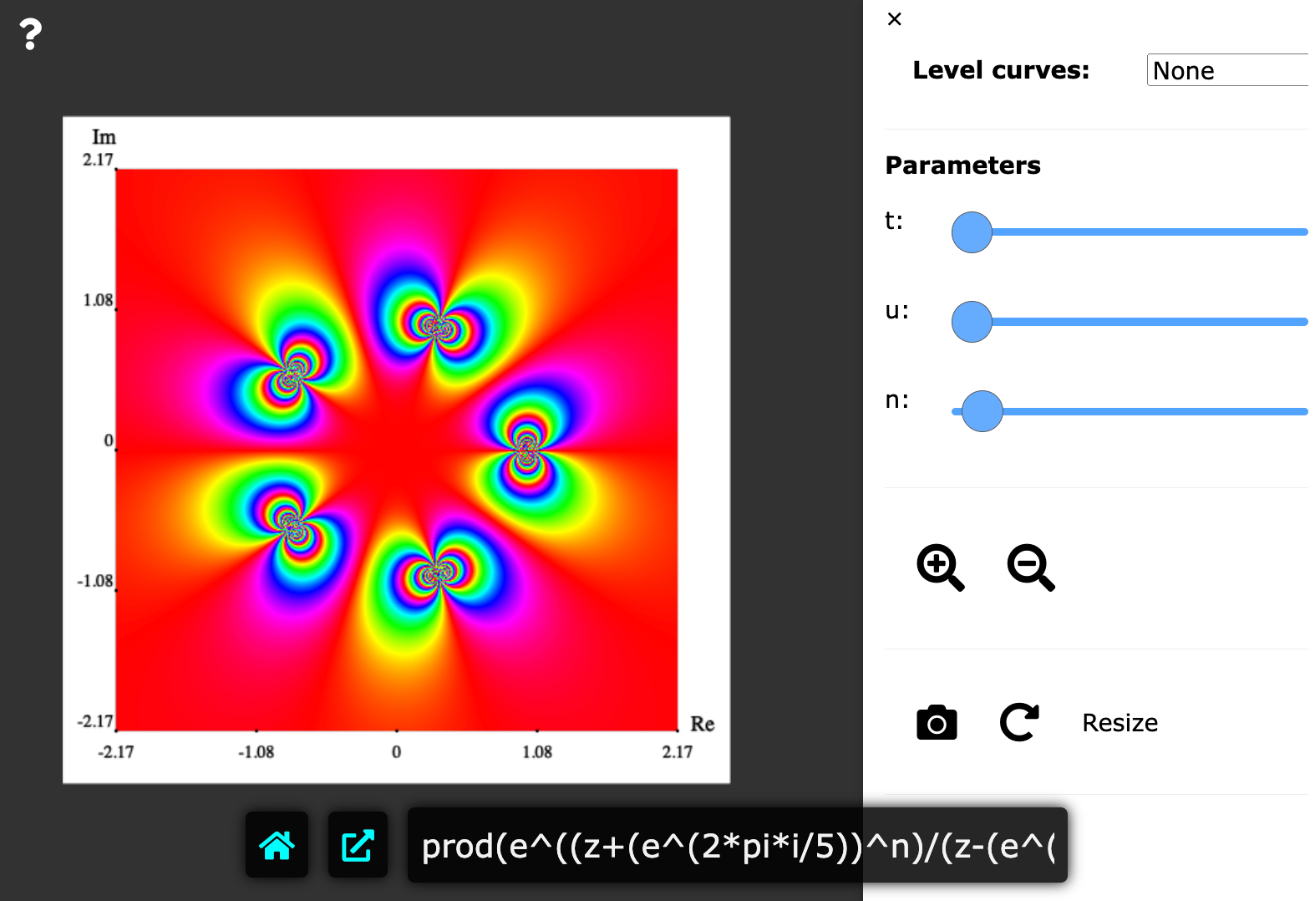
Online tools
www.dynamicmath.xyz


Complex Analysis
A visual and Interactive Introduction
complex-analysis.com
Thanks for
watching!
Patreons:
Ruan Ramon, Miguel Díaz, bleh, Dennis Watson, Doug Kuhlmann, mirror, Newnome Beauton, Adam Parrott, Sophia Wood (Fractal Kitty), pmben, Abei, Edward Huff.

Thanks for
watching!
Patreons:
Ruan Ramon, Miguel Díaz, bleh, Dennis Watson, Doug Kuhlmann, mirror, Newnome Beauton, Adam Parrott, Sophia Wood (Fractal Kitty), pmben, Abei, Edward Huff.

