The mathematical
beauty of epicycles
Juan Carlos Ponce Campuzano

School of Environment and Science
A mysterious curve
The mathematical beauty of epicycles

What are epicycles?
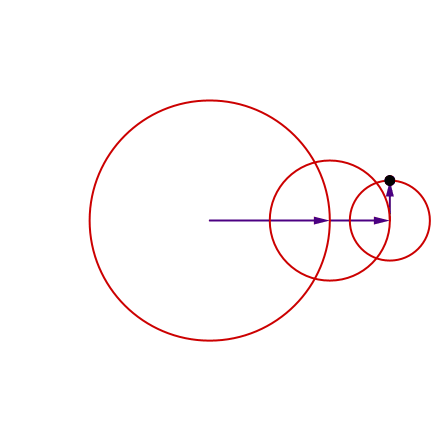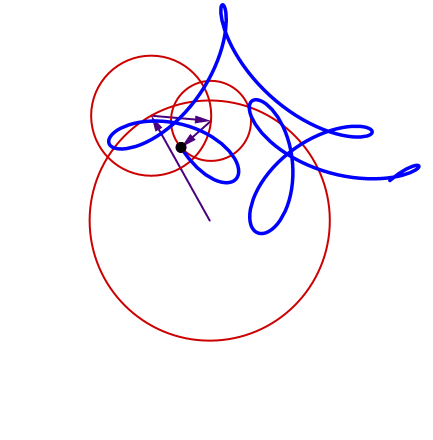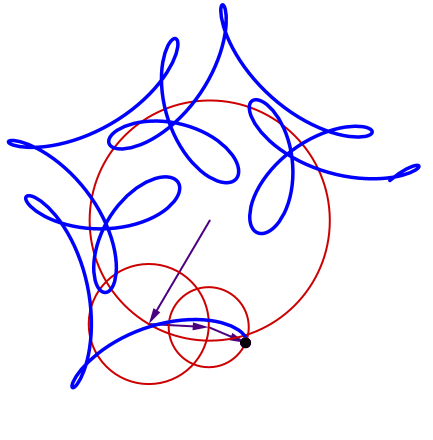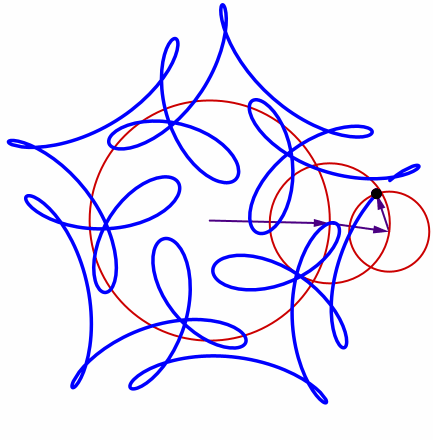
A circle moving on another circle.


What are epicycles?
A circle moving on another circle, on another circle.


What are epicycles?
A circle moving on another circle, on another circle, on another circle...
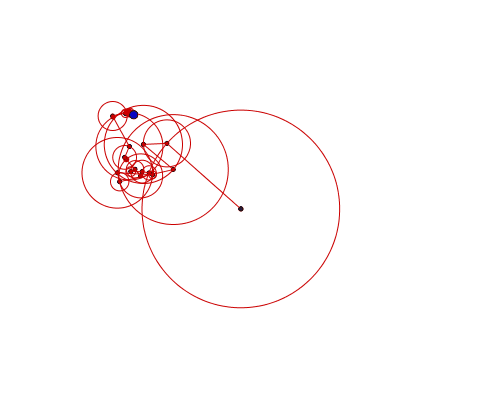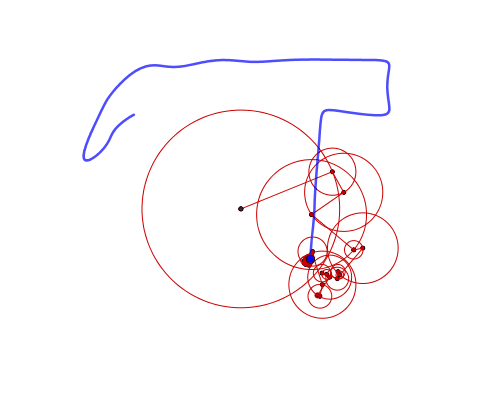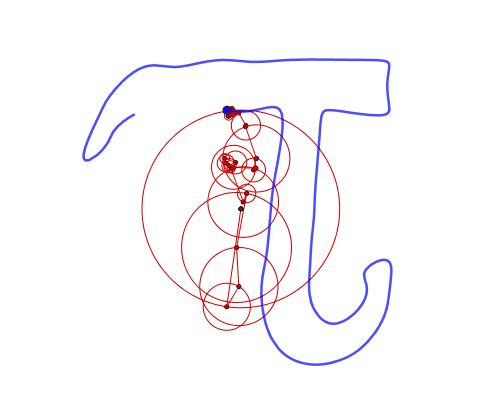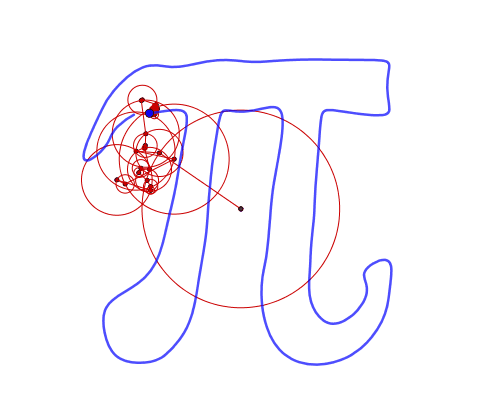

What are epicycles?
How can we represent them mathematically?
A parametric function!

What are epicycles?

🔍
Code:
ABEV FXP8
What are epicycles?
🔍
Work only with
- Simple rotation
- Double rotation

Code:
ABEV FXP8
Simple rotations

Both represent
the same thing!
Simple rotations
\(\sin x\)
Simple rotations
\(\sin x\) and \(\cos x\)
Double rotations

Triple rotations

Triple rotations
👉
Complete last task!
6
-14

Triple rotations
6
-14

Why there is rotational symmetry?
Triple rotations
6
-14

Is this symmetry related to these numbers?

A parametric function with sin and cos functions
What are epicycles?
What are epicycles?
In general we have:
This new symbol \(\phi_k\) indicates how much the disk \(k\) is initially rotated at time \(t = 0\), and we called a phase offset.
What are epicycles?
If we do not specify a phase offset, we can only describe epicycles where the circles start aligned.
\(\phi_k\) is called a phase offset

mysterious curve
Remember our
mysterious curve

How can we determine the epicycles for our mysterious curve?

mysterious curve


- \(R_1, R_2, R_3\) are positive real numbers
- \(\omega_1, \omega_2, \omega_3\) are integers (\(\ldots,-2,-1,0,1,2,\ldots\))
How can we determine the epicycles for our mysterious curve?

It is going to get complex!


It is going to get complex!


It is going to get complex!


It is going to get complex!


The mysterious curve

The mysterious curve
Using properties of complex numbers:
\(i\cdot i = -1\)

More mystery curves

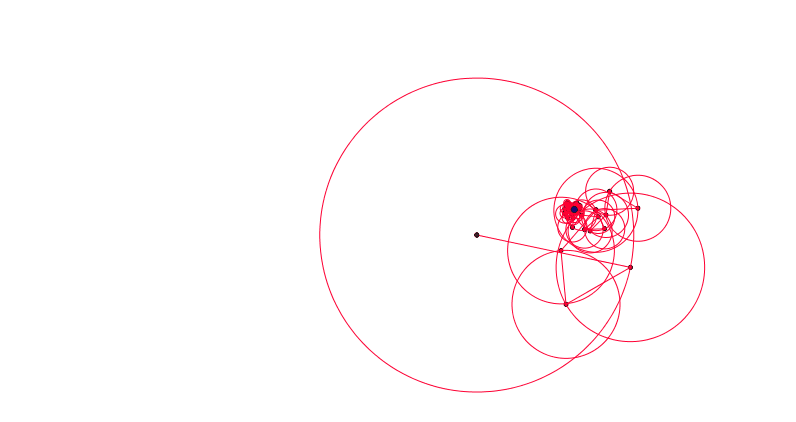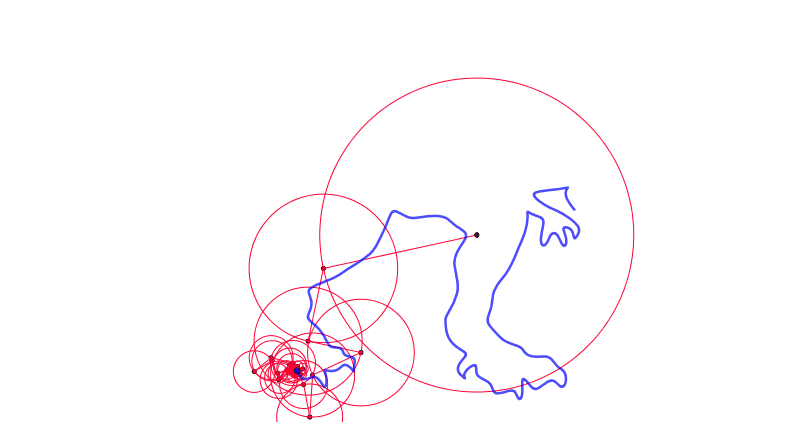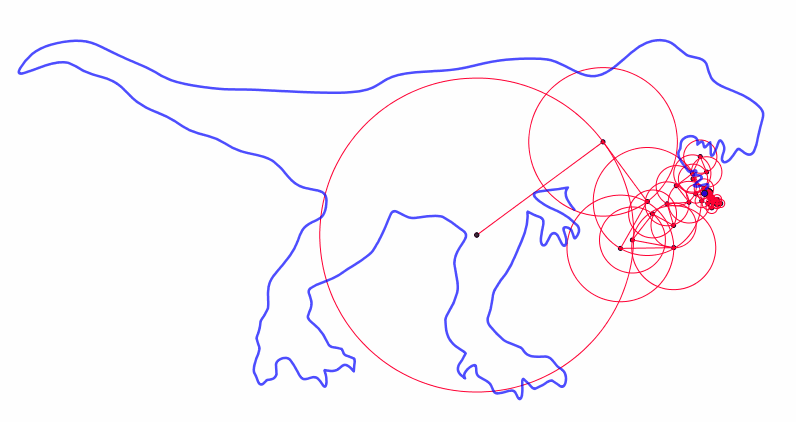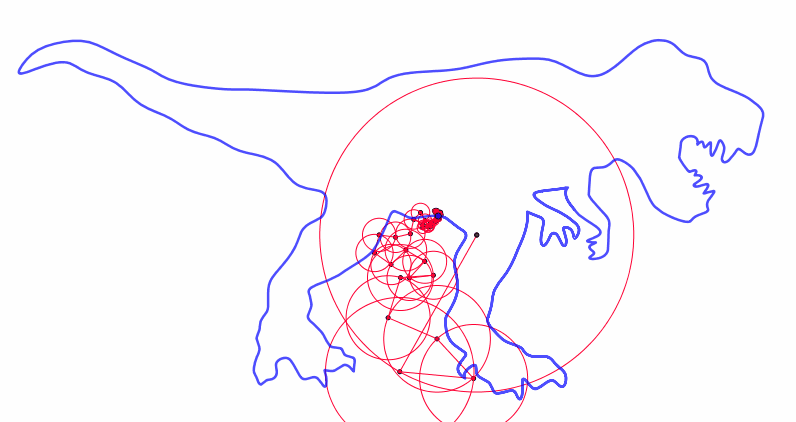
In fact we can use this equation to create more complex epicycles!

Discrete Fourier Transform
In fact we can use this equation to create more complex epicycles!

\(\Bigg\{\Bigg.\)
Discrete Fourier Transform
👈 DFT
The inverse of the DFT
👈

(DFT)
They are very similar to this:
\(\Bigg\{\Bigg.\)
Discrete Fourier Transform

(DFT)
They are very similar to this:
\(\Bigg\{\Bigg.\)
Discrete Fourier Transform

(DFT)
Discrete Fourier Transform
(DFT)
A nice methaphor 😃
What does the Discrete Fourier Transform do?
Given a smoothie, it finds the recipe.
A nice methaphor 😃
🍓 🍌🥭🍏
🫐🍍🥝🍫
How does it do that?
A nice methaphor 😃
How does it do that?
Run the smoothie through filters to extract each ingredient.
🍓 🍌🥭🍏
🫐🍍🥝🍫
A nice methaphor 😃
🍓 🍌🥭🍏
🫐🍍🥝🍫
Why do we want to do this?
Recipes are easy to analyse, compare, than the smoothie itself.
A nice methaphor 😃
🍓 🍌🥭🍏
🫐🍍🥝🍫
How do we get the smoothie back?
Blend the ingredients.
A nice methaphor 😃
🍓 🍌🥭🍏
🫐🍍🥝🍫
How do we get the smoothie back?
Blend the ingredients.
Applications of the DFT

Modern digital media
Applications of the DFT

Video
Applications of the DFT
Images

Applications of the DFT
Magnetic Resonance Imaging
Applications of the DFT

Sound
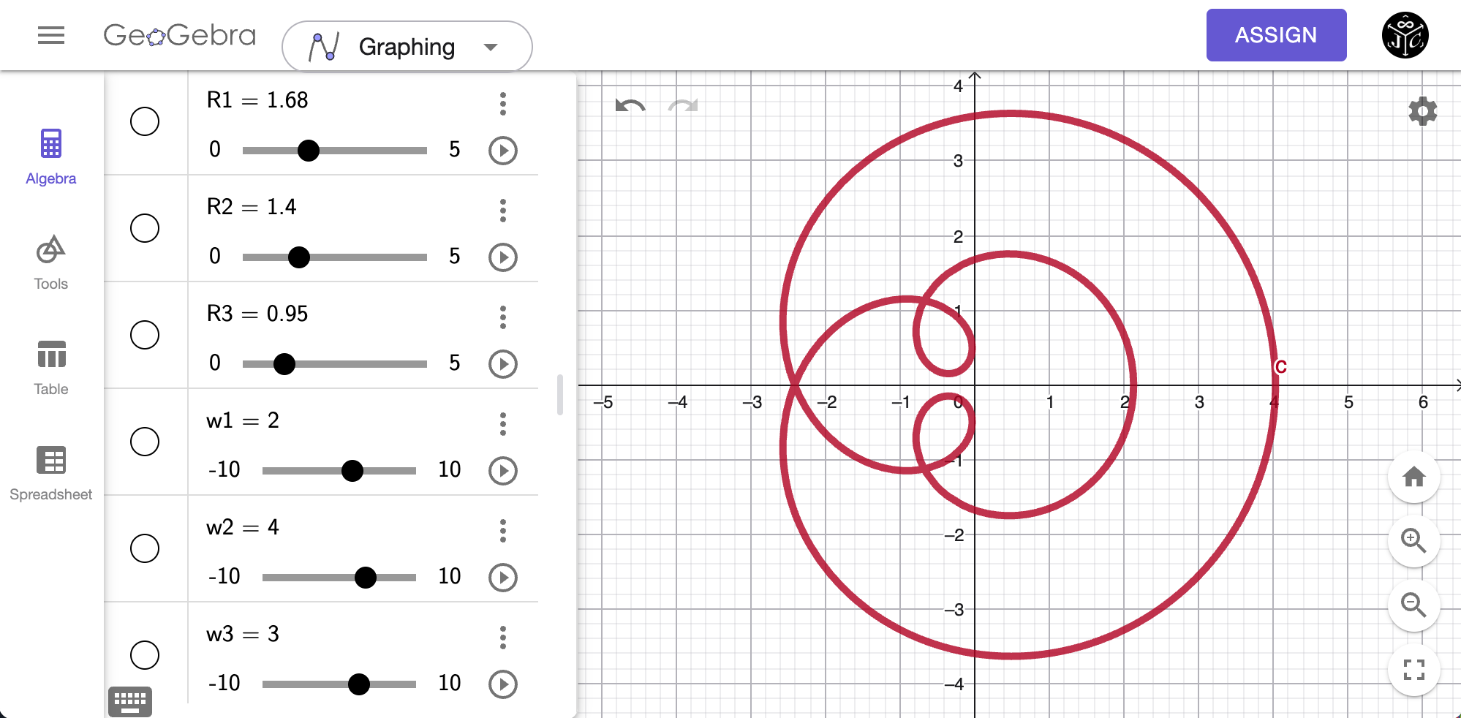
Try it yourself!
R1 = Slider(0, 5, 0.01, 1, 200)
R2 = Slider(0, 5, 0.01, 1, 200)
R3 = Slider(0, 5, 0.01, 1, 200)
w1 = Slider(-10, 10, 1, 1, 200)
w2 = Slider(-10, 10, 1, 1, 200)
w3 = Slider(-10, 10, 1, 1, 200)
fx(x) = R1 * cos(w1 * x) + R2 * cos(w2 * x) + R3 * cos(w3 * x)
fy(x) = R1 * sin(w1 * x) + R2 * sin(w2 * x) + R3 * sin(w3 * x)
c = Curve(fx(t), fy(t), t, 0, 2pi)
The beauty of mathematics shows itself to patient followers.
- Maryam Mirzakhani