Diseño e Integración de Applets Interactivos
de Matemáticas y Actividades de Aprendizaje
en la Universidad de Queensland
Seminario de Innovación Docente
Universidade da Coruña

Dr. Juan Carlos Ponce Campuzano

Agradecimientos
Andrés Prieto Anerios
Grupo de Innovación Docente en Modelización Matemática e Simulación Numérica (M2SINUM)

Contenido
- Breve introducción al contexto educativo en la Universidad de Queensland.
- Diseño e integración de applets interactivos y actividades de aprendizaje.
- Actualización de la componente de programación.

1. Contexto


1. Contexto



1. Contexto


1. Contexto
Cursos de matemáticas
Conferencias (Lectures)
Tutoriales/Talleres
(Tutorials/Workshops)

2 Semestres por año
13 semanas por semestre
1. Contexto
Cursos de matemáticas
Conferencias (Lectures)
~3 horas por semana
Estudiantes por curso:
~800 a 1500
(primer año de la universidad)


1. Contexto

Tutoriales/Talleres
(Tutorials/Workshops)
Cursos de matemáticas
1. Contexto
~1 o 2 horas por semana
Trabajo grupal:
~20 a 30 estudiantes

Tutoriales/Talleres
(Tutorials/Workshops)
Cursos de matemáticas
1. Contexto

Conferencias (Lectures)
Tutoriales/Talleres
(Tutorials/Workshops)

Proyecto (2018):
Diseño e integración de applets interactivos y actividades de aprendizaje.
- Mejorar el aprendizaje de contenido matemático.
- Fomentar la interacción en cursos.
- Actualizar contenido y actividades relacionadas con programación.
Cursos de matemáticas
1. Contexto
Proyecto (2018):
Diseño e integración de applets interactivos y actividades de aprendizaje.
MATH1050: Fundamentos de matemáticas
MATH1051: Cálculo y Álgebra Lineal
MATH1052: Cálculo Multivariable y Ecuaciones Diferenciales Ordinarias
Grandes cursos de primer año universitario.
Obligatorios para las carreras de matemáticas, ingeniería y otras ciencias.
MATLAB
Fundamentos de programación
1. Contexto
Colaboración entre académicos, estudiantes y diseñadores didácticos:
Poh Hillock, Sam Kault, Wenbo Li, Michael Jennings,
Kyle Clunies-Ross, Thomas Reay, Marcus Flook, Dylan Cowley, Liam Timms, Emma Comino, Montana Wickens, Christina Tang-Fujiwara, Andre Mengene,
Juan Carlos Ponce Campuzano
Proyecto (2018):
Diseño e integración de applets interactivos y actividades de aprendizaje.
2. Diseño e integración de applets interactivos y actividades de aprendizaje
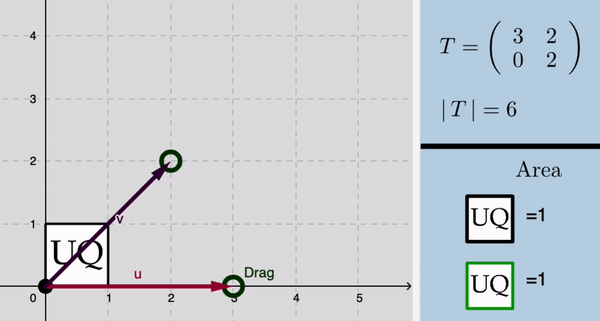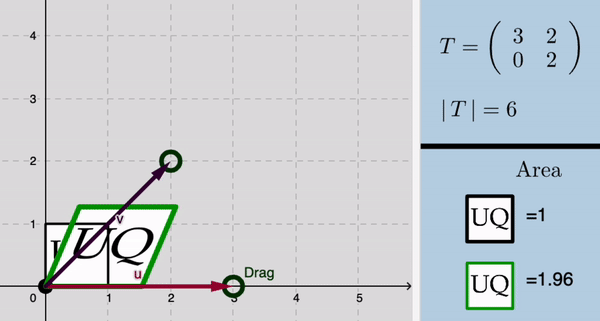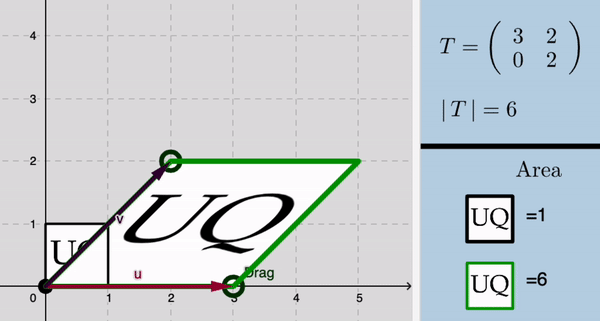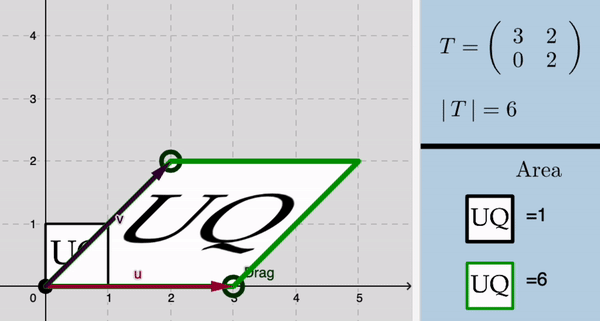
2. Diseño e integración de applets interactivos y actividades de aprendizaje
Multiple representaciones semióticas

Actividades de aprendizaje
Applets interactivos
2. Diseño e integración de applets interactivos y actividades de aprendizaje
Applets interactivos
GeoGebra
- Programa de acceso libre
- Múltiple representaciones semióticas:
- Álgebra
- Geometría dinámica 2D y 3D
- Hojas de cálculo
- Systema algebraico de cómputo
- "Fácil" uso para la creación y diseño de applets
- Compatibilidad con differentes navegadores
- Potencialmente de fácil mantenimiento a largo plazo

2. Diseño e integración de applets interactivos y actividades de aprendizaje
Applets interactivos
JavaScript (JS)
- Lenguaje de programación libre
- Compatibilidad con diferentes navegadores
- Potencial de crear casi cualquier tipo de simulaciones o applets interactivos en 2D y 3D
- Requiere mayor conocimiento en programación
function draw() {
v[halfWidth][halfHeight] = 0;
p[halfWidth][halfHeight] = (sin(frameCount * f1 * vel) + sin(frameCount * f2 * vel) + sin(frameCount * f3 * vel)) * 8;
for (let x = 1; x < widt; x++) {
for (let y = 1; y < heigh; y++) {
v[x][y] += (p[x - 1][y] + p[x + 1][y] + p[x][y - 1] + p[x][y + 1]) * 0.25 - p[x][y];
}
}
loadPixels(); // Load the pixel data into the pixels[] array
for (let x = 1; x < widt; x++) {
for (let y = 1; y < heigh; y++) {
p[x][y] += v[x][y];
let c = 1 - abs(constrain(p[x][y], -1, 1));
let index = (x + y * width) * 4;
pixels[index] = c * 255; // Red
pixels[index + 1] = c * 255; // Green
pixels[index + 2] = c * 255; // Blue
pixels[index + 3] = 255; // Alpha
}
}
updatePixels(); // Update the display window with the new pixel data
}Entre los más populares lenguajes de programación
JS Frameworks:
2. Diseño e integración de applets interactivos y actividades de aprendizaje

Conferencias
(Lectures)
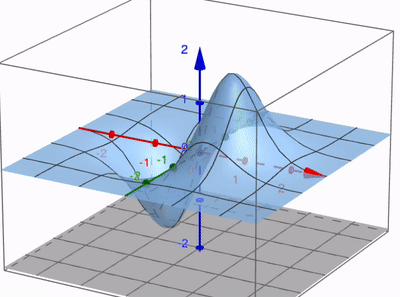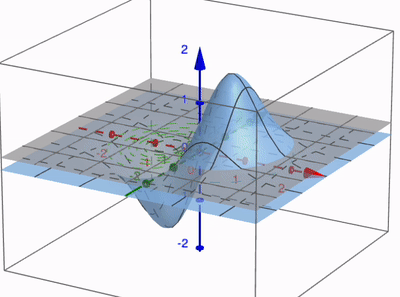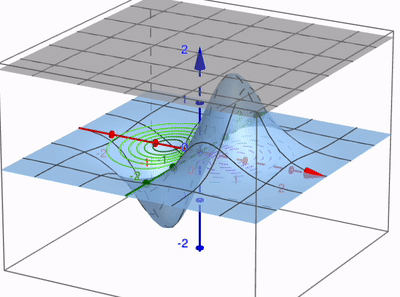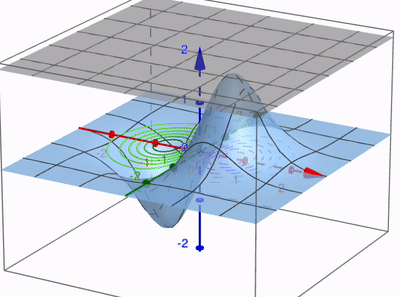
2. Diseño e integración de applets interactivos y actividades de aprendizaje
Conferencias
(Lectures)
Tutoriales/Talleres
(Tutorials/Workshops)



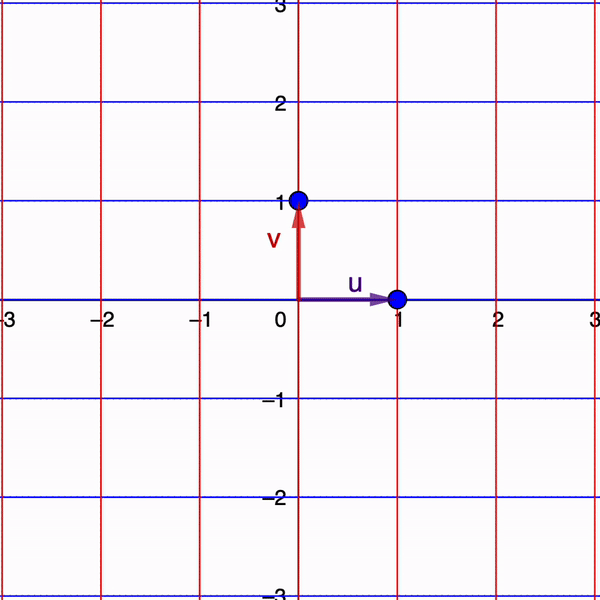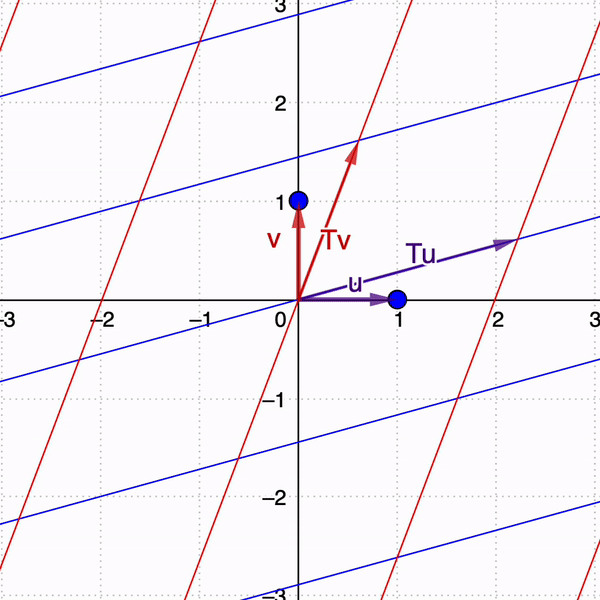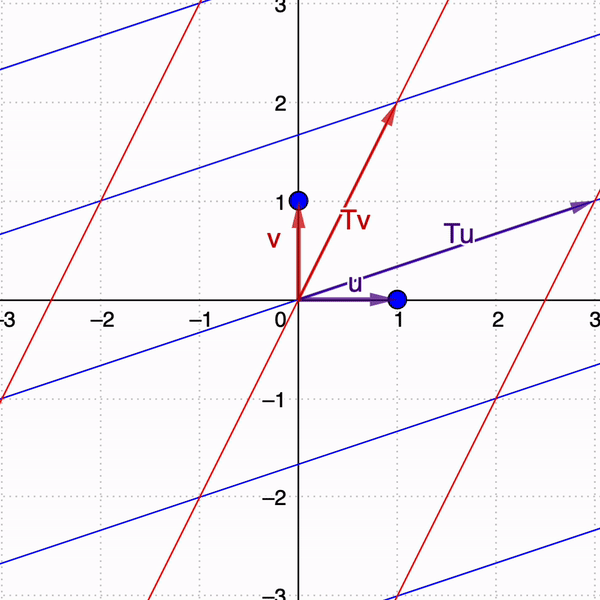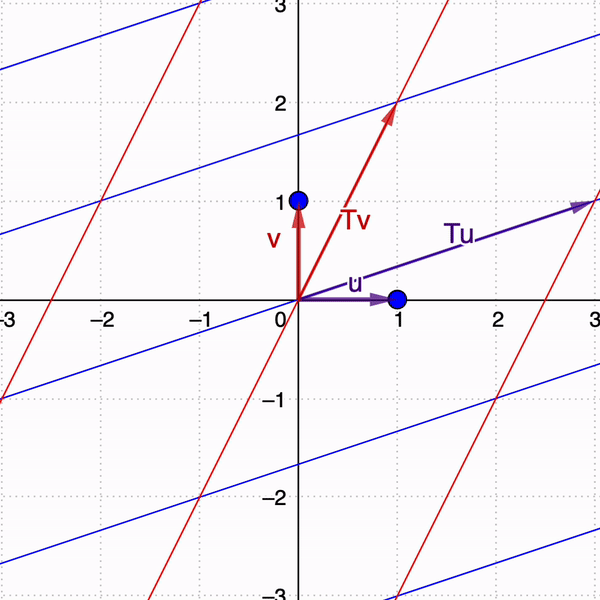
2. Diseño e integración de applets interactivos y actividades de aprendizaje
Ejemplo 1: Sucesiones
2. Diseño e integración de applets interactivos y actividades de aprendizaje
Ejemplo 2: Geometría de eigenvectores
2. Diseño e integración de applets interactivos y actividades de aprendizaje
Ejemplo 3: Campos de direcciones
2. Diseño e integración de applets interactivos y actividades de aprendizaje
Tutoriales/Talleres
(Tutorials/Workshops)



2. Diseño e integración de applets interactivos y actividades de aprendizaje
Tutoriales/Talleres
(Tutorials/Workshops)



Trabajo colaborativo dentro de un contexto de resolución de problemas
2. Diseño e integración de applets interactivos y actividades de aprendizaje
Flujo de trabajo
Diseño de applets y actividades de aprendizaje
Revisión y prueba
Incorporación en cursos
Entre Febrero y Diciembre de 2018
2. Diseño e integración de applets interactivos y actividades de aprendizaje
Flujo de trabajo
Diseño de applets y actividades de aprendizaje
Revisión y prueba
Incorporación en cursos
Entre Febrero y Diciembre de 2018
Creación de videos de contenido matemático
Opciones de estudio:
- Presenciales
- En línea
2. Diseño e integración de applets interactivos y actividades de aprendizaje
Conferencias
(Lectures)
Tutoriales/Talleres
(Tutorials/Workshops)




Actualmente en vigencia
4 Cursos de primer año
(Algunos cursos más avanzados)
3. Actualización de la componente de programación
% Define anonymous function
f = @(t,y) 1 - exp(-4 * t) - 2 * y;
t = zeros(1, 10+1);
y = zeros(1, 10+1);
t(1) = 0;
y(1) = 1;
dt = 0.2;
for k = 1:10
t(k+1) = t(k) + dt;
% Here we use the anonymous function
y(k+1) = y(k) + dt * f(t(k), y(k));
end
plot(t, y, 'bo-')3. Actualización de la componente de programación
% Define anonymous function
f = @(t,y) 1 - exp(-4 * t) - 2 * y;
t = zeros(1, 10+1);
y = zeros(1, 10+1);
t(1) = 0;
y(1) = 1;
dt = 0.2;
for k = 1:10
t(k+1) = t(k) + dt;
% Here we use the anonymous function
y(k+1) = y(k) + dt * f(t(k), y(k));
end
plot(t, y, 'bo-')MATH1051: Cálculo y Álgebra Lineal
MATH1052: Cálculo Multivariable y Ecuaciones Diferenciales Ordinarias
MATLAB
Fundamentos de programación
MATH1051: Cálculo y Álgebra Lineal
MATH1052: Cálculo Multivariable y Ecuaciones Diferenciales Ordinarias
MATLAB
Fundamentos de programación

Hoja de trabajo

MATLAB en el ordenador
+
3. Actualización de la componente de programación
MATH1051: Cálculo y Álgebra Lineal
MATH1052: Cálculo Multivariable y Ecuaciones Diferenciales Ordinarias
MATLAB Live Scripts
Fundamentos de programación
3. Actualización de la componente de programación
MATLAB Live Script
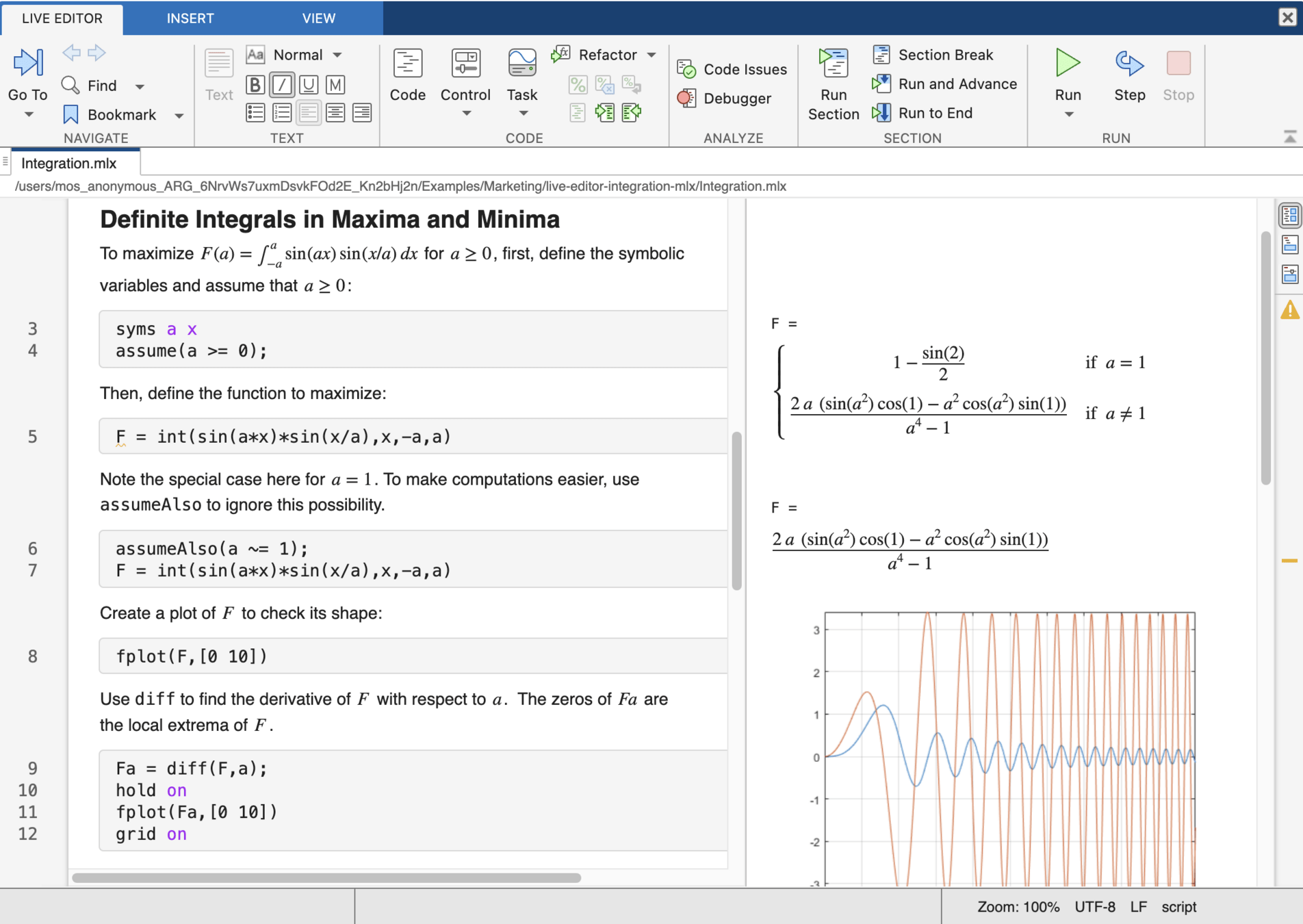

Hoja de trabajo

MATLAB en el ordenador
2022
3. Actualización de la componente de programación
MATLAB Live Script

3. Actualización de la componente de programación
MATLAB Live Script

3. Actualización de la componente de programación
MATLAB Live Script
Objetivos principales:
- Cubrir conceptos elementales de programación vinculados directamente con el contenido de cada curso.
- Facilitar la transición al uso de otros lenguajes de programación de acceso libre tales como Python, R o Julia.
Applets de GeoGebra y JavaScript disponibles en:
Applets de GeoGebra disponibles también en:
MATLAB Live scripts disponibles en:

Complex Analysis
A visual and Interactive Introduction