MATH2400

Mathematical Analysis

Juan Carlos Ponce Campuzano

@jcponcemath

I acknowledge the Traditional Owners and their custodianship of the lands on which we meet today and pay my respect to their Ancestors and their descendants.

Acknowledgement
of Country

Image: Digital reproduction of A guidance through timeΒ by Casey Coolwell and Kyra Mancktelow

What is Mathematical Analysis?

\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}
\displaystyle e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}
\displaystyle \int_a^b f(x) dx=\lim_{n\to \infty} \sum_{n=0}^{n} f(x_i)\Delta x_i
\displaystyle f'(a) = \lim_{x\to a} \frac{f(x)- f(a)}{x-a}

What is Mathematical Analysis?

Essentially, it is the study of limts (and related theories) using the axiomatic properties of real numbers.

\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}
\displaystyle e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}
\displaystyle \int_a^b f(x) dx=\lim_{n\to \infty} \sum_{n=0}^{n} f(x_i)\Delta x_i
\displaystyle f'(a) = \lim_{x\to a} \frac{f(x)- f(a)}{x-a}

This course is proof oriented instead of an application oriented course

What are Axioms?

Axioms

Definitions

All Mathematical Theories

Non-Euclidian Geometry

Group Theory

Algebra

Linear Algebra

Game Theory

Topology

Category Theory

\vdots

Euclidian Geometry

Calculus

Number Theory

What are Axioms?

Euclidian Geometry

Euclid's Elements (~2300 years old)

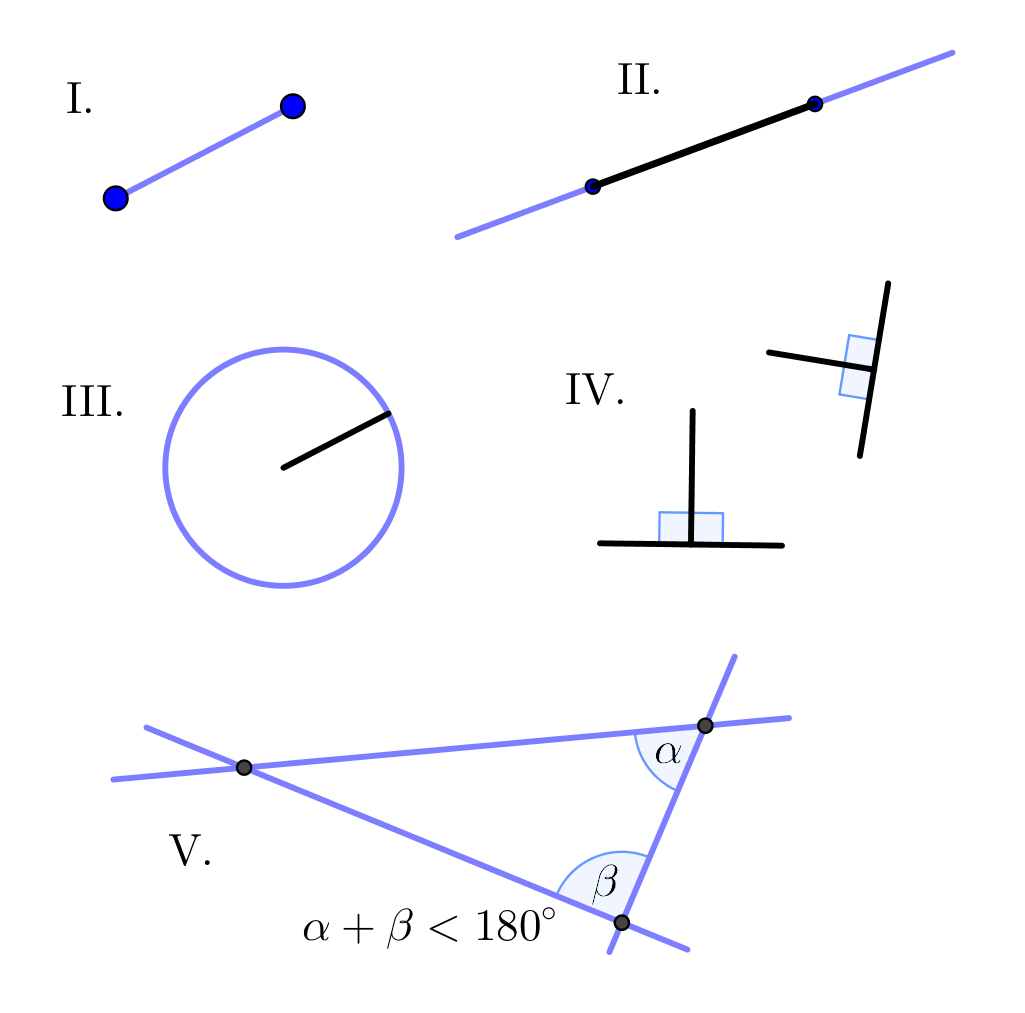
Definitions

Point

Straight line

Circle

Right angle (\(90^\circ\))

What are Axioms?

Euclidian Geometry

Euclid's Elements (~2300 years old)

Axioms

  1. It is possible to draw a straight line from any point to any other point.
  2. It is possible to extend a line segment continuosly in both directions.
  3. It is possible to describe a circle with any center and any radius.
  4. It is true that all righ angle are equal to one another.
  5. Two distinct intersecting lines cannot be parallel to the same line.

What are Axioms?

Euclidian Geometry

Euclid's Elements (~2300 years old)

Axioms

  1. It is possible to draw a straight line from any point to any other point.
  2. It is possible to extend a line segment continuosly in both directions.
  3. It is possible to describe a circle with any center and any radius.
  4. It is true that all righ angle are equal to one another.
  5. Two distinct intersecting lines cannot be parallel to the same line.

Proposition 47, Book I

What are Axioms?

Euclidian Geometry

Euclid's Elements (~2300 years old)

Axioms

  1. It is possible to draw a straight line from any point to any other point.
  2. It is possible to extend a line segment continuosly in both directions.
  3. It is possible to describe a circle with any center and any radius.
  4. It is true that all righ angle are equal to one another.
  5. Two distinct intersecting lines cannot be parallel to the same line.

Elisha S. Loomis (1940)

Mathematical Analysis

We are going to prove statements like:

0\cdot x = 0
\displaystyle \lim_{n\to\infty} \int_0^1 \frac{nx+ \sin(nx^2)}{n} \,dx = 0

Mathematical Analysis

Traditionall, a rigorous first corse in Analysis progresses (more or less) in the follwoing order:

In the other hand, the historical development of these subjects ocurred in reverse order:

sets,

real numbers

limits,

continuous functionns

derivatives

integration

Cantor 1874,

Dedekin

Cauchy 1823,

Riemann,

Weiestrass

Newton 1669

Leibniz 1684

Archimedes

3rd B.C.

Archimedes

c. 287 BC - c. 212 BC

0

1600

Liu Hui

c. 220 - c. 280

200

Hindu-Arabic numerical system

Algebra: Muhammad ibn Musa al-Khwarizmi

Analytic Geometry:

Descartes & Fermat

-200

Time line

Archimedes

c. 287 BC - c. 212 BC

1669

Newton

1684

Leibniz

1872

Dedekin

1874

Cantor

1854

Riemann

1755

Euler

...

0

1600

1900

1700

1800

2000

Cauchy

1823

Liu Hui

c. 220 - c. 280

1748

Agnesi

1861

Weiestrass

Time line

~300 years of mathematical development

(roughly)

Mathematical Analysis

Mathematical Analysis

13 Weeks

Good news!

You already know most of the content.

Lectures

Tutorials

How are we going to work in this course?

How are we going to work in this course?

- Every week you will practice with a set of problems.

It covers core material not covered in lectures!

  • Internal students: on Campus
  • External students: via Zoom πŸ–₯️ 

Lectures

- We will cover the theory with examples.

Most weeks there will be at most

one complementary reading πŸ“– πŸ‘€

Important:

How are we going to work in this course?

Available in Blackboard under Learning Resources

Most weeks there will be at most

one complementary reading πŸ“– πŸ‘€

Important:

via weekly modules:

πŸš€

Why should I read the complementary material? πŸ€”

  1. Reading is, in general, a very useful cognitive exercise.
  2. In mathematical analysis, it can help you gain a deeper understanding of the concepts and theorems being presented, and develop your ability to think logically and rigorously.
  3. You are studing maths!

Most weeks there will be at most

one complementary reading πŸ“– πŸ‘€

Important:

How are we going to work in this course?

Ingrid Deubechies

Maryam Mirzakhani†

You will gain some experience to read maths papers:

How are we going to work in this course?

Tutorials

Consult your timetable.

How are we going to work in this course?

πŸ‘‰ Tutorials begin in week 2.

Ask questions about assignments, content and

problem sheets (available in Blackboard).

πŸ“ You should attempt problems beforehand.

  • Internal students: on Campus
  • External students: via Zoom πŸ–₯️ 

How are we going to work in this course?

Link in Blackboard

  • Post questions
  • Try answering questions
  • 3 Assignments - 36%
  • Final exam - 64%

MATH2400 & MATH7400

Assessment

Assessment

Sumbission will be online through Blackboard

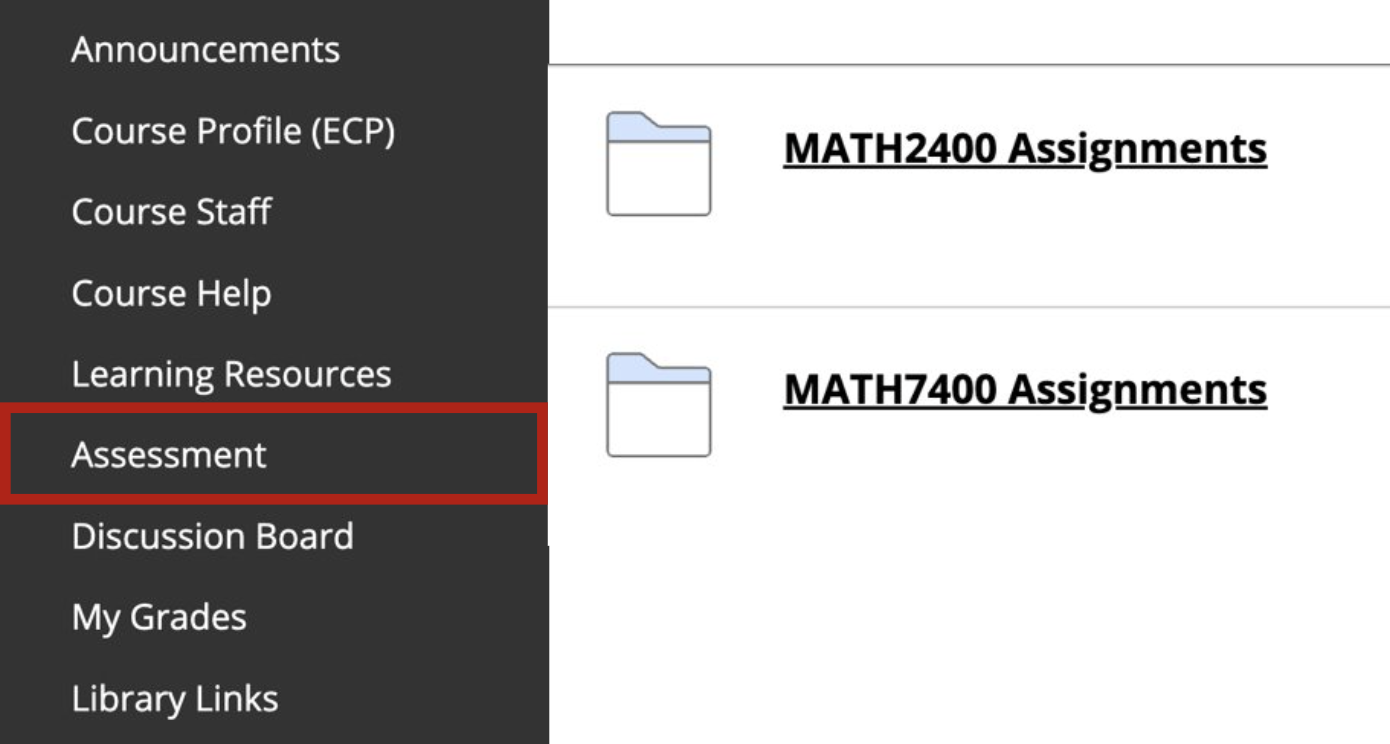
Under Assessment look for the folder corresponding

to your course code MATH2400 or MATH7400

Check the Submission Instructions ‼️

Assignments

Assessment

Final Exam

Invigilated on-campus & over Zoom

Β for internal and external students, respectively

You will have two hours to

solve problems and formulate proofs

Final Exam

Assessment

In which you may encounter some beautiful expressions such as:

\displaystyle\lim_{\substack{h \to 0\\h\in \R^n}} \frac{||f(x+h)-f(x) - Df(x)h||}{||h||} = 0
\displaystyle {\biggl( \sum_{k=1}^n x_k y_k \biggr)}^2 \leq \biggl(\sum_{k=1}^n x_k^2 \biggr) \biggl(\sum_{k=1}^n y_k^2 \biggr)
\displaystyle (f^{-1})'(y_0) = \frac{1}{f'\bigl( f^{-1}(y_0) \bigr)} = \frac{1}{f'(x_0)}
\displaystyle f'(p) \, e_j = \sum_{k=1}^m \frac{\partial f_k}{\partial x_j}(p) \,e_k
\displaystyle \limsup_{n \to \infty} \, x_n = \inf \{ a_n : n \in \N \}
\displaystyle \liminf_{n \to \infty} \, x_n \leq \limsup_{n \to \infty} \, x_n
\displaystyle \lim_{n\to\infty} \int_0^1 \frac{nx+ \sin(nx^2)}{n} \,dx = 0

Final Exam

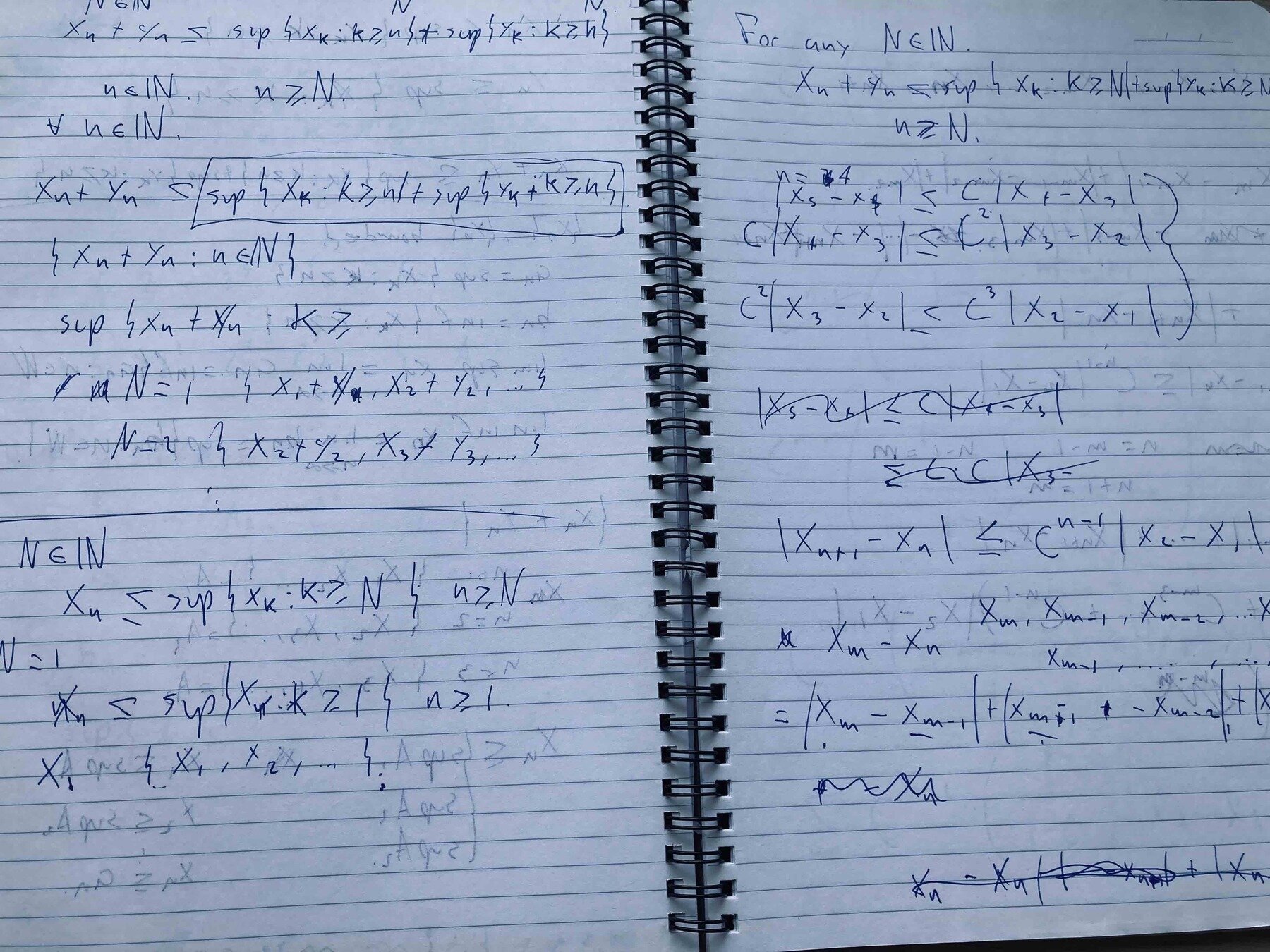
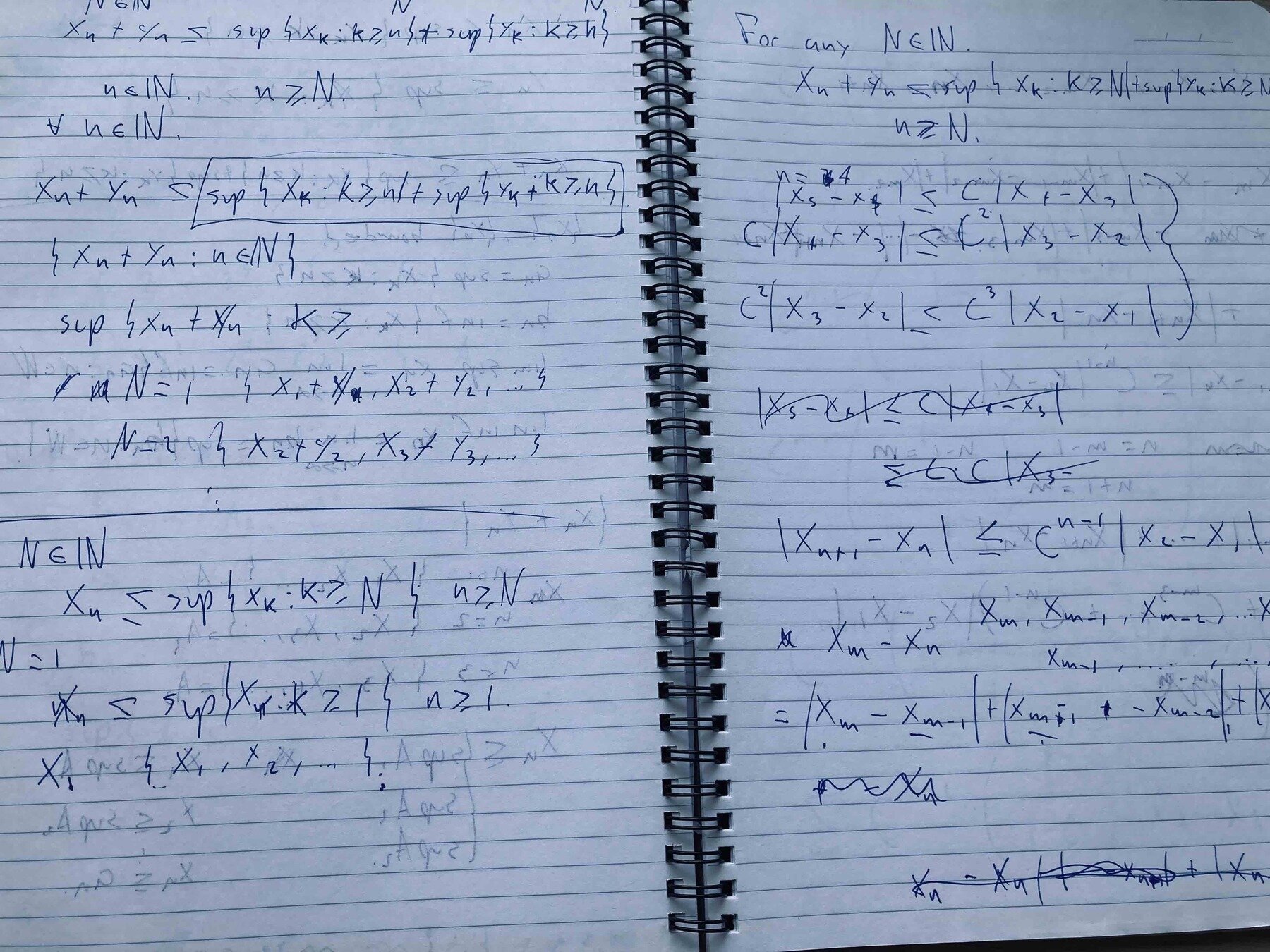
But before, we need to practice a lot πŸ“ ✍️

\displaystyle\lim_{\substack{h \to 0\\h\in \R^n}} \frac{||f(x+h)-f(x) - Df(x)h||}{||h||} = 0
\displaystyle {\biggl( \sum_{k=1}^n x_k y_k \biggr)}^2 \leq \biggl(\sum_{k=1}^n x_k^2 \biggr) \biggl(\sum_{k=1}^n y_k^2 \biggr)
\displaystyle (f^{-1})'(y_0) = \frac{1}{f'\bigl( f^{-1}(y_0) \bigr)} = \frac{1}{f'(x_0)}
\displaystyle f'(p) \, e_j = \sum_{k=1}^m \frac{\partial f_k}{\partial x_j}(p) \,e_k
\displaystyle \limsup_{n \to \infty} \, x_n = \inf \{ a_n : n \in \N \}
\displaystyle \liminf_{n \to \infty} \, x_n \leq \limsup_{n \to \infty} \, x_n
\displaystyle \lim_{n\to\infty} \int_0^1 \frac{nx+ \sin(nx^2)}{n} \,dx = 0

😎

More Questions?

  1. For general inquiries: smp.student@uq.edu.au
  2. Questions about Tutorial sheets: In your Tutorial
  3. email: j.ponce@uq.edu.au
  4. Consultation hours on Mondays from week 2:
    • In person: 1 pm, 67-741 Priestley Bld.
    • On Zoom: 2 pm (link in BB).