Mysterious
Rotating
Circles

Centers
Radii
\(\overline{C_1P_1}\)
\(= r_1\)
\(\overline{C_1P_1}= r_1\)
\(\overline{C_2P_2}= r_2\)
\(= r_1 s\)
\(\overline{C_1P_1}= r_1\)
\(\overline{C_2P_2}= r_2\)
\(\overline{C_3P_3}= r_3\)
\(= r_1 s\)
\(=r_1 s^2 \)
\(= r_2 s \)
\(=\left( r_1 s \right) s\)

\(\overline{C_1P_1}= r_1\)
\(\overline{C_2P_2}= r_2\)
\(\overline{C_3P_3}= r_3\)
Here \(\,0<s<1\)
\(\vdots \)
\(\overline{C_nP_n}= r_n = r_1 s^{n-1} \)
\(= r_1 s\)
\(=r_1 s^2 \)
\(= r_2 s \)
\(=\left( r_1 s \right) s\)
\(\,r_1 = \overline{C_1C_2} + \overline{C_2P_1},\)
\(\Rightarrow \overline{C_1C_2} = r_1-\overline{C_2P_1}\)
\(= r_1-r_1s\)
\(= r_1\left(1-s\right)\)
\(\,r_1 = \overline{C_1C_2} + \overline{C_2P_1},\)
\(\Rightarrow \overline{C_1C_2} = r_1-\overline{C_2P_1}\)
\(\,r_2 = \overline{C_2C_3} + \overline{C_3P_2},\)
\(\Rightarrow \overline{C_2C_3} = r_2-\overline{C_3P_2}\)
\(= r_1-r_1s\)
\(= r_1\left(1-s\right)\)
\(= r_1s-r_1 s^2\)
\(= r_1s\left(1- s\right)\)
\(\,r_1 = \overline{C_1C_2} + \overline{C_2P_1},\)
\(\Rightarrow \overline{C_1C_2} = r_1-\overline{C_2P_1}\)
\(\,r_2 = \overline{C_2C_3} + \overline{C_3P_2},\)
\(\Rightarrow \overline{C_2C_3} = r_2-\overline{C_3P_2}\)
\(= r_1-r_1s\)
\(= r_1\left(1-s\right)\)
\(= r_1s-r_1 s^2\)
\(= r_1s\left(1- s\right)\)
\(\overline{C_3C_4}= r_1 s^{2}\left(1-s\right) \)

\(\,r_1 = \overline{C_1C_2} + \overline{C_2P_1},\)
\(\Rightarrow \overline{C_1C_2} = r_1-\overline{C_2P_1}\)
\(\vdots \)
\(\overline{C_nC_{n+1}}= r_1 s^{n-1}\left(1-s\right) \)
\(\,r_2 = \overline{C_2C_3} + \overline{C_3P_2},\)
\(\Rightarrow \overline{C_2C_3} = r_2-\overline{C_3P_2}\)
\(= r_1-r_1s\)
\(= r_1\left(1-s\right)\)
\(= r_1s-r_1 s^2\)
\(= r_1s\left(1- s\right)\)
\(\overline{C_3C_4}= r_1 s^{2}\left(1-s\right) \)

Again \(\,0<s<1!\)
\(\overline{C_1C_2} =r_1(1-s)\)
\(\vdots \)
\(\overline{C_nC_{n+1}}= r_1 s^{n-1}\left(1-s\right) \)
\(\overline{C_2C_3} = r_1s\left(1-s\right)\)
\(\overline{C_3C_4}= r_1 s^{2}\left(1-s\right) \)

Lenght of segments
Now let's find the coordinates of each point
\(C_n =\left(?, ?\right)\)

Set

Set
\(\leftarrow\)Polar form
Set

Set

Set

Set


Set


Set


Set

Radii
Centers


Radii
Centers

s = Slider(0.1, 1.5, 0.01)
t = Slider(0, 2pi, 0.01)
n = Slider(0, 50, 1)
Ln = 0...n
LR = Zip(s^k, k, Ln)
LP = Join({(0, 0)}, Zip((s^k * (1 - s); (k+1) * t), k, Ln))
LS = Zip(Sum(LP, k), k, Ln+1)
LC = Zip(Circle(P, r), P, LS, r, LR)GeoGebra Script
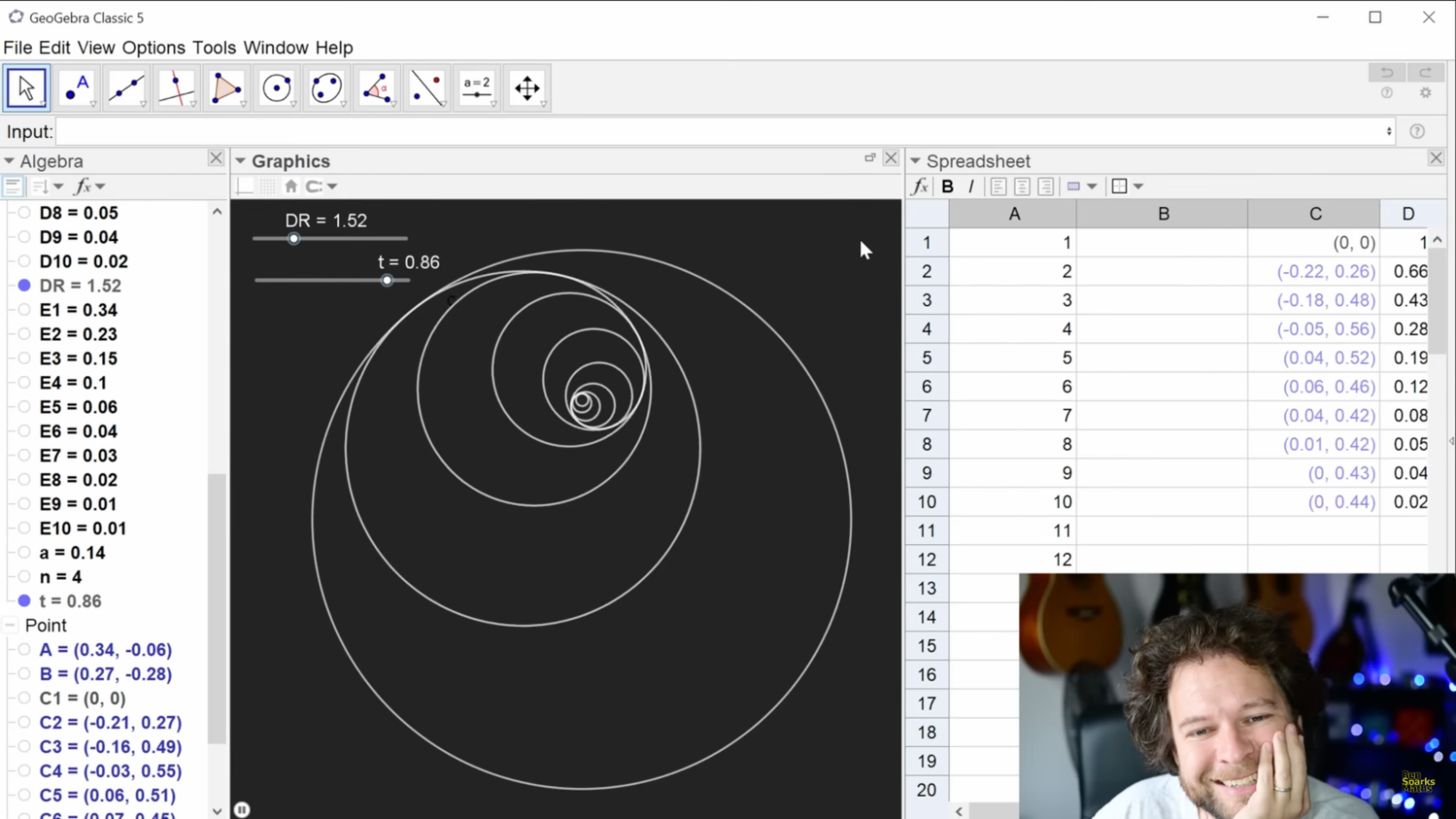
Check Ben Sparks' construction
using the Spreadsheet in GeoGebra
Link in the description


Mathematical topics
- Geometry:
- Rotations, Dilations, Tangency of circles
- Analytic geometry:
- Cartesian and polar coordinates
- Recursive Sequences and Series
There is also a conexion with
Complex Numbers!


Plot all the centers

and join them
for \(z=x+iy\)
Geometrical representation
of the geometric series



Geometrical representation of the
Geometric series



Geometric series
Relationship between the Geometric series and the points \(C_n\)

Relationship between the Geometric series and the points \(C_n\)

Re-write both in cartesian form!
Relationship between the Geometric series and the points \(C_n\)

Factorize \((1-s)\)
Relationship between the Geometric series and the points \(C_n\)

Relationship between the Geometric series and the points \(C_n\)

Relationship between the Geometric series and the points \(C_n\)

Relationship between the Geometric series and the points \(C_n\)

Relationship between the Geometric series and the points \(C_n\)

Relationship between the Geometric series and the points \(C_n\)


Relationship between the Geometric series and the points \(C_n\)

Relationship between the Geometric series and the points \(C_n\)


we just need to adjust the expression
To obtain the same result
with

with
Multiply by
Add this
with
Challenge: Use this approach to built it in GeoGebra

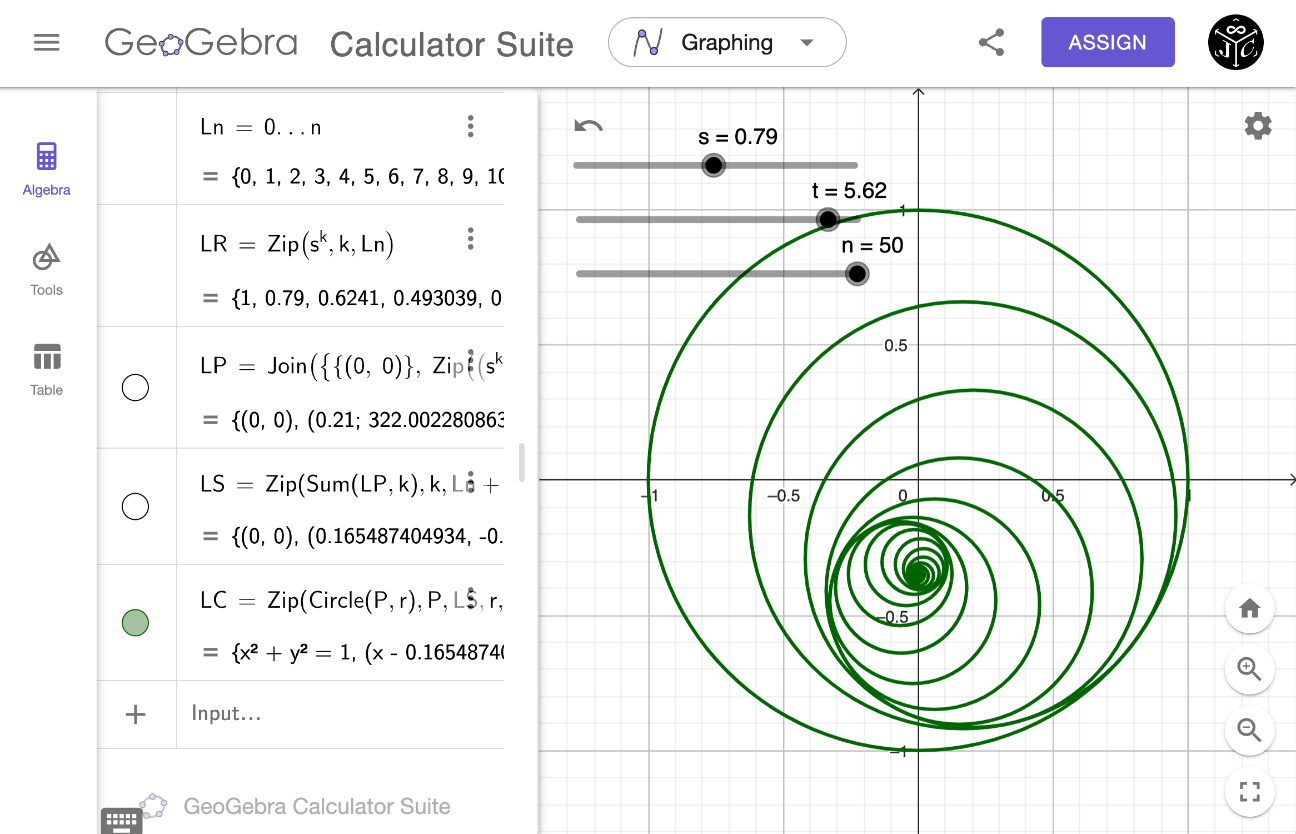
GeoGebra
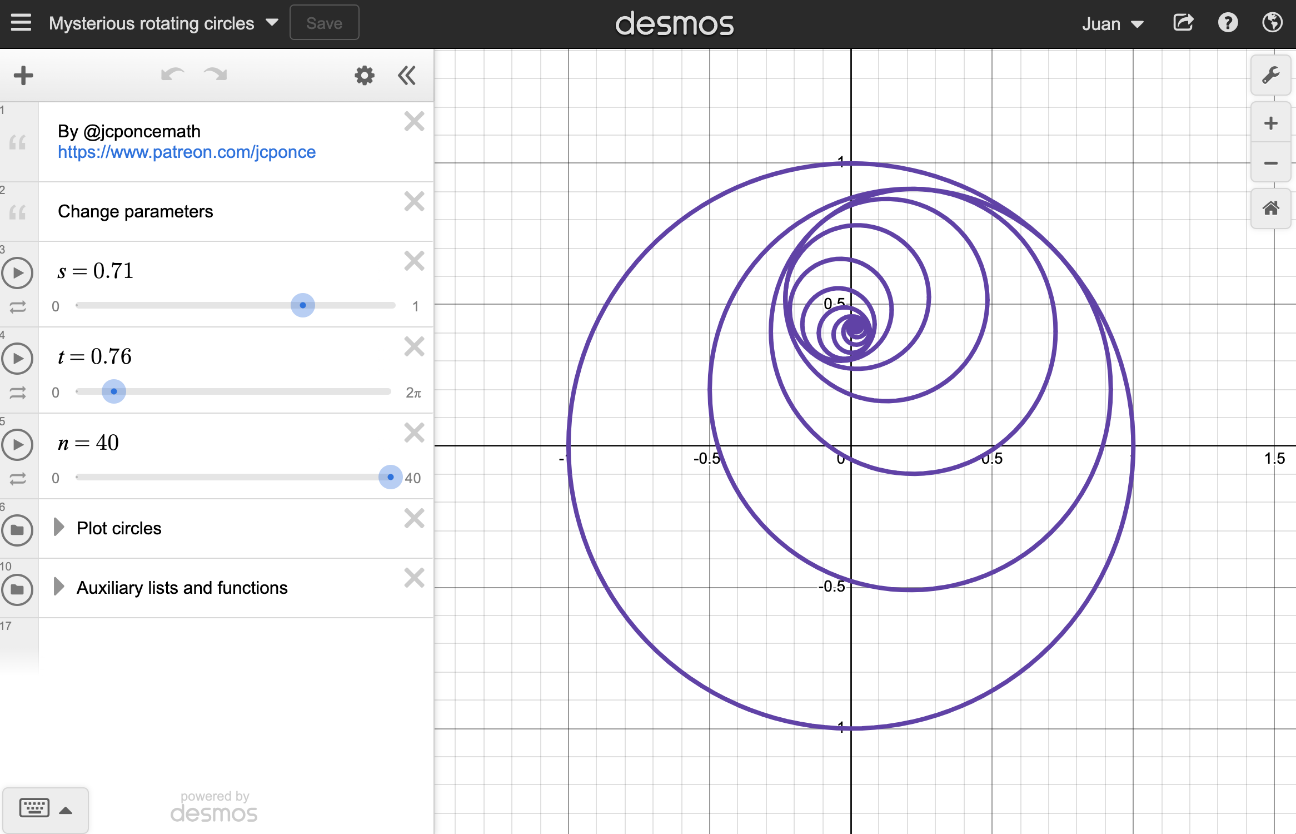
Desmos
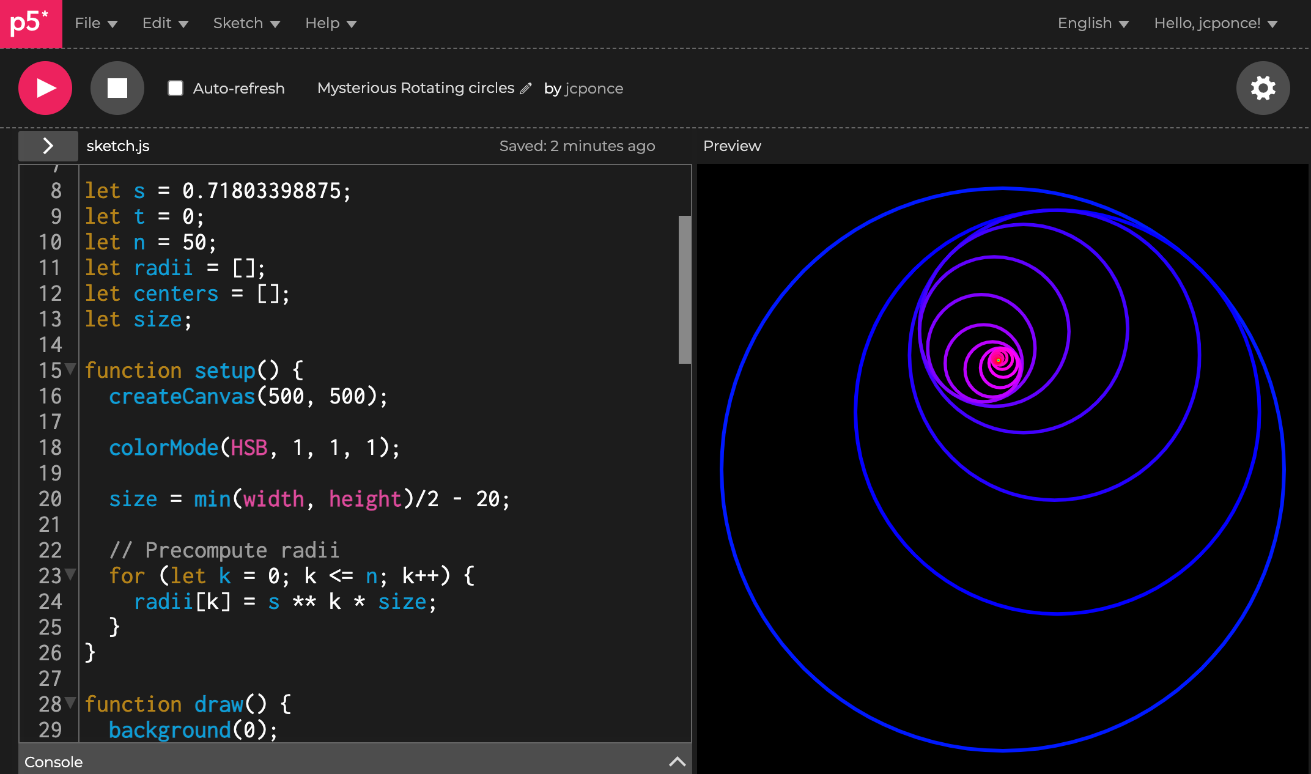
p5.js
Links in the description

Thanks for
watching!
Patreons:
Christopher-Alexander Hermans, Maciej Lasota, Miguel Díaz, bleh, Dennis Watson, Doug Kuhlmann, Newnome Beauton, Adam Parrott, Sophia Wood (Fractal Kitty), pmben, Abei, Edward Huff.

Thanks for
watching!

Patreons:
Christopher-Alexander Hermans, Maciej Lasota, Miguel Díaz, bleh, Dennis Watson, Doug Kuhlmann, Newnome Beauton, Adam Parrott, Sophia Wood (Fractal Kitty), pmben, Abei, Edward Huff.
