A didactic proposal for applying matrix diagonalisation:

Parametrising the intersection of a sphere and plane with the aid of GeoGebra

Work done in collaboration with Bradley Welch

Part 1:

Context and problem formulation

Main Problem: Find the parametrisation of the intersection curve of a sphere and a plane.

  • What are the conditions for a sphere and a plane to intersect?
  • How can we determine the parametric equations of the intersection curve of these geometric objects?

Part 1: Context and problem formulation

Part 1: Context and problem formulation

  • What are the conditions for a sphere and a plane to intersect?
S: (x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2
\Pi: Ax+By+Cz=D

Sphere of radius \(R>0,\) centred at \((x_0,y_0,z_0)\):

Plane defined by:

\(A,B\) and \(C\) real constants, not all simultaneaously zero.

Part 1: Context and problem formulation

  • What are the conditions for a sphere and a plane to intersect?
S: (x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2
\Pi: Ax+By+Cz=D

Let \(\rho\) be the shortest signed distance between the centre of the sphere and the plane.

\rho = \dfrac{Ax_0+By_0+ Cy_0-D}{\sqrt{A^2+B^2+C^2}}

That is,

Part 1: Context and problem formulation

  • What are the conditions for a sphere and a plane to intersect?
S: (x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2
\Pi: Ax+By+Cz=D
\rho = \dfrac{Ax_0+By_0+ Cy_0-D}{\sqrt{A^2+B^2+C^2}}

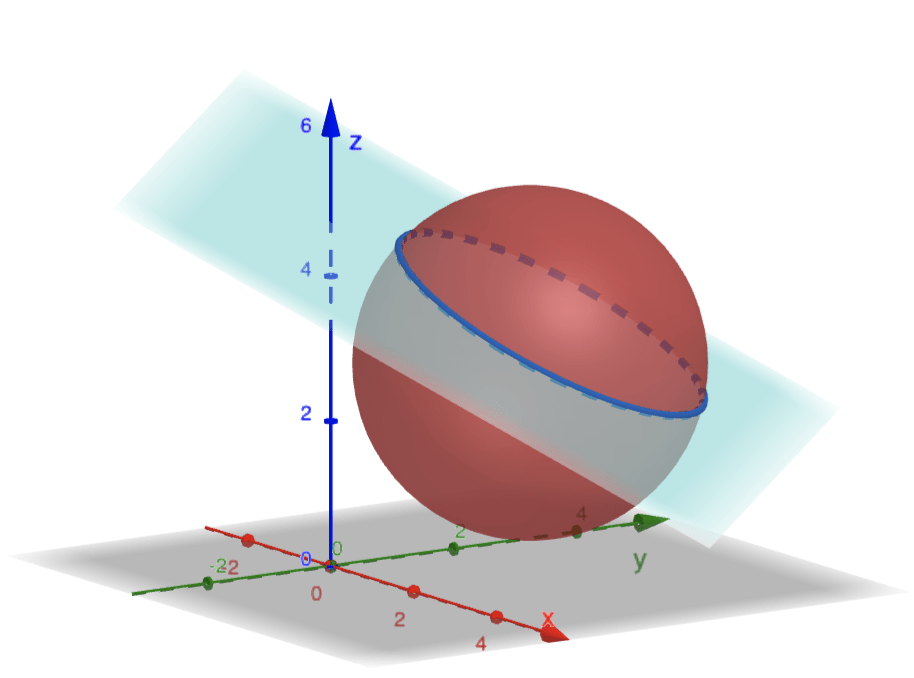
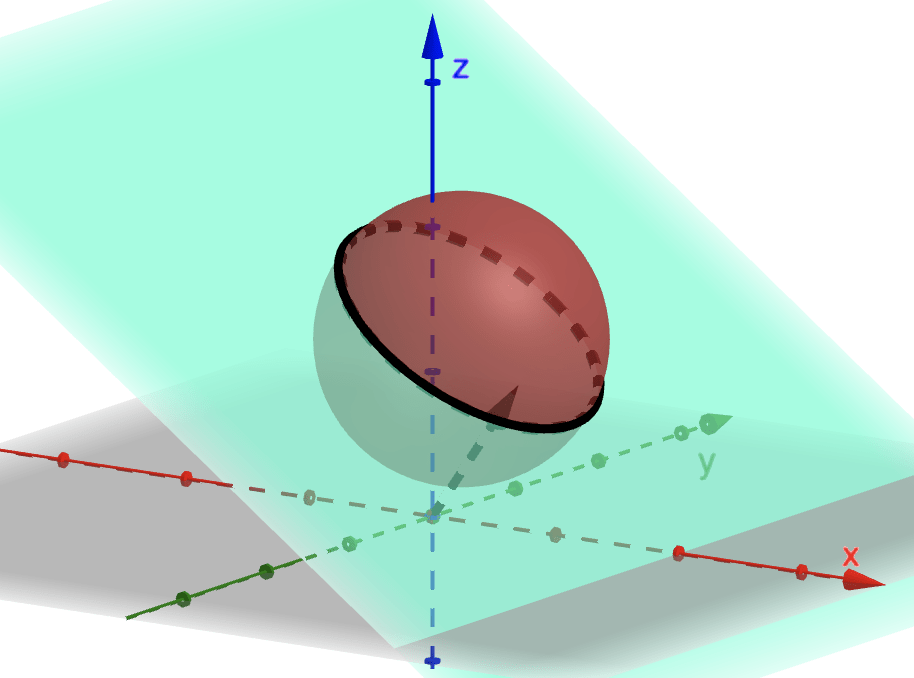
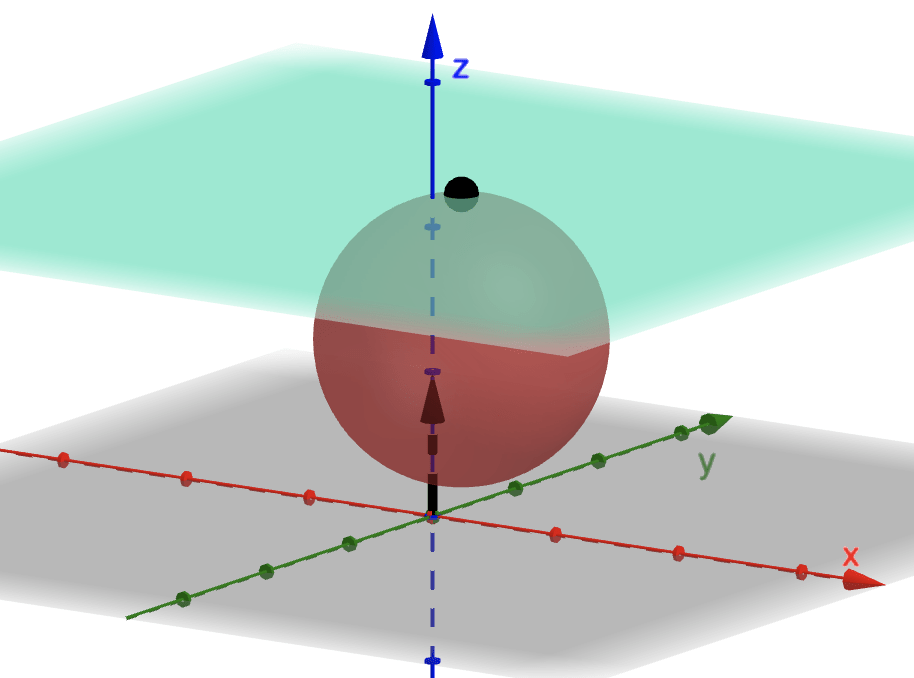
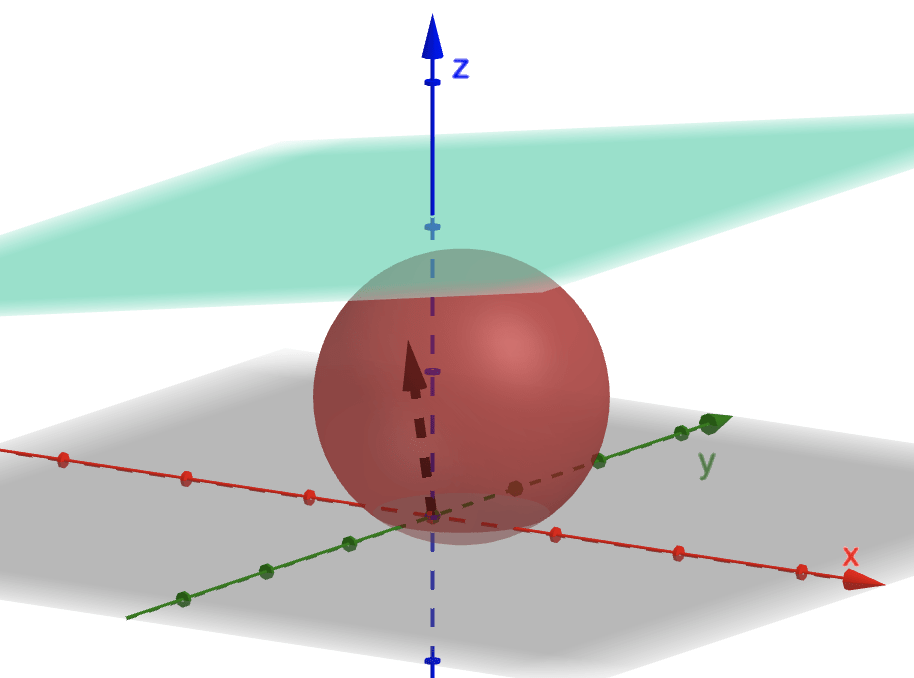
We can set the following cases for the intersection \(\Pi\cap S\):

1. If \(|\rho|<R,\) then \(\Pi\cap S\) is a circle.

2. If \(|\rho|=R,\) then \(\Pi\cap S\) is a point.

3. If \(|\rho|>R,\) then \(\Pi\cap S\) is a empty.

Part 1: Context and problem formulation

  • What are the conditions for a sphere and a plane to intersect?

Part 1: Context and problem formulation

Find the parametrisation of the intersection curve of a sphere and a plane.

X=\left(x_c,y_c,z_c\right)+\left(C_1 \cos(t)+ C_2\sin(t), C_3 \cos(t)+ C_4\sin(t), C_5\sin(t)\right)
\left\{ \begin{array}{l} x=C_1 \cos(t)+ C_2\sin(t)+x_c\\ y= C_3 \cos(t)+ C_4\sin(t)+y_c\\ z=C_5\sin(t)+z_c \end{array} \right.

or

Conjecture: The solution provided by Geogebra takes the general vector form given as

The dynamic exploration in GeoGebra with different semiotic representations provides some clues to solve our main problem:

Part 1: Context and problem formulation

\left\{ \begin{array}{l} x=C_1 \cos(t)+ C_2\sin(t)+x_c\\ y= C_3 \cos(t)+ C_4\sin(t)+y_c\\ z=C_5\sin(t)+z_c \end{array} \right.
  • But how does GeoGebra compute this parametrisation?
  • What are the mathematical concepts or relationships necessary to determine the values for the constants \(C_k, \;x_c, y_c, z_c\)?

Conjecture: The solution provided by Geogebra takes the general vector form given as

Part 2: Learning trajectory

Part 2: Learning trajectory

Problem 1: Find the parametric equation of the curve obtained by intersecting the sphere \(S:x^2 +y^2 +z^2 =1\) and the plane \(\Pi:z= \dfrac{1}{2}.\)

Find the parametrisation of the intersection curve of a sphere and a plane.

Before solving the general problem:

Let's try to relax the conditions and solve the simplest case:

Part 2: Learning trajectory

Problem 1: Find the parametric equation of the curve obtained by intersecting the sphere \(S:x^2 +y^2 +z^2 =1\) and the plane \(\Pi:z= \dfrac{1}{2}.\)

Substitute \(z=\dfrac{1}{2}\) in the equation of the sphere:

\(x^2+y^2+\left(\dfrac{1}{2}\right)^2=1\)

Using the identity \(\;\cos^2(t)+\sin^2(t)=1\)

 \(\Rightarrow\;\dfrac{4}{3}x^2+\dfrac{4}{3}y^2=1\)

\Rightarrow \left\{ \begin{array}{rcl} x&=&\dfrac{\sqrt{3}}{2}\cos(t) \\ \\ y&=&\dfrac{\sqrt{3}}{2}\sin(t) \\ \\ z&=&\dfrac{1}{2} \end{array} \right. \qquad t\in[0, 2\pi].

Part 2: Learning trajectory

\Rightarrow \left\{ \begin{array}{rcl} x&=&\dfrac{\sqrt{3}}{2} \cos(t) \\ y&=&\dfrac{\sqrt{3}}{2}\sin(t) \\ z&=&\dfrac{1}{2} \end{array} \right. \qquad t\in[0, 2\pi].

Part 2: Learning trajectory

\Rightarrow \left\{ \begin{array}{rcl} x&=&\dfrac{\sqrt{3}}{2} \cos(t) \\ y&=&\dfrac{\sqrt{3}}{2}\sin(t) \\ z&=&\dfrac{1}{2} \end{array} \right. \qquad t\in[0, 2\pi].

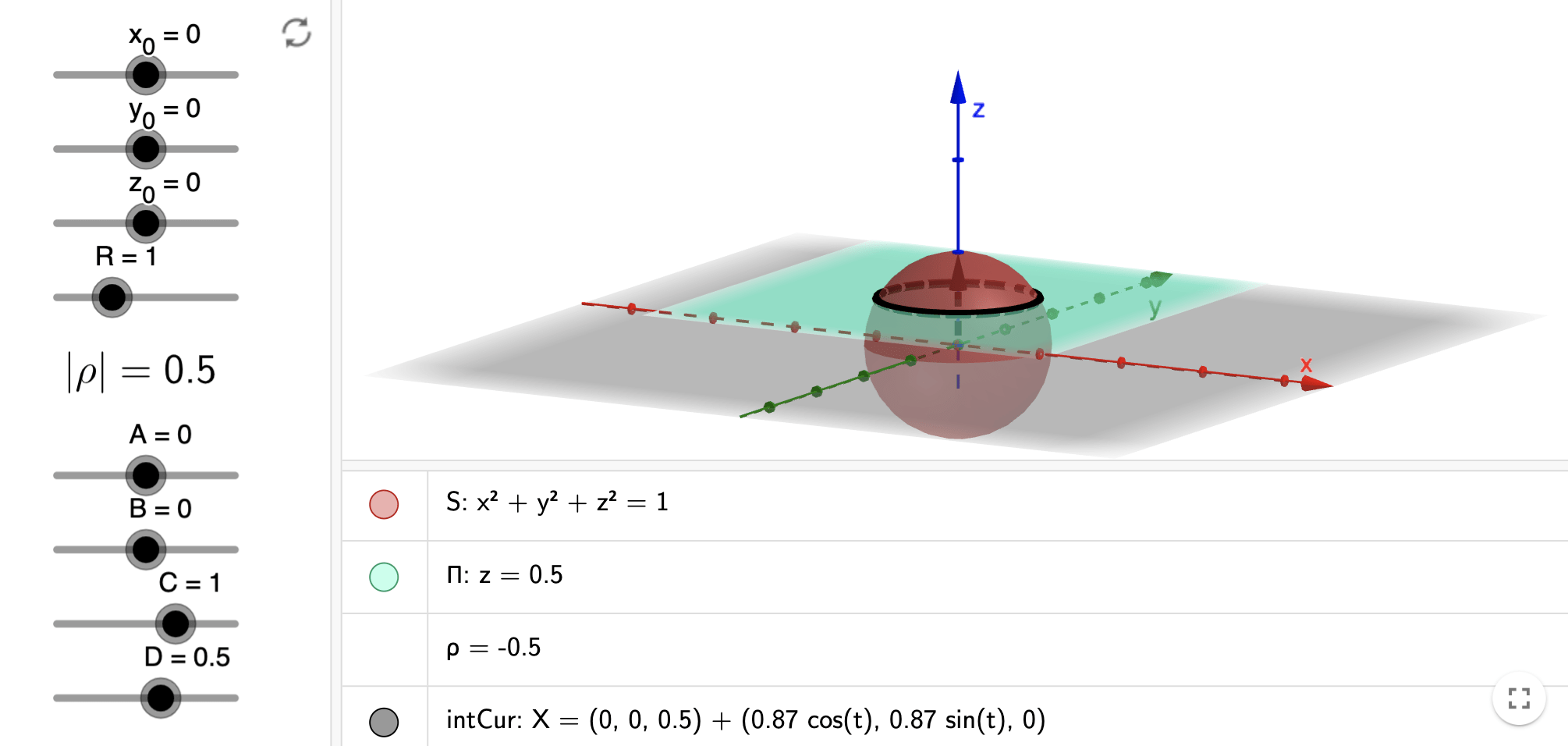
Part 2: Learning trajectory

Problem 2: Compute the parametric equations of the curve obtained by intersecting the sphere and plane given by

\(S:x^2 +y^2 +z^2 =4\;\) and \(\;\Pi:2x+2y+z=-3,\)

respectively.

Rewrite the plane as \(\;z=-3-2x-2y\)

Then we obtain \(\;x^2+y^2+\left(-3-2-x-2y\right)^2=4\)

That is \(\;5x^2+8xy+5y^2+12x+12y+5=0\)

This is a conic section, also known as a quadratic form in \(\mathbb R^2,\) and can be written in matrix form as

\[\mathbf x^T M \mathbf x+ K \mathbf x+f=0\]

Now let's try a slightly more difficult problem!

Part 2: Learning trajectory

Problem 2: Compute the parametric equations of the curve obtained by intersecting the sphere and plane given by

\(S:x^2 +y^2 +z^2 =4\;\) and \(\;\Pi:2x+2y+z=-3,\)

respectively.

That is \(\;5x^2+8xy+5y^2+12x+12y+5=0\)

Let \(\mathbf{x}=\begin{pmatrix}x\\y\end{pmatrix}.\)

\(\mathbf x^T M \mathbf x+ K \mathbf x+f=0\)

Then we have

\begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} 5&4\\4&5 \end{pmatrix} \begin{pmatrix}x\\y \end{pmatrix}+ \begin{pmatrix} 12&12\end{pmatrix} \begin{pmatrix}x\\ y \end{pmatrix}+5=0.

By means of a rotation of the plane about the origin, a translation of the plane, or both, it is possible to represent every conic in a simplified standard, or canonical, form.

Part 2: Learning trajectory

That is \(\;5x^2+8xy+5y^2+12x+12y+5=0\)

\(\mathbf x^T M \mathbf x+ K \mathbf x+f=0\)

By means of a rotation of the plane about the origin, a translation of the plane, or both, it is possible to represent every conic in a simplified standard, or canonical, form.

This process is known as diagonalisation of quadratic forms.

Let \(\mathbf{x}=\begin{pmatrix}x\\y\end{pmatrix}.\)

Then we have

\begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} 5&4\\4&5 \end{pmatrix} \begin{pmatrix}x\\y \end{pmatrix}+ \begin{pmatrix} 12&12\end{pmatrix} \begin{pmatrix}x\\ y \end{pmatrix}+5=0.

Problem 2: Compute the parametric equations of the curve obtained by intersecting the sphere and plane given by

\(S:x^2 +y^2 +z^2 =4\;\) and \(\;\Pi:2x+2y+z=-3,\)

respectively.

Part 2: Learning trajectory

That is \(\;5x^2+8xy+5y^2+12x+12y+5=0\)

\(\mathbf x^T M \mathbf x+ K \mathbf x+f=0\)

Let \(\mathbf{x}=\begin{pmatrix}x\\y\end{pmatrix}.\)

Then we have

The diagonalisation process and a change of variables provides the following expression:

9u^2+v^2+12\sqrt{2}u+5=0

the simplified standard form of

Problem 2: Compute the parametric equations of the curve obtained by intersecting the sphere and plane given by

\(S:x^2 +y^2 +z^2 =4\;\) and \(\;\Pi:2x+2y+z=-3,\)

respectively.

\begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} 5&4\\4&5 \end{pmatrix} \begin{pmatrix}x\\y \end{pmatrix}+ \begin{pmatrix} 12&12\end{pmatrix} \begin{pmatrix}x\\ y \end{pmatrix}+5=0.

Part 2: Learning trajectory

Using again the identity \(\cos^2(t)+\sin^2(t)=1\) and rewriting everything back with the variables \(x,y\) and \(z;\)

\left\{ \begin{array} {rcl} x &=&\dfrac{\sqrt{6}}{6}\cos(t)-\dfrac{\sqrt{6}}{2}\sin(t)-\dfrac{2}{3} \\ \\ y &=&\dfrac{\sqrt{6}}{6}\cos(t)+\dfrac{\sqrt{6}}{2}\sin(t)-\dfrac{2}{3} \\ \\ z &=&-\dfrac{2\sqrt{6}}{3}\cos(t)-\dfrac{1}{3} \end{array} \right. \qquad t\in[0, 2\pi].

Problem 2: Compute the parametric equations of the curve obtained by intersecting the sphere and plane given by

\(S:x^2 +y^2 +z^2 =4\;\) and \(\;\Pi:2x+2y+z=-3,\)

respectively.

we obtain the solution:

Part 2: Learning trajectory

\left\{ \begin{array} {rcl} x &=&\dfrac{\sqrt{6}}{6}\cos(t)-\dfrac{\sqrt{6}}{2}\sin(t)-\dfrac{2}{3} \\ y &=&\dfrac{\sqrt{6}}{6}\cos(t)+\dfrac{\sqrt{6}}{2}\sin(t)-\dfrac{2}{3} \\ z &=&-\dfrac{2\sqrt{6}}{3}\cos(t)-\dfrac{1}{3} \end{array} \right. \qquad t\in[0, 2\pi].

Part 2: Learning trajectory

Problem 3:  Find the parametrisation of the intersection curve of the sphere and plane \[ \left\{ \begin{array} {rl} S: &(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2 \\ \\ \Pi: & Ax+By+Cz=D,  \\ \end{array} \right. \] where \(A,B,C\) are not all simultaneously zero.

General problem!

To simplify some calculations, first we translate both objects to the origin: \[ \left\{ \begin{array} {rl} S_0: &x^2+y^2+z^2=R^2 \\ \\ \Pi_0: & A(x+x_0)+B(y+y_0)+C(z+z_0)=D  \\ \end{array} \right. \] 

Part 2: Learning trajectory

Problem 3:  Find the parametrisation of the intersection curve of the sphere and plane \[ \left\{ \begin{array} {rl} S: &(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2 \\ \\ \Pi: & Ax+By+Cz=D,  \\ \end{array} \right. \] where \(A,B,C\) are not all simultaneously zero.

Substituing the equation of the plane \(\Pi_0\) into the sphere \(S_0\) yields

\[ \left\{ \begin{array} {rl} S_0: &x^2+y^2+z^2=R^2 \\ \\ \Pi_0: & A(x+x_0)+B(y+y_0)+C(z+z_0)=D  \\ \end{array} \right. \] 

x^2+y^2+(\alpha_0-\alpha_1x-\alpha_2y -\alpha_3)^2=R^2
\text{where}\quad \alpha_0=\frac{D}{C}, \quad \alpha_1=\frac{A}{C}, \quad \alpha_2=\frac{B}{C} \quad \text{and} \quad \alpha_3=z_0+ \frac{A}{C} x_0 + \frac{B}{C}{y_0}

Part 2: Learning trajectory

Problem 3:  Find the parametrisation of the intersection curve of the sphere and plane \[ \left\{ \begin{array} {rl} S: &(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2 \\ \\ \Pi: & Ax+By+Cz=D,  \\ \end{array} \right. \] where \(A,B,C\) are not all simultaneously zero.

x^2+y^2+(\alpha_0-\alpha_1x-\alpha_2y -\alpha_3)^2=R^2

This expression is in fact a quadratic form:

\(ax^2+bxy+cy^2+dx+ey+f=0\)

So we can rewrite it as

\(\mathbf{x}^{T} M\mathbf{x}+K\mathbf{x}+f=0\)

Thus we can apply the process of diagonalisation

to obtain the solution of the general problem.

Part 2: Learning trajectory

Problem 3:  Find the parametrisation of the intersection curve of the sphere and plane \[ \left\{ \begin{array} {rl} S: &(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2 \\ \\ \Pi: & Ax+By+Cz=D,  \\ \end{array} \right. \] where \(A,B,C\) are not all simultaneously zero.

Thus we can apply the process of diagonalisation

to obtain the solution of the general problem.

\left\{ \begin{array} {rcl} x &=& p_{1,1}u+p_{1,2}v \\ \\ y &=&p_{2,1}u+p_{2,2}v \\ \\ z &=&\alpha_0-\alpha_1x-\alpha_2y -\alpha_3 \end{array} \right. \quad\quad t\in[0, 2\pi].
+\,x_0
+\,y_0
+\,z_0

Part 3: Final comments

Part 3: Final comments

  • The sequence of problems mentioned before can be adapted within a problem-solving learning environment for:
    • discussing the geometric properties of the intersection curve of the sphere and plane,
S: (x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2
\Pi: Ax+By+Cz=D
\rho = \dfrac{Ax_0+By_0+ Cy_0-D}{\sqrt{A^2+B^2+C^2}}

Part 3: Final comments

  • The sequence of problems mentioned before can be adapted within a problem-solving learning environment for:
    • discussing the geometric properties of the intersection curve of the sphere and plane,
    • establishing mathematical connections, in this case, with the process of diagonalisation of quadratic forms to solve a geometric problem.
S: (x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2
\Pi: Ax+By+Cz=D
\rho = \dfrac{Ax_0+By_0+ Cy_0-D}{\sqrt{A^2+B^2+C^2}}

\(\mathbf{x}^{T} M\mathbf{x}+K\mathbf{x}+f=0\)

\left\{ \begin{array} {rcl} x &=& p_{1,1}u+p_{1,2}v + x_0 \\ y &=&p_{2,1}u+p_{2,2}v + y_0 \\ z &=&\alpha_0-\alpha_1x-\alpha_2y -\alpha_3 + z_0 \end{array} \right. \\t\in[0, 2\pi].

Part 3: Final comments

  • GeoGebra offers different semiotic representations (e.g. geometric, algebraic, CAS) and a set of affordances for students to explore and model these problems dynamically.
Algebraic view
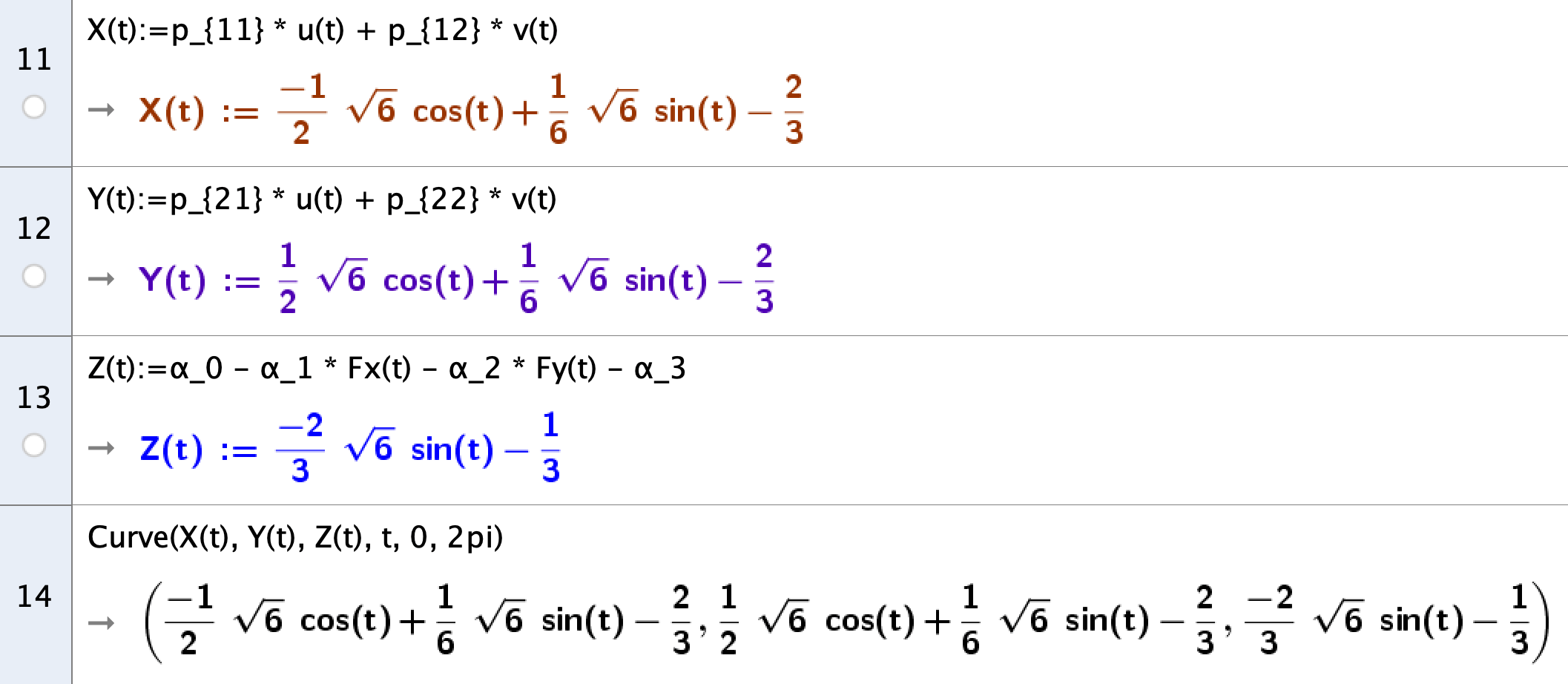
CAS view
3D view

Part 3: Final comments

  • The exploration of these models opens up novel approaches for learners to engage in mathematical thinking since they can generate different representations of a problem to visualise and contrast how numeric, graphic, and algebraic approaches are connected.
Algebraic view
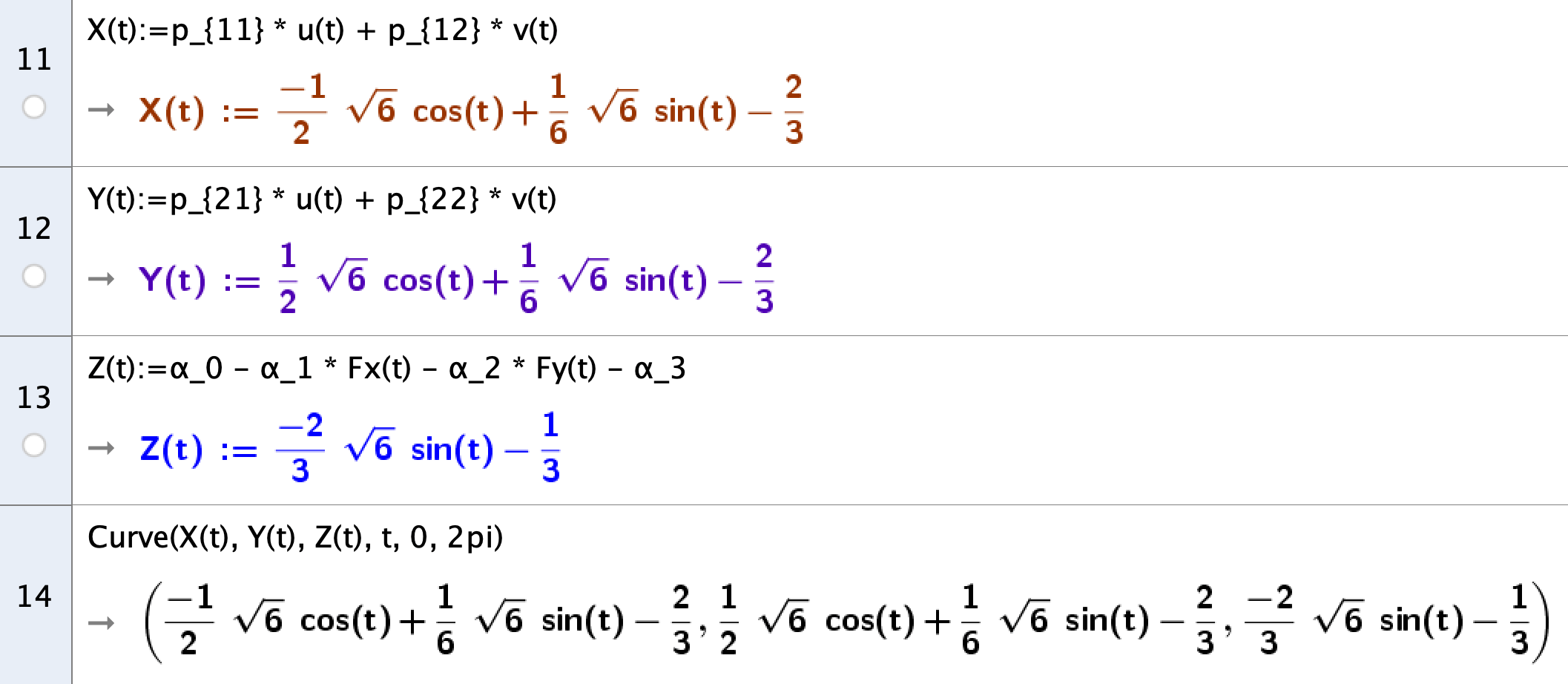
CAS view
3D view

Part 3: Final comments

  • Collaboration with Bradley Welch, a UQ student soon to become a senior maths and chemistry teacher.
  • Future work: Implement the didactic proposal in the classroom to analise how this can help students to develop their problem-solving skills and create more meaningful mathematical connections.
  • The general solution, together with the didactic proposal, has been recently published in the International Journal of Mathematical Education in Science and Technology:
  • But how does GeoGebra compute this parametrisation?
  • What are the mathematical concepts or relationships necessary to determine the values for the constants \(C_k, \;x_c, y_c, z_c\)?
\left\{ \begin{array}{l} x=C_1 \cos(t)+ C_2\sin(t)+x_c\\ y= C_3 \cos(t)+ C_4\sin(t)+y_c\\ z=C_5\sin(t)+z_c \end{array} \right.
/* 
GeoGebra - Dynamic Mathematics for Everyone
http://www.geogebra.org

This file is part of GeoGebra.

This program is free software; you can redistribute it and/or modify it 
under the terms of the GNU General Public License as published by 
the Free Software Foundation.

 */

/*
 * AlgoJoinPointsSegment
 *
 * Created on 21. August 2003
 */

package org.geogebra.common.geogebra3D.kernel3D.algos;

import org.geogebra.common.geogebra3D.kernel3D.geos.GeoConic3D;
import org.geogebra.common.kernel.Construction;
import org.geogebra.common.kernel.StringTemplate;
import org.geogebra.common.kernel.commands.Commands;
import org.geogebra.common.kernel.geos.GeoElement;
import org.geogebra.common.kernel.kernelND.GeoCoordSys2D;
import org.geogebra.common.kernel.kernelND.GeoQuadricND;
import org.geogebra.common.kernel.matrix.CoordMatrix;

/**
 *
 * @author ggb3D
 * 
 */
public class AlgoIntersectPlaneQuadric extends AlgoElement3D {

	// inputs
	/** plane */
	protected GeoCoordSys2D plane;
	/** second coord sys */
	protected GeoQuadricND quadric;

	// output
	/** intersection */
	protected GeoConic3D conic;

	private CoordMatrix cm = new CoordMatrix(3, 3);
	private CoordMatrix tmpMatrix = new CoordMatrix(3, 4);
	private CoordMatrix parametricMatrix;

	/**
	 * Creates new AlgoIntersectLinePlane
	 * 
	 * @param cons
	 *            the construction
	 * @param plane
	 *            plane
	 * @param quadric
	 *            quadric
	 * @param addToCons
	 *            whether to add to cons
	 */
	AlgoIntersectPlaneQuadric(Construction cons, GeoCoordSys2D plane,
			GeoQuadricND quadric, boolean addToCons) {

		super(cons, addToCons);

		this.plane = plane;
		this.quadric = quadric;

		conic = newConic(cons);

		// end
		if (addToCons) {
			end();
		}
	}

	/**
	 * Creates new AlgoIntersectLinePlane
	 * 
	 * @param cons
	 *            the construction
	 * @param plane
	 *            plane
	 * @param quadric
	 *            quadric
	 */
	AlgoIntersectPlaneQuadric(Construction cons, GeoCoordSys2D plane,
			GeoQuadricND quadric) {

		this(cons, plane, quadric, true);

	}

	/**
	 * end of contructor for this algo
	 */
	protected void end() {
		setInputOutput(new GeoElement[] { plane.toGeoElement(), quadric },
				new GeoElement[] { conic });
	}

	/**
	 * 
	 * @param cons1
	 *            construction
	 * @return new conic for intersection
	 */
	protected GeoConic3D newConic(Construction cons1) {
		return new GeoConic3D(cons1, true);
	}

	/**
	 * return the intersection
	 * 
	 * @return the intersection
	 */
	public GeoConic3D getConic() {
		return conic;
	}

	// /////////////////////////////////////////////
	// COMPUTE

	@Override
	public void compute() {
		conic.setCoordSys(plane.getCoordSys());
		if (!quadric.isDefined() || !plane.isDefined()) {
			conic.setUndefined();
			return;
		}
		intersectPlaneQuadric(plane, quadric, conic);
	}

	private void intersectPlaneQuadric(GeoCoordSys2D inputPlane,
			GeoQuadricND inputQuad, GeoConic3D outputConic) {
		if (parametricMatrix == null) {
			parametricMatrix = new CoordMatrix(4, 3);
		}
		CoordMatrix qm = inputQuad.getSymetricMatrix();
		CoordMatrix pm = inputPlane.getCoordSys()
				.getParametricMatrix(parametricMatrix);

		// sets the conic matrix from plane and quadric matrix
		cm.setMul(tmpMatrix.setMulT1(pm, qm), pm);

		outputConic.setCoordSys(inputPlane.getCoordSys());
		outputConic.setMatrix(cm);

	}

	@Override
	public Commands getClassName() {
		return Commands.IntersectPath;
	}

	@Override
	final public String toString(StringTemplate tpl) {
		StringBuilder sb = new StringBuilder();

		sb.append(getLoc().getPlain("IntersectionCurveOfAB",
				plane.getLabel(tpl), quadric.getLabel(tpl)));

		return sb.toString();
	}

}

We need to study the source code of  GeoGebra, which is written in Java.

For example this:

  • Future work: Investigate more in depth the source code of GeoGebra