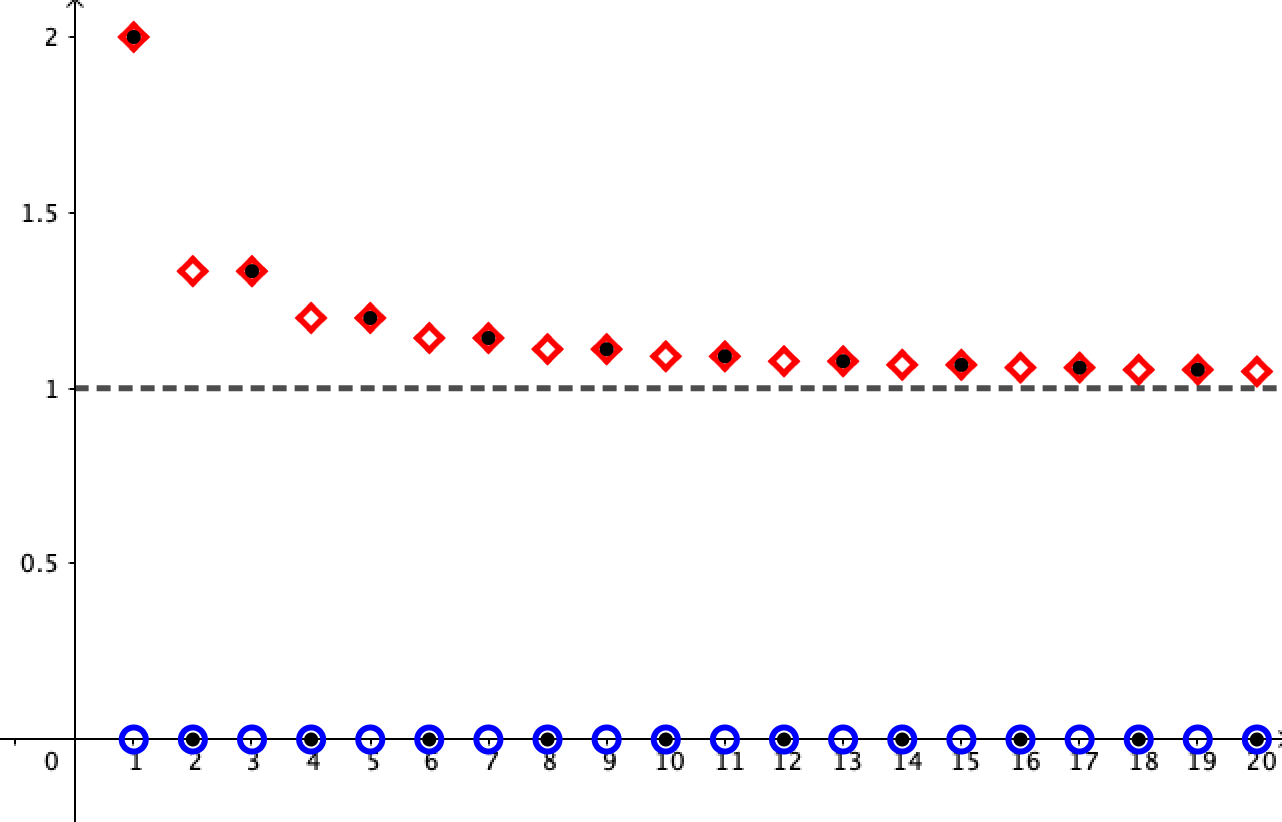
Upper & Lower limits

Example - Week 2

Example 2.4.1.

\(\{x_n\}\) where,

x_n := \begin{cases} \frac{n+1}{n} & \text{if } n \text{ is odd,} \\ 0 & \text{if } n \text{ is even.} \end{cases}

Example 2.4.1.

\(\{x_n\}\) where,

x_n := \begin{cases} \frac{n+1}{n} & \text{if } n \text{ is odd,} \\ 0 & \text{if } n \text{ is even.} \end{cases}

\left\{ 2, 0, \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, 0, \frac{16}{15}, 0, \frac{18}{17} \ldots \right\}

\(n=1\)

\(2\)

\(n=2\)

\(0\)

\(n=3\)

\(\displaystyle\frac{4}{3}\)

\(n=4\)

\(0\)

\(n=5\)

\(\displaystyle \frac65\)

Example 2.4.1.

\left\{ 2, 0, \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, 0, \frac{16}{15}, 0, \frac{18}{17} \ldots \right\}

\(\{x_n\}\) where,

x_n := \begin{cases} \frac{n+1}{n} & \text{if } n \text{ is odd,} \\ 0 & \text{if } n \text{ is even.} \end{cases}

Example 2.4.1.

\(b_n=\inf\{x_k:k\geq n\}\)

\(\displaystyle\liminf_{n\rightarrow \infty}x_n\)

\(b_1=\inf\{x_k:k\geq 1\}\)

\(b_2=\inf\{x_k:k\geq 2\}\)

\(b_3=\inf\{x_k:k\geq 3\}\)

\(=\displaystyle\lim_{n\rightarrow \infty}b_n\)

\left\{ 2, 0, \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, 0, \frac{16}{15}, 0, \frac{18}{17} \ldots \right\}

=\inf\left\{ 2, 0, \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, \ldots \right\}

=\inf \left\{ 0, \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, \ldots \right\}

=\inf \left\{ \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, \ldots \right\}

\(=0\)

Example 2.4.1.

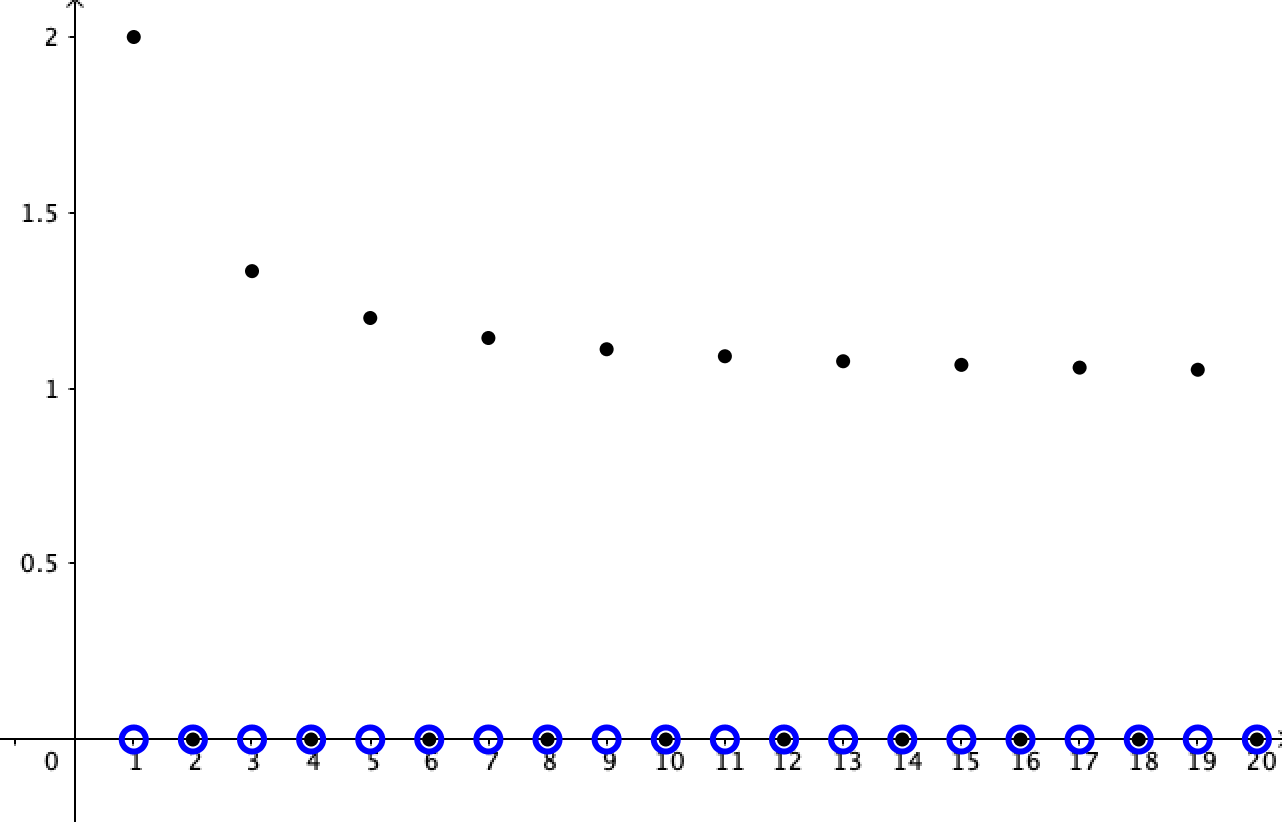
\left\{ 2, 0, \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, 0, \frac{16}{15}, 0, \frac{18}{17} \ldots \right\}

\(\displaystyle\liminf_{n\rightarrow \infty}x_n\)

\(=\displaystyle\lim_{n\rightarrow \infty}b_n\)

\(=0\)

Example 2.4.1.

\(a_n=\sup\{x_k:k\geq n\}\)

\(\displaystyle\limsup_{n\rightarrow \infty}x_n\)

\(a_1=\sup\{x_k:k\geq 1\}\)

\(a_2=\sup\{x_k:k\geq 2\}\)

\(a_3=\sup\{x_k:k\geq 3\}\)

\(=\displaystyle\lim_{n\rightarrow \infty}a_n\)

\left\{ 2, 0, \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, 0, \frac{16}{15}, 0, \frac{18}{17} \ldots \right\}

=\sup\left\{ 2, 0, \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, \ldots \right\}

=\sup \left\{ 0, \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, \ldots \right\}

=\sup \left\{ \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, \ldots \right\}

\(=2\)

\(=\dfrac43\)

\(=1\)

\(a_4=\sup\{x_k:k\geq 4\}\)

=\sup \left\{ 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, \ldots \right\}

\(=\dfrac65\)

= \begin{cases} \frac{n+1}{n} & \text{if } n \text{ is odd,} \\ \frac{n+2}{n+1} & \text{if } n \text{ is even.} \end{cases}

Example 2.4.1.

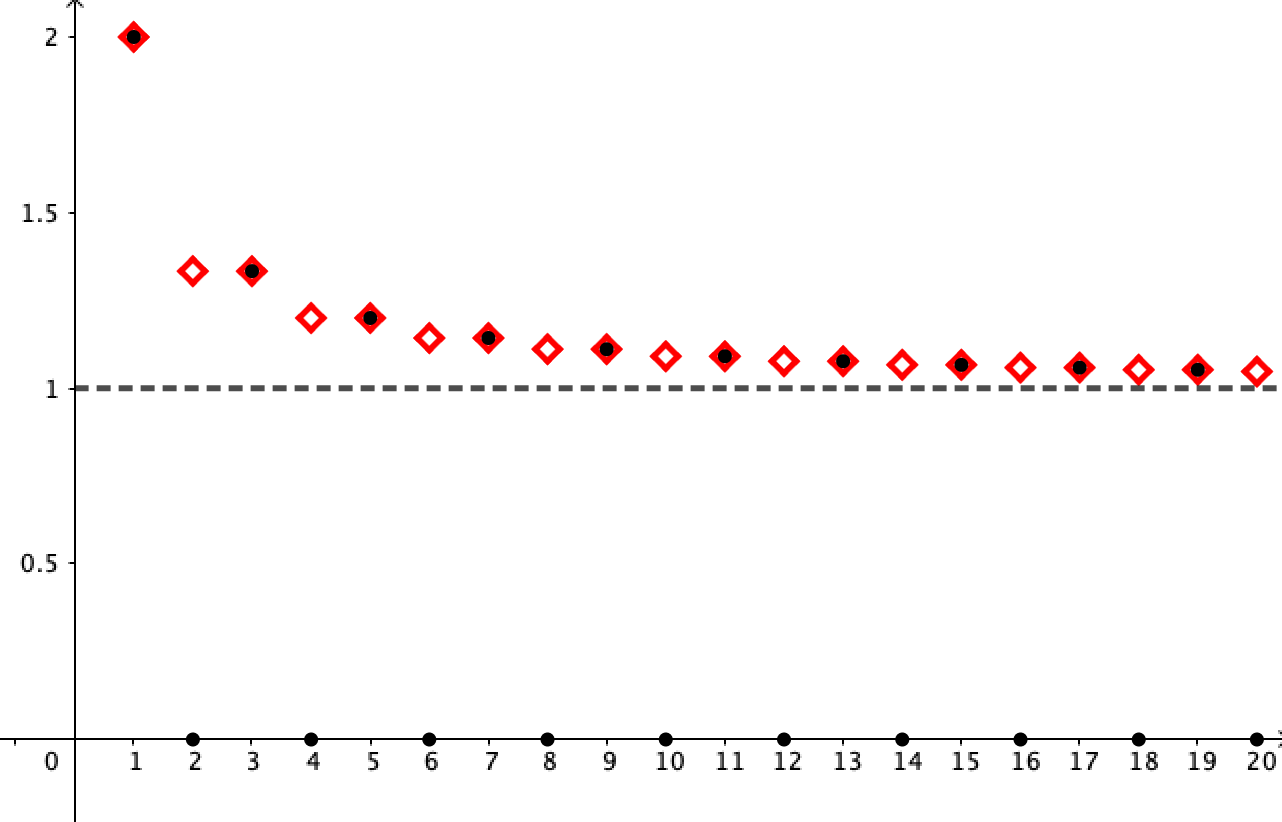
\left\{ 2, 0, \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, 0, \frac{16}{15}, 0, \frac{18}{17} \ldots \right\}

\(\displaystyle\limsup_{n\rightarrow \infty}x_n\)

\(=\displaystyle\lim_{n\rightarrow \infty}a_n\)

\(=1\)

Example 2.4.1.

\(\displaystyle\limsup_{n\rightarrow \infty}x_n=1\)

\left\{ 2, 0, \frac{4}{3}, 0, \frac{6}{5}, 0, \frac{8}{7}, 0, \frac{10}{9}, 0, \frac{12}{11}, 0, \frac{14}{13}, 0, \frac{16}{15}, 0, \frac{18}{17} \ldots \right\}

\(\displaystyle\liminf_{n\rightarrow \infty}x_n=0\)