Visualising
Complex Functions
Enhanced phase portraits
- What domain colouring is
- How it can be implemented in the computer
- How we can use it to explore complex functions
Complex functions
f:\mathbb C \rightarrow \mathbb C
live in a 4-dimensional space
Methods to visualize complex functions
- Real and Imaginary components
- Analytic Landscapes
- Mappings
- Domain colouring
Real and Imaginary components
f(z) = \text{Re}(z) + i \, \text{Im}(z)
f(z) = z^2
f(z) = x^2-y^2 + 2xy\,i
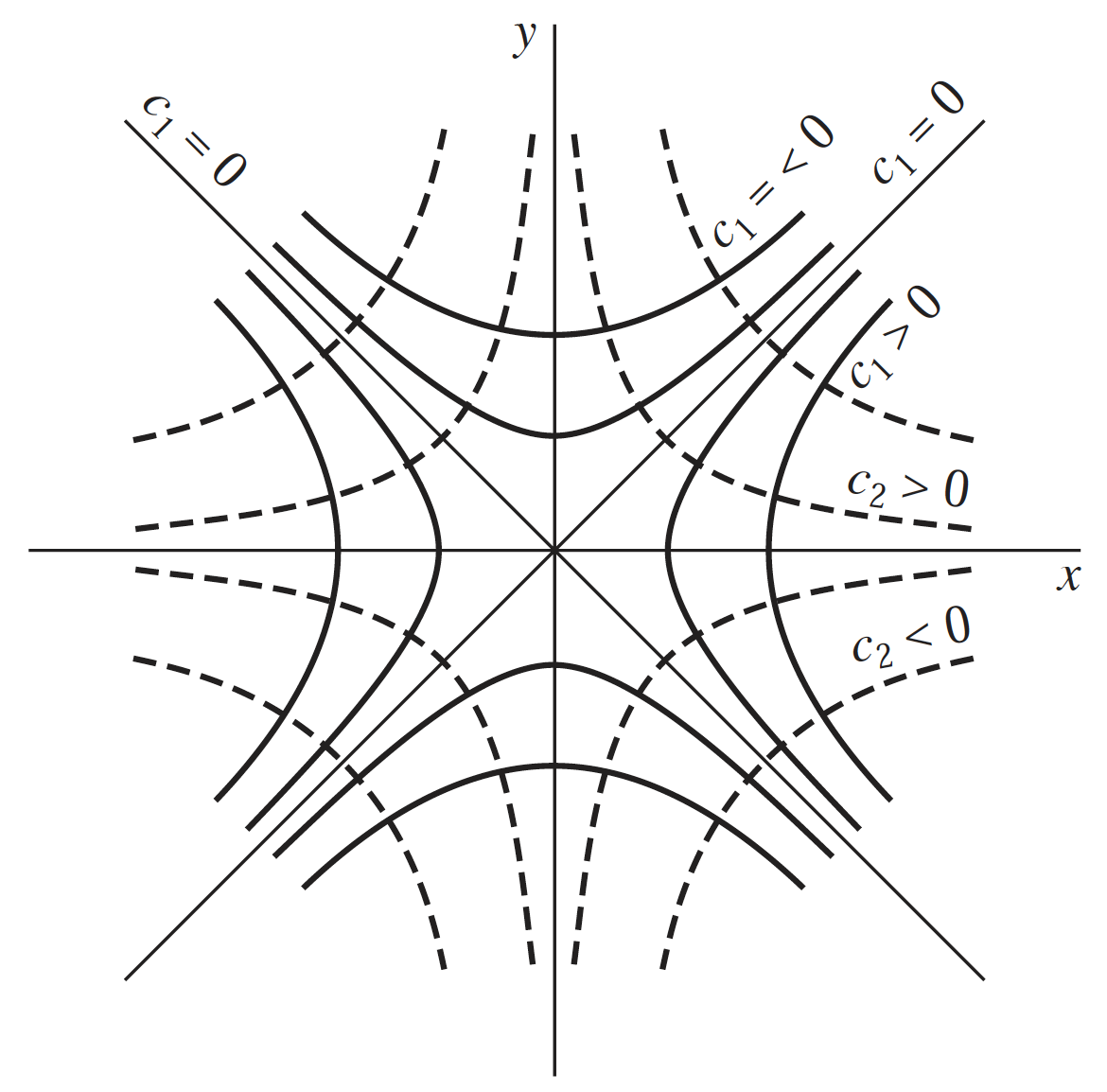
f(z) = x^2-y^2 + 2xy\,i
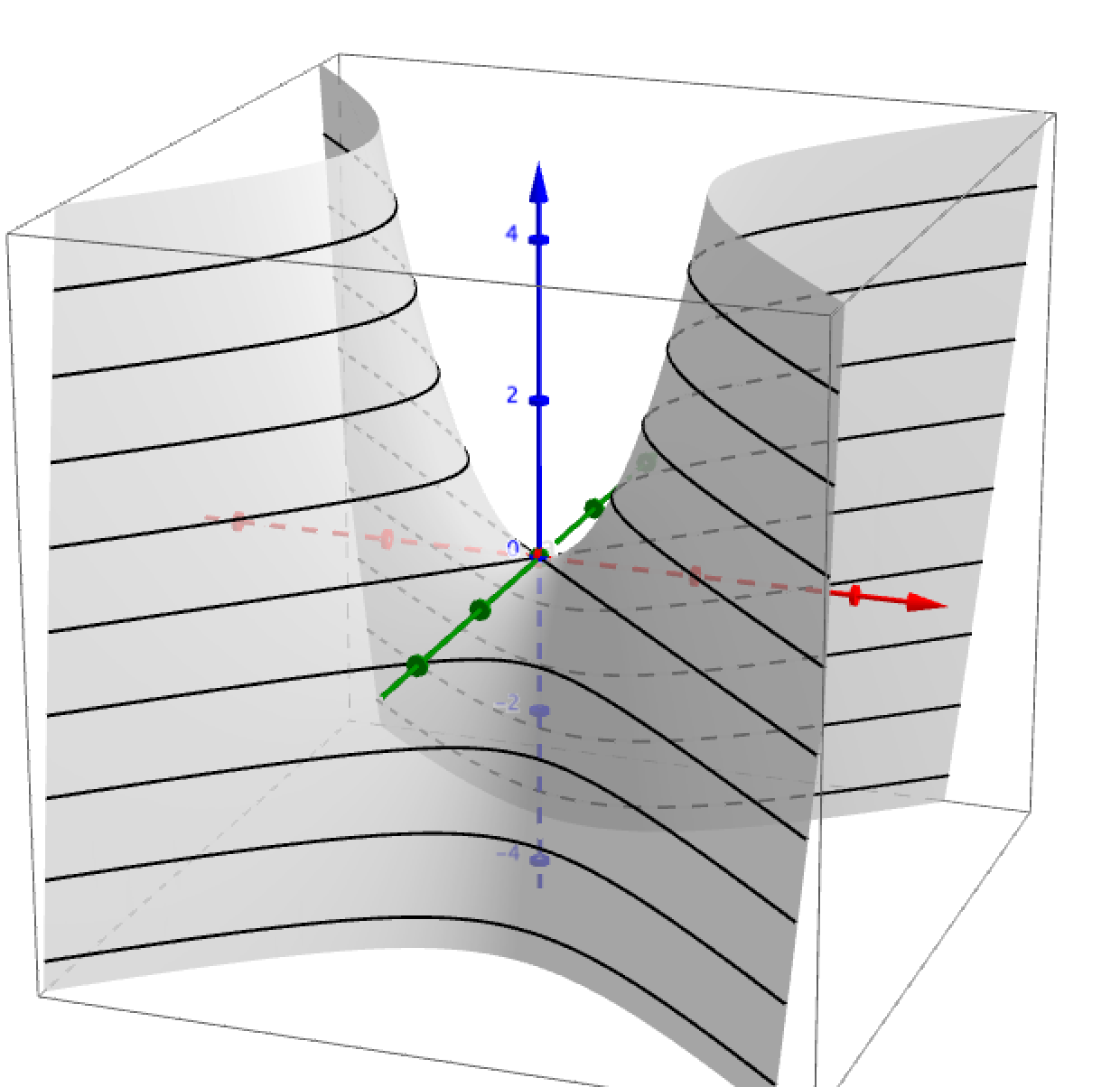
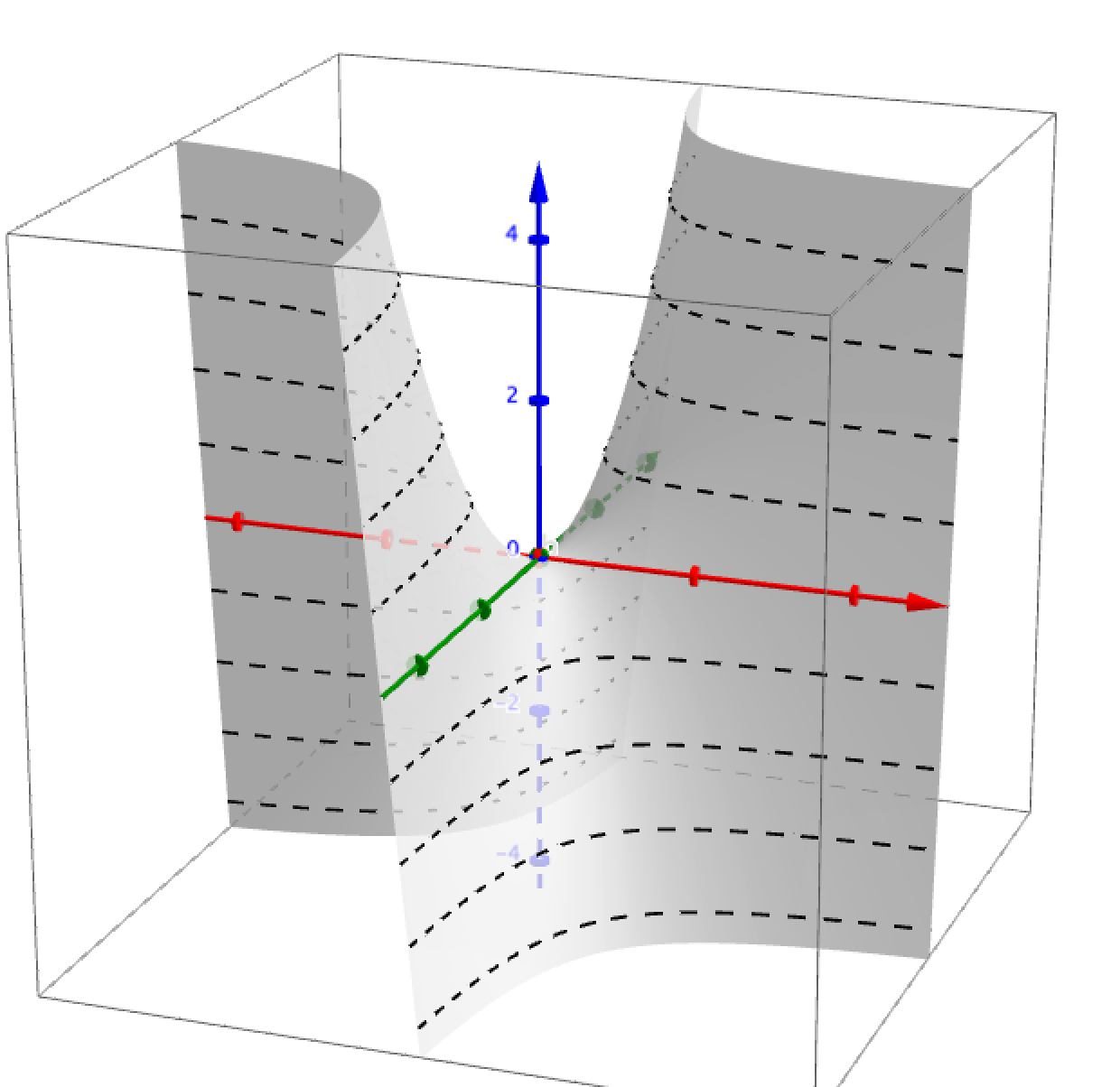
\text{Re}(z^2)
\text{Im}(z^2)
Analytic Landscapes
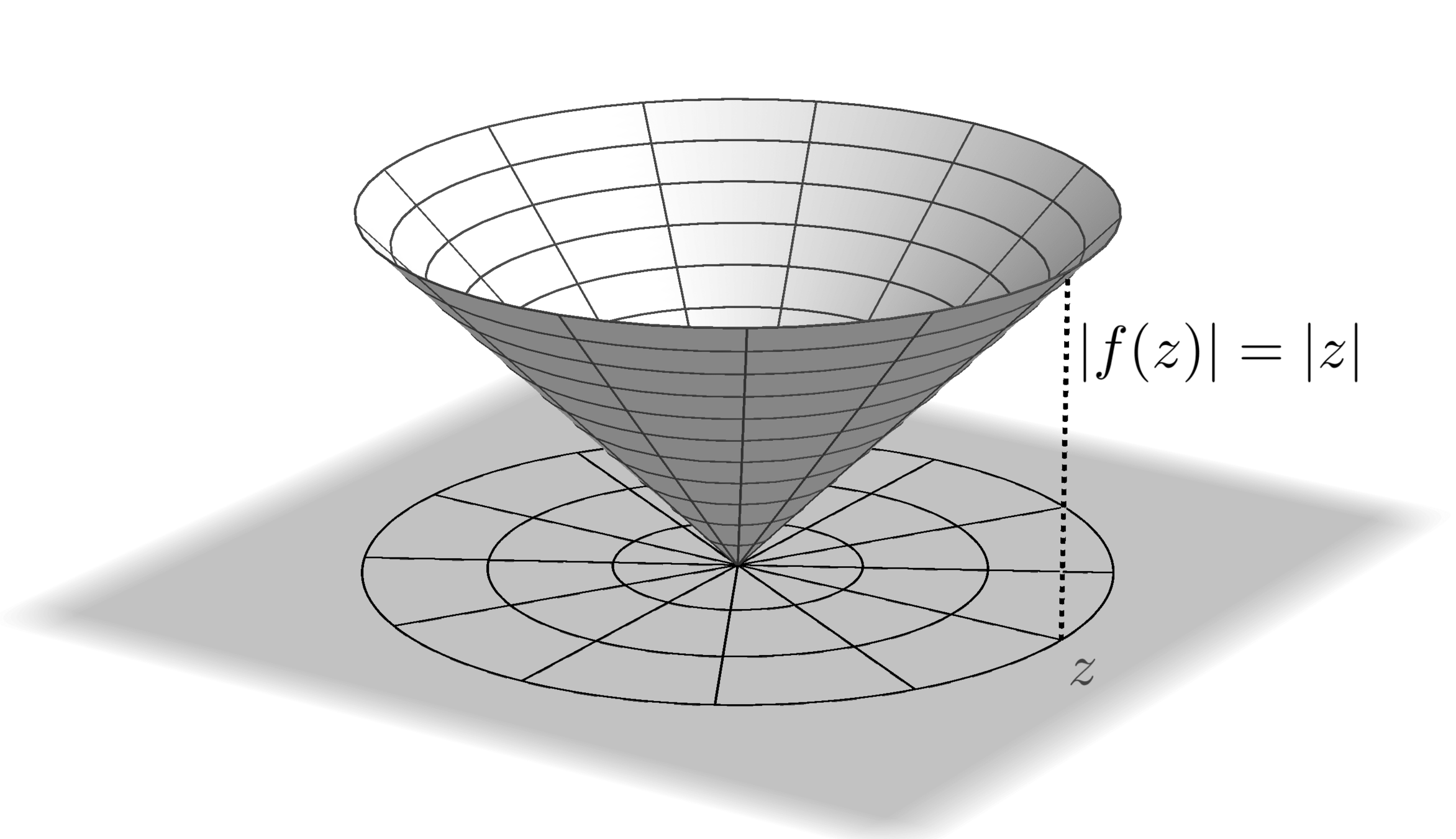
\big| f(z) \big|
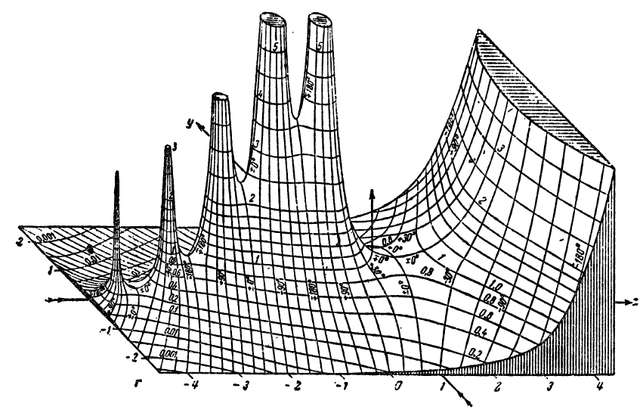
A historical analytic landscape of \(\big|\Gamma(z)\big|\) from 1909
Funktionentafeln mit Formeln und Kurven by Eugene Jahnke & Fritz Emde
Mappings
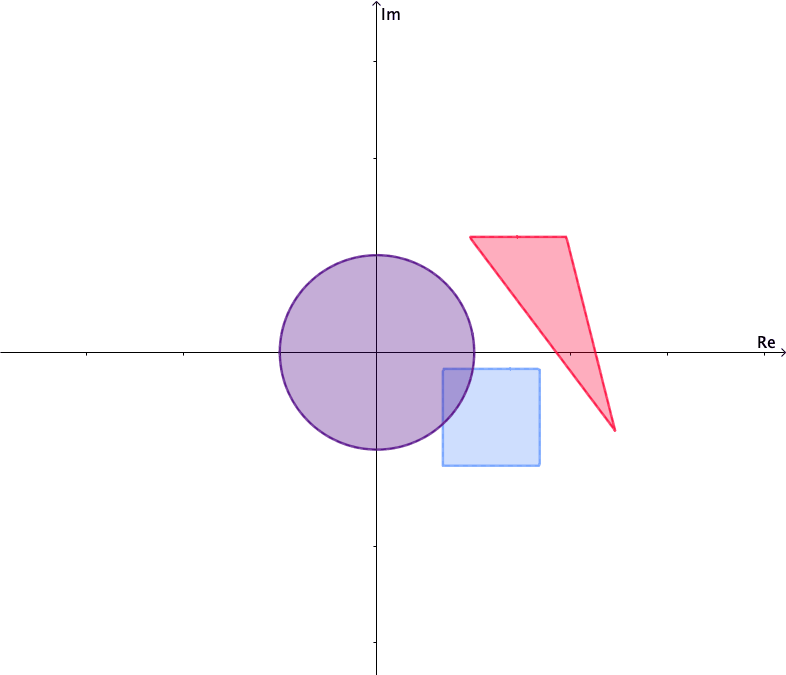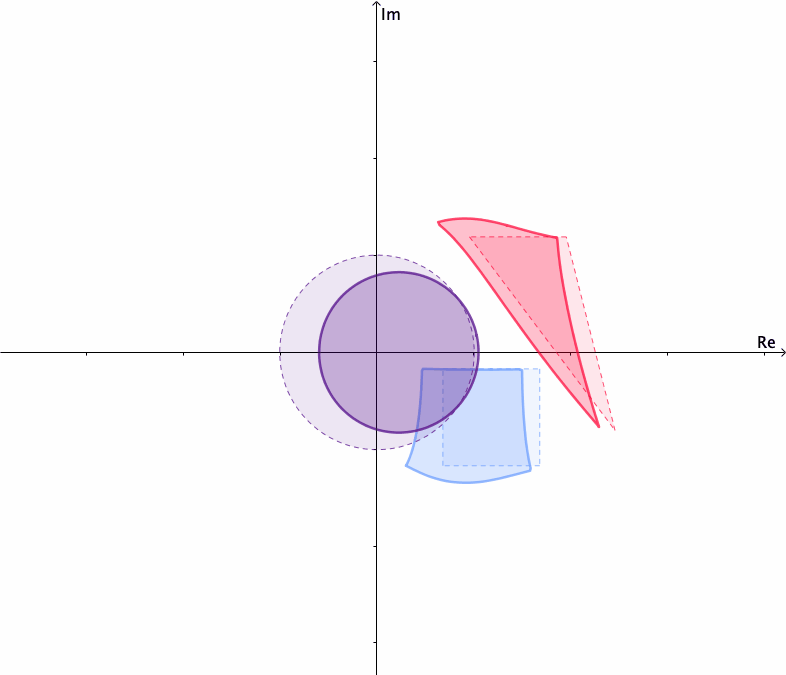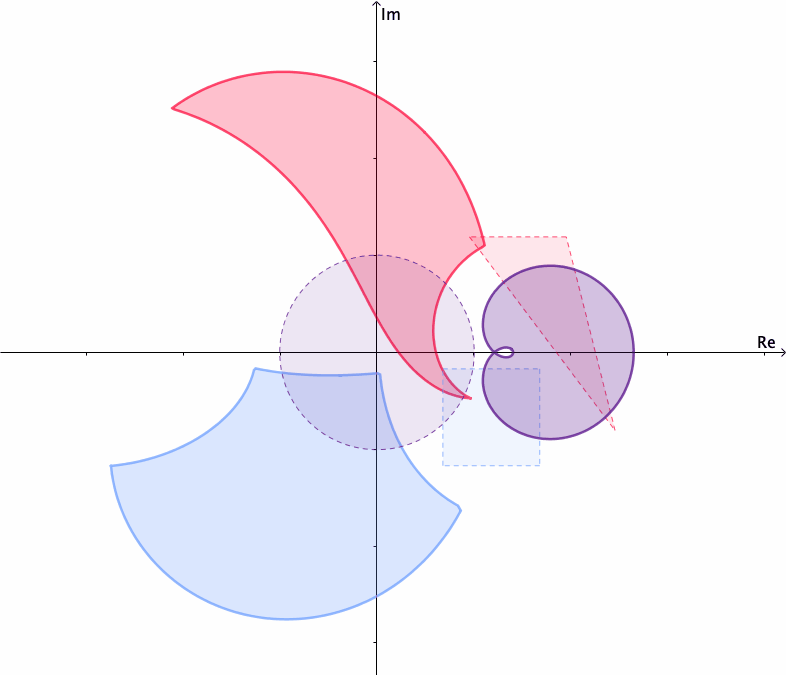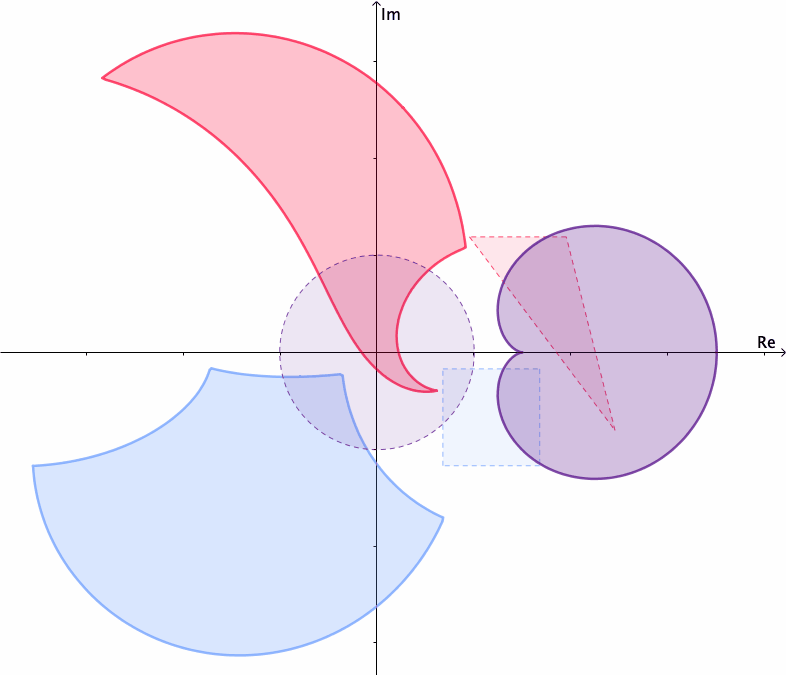
Mappings
Domain colouring
Phase portraits
Domain colouring
- Assign a colour to every point in the complex plane.
- Colour the domain of \(f\) by painting the location \(z\) with the colour determined by the value \(f(z)\).
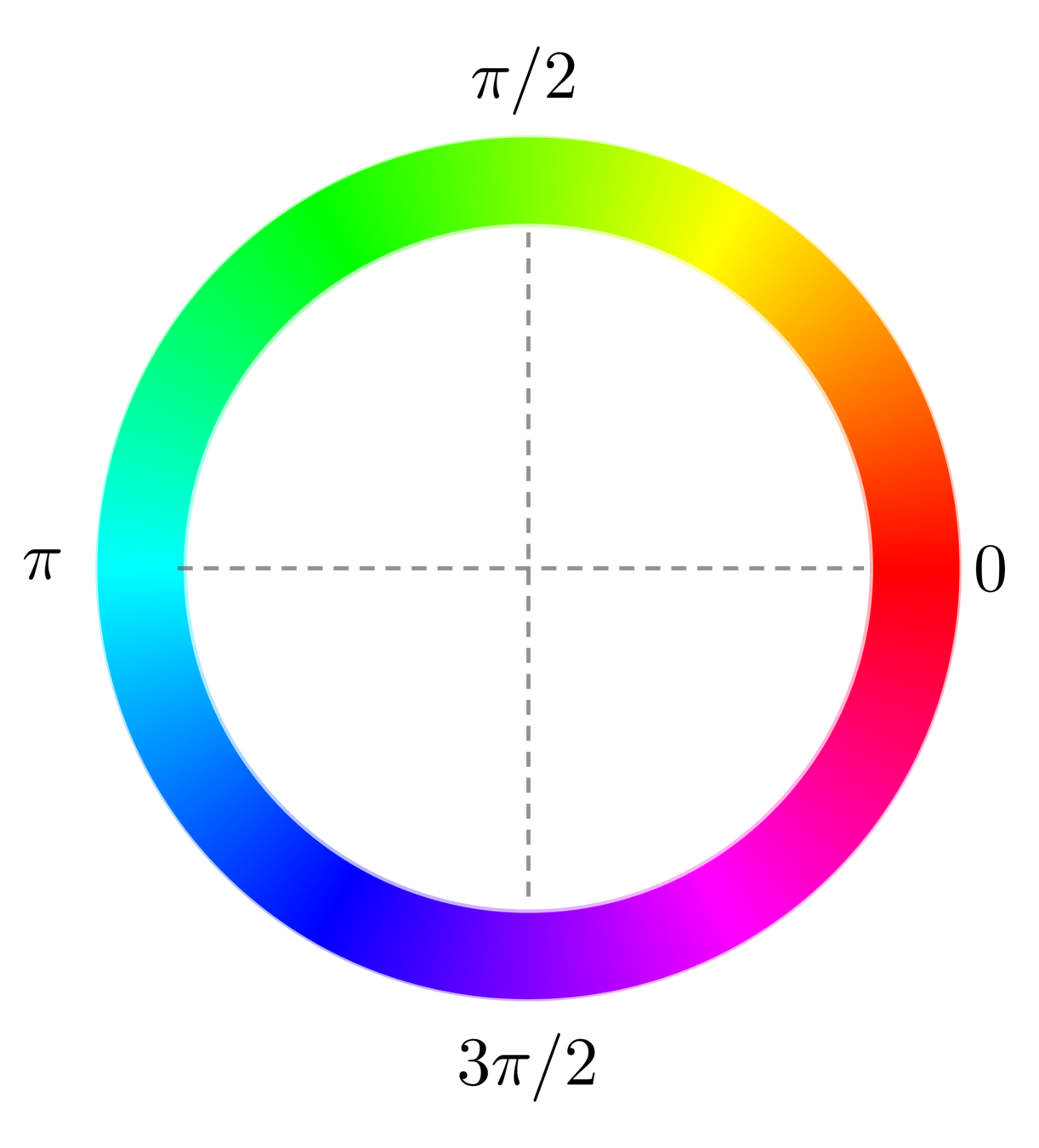
The colour wheel
- H = Phase
-
S = 1
- B = 1
Hue , Saturation & Brightness
(HSB)
Implementation in the computer
- Mathematica
- MATLAB
- Python
- Java
- C++
- GeoGebra
- JavaScript
- CindyJS
- p5.js
Implementation in the computer
Basic Examples
Phase portraits
Phase portrait
f(z)=z\\
[-2,2] \times [-2,2]

Phase portrait
f(z)=\dfrac{1}{z}\\
[-2,2] \times [-2,2]

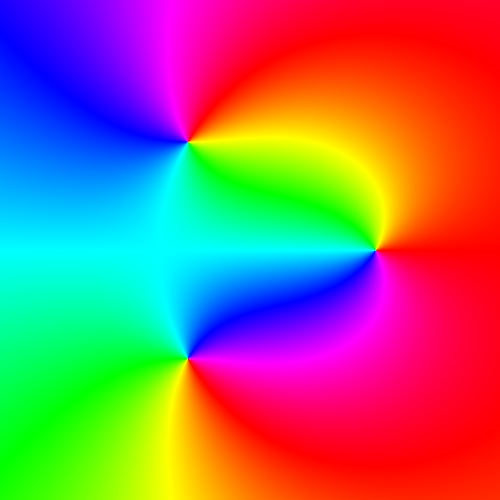
Phase portrait
f(z)=\dfrac{z-1}{z^2+z+1}\\
[-2,2] \times [-2,2]
Enhanced phase portraits
- H = Phase
-
S = 1
- B = \(\log\big|f\big|- \lfloor \log |f| \rfloor\)
Elias Wegert's work from 2012

=\text{Phase}-\lfloor \text{Phase} \rfloor
Enhanced phase portraits: Level curves



f(z)=z
Phase
Modulus
Enhanced phase portraits: Level curves



f(z)=z
Phase
Modulus
Combined
Enhanced phase portraits: Modulus

f(z)=z
f(z)=1/z

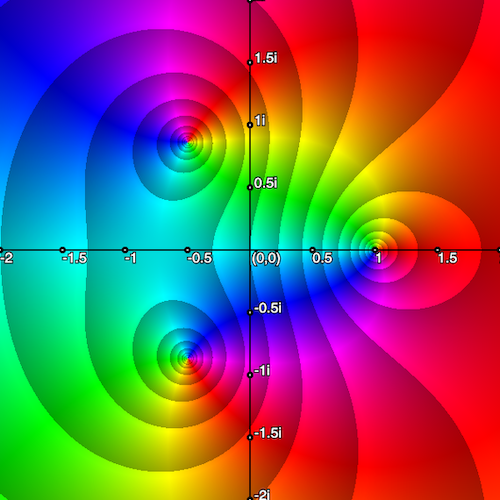
Enhanced phase portraits: \(f(z)=\dfrac{z-1}{z^2+z+1}\)

More examples...
Roots of unity: \(z^n-1,\;n=2,3,\ldots,10\)
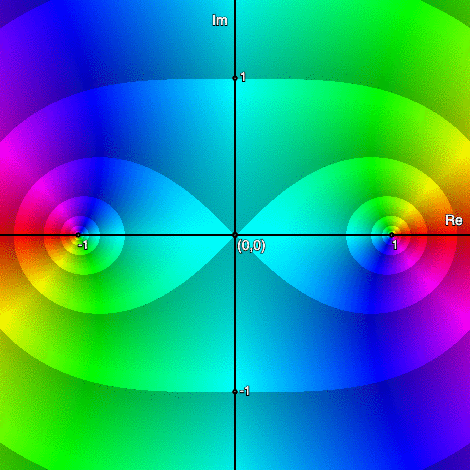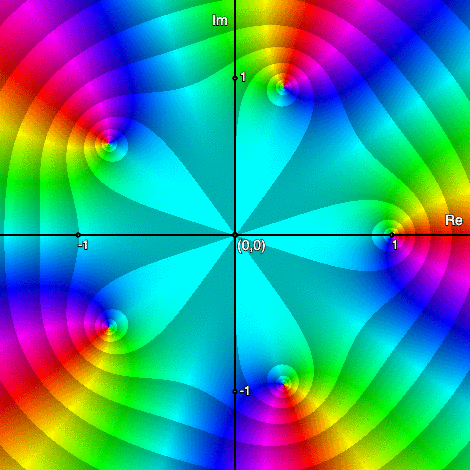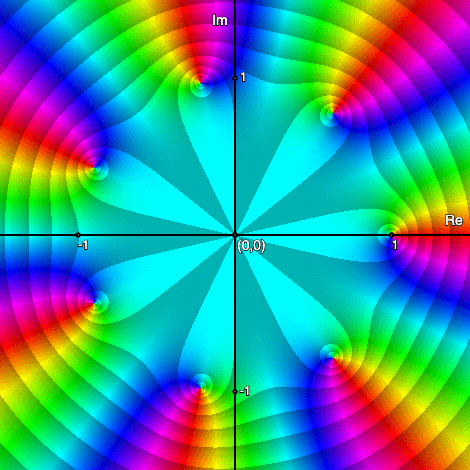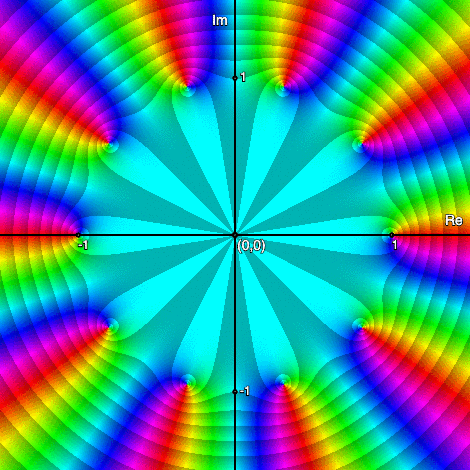
Multiplicity of zeros & Order of poles

f(z)=(z+1)z^2(z-1)^3
g(z)=1/f(z)

Analytic vs Non-Analytic functions

f(z)=\frac{3}{2}z(1+iz)
g(z)=\frac{3}{2}z(1-i\overline{z})

Laurent series
f(z)=\displaystyle\sum_{n=0}^{\infty} a_n(z-z_0)^n+\displaystyle\sum_{n=1}^{\infty}\frac{b_n}{(z-z_0)^n},
R_1 <|z-z_0|< R_2.
a_n=\frac{1}{2\pi i}\displaystyle \oint_C \frac{f(z)dz}{(z-z_0)^{n+1}}\quad (n=0,1,2,\ldots)
b_n=\frac{1}{2\pi i}\displaystyle \oint_C \frac{f(z)dz}{(z-z_0)^{-n+1}}\quad (n=1,2,\ldots)




\dfrac{1-\cosh(z)}{z^3}
Poles of order \(m\): \(\exists m \geq 1, \, b_m\neq 0\) and \(b_k=0\) for \(k>m\).
\dfrac{\exp(2z)}{(z-1)^2}
\dfrac{\sinh(z)}{z^4}
Removable singularities: If \(b_n=0,\; \forall n\)

\dfrac{\sin(z)}{z}
\dfrac{z}{e^z-1}

Essential singularities: If \(b_k\neq0\) for infinitely many \(k\)

\sin \left(\dfrac{1}{z}\right)
\exp \left(\dfrac{1}{z}\right)

Zooming in
\(f(z)=\exp\left(\dfrac{1}{z}\right)\)

Other colour schemes



\(f(z)=0.926(z+0.073857 z^5+0.0045458 z^9)\)
Discrete HSV
RGB
B&W
Thank you!
Online resources:
https://www.dynamicmath.xyz/domain-coloring/
Contact:
j.ponce@uq.edu.au
Slides: reveal.js