The Zip Command in

GeoGebra

\{1,2,3,4,5\}\\ \{2,4,8,16,32,64\}\\ \{0, 0.1, 0.2, 0.3, 0.4, 0.5\}\\ \vdots
\{(2, 1), (2, 2), (2, 3), (2, 4), (2, 5)\}\\ \left\{x, x^2, x^3, x^4, x^5, x^6, x^7, x^8, x^9, x^{10}\right\}\\ \{\text{Sphere1}, \text{Sphere2}, \text{Sphere3},\text{Sphere4}\}\\

Command

Zip()

Command

Zip()
\{1,2,3,4,5\}\\ \{2,4,8,16,32,64\}\\ \{0, 0.1, 0.2, 0.3, 0.4, 0.5\}\\ \vdots

Sequence (list) of numbers

Sequence (list) of objects

\{(1, 2), (2, 2), (3, 2), (4, 2), (5, 2)\}\\

Command

Zip()
\left\{x, x^2, x^3, x^4, x^5, x^6, x^7, x^8, x^9, x^{10}\right\}

Command

Zip()

Sequence (list) of objects

\{\text{Polygon1}, \text{Polygon2}, \text{Polygon3},\text{Polygon4}\}

Command

Zip()

Sequence (list) of objects

Wait a second!

Sequence()

The

command

does exactly that!

Why do we need another command that does the same?

Command

Zip()
Sequence( End Value )

Sequence( Start Value, End Value )

Sequence( Start Value, End Value, Increment )

Sequence( Expression, Variable, Start Value, End Value )

Sequence( Expression, Variable, Start Value, End Value, Increment )

It is an efficient and intuitive way to create

lists of numbers and objects

Sequence( End Value )
Sequence( Start Value, End Value )
Sequence( Start Value, End Value, Increment )
Sequence( Expression, Variable, Start Value, End Value )
Sequence( Expression, Variable, Start Value, End Value, Increment )
Zip( Expression, Var1, List1, Var2, List2, ...)

Looks like we're limited to just one input option!

What exactly does the Zip command do?
Zip( Expression, Var1, List1, Var2, List2, ...)

Creates a list of objects

by elements of corresponding lists

obtained by substitution of variables in the expression

According to the GeoGebra Manual

Examples

Lists of numbers

GeoGebra Classic 5

Desktop

GeoGebra Classic 6

Desktop & Online

Type the scripts (or GeoGebra code) in the Input box

Lists of numbers: Example 1

list1 = {1, 2, 3, 4, 5}
L = Zip(2*k+1, k, list1)

Input:

 L = {3, 5, 7, 9, 11}

Output:

Sequence(2*k+1, k, 1, 5)

Equivalent to:

Lists of numbers: Example 2

list1 = {0, 0.5, 1, 1.5, 2}
L = Zip(i^2+1, i, list1)

Input:

 L = {1, 1.25, 2, 3.35, 5}

Output:

Sequence(i^2+1, i, 0, 2, 0.5)

Equivalent to:

Lists of numbers: Example 3

list1 = Sequence(k, k, -4, 4, 0.2)
L = Zip(2*k, k, list1)

Input:

Lists of numbers: Example 3

list1 = Sequence(k, k, -4, 4, 0.2)
L = Zip(2*k, k, list1)

Input:

Sequence(2*k, k, -4, 4, 0.2)

Equivalent to:

Output:

 list1 = {-4, -3.8, -3.6, ..., 3.6, 3.8, 4}
 L = {-8, -7.6, -7.2, -6.8,..., 7.2, 7.6, 8}
Sequence(2*k, k, -4, 4, 0.2)
list1 = {1, 2, 3, 4, 5}
L = Zip(2*k+1, k, list1)
Sequence(2*k+1, k, 1, 5)
Sequence(i^2+1, i, 0, 2, 0.5)
list1 = {0, 0.5, 1, 1.5, 2}
L = Zip(i^2+1, i, list1)
list1 = Sequence(k, k, -4, -4, 0.2)
L = Zip(2*k, k, list1)
Here, both commands do pretty much the same.

An additional list needs to be predefined for the Zip command

Examples

Lists of objects

Lists of objects: Example 4

P = (-2, -2)
Q = (2, -2)
R = (-2, 2)
S = (2, 2)
Zip(Midpoint(A, B), A, {P, Q}, B, {R, S})

Lists of objects: Example 4

P = (-2, -2)
Q = (2, -2)
R = (-2, 2)
S = (2, 2)
Zip(Midpoint(A, B), A, {P, Q}, B, {R, S})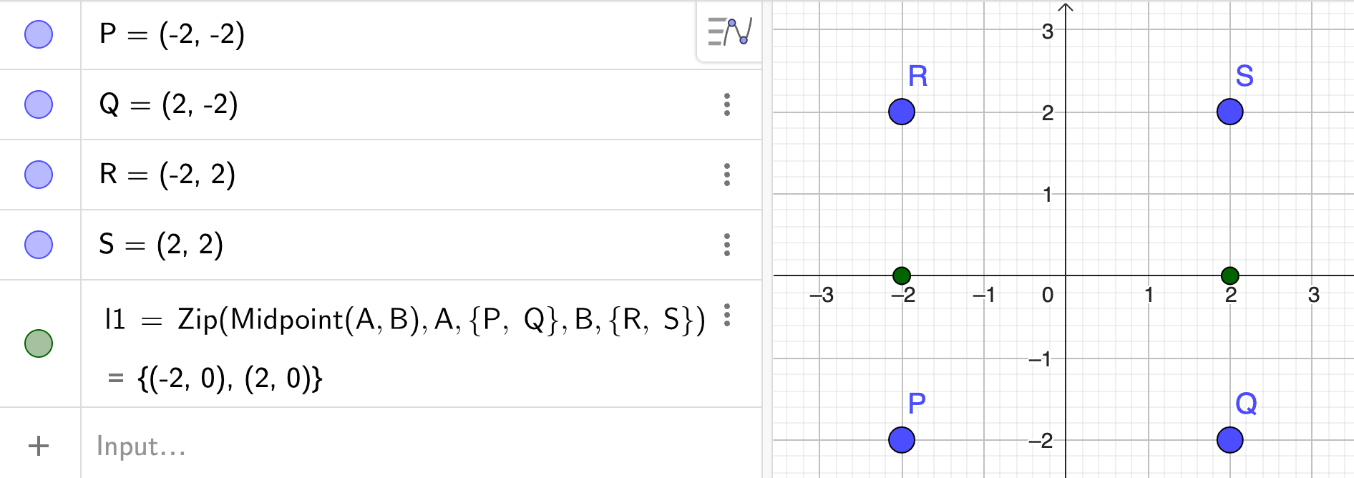

Lists of objects: Example 4

Zip(Midpoint(A, B), A, {P, Q}, B, {R, S})

Creates a list of objects (midpoints)

by elements of corresponding lists

obtained by substitution of variables in the expression

Lists of objects: Example 4

Sequence(Midpoint(Element({P,Q}, k), Element({R,S}, k)), k, 1, 2)

We can also use the Sequence command:

But we need to introduce an extra command: Element()

Zip(Midpoint(A, B), A, {P, Q}, B, {R, S})

Lists of objects: Example 4

Sequence(Midpoint(Element({P,Q}, k), Element({R,S}, k)), k, 1, 2)
Zip(Midpoint(A, B), A, {P, Q}, B, {R, S})

Using the Zip command not only reduces code

but also makes it more concise

Lists of objects: Example 5

A = (1, -3)
B = (3, -3)
C = (1, 1)
D = (3, 1)
E = (-3, 1)
F = (-1, 1)
G = (-3, -3)
H = (-1, -3)

Lk = {3, 4, 5, 6}

Zip(Polygon(P, Q, k), P, {A, C, G, E}, Q, {B, D, H, F}, k, Lk)

Lists of objects: Example 5

A = (1, -3)
B = (3, -3)
C = (1, 1)
D = (3, 1)
E = (-3, 1)
F = (-1, 1)
G = (-3, -3)
H = (-1, -3)

Lk = {3, 4, 5, 6}

Zip(Polygon(P, Q, k), P, {A, C, G, E}, Q, {B, D, H, F}, k, Lk)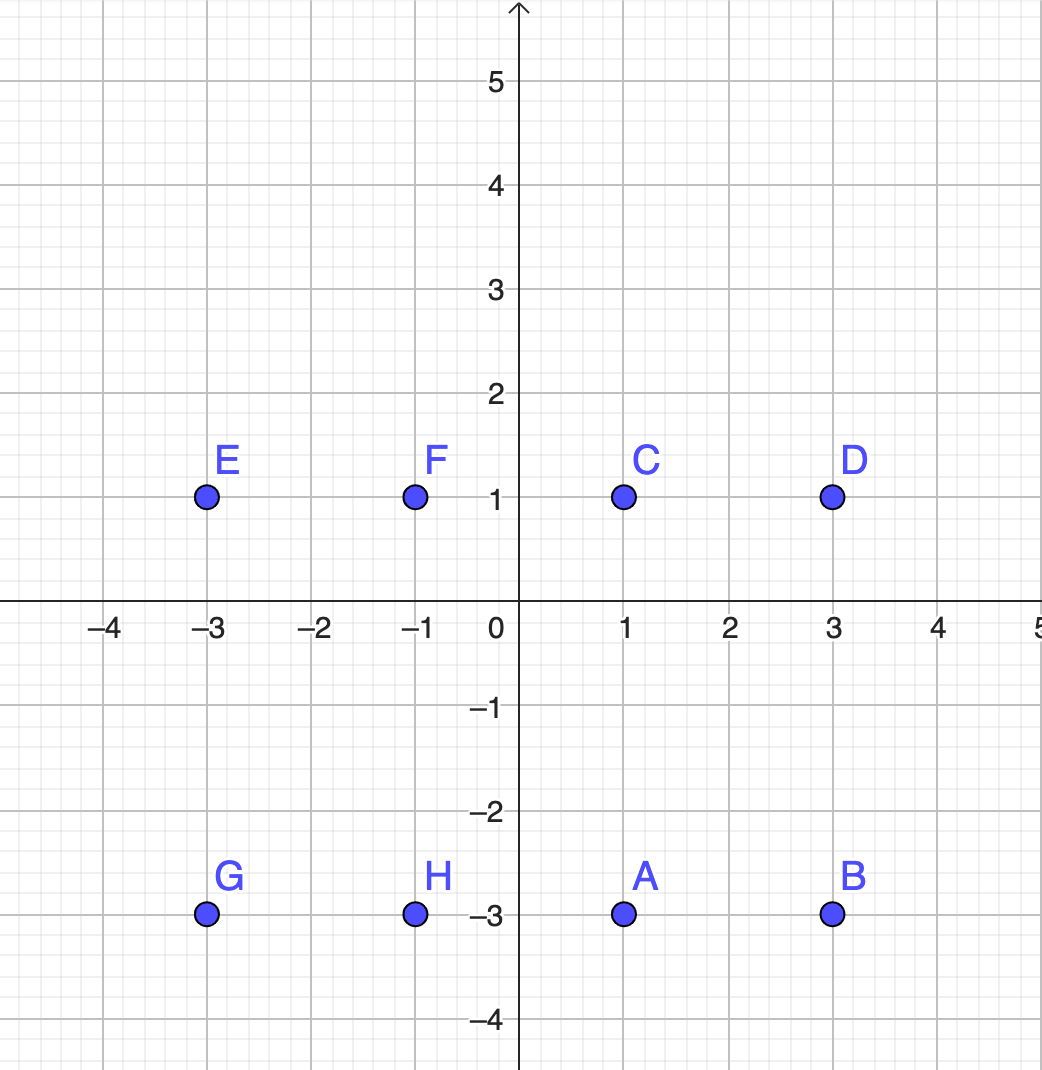

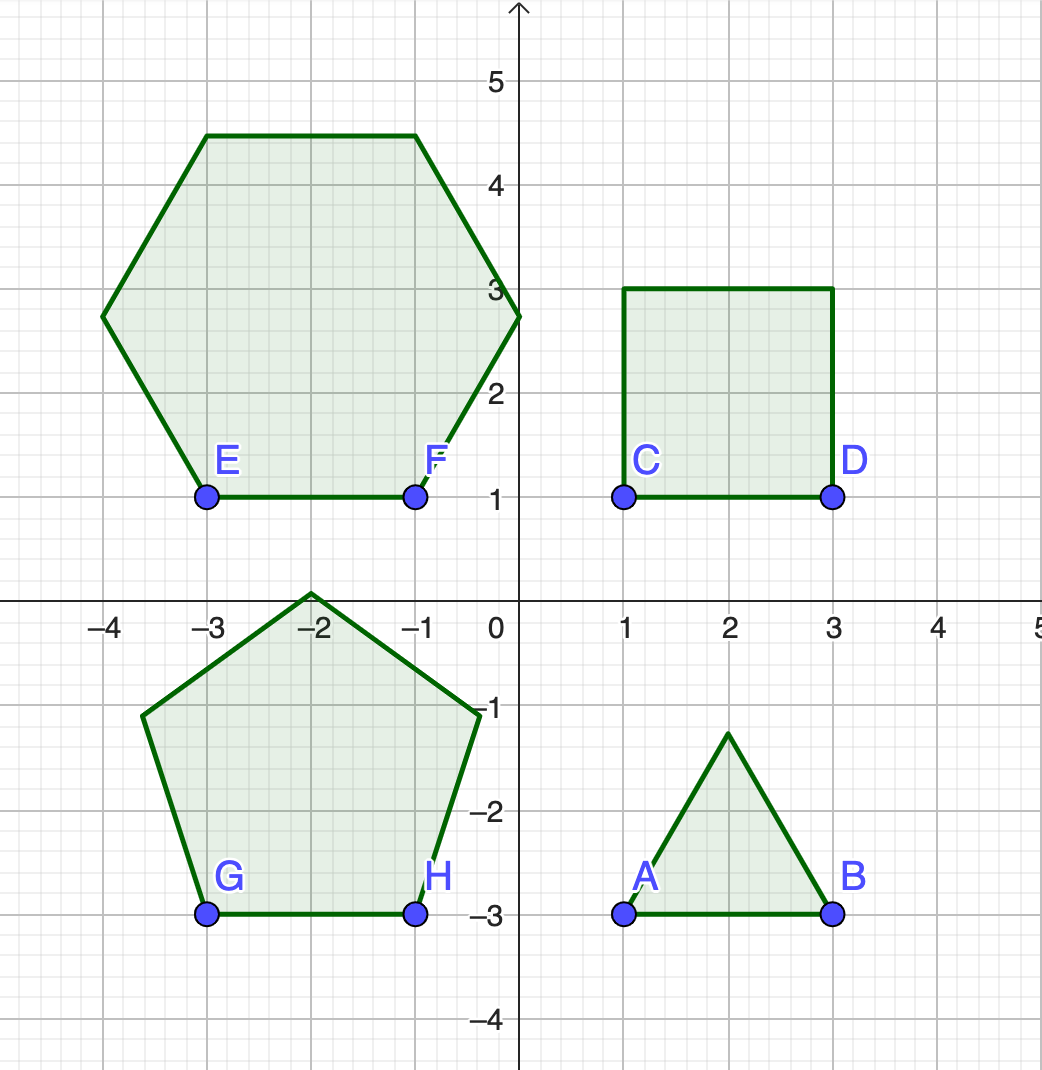
Lists of objects: Example 5

A = (1, -3)
B = (3, -3)
C = (1, 1)
D = (3, 1)
E = (-3, 1)
F = (-1, 1)
G = (-3, -3)
H = (-1, -3)

Lk = {3, 4, 5, 6}
LP = {A, C, G, E}
LQ = {B, D, H, F}

Zip(Polygon(P, Q, k), P, LP, Q, LQ, k, Lk)

Lists of objects: Example 5

Zip(Polygon(P, Q, k), P, LP, Q, LQ, k, Lk)
Sequence(Polygon(Element(LP, k), Element(LQ, k), Element(Lk, k)), k, 1, 4)

✔

Lists of objects: Example 6

Lk = -4..4 
LP = Flatten(Zip(Zip(Zip((i, j, k), i, Lk), j, Lk), k, Lk))
Lr = Zip(0.5*random(), k, 1..Length(LP))

LS = Zip(Sphere(P, r), P, LP, r, Lr)

Lists of objects: Example 6

Lk = -4..4 
LP = Flatten(Zip(Zip(Zip((i, j, k), i, Lk), j, Lk), k, Lk))
Lr = Zip(0.5*random(), k, 1..Length(LP))

LS = Zip(Sphere(P, r), P, LP, r, Lr)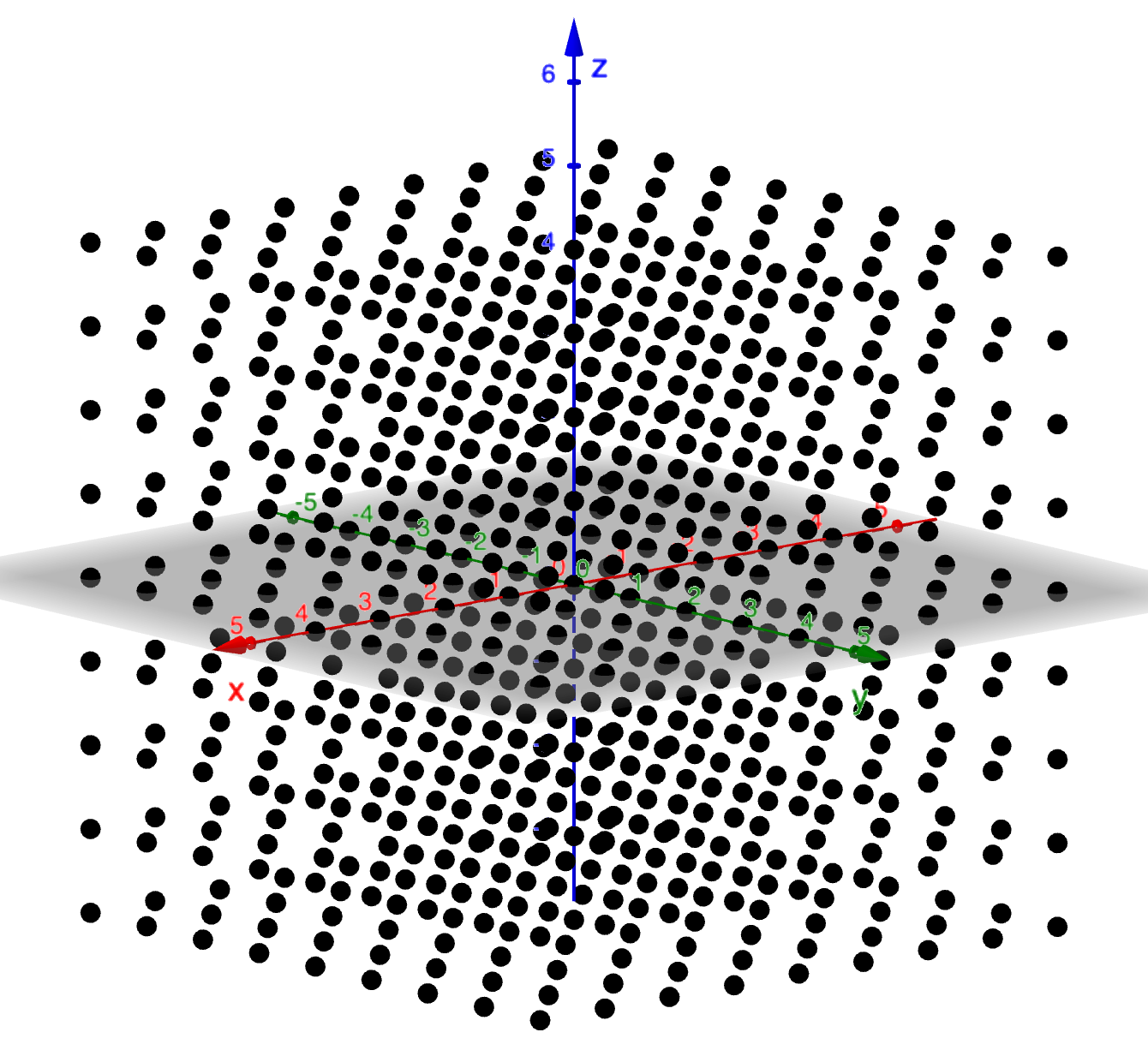
Sequence(k, k, -4, 4)

You can also type:

Create a list of numbers:

Lk = {-4, -3, -2, -1, 0, 1, 2, 3, 4}

Creates a 3D array of points

{{a, b, c}, {x, y,z}}
  →{a, b, c, x, y, z}

Flattens list to a one dimensional list

Flatten()

Lists of objects: Example 6

Lk = -4..4 
LP = Flatten(Zip(Zip(Zip((i, j, k), i, Lk), j, Lk), k, Lk))
Lr = Zip(0.5*random(), k, 1..Length(LP))

LS = Zip(Sphere(P, r), P, LP, r, Lr)

Creates a list of random numbers between 0 and 0.5 based on the number of elements of the list LP

1..Length(LP) = Sequence(k, k, 1, Length(LP))

Lists of objects: Example 6

Lk = -4..4 
LP = Flatten(Zip(Zip(Zip((i, j, k), i, Lk), j, Lk), k, Lk))
Lr = Zip(0.5*random(), k, 1..Length(LP))

LS = Zip(Sphere(P, r), P, LP, r, Lr)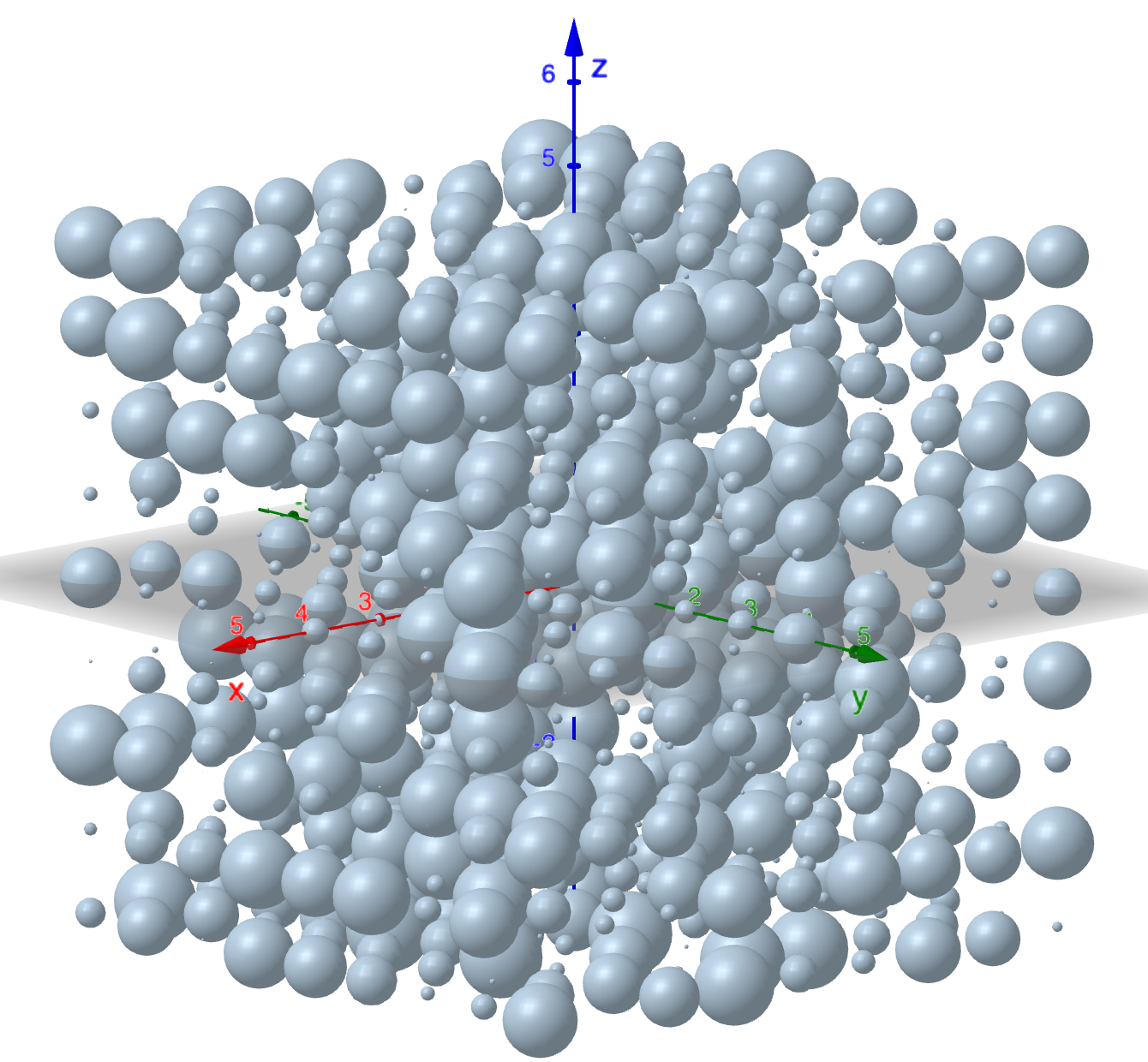

Creates a 3D array of spheres

Lists of objects: Example 6

Lk = -4..4 
LP = Flatten(Zip(Zip(Zip((i, j, k), i, Lk), j, Lk), k, Lk))
Lr = Zip(0.5*random(), k, 1..Length(LP))

LS = Zip(Sphere(P, r), P, LP, r, Lr)

As an exercise try to rewrite this code using the

Sequence()

command

Lists of objects: Example 6

Lk = -4..4 
LP = Flatten(Zip(Zip(Zip((i, j, k), i, Lk), j, Lk), k, Lk))
Lr = Zip(0.5*random(), k, 1..Length(LP))

LS = Zip(Sphere(P, r), P, LP, r, Lr)

I am sure you will see the benefits of using the

Zip()

command

In Summary

We can create lists of numbers and objects

by writing GeoGebra code in a more

efficient and concise manner

Zip()

command

In Summary

Zip()

command

which works fine if your goal is to create simple lists of numbers and objects

This is similar to the 

Sequence()

command

Think about the 

Zip()

command

In Summary

as an advanced version of the 

Sequence()

command

Think about the 

Zip()

as an advanced version of the 

command

Sequence()

command

In Summary

that will help you discover the full potential of GeoGebra to write code

Thanks for

watching!

Patreons:

David Arso Civil, bleh, Dennis Watson, Neil, Doug Kuhlmann, mirror, Newnome Beauton, Adam Parrott, Sophia Wood (Fractal Kitty), pmben, Abei, Edward Huff.

Thanks for

watching!

Patreons:

David Arso Civil, bleh, Dennis Watson, Neil, Doug Kuhlmann, mirror, Newnome Beauton, Adam Parrott, Sophia Wood (Fractal Kitty), pmben, Abei, Edward Huff.

Thanks for

watching!

Patreons:

David Arso Civil, bleh, Dennis Watson, Neil, Doug Kuhlmann, mirror, Newnome Beauton, Adam Parrott, Sophia Wood (Fractal Kitty), pmben, Abei, Edward Huff.

Thanks for

watching!

Patreons:

David Arso Civil, bleh, Dennis Watson, Neil, Doug Kuhlmann, mirror, Newnome Beauton, Adam Parrott, Sophia Wood (Fractal Kitty), pmben, Abei, Edward Huff.