Jeanne Colbois | CNRS - LPT Toulouse | France
IQTN workshop | Tensor networks for constrained systems | Delft, 18.10.2023



tensor networks and LIMITS
oF classical frustrated Ising models

1
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Trailer...
Classical frustrated systems
The constraints appearing in the low-temperature limit need to be correctly described at the level of a single tensor for the contraction to converge
2
Short-range, classical spin Hamiltonian on a lattice...
- How to write the partition function as a TN?
- Consequences?
- Interesting physics?
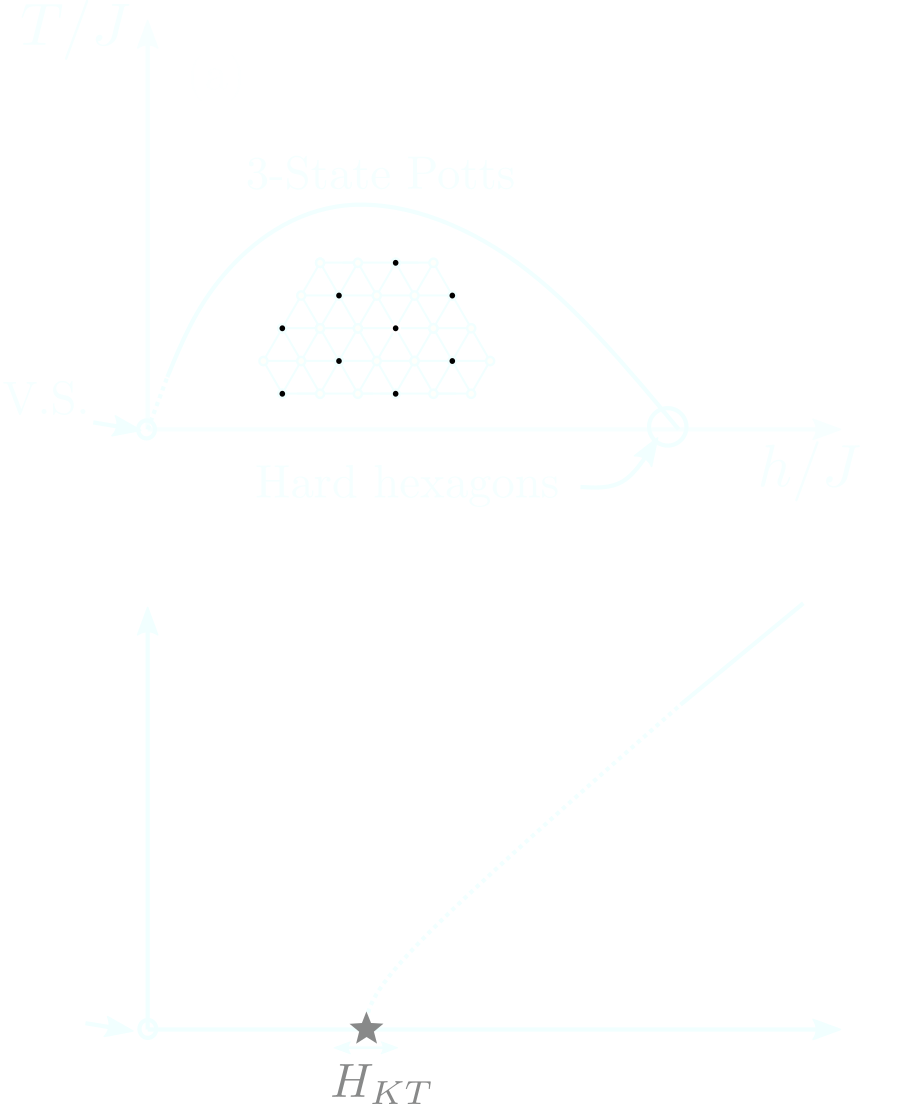
TIAFM in a field


Kagome lattice
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Scope
Scope
3
1. Motivation : classical frustrated Ising models
2. The frustration problem
3. A simple case: the triangular lattice Ising antiferromagnet
4. Farther-neighbor models on the kagome lattice
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Acknowledgments
4

Andrew Smerald
KIT | Germany
Frédéric Mila
EPFL | Switzerland

Frank Verstraete
Ghent University | Belgium

Laurens Vanderstraeten
Ghent University | Belgium


Samuel Nyckees
EPFL | Switzerland

Afonso Rufino
EPFL | Switzerland
Bram Vanhecke
University of Vienna | Austria

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Acknowledgments

Andrew Smerald
KIT | Germany
Frédéric Mila
EPFL | Switzerland

Frank Verstraete
Ghent University | Belgium

Laurens Vanderstraeten
Ghent University | Belgium


Samuel Nyckees
EPFL | Switzerland

Afonso Rufino
EPFL | Switzerland
Bram Vanhecke
University of Vienna | Austria

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
4
Acknowledgments

Andrew Smerald
KIT | Germany
Frédéric Mila
EPFL | Switzerland

Frank Verstraete
Ghent University | Belgium

Laurens Vanderstraeten
Ghent University | Belgium


Samuel Nyckees
EPFL | Switzerland

Afonso Rufino
EPFL | Switzerland
Bram Vanhecke
University of Vienna | Austria

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
4
Acknowledgments

Andrew Smerald
KIT | Germany
Frédéric Mila
EPFL | Switzerland

Frank Verstraete
Ghent University | Belgium

Laurens Vanderstraeten
Ghent University | Belgium


Samuel Nyckees
EPFL | Switzerland

Afonso Rufino
EPFL | Switzerland
Bram Vanhecke
University of Vienna | Austria

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
4
Motivation : frustration...
Frustrated Ising models
5


G.H. Wannier, PR 79, (1950, 1973)
K. Kano and S. Naya, Prog. Theor. Phys. 10, (1953)


2-up 1-down (UUD),
2-down 1-up (DDU)
A. Sütö, Z. Phys. B 44, (1981)
W. Apel, H.-U. Everts, J. Stat. Mech, (2011)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Simple models of complex behavior
6
In-plane artificial kagome /square ice

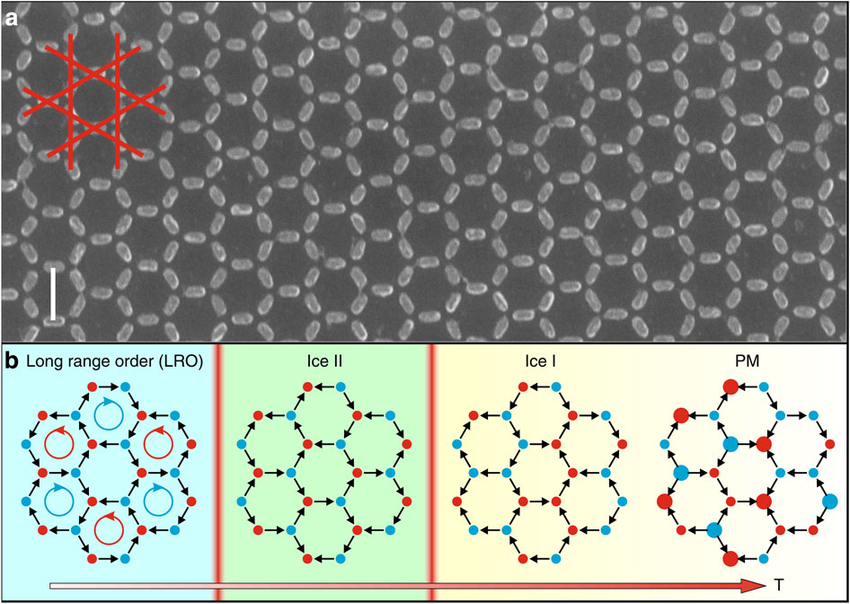
L. Anghinolfi et al.,
Nat. Commun. 6, (2015)
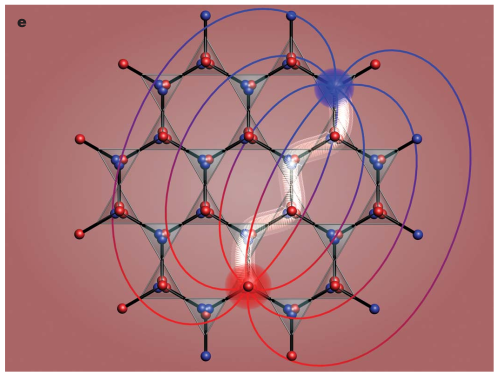
Monopoles in spin ice
C. Castlenovo, R. Moessner, S. L. Sondhi, Nature 451 (2008)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
T. Mizoguichi, L. Jaubert, M. Udagawa, PRL 119, 077207 (2017)
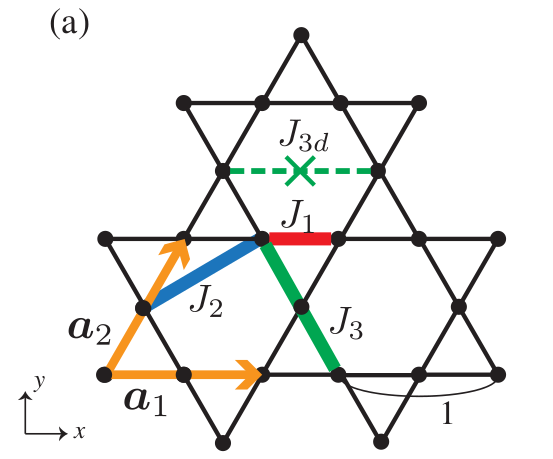
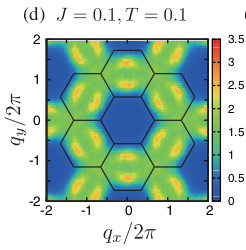
D. Kiese, F. Ferrari, N. Astrakhantsev, N. Niggemann, P. Ghosh et al. , PRR 5, L012025 (2023)
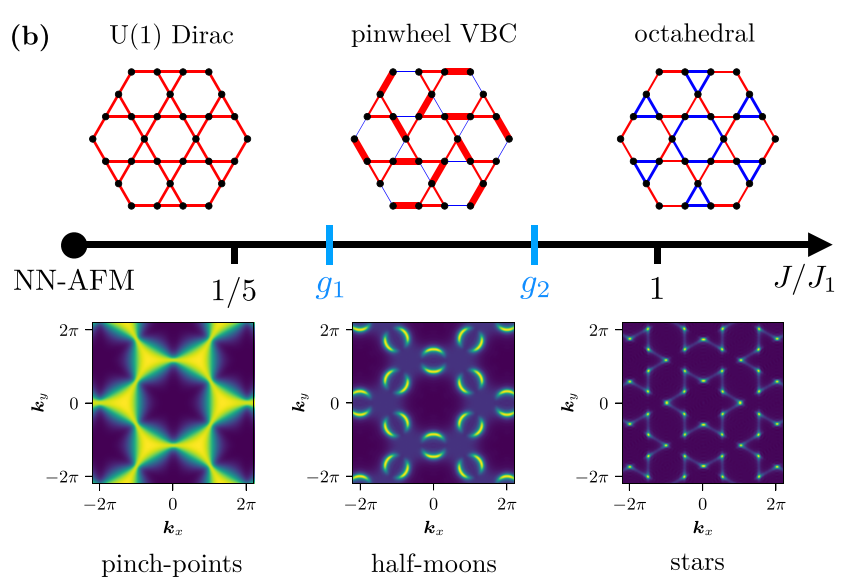
Hexamer spin liquid
7
I. A. Chioar, N. Rougemaille, B. Canals, PRB 93, (2016)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
L. Cugliandolo, L. Foini, M. Tarzia, PRB 101 (2020)

Chioar et al., PRB 90, (2014)

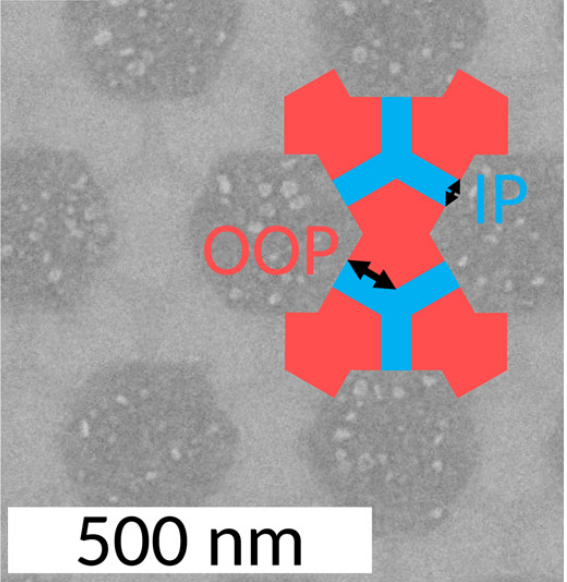
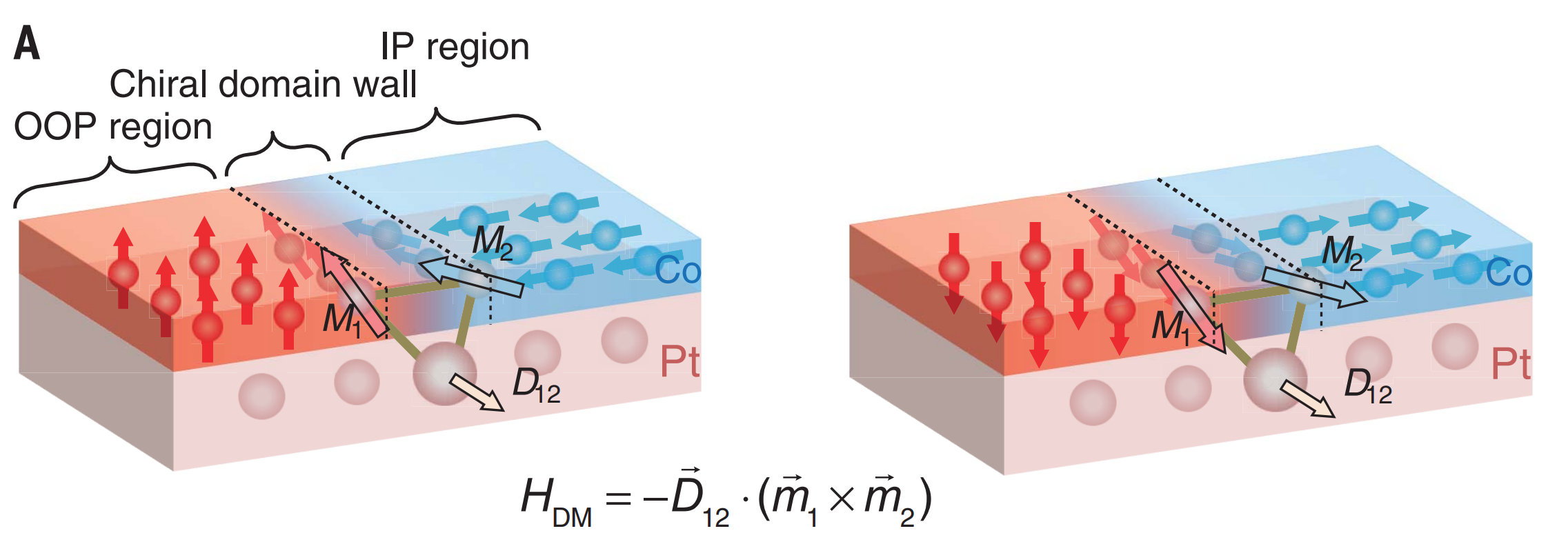
Luo et al. Science 363, (2019)
Colbois et al., PRB 104 (2021)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Artificial spin systems
TN for classical Frustrated models
TNs for 2D classical Frustrated systems - Why?
8
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Monte Carlo?
no sign problem (classical)
ergodicity
Entanglement scaling vs finite-size scaling
TNs give direct access to the partition function per site
2D partition function
R. J. Baxter, J. Math. Phys. 9, 1968
R. Orús, G. Vidal, PRB 78, 2008
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996

9
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
2D partition function contraction
R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
10


R. J. Baxter, J. Math. Phys. 9, 1968
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
P. Corboz, T. M. Rice, and M. Troyer, PRL 113, 2014
Row to row transfer matrix \(\rightarrow\) MPO
2D partition function contraction
R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
10




R. J. Baxter, J. Math. Phys. 9, 1968
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
P. Corboz, T. M. Rice, and M. Troyer, PRL 113, 2014
Row to row transfer matrix \(\rightarrow\) MPO
2D partition function contraction
R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
10




R. J. Baxter, J. Math. Phys. 9, 1968
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
P. Corboz, T. M. Rice, and M. Troyer, PRL 113, 2014
Row to row transfer matrix \(\rightarrow\) MPO
2D partition function contraction
R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
10




R. J. Baxter, J. Math. Phys. 9, 1968
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
P. Corboz, T. M. Rice, and M. Troyer, PRL 113, 2014

Measurements
11

R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
\(\langle m \rangle\) =
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023

R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
\(\langle m \rangle\) =
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023


\(\rightarrow\) patches of the infinite lattice
11
Measurements
Ueda, et al. JSPS 74, 111-124 (2005)
T. Viejira, J. Haegeman, F. Verstraete, L. Vanderstraeten, PRB 104, 235141 (2021)

R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
\(\langle m \rangle\) =
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023

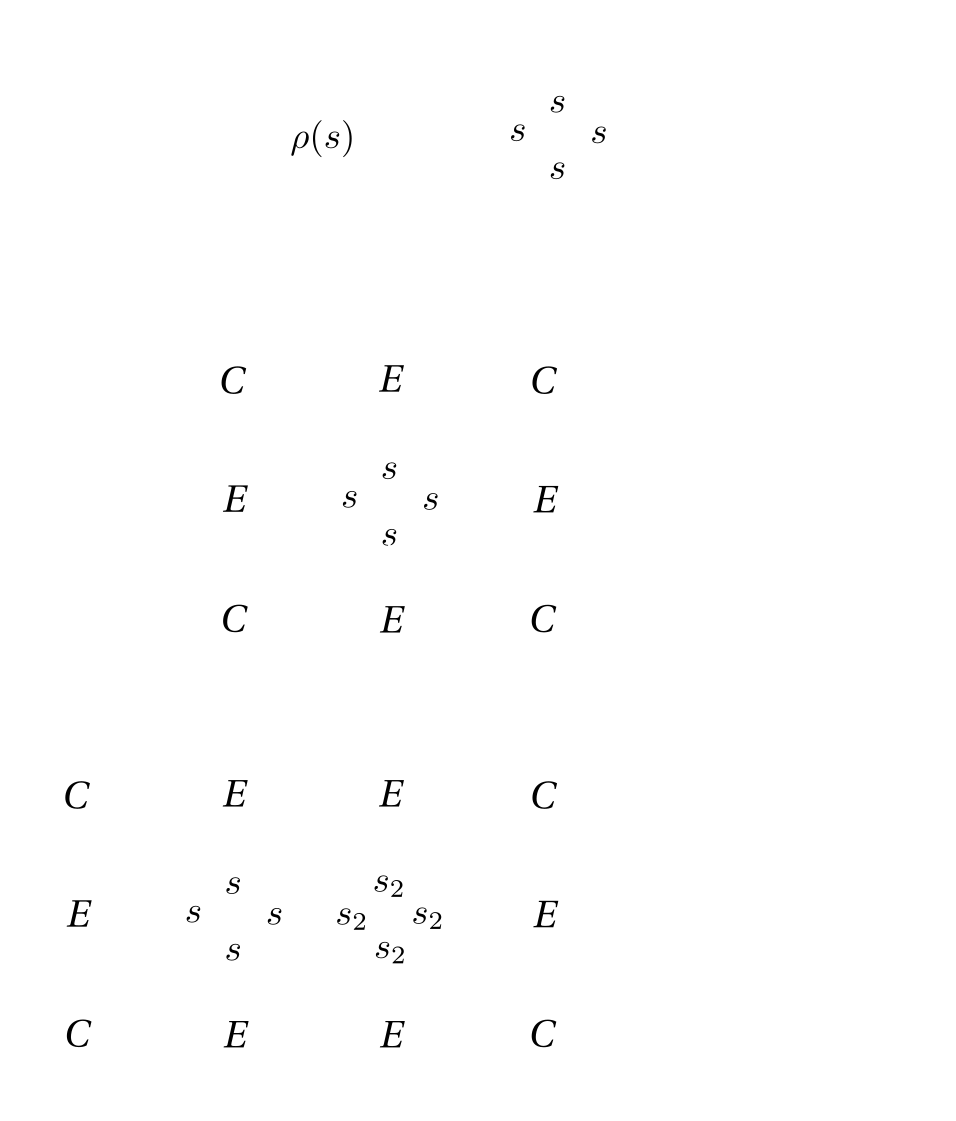
\(\rightarrow\) patches of the infinite lattice
11
Ueda, et al. JSPS 74, 111-124 (2005)
T. Viejira, J. Haegeman, F. Verstraete, L. Vanderstraeten, PRB 104, 235141 (2021)
Measurements
The frustration problem
12

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
The frustration problem

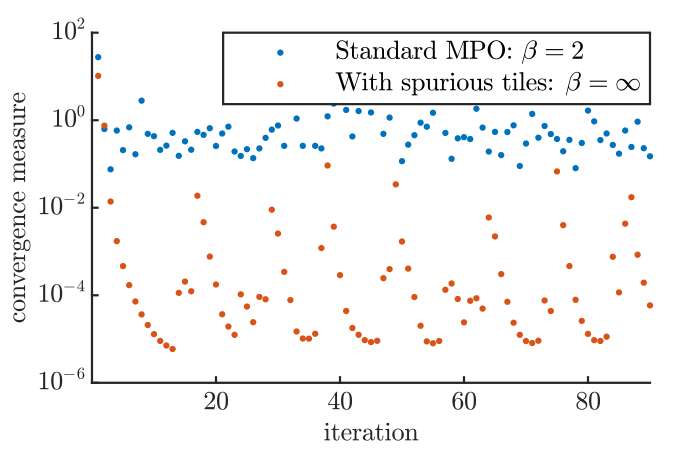
Fails in the presence of
frustration and macroscopic g.s. degeneracy
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
12
\(\rightarrow\) in spin glasses
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
J. G. Liu, L. Wang, P. Zhang, PRL 126, (2021)
The frustration problem


Fails in the presence of
frustration and macroscopic g.s. degeneracy
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
B. Vanhecke, JC, et al. PRR 3, (2021)
\(\rightarrow\) in spin glasses
\(\rightarrow \) in translation-invariant frustrated Ising models
12
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
J. G. Liu, L. Wang, P. Zhang, PRL 126, (2021)
The frustration problem


Fails in the presence of
frustration and macroscopic g.s. degeneracy
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
B. Vanhecke, JC, et al. PRR 3, (2021)
\(\rightarrow\) in spin glasses
\(\rightarrow \) in translation-invariant frustrated Ising models
\(\rightarrow\) in lattice gas models
S. A. Akimenko, PRE 107, (2023)
12
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
J. G. Liu, L. Wang, P. Zhang, PRL 126, (2021)
The frustration problem


Fails in the presence of
frustration and macroscopic g.s. degeneracy
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
B. Vanhecke, JC, et al. PRR 3, (2021)
\(\rightarrow\) in spin glasses
\(\rightarrow \) in translation-invariant frustrated Ising models
\(\rightarrow\) in lattice gas models
\(\rightarrow\) in frustrated XY models
S. A. Akimenko, PRE 107, (2023)
F.F. Song, T.-Y. Lin, G. M. Zhang, arXiv:2309.05321
12
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
J. G. Liu, L. Wang, P. Zhang, PRL 126, (2021)
Points of view
13
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Contracting the TN of a frustrated model
Numerical problem
Cancellation of small and large factors
Points of view
13
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Contracting the TN of a frustrated model
Numerical problem
Cancellation of small and large factors
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
\(\rightarrow\) precision?
Points of view
13
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Contracting the TN of a frustrated model
Numerical problem
Cancellation of small and large factors
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
\(\rightarrow\) precision?
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
\(\rightarrow\) log?
Points of view
13
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Contracting the TN of a frustrated model
Numerical problem
Cancellation of small and large factors
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
\(\rightarrow\) precision?
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
\(\rightarrow\) log?
MPO
The MPO is badly conditioned (e.g. not hermitian, ...). Fix it?
Points of view
13
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Contracting the TN of a frustrated model
Numerical problem
Ground-state rule
Cancellation of small and large factors
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
\(\rightarrow\) precision?
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
\(\rightarrow\) log?
MPO
The MPO is badly conditioned (e.g. not hermitian, ...). Fix it?
Failure to minimize simultaneously all local Hamiltonians.
B. Vanhecke, JC, et al. PRR 3, (2021)
F.F. Song, T.-Y. Lin, G. M. Zhang, arXiv:2309.05321
Points of view
13
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Contracting the TN of a frustrated model
Numerical problem
Ground-state rule
Cancellation of small and large factors
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
\(\rightarrow\) precision?
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
\(\rightarrow\) log?
MPO
The MPO is badly conditioned (e.g. not hermitian, ...). Fix it?
Failure to minimize simultaneously all local Hamiltonians.
B. Vanhecke, JC, et al. PRR 3, (2021)
F.F. Song, T.-Y. Lin, G. M. Zhang, arXiv:2309.05321
Bram Vanhecke
University of Vienna | Austria

Relaxing THE frustration
14
1. Split
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969);
M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975);
B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981);
W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016)

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
P. W. Anderson, PR 83, (1951).
Essential idea : Anderson bounds
Relaxing THE frustration
1. Split
2. Lower bound on GS energy
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969);
M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975);
B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981);
W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016)

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
14
P. W. Anderson, PR 83, (1951).
Essential idea : Anderson bounds
Relaxing THE frustration
1. Split
2. Lower bound on GS energy
3. Maximize with respect to the weights:
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969);
M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975);
B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981);
W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016)


J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
14
P. W. Anderson, PR 83, (1951).
Essential idea : Anderson bounds
Relaxing THE frustration
1. Split
2. Lower bound on GS energy
3. Maximize with respect to the weights:
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969);
M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975);
B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981);
W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016)



J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Ground states
tiling of configurations that minimize the local Hamiltonian
14
P. W. Anderson, PR 83, (1951).
Essential idea : Anderson bounds
Relaxing THE frustration
1. Split
2. Lower bound on GS energy
3. Maximize with respect to the weights:
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969);
M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975);
B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981);
W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016)




J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
14
P. W. Anderson, PR 83, (1951).
Essential idea : Anderson bounds
Ground states
tiling of configurations that minimize the local Hamiltonian
remarks
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
15
remarks
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
15
Turned the problem into a tiling problem.
L. Vanderstraeten , B. Vanhecke, F. Verstraete, PRE 98, (2018)
remarks
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
15
Turned the problem into a tiling problem.
For NN models, naturally occurs from the "interactions-round-a-face" construction
see e.g. R. J. Baxter, J. Stat. Phys. 19, (1978)
L. Vanderstraeten , B. Vanhecke, F. Verstraete, PRE 98, (2018)
remarks
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
15
Turned the problem into a tiling problem.
For NN models, naturally occurs from the "interactions-round-a-face" construction
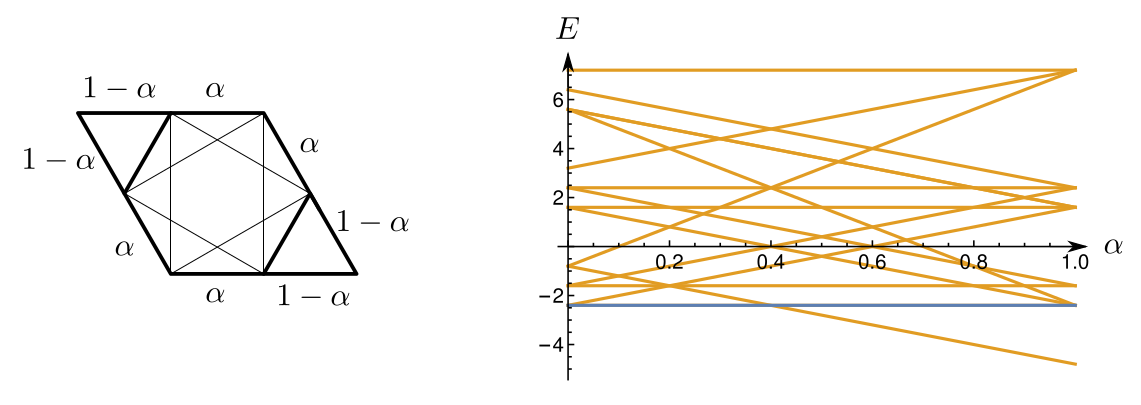
\(J_1 - J_2\) on kagome
see e.g. R. J. Baxter, J. Stat. Phys. 19, (1978)
L. Vanderstraeten , B. Vanhecke, F. Verstraete, PRE 98, (2018)
Finite temperature
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
16
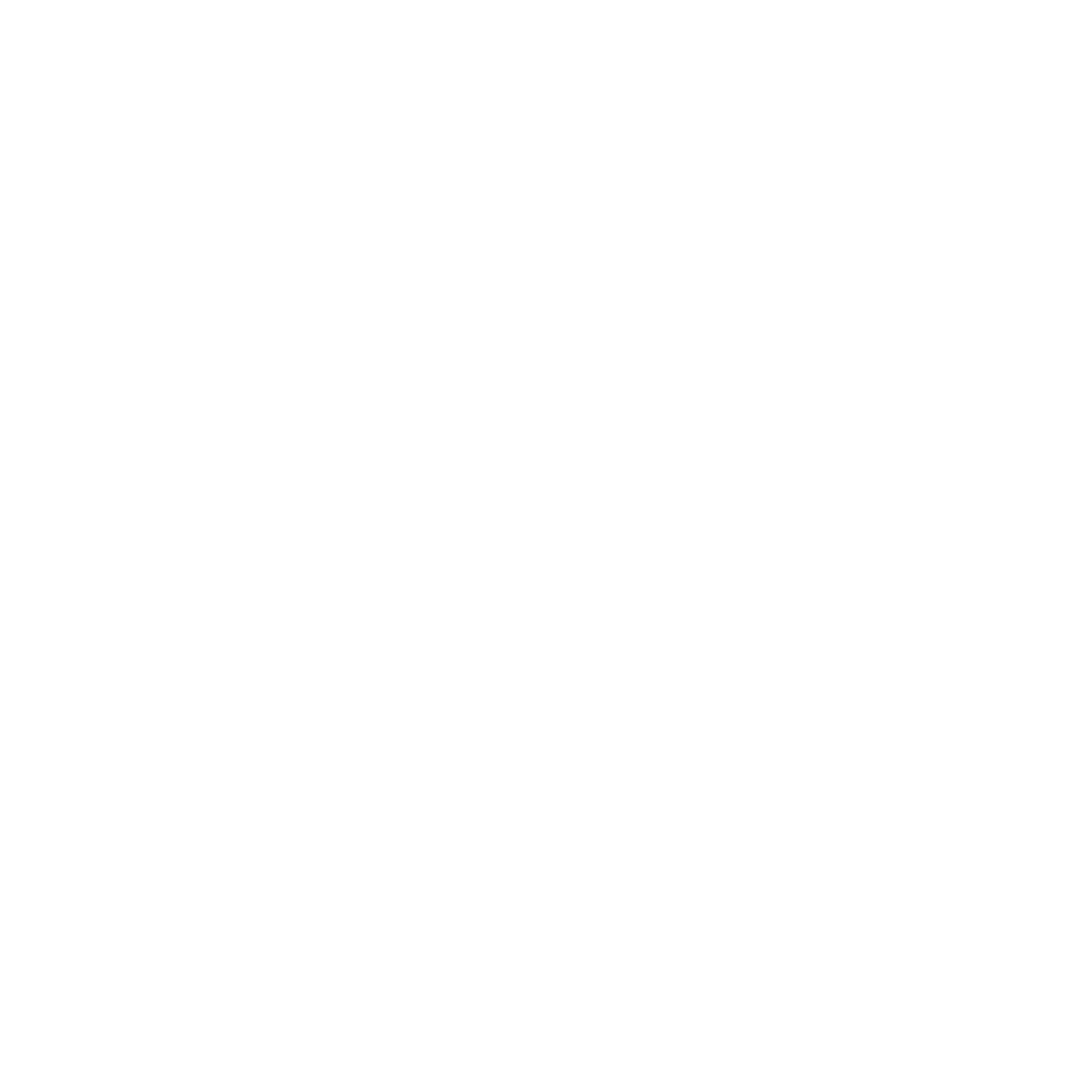
Contraction
17
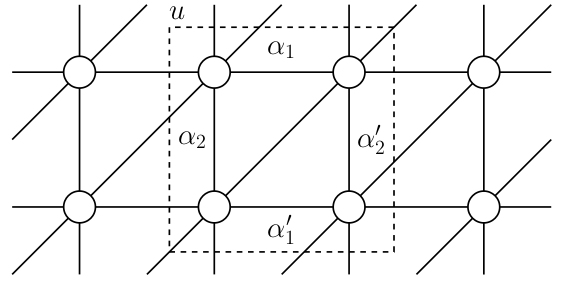
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023

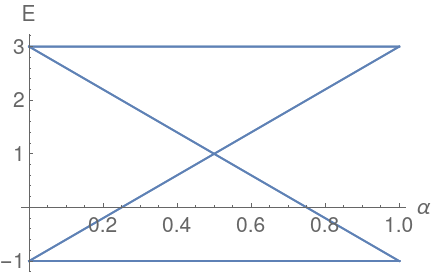
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Contraction
17


B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)

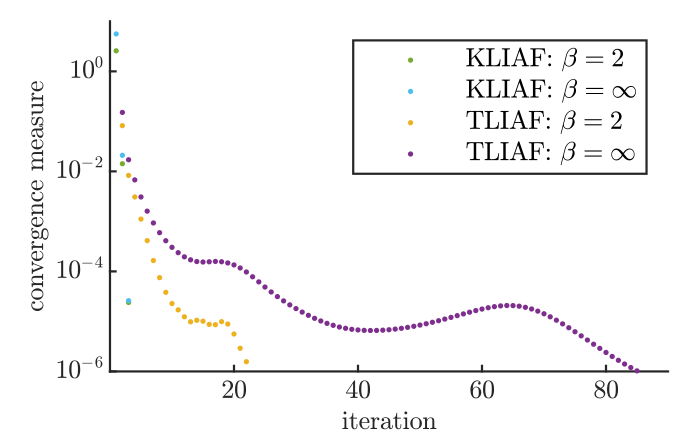
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Contraction
17
Spurious tiles



B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
17
Spurious tiles



B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)

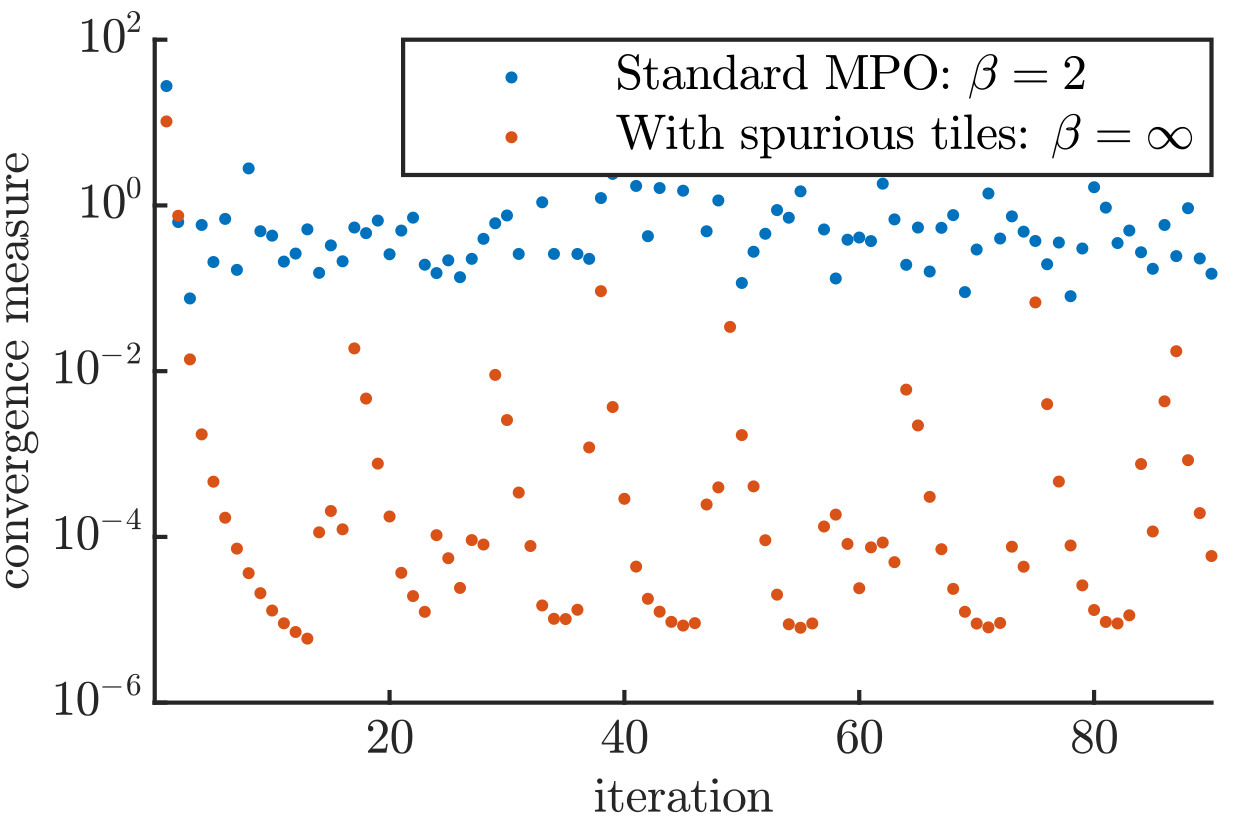
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
17
18
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
F.F. Song, T.-Y. Lin, G. M. Zhang, arXiv:2309.05321
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)

Charges and strings
See e.g. Henley (2010) or Nienhuis (1984)
18
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
F.F. Song, T.-Y. Lin, G. M. Zhang, arXiv:2309.05321
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)

Charges and strings
See e.g. Henley (2010) or Nienhuis (1984)
18
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
F.F. Song, T.-Y. Lin, G. M. Zhang, arXiv:2309.05321
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)

Charges and strings
See e.g. Henley (2010) or Nienhuis (1984)
18
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
F.F. Song, T.-Y. Lin, G. M. Zhang, arXiv:2309.05321
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)

Charges and strings
See e.g. Henley (2010) or Nienhuis (1984)
18
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
F.F. Song, T.-Y. Lin, G. M. Zhang, arXiv:2309.05321
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)

Charges and strings
See e.g. Henley (2010) or Nienhuis (1984)
18
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
F.F. Song, T.-Y. Lin, G. M. Zhang, arXiv:2309.05321
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)

Charges and strings
See e.g. Henley (2010) or Nienhuis (1984)
Charges and strings
18
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
F.F. Song, T.-Y. Lin, G. M. Zhang, arXiv:2309.05321
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)

See e.g. Henley (2010) or Nienhuis (1984)
Triangular lattice Ising antiferromagnet
Phase diagram & Question
19
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Phase diagram & Question

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
19
Phase diagram & Question

G.S. critical
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
G. H. Wannier, PR 79, 1950
Stephenson, J. Math. Phys. 11, 1970
Height model!
19
B. Nienhuis, H. J. Hilhorst, and H. W. J. Blote, J. Phys. A. 17, (1984).
Phase diagram & Question

No transition at finite temperature
Stephenson, J. Math. Phys. 11, 1970
Jacobsen, Fogedby, Physica A 246, 1997
Houtappel, Physica 16, 1950
G.S. critical
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
G. H. Wannier, PR 79, 1950
Stephenson, J. Math. Phys. 11, 1970
19
Height model!
B. Nienhuis, H. J. Hilhorst, and H. W. J. Blote, J. Phys. A. 17, (1984).
Phase diagram & Question


J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
20
Phase diagram & Question


Alexander P.L.A 54 (1975)
Kinzel & Schick PRB 23 (1981)
Noh & Kim, Int. J. Phys. B 06 ( 1992)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
20
Phase diagram & Question

Racz PRB 21, 1980;
Qian, Wegewijs, Blöte PRE 69, 2004;
Baxter, Exactly solved models

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Alexander P.L.A 54 (1975)
Kinzel & Schick PRB 23 (1981)
Noh & Kim, Int. J. Phys. B 06 ( 1992)
20
Phase diagram & Question

Racz PRB 21, 1980;
Qian, Wegewijs, Blöte PRE 69, 2004;
Baxter, Exactly solved models

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Alexander P.L.A 54 (1975)
Kinzel & Schick PRB 23 (1981)
Noh & Kim, Int. J. Phys. B 06 ( 1992)
20
Phase diagram & Question


Blöte, Nightingale, Wu, Hoogland, PRB 43, (1991)
Blöte, Nightingale, PRB 47, (1993)
Qian, Wegewijs, Blöte, PRE 69 (2004)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
21
Flat
Rough
tensor network
22
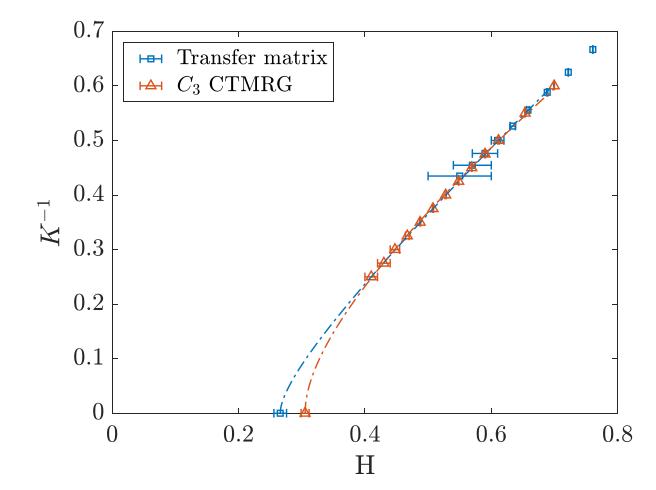
S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023

Limit at T = 0 where H = h/T is constant

ctmrg on the honeycomb lattice
23

Samuel Nyckees
EPFL | Switzerland
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023

S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)
I. V. Lukin and A. G. Sotnikov, PRB 107, 054424 (2023)
A. Gendiar, R. Krcmar, S. Andergassen, M. Daniška,
and T. Nishino, PRE 86, 021105 (2012)

Samuel Nyckees
EPFL | Switzerland
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
23
ctmrg on the honeycomb lattice

S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)
I. V. Lukin and A. G. Sotnikov, PRB 107, 054424 (2023)
A. Gendiar, R. Krcmar, S. Andergassen, M. Daniška,
and T. Nishino, PRE 86, 021105 (2012)

Samuel Nyckees
EPFL | Switzerland
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
23
ctmrg on the honeycomb lattice
S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)

I. V. Lukin and A. G. Sotnikov, PRB 107, 054424 (2023)
A. Gendiar, R. Krcmar, S. Andergassen, M. Daniška,
and T. Nishino, PRE 86, 021105 (2012)

Samuel Nyckees
EPFL | Switzerland
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
23
ctmrg on the honeycomb lattice
S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)

I. V. Lukin and A. G. Sotnikov, PRB 107, 054424 (2023)
A. Gendiar, R. Krcmar, S. Andergassen, M. Daniška,
and T. Nishino, PRE 86, 021105 (2012)

Samuel Nyckees
EPFL | Switzerland
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
23
ctmrg on the honeycomb lattice
S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)
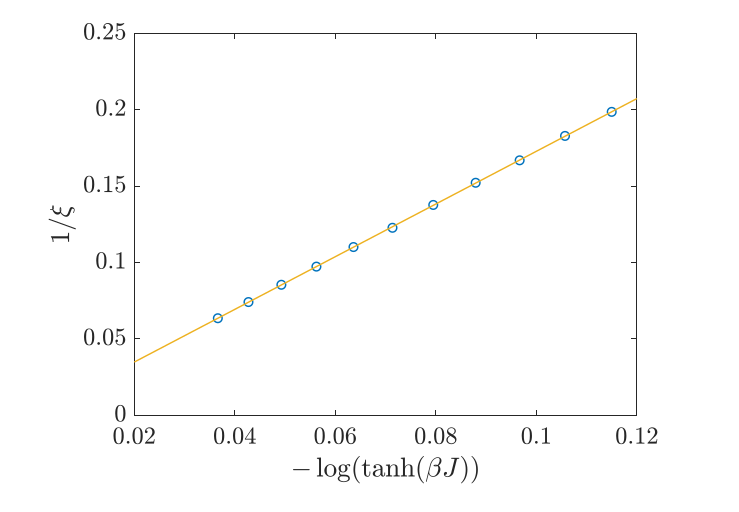


Samuel Nyckees
EPFL | Switzerland
24
Large Field
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Order parameter for 3-sublattice order (3 states of the triangle)

S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)

Samuel Nyckees
EPFL | Switzerland
24
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023

S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)
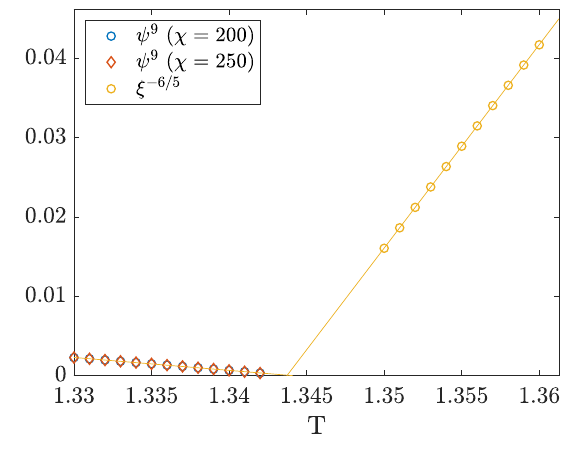
Order parameter for 3-sublattice order (3 states of the triangle)
Single-site -> no access to TM
Large Field

Samuel Nyckees
EPFL | Switzerland
24
Constrained limit
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Order parameter for 3-sublattice order (3 states of the triangle)
Single-site -> no access to TM

S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)
F. Pollmann, S. Mukerjee, A. M. Turner, J.E. Moore, PRL 102 (2009)
L. Tagliacozzo, T. R. de Oliveira, S. Iblisdir, J.I. Latorre, PRB 78 (2008)
\(\Rightarrow\) exponents from log. fits, assuming \(c\).
Constrained limit

Samuel Nyckees
EPFL | Switzerland
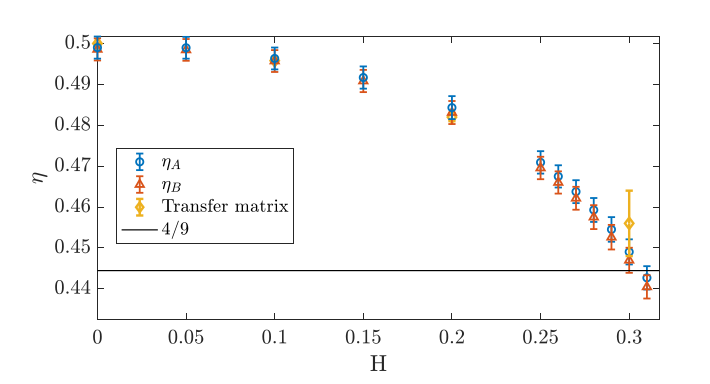
Qian, Wegewijs, Blöte PRE 69 (2004) : TM results
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
23

A, B : convergence modulo 3 (B=C)
S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)
Approaching the Constrained limit

Samuel Nyckees
EPFL | Switzerland
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
24
S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)
\(\eta\) in agreement with 3-state Potts
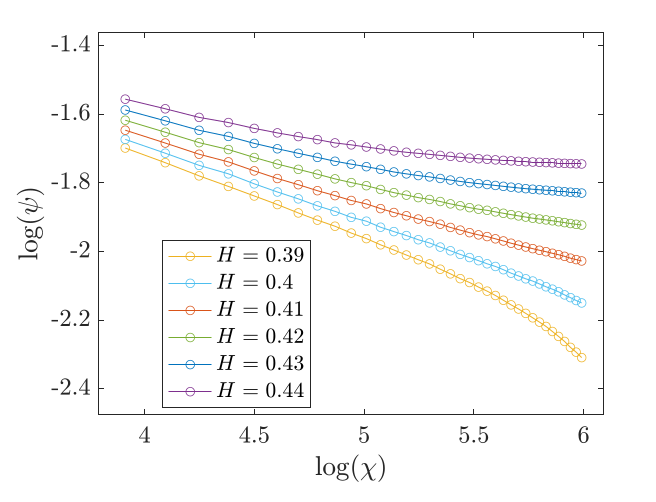
Qian, Wegewijs, Blöte PRE 69 (2004)
Approaching the Constrained limit

Samuel Nyckees
EPFL | Switzerland
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
24
\(\eta\) in agreement with 3-state Potts

S. Nyckees, A. Rufino, F. Mila & JC, arXiv:2306.0904 (2023)
Qian, Wegewijs, Blöte PRE 69 (2004)
Farther-neighbors on kagome
Artificial Out-of-plane kagome
I. A. Chioar, N. Rougemaille, B. Canals, PRB 93, (2016)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
L. Cugliandolo, L. Foini, M. Tarzia, PRB 101 (2020)

Chioar et al., PRB 90, (2014)


J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
25


Tensor network construction
26

JC, B. Vanhecke et. al., PRB 106 (2022)


J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Ground state Phase diagram
27

JC, B. Vanhecke et. al., PRB 106 (2022)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023

Emergent degrees-of-freedom
28



JC, B. Vanhecke et. al., PRB 106 (2022)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Emergent degrees-of-freedom
28

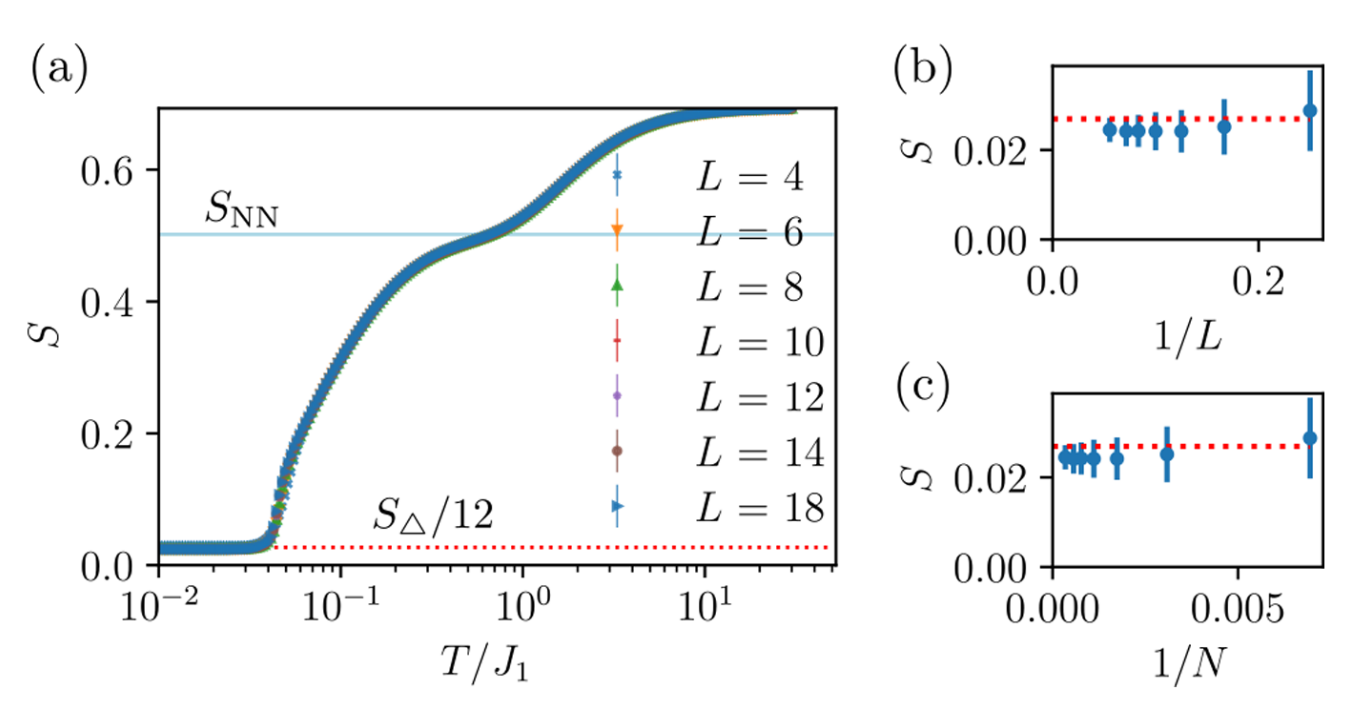
JC, B. Vanhecke et. al., PRB 106 (2022)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Emergent degrees-of-freedom
28

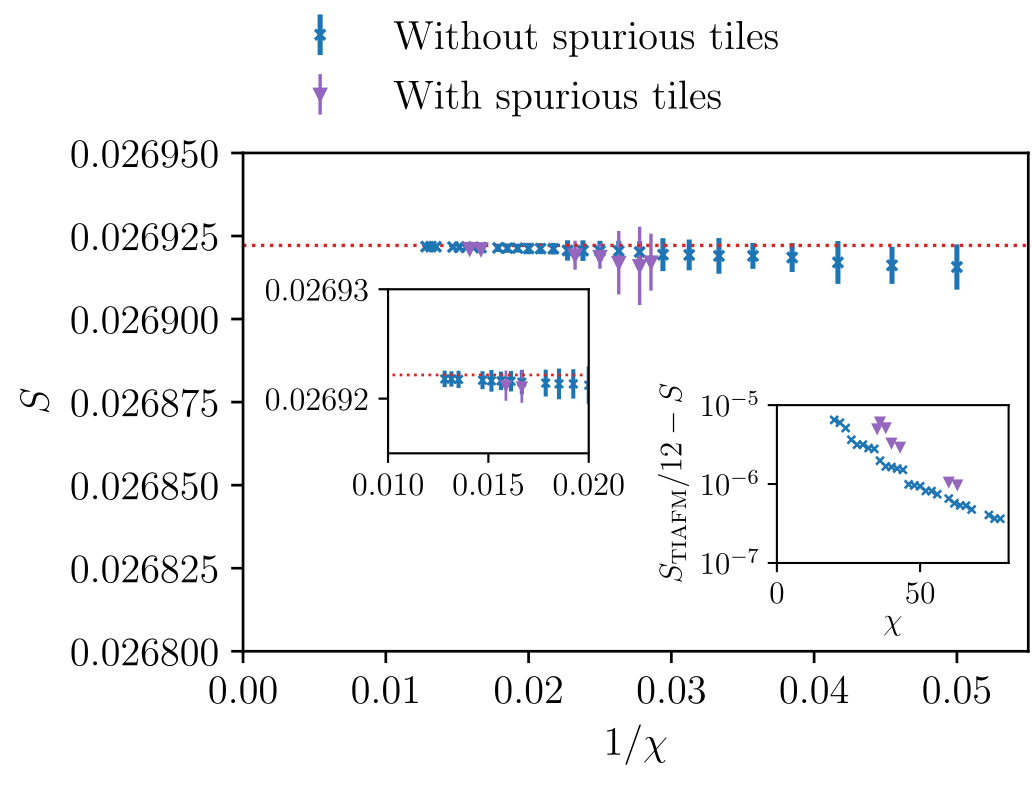
JC, B. Vanhecke et. al., PRB 106 (2022)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Emergent degrees-of-freedom
29

JC, B. Vanhecke et. al., PRB 106 (2022)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
\(\mathbb{Z}_2 \times \mathbb{Z}_3\) symmetry breaking
Relation to the TIAFM

Outlook
32
TNs
Is there always a cell relaxing the frustration? (Hard vs weak frustration)
Can the problem be fixed at the level of the MPO?
Consequences for iPEPS?
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Outlook
32
TNs
Is there always a cell relaxing the frustration? (Hard vs weak frustration)
Can the problem be fixed at the level of the MPO?
Consequences for iPEPS?
Beyond
classical, short-range
Ising
Effect of quantum fluctuations?
Other classical constrained models? Other challenges?
NN Frustrated XY models. Farther-neighbors? Heisenberg?
Long-range interactions? (TNMH)
Spin glasses ? (Tropical TNs)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Thank you for the question!
Strings phase ground state

JC, B. Vanhecke et. al., PRB 106 (2022)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Strings phase ground state

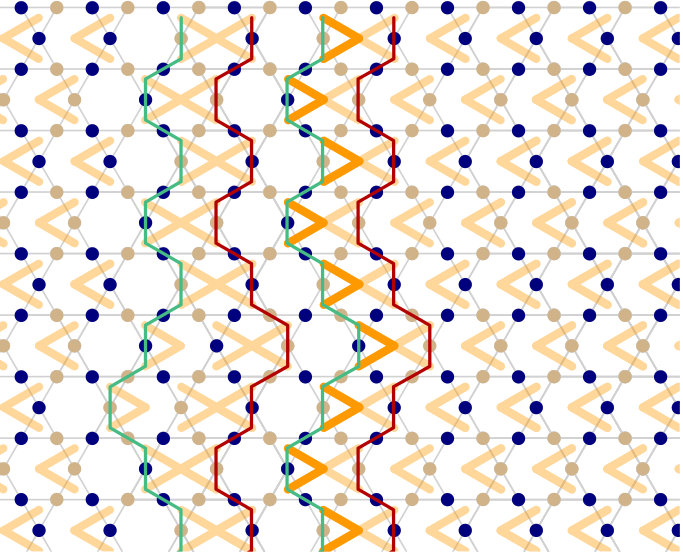
JC, B. Vanhecke et. al., PRB 106 (2022)
JC, B. Vanhecke et. al., PRB 106 (2022)
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Strings phase ground state


\(\mathbb{Z}_2 \times \mathbb{Z}_3\) symmetry breaking
Relation to the TIAFM
AF. order in horizontal direction
Absence of vertical dimers
JC, B. Vanhecke et. al., PRB 106 (2022); A. Rufino, S. Nyckees, JC, F. Mila, in preparation
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Tensor networks : inspired by transfer matrices
Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Tensor networks : inspired by transfer matrices
Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Tensor networks : inspired by transfer matrices
Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Tensor networks : inspired by transfer matrices
Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)

"Exact contraction"
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Tensor networks : inspired by transfer matrices
Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)

"Exact contraction"
"Approximate contraction"
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
TN language
Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)
"Contraction"
Matrix / tensor
Vector
Open legs = number of indices = "rank"

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
Tensor networks : inspired by transfer matrices
Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)

"Exact contraction"
"Approximate contraction"
J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023
TN language
Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)
"Contraction"
Matrix / tensor
Vector
Open legs = number of indices = "rank"

J. COLBOIS | TENSOR NETWORKS FOR CONSTRAINED SYSTEMS | DELFT | 18.10.2023