Majulab day | NTU Singapore | 2024/07/24

Jeanne Colbois

NUS & Majulab

PRB 108, 144206 (2023)

arXiv:2403.09608

arXiv:240x.xxxxxx

Instabilities in random spin chainS:

Extreme magnetizations and correlations

Majulab day | NTU Singapore | 2024/07/24

PRB 108, 144206 (2023)

arXiv:2403.09608

arXiv:240x.xxxxxx

Nicolas Laflorencie

Laboratoire de Physique Théorique

Toulouse, France

Fabien Alet

Jeanne Colbois

NUS & Majulab

Instabilities in random spin chainS:

Extreme magnetizations and correlations

1

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

$|\psi(x)|^2$

1

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

Jump

Random on-site

energy

$|\psi(x)|^2$

Anderson, Phys. Rev. 109, 1492 (1958)

Mott & Twose, Advances in Physics, 10 (1961)

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

$|\psi(x)|^2$

$\xi(h, E)$

$h$

$\forall h , \, \forall E$ : localization !!

(1D, NN)

\mathcal{P}(h_i)

\mathcal{P}(h_i)

$-h$

$h$

1

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

Jump

Random on-site

energy

$|\psi(x)|^2$

Anderson, Phys. Rev. 109, 1492 (1958)

Mott & Twose, Advances in Physics, 10 (1961)

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

$|\psi(x)|^2$

$\xi(h, E)$

$h$

Anderson localization

$\forall h , \, \forall E$ : localization !!

(1D, NN)

\mathcal{P}(h_i)

\mathcal{P}(h_i)

$-h$

$h$

Magnetization / correlations

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

High energy eigenstates of an isolated many-body quantum spin chain in random field

... through simple observables

2

Many-body effects...

Scope

Why care about many-body effects?

3

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

Can we still say that high-energy many-body eigenstates are localized?

Why care about many-body effects?

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

Can we still say that high-energy many-body eigenstates are localized?

If yes: no transport.

Simple example of an isolated quantum system that cannot thermalize

See Anderson, 1958

3

Program

4

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

1. From single fermion to many-body Anderson localization

2. Extreme magnetization

3. The role of interactions : instabilities

1. From single- to many-body Anderson localization

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

From fermions to spins

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

P. Jordan and E. Wigner, Z. Physik 47, 631–651 (1928)

Anderson, Phys. Rev. 109, 1492 (1958)

$|\psi(x)|^2$

$\xi(h, E)$

Charge is conserved

1 fermion

5

\mathcal{P}(h_i)

\mathcal{P}(h_i)

$-h$

$h$

From fermions to spins

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

P. Jordan and E. Wigner, Z. Physik 47, 631–651 (1928)

Anderson, Phys. Rev. 109, 1492 (1958)

Magnetic field

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} \right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} \right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

Spin-flip

S^{x,y,z} = \frac{1}{2} \sigma^{x,y,z}

S^{x,y,z} = \frac{1}{2} \sigma^{x,y,z}

Charge is conserved

Magnetization is conserved

1 fermion

1 spin up

5

$|\psi(x)|^2$

$\xi(h, E)$

\mathcal{P}(h_i)

\mathcal{P}(h_i)

$-h$

$h$

Jordan-Wigner

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

$L/2$ fermions

$\sum_i S_i^{z} = 0$

P. Jordan and E. Wigner, Z. Physik 47, 631–651 (1928)

mANY-BODY aNDERSON LOCALIZATION

6

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

Magnetic field

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} \right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} \right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

Spin-flip

Charge is conserved

Magnetization is conserved

\mathcal{P}(h_i)

\mathcal{P}(h_i)

$-h$

$h$

Jordan-Wigner

Anderson, Phys. Rev. 109, 1492 (1958)

mANY-BODY aNDERSON LOCALIZATION

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

$L/2$ fermions

Jordan-Wigner

$L/2$ fermions

$\sum_i S_i^{z} = 0$

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

Magnetic field

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} \right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} \right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

Spin-flip

Magnetization is conserved

\mathcal{P}(h_i)

\mathcal{P}(h_i)

$-h$

$h$

Charge is conserved

P. Jordan and E. Wigner, Z. Physik 47, 631–651 (1928)

Anderson, Phys. Rev. 109, 1492 (1958)

6

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

7

Many-body lOCALIZATION LENGTH?

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

7

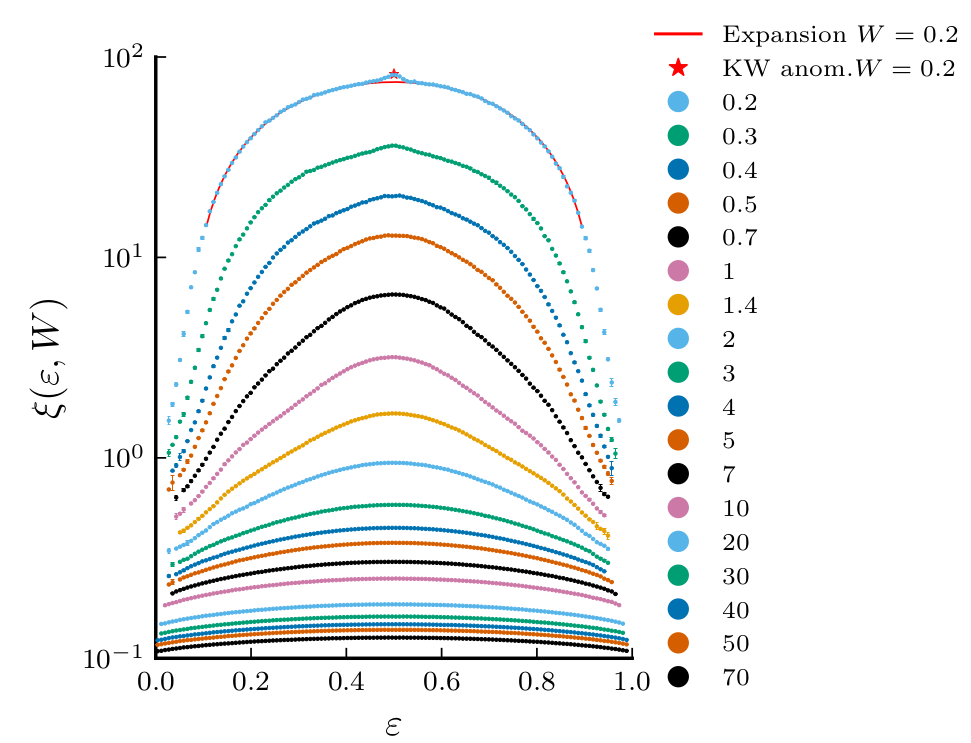
$\epsilon$

$\xi(\epsilon, W)$

Many-body lOCALIZATION LENGTH?

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

$\epsilon$

$\xi(\epsilon, W)$

7

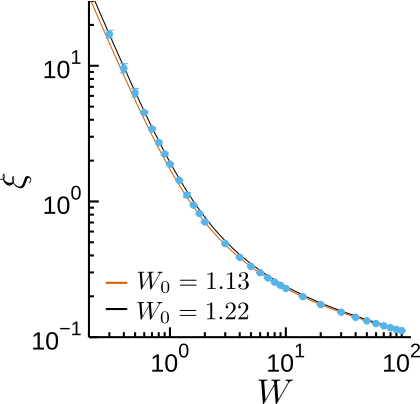
Many-body lOCALIZATION LENGTH?

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

$\epsilon$

$\xi(\epsilon, W)$

\xi \ll 1

\xi \ll 1

h \gg 2

h \gg 2

\xi = \frac{1}{\ln\left(1+\left(\frac{h}{h_0}\right)^2 \right)}

\xi = \frac{1}{\ln\left(1+\left(\frac{h}{h_0}\right)^2 \right)}

7

Many-body lOCALIZATION LENGTH?

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

$\epsilon$

$\xi(\epsilon, W)$

\xi \ll 1

\xi \ll 1

h \gg 2

h \gg 2

\xi = \frac{1}{\ln\left(1+\left(\frac{h}{h_0}\right)^2 \right)}

\xi = \frac{1}{\ln\left(1+\left(\frac{h}{h_0}\right)^2 \right)}

7

Many-body lOCALIZATION LENGTH?

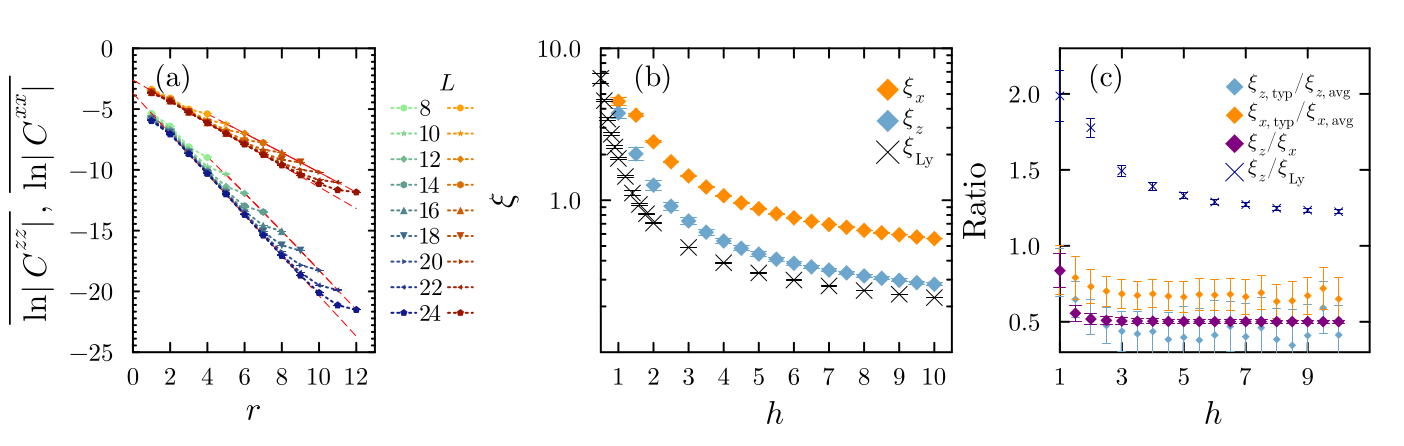
Related to correlation length!

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

2. A simple many-body effect

\delta_i = 1/2 -| \langle S_i^z \rangle|

\delta_i = 1/2 -| \langle S_i^z \rangle|

Some eigenstate

J. C., N. Laflorencie, PRB (2023)

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

8

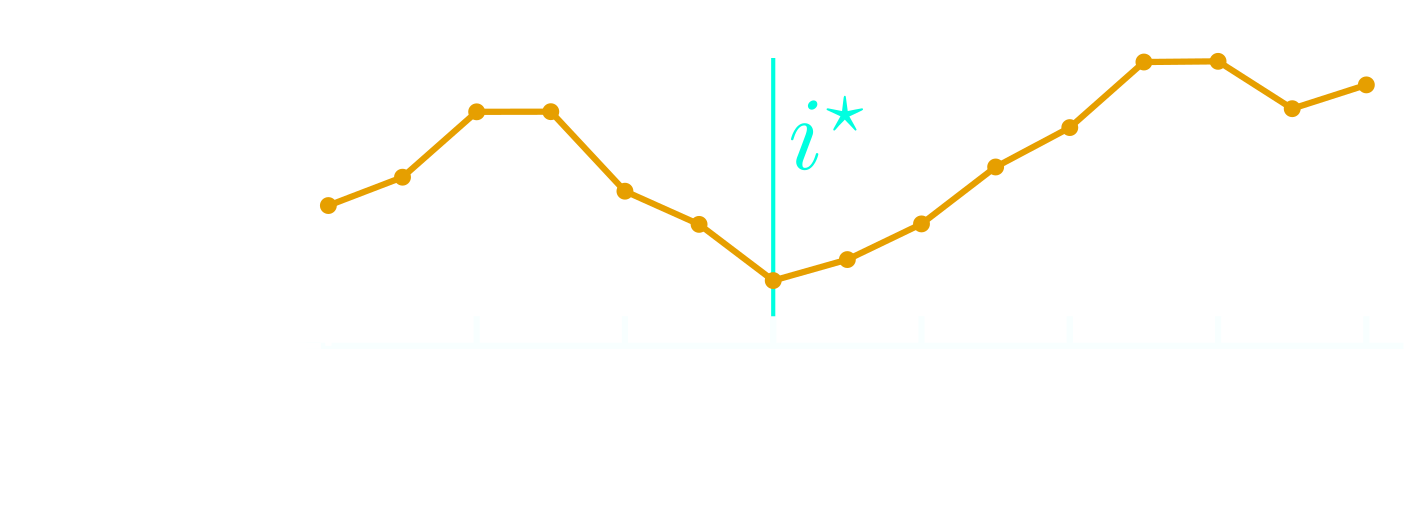
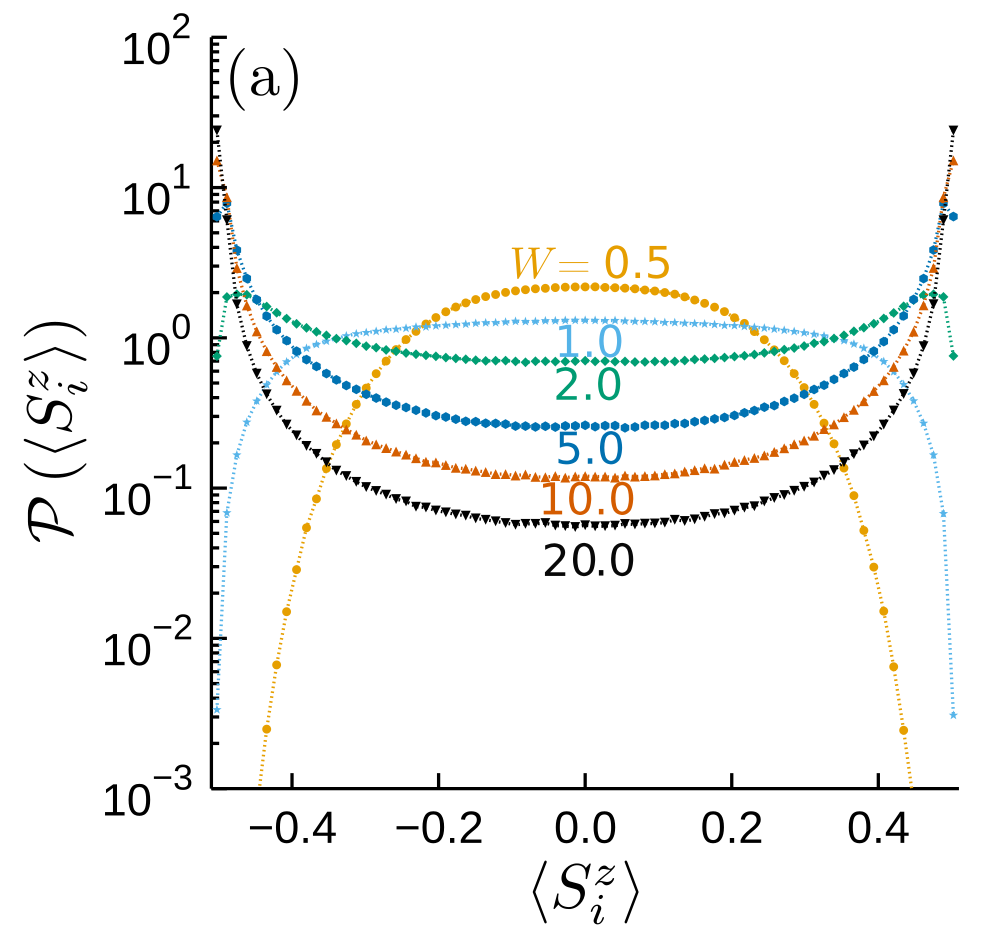
Extreme magnetization

$|\langle S_i^{z}\rangle| < 1/2$

\delta_i = 1/2 -| \langle S_i^z \rangle|

\delta_i = 1/2 -| \langle S_i^z \rangle|

Some eigenstate

J. C., N. Laflorencie, PRB (2023)

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

8

$|\langle S_i^{z}\rangle| < 1/2$

Extreme magnetization

\delta_i = 1/2 -| \langle S_i^z \rangle|

\delta_i = 1/2 -| \langle S_i^z \rangle|

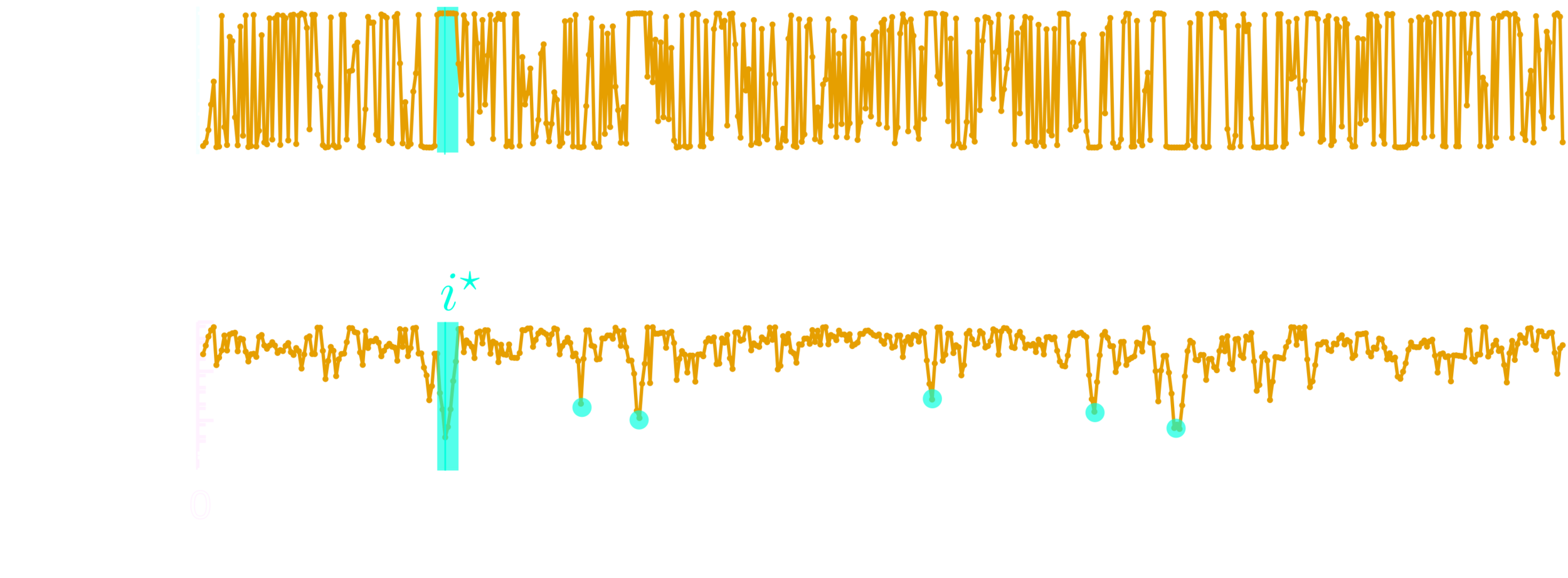
Some eigenstate

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

J. C., N. Laflorencie, PRB (2023)

8

$|\langle S_i^{z}\rangle| < 1/2$

Extreme magnetization

\delta_i = 1/2 -| \langle S_i^z \rangle|

\delta_i = 1/2 -| \langle S_i^z \rangle|

Some eigenstate

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

J. C., N. Laflorencie, PRB (2023)

8

$|\langle S_i^{z}\rangle| < 1/2$

Extreme magnetization

how to predict it?

8

A little game...

Tossing a coin

M. F. Schilling, The College Mathematics Journal 21(3), 196-207 (1990)

P. Révész, Proc. 1978 Int'l Cong. of Mathematicians, 749-754 (1980)

$L = 176$

HTTHTHH

THTHHT

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

9

HTTHTHTTHTHHHTHTTHHTTHHTHTTTHHHTTHTHTHTHHTHTHTHTHTHHTHTHHTHTHTHHTHTHTHHTHTHTTHTHTHTHHHTHTHTHTTHHTHTHTHTHHTHHHTTTHHTHTHTHTHTHTHHTHTHTHHTHTHHTTHTHHTHTHTHHTHTHHTHTHTHTHTHHTHTHHTHT

176 (81 T / 95 H )

HTTTHTTTHTHTHHTHHHHHHTTTTHHHHHHHTHTHHHTTHTHHTHHTTTHHHTHHHTTHHHHTHHTHHHTTTHTHTTHTHTTHHTHTTHTHTTTTTTTHHTHTHHHTHHTTHHTTTTTHHHTTHTHTHHTHTTHTTHHHHTHTHHHTTTTTHTHTTHHTHTTHHTHHHHTHHTHT

176 (83 T / 93 H )

M. F. Schilling, The College Mathematics Journal 21(3), 196-207 (1990)

P. Révész, Proc. 1978 Int'l Cong. of Mathematicians, 749-754 (1980)

Tossing a coin

10

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

HTTHTHTTHTHHHTHTTHHTTHHTHTTTHHHTTHTHTHTHHTHTHTHTHTHHTHTHHTHTHTHHTHTHTHHTHTHTTHTHTHTHHHTHTHTHTTHHTHTHTHTHHTHHHTTTHHTHTHTHTHTHTHHTHTHTHHTHTHHTTHTHHTHTHTHHTHTHHTHTHTHTHTHHTHTHHTHT

176 (81 T / 95 H )

HTTTHTTTHTHTHHTHHHHHHTTTTHHHHHHHTHTHHHTTHTHHTHHTTTHHHTHHHTTHHHHTHHTHHHTTTHTHTTHTHTTHHTHTTHTHTTTTTTTHHTHTHHHTHHTTHHTTTTTHHHTTHTHTHHTHTTHTTHHHHTHTHHHTTTTTHTHTTHHTHTTHHTHHHHTHHTHT

176 (83 T / 93 H )

M. F. Schilling, The College Mathematics Journal 21(3), 196-207 (1990)

P. Révész, Proc. 1978 Int'l Cong. of Mathematicians, 749-754 (1980)

Tossing a coin

10

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

HTTHTHTTHTHHHTHTTHHTTHHTHTTTHHHTTHTHTHTHHTHTHTHTHTHHTHTHHTHTHTHHTHTHTHHTHTHTTHTHTHTHHHTHTHTHTTHHTHTHTHTHHTHHHTTTHHTHTHTHTHTHTHHTHTHTHHTHTHHTTHTHHTHTHTHHTHTHHTHTHTHTHTHHTHTHHTHT

176 (81 T / 95 H )

HTTTHTTTHTHTHHTHHHHHHTTTTHHHHHHHTHTHHHTTHTHHTHHTTTHHHTHHHTTHHHHTHHTHHHTTTHTHTTHTHTTHHTHTTHTHTTTTTTTHHTHTHHHTHHTTHHTTTTTHHHTTHTHTHHTHTTHTTHHHHTHTHHHTTTTTHTHTTHHTHTTHHTHHHHTHHTHT

176 (83 T / 93 H )

\ell_{\max} \sim \ln L / \ln 2 \sim 7.45

\ell_{\max} \sim \ln L / \ln 2 \sim 7.45

M. F. Schilling, The College Mathematics Journal 21(3), 196-207 (1990)

P. Révész, Proc. 1978 Int'l Cong. of Mathematicians, 749-754 (1980)

Tossing a coin

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

10

11

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

Toy model

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

|\phi_m(i)|^2 \propto \exp\left(-\frac{|i - i_0^m|}{{\xi}}\right)

|\phi_m(i)|^2 \propto \exp\left(-\frac{|i - i_0^m|}{{\xi}}\right)

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

11

Toy model

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

|\phi_m(i)|^2 \propto \exp\left(-\frac{|i - i_0^m|}{{\xi}}\right)

|\phi_m(i)|^2 \propto \exp\left(-\frac{|i - i_0^m|}{{\xi}}\right)

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

11

\Rightarrow \langle n_i \rangle = \langle S_i^z \rangle + 1/2 = \sum_{m \in {\color{#56B4E9}\mathrm{occ}}}

\Rightarrow \langle n_i \rangle = \langle S_i^z \rangle + 1/2 = \sum_{m \in {\color{#56B4E9}\mathrm{occ}}}

Toy model

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

|\phi_m(i)|^2 \propto \exp\left(-\frac{|i - i_0^m|}{{\xi}}\right)

|\phi_m(i)|^2 \propto \exp\left(-\frac{|i - i_0^m|}{{\xi}}\right)

r

r

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

11

\Rightarrow \langle n_i \rangle = \langle S_i^z \rangle + 1/2 = \sum_{m \in {\color{#56B4E9}\mathrm{occ}}}

\Rightarrow \langle n_i \rangle = \langle S_i^z \rangle + 1/2 = \sum_{m \in {\color{#56B4E9}\mathrm{occ}}}

\delta_i = \langle n_i \rangle\approx e^{-\frac{r}{\xi} } + \dots

\delta_i = \langle n_i \rangle\approx e^{-\frac{r}{\xi} } + \dots

:

Toy model

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

|\phi_m(i)|^2 \propto \exp\left(-\frac{|i - i_0^m|}{{\xi}}\right)

|\phi_m(i)|^2 \propto \exp\left(-\frac{|i - i_0^m|}{{\xi}}\right)

\Rightarrow \langle n_i \rangle = \langle S_i^z \rangle + 1/2 = \sum_{m \in {\color{#56B4E9}\mathrm{occ}}}

\Rightarrow \langle n_i \rangle = \langle S_i^z \rangle + 1/2 = \sum_{m \in {\color{#56B4E9}\mathrm{occ}}}

\delta_i = \langle n_i \rangle\approx e^{-\frac{r}{\xi} } + \dots

\delta_i = \langle n_i \rangle\approx e^{-\frac{r}{\xi} } + \dots

:

r

r

\ell_{\mathrm{cluster}}

\ell_{\mathrm{cluster}}

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

11

\Rightarrow \quad \delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\Rightarrow \quad \delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

Toy model

\Rightarrow \quad \delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\Rightarrow \quad \delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

|\phi_m(i)|^2 \propto \exp\left(-\frac{|i - i_0^m|}{{\xi}}\right)

|\phi_m(i)|^2 \propto \exp\left(-\frac{|i - i_0^m|}{{\xi}}\right)

\Rightarrow \langle n_i \rangle = \langle S_i^z \rangle + 1/2 = \sum_{m \in {\color{#56B4E9}\mathrm{occ}}}

\Rightarrow \langle n_i \rangle = \langle S_i^z \rangle + 1/2 = \sum_{m \in {\color{#56B4E9}\mathrm{occ}}}

\delta_i = \langle n_i \rangle\approx e^{-\frac{r}{\xi} } + \dots

\delta_i = \langle n_i \rangle\approx e^{-\frac{r}{\xi} } + \dots

:

r

r

\ell_{\mathrm{cluster}}

\ell_{\mathrm{cluster}}

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

11

\Rightarrow \quad \delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\Rightarrow \quad \delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\ell_{\mathrm{cluster}}

\ell_{\mathrm{cluster}}

Toy model

12

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

Toy model validity

\ell_{\mathrm{cluster}}

\ell_{\mathrm{cluster}}

12

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

Toy model validity

\ell_{\mathrm{cluster}}

\ell_{\mathrm{cluster}}

Chain breaking

13

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

Chain breaking

13

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\gamma

\gamma

Chain breaking

13

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

SPIN FREEZING !

\gamma

\gamma

CHAIN BREAKING !

Chain breaking : not just a toy model

14

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

14

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\quad h

\quad h

Chain breaking : not just a toy model

14

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\overline{\ell_{\mathrm{cluster}}} \approx \frac{\ln L}{ \ln 2}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

\delta^{\mathrm{typ}}_{\min} \approx L^{-\frac{1}{2\xi \ln2}}

Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)

Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)

JC, Laflorencie, PRB 108, 144206 (2023)

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

\delta_{\min} \approx e^{-\frac{\ell_{\mathrm{cluster}}}{2\xi}}

h

h

Chain breaking : not just a toy model

Extreme magnetization outlook

15

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

Extreme value transition

Novel numerical methods?

$h$

Distributions predicted by extreme value

3. Interactions

rOLE OF INTERACTIONS

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

16

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}\right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} \right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} \right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

rOLE OF INTERACTIONS

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}+{\color{salmon}2 \Delta n_i n_{i+1}} \right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}+{\color{salmon}2 \Delta n_i n_{i+1}} \right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} + {\color{salmon} 2\Delta S_i^z S_{i+1}^z}\right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} + {\color{salmon} 2\Delta S_i^z S_{i+1}^z}\right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

Attraction /Repulsion

Ising

16

rOLE OF INTERACTIONS

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}+{\color{salmon}2 \Delta n_i n_{i+1}} \right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}+{\color{salmon}2 \Delta n_i n_{i+1}} \right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} + {\color{salmon} 2\Delta S_i^z S_{i+1}^z}\right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} + {\color{salmon} 2\Delta S_i^z S_{i+1}^z}\right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

Polynomial $\rightarrow$ Exponential

Simulations of MBL lattice models | Fabien Alet | Cargese

Attraction /Repulsion

Ising

16

rOLE OF INTERACTIONS

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}+{\color{salmon}2 \Delta n_i n_{i+1}} \right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}+{\color{salmon}2 \Delta n_i n_{i+1}} \right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} + {\color{salmon} 2\Delta S_i^z S_{i+1}^z}\right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} + {\color{salmon} 2\Delta S_i^z S_{i+1}^z}\right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

Polynomial $\rightarrow$ Exponential

See for instance Pietracaprina et al., SciPost Phys. 5, 045

Simulations of MBL lattice models | Fabien Alet | Cargese

Attraction /Repulsion

Ising

16

rOLE OF INTERACTIONS

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}+{\color{salmon}2 \Delta n_i n_{i+1}} \right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H}_f = \sum_{i} \frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}}+{\color{salmon}2 \Delta n_i n_{i+1}} \right) -\sum_i{\color{gray}h_i n_i}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} + {\color{salmon} 2\Delta S_i^z S_{i+1}^z}\right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

\mathcal{H} = \sum_{i} \frac{J}{2}\left({\color{lightgreen}S_i^{+} S_{i+1}^{-} + S_i^{-} S_{i+1}^{+}} + {\color{salmon} 2\Delta S_i^z S_{i+1}^z}\right) - \sum_{i} {\color{gray} h_i S_i^z} {\color{black}+ E_0 + \mathcal{H}_{\mathrm{BC}}}

Polynomial $\rightarrow$ Exponential

See for instance Pietracaprina et al., SciPost Phys. 5, 045

Simulations of MBL lattice models | Fabien Alet | Cargese

Attraction /Repulsion

Ising

16

The question

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

17

Anderson localized

(insulator)

disorder $h$

Interaction $\Delta$

Recent review : Sierant et al., arXiv:2403.07111

The question

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

Anderson localized

(insulator)

disorder $h$

Ergodic

("metal")

Interaction $\Delta$

Many-body localized

Recent review : Sierant et al., arXiv:2403.07111

17

The question

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

Anderson localized

(insulator)

disorder $h$

Ergodic

("metal")

Many-body localized

Interaction $\Delta$

Recent review : Sierant et al., arXiv:2403.07111

Debate :

Stability of MBL
Location of the transition
Intermediate phase

17

The question

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

Anderson localized

(insulator)

disorder $h$

Ergodic

("metal")

?

Interaction $\Delta$

Many-body localized

Debate :

Stability of MBL
Location of the transition
Intermediate phase

Recent review : Sierant et al., arXiv:2403.07111

17

Ergodic instability

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

18

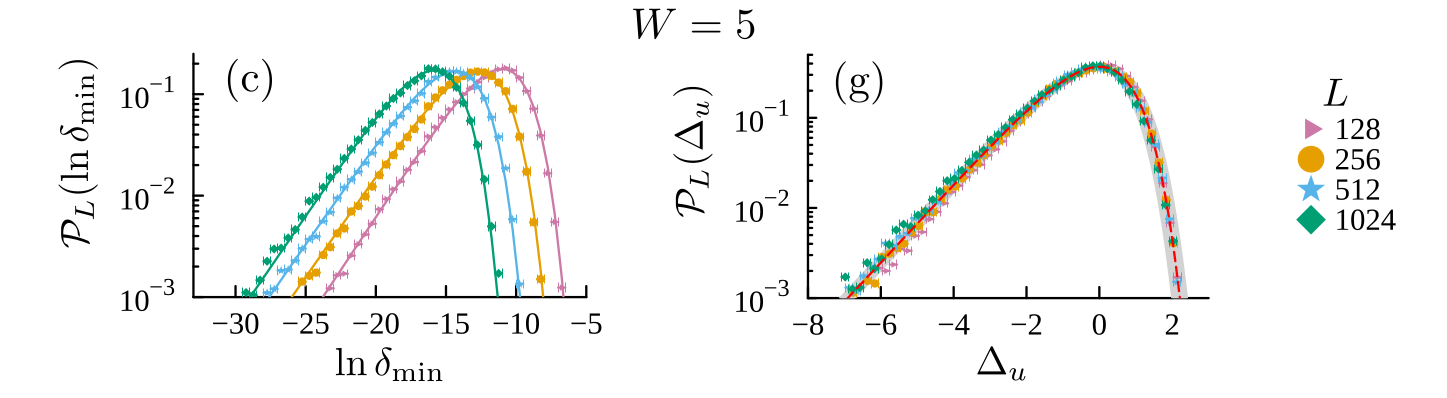
$\delta_{\min} \rightarrow 1/2$

$\delta_{\min} \sim L^{-\gamma}\rightarrow 0$

JC, F. Alet, N. Laflorencie, arXiv:2403.09608

(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5)

Anderson localized

(insulator)

disorder $h$

?

Interaction $\Delta$

Ergodic instability

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5)

Anderson localized

(insulator)

disorder $h$

?

Interaction $\Delta$

Avalanche theory:

if $\xi > \xi_{\mathrm{av.}}$ then the system becomes ergodic

18

JC, F. Alet, N. Laflorencie, arXiv:2403.09608

Ergodic instability

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

$\Delta/J$

$h/J$

Anderson localized

(insulator)

1

0.75

0.5

0.25

0

1

2

3

4

5

6

7

8

9

10

$\delta_{\min} \rightarrow 1/2$

$\delta_{\min} \sim L^{-\gamma}\rightarrow 0$

(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5)

Avalanche theory:

if $\xi > \xi_{\mathrm{av.}}$ then the system becomes ergodic

18

JC, F. Alet, N. Laflorencie, arXiv:2403.09608

Ergodic instability

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

$\Delta/J$

$h/J$

Anderson localized

(insulator)

1

0.75

0.5

0.25

0

1

2

3

4

5

6

7

8

9

10

In the XXZ spin-chain

Avalanche theory + numerical results:

weak interactions $\rightarrow$ ergodic!

$\delta_{\min} \rightarrow 1/2$

$\delta_{\min} \sim L^{-\gamma}\rightarrow 0$

(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5)

Avalanche theory:

if $\xi > \xi_{\mathrm{av.}}$ then the system becomes ergodic

18

JC, F. Alet, N. Laflorencie, arXiv:2403.09608

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

19

(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5)

Avalanche theory:

if $\xi > \xi_{\mathrm{av.}}$ then the system becomes ergodic

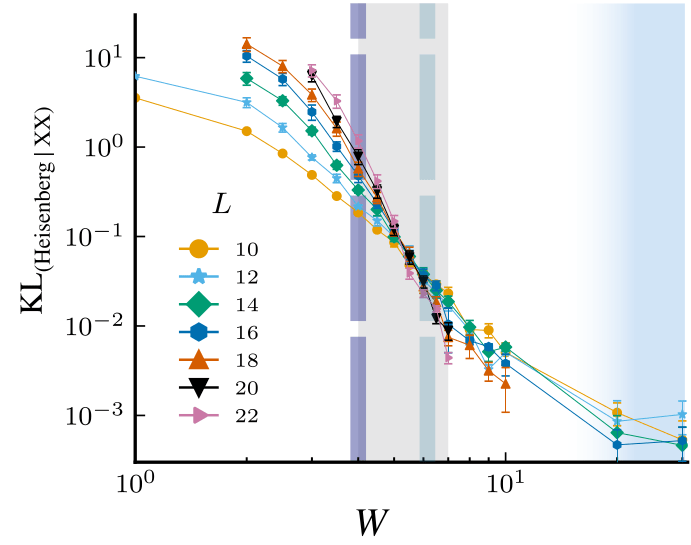
How to evaluate $\xi$ in the presence of interactions?

Instabilities in the spin-spin correlations

JC, F. Alet, N. Laflorencie, arXiv:2403.09608

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5)

Avalanche theory:

if $\xi > \xi_{\mathrm{av.}}$ then the system becomes ergodic

How to evaluate $\xi$ in the presence of interactions?

$\Delta/J$

$h/J$

Anderson localized

(insulator)

1

0.75

0.5

0.25

0

1

2

3

4

5

6

7

8

9

10

Instabilities in the spin-spin correlations

19

JC, F. Alet, N. Laflorencie, arXiv:2403.09608

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5)

Avalanche theory:

if $\xi > \xi_{\mathrm{av.}}$ then the system becomes ergodic

How to evaluate $\xi$ in the presence of interactions?

$\Delta/J$

$h/J$

Anderson localized

(insulator)

1

0.75

0.5

0.25

0

1

2

3

4

5

6

7

8

9

10

Instabilities in the spin-spin correlations

19

JC, F. Alet, N. Laflorencie, arXiv:2403.09608

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5)

Avalanche theory:

if $\xi > \xi_{\mathrm{av.}}$ then the system becomes ergodic

How to evaluate $\xi$ in the presence of interactions?

$\Delta/J$

$h/J$

Anderson localized

(insulator)

1

0.75

0.5

0.25

0

1

2

3

4

5

6

7

8

9

10

Instabilities in the spin-spin correlations

19

JC, F. Alet, N. Laflorencie, arXiv:2403.09608

tAKE-HOME MESSAGEs

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

$|\psi(x)|^2$

$\xi(h, E)$

Anderson localization

in 1D: $\forall E$

20

tAKE-HOME MESSAGEs

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

$|\psi(x)|^2$

$\xi(h, E)$

Anderson localization

in 1D: $\forall E$

SPIN FREEZING!

CHAIN BREAKING!

20

tAKE-HOME MESSAGEs

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

$|\psi(x)|^2$

$\xi(h, E)$

Anderson localization

in 1D: $\forall E$

SPIN FREEZING!

CHAIN BREAKING!

disorder $h$

Interaction $\Delta$

@ High energy!

20

Four Questions for you!

COLBOIS | INSTABILITIES IN RANDOM SPIN CHAINS | MAJULAB | 07.2024

\ell_{\max} \sim \ln L / \ln 2 \sim 7.45

\ell_{\max} \sim \ln L / \ln 2 \sim 7.45

1. How to show

2. True or false: Anderson localization is a purely quantum phenomenon

3. Is many-body localization different from "many-body Anderson" localization?

4. How can you use tensor networks to count

the number of ground states of a generalized Ising model?

21

22

Weitao CHEN

Sen MU

Nyayabanta SWAIN

Noam IZEM

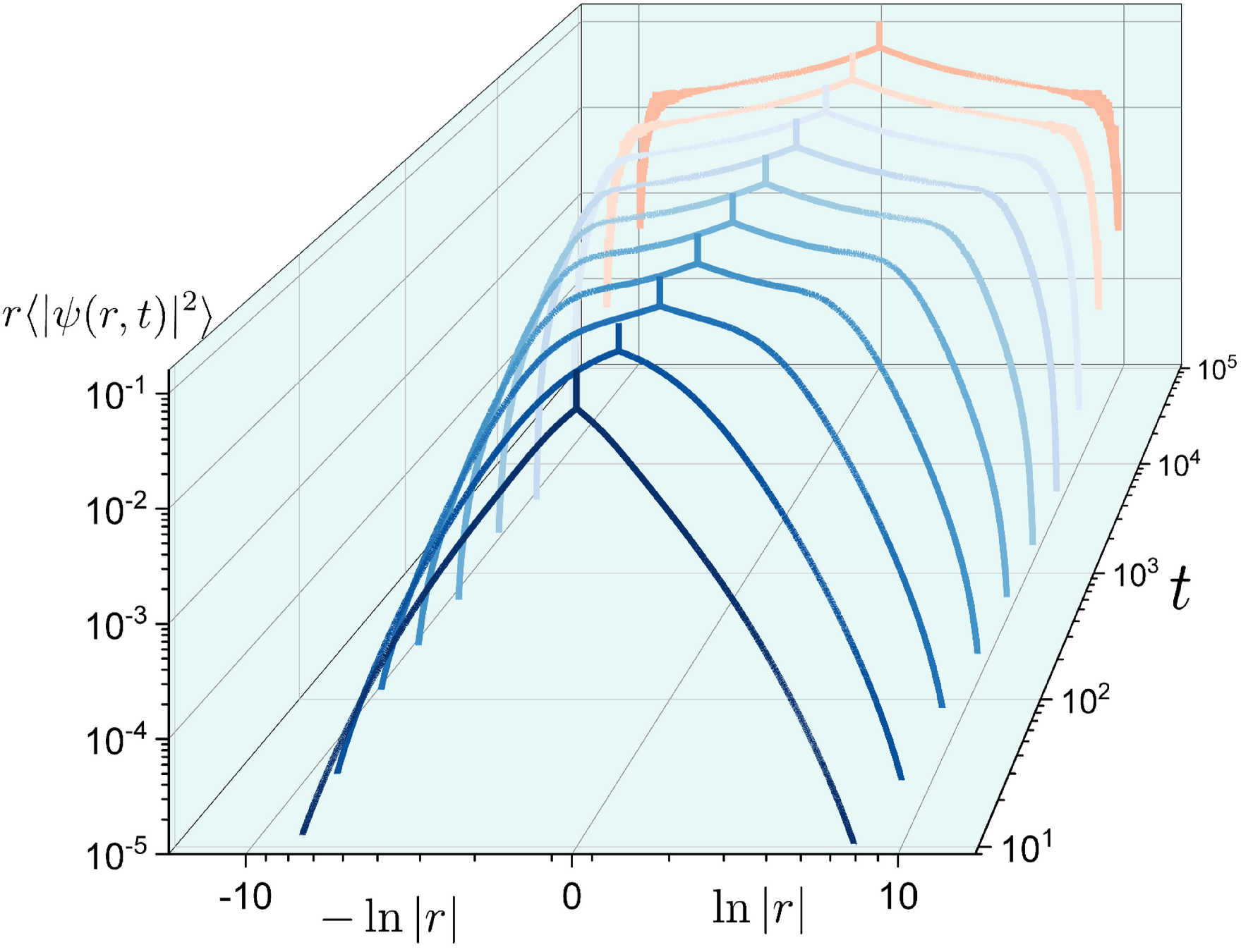
Logarithmically slow expansion of a

quantum logarithmic-multifractal

wave packet over time

Localization, Multifractality and Chaos in complex quantum systems;

Random Matrices

Anderson localization/transition in cold atom systems

Multifractality

Numerical simulations

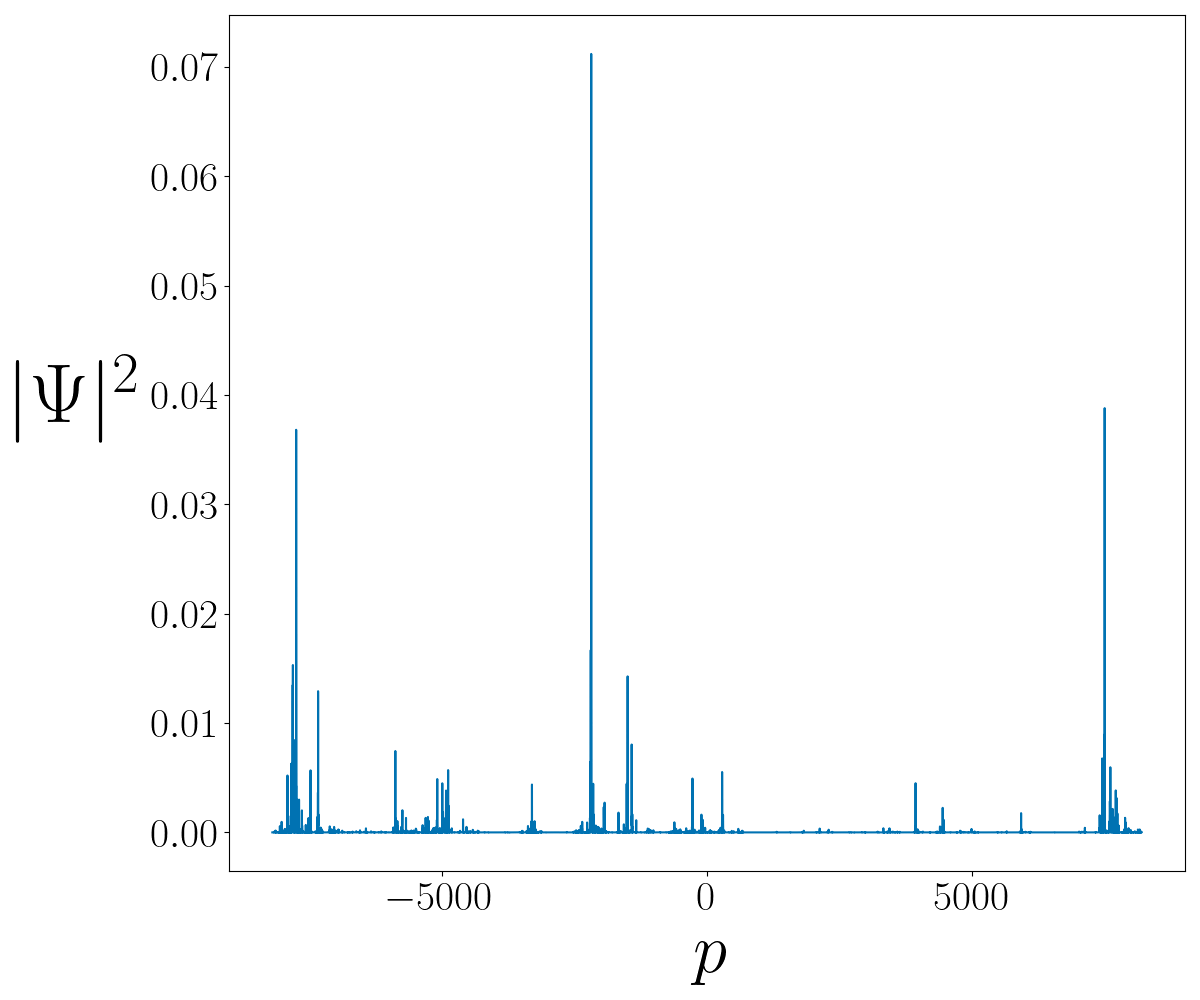
Example of a

multifractal eigenstate for one electron in a disordered potential:

neither localized nor metallic

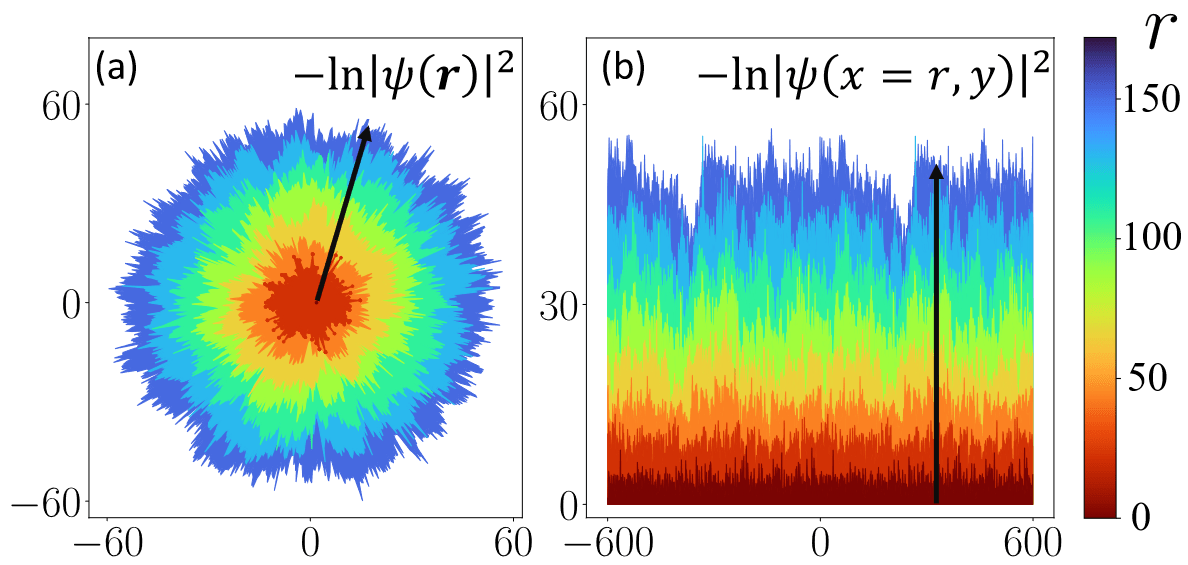
The logarithm of the wave density

of a localized wave packet in 2D

exhibits similar scaling behaviors as a

growing interface

in the KPZ class

Quantum information and topological phases of matter

Kardar-Parisi-Zhang

universality class

Gabriel

LEMARIE

Quantum Monte Carlo

Eigenstate to Hamiltonian construction

Kardar-Parisi-Zhang universality class

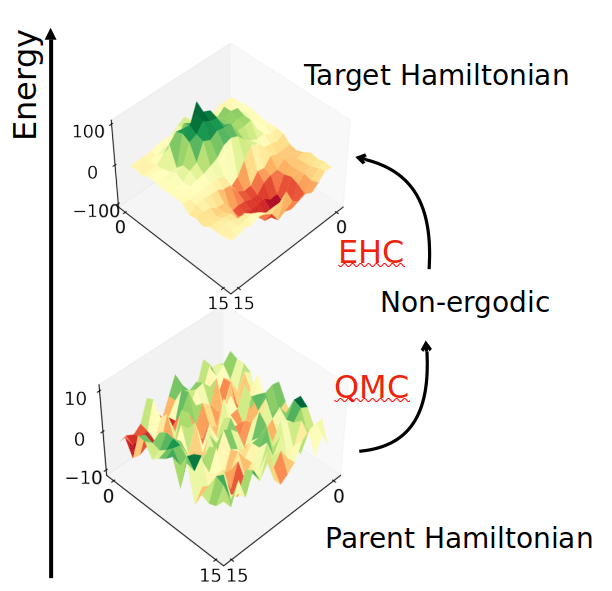
Using EHC, we map the ground state of a 2D Hamiltonian in random disorder to an exotic excited state of a target Hamiltonian

Bonus slide unlocked

$L/2$ fermions

$S_z = 0$

|\Psi \rangle = | \left\{\phi_m, m \in {\color{#56B4E9}\mathrm{occ}} \right\}\rangle

|\Psi \rangle = | \left\{\phi_m, m \in {\color{#56B4E9}\mathrm{occ}} \right\}\rangle

\mathcal{H}_f = \sum_{i} \Bigl[\frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}} \right) -{\color{#76a5af}h_i n_i}\Bigr]

\mathcal{H}_f = \sum_{i} \Bigl[\frac{J}{2}\left({\color{lightgreen}c_i^{\dagger} c_{i+1}^{\vphantom{\dagger}} + c_{i+1}^{\dagger}c_i^{\vphantom{\dagger}}} \right) -{\color{#76a5af}h_i n_i}\Bigr]

\epsilon_m

\epsilon_m

E_m

E_m

\mathcal{H} = \sum_m \epsilon_m b_m^{\dagger} b_m + \sum_{j,k,l,m} {\color{#ff9900}V_{j,k,l,m} b_j^{\dagger} b_k^{\dagger} b_l b_m}

\mathcal{H} = \sum_m \epsilon_m b_m^{\dagger} b_m + \sum_{j,k,l,m} {\color{#ff9900}V_{j,k,l,m} b_j^{\dagger} b_k^{\dagger} b_l b_m}

In the Anderson basis:

Anderson

orbitals $m$

What about high temperatures / high energy eigenstates?

Do isolated quantum systems thermalize?

Thermal average

?

ETH

Time average

Anderson

No growth

of entanglement

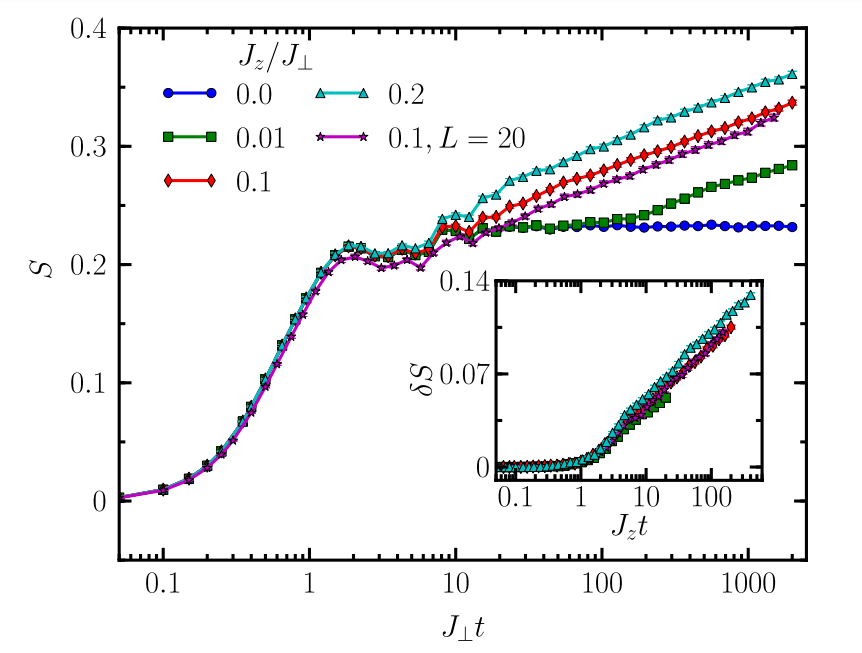
J. H. Bardarson, F. Pollmann, and J. E. Moore, PRL 109, 017202 (2012)

M. Znidaric, T. Prosen, and P. Prelovsek PRB 77, 064426 (2008)

Log growth

of entanglement

Initial $S^z$ basis random product state

+

TEBD

W = 5

W

Ergodic

MBL

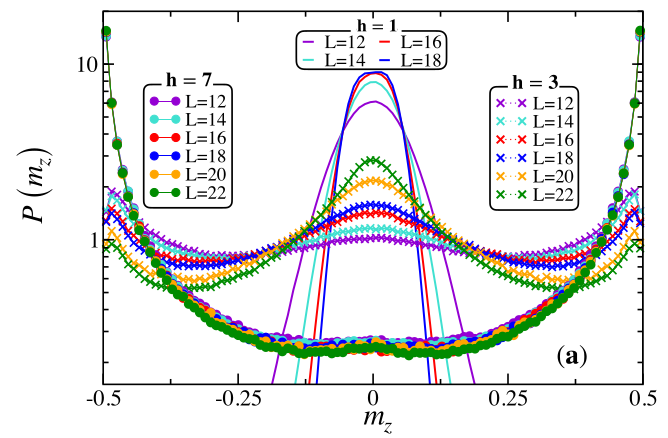
2016

Finite L

Finite-size scaling? Location of the transition?
Destabilization by ergodic bubbles even at strong disorder?
Immediate onset of quantum chaos? Intermediate phase(s)?

W

Ergodic

MBL phase/ regimes?

Prethermal

regime?

2023

$L$ increases

Anderson chain / XX chain

Heisenberg chain

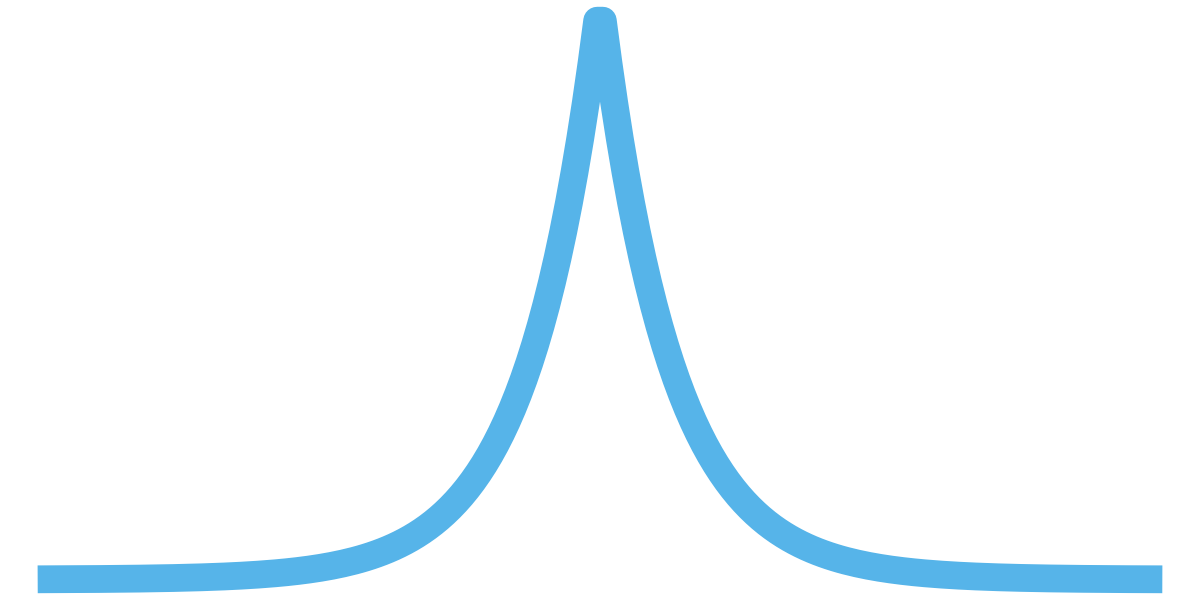
Fréchet

$10^5$ samples

\mathcal{P}(\delta) \overset{\delta \rightarrow 0}{\sim} A\delta^{\alpha}

\mathcal{P}(\delta) \overset{\delta \rightarrow 0}{\sim} A\delta^{\alpha}

\mathcal{P}(\ln\delta_{\min}) \rightarrow AL\delta_{\min}^{\alpha} \exp\left({-\frac{AL}{\alpha+1}\delta_{\min}^{\alpha+1}}\right)

\mathcal{P}(\ln\delta_{\min}) \rightarrow AL\delta_{\min}^{\alpha} \exp\left({-\frac{AL}{\alpha+1}\delta_{\min}^{\alpha+1}}\right)

\delta_{\mathrm{\min}}^{\mathrm{typ}}(L) \approx \left(\frac{A}{1+\alpha} L \right)^{-\frac{1}{1+\alpha}}

\delta_{\mathrm{\min}}^{\mathrm{typ}}(L) \approx \left(\frac{A}{1+\alpha} L \right)^{-\frac{1}{1+\alpha}}

\Delta_u= (\alpha+1)(\ln\delta_{\min}- \ln\delta_{\min}^{\mathrm{typ}})

\Delta_u= (\alpha+1)(\ln\delta_{\min}- \ln\delta_{\min}^{\mathrm{typ}})

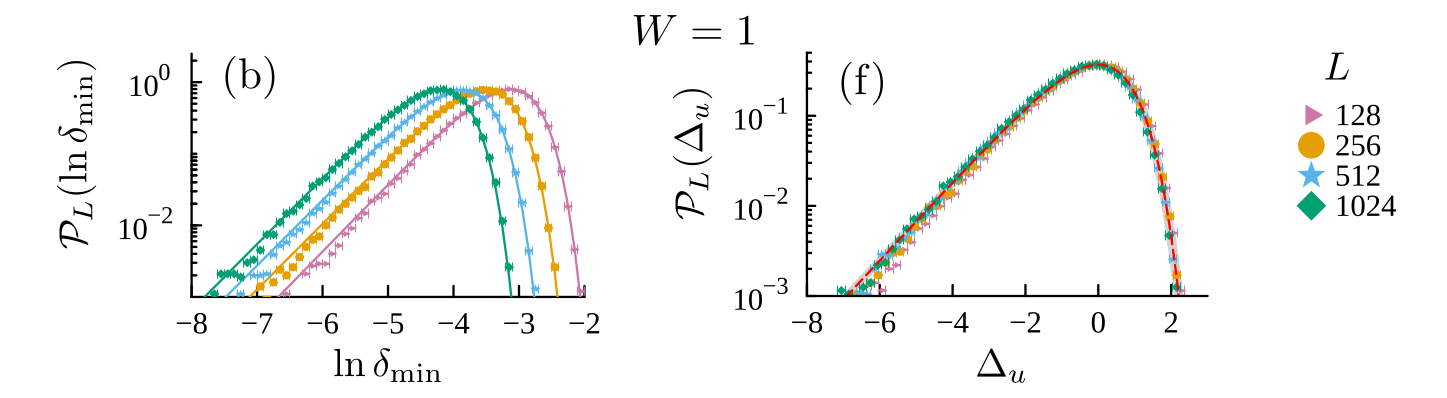
Fréchet

$10^5$ samples

\mathcal{P}(\delta) \overset{\delta \rightarrow 0}{\sim} A\delta^{\alpha}

\mathcal{P}(\delta) \overset{\delta \rightarrow 0}{\sim} A\delta^{\alpha}

\mathcal{P}(\ln\delta_{\min}) \rightarrow AL\delta_{\min}^{\alpha} \exp\left({-\frac{AL}{\alpha+1}\delta_{\min}^{\alpha+1}}\right)

\mathcal{P}(\ln\delta_{\min}) \rightarrow AL\delta_{\min}^{\alpha} \exp\left({-\frac{AL}{\alpha+1}\delta_{\min}^{\alpha+1}}\right)

\Delta_u= (\alpha+1)(\ln\delta_{\min}- \ln\delta_{\min}^{\mathrm{typ}})

\Delta_u= (\alpha+1)(\ln\delta_{\min}- \ln\delta_{\min}^{\mathrm{typ}})

\delta_{\mathrm{\min}}^{\mathrm{typ}}(L) \approx \left(\frac{A}{1+\alpha} L \right)^{-\frac{1}{1+\alpha}}

\delta_{\mathrm{\min}}^{\mathrm{typ}}(L) \approx \left(\frac{A}{1+\alpha} L \right)^{-\frac{1}{1+\alpha}}