Motivation / promise

1

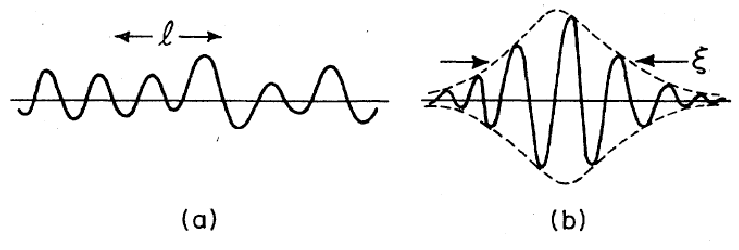
Large systems
Any energy / eigenfunctions

Need

Idea

Promise

M

+ Combine efficiently

$10^9$ non-interacting

$10^6$ Two interacting particles

Time evolution

arXiv:2211.13089 (v1)

Plan

Models
Observables
Algorithm(s)
Some results

2

arXiv:2211.13089 (v1)

Models

3

arXiv:2211.13089 (v1)

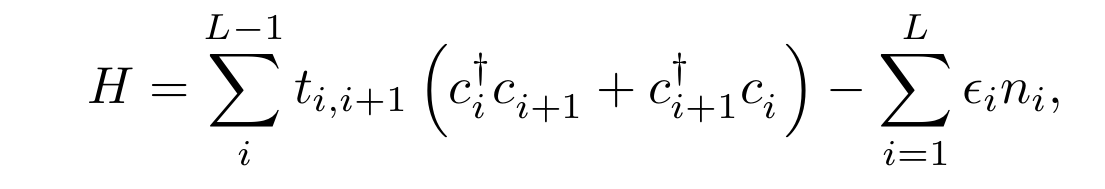
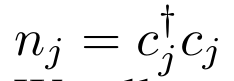
(1) Mostly: $t_{i, i+1} = t = 1$ , $\epsilon_i$ :

Irrational $\beta$

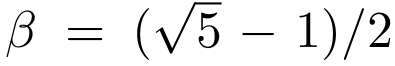
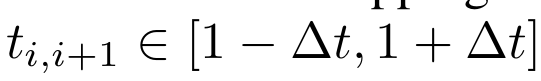
(2) Also:

$\epsilon_i$ constant

Models

3

arXiv:2211.13089 (v1)

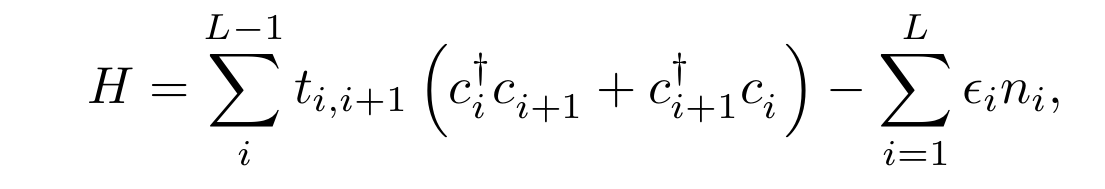
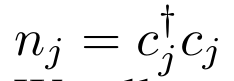
(1) Mostly: $t_{i, i+1} = t = 1$ , $\epsilon_i$ :

Irrational $\beta$

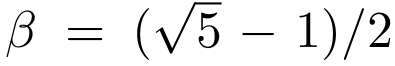
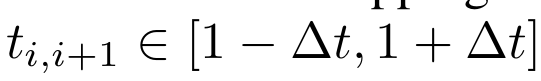
(2) Also:

$\epsilon_i$ constant

More delocalized

locally clean
translation invariance partially restored

Chiral (particle-hole) symmetry:

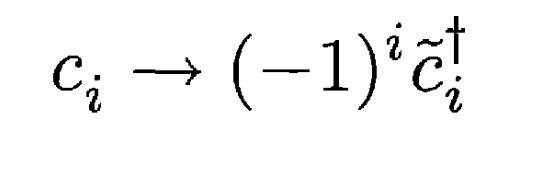
Delocalized region

Models : TIP

4

arXiv:2211.13089 (v1)

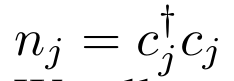
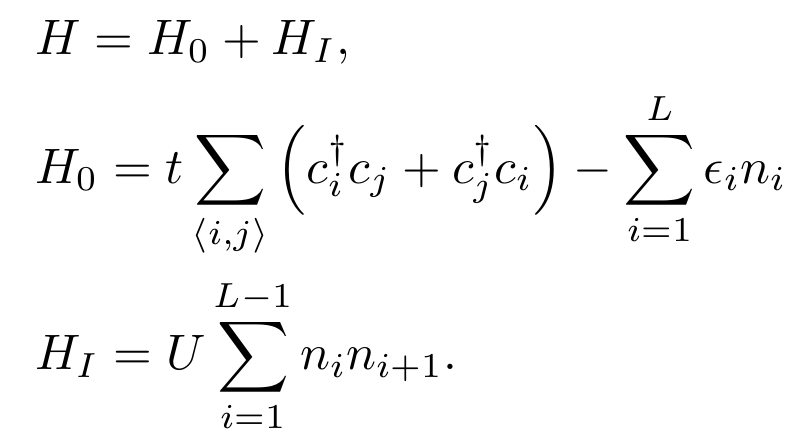
Only at strong disorder

Measurements

5

arXiv:2211.13089 (v1)

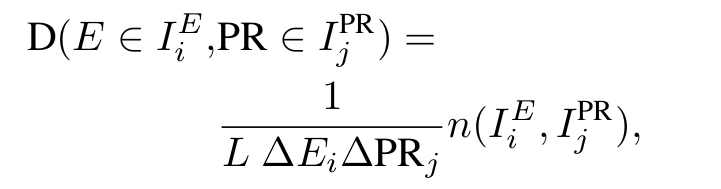
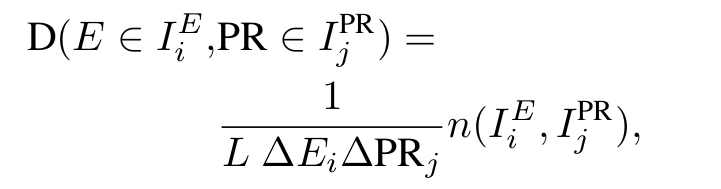
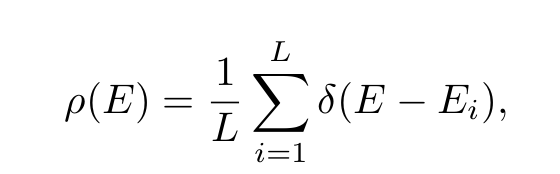
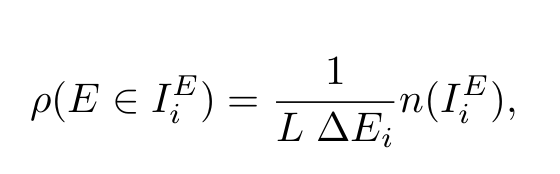
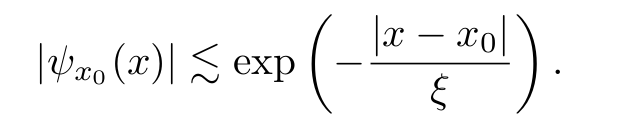
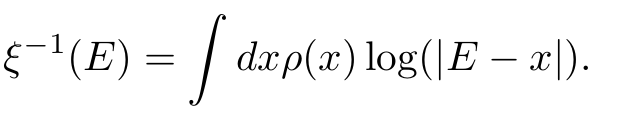
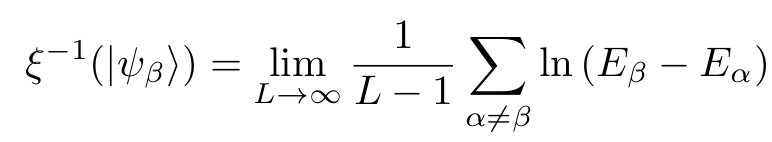
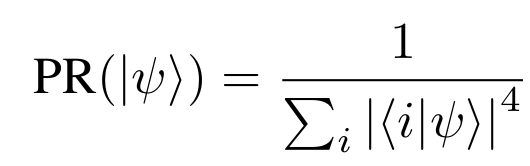
Density of states

Localization length

Participation ratio

D J Thouless 1972 J. Phys. C: Solid State Phys. 5 77

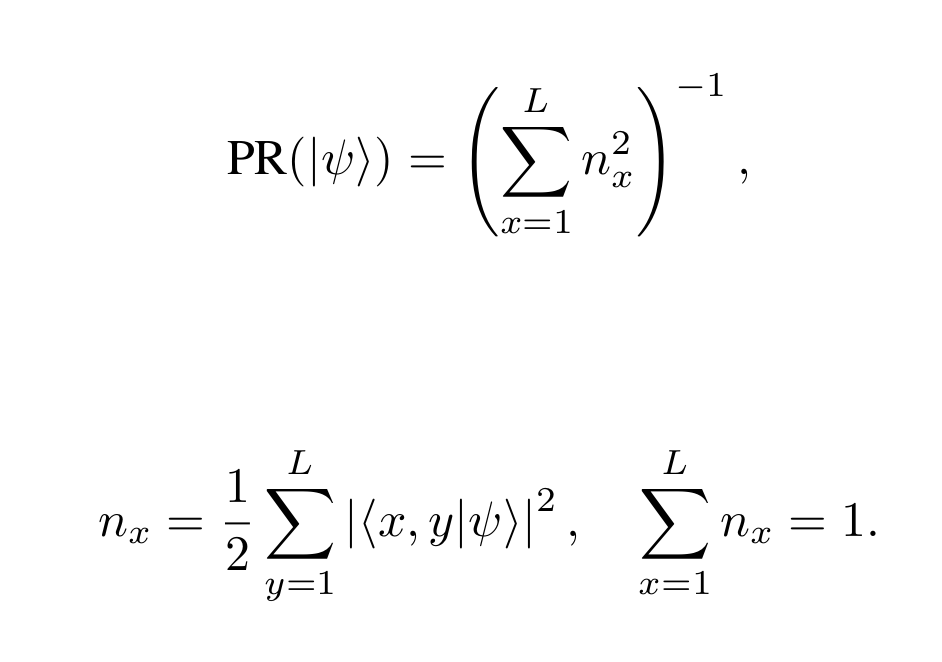
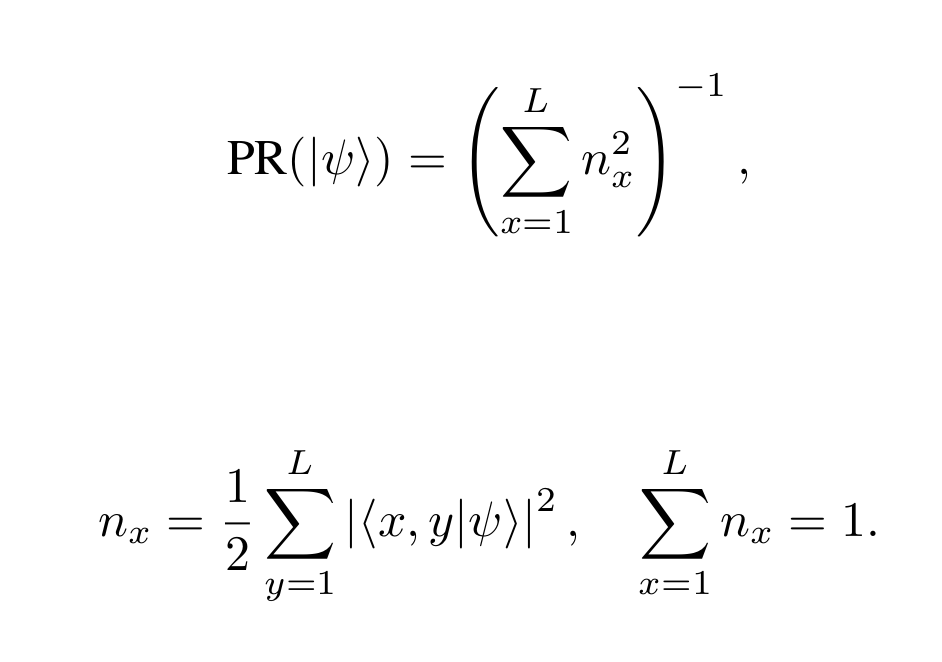
Algorithm(s)

arXiv:2211.13089 (v1)

General idea

H = H^S + H^{\mathrm{Env}}

H = H^S + H^{\mathrm{Env}}

H^S

H^S

Partition and solve $H_s$
Embed
Eliminate
(Time-evolve)

6

arXiv:2211.13089 (v1)

General idea

H = H^S + H^{\mathrm{Env}}

H = H^S + H^{\mathrm{Env}}

H^S

H^S

Partition and solve $H_s$
Embed
Eliminate
(Time-evolve)

Parallelization

6

arXiv:2211.13089 (v1)

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

7

arXiv:2211.13089 (v1)

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

7

arXiv:2211.13089 (v1)

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

7

arXiv:2211.13089 (v1)

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

7

arXiv:2211.13089 (v1)

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

7

arXiv:2211.13089 (v1)

i \in [0, L-M]

i \in [0, L-M]

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

$\left \lceil \frac{2L}{M}\right\rceil$ sub-systems

Far less repetitions

$M$ twice as large

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

x_1

x_1

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\langle x_1 | N \rho_1 | x_1 \rangle < 1

\langle x_1 | N \rho_1 | x_1 \rangle < 1

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

$\left \lceil \frac{2L}{M}\right\rceil$ sub-systems

Far less repetitions

$M$ twice as large

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

x_1

x_1

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\langle x_1 | N \rho_1 | x_1 \rangle < 1

\langle x_1 | N \rho_1 | x_1 \rangle < 1

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

$\left \lceil \frac{2L}{M}\right\rceil$ sub-systems

Far less repetitions

$M$ twice as large

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

x_1

x_1

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\langle x_1 | N \rho_1 | x_1 \rangle = 1

\langle x_1 | N \rho_1 | x_1 \rangle = 1

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

$\left \lceil \frac{2L}{M}\right\rceil$ sub-systems

Far less repetitions

$M$ twice as large

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

x_1

x_1

x_2

x_2

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\langle x_1 | N \rho_1 | x_1 \rangle = 1

\langle x_1 | N \rho_1 | x_1 \rangle = 1

\langle x_2 | N \rho_1 | x_2 \rangle < 1

\langle x_2 | N \rho_1 | x_2 \rangle < 1

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

$\left \lceil \frac{2L}{M}\right\rceil$ sub-systems

Far less repetitions

$M$ twice as large

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

1. Partitions: $M$ sites

x_1

x_1

x_2

x_2

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\langle x_1 | N \rho_1 | x_1 \rangle = 1

\langle x_1 | N \rho_1 | x_1 \rangle = 1

\langle x_2 | N \rho_1 | x_2 \rangle < 1

\langle x_2 | N \rho_1 | x_2 \rangle < 1

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

A_i = ] i, i+M] ,\quad i \in ]0, L-M]

Repetitions

$L-M$ sub-systems

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

B_i = ]i \times \frac{M}{2}, i\times \frac{M}{2}+M] ,\quad 0 \leq i \leq \left \lceil \frac{2L}{M} \right \rceil

7

arXiv:2211.13089 (v1)

$\left \lceil \frac{2L}{M}\right\rceil$ sub-systems

Far less repetitions

$M$ twice as large

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

0 \leq i < \left \lfloor \frac{2L}{M} \right \rfloor

i \in [0, L-M]

i \in [0, L-M]

2. Embed

8

arXiv:2211.13089 (v1)

H = H^S + H^{\mathrm{Env}}

H = H^S + H^{\mathrm{Env}}

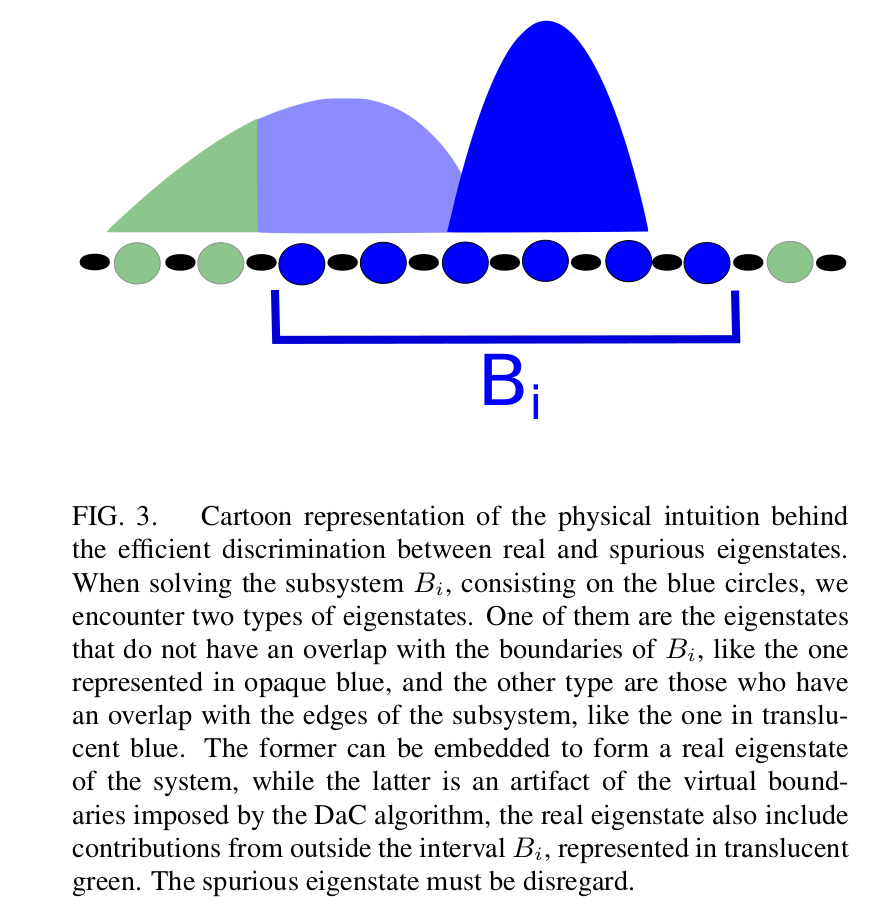
Real

Spurious

$B_{i-1}$

\ln(\tilde{\Phi}(x))

\ln(\tilde{\Phi}(x))

2. Embed

8

arXiv:2211.13089 (v1)

H = H^S + H^{\mathrm{Env}}

H = H^S + H^{\mathrm{Env}}

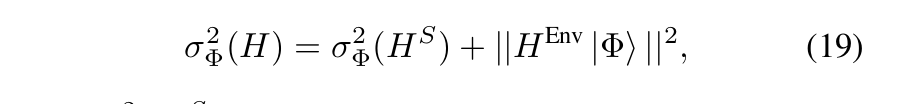
$|\Phi\rangle$ localized in $S$ :

Variance w.r.t environment

$|\Phi\rangle$ eigenvector of $H^S$ :

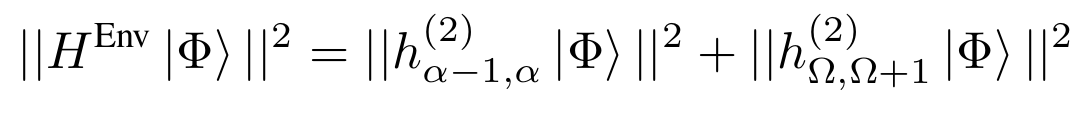
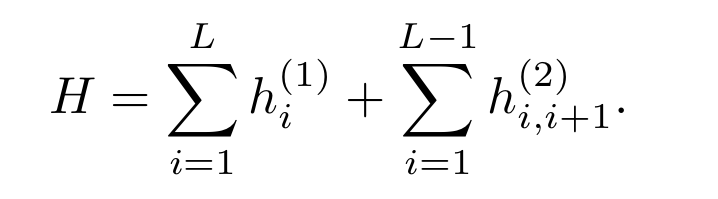
\sigma_{\Phi}^2(H) = ||H^{\mathrm{Env}}|\Phi\rangle||^2

\sigma_{\Phi}^2(H) = ||H^{\mathrm{Env}}|\Phi\rangle||^2

3. COMBINE / ELIMINATE

9

arXiv:2211.13089 (v1)

Alternative : Gram-Schmidt

Two steps:

No arbitrary cut-off

Much slower

1. $|E_{\Phi} - E_{\Phi_k}| > \mathrm{num. }\, \mathrm{err} \quad \forall \, k \in \mathrm{rel.}\, \mathrm{clusters}$

2. $\langle \Phi_{j} | \Phi \rangle < \theta$ for all relevant $k$

$\Rightarrow | \Phi \rangle$ is a new eigenfunction

Setting $\theta$ :

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

Pop. on each site should not be larger than 1.

3. COMBINE / ELIMINATE

9

arXiv:2211.13089 (v1)

Two steps:

1. $|E_{\Phi} - E_{\Phi_k}| > \mathrm{num. }\, \mathrm{err} \quad \forall \, k \in \mathrm{rel.}\, \mathrm{clusters}$

2. $\langle \Phi_{j} | \Phi \rangle < \theta$ for all relevant $k$

$\Rightarrow | \Phi \rangle$ is a new eigenfunction

Setting $\theta$ :

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

Pop. on each site should not be larger than 1.

Before storing
Previous overlapping subsystems

Parallelization:

4. Time evolution

10

arXiv:2211.13089 (v1)

|\psi_0\rangle = \sum_{\mu} |\Phi_{\mu} \rangle \langle \Phi_{\mu} | \psi_0\rangle

|\psi_0\rangle = \sum_{\mu} |\Phi_{\mu} \rangle \langle \Phi_{\mu} | \psi_0\rangle

Prec. $\epsilon$ on $\langle\hat{O}\rangle$ $\Rightarrow$

# Eigenfunctions:

Accuracy of eigenfunctions:

\langle \Phi_{\mu} | \psi_0\rangle < \delta

\langle \Phi_{\mu} | \psi_0\rangle < \delta

Valid eigenfunctions : variance smaller than $\delta^2$

(Err. $\delta$ in amplitude)

Single particle specificities

11

arXiv:2211.13089 (v1)

$L$ eigenfunctions
Orthogonality : $\mathrm{Tr}(\rho_1)$ = 1
If missing: sites s.t. $\langle x | N \rho_1| x \rangle < 1$

Termination criteria

Variance

$S = [\alpha, \Omega]$

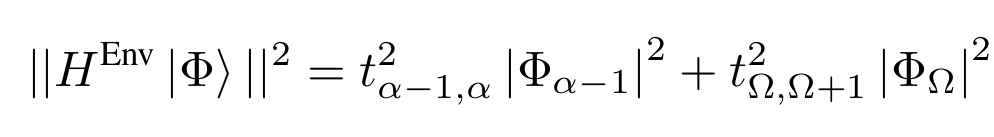
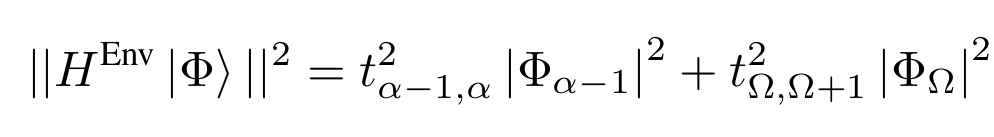
TIP specificities (1)

12

arXiv:2211.13089 (v1)

Idea

$L \times (L-1) /2$ eigenfunctions
Most pairs unaffected
Focus on subsystems of size M

BASIS

$M \times (M-1) /2$ , but sparse
Bandwidth $M$ in $\{|1,2\rangle, \dots , |1,M \rangle, |2,3 \rangle , \dots, |M-1, M \rangle\}$
Can be made $M/2$ [Reverse Cuthill-McKee]

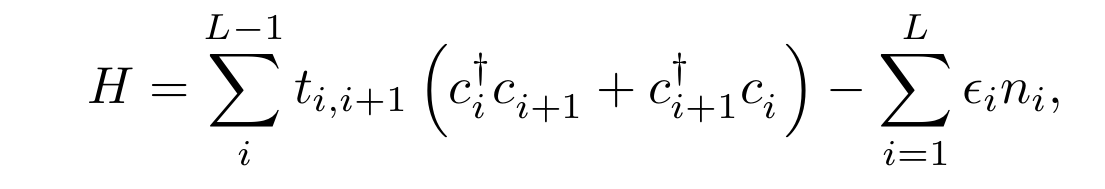
TIP specificities (2)

13

arXiv:2211.13089 (v1)

Variance

Termination criterion

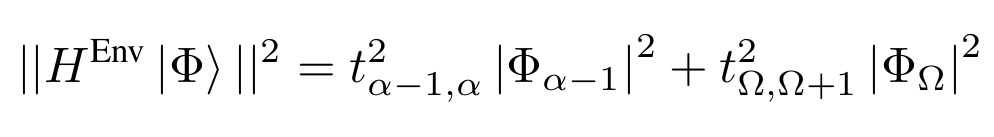
Here $|\Phi_{i}| ^2 = \sum_{j} |\langle i,j |\Phi\rangle |^2$

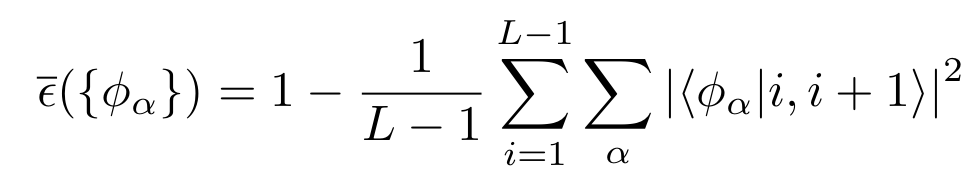
Smaller than a given cut-off.

Increase $M$ : new eigenstates, but independent of the value of the interaction

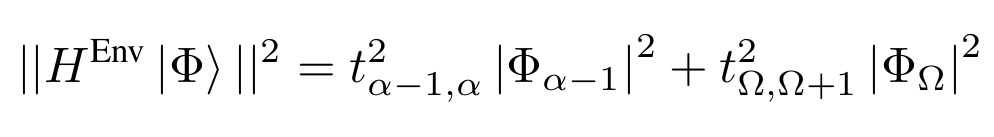
Algorithm Summary

arXiv:2211.13089 (v1)

Parameters

$\sigma$

$\theta, \, \delta (\epsilon)$

Simulation settings

14

$M_{\mathrm{Max}} = 26000$

$\Rightarrow V_{\mathrm{Min}} = 0.05$ : $W^{\mathrm{box}}_{\mathrm{And.}} \sim 0.77$ ; $W^{\mathrm{Gauss.}}_{\mathrm{And.}} = W^{\mathrm{Bin.}}_{\mathrm{And.}} \sim 0.44$

Single particle

INteracting particles

Variance:

\sigma_0^2 = \begin{cases} 10^{-32} & \text{ strong disorder}\\ 10^{-16} & \text{ weak disorder} \end{cases}

\sigma_0^2 = \begin{cases} 10^{-32} & \text{ strong disorder}\\ 10^{-16} & \text{ weak disorder} \end{cases}

Time evolution:

$M_{\mathrm{Max}} = 200$

Variance:

\sigma_0^2 = 10^{-16}

\sigma_0^2 = 10^{-16}

\epsilon = \begin{cases} 10^{-3} & \text{ strong disorder}\\ 10^{-1} & \text{ weak disorder} \end{cases}

\epsilon = \begin{cases} 10^{-3} & \text{ strong disorder}\\ 10^{-1} & \text{ weak disorder} \end{cases}

Overlap:

$\theta = 10^{-5}$

Overlap:

$\theta = 10^{-7}$

Time evolution:

\epsilon = \begin{cases} 10^{-5} & \text{ strong disorder}\\ 10^{-2} & \text{ weak disorder} \end{cases}

\epsilon = \begin{cases} 10^{-5} & \text{ strong disorder}\\ 10^{-2} & \text{ weak disorder} \end{cases}

Performance

15

$M \propto \xi$

Assume

$M$ being $L$ -independent
$M$ large enough

Limitations:

\mathcal{O}(\frac{L}{M} \times F(M)) = \begin{cases} \mathcal{O}(L \times M^2) & \text{ generic } \\ \mathcal{O}(L \times M) & \text{ tridiagonal } \end{cases}

\mathcal{O}(\frac{L}{M} \times F(M)) = \begin{cases} \mathcal{O}(L \times M^2) & \text{ generic } \\ \mathcal{O}(L \times M) & \text{ tridiagonal } \end{cases}

$\xi \sim L$ (ergodic) $\rightarrow$ usual complexity

$\xi \ll L$ $\rightarrow$ Dep. $L$ : locally larger $M$

arXiv:2211.13089 (v1)

Performance

16

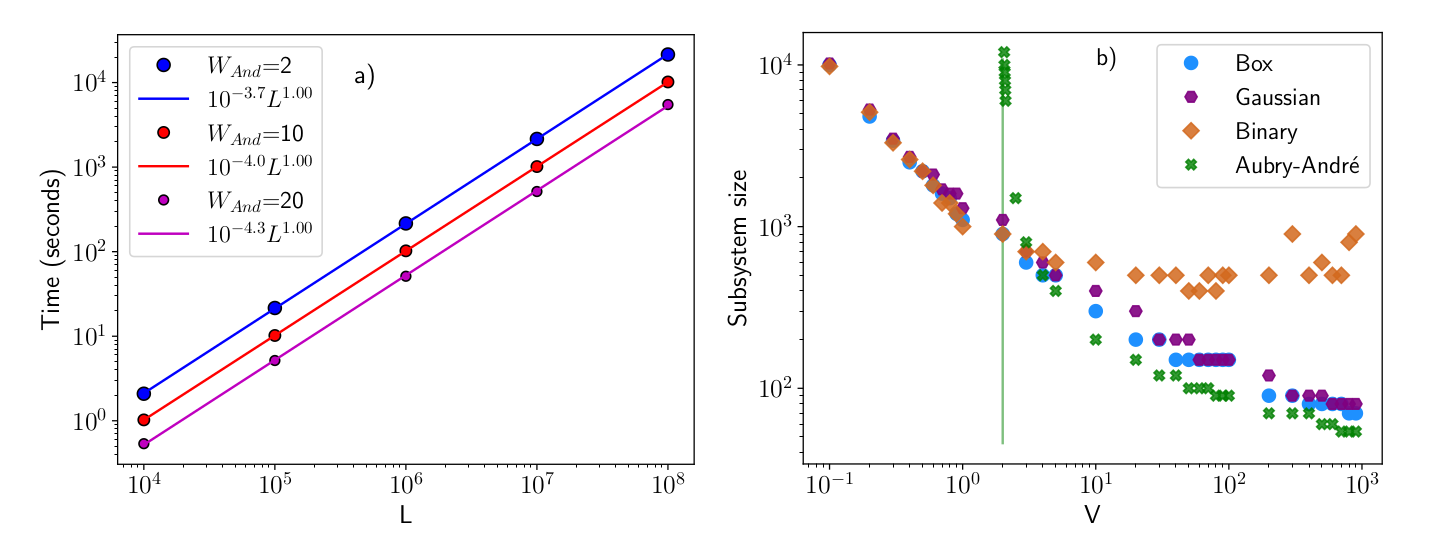
4 cores Inter Core i7-7700 CPU

Box distribution
$M = 1000,500, 250$

arXiv:2211.13089 (v1)

Performance

17

$M$

Saturation : binary potential

Aubry-André : delocalized eigenstates

Potential variance

arXiv:2211.13089 (v1)

S. Aubry and G. André, Ann. Israel Phys. Soc 3, 18, (1980)

Results

Strong

Weak

Single Particle

Two Interacting Particles

Eigenfunctions / Dynamics

Disorder

Properties of eigenfunctions

Strong disorder - single particle

18

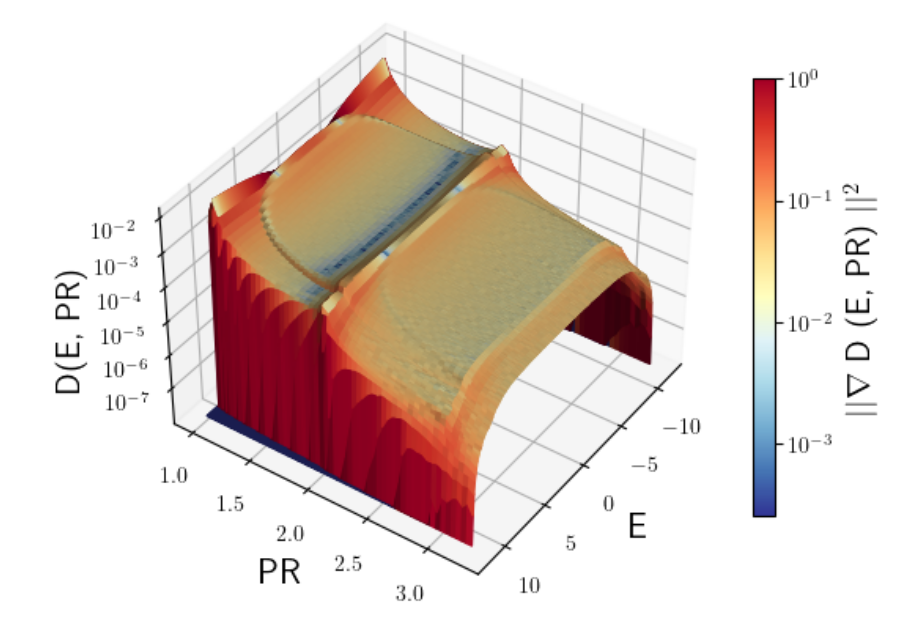
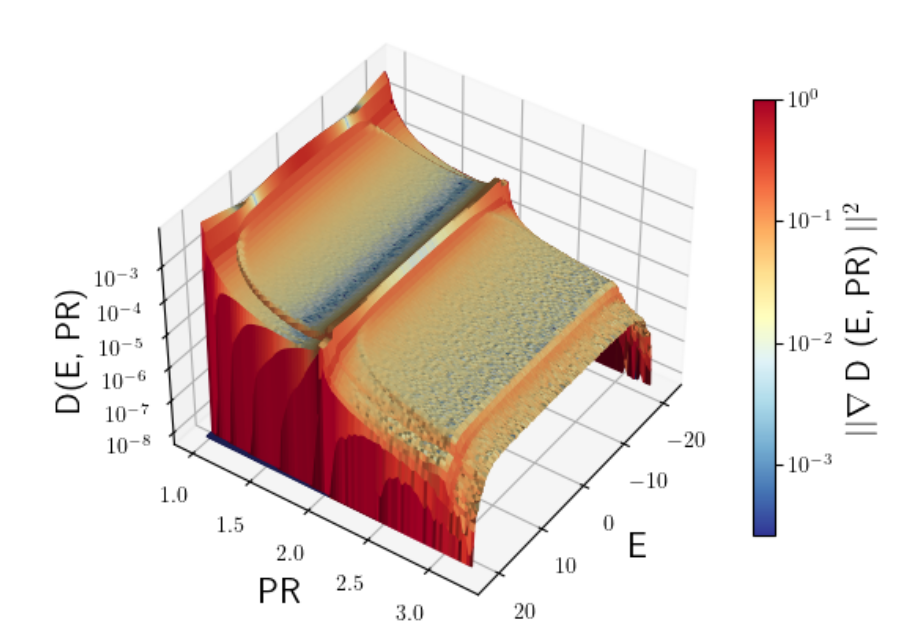
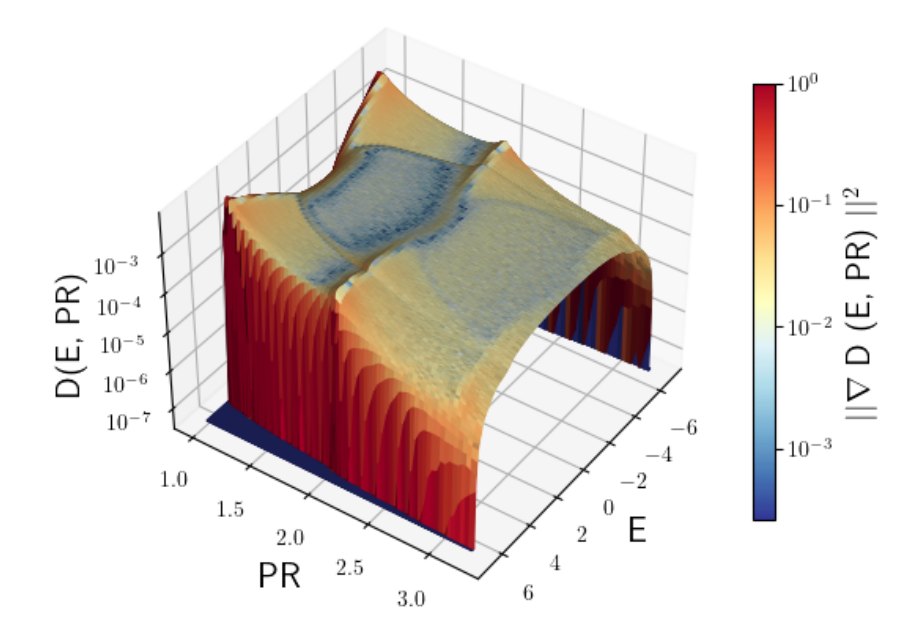
$10^9$ sites, Box distribution

$W_{\mathrm{And.}} = 10$

$W_{\mathrm{MBL}} = 2.5$

$W_{\mathrm{And.}} = 20$

$W_{\mathrm{MBL}} = 5$

$W_{\mathrm{And.}} = 40$

$W_{\mathrm{MBL}} = 10$

arXiv:2211.13089 (v1)

Strong disorder - TIP

19

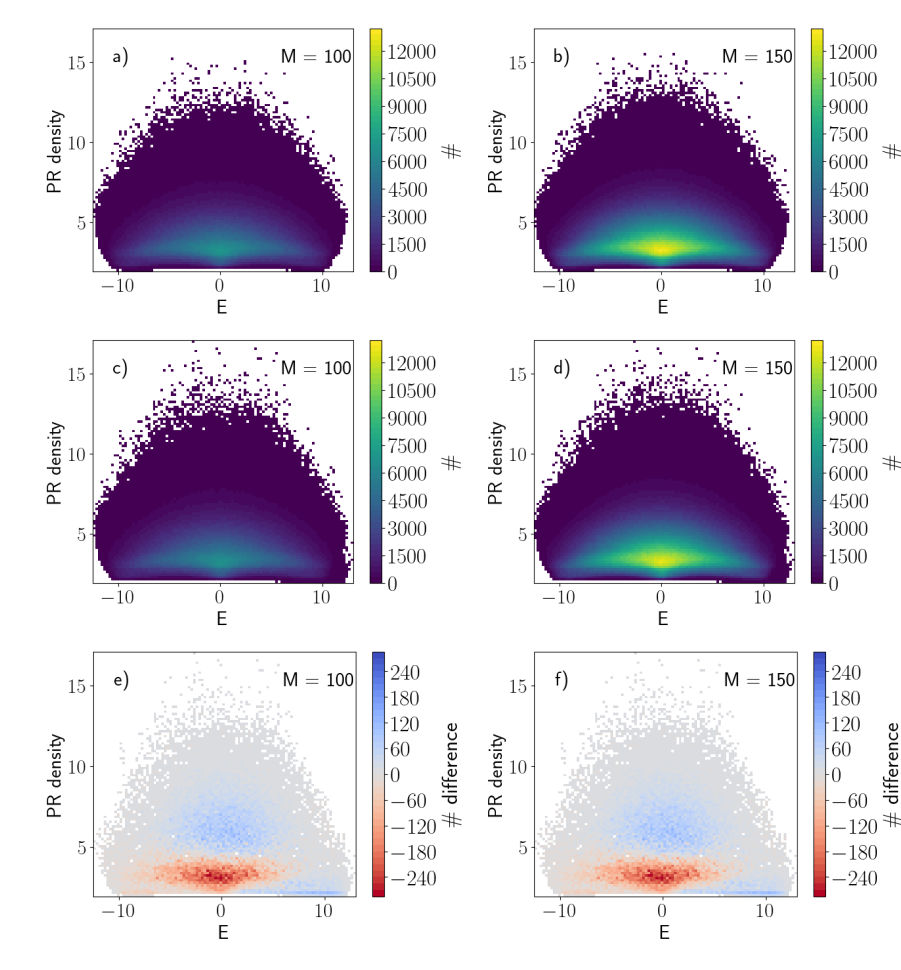
Diff.

$U = 0$

$U = 2$

$L = 10^5, W_{\mathrm{And.}} = 10$

Box distribution

arXiv:2211.13089 (v1)

Strong disorder - TIP

20

$U = 10, L = 10^6, W_{\mathrm{And.}} = 40$

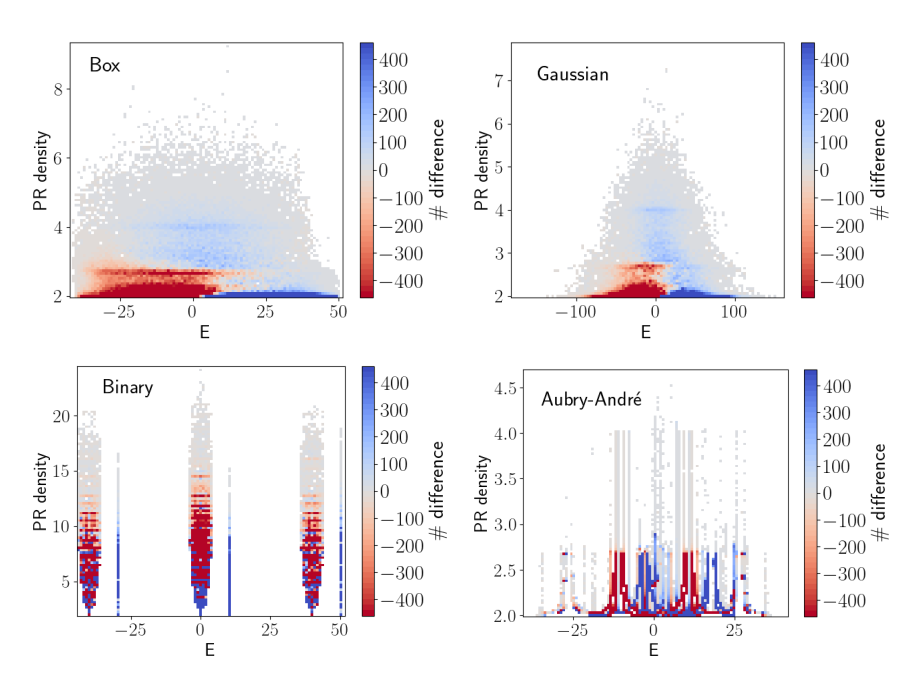
arXiv:2211.13089 (v1)

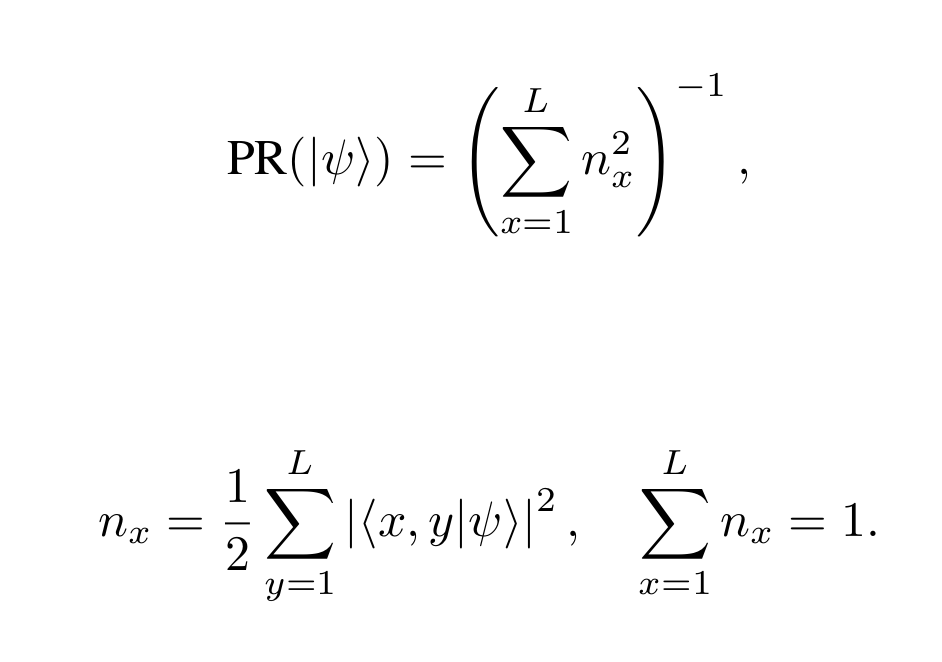
Strong disorder - TIP

20

$U = 10, L = 10^6, W_{\mathrm{And.}} = 40$

arXiv:2211.13089 (v1)

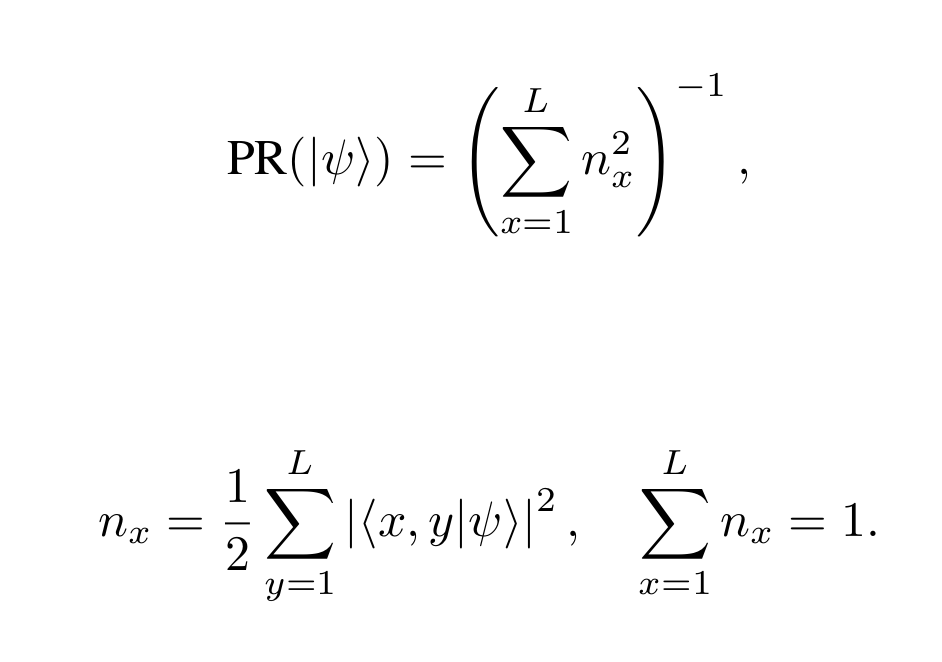
Weak disorder - Single particle

21

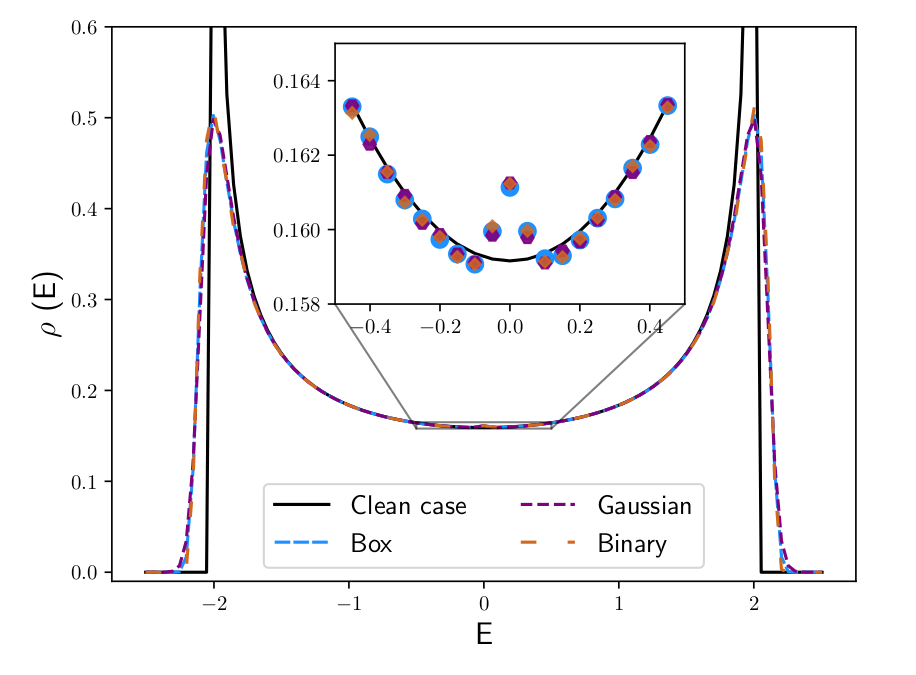
D.O.S., $V = 0.05$ , i.e. $W_{\mathrm{Box, MBL}} =$ ; $L = 10^8$ sites

arXiv:2211.13089 (v1)

Cusp : M. Kappus and F. Wegner,

Zeit. Phys. B 45,15–21 (1981)

Weak disorder - Single particle

22

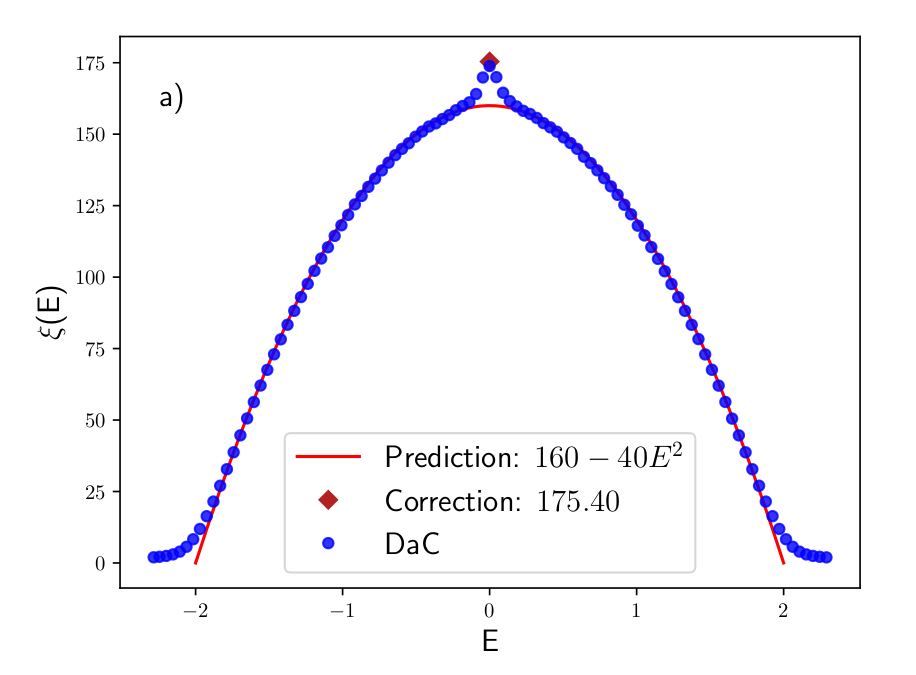
Localization length, $V = 0.05$ , i.e. $W_{\mathrm{Box, MBL}} =$ ; $L = 10^8$ sites

arXiv:2211.13089 (v1)

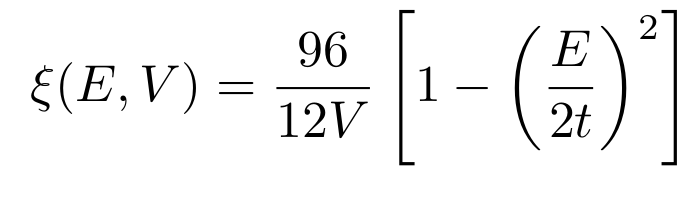
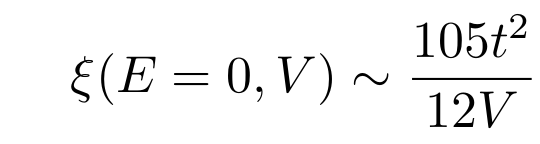
G. Czycholl, B. Kramer, and A. MacKinnon, Zeit. Phys. B 43, 5–11 (1981)

M. Kappus and F. Wegner, Zeit. Phys. B 45,15–21 (1981)

B. Kramer and A. MacKinnon, Rep. Prog. Phys. 56, 1469 (1993)

Weak disorder - Single particle

23

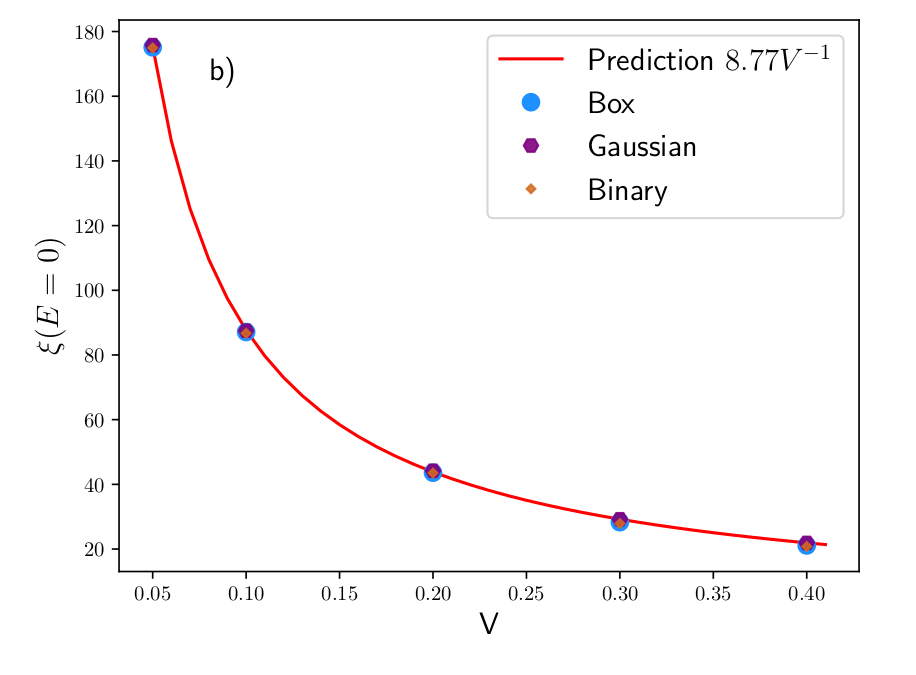
Localization length, $L = 10^8$ sites

arXiv:2211.13089 (v1)

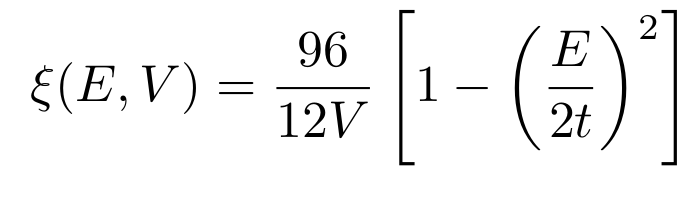
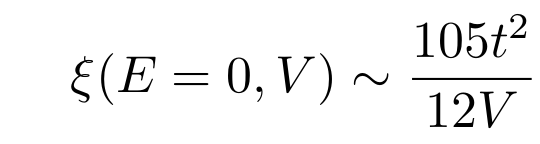
G. Czycholl, B. Kramer, and A. MacKinnon, Zeit. Phys. B 43, 5–11 (1981)

M. Kappus and F. Wegner, Zeit. Phys. B 45,15–21 (1981)

B. Kramer and A. MacKinnon, Rep. Prog. Phys. 56, 1469 (1993)

Weak disorder - Single particle

24

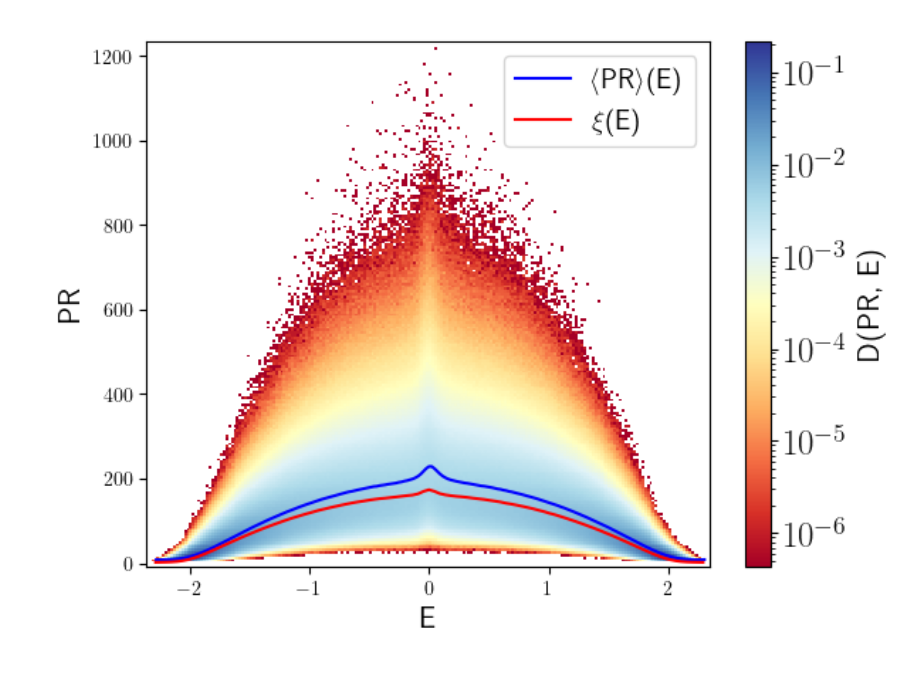
$L = 10^8$ , Box distribution, $V = 0.05$

arXiv:2211.13089 (v1)

Weak disorder - Single particle

24

$L = 10^8$ , Box distribution, $V = 0.05$

arXiv:2211.13089 (v1)

Weak disorder - Single particle

24

$L = 10^8$ , Box distribution, $V = 0.05$

arXiv:2211.13089 (v1)

Weak disorder - TIP

25

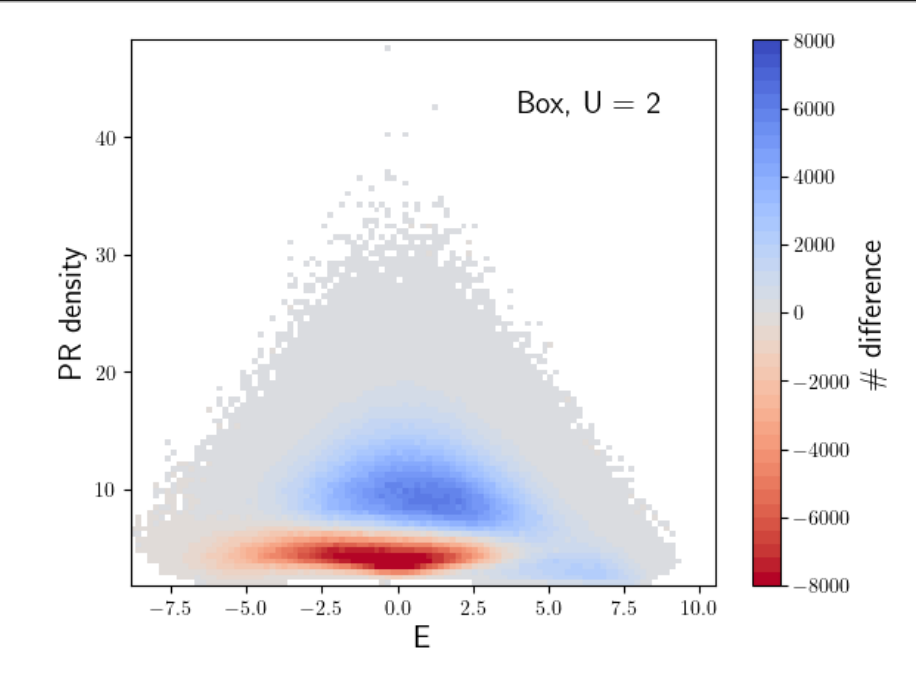
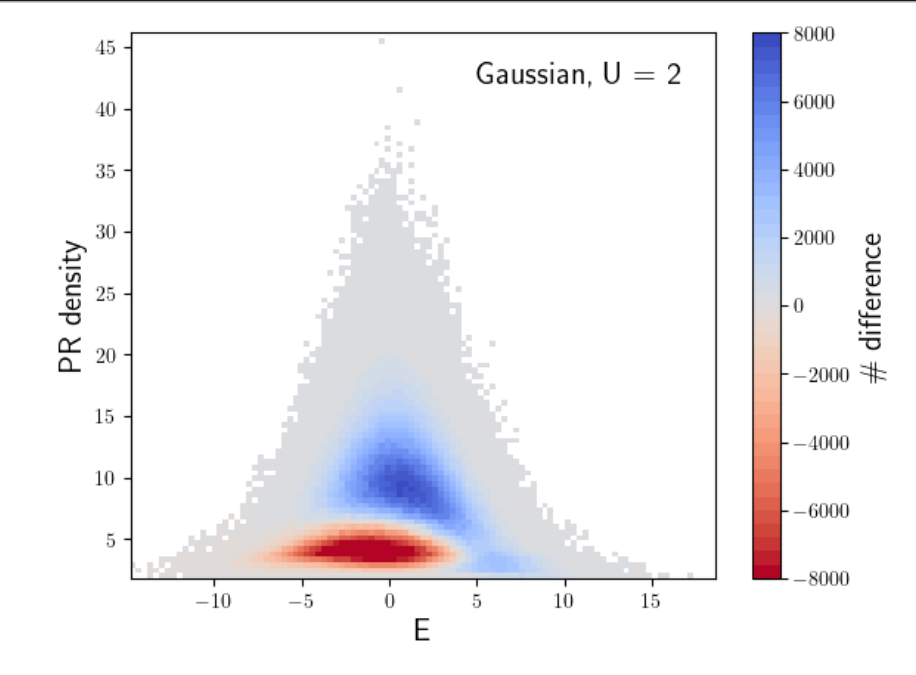
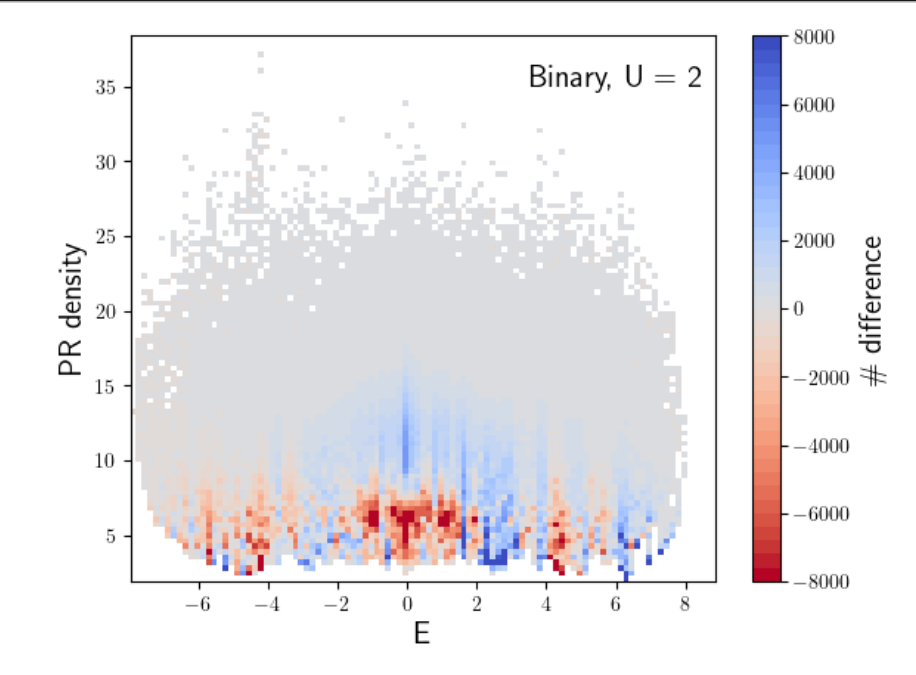
$L = 10^6$ , $W_{\mathrm{And}} = 4$

$V = 4$

$L = 10^6$ , $W_{\mathrm{And}} = 6$

$V = 3$

arXiv:2211.13089 (v1)

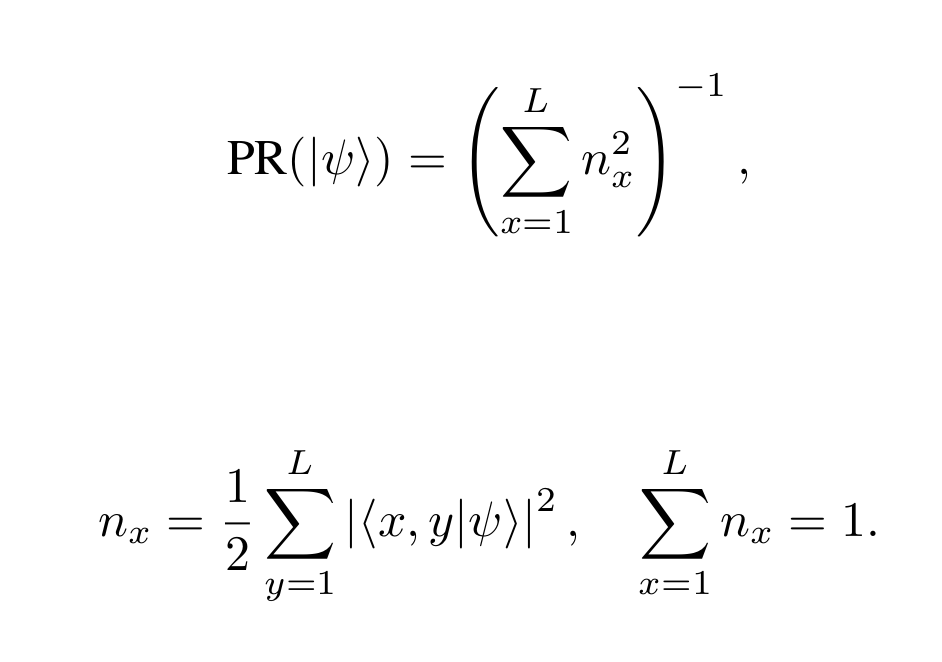
Weak disorder - TIP

25

$L = 10^6$ , $W_{\mathrm{And}} = 4$

$V = 4$

$L = 10^6$ , $W_{\mathrm{And}} = 6$

$V = 3$

arXiv:2211.13089 (v1)

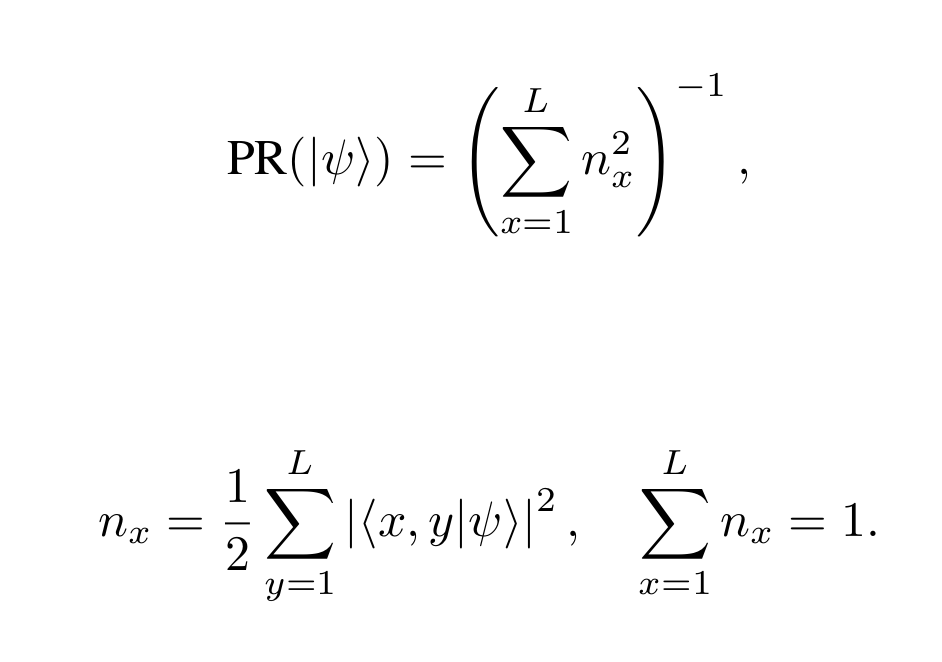
Weak disorder - TIP

25

$L = 10^6$ , $W_{\mathrm{And}} = 4$

$V = 4$

$L = 10^6$ , $W_{\mathrm{And}} = 6$

$V = 3$

arXiv:2211.13089 (v1)

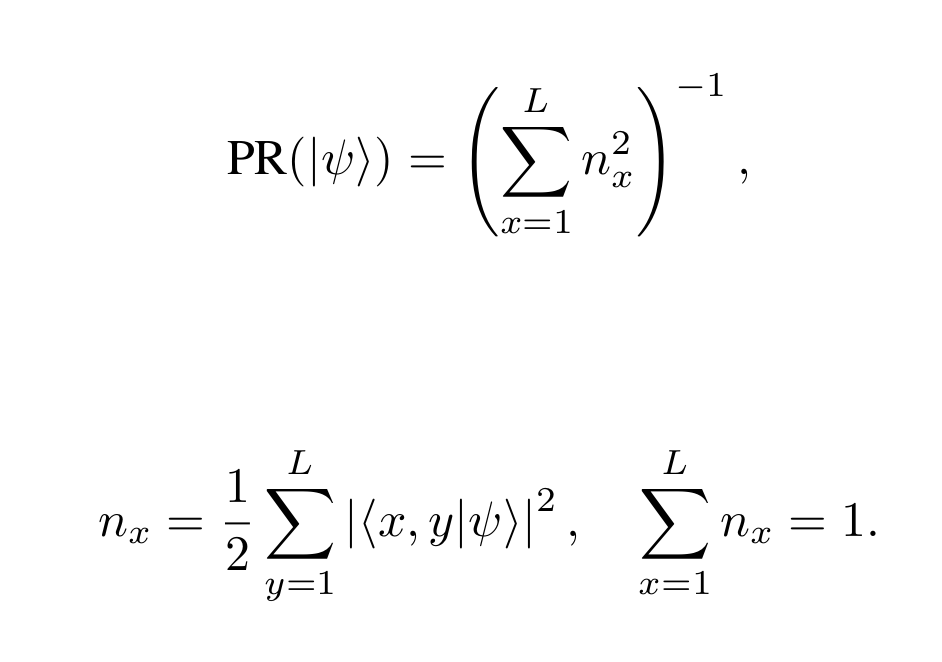
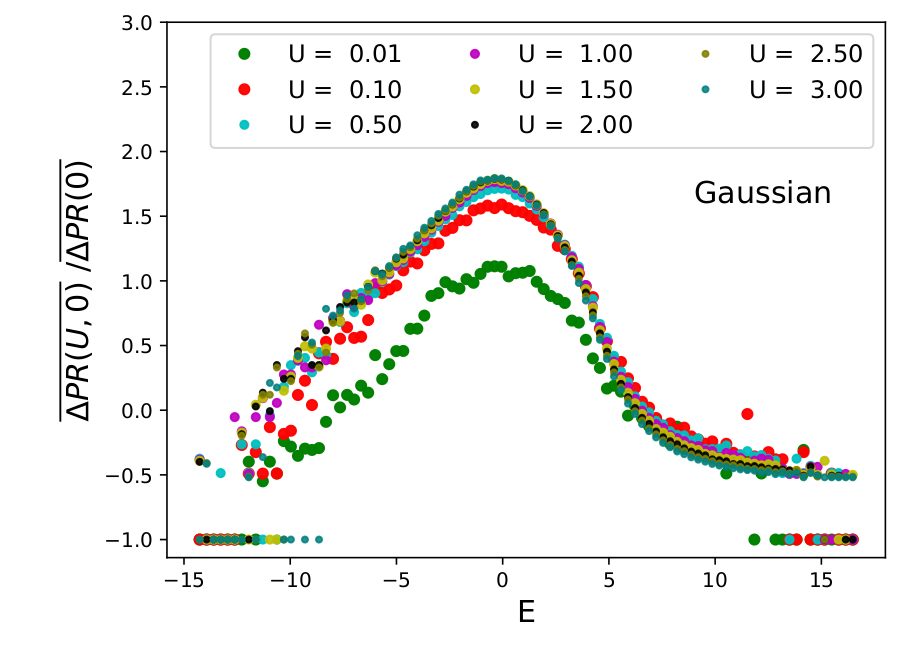
Weak disorder - TIP

26

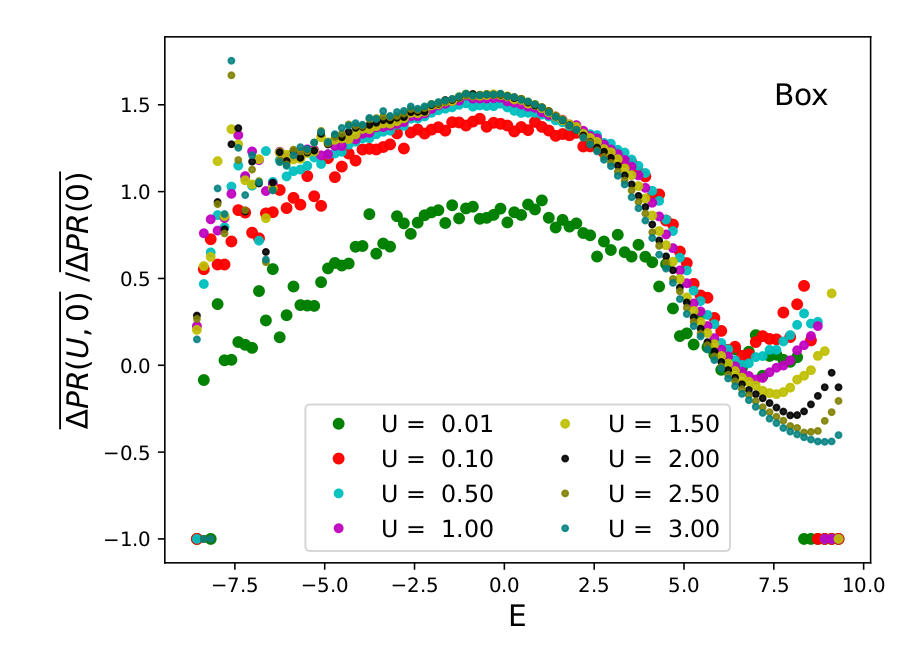
$L = 10^6$ , $W_{\mathrm{And}} = 6$

$V = 3$

$L = 10^6$ , $W_{\mathrm{And}} = 4$

$V = 4$

arXiv:2211.13089 (v1)

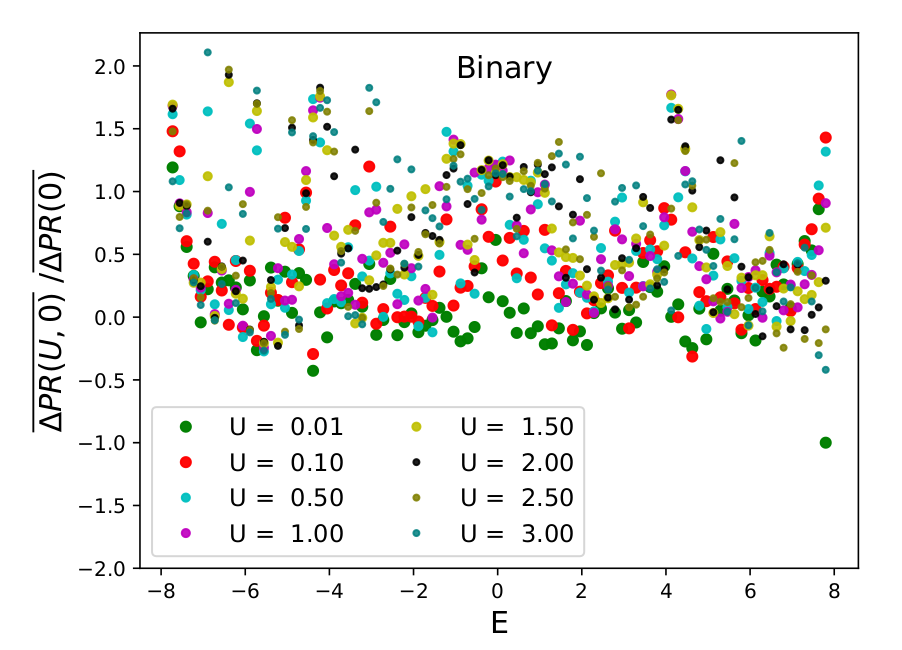
Weak disorder - TIP

26

$L = 10^6$ , $W_{\mathrm{And}} = 6$

$V = 3$

$L = 10^6$ , $W_{\mathrm{And}} = 4$

$V = 4$

arXiv:2211.13089 (v1)

Weak disorder - TIP

26

$L = 10^6$ , $W_{\mathrm{And}} = 6$

$V = 3$

$L = 10^6$ , $W_{\mathrm{And}} = 4$

$V = 4$

arXiv:2211.13089 (v1)

Weak disorder - TIP

26

$L = 10^6$ , $W_{\mathrm{And}} = 6$

$V = 3$

$L = 10^6$ , $W_{\mathrm{And}} = 4$

$V = 4$

arXiv:2211.13089 (v1)

Localized VS extended

27

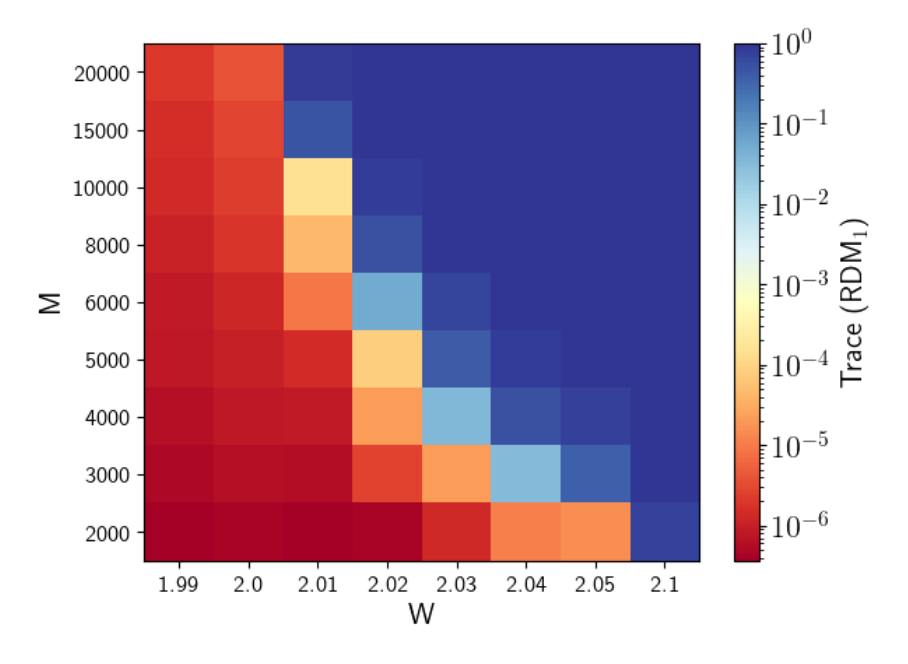
Aubry-André model

$L = 10^8$ sites

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

\rho_1 = \frac{1}{N} \sum_{\alpha} |\tilde{\Phi}_{\alpha} \rangle \langle \tilde{\Phi}_\alpha|

x_1

x_1

x_2

x_2

S. Aubry and G. André, Ann. Israel Phys. Soc 3, 18, (1980)

arXiv:2211.13089 (v1)

Localized VS extended

28

Bond disorder

$L = 10^8$ sites

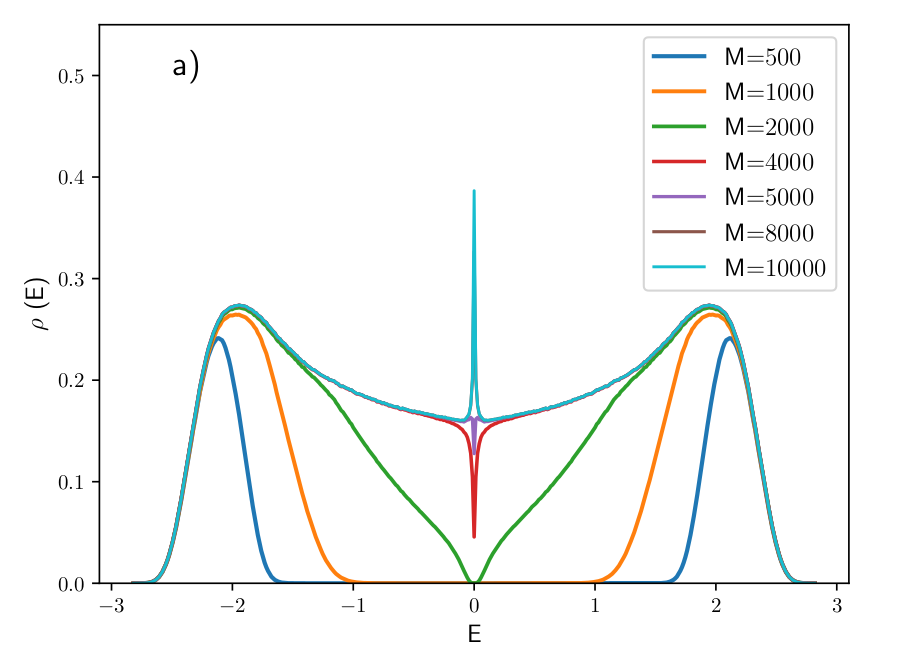
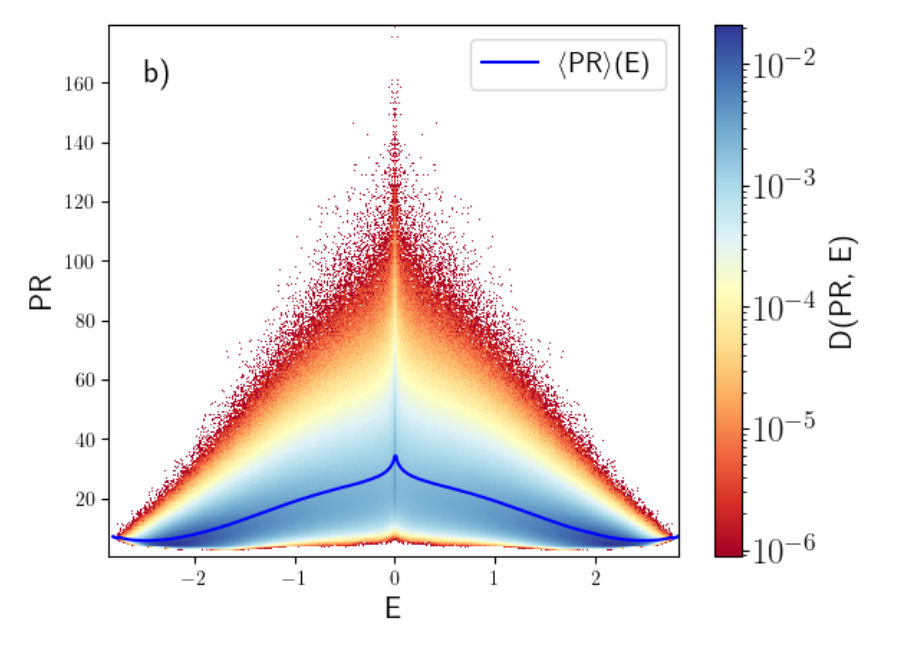
arXiv:2211.13089 (v1)

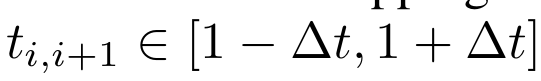
$M = 10^4, 99.8\%$ of eigenstates

$\Delta t = 0.5$

Divergence : L. Balents and M. P. A. Fisher, Phys. Rev. B 56, 12970 (1997)

Localized VS extended

28

Bond disorder

$L = 10^8$ sites

arXiv:2211.13089 (v1)

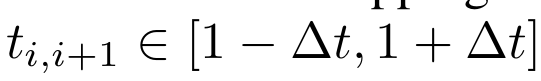
$M = 10^4, 99.8\%$ of eigenstates

$\Delta t = 0.5$

Divergence : L. Balents and M. P. A. Fisher, Phys. Rev. B 56, 12970 (1997)

Localized VS extended

28

Bond disorder

$L = 10^8$ sites

arXiv:2211.13089 (v1)

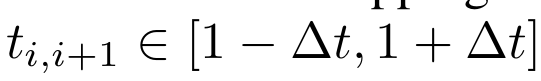
$M = 10^4, 99.8\%$ of eigenstates

$\Delta t = 0.5$

Divergence : L. Balents and M. P. A. Fisher, Phys. Rev. B 56, 12970 (1997)

Localized VS extended

28

Bond disorder

$L = 10^8$ sites

arXiv:2211.13089 (v1)

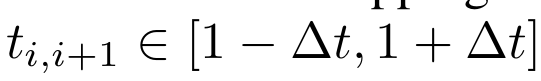
$M = 10^4, 99.8\%$ of eigenstates

$\Delta t = 0.5$

Divergence : L. Balents and M. P. A. Fisher, Phys. Rev. B 56, 12970 (1997)

BONUS : Dynamics

Evolution of localized wavefunctions

Strong disorder dynamics

29

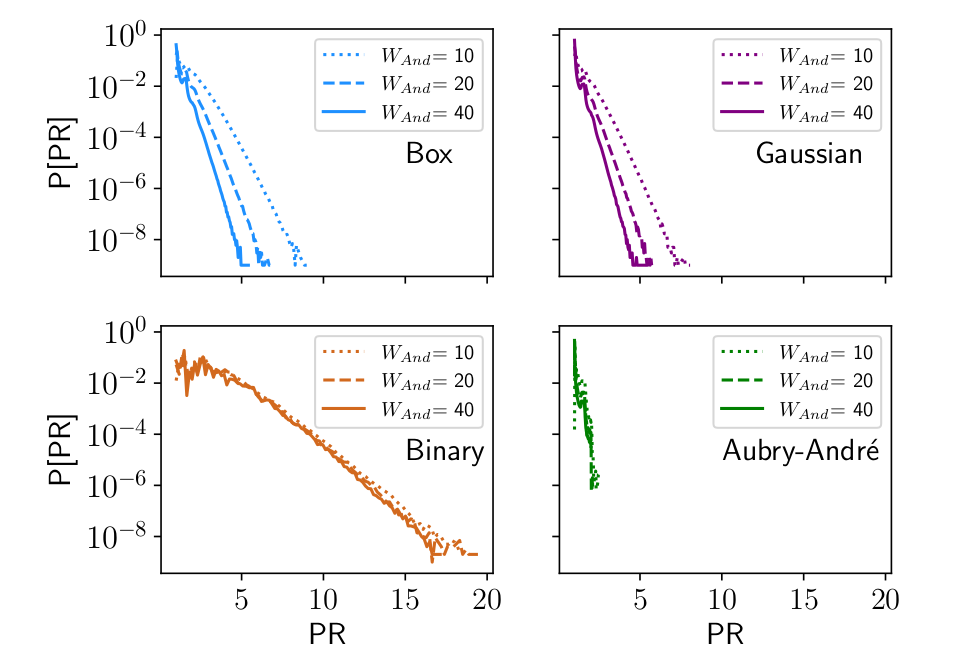
Long-time limit

Strong disorder, $L = 10^9$

$t \in [9.500, 10.500]$

arXiv:2211.13089 (v1)

Strong disorder dynamics

29

Long-time limit

Strong disorder, $L = 10^9$

$t \in [9.500, 10.500]$

arXiv:2211.13089 (v1)

Strong disorder dynamics

29

Long-time limit

Strong disorder, $L = 10^9$

$t \in [9.500, 10.500]$

arXiv:2211.13089 (v1)

Strong disorder dynamics

29

Long-time limit

Strong disorder, $L = 10^9$

$t \in [9.500, 10.500]$

arXiv:2211.13089 (v1)

Effect of interactions on strong disorder dynamics

30

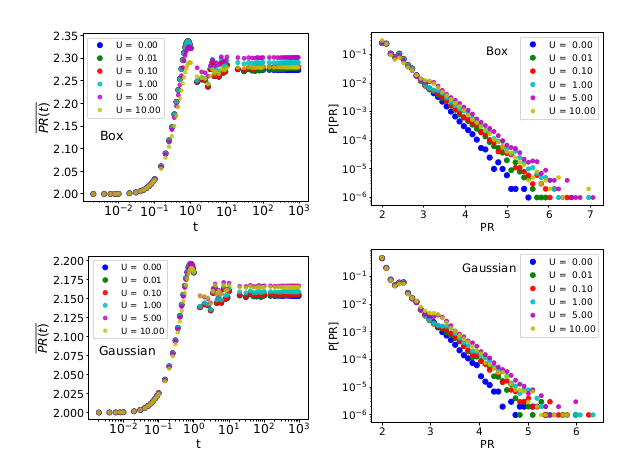
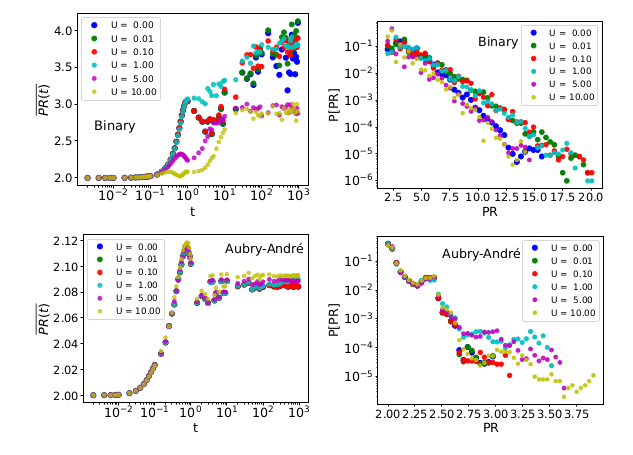
arXiv:2211.13089 (v1)

$L= 10^6$

Effect of interactions on strong disorder dynamics

30

arXiv:2211.13089 (v1)

$L= 10^6$

Effect of interactions on strong disorder dynamics

30

arXiv:2211.13089 (v1)

Long-time limit

$L= 10^6$

weak disorder dynamics

31

arXiv:2211.13089 (v1)

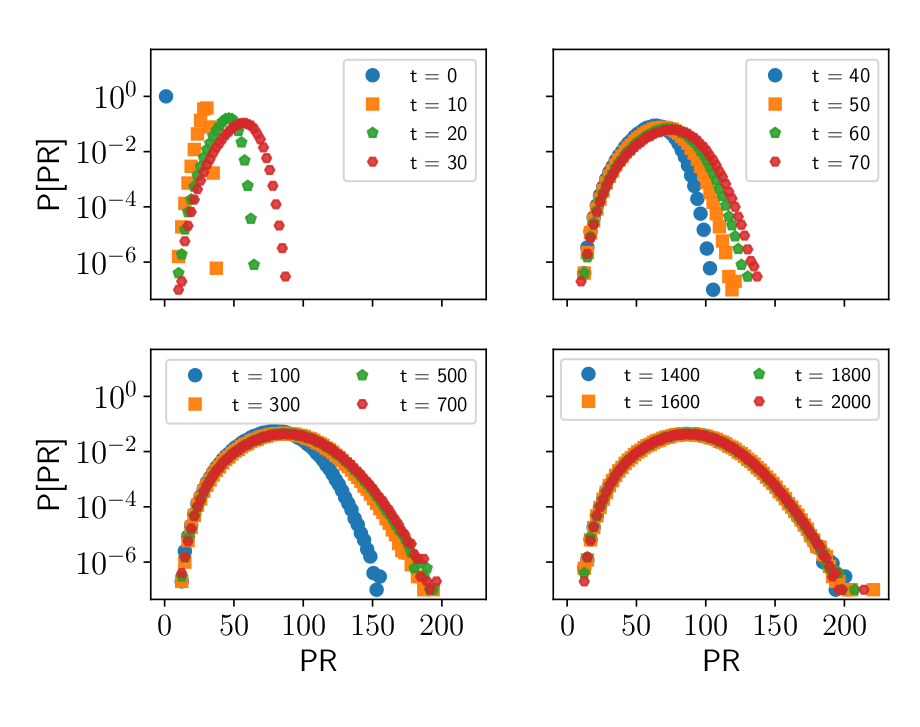
Weak disorder,

$L = 10^8$

Box, $V = 0.05$

weak disorder dynamics

31

arXiv:2211.13089 (v1)

Weak disorder,

$L = 10^8$

Box, $V = 0.05$

Effect of interactions on weak disorder dynamics

32

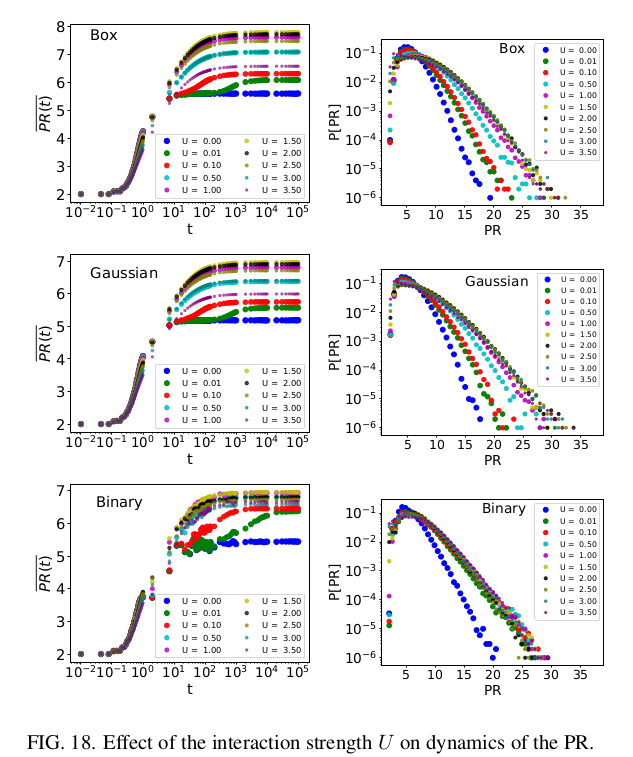
arXiv:2211.13089 (v1)

Effect of interactions on weak disorder dynamics

32

arXiv:2211.13089 (v1)

Effect of interactions on weak disorder dynamics

32

arXiv:2211.13089 (v1)

Summary

arXiv:2211.13089 (v1)

Approach from localized
Diagnose missing eigenfunctions
Large system sizes