
Partial lifting of degeneracy in the J1-J2-J3
Ising antiferromagnet on the kagome lattice
JC, B. Vanhecke et al., arXiv:2206.11788 (2022)
B. Vanhecke, JC, et al., Phys. Rev. Research 3 (2021)

Jeanne Colbois | Laboratoire de Physique Théorique, Université de Toulouse CNRS/UPS | France

Andrew Smerald
KIT | Germany
Frank Verstraete
Ghent University | Belgium
Laurens Vanderstraeten
Ghent University | Belgium
Bram Vanhecke
University of Vienna | Austria
Frédéric Mila
EPFL | Switzerland






Magnetism and Magnetic Materials 2022 - Minneapolis and Online - Nov. 2022
Frustration and motivation: artificial spin systems
A model with several macroscopically degenerate phases
Tensor networks for frustrated Ising models
Proving the ground-state energy?
Scope
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
1
J. Colbois


2-up 1-down (UUD),
2-down 1-up (DDU)
2
J. Colbois
Frustration
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME




2-up 1-down (UUD),
2-down 1-up (DDU)
2
J. Colbois
Frustration
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME


G.H. Wannier, PR 79, (1950, 1973)
K. Kano and S. Naya, Prog. Theor. Phys. 10, (1953)


2-up 1-down (UUD),
2-down 1-up (DDU)
2
J. Colbois
Frustration
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
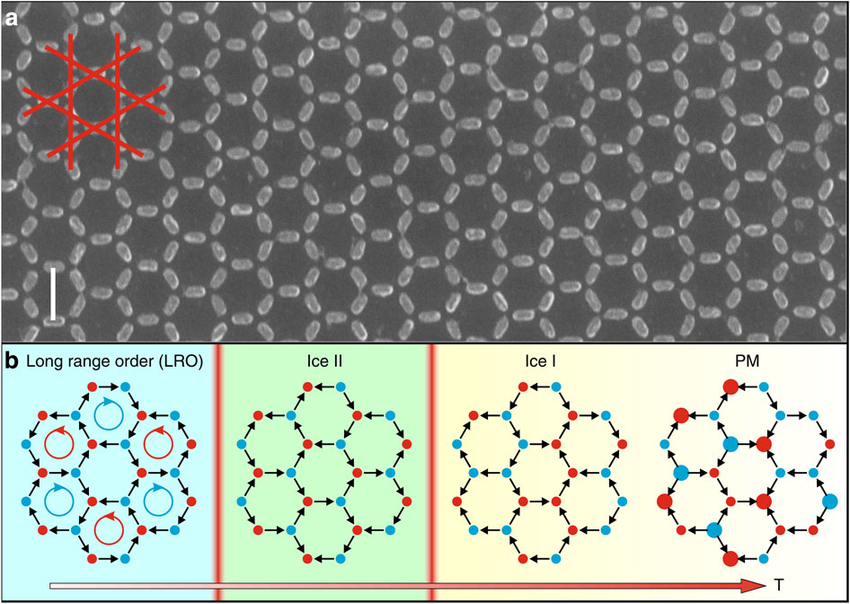
Anghinolfi et al.,
Nat. Commun. 6, (2015)

J. Colbois
3
In-plane
Artificial spin systems
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME

Chioar et al., PRB 90, (2014)
TbCo
Out-of-plane


Anghinolfi et al.,
Nat. Commun. 6, (2015)

J. Colbois
3
In-plane
Artificial spin systems
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
I. A. Chioar, N. Rougemaille, B. Canals, PRB 93, (2016)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
L. Cugliandolo, L. Foini, M. Tarzia, PRB 101 (2020)
J. Colbois
4

Chioar et al., PRB 90, (2014)


Dipolar kagome Ising antiferromagnet (DKIAFM)
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois
4

Chioar et al., PRB 90, (2014)

Dipolar kagome Ising antiferromagnet (DKIAFM)
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME


I. A. Chioar, N. Rougemaille, B. Canals, PRB 93, (2016)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
L. Cugliandolo, L. Foini, M. Tarzia, PRB 101 (2020)
J. Colbois
4

Chioar et al., PRB 90, (2014)

Dipolar kagome Ising antiferromagnet (DKIAFM)
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME


I. A. Chioar, N. Rougemaille, B. Canals, PRB 93, (2016)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
L. Cugliandolo, L. Foini, M. Tarzia, PRB 101 (2020)
How does the degeneracy get lifted?

J. Colbois
5
Short-range model and questions
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME


J. Colbois
5
Short-range model and questions
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME


J. Colbois
5
Short-range model and questions
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
Proving the ground-state energy?
Evaluating the residual entropy precisely?


J. Colbois
5
Short-range model and questions
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
- Short-range model :
- MC falls out-of-equilibrium
- Negative results from simple Pauling estimates assuming the UUD/DDU rule is respected on each triangle
Proving the ground-state energy?
Evaluating the residual entropy precisely?
(How) Does the degeneracy get lifted?
J. Colbois
6
Expectations (1)
T. Takagi and M. Mekata, JSPS 62, (1993)
A. Wills, R. Ballou, C. Lacroix, PRB 66, (2002)
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
The macroscopic g.s. degeneracy gets completely lifted by second-neighbor interactions.
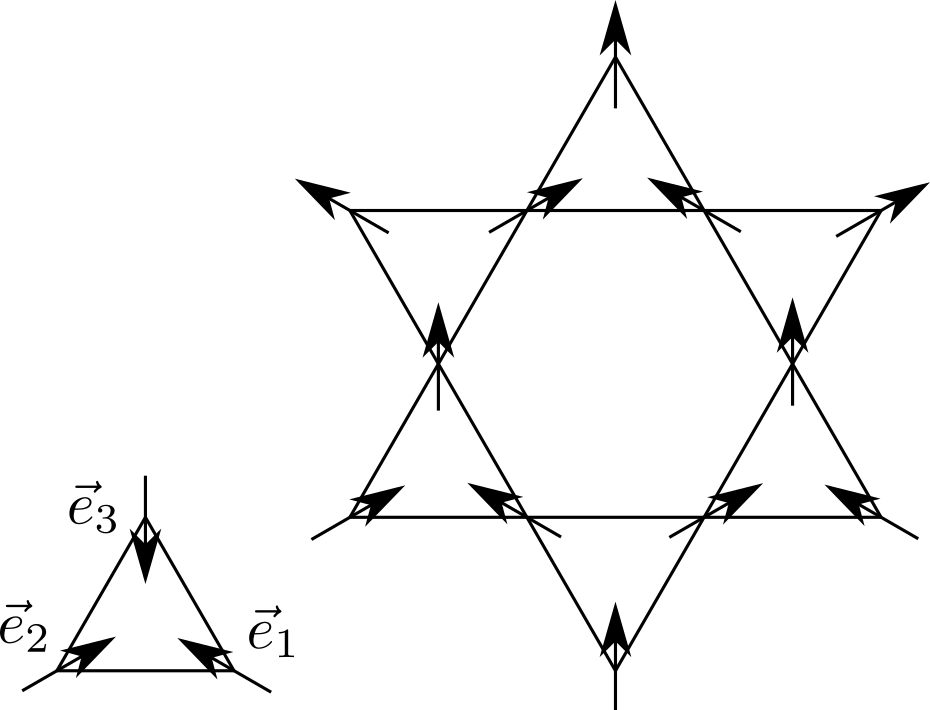

T. Takagi and M. Mekata, JSPS 62, (1993)
A. Wills, R. Ballou, C. Lacroix, PRB 66, (2002)
J. Colbois
Expectations (1)
(How) Does the degeneracy get lifted?
6
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
The macroscopic g.s. degeneracy gets completely lifted by second-neighbor interactions.


T. Takagi and M. Mekata, JSPS 62, (1993)
A. Wills, R. Ballou, C. Lacroix, PRB 66, (2002)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
JC, K. Hofhuis, et al., PRB 104, (2022)
J. Colbois
7
Expectations (1) vs Reality

(How) Does the degeneracy get lifted?
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
The macroscopic g.s. degeneracy gets completely lifted by second-neighbor interactions.


T. Takagi and M. Mekata, JSPS 62, (1993)
A. Wills, R. Ballou, C. Lacroix, PRB 66, (2002)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
JC, K. Hofhuis, et al., PRB 104, (2022)
J. Colbois
7
Expectations (1) vs Reality

(How) Does the degeneracy get lifted?
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
The macroscopic g.s. degeneracy gets completely lifted by second-neighbor interactions.


T. Takagi and M. Mekata, JSPS 62, (1993)
A. Wills, R. Ballou, C. Lacroix, PRB 66, (2002)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
JC, K. Hofhuis, et al., PRB 104, (2022)
J. Colbois
7
Expectations (1) vs Reality

(How) Does the degeneracy get lifted?
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
The macroscopic degeneracy can survive in the presence of third-neighbor interactions but only at very fine-tuned points.
J. Colbois
Expectations (2)
(How) Does the degeneracy get lifted?
8
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME

The macroscopic degeneracy can survive in the presence of third-neighbor interactions but only at very fine-tuned points.
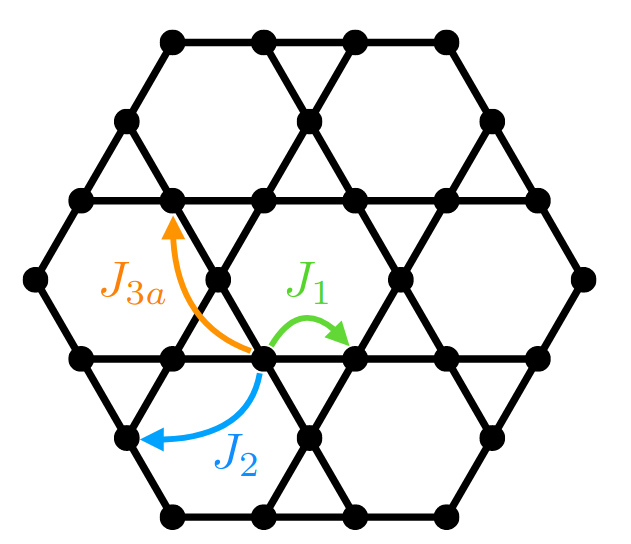
J. Colbois
Expectations (2)
(How) Does the degeneracy get lifted?
8
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME

The macroscopic degeneracy can survive in the presence of third-neighbor interactions but only at very fine-tuned points.

J. Colbois
Expectations (2) vs Reality
(How) Does the degeneracy get lifted?
This talk: a series of macroscopically degenerate phases
8
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
Frustration and motivation: artificial spin systems
Ground-state energy lower bounds


J. Colbois
Kanamori's method : applied to our problem
9
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME



J. Colbois
Kanamori's method : applied to our problem
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
9
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME



Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
Kanamori's method : applied to our problem
9
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME



Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
Kanamori's method : applied to our problem
9
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME


Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
Kanamori's method : applied to our problem
Not all triangles can respect the UUD/DDU rule at the same time
9
All the corners must be verified
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
Proving the ground-state energy
10



MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois
10
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
All the corners must be verified
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Proving the ground-state energy



J. Colbois
10
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
All the corners must be verified
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Proving the ground-state energy



J. Colbois
10
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
All the corners must be verified
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Proving the ground-state energy



Frustration and motivation: artificial spin systems
Tensor networks for frustrated Ising models
Proving the ground-state energy?
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois
11
Idea: why tensor networks
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois
11
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
Idea: why tensor networks
J. Colbois
11
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
Idea: why tensor networks
We "just" have to compute the (normalized) partition function for one site...
... which is the result that naturally comes out with a large precision from tensor networks.
J. Colbois
11
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
Idea: why tensor networks

Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)
J. Colbois
12
Tensor networks : inspired by transfer matrices

MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME

Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)
J. Colbois
Tensor networks : inspired by transfer matrices

MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME

"Legs"
"Contraction"
Open legs = number of indices
Tensor network language:

"vector"
"Tensor"
12
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois
Partition function of a 2D problem as a TN


R. J. Baxter, J. Math. Phys. 9, 1968
R. Orús, G. Vidal, PRB 78, 2008
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
13
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois
Partition function of a 2D problem as a TN


R. J. Baxter, J. Math. Phys. 9, 1968
R. Orús, G. Vidal, PRB 78, 2008
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
13
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois
Partition function of a 2D problem as a TN
R. J. Baxter, J. Math. Phys. 9, 1968
R. Orús, G. Vidal, PRB 78, 2008
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996

13
(1 + 1)D
iTEBD / VUMPS
R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
J. Colbois
(1+1)D versus 2D

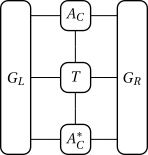

MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
14
(1 + 1)D
iTEBD / VUMPS
R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
J. Colbois
(1+1)D versus 2D


2D



R. J. Baxter, J. Math. Phys. 9, 1968
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
14
(1 + 1)D
iTEBD / VUMPS
R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
J. Colbois
(1+1)D versus 2D


2D



R. J. Baxter, J. Math. Phys. 9, 1968
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
Environment
Iteratively solving fixed-point equations
T tensor can be replaced by observables
14

J. Colbois
The issue
15
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME

J. Colbois
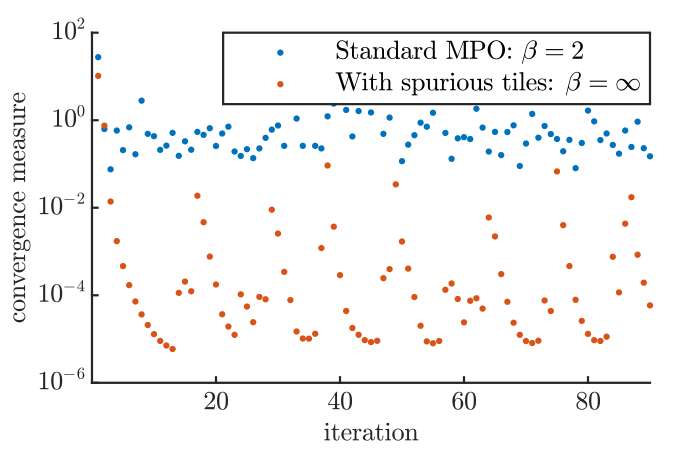
The issue
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
B. Vanhecke, JC, et al. PRR 3, (2021)
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
M. Friaz-Pérez, M, Mariën et al, arXiv:2104.13264, (2021)
Fails in the presence of frustration and macroscopic g.s. degeneracy
15

J. Colbois
The issue
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
B. Vanhecke, JC, et al. PRR 3, (2021)
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
M. Friaz-Pérez, M, Mariën et al, arXiv:2104.13264, (2021)
Fails in the presence of frustration and macroscopic g.s. degeneracy

C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
Related to the inexact cancellation of very large
and very small factors.
15
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois

1. Split the Hamiltonian in a different way

J. Colbois
Systematically finding the local rule
16
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois

1. Split the Hamiltonian in a different way
2. Lower bound on the ground-state energy:

J. Colbois
Systematically finding the local rule
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
16
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois

1. Split the Hamiltonian in a different way
2. Lower bound on the ground-state energy:
3. This lower bound can be maximized with respect to the weights (max-min approach):


J. Colbois
Systematically finding the local rule
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
16
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois

1. Split the Hamiltonian in a different way
2. Lower bound on the ground-state energy:
3. This lower bound can be maximized with respect to the weights (max-min approach):
4. When the lower bound is saturated:


All the ground states are made of configurations that minimize the local Hamiltonian.

J. Colbois
Systematically finding the local rule
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
16
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME

J. Colbois
Does it work?
17
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME

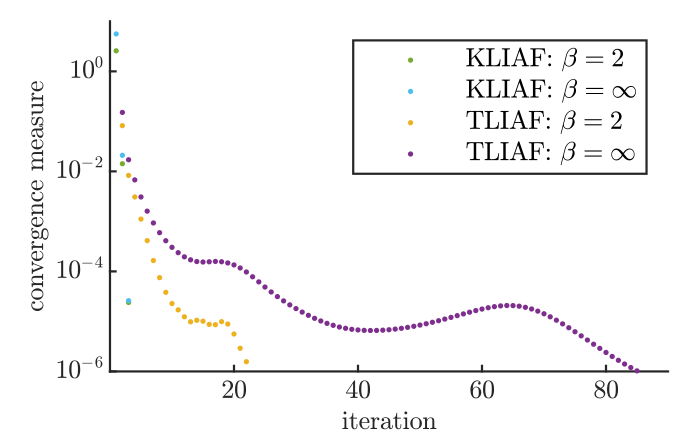
J. Colbois
Does it work?
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
17
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME


B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. Colbois
Does it work?
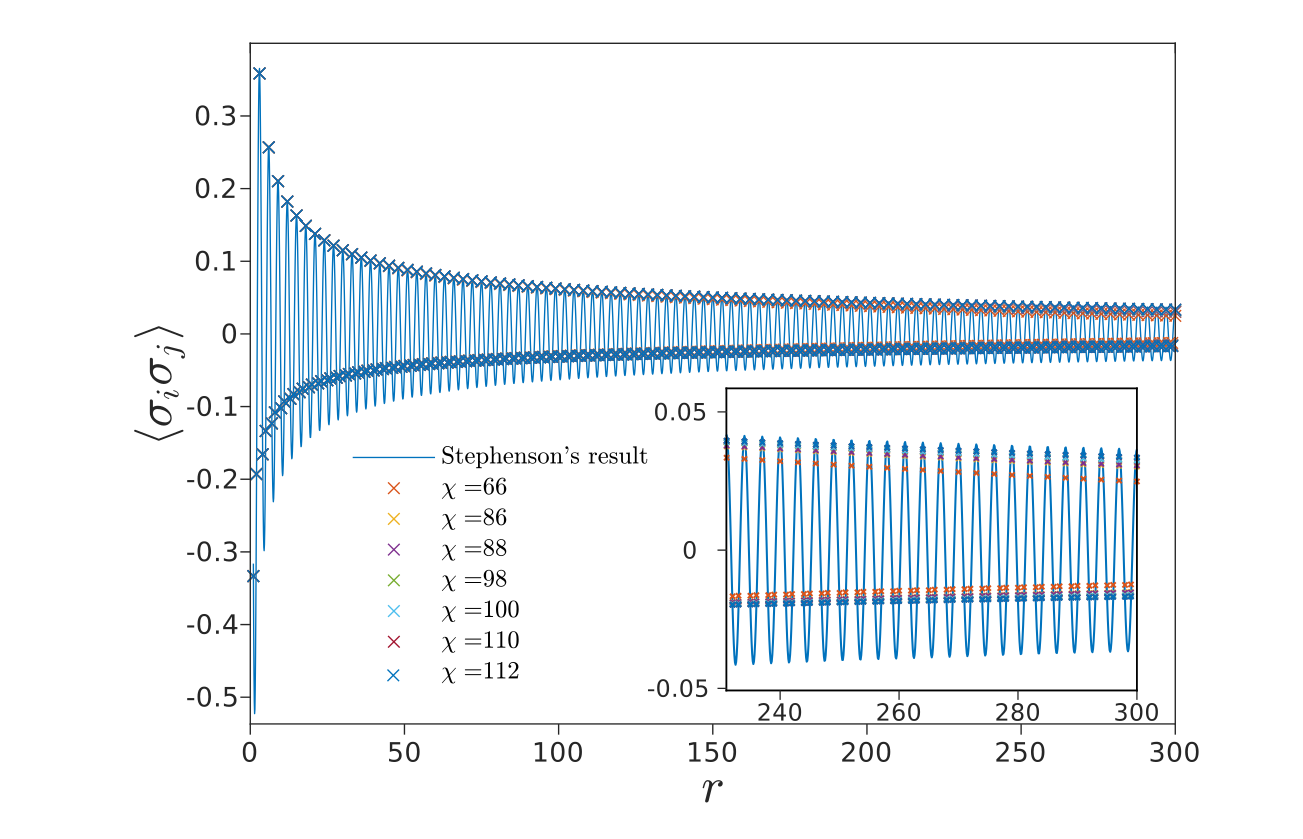
17
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME


B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. Colbois
Does it work?

17
Frustration and motivation: artificial spin systems
A model with several macroscopically degenerate phases
Tensor networks for frustrated Ising models
Proving the ground-state energy?
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)

Phase diagram
J. Colbois
18

MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois
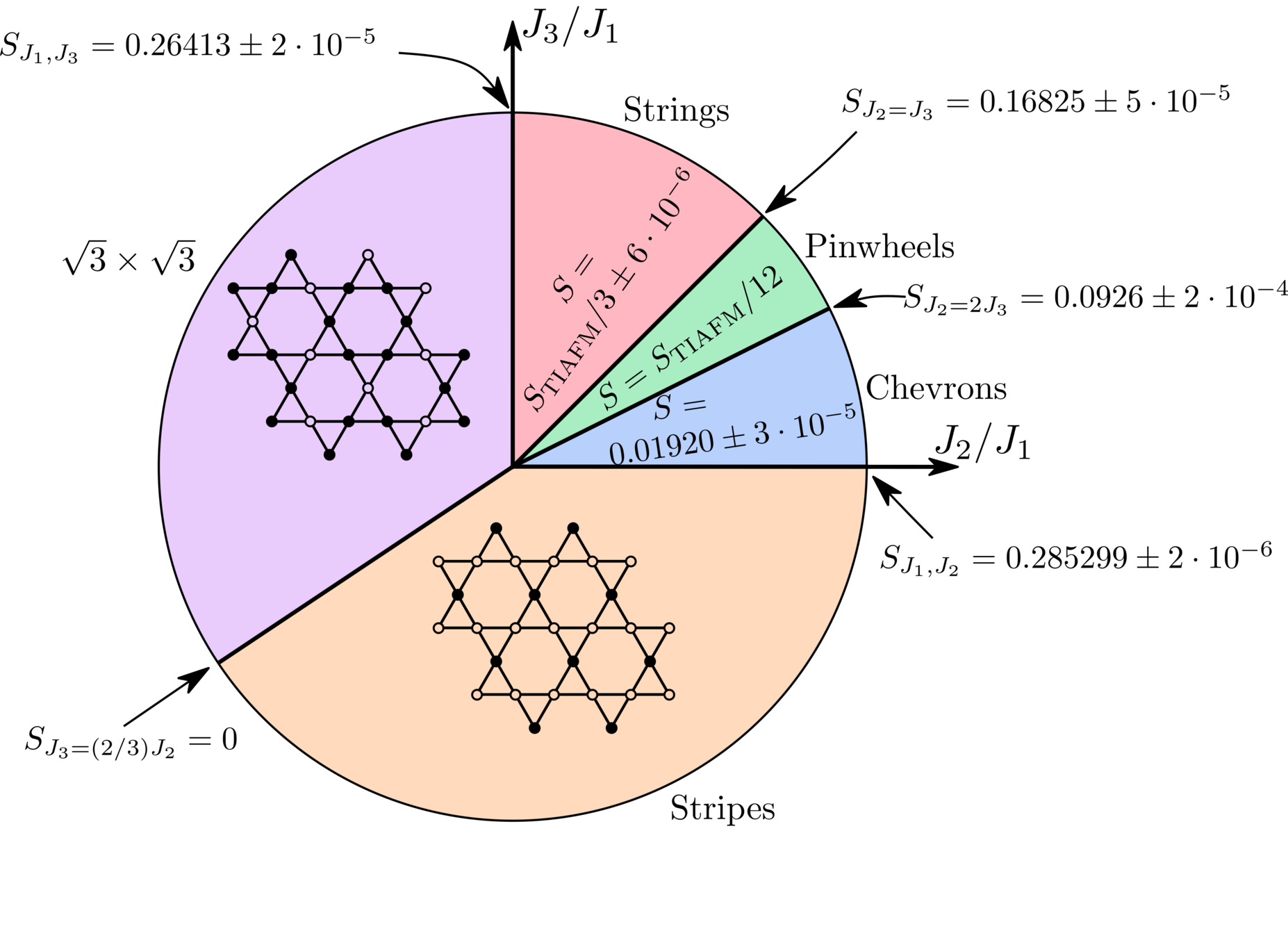
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Residual entropies
19

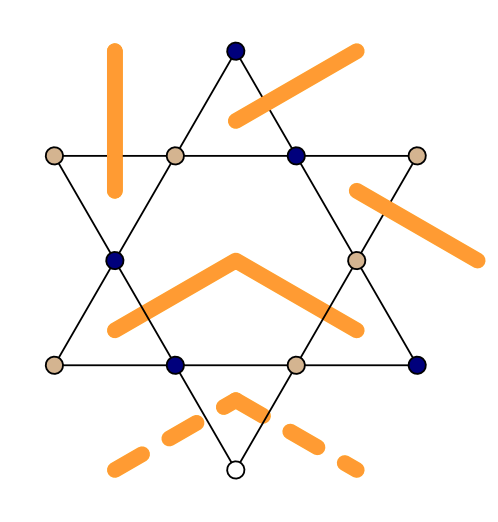
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Residual entropies
19





MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
J. Colbois
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Residual entropies
19



MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME


J. Colbois
20
Discussion
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME



J. Colbois
Discussion
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
20
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
The convergence of the tensor network contraction depends on the formulation of the partition function
J. Colbois
21
Take home...
JC, B. Vanhecke et al., arXiv:2206.11788 (2022)
B. Vanhecke, JC, et al., Phys. Rev. Research 3 (2021)
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
If the ground-state rule is implemented at the level of the tensor, approximate contraction aglorithms converge
The convergence of the tensor network contraction depends on the formulation of the partition function
J. Colbois
Take home...
JC, B. Vanhecke et al., arXiv:2206.11788 (2022)
B. Vanhecke, JC, et al., Phys. Rev. Research 3 (2021)
21
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
If the ground-state rule is implemented at the level of the tensor, approximate contraction aglorithms converge
The convergence of the tensor network contraction depends on the formulation of the partition function
J. Colbois
Take home...
Tensor networks are a powerful tool to study 2D classical spin systems!
JC, B. Vanhecke et al., arXiv:2206.11788 (2022)
B. Vanhecke, JC, et al., Phys. Rev. Research 3 (2021)
21
MMM2022 | 11.2022 | PARTIAL LIFTING OF G. S. DEG. IN THE J1-J2-J3 AF ISING MODEL ON KAGOME
If the ground-state rule is implemented at the level of the tensor, approximate contraction aglorithms converge
The convergence of the tensor network contraction depends on the formulation of the partition function

J. Colbois
Take home...
Tensor networks are a powerful tool to study 2D classical spin systems!
JC, B. Vanhecke et al., arXiv:2206.11788 (2022)
B. Vanhecke, JC, et al., Phys. Rev. Research 3 (2021)
Thank you!
See you in the chat!
21