

Tensor networks for frustrated Ising models,
and partial lifting of a macroscopic degeneracy

JC et al., arXiv:2206.11788 (2022)
B. Vanhecke, JC, et al., Phys. Rev. Research 3 (2021)

Jeanne Colbois
Laboratoire de Physique Théorique, Université de Toulouse CNRS/UPS, France

Laurens Vanderstraeten

Bram Vanhecke

Frank Verstraete
Ghent University (Ghent, Belgium)

Andrew Smerald,
KIT (Germany)

Frédéric Mila, EPFL (Lausanne, Switzerland)
CMT Seminar, Göttingen, 25.06.2022

Laurens Vanderstraeten

Bram Vanhecke

Frank Verstraete
Ghent University (Ghent, Belgium)

Andrew Smerald,
KIT (Germany)

Frédéric Mila, EPFL (Lausanne, Switzerland)
CMT Seminar, Göttingen, 25.06.2022

CMT Seminar, Göttingen, 25.06.2022


CMT Seminar, Göttingen, 25.06.2022



CMT Seminar, Göttingen, 25.06.2022




CMT Seminar, Göttingen, 25.06.2022







Tensor networks for frustrated Ising models,
and partial lifting of a macroscopic degeneracy

JC et al., arXiv:2206.11788 (2022)
B. Vanhecke, JC, et al., Phys. Rev. Research 3 (2021)

Jeanne Colbois
Laboratoire de Physique Théorique, Université de Toulouse CNRS/UPS, France
CMT Seminar, Göttingen, 25.06.2022

Laurens Vanderstraeten

Bram Vanhecke

Frank Verstraete
Ghent University (Ghent, Belgium)

Andrew Smerald,
KIT (Germany)

Frédéric Mila, EPFL (Lausanne, Switzerland)
Scope
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Frustration and motivation: artificial spin systems
A model with several macroscopically degenerate phases
Tensor networks for frustrated Ising models
Proving the ground-state energy?
1
Scope
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Frustration and motivation: artificial spin systems
A model with several macroscopically degenerate phases
Tensor networks for frustrated Ising models
Proving the ground-state energy?
> Why study frustrated Ising models?
1
Scope
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Frustration and motivation: artificial spin systems
A model with several macroscopically degenerate phases
Tensor networks for frustrated Ising models
Proving the ground-state energy?
> Why study frustrated Ising models?
> Can we obtain exact results? An approach from the 60's
1
Scope
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Frustration and motivation: artificial spin systems
A model with several macroscopically degenerate phases
Tensor networks for frustrated Ising models
Proving the ground-state energy?
> Why study frustrated Ising models?
> Can we obtain exact results? An approach from the 60's
> A problem of contraction
> To be solved by implementing the local ground-state rule
1
Scope
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Frustration and motivation: artificial spin systems
A model with several macroscopically degenerate phases
Tensor networks for frustrated Ising models
Proving the ground-state energy?
> Why study frustrated Ising models?
> Can we obtain exact results? An approach from the 60's
> A problem of contraction
> To be solved by implementing the local ground-state rule
> In contrast to what is usually expected in frustrated models
> Some understanding of emergent degrees-of-freedom
1
J. Colbois

Frustration
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
2

Frustration
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
2
2-up 1-down (UUD),
2-down 1-up (DDU)

Frustration

J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
2
2-up 1-down (UUD),
2-down 1-up (DDU)

Frustration



J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
2-up 1-down (UUD),
2-down 1-up (DDU)
2

Frustration



J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
2-up 1-down (UUD),
2-down 1-up (DDU)
2

Frustration



J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
2-up 1-down (UUD),
2-down 1-up (DDU)
2

Frustration

G.H. Wannier, PR 79, (1950, 1973)
K. Kano and S. Naya, Prog. Theor. Phys. 10, (1953)


J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
2-up 1-down (UUD),
2-down 1-up (DDU)
2

Frustration

G.H. Wannier, PR 79, (1950, 1973)
A. Sütö, Z. Phys. B 44, (1981)
W. Apel, H.-U. Everts, J. Stat. Mech, (2011)


J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
2-up 1-down (UUD),
2-down 1-up (DDU)
2
Artificial spin systems
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
In-plane

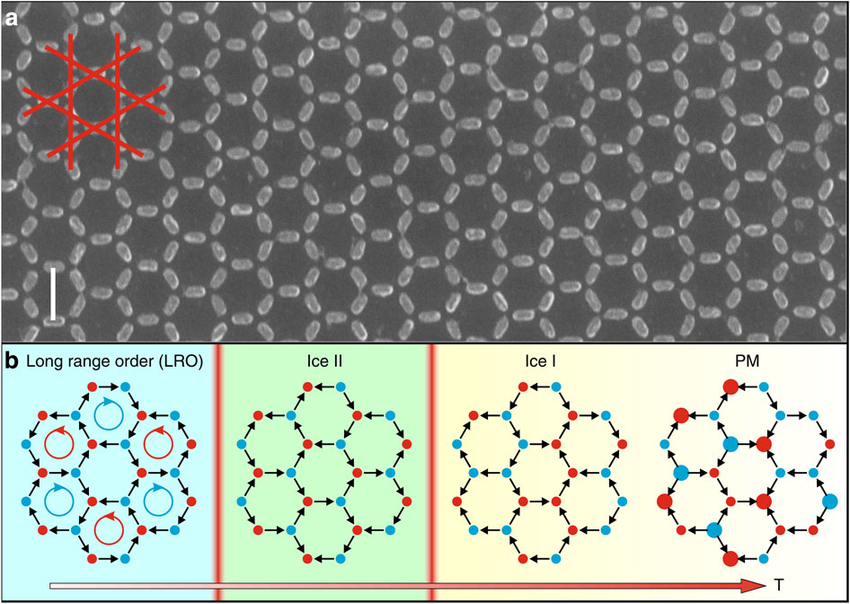
Anghinolfi et al.,
Nat. Commun. 6, (2015)
3
Artificial spin systems

Chioar et al., PRB 90, (2014)
TbCo
In-plane
Out-of-plane

J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.


Anghinolfi et al.,
Nat. Commun. 6, (2015)
3
Dipolar kagome Ising antiferromagnet (DKIAFM)
I. A. Chioar, N. Rougemaille, B. Canals, PRB 93, (2016)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
L. Cugliandolo, L. Foini, M. Tarzia, PRB 101 (2020)
4
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

Chioar et al., PRB 90, (2014)

Dipolar kagome Ising antiferromagnet (DKIAFM)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
I. A. Chioar, N. Rougemaille, B. Canals, PRB 93, (2016)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
L. Cugliandolo, L. Foini, M. Tarzia, PRB 101 (2020)

Chioar et al., PRB 90, (2014)

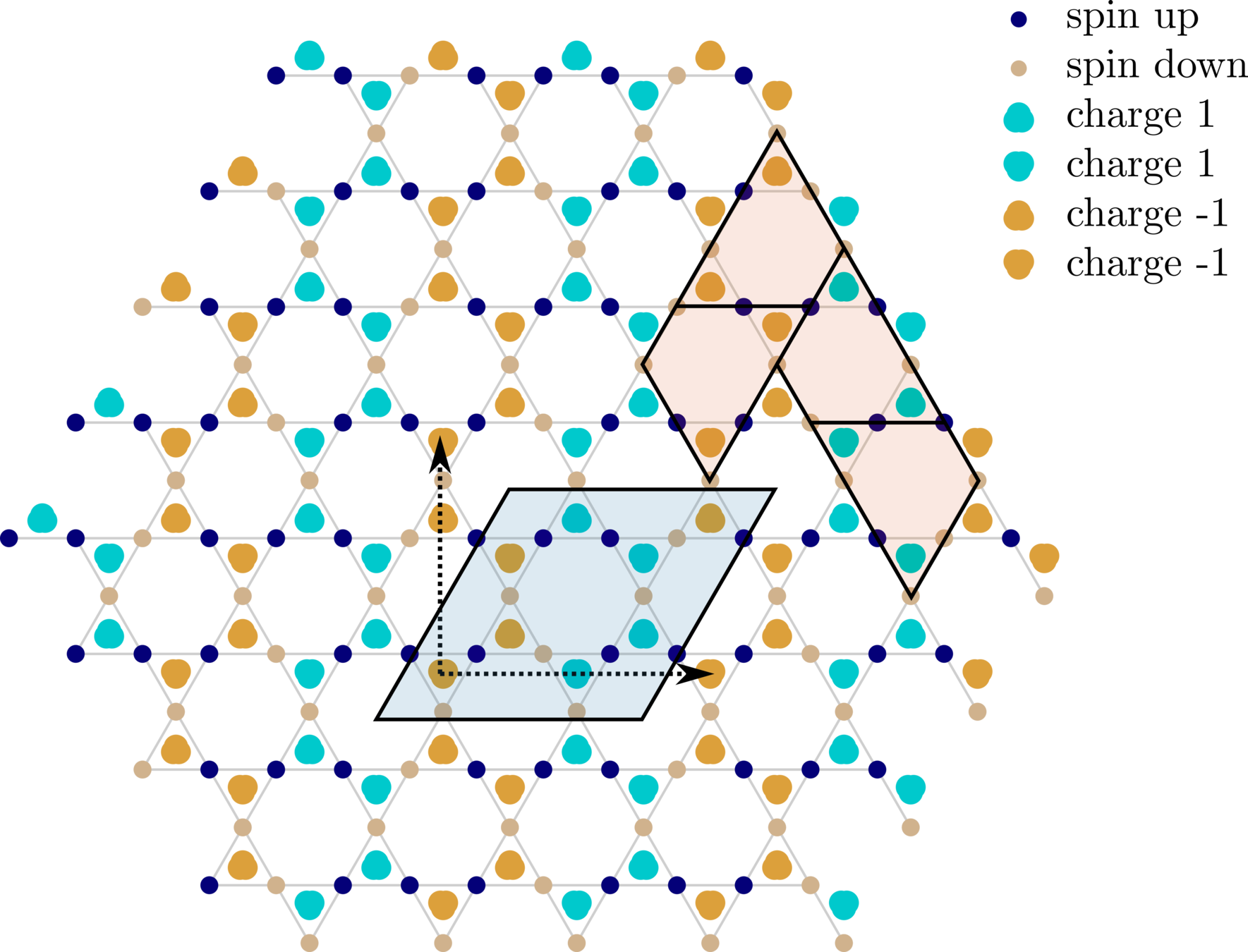
4
Dipolar kagome Ising antiferromagnet (DKIAFM)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
I. A. Chioar, N. Rougemaille, B. Canals, PRB 93, (2016)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
L. Cugliandolo, L. Foini, M. Tarzia, PRB 101 (2020)

Chioar et al., PRB 90, (2014)



4
Dipolar kagome Ising antiferromagnet (DKIAFM)


(How) Does the degeneracy get lifted?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
I. A. Chioar, N. Rougemaille, B. Canals, PRB 93, (2016)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
L. Cugliandolo, L. Foini, M. Tarzia, PRB 101 (2020)

Chioar et al., PRB 90, (2014)

4
Expectations (1)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
(How) Does the degeneracy get lifted?
5
The macroscopic g.s. degeneracy gets completely lifted by second-neighbor interactions.
Expectations (1)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
(How) Does the degeneracy get lifted?
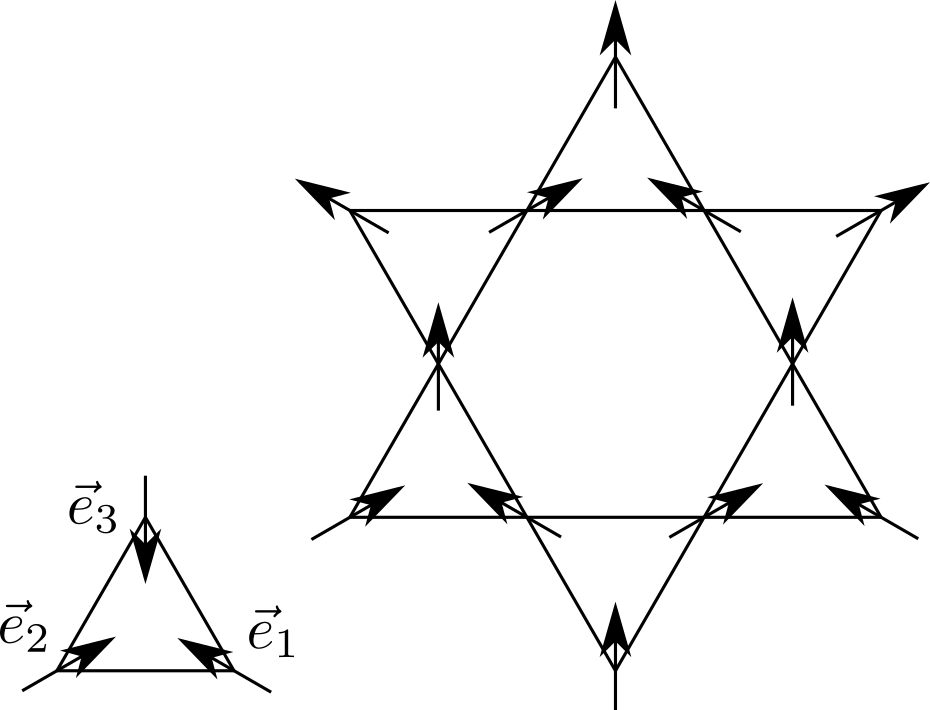

The macroscopic g.s. degeneracy gets completely lifted by second-neighbor interactions.
T. Takagi and M. Mekata, JSPS 62, (1993)
A. Wills, R. Ballou, C. Lacroix, PRB 66 , (2002)
5
Expectations (1)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
(How) Does the degeneracy get lifted?


The macroscopic degeneracy can survive in the presence of third-neighbor interactions but only at very fine-tuned points.
The macroscopic g.s. degeneracy gets completely lifted by second-neighbor interactions.
T. Takagi and M. Mekata, JSPS 62, (1993)
A. Wills, R. Ballou, C. Lacroix, PRB 66 , (2002)
5

Expectations (1)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
(How) Does the degeneracy get lifted?


The macroscopic degeneracy can survive in the presence of third-neighbor interactions but only at very fine-tuned points.
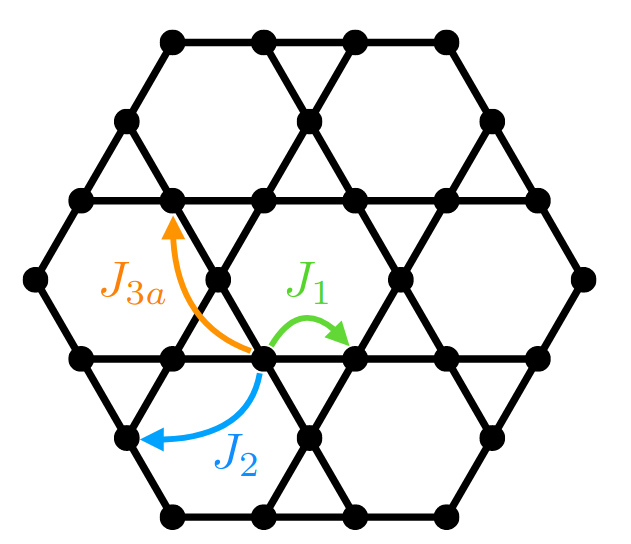
The macroscopic g.s. degeneracy gets completely lifted by second-neighbor interactions.
5
The macroscopic g.s. degeneracy gets completely lifted by second-neighbor interactions.
Expectations (1) vs reality
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
(How) Does the degeneracy get lifted?
6


T. Takagi and M. Mekata, JSPS 62, (1993)
A. Wills, R. Ballou, C. Lacroix, PRB 66, (2002)
The macroscopic g.s. degeneracy gets completely lifted by second-neighbor interactions.
Expectations (1) vs reality
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
(How) Does the degeneracy get lifted?


T. Takagi and M. Mekata, JSPS 62, (1993)
A. Wills, R. Ballou, C. Lacroix, PRB 66, (2002)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
JC, K. Hofhuis, et al., PRB 104, (2022)
6
The macroscopic g.s. degeneracy gets completely lifted by second-neighbor interactions.
Expectations (1) vs reality
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
(How) Does the degeneracy get lifted?


T. Takagi and M. Mekata, JSPS 62, (1993)
A. Wills, R. Ballou, C. Lacroix, PRB 66, (2002)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
JC, K. Hofhuis, et al., PRB 104, (2022)

6
Expectations (1) vs reality
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
(How) Does the degeneracy get lifted?
7

The macroscopic degeneracy can survive in the presence of third-neighbor interactions but only at very fine-tuned points.

Expectations (1) vs reality
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
(How) Does the degeneracy get lifted?

The macroscopic degeneracy can survive in the presence of third-neighbor interactions but only at very fine-tuned points.

This talk: a series of macroscopically degenerate phases
7
Short-range model and questions
8
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

Chioar et al., PRB 90, (2014)


Short-range model and questions
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

Chioar et al., PRB 90, (2014)


- Proving the ground-state energy?
- Evaluating the residual entropy precisely?
8
Expectations (2)
Ising model = easy to solve?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
9
Ising model = easy to solve?
- The long-range model is challenging (~300 spins) (glassy behavior)
I. A. Chioar, N. Rougemaille, B. Canals, PRB 93, (2016)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
L. Cugliandolo, L. Foini, M. Tarzia, PRB 101 (2020)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

Expectations (2) vs reality
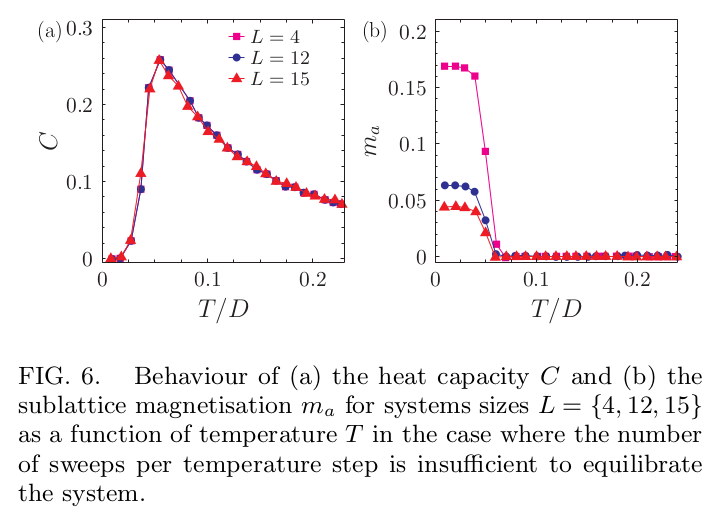
9
Ising model = easy to solve?
- The long-range model is challenging (~300 spins) (glassy behavior)
I. A. Chioar, N. Rougemaille, B. Canals, PRB 93, (2016)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
L. Cugliandolo, L. Foini, M. Tarzia, PRB 101 (2020)
J. Hamp, C. Castelnovo, R. Moessner, PRB 98, (2018)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

Expectations (2) vs reality


- Short-range model :
- MC falls out-of-equilibrium
- Negative results from simple Pauling estimates
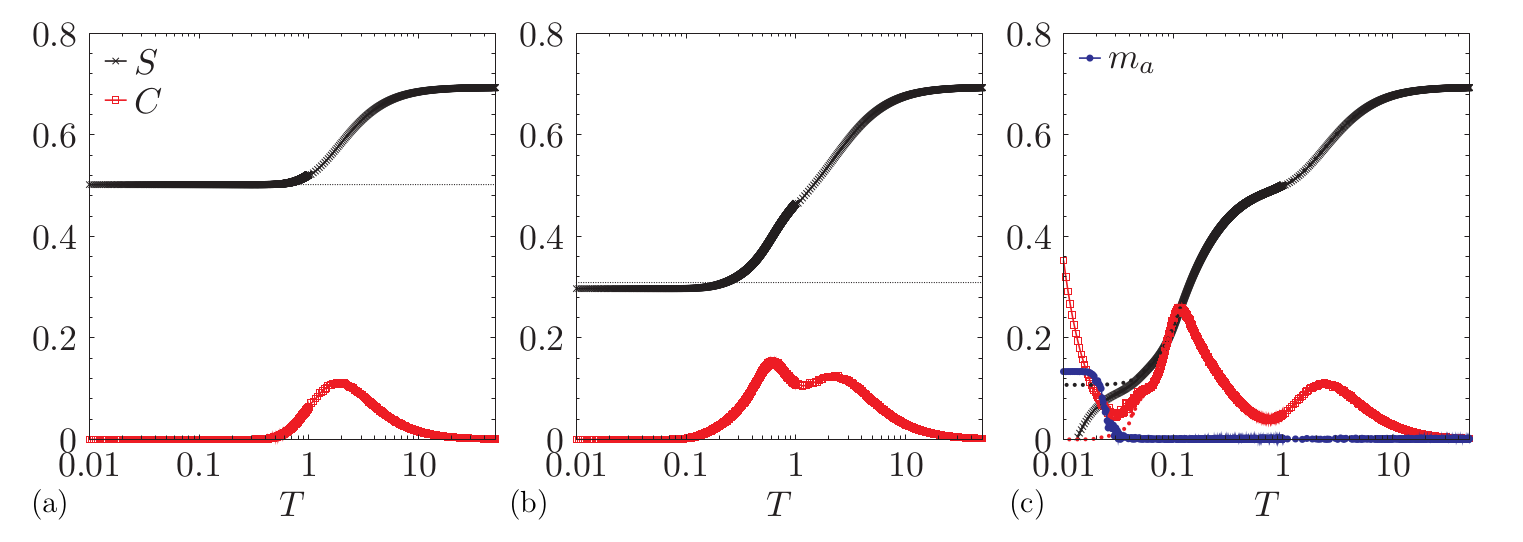
9
Proving the ground-state energy
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Kanamori's method
10
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Constrain the possible values of the correlations:
Kanamori's method
10
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Constrain the possible values of the correlations:
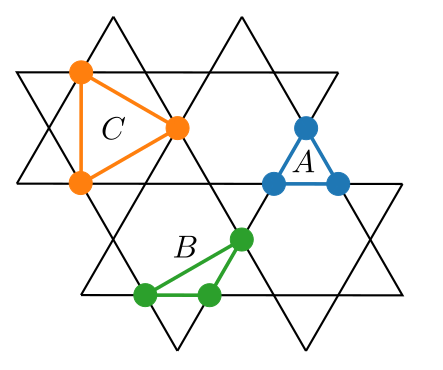
Kanamori's method
10
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)

Translations + rotations
to cover the lattice
Constrain the possible values of the correlations:
Kanamori's method
10
11
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Kanamori's method : applied to our problem
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)

Kanamori's method : applied to our problem
11
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)

Kanamori's method : applied to our problem

11

J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)


Kanamori's method : applied to our problem
11

J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)


Kanamori's method : applied to our problem
11
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)



Kanamori's method : applied to our problem
11



Not all triangles can respect the UUD/DDU rule at the same time
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Kanamori's method : applied to our problem
11
Obtaining the ground state phase diagram
12
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Corners directly correspond to G.S. phases:

Obtaining the ground state phase diagram
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)

12
Corners directly correspond to G.S. phases:
Obtaining the ground state phase diagram
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)

12
Corners directly correspond to G.S. phases:
Obtaining the ground state phase diagram
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)

12
Corners directly correspond to G.S. phases:
Proving the ground-state energy
13

J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
All corners must be verified
Proving the ground-state energy
14



J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Proving the ground-state energy



J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
14
Proving the ground-state energy



J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Methods: J. Kanamori, Prog. Theor. Phys. 35, (1966)
F. Ducastelle, Cohesion and Structure No 3, (1990)
G. Rakala, K. Damle, PRE 96, (2017)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
14
Tensor networks for frustrated Ising models
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Why?
15
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
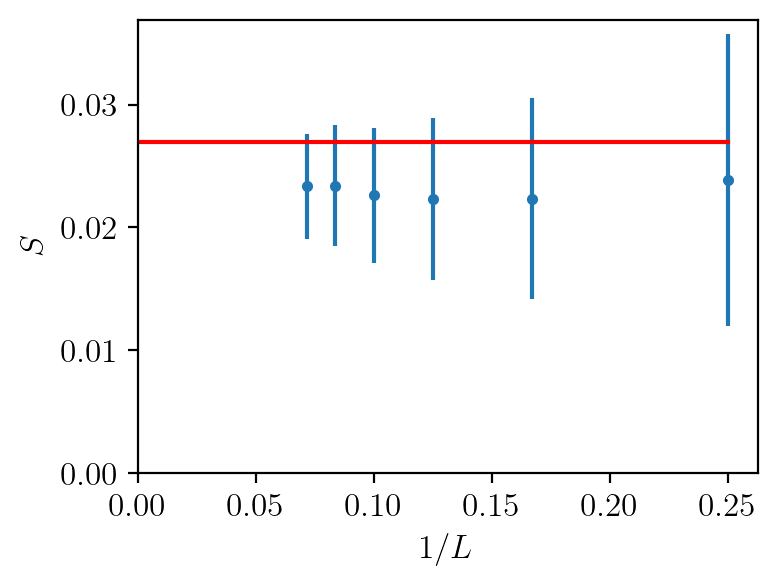
- Determining the residual entropy precisely.
Why?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
- Determining the residual entropy precisely.
Monte Carlo challenges:
- "Good" update
- Thermodynamic integration
- Good control over the finite-size scaling behavior
15
Why?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
- Determining the residual entropy precisely.
Monte Carlo challenges:
- "Good" update
- Thermodynamic integration
- Good control over the finite-size scaling behavior
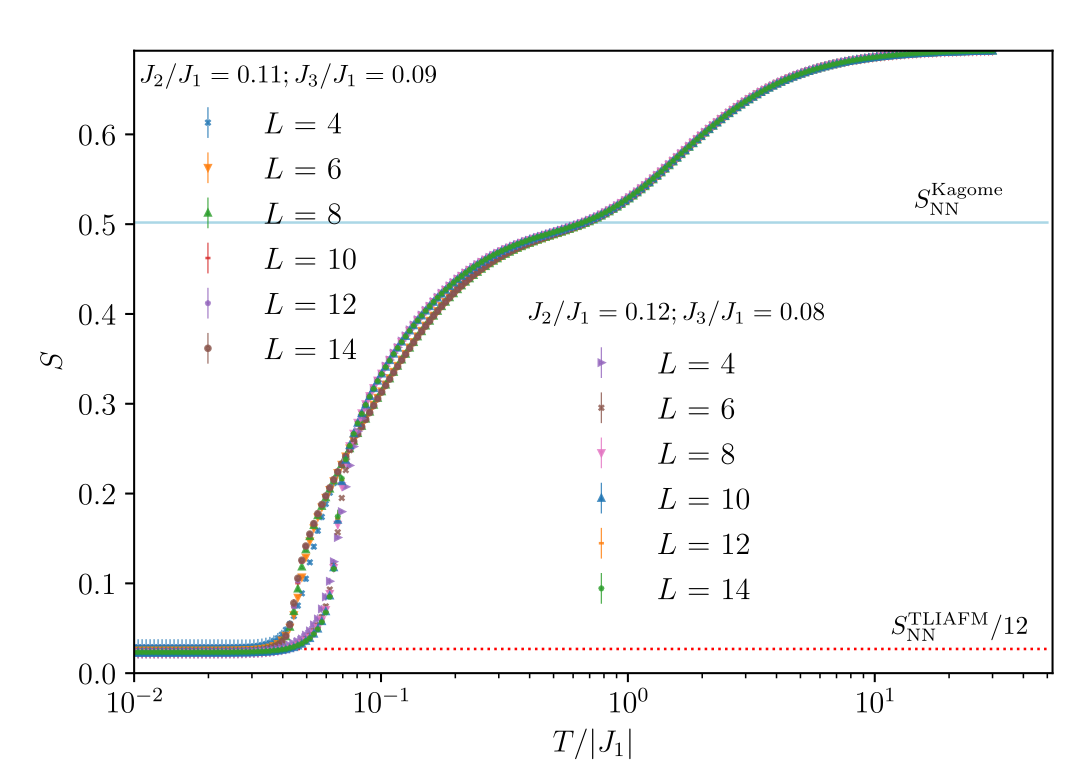
15
Why?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
- Determining the residual entropy precisely.
Monte Carlo challenges:
- "Good" update
- Thermodynamic integration
- Good control over the finite-size scaling behavior

15
Why?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
- Determining the residual entropy precisely.
Monte Carlo challenges:
- "Good" update
- Thermodynamic integration
- Good control over the finite-size scaling behavior

15
Why?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
- Determining the residual entropy precisely.
Monte Carlo challenges:
- "Good" update
- Thermodynamic integration
- Good control over the finite-size scaling behavior
15
Why?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
- Determining the residual entropy precisely.
Monte Carlo challenges:
- "Good" update
- Thermodynamic integration
- Good control over the finite-size scaling behavior

15
The idea
16
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
The idea
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
16
The idea
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
16
The idea
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
We "just" have to compute the (normalized) partition function for one site...
16
The idea
We "just" have to compute the (normalized) partition function for one site...
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
No need to control the whole temperature range
16
Transfer matrix inspiring tensor networks


Transfer matrix
Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
17

Transfer matrix




Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
17
Transfer matrix inspiring tensor networks
Tensor networks for classical spin systems

Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
18
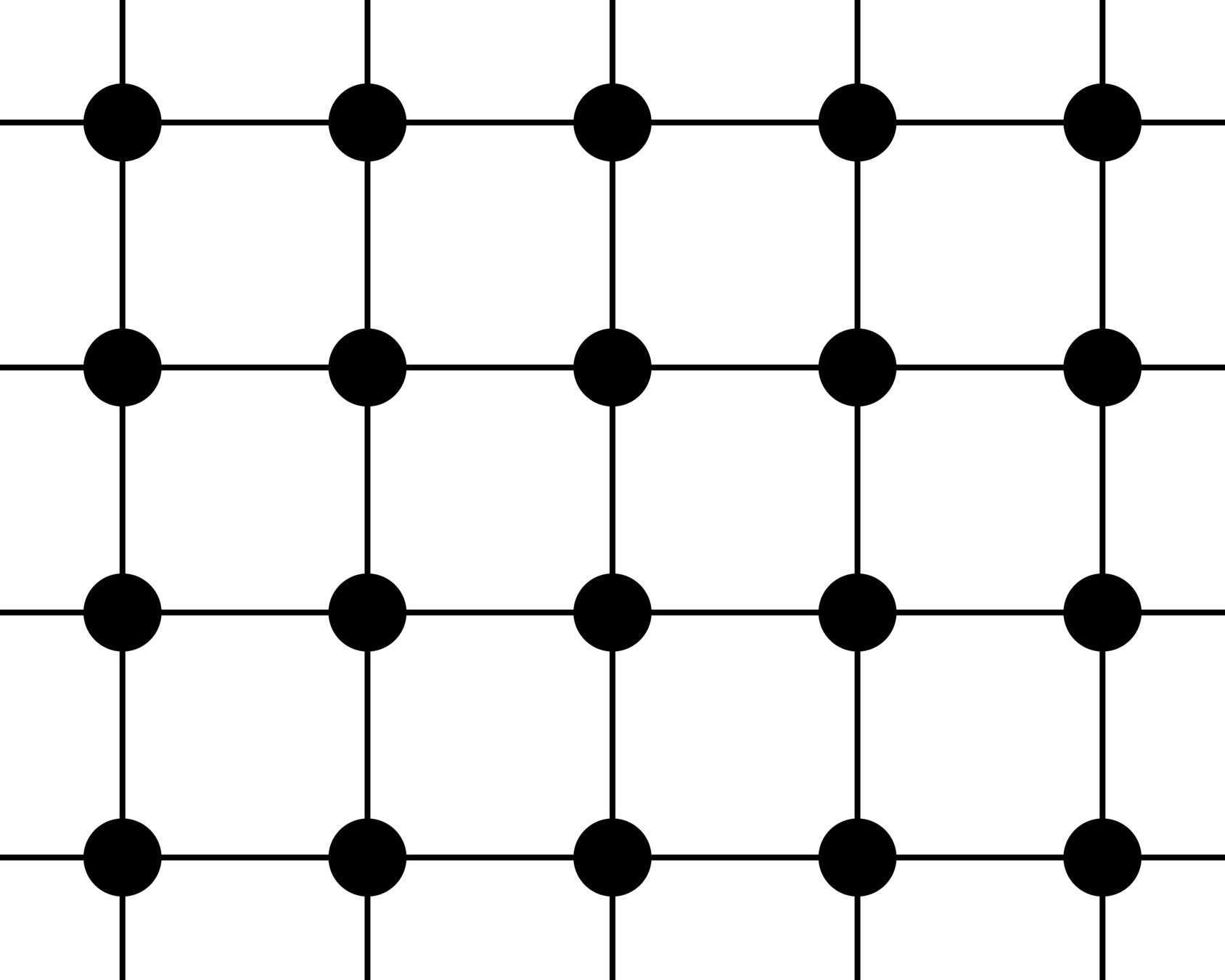
Tensor networks for classical spin systems

Tensor notation: R. Penrose, in Combinatorial Mathematics and its applications, Academic Press (1971)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
18
Tensor networks for classical spin systems


(1 + 1)D
iTEBD / VUMPS
R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
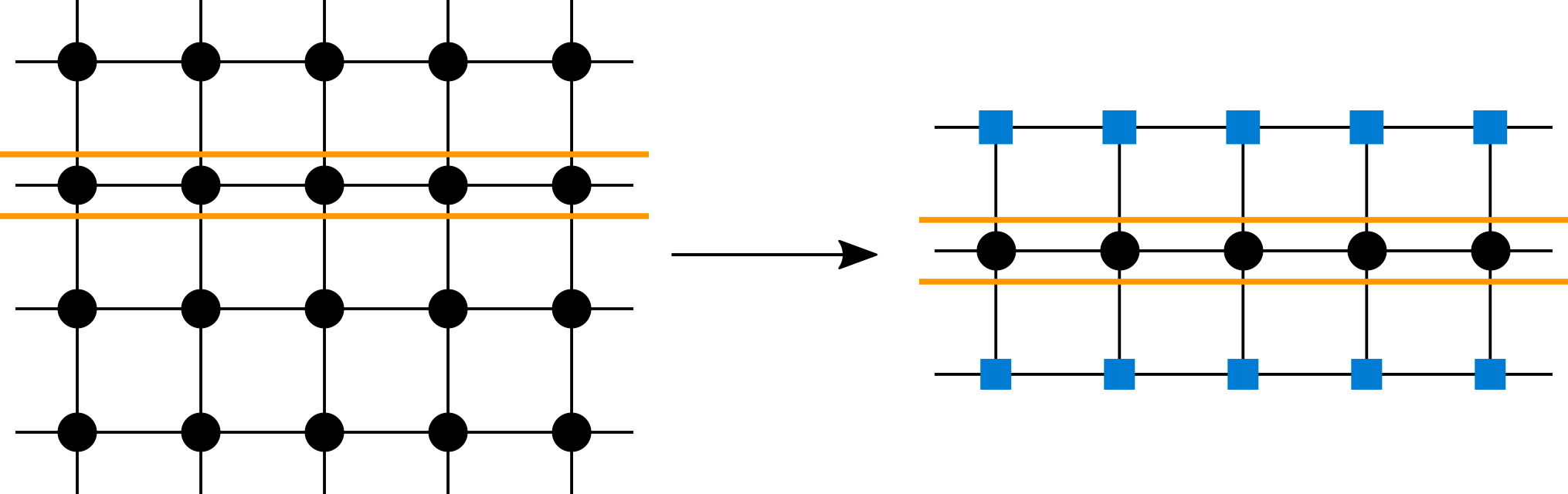
18
Tensor networks for classical spin systems


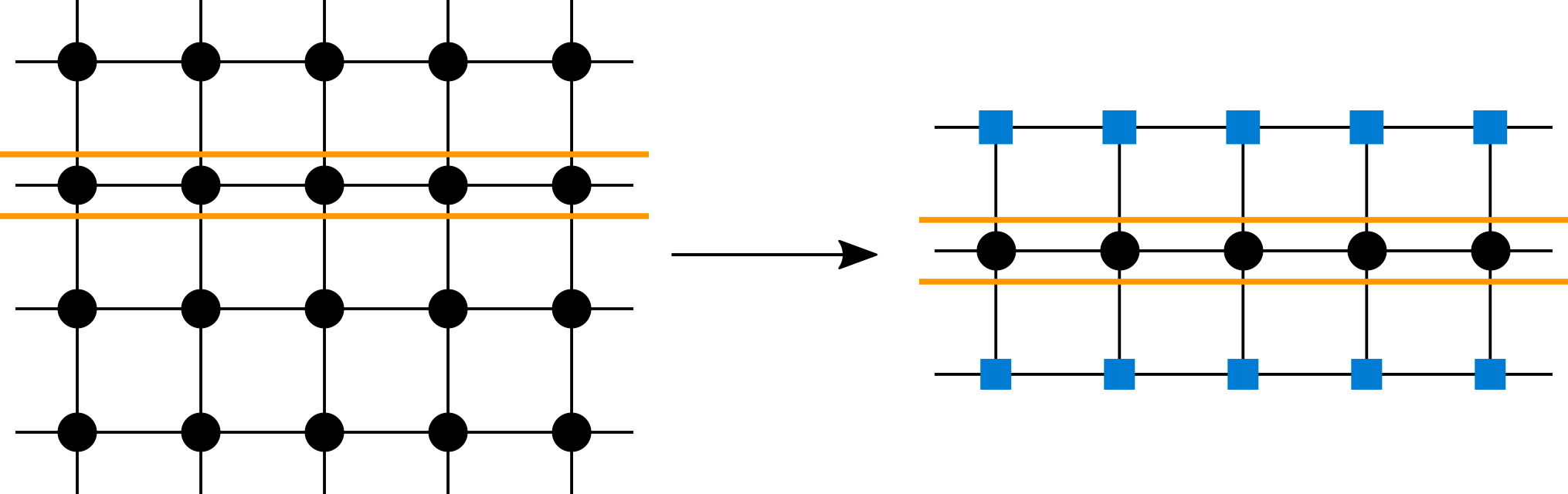
(1 + 1)D
iTEBD / VUMPS
R. J. Baxter, J. Math. Phys. 9, 1968
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn 65, 1996
2D
CTMRG
TRG

M. Levin, C. P. Nave, PRL 99, 2007

J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
R. J. Baxter, J. Math. Phys. 9, 1968
Orús, Vidal, PRB 78, 2008;
V. Zauner-Stauber et. al. PRB 97,2018;
M. Fishman et. al PRB 98, 2018
12
The issue
19

J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
The issue

J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
B. Vanhecke, JC, et al. PRR 3, (2021)
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
M. Friaz-Pérez, M, Mariën et al, arXiv:2104.13264, (2021)
Fails in the presence of frustration and macroscopic g.s. degeneracy
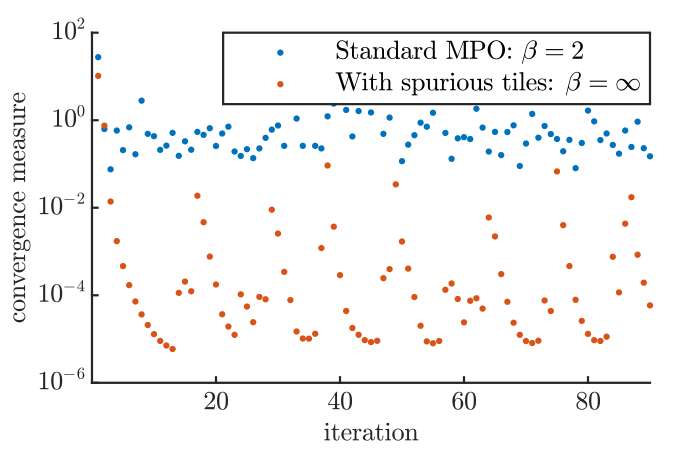
19
The issue

J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
B. Vanhecke, JC, et al. PRR 3, (2021)
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
M. Friaz-Pérez, M, Mariën et al, arXiv:2104.13264, (2021)
Fails in the presence of frustration and macroscopic g.s. degeneracy

19
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
Related to the inexact cancellation of very large
and very small factors.
What is going on?
20
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Non-frustrated models:
What is going on?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Non-frustrated models:
20
What is going on?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Non-frustrated models:
Triangular/ kagome lattices:
20
Why is it intriguing?
21
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
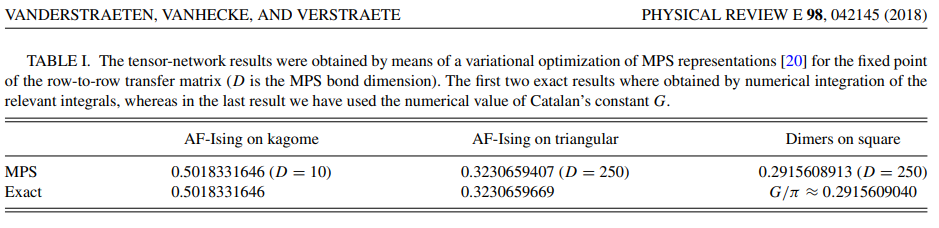
TNs : 10 digits, vs 5 digits for MC
Why is it intriguing?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

TNs : 10 digits, vs 5 digits for MC


21
Why is it intriguing?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

TNs : 10 digits, vs 5 digits for MC




21
Why is it intriguing?
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

TNs : 10 digits, vs 5 digits for MC




The convergence of the tensor network contraction depends on the formulation of the partition function
21
Systematically finding the local rule
22
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969);
M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975);
B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981);
W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

1. Split the Hamiltonian in a different way

Systematically finding the local rule
22
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969);
M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975);
B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981);
W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

1. Split the Hamiltonian in a different way
2. Lower bound on the ground-state energy:

Systematically finding the local rule
22
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969);
M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975);
B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981);
W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

1. Split the Hamiltonian in a different way
2. Lower bound on the ground-state energy:
3. This lower bound can be maximized with respect to the weights (max-min approach):


Systematically finding the local rule
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

1. Split the Hamiltonian in a different way
2. Lower bound on the ground-state energy:
3. This lower bound can be maximized with respect to the weights (max-min approach):
4. When the lower bound is saturated:


All the ground states are made of configurations that minimize the local Hamiltonian.

22
Does it work?
23

B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Does it work?

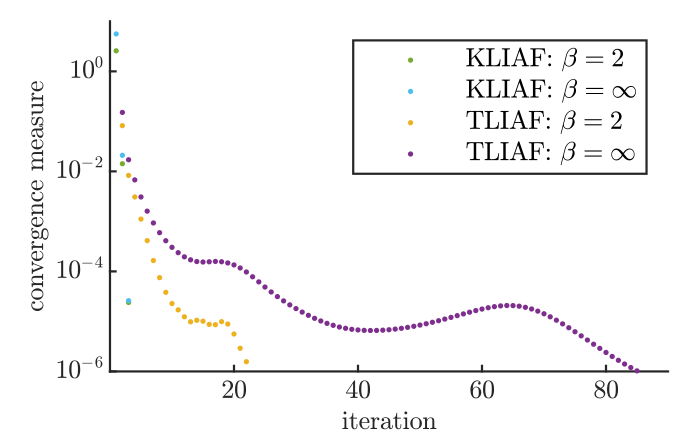
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
23
Does it work?


B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
23
24
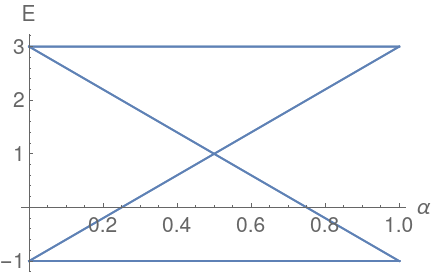
Spurious tiles
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
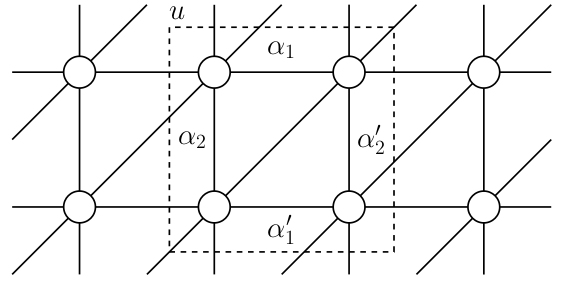
Spurious tiles
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

24
Spurious tiles
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.


24

Spurious tiles
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.



24

Spurious tiles
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.





24
TNs for frustrated Ising models
25
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
The convergence of the tensor network contraction depends on the formulation of the partition function
TNs for frustrated Ising models
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
The convergence of the tensor network contraction depends on the formulation of the partition function
If the ground-state rule is implemented at the level of the tensor, approximate contraction aglorithms converge
25
TNs for frustrated Ising models
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
The convergence of the tensor network contraction depends on the formulation of the partition function
If the ground-state rule is implemented at the level of the tensor, approximate contraction aglorithms converge

25
A model with several macroscopically degenerate phases
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

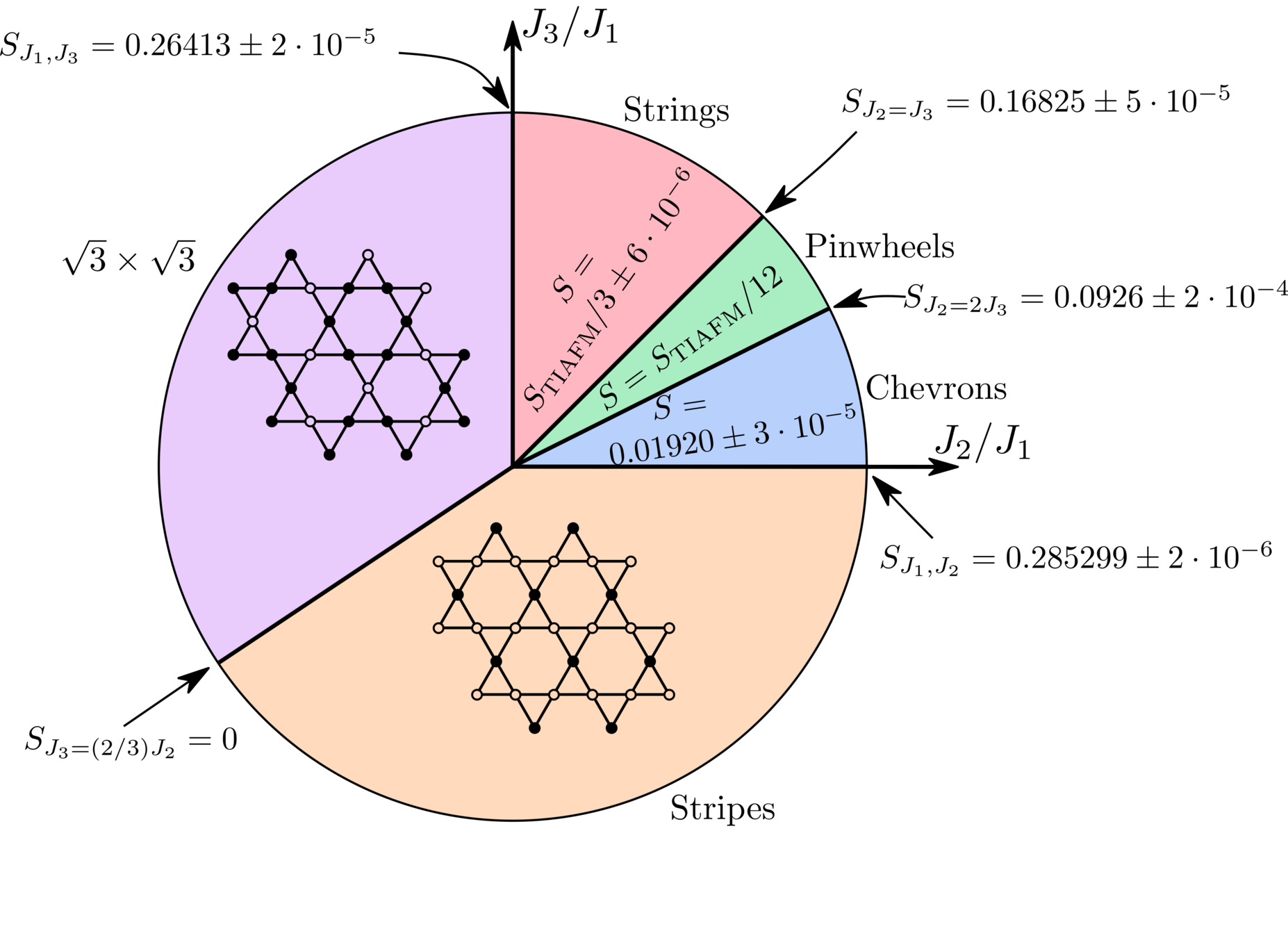
Phase diagram
26
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

Phase diagram
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
26

Residual entropies

JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
27
Residual entropies


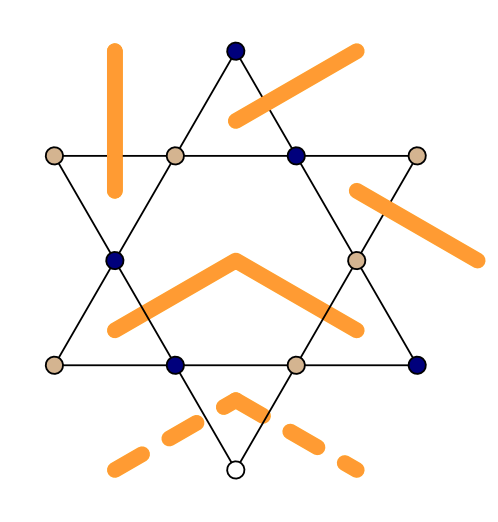
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
27
Residual entropies



JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

27
Residual entropies


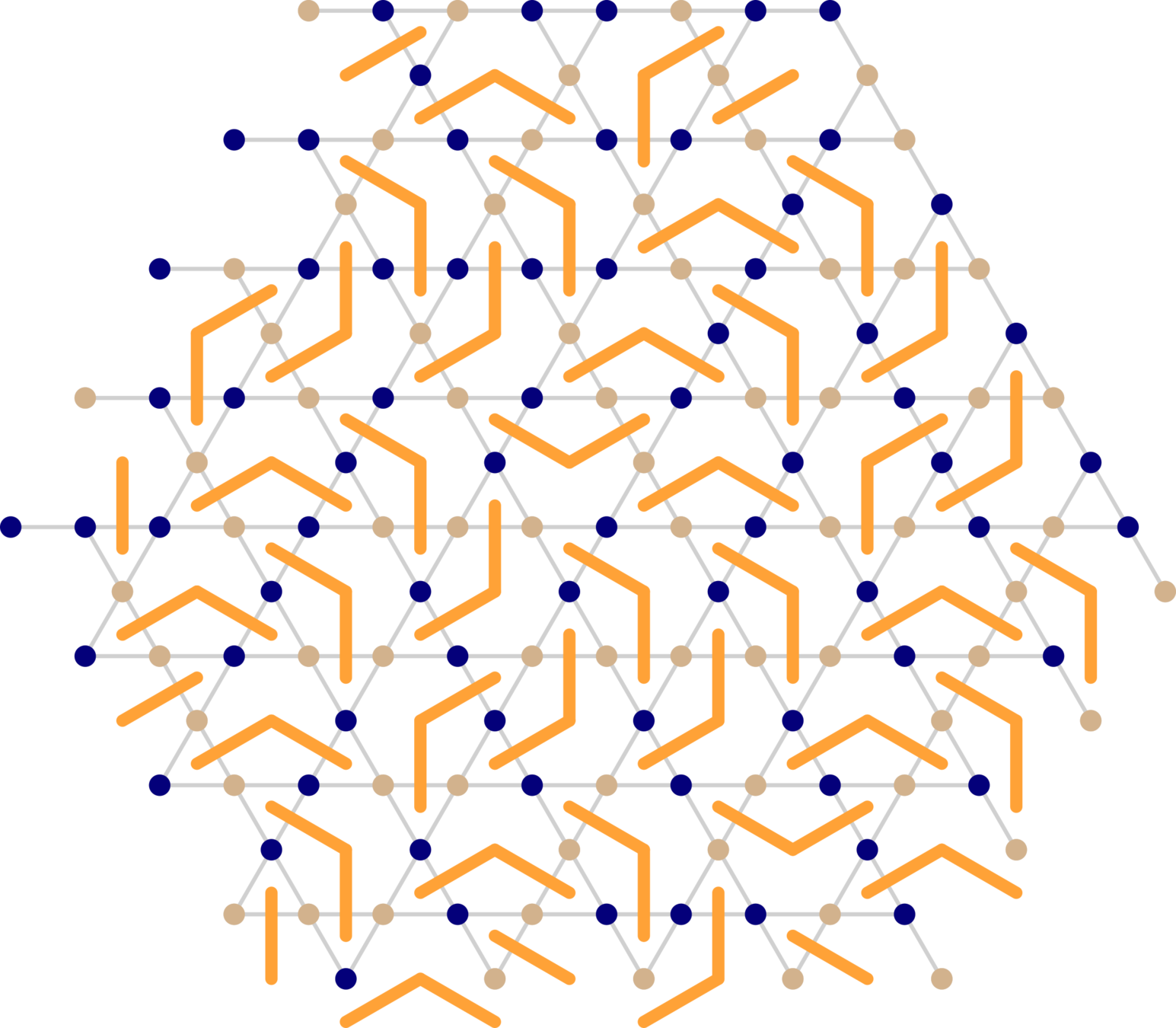


JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
28
Residual entropies

29

JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Residual entropies

29


JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Residual entropies

29


JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

Residual entropies




JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
29
Residual entropies






JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
29
Residual entropies





JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
30
Residual entropies


JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
31
Residual entropies



JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
31
Residual entropies



JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
31

Residual entropies



JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
32
Residual entropies




JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
32
Residual entropies




JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
32
Discussion
33

JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Discussion


JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
33
Discussion



JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
33
Open questions...
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
34
Nature of the phase transitions?
Open questions...
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
34
Tensor network "problem": does this solution work for TNR?
Nature of the phase transitions?
Open questions...
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
34
Tensor network "problem": does this solution work for TNR?
Nature of the phase transitions?
Contraction of PEPS wavefunctions?
Open questions...
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
34
Tensor network "problem": does this solution work for TNR?
Nature of the phase transitions?
Contraction of PEPS wavefunctions?
A different approach for spin glasses: extend to approximate contraction?
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
Open questions...
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
34
Tensor network "problem": does this solution work for TNR?
Contraction of PEPS wavefunctions?
Use of the ground-state local rule: existence of the cluster?
Nature of the phase transitions?
A different approach for spin glasses: extend to approximate contraction?
Ronceray and Le Floch, PRE 100, (2019)
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
Take home...
35
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
Take home...
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
The convergence of the tensor network contraction depends on the formulation of the partition function
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
35
Take home...
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
The convergence of the tensor network contraction depends on the formulation of the partition function
If the ground-state rule is implemented at the level of the tensor, approximate contraction aglorithms converge
35
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
Take home...
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
If the ground-state rule is implemented at the level of the tensor, approximate contraction aglorithms converge
The convergence of the tensor network contraction depends on the formulation of the partition function
35
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
Take home...
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
If the ground-state rule is implemented at the level of the tensor, approximate contraction aglorithms converge
The convergence of the tensor network contraction depends on the formulation of the partition function

Thank you!
35
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021)
Bonus slides
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
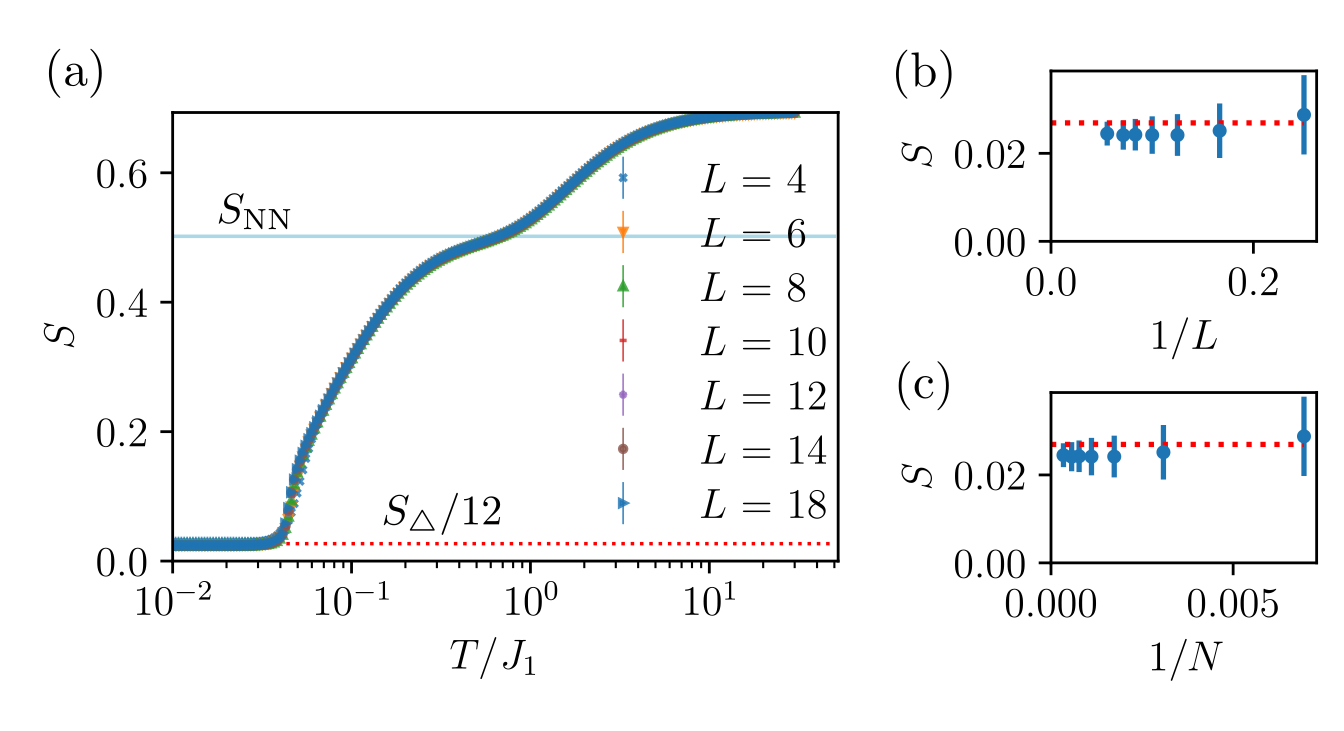
Farther-neighbor interactions : the question of the residual entropy



Very small residual entropy. How can we evaluate it precisely?
Challenges with MC
- Good update
- Thermodynamic integration
- Good control over the finite-size scaling behavior
Postulate:
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
JC, B. Vanhecke, L. Vanderstraeten, et al., arXiv:2206.11788 (2022)
Emergent U(1) symmetry and infinite correlation length
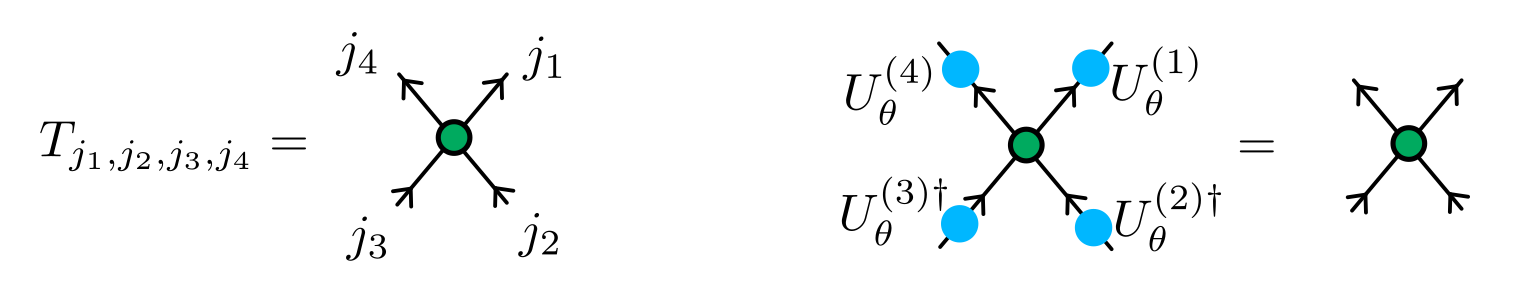
Invariance of a tensor
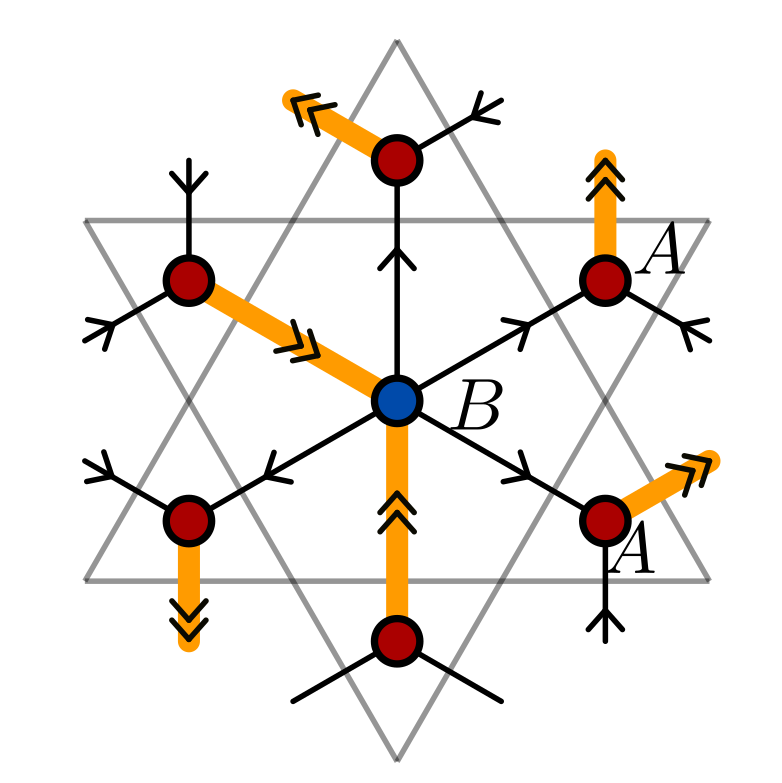
Gauss's law for the J1-J2 model
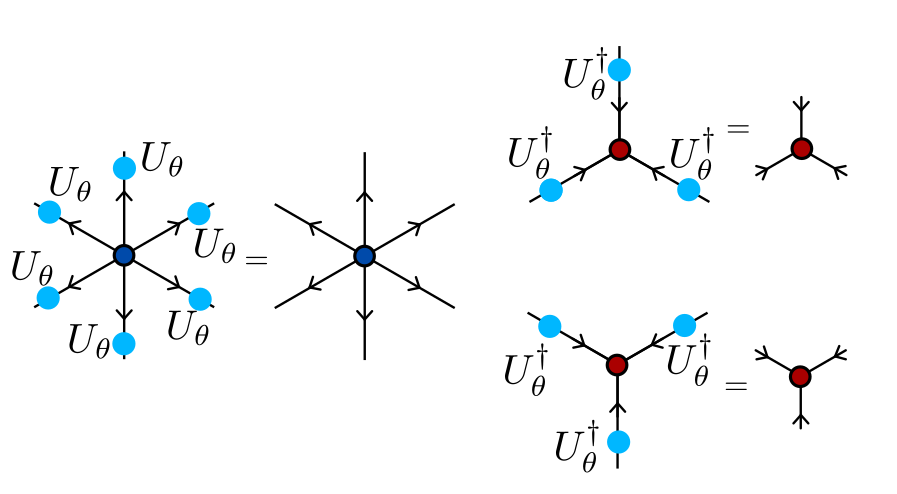
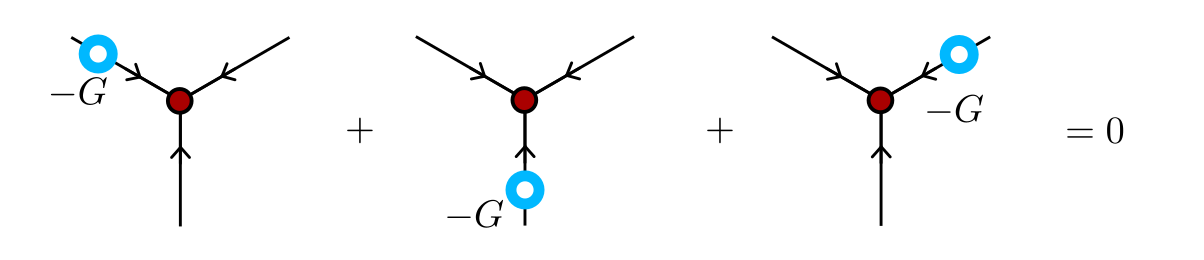
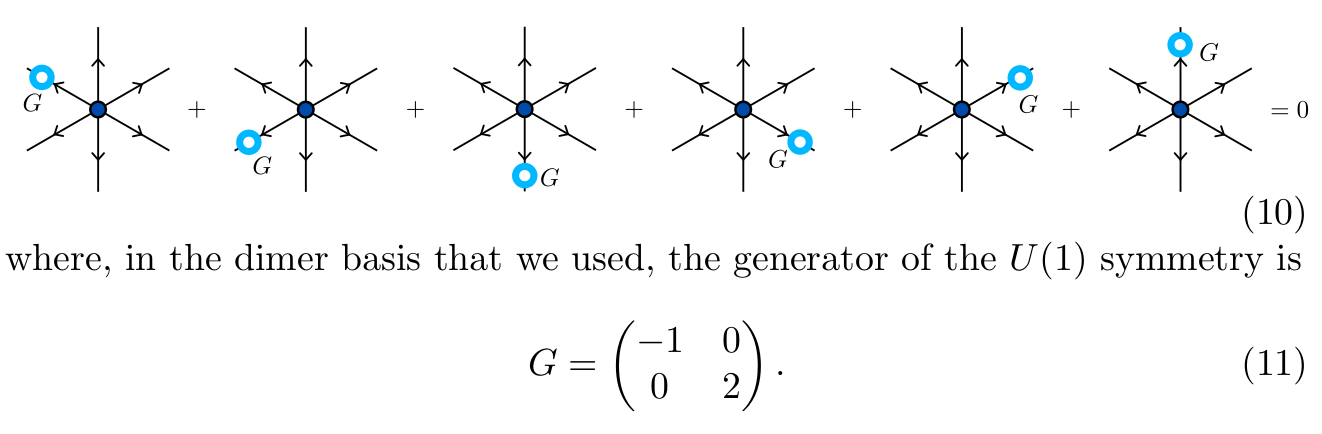
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
JC, B. Vanhecke, Unpublished

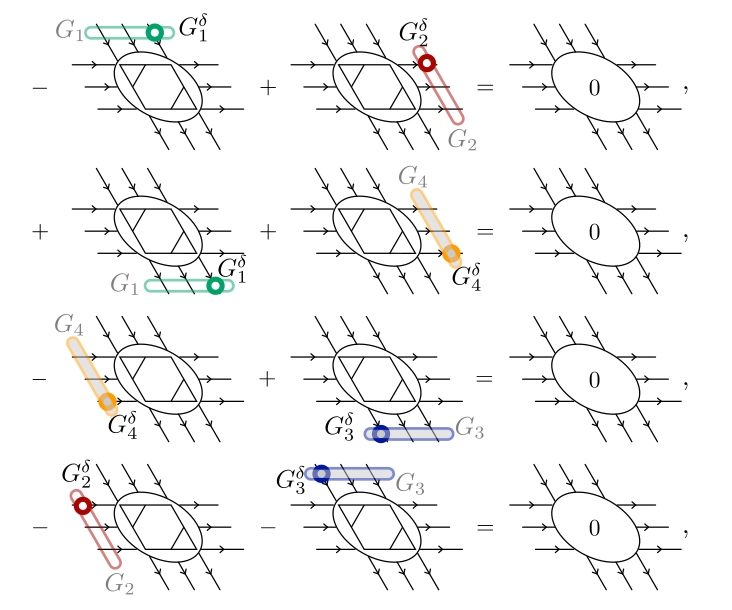
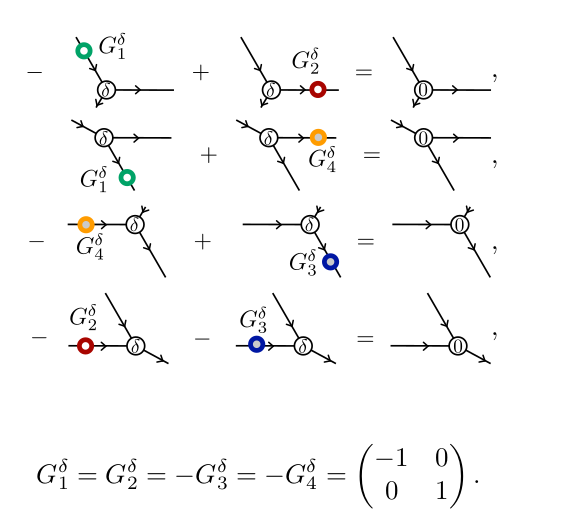
Emergent U(1) symmetry and infinite correlation length
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
JC, B. Vanhecke, Unpublished

Look for solutions to
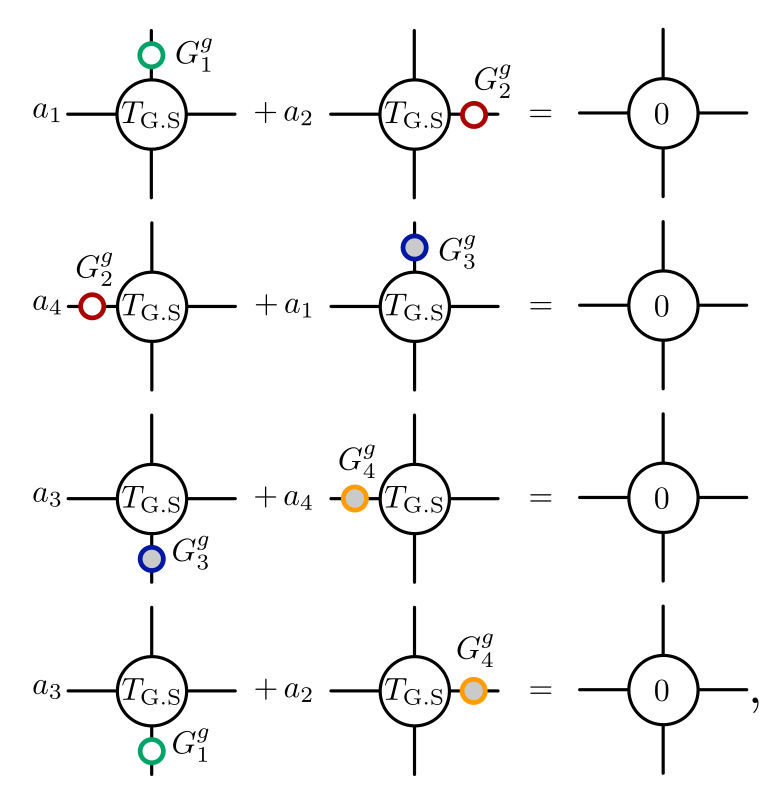
Remove solutions corresponding to:

Emergent U(1) symmetry and infinite correlation length
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
JC, B. Vanhecke, Unpublished
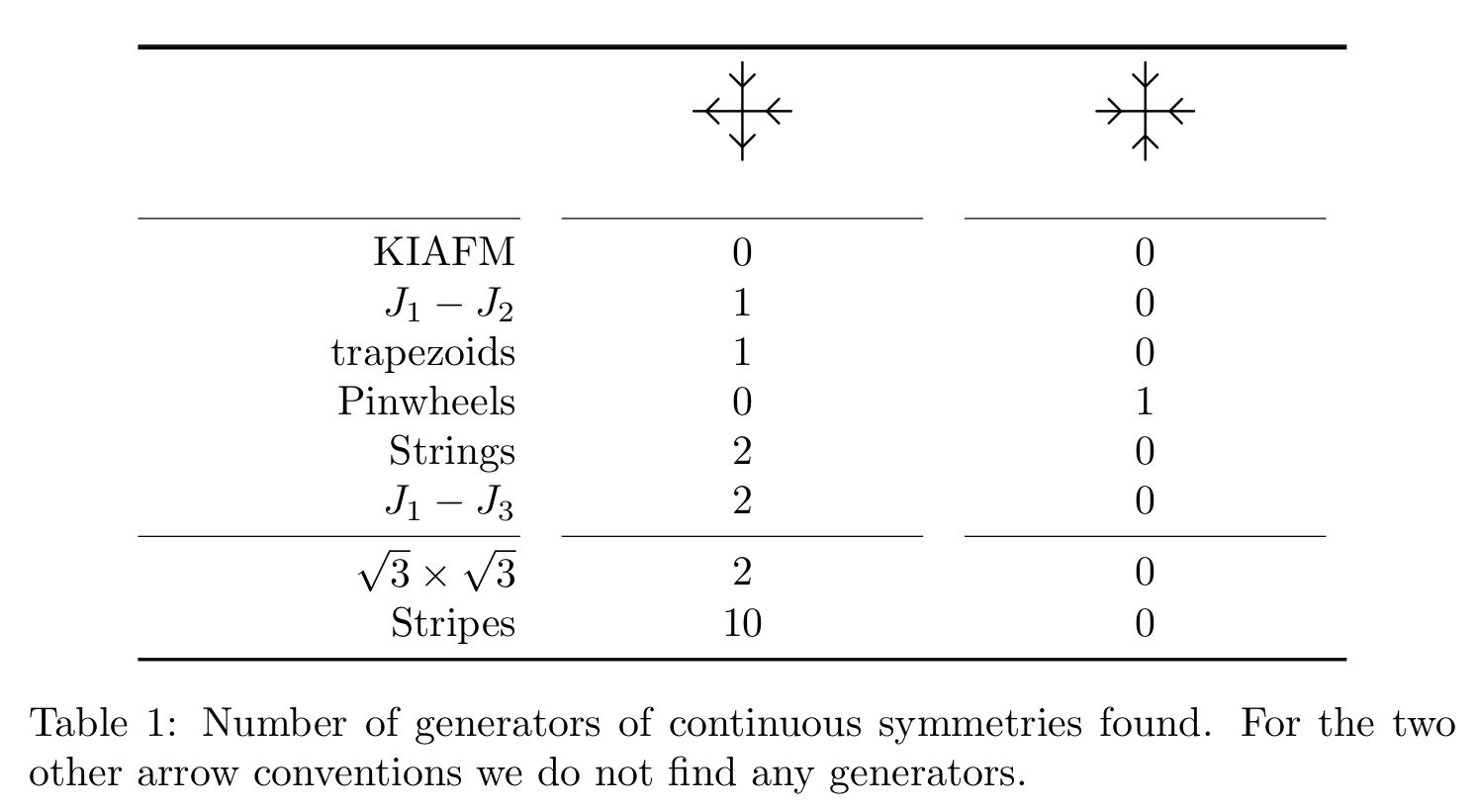
Emergent U(1) symmetry and infinite correlation length
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
JC, B. Vanhecke, Unpublished


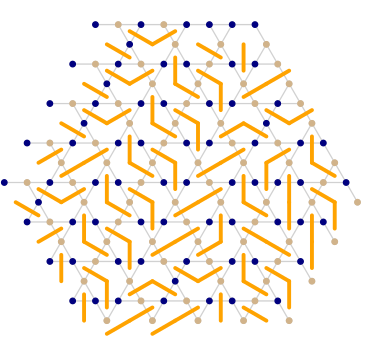
Phase boundaries
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
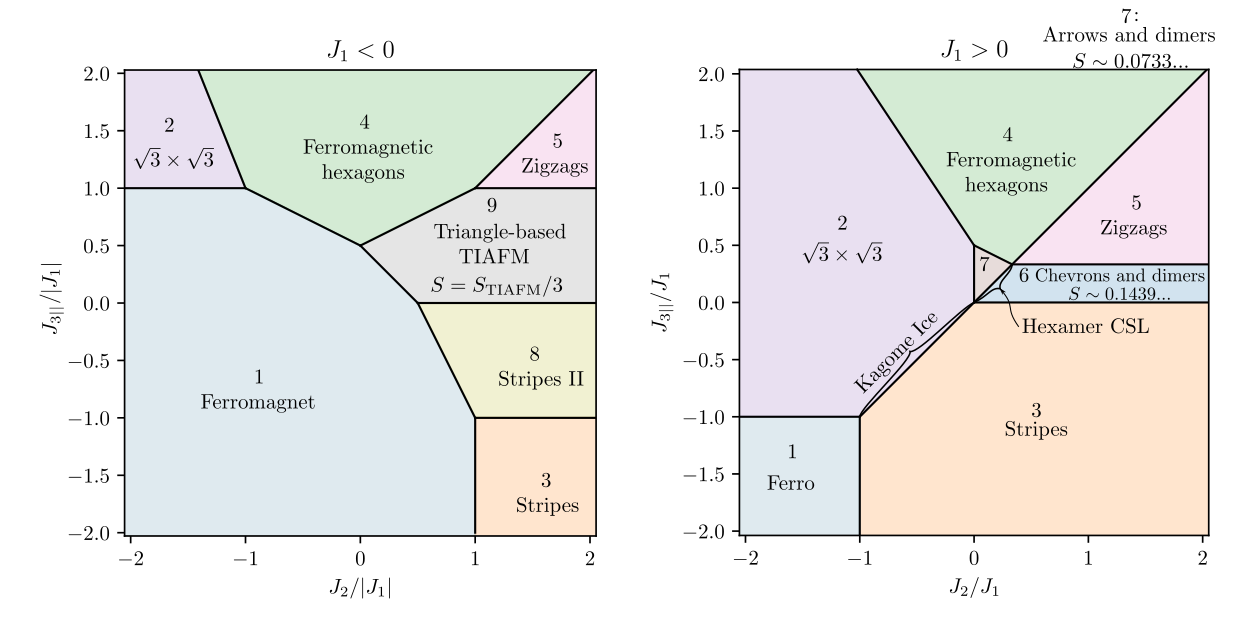
Phase diagrams
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
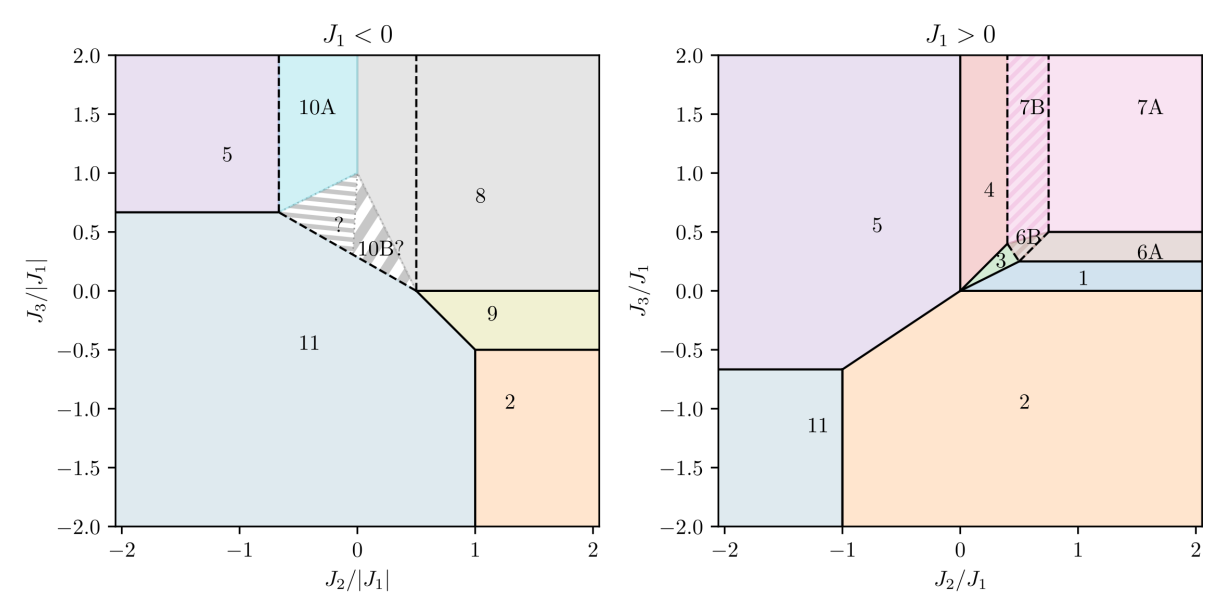
Phase diagrams
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

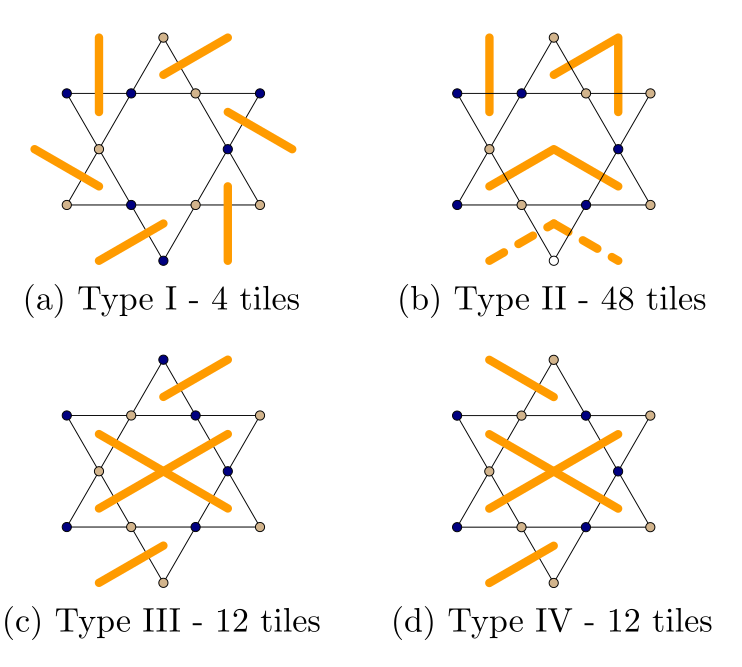
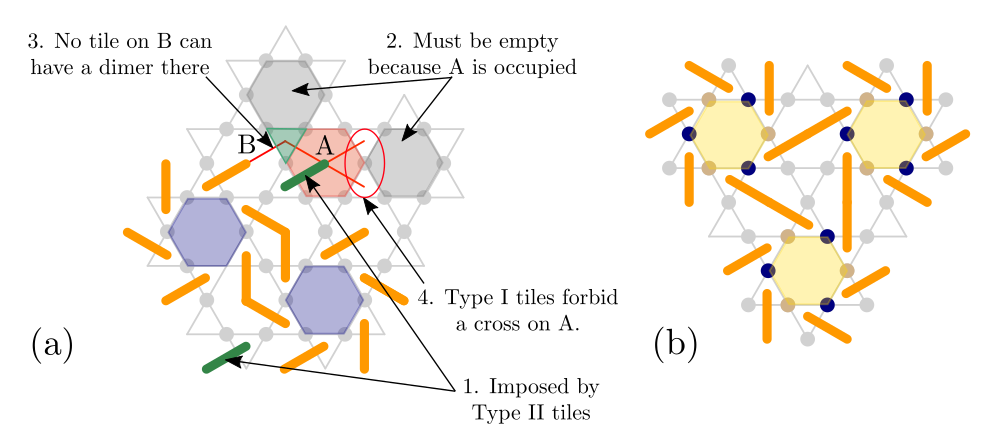


1. Ratios are fixed by energy and PBC
2. The ratios are fixed locally because
- occupied tiles have to have at least two nearest-neighbor empty tiles
- emtpy tiles cannot be 2nd NN
3. The tiles have to have different chiralities
Elements of proof for the pinwheels phase
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
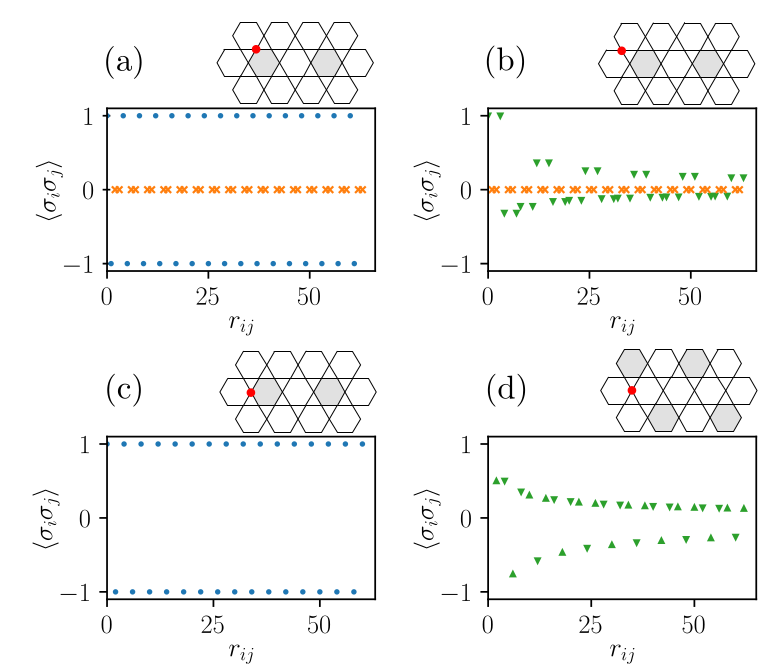
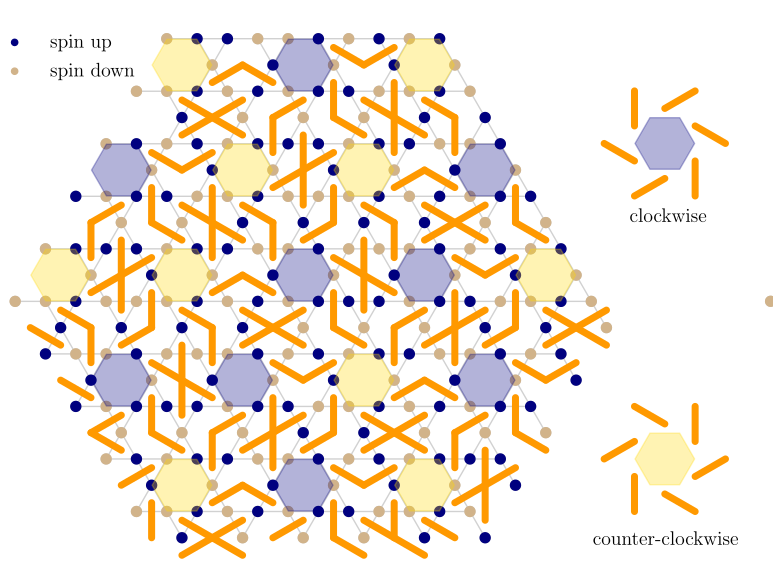
Spin-Spin correlations in the pinwheels phase
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
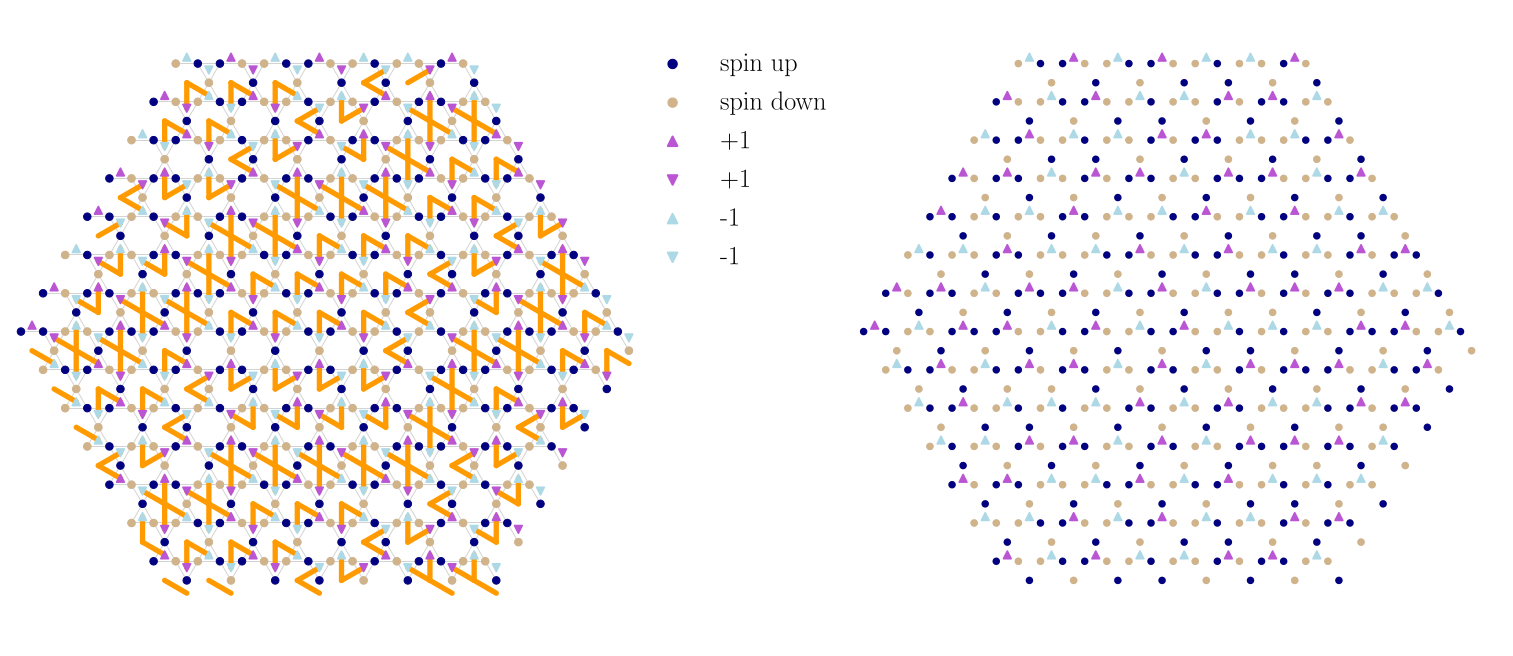
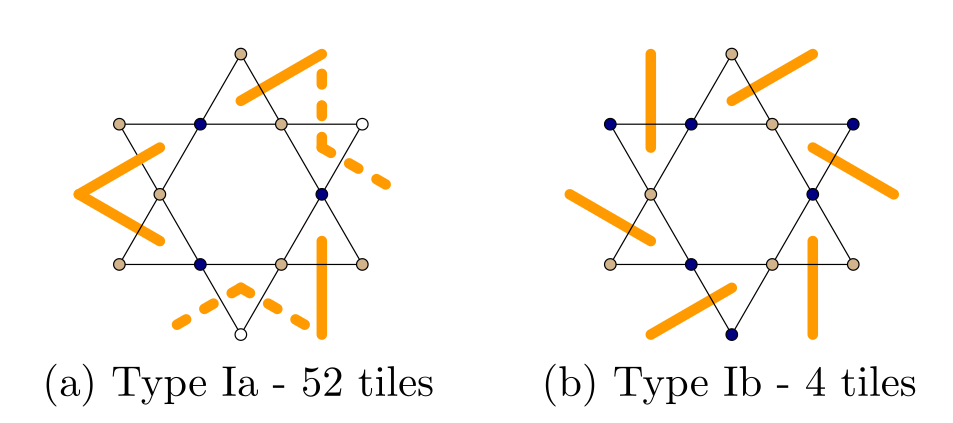
Strings phase
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
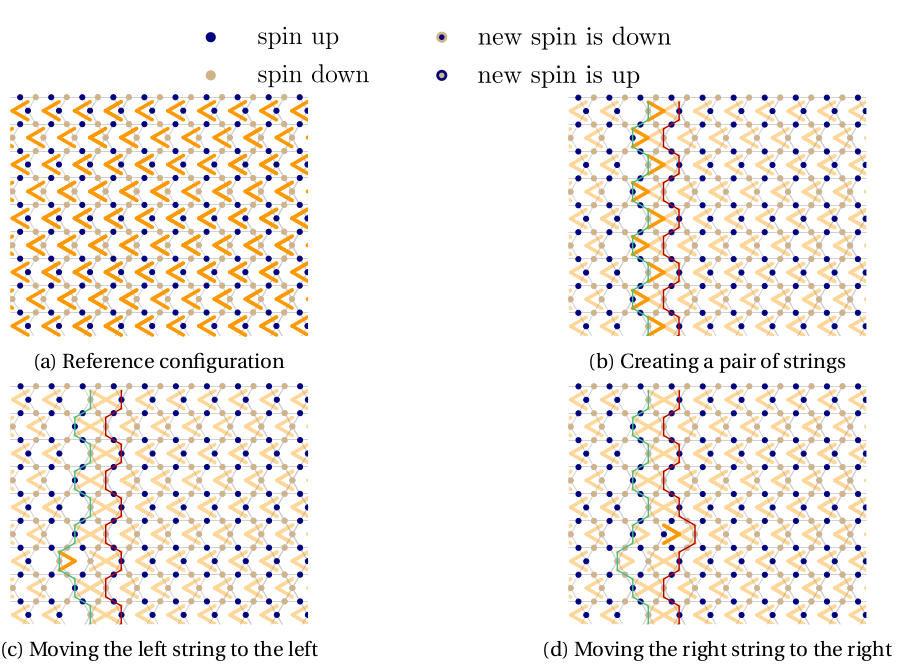
Strings phase
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Strings phase
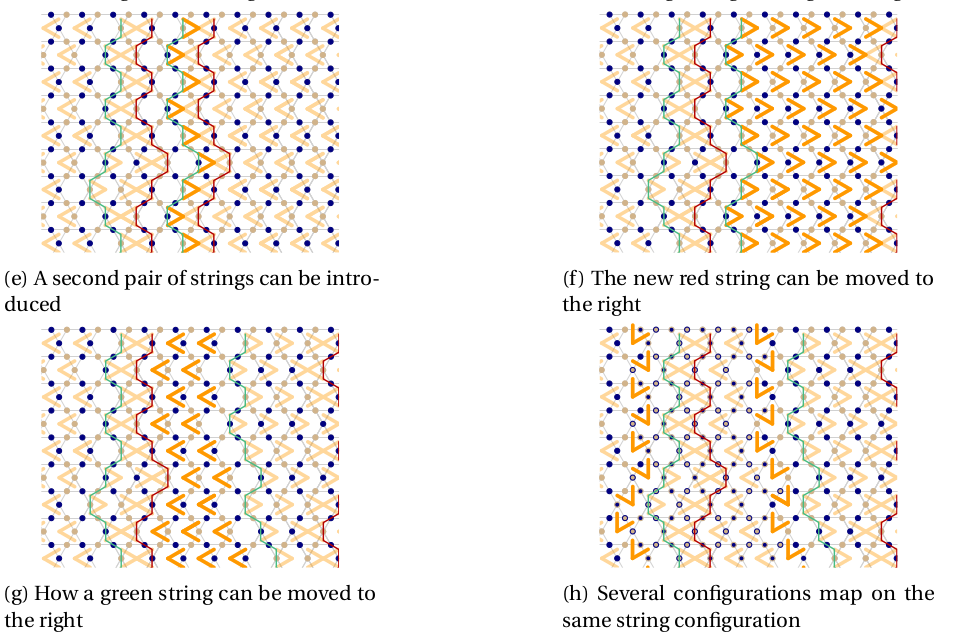
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Strings phase
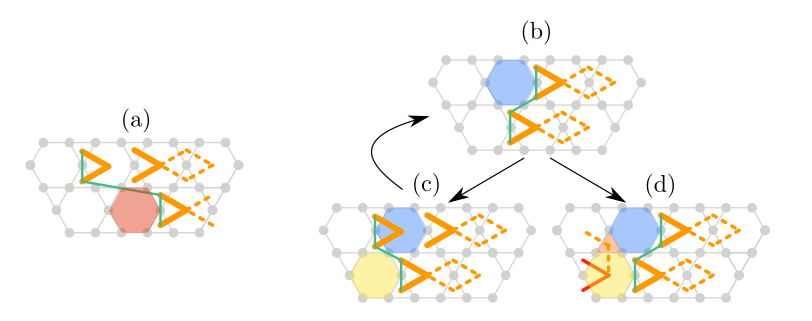
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Bonus slides
Technical aspects
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
It works...
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
17
(2D Ising square lattice)
Chiral 3-state Potts model
Six-state clock model
Kagome ferromagnet
J1-J2 square lattice away from the frustrated line
Hard rods
Nearest-neighbor kagome Ising
Nearest-neighbor triangular Ising
Tensor networks for classical spin systems

Transfer matrix for the 1D Ising model
Partition function and leading left/right eigenvectors

"Exact contraction"
"Approximate contraction"
The aim is essentially to find the leading eigenvectors and the largest eigenvalue
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.

VUMPS
CTMRG
Tensor networks for classical spin systems
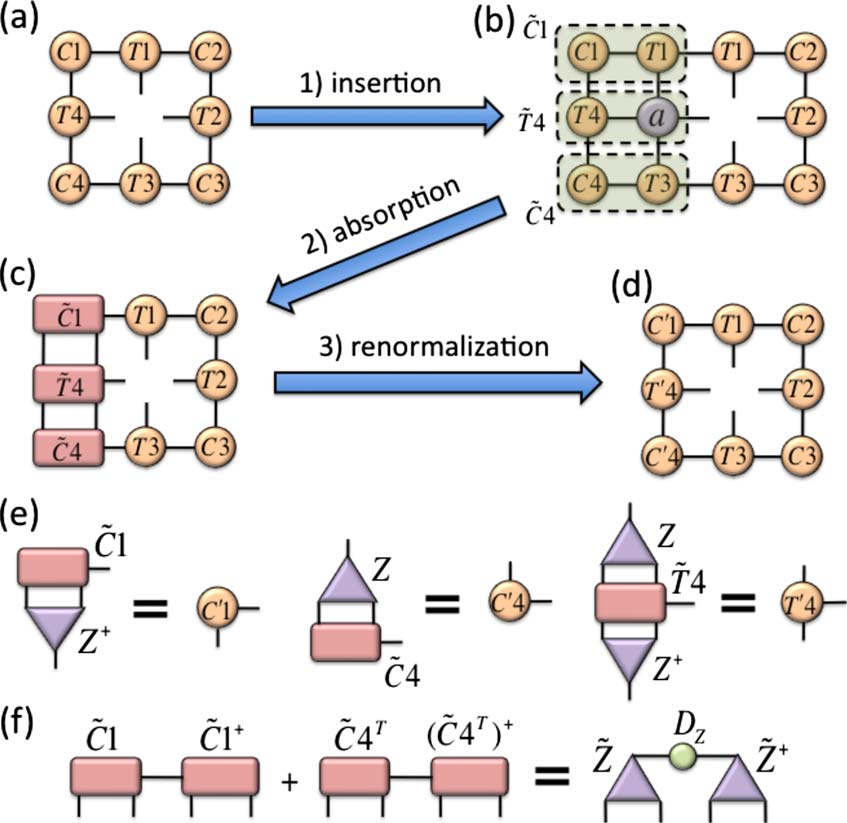
T. Nishino, K. Okunishi, J. Phys. Soc. Jpn. 65, (1996)
R. Orús, G. Vidal, PRB 80, 2009
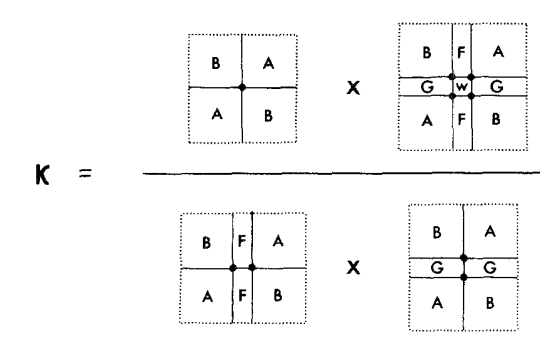
R. J. Baxter, J. Stat. Phys. 19, 1978
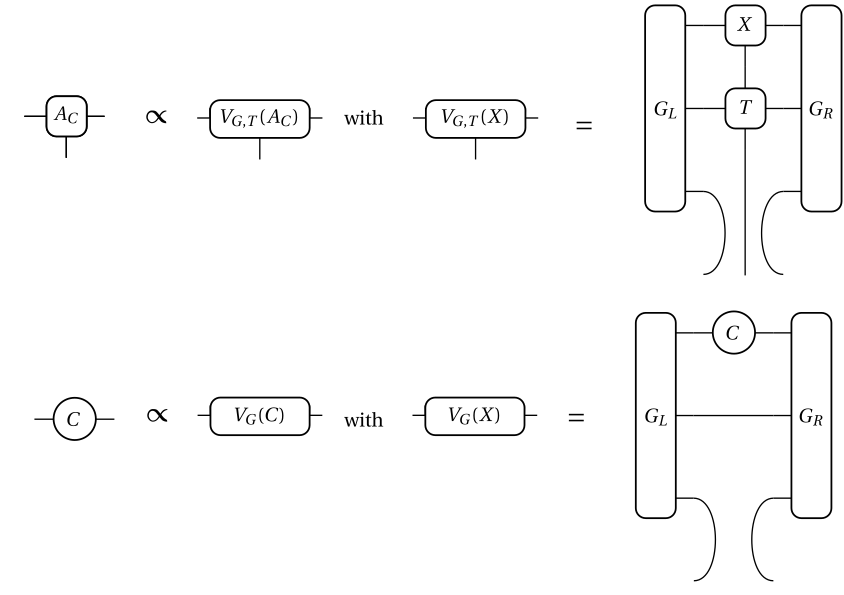
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Temperature and tensor networks
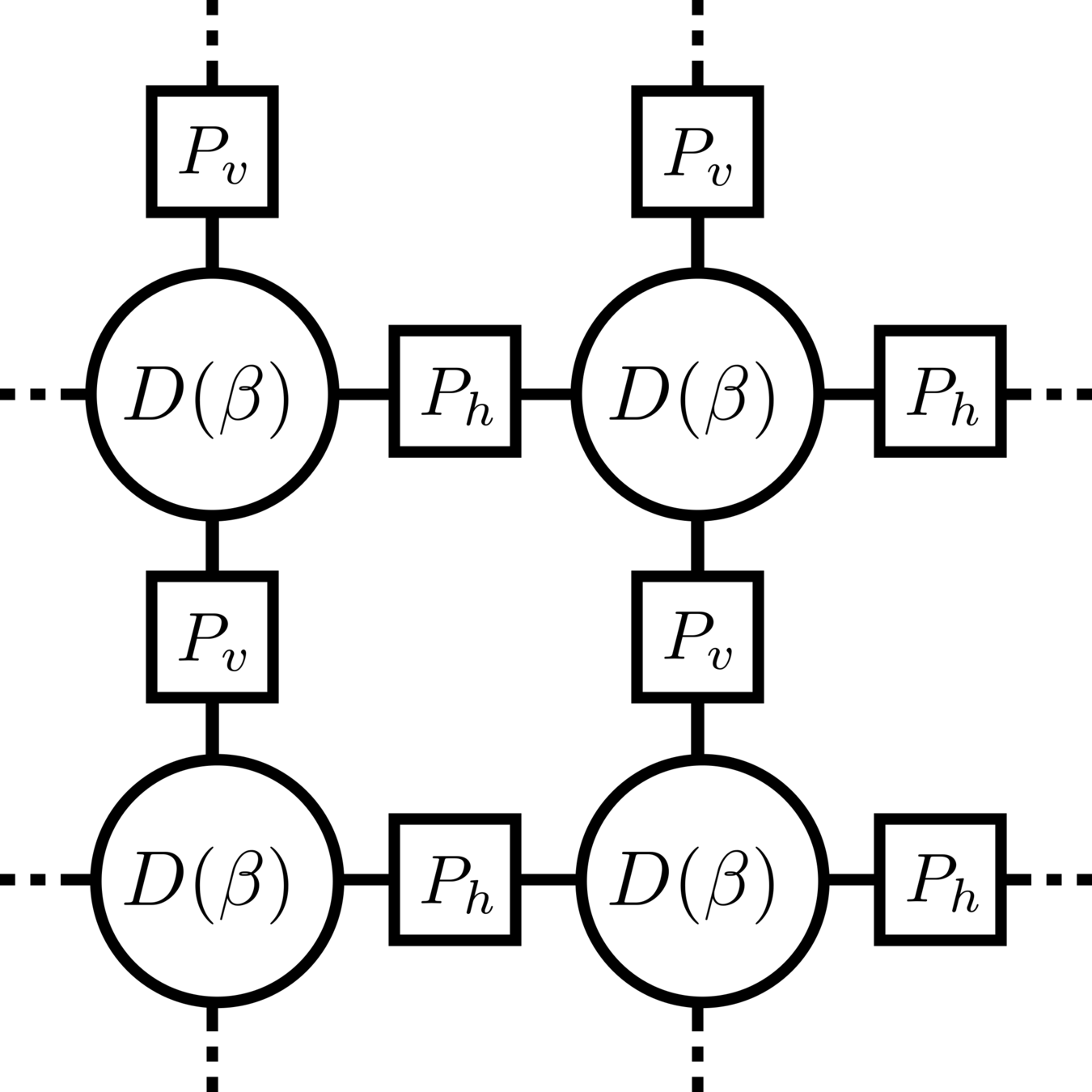
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
J1-J2 vs TIAFM
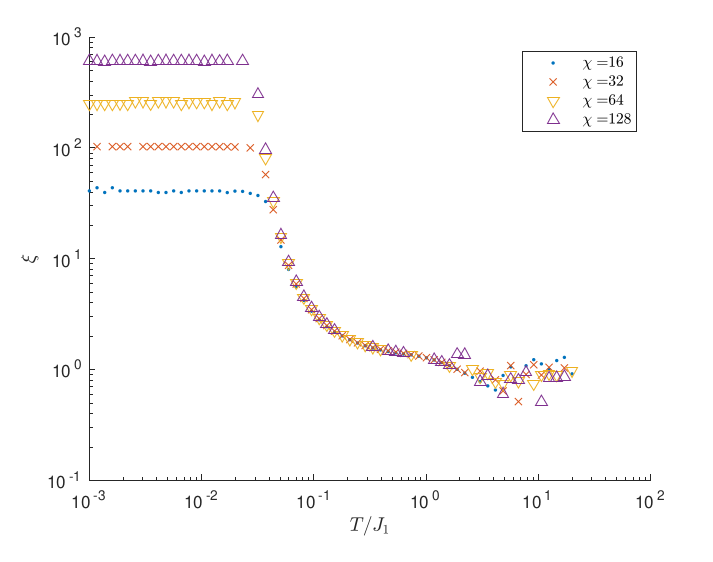
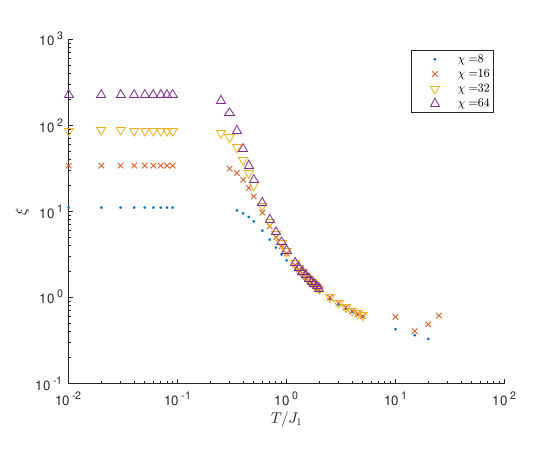
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
J. F. Nagle versus tensor networks

L. Vanderstraeten, B. Vanhecke, F. Verstraete, PRE 98 (2018)
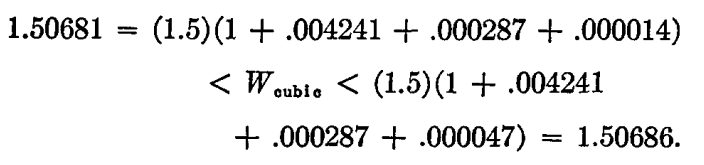
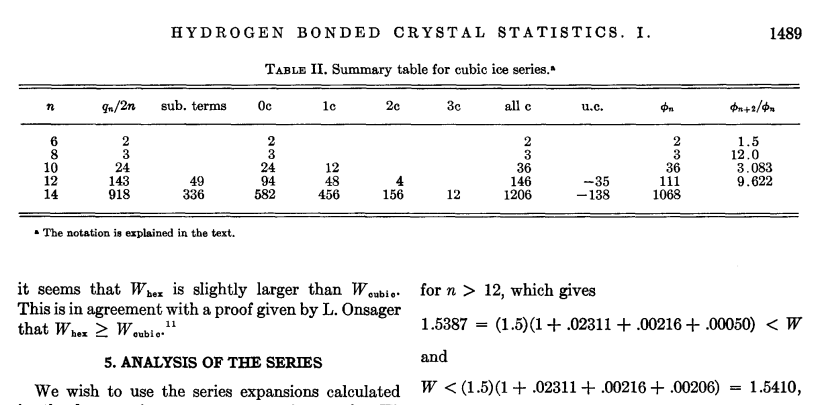
J. F. Nagle, J. Math. Phys. 7, (1966)
J. F. Nagle, J. Math. Phys. 7, (1966)
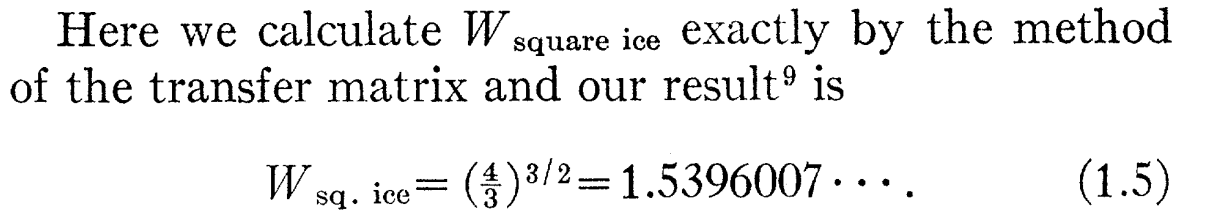
E. H. Lieb, PR 162, (1967)

J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Dual worm algorithm
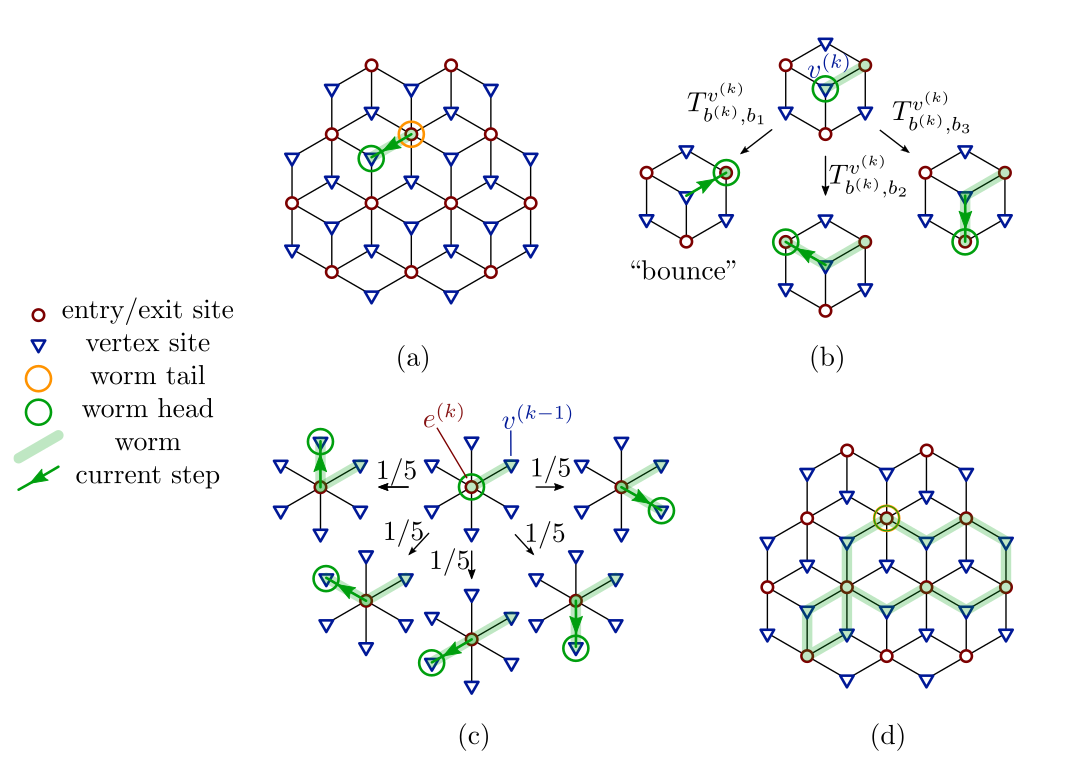
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
Linear program
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
1. A function computing A and b with the energy shift
2. A linear program solver

= Find one solution
= Find orthogonal solutions
If the energy is known
Linear program
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
1. A function computing A and b with the energy shift
2. A linear program solver

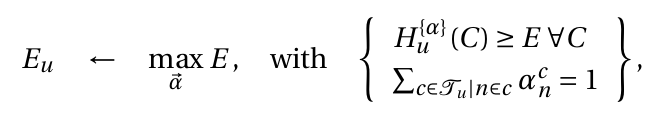
Start by calling the previous algorithm
call the previous algorithm
If the energy is not known
Linear program
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.
- For each configuration on the cluster
- going through the parameters/pairs
- The contribution to b is the pair interaction if the parameter is fixed
- If the parameter is free, then the contribution to A is the pair interaction.
- going through the parameters/pairs
Linear program
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.


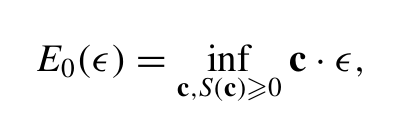
- Finite range frustration
- Existence of long-range frustration?
- Proving ground-state energies
Ronceray and Le Floch, PRE 100, (2019)
Finite range of frustration
J. Colbois
CMT SEMINAR, GÖTTINGEN, 06.2022 / TNS FOR FRUSTRATED ISING MODELS AND PARTIAL LIFTING OF GS DEG.