Studying frustrated Ising models
using tensor networks
MPQ Theory seminar
27.01.2021
Bram Vanhecke, Jeanne Colbois, Laurens Vanderstraeten, Frank Verstraete, Frédéric Mila, Phys. Rev. Research 3, 01304, 2021
MPQ Theory seminar - 27.01.2021

Plan
- Computing the residual entropy of (classical) frustrated systems
- Motivation: classical frustrated spin systems
- "Standard" TN formulation of partition functions
- Issues with the low temperature limit
- Solving the convergence problem of tensor networks on frustrated spin systems
- Finding the ground state local rule
- An example of ground state phase
MPQ Theory seminar - 27.01.2021
1
MPQ Theory seminar - 27.01.2021
Motivation
Frustrated models, residual entropies and methods to compute them
MPQ Theory seminar - 27.01.2021
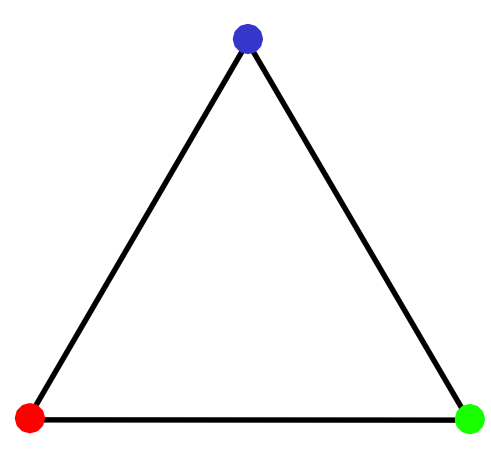
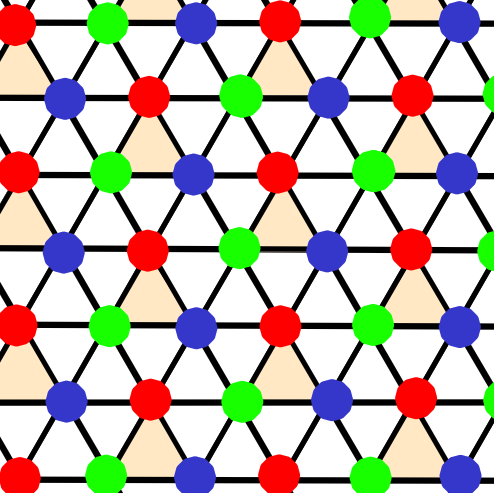
Nearest neighbour Ising antiferromagnet on the triangular lattice
2
We cannot minimize the Hamiltonian on each bond simultaneously
MPQ Theory seminar - 27.01.2021
Nearest neighbour Ising antiferromagnet on the triangular lattice


Wannier, Antiferromagnetism. The triangular Ising net. PR 79 1950 (Erratum PRB 7, 1973)
2
MPQ Theory seminar - 27.01.2021
Computing/estimating residual entropies
- Exactly solvable cases
- Mapping to free fermions, Kasteleyn's method, height mappings
- In further-neighbour models : integrable points, mapping to charge models
Baxter, Exactly solved models in statistical mechanics
3
MPQ Theory seminar - 27.01.2021
Computing/estimating residual entropies
- Exactly solvable cases
- Mapping to free fermions, Kasteleyn's method, height mappings
- In further-neighbour models : integrable points, mapping to charge models
- What about non-integrable models?
- Pauling estimates (entropy of ice)
- Monte Carlo simulations
- Tensor network contractions
Baxter, Exactly solved models in statistical mechanics
Pauling, J. Am. Chem. Soc. 57 , 1935
3
MPQ Theory seminar - 27.01.2021
Computing residual entropies
Using Monte Carlo simulations
4
MPQ Theory seminar - 27.01.2021
Computing residual entropies
Using Monte Carlo simulations
Difficulties
1. Critical slowing down, ergodicity
2. Thermodynamic integration
4
MPQ Theory seminar - 27.01.2021
Computing residual entropies
Using Monte Carlo simulations
Difficulties
1. Critical slowing down, ergodicity
2. Thermodynamic integration
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
Mizoguchi, Jaubert, Udagawa, PRL 119, 2017
4
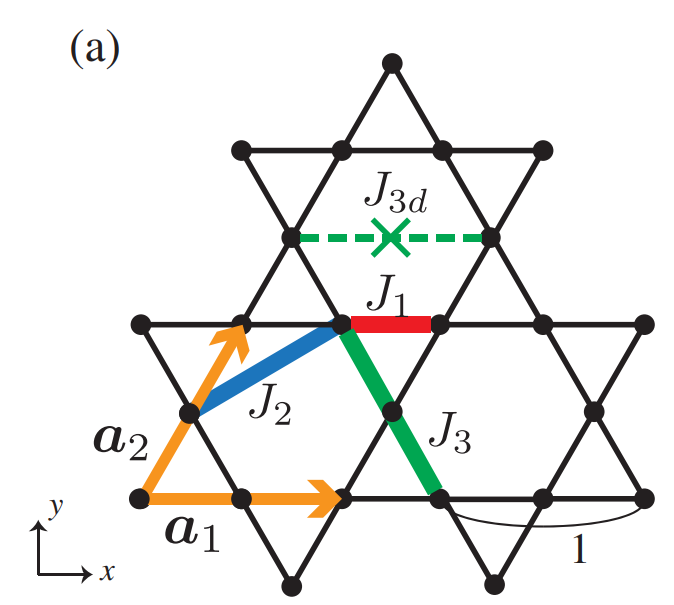
MPQ Theory seminar - 27.01.2021
Computing residual entropies
Using Monte Carlo simulations
Mizoguchi, Jaubert, Udagawa, PRL 119, 2017
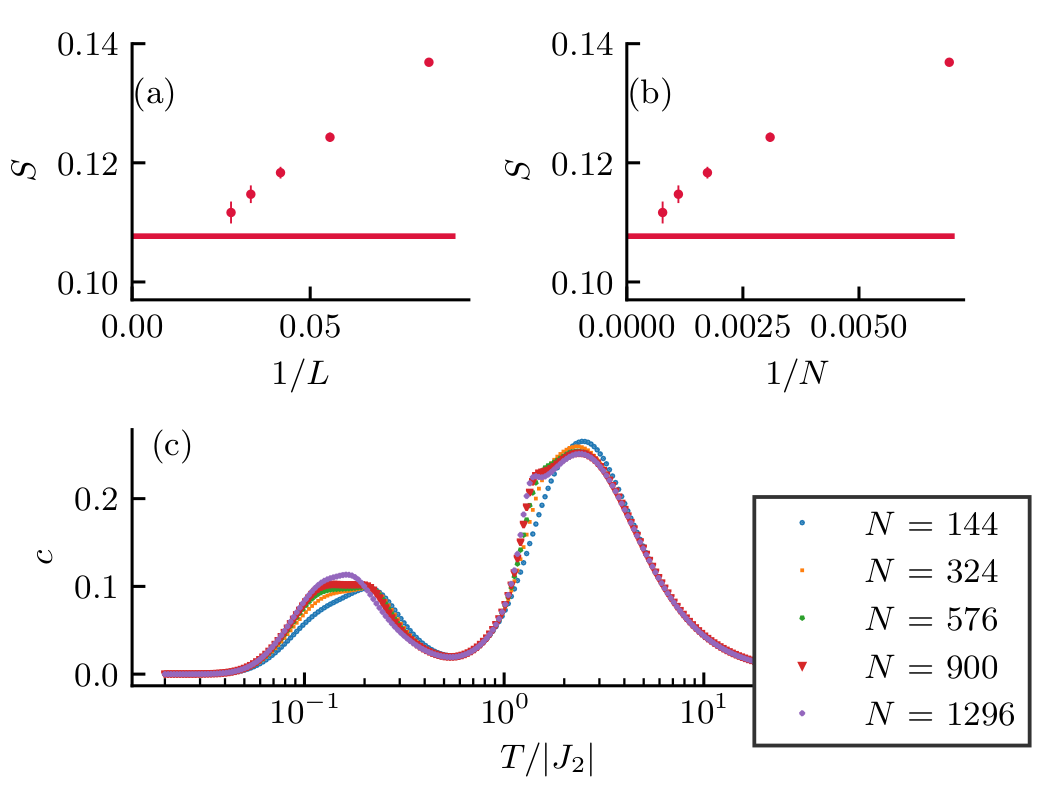
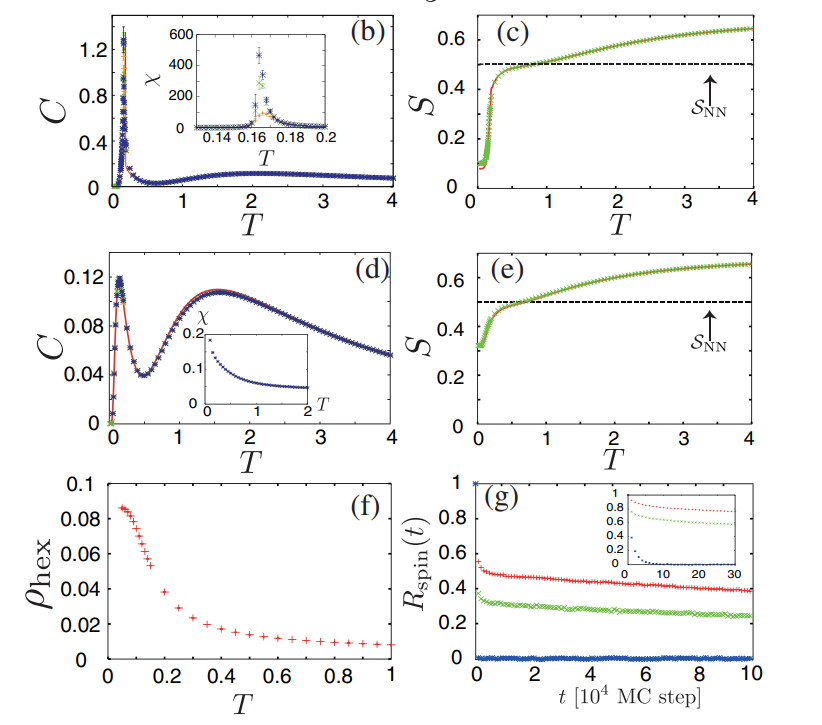


(2 digits)
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
5
MPQ Theory seminar - 27.01.2021
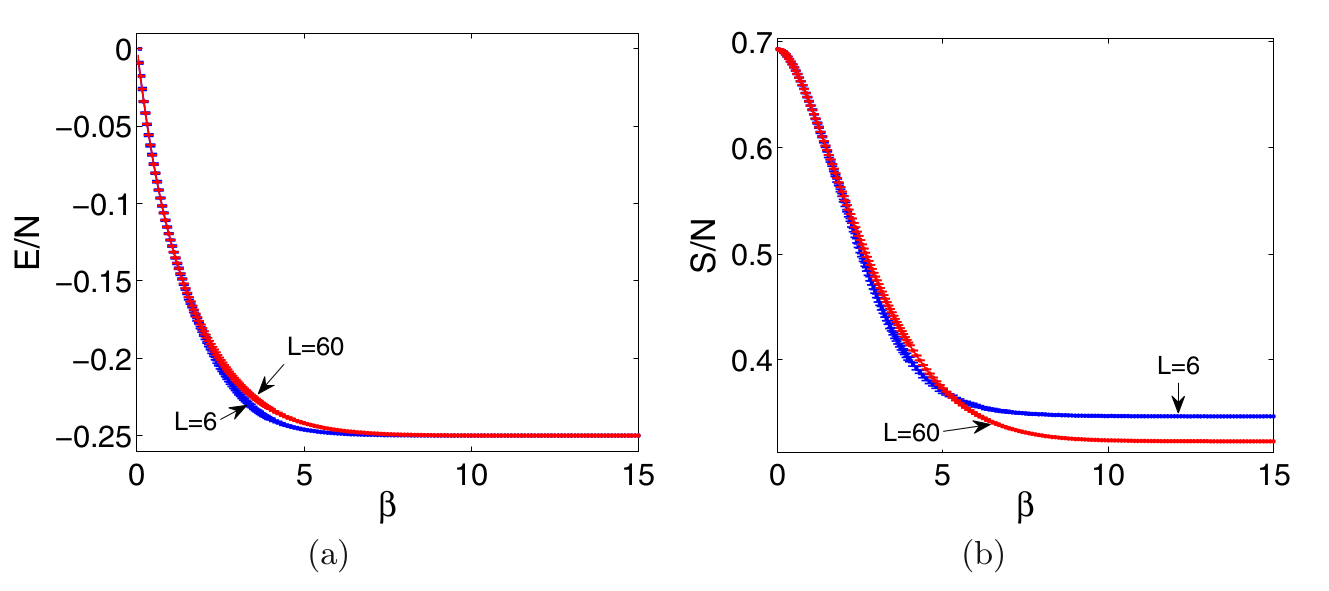
Computing residual entropies
Using Monte Carlo simulations
Zukovic, Eur. Phys. J. B, 2013
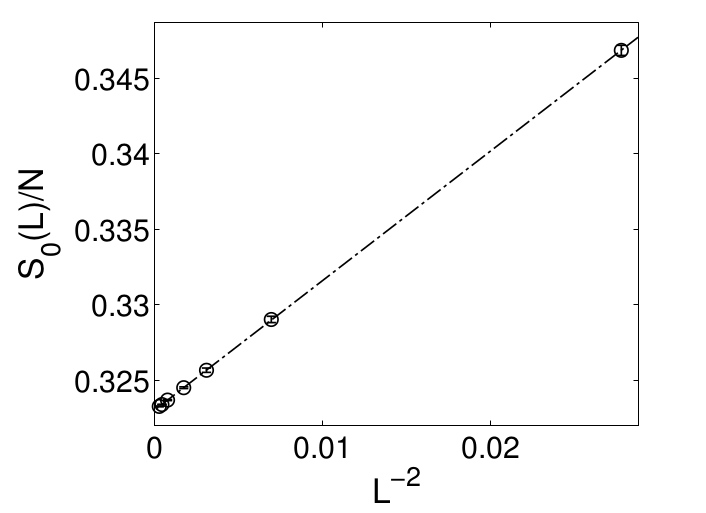
6
MPQ Theory seminar - 27.01.2021
Computing residual entropies
Using Monte Carlo simulations
Zukovic, Eur. Phys. J. B, 2013
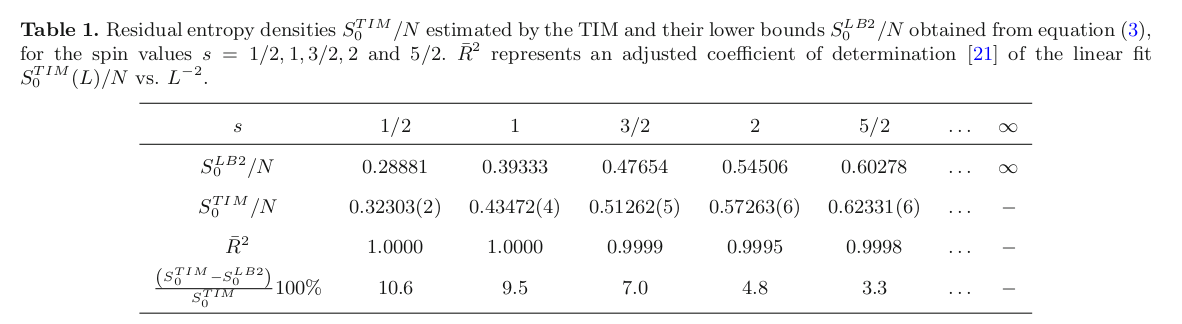
Wannier:
6
MPQ Theory seminar - 27.01.2021
Computing residual entropies
Using tensor networks and ground state local rules
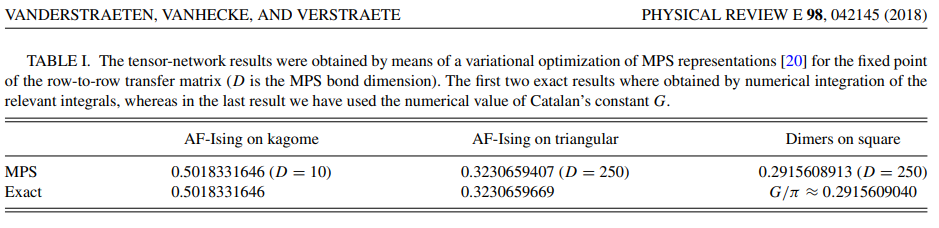
Vanderstraeten, Vanhecke, Verstraete, PRE 98, 2018
7
MPQ Theory seminar - 27.01.2021
Computing residual entropies
Using tensor networks and ground state local rules

TNs : 10 digits, vs 5 digits for MC
Vanderstraeten, Vanhecke, Verstraete, PRE 98, 2018
7
MPQ Theory seminar - 27.01.2021
Computing residual entropies
Using tensor networks and ground state local rules

No need to understand the whole temperature range to understand the ground state
Vanderstraeten, Vanhecke, Verstraete, PRE 98, 2018
TNs : 10 digits, vs 5 digits for MC
7
TN
"Standard" tensor network construction for partition functions
MPQ Theory seminar - 27.01.2021
MPQ Theory seminar - 27.01.2021
"Standard" construction
Partition functions of classical spin systems as a tensor network

Baxter, Exactly solved models in statistical mechanics;
Nishino, Okunishi, J. Phys. Soc. Jpn 65, 1996; Orús, Vidal, PRB 78, 2008;
Zhao, Xie, et. al. PRB 81, 2010; Xie, Chen et. al. PRB 86, 2012;
Zhu, Katzgraber, arXiv:1903.0772, 2019;
Nyckees, JC, Mila, arXiv:2008.08408, 2020
8
MPQ Theory seminar - 27.01.2021
"Standard" construction
Partition functions of classical spin systems as a tensor network


Baxter, Exactly solved models in statistical mechanics;
Nishino, Okunishi, J. Phys. Soc. Jpn 65, 1996; Orús, Vidal, PRB 78, 2008;
Zhao, Xie, et. al. PRB 81, 2010; Xie, Chen et. al. PRB 86, 2012;
Zhu, Katzgraber, arXiv:1903.0772, 2019;
Nyckees, JC, Mila, arXiv:2008.08408, 2020

8
MPQ Theory seminar - 27.01.2021
Contraction algorithms




1 + 1
2 D
CTMRG
TRG
iTEBD
VUMPS
Nishino, Okunishi, J. Phys. Soc. Jpn 65, 1996;
Levin, Nave, PRL 99, 2007
9
Orús, Vidal, PRB 78, 2008;
Zauner-Stauber et. al. PRB 97,2018; Fishman et. al PRB 98, 2018
MPQ Theory seminar - 27.01.2021
Contraction algorithms




1 + 1
2 D
CTMRG
TRG
iTEBD
VUMPS
Nishino, Okunishi, J. Phys. Soc. Jpn 65, 1996;
Levin, Nave, PRL 99, 2007
9
Orús, Vidal, PRB 78, 2008;
Zauner-Stauber et. al. PRB 97,2018; Fishman et. al PRB 98, 2018
MPQ Theory seminar - 27.01.2021
Contraction and leading eigenvalue
(1+1)D : Look for the leading eigenvector of the row-to-row transfer matrix


10
Haegeman, Verstraete, Annu. Rev. Condens. Matter Phys. 2017
MPQ Theory seminar - 27.01.2021
Contraction and leading eigenvalue
(1+1)D : Look for the leading eigenvector of the row-to-row transfer matrix


Just like in the 1D chain, because the partition function is the trace of the transfer matrix:
10
Haegeman, Verstraete, Annu. Rev. Condens. Matter Phys. 2017
Residual entropy from the leading eigenvalue
MPQ Theory seminar - 27.01.2021
11
Residual entropy from the leading eigenvalue
MPQ Theory seminar - 27.01.2021
11
Residual entropy from the leading eigenvalue
MPQ Theory seminar - 27.01.2021
11
Issues with taking the low temperature limit
MPQ Theory seminar - 27.01.2021
Non-frustrated models
(e.g. ferromagnet)
MPQ Theory seminar - 27.01.2021
12
Non-frustrated models
(e.g. antiferromagnet, square lattice)
MPQ Theory seminar - 27.01.2021
12
Triangular lattice Ising antiferromagnet
Kagome lattice Ising antiferromagnet
MPQ Theory seminar - 27.01.2021
13
Triangular lattice Ising antiferromagnet
Kagome lattice Ising antiferromagnet
MPQ Theory seminar - 27.01.2021
13
Why was that not a problem?
MPQ Theory seminar - 27.01.2021
Why was that not a problem?
... in general ...
MPQ Theory seminar - 27.01.2021
- It is a problem, e.g. in spin glasses
Wang, Qin, Zhou, PRB 90, 2014
Zhu, Katzgraber, arXiv:1903.07721, 2019
14
Why was that not a problem?
... in general ...
MPQ Theory seminar - 27.01.2021
- It is a problem, e.g. in spin glasses
Wang, Qin, Zhou, PRB 90, 2014
Zhu, Katzgraber, arXiv:1903.07721, 2019
2. The problem can be avoided when one knows how to write the partition function in a different way
Kramers, Wannier, PR 60, 1941; Wannier, PR 79 1950;
Kano, Naya, Prog. Theor. Phys. 10 , 1953
Levin, Nave, PRL 99, 2007
14
Why was that not a problem?
... in general ...
MPQ Theory seminar - 27.01.2021
- It is a problem, e.g. in spin glasses
Wang, Qin, Zhou, PRB 90, 2014
Zhu, Katzgraber, arXiv:1903.07721, 2019
2. The problem can be avoided when one knows how to write the partition function in a different way
Kramers, Wannier, PR 60, 1941; Wannier, PR 79 1950;
Kano, Naya, Prog. Theor. Phys. 10 , 1953
Levin, Nave, PRL 99, 2007
=> First build a tensor network which describes the ground states and can be contracted
14
MPQ Theory seminar - 27.01.2021
Can we just split the Hamiltonian differently?
15
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, 1969;
M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , 1975;
B. Sriram Shastry and B. Sutherland, Physica 108 B+C, 1981;
W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, 2016;
Z. Wang, M. Navascues, Proc. Roy. Soc. A 474, 2018
Splitting the Hamiltonian
... on the triangular lattice
MPQ Theory seminar - 27.01.2021
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
16
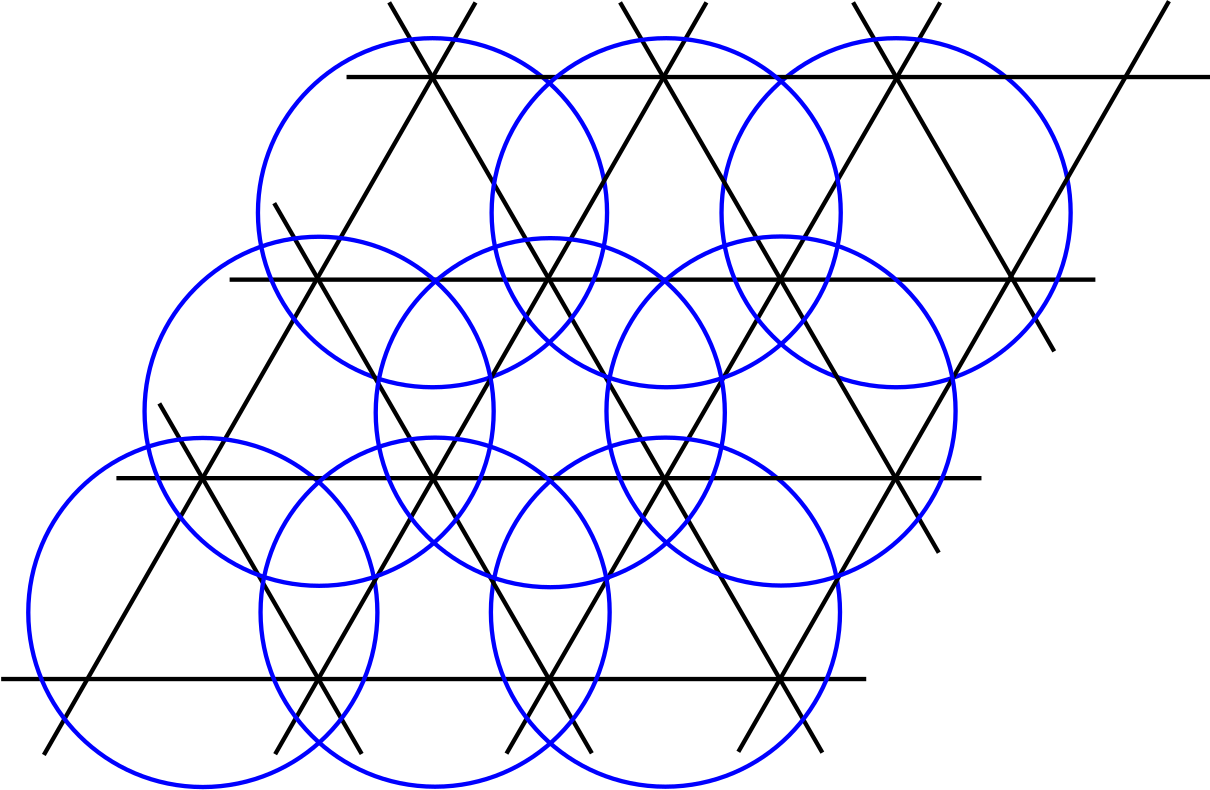
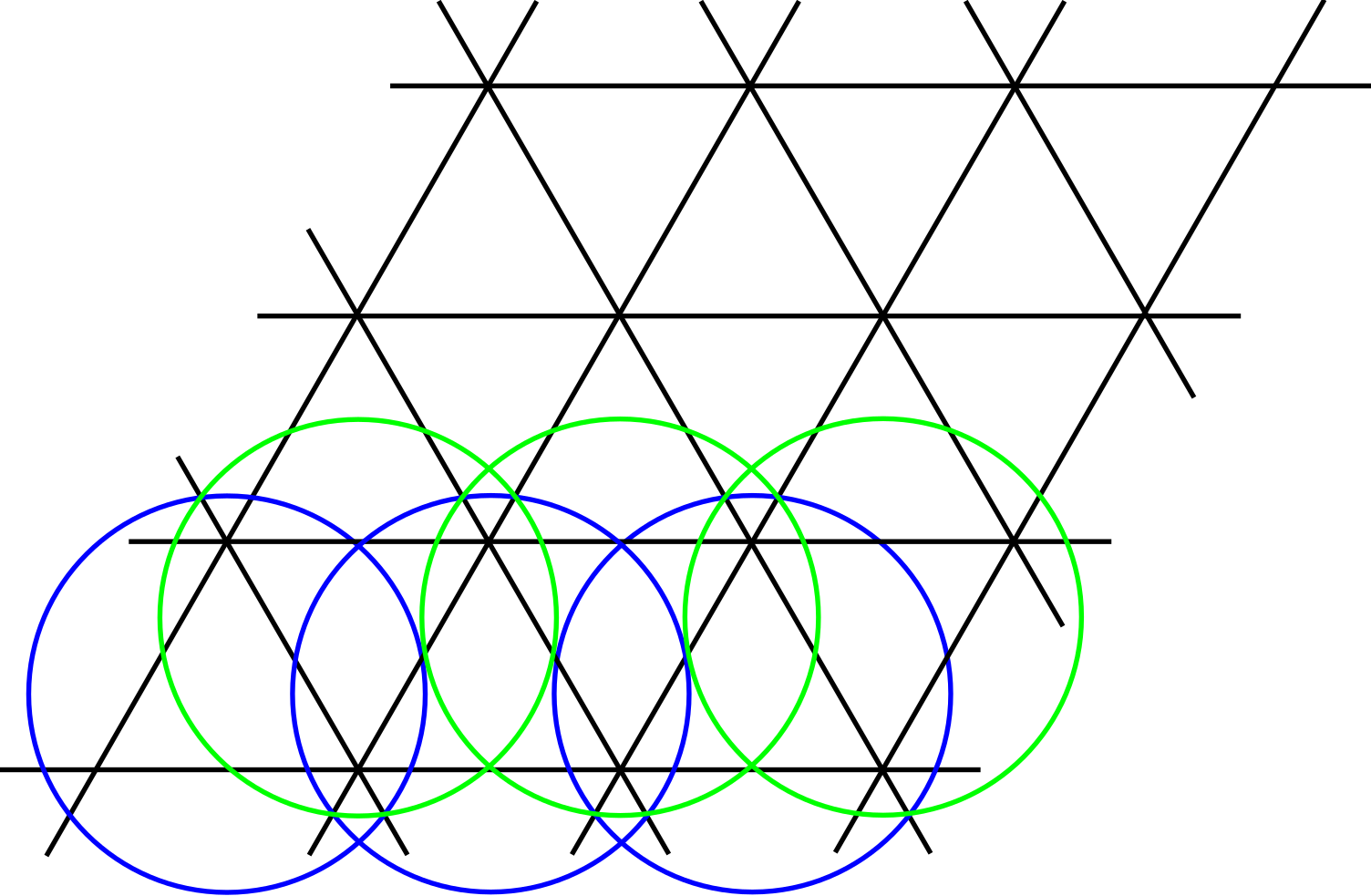
Splitting the Hamiltonian
... on the triangular lattice
MPQ Theory seminar - 27.01.2021
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
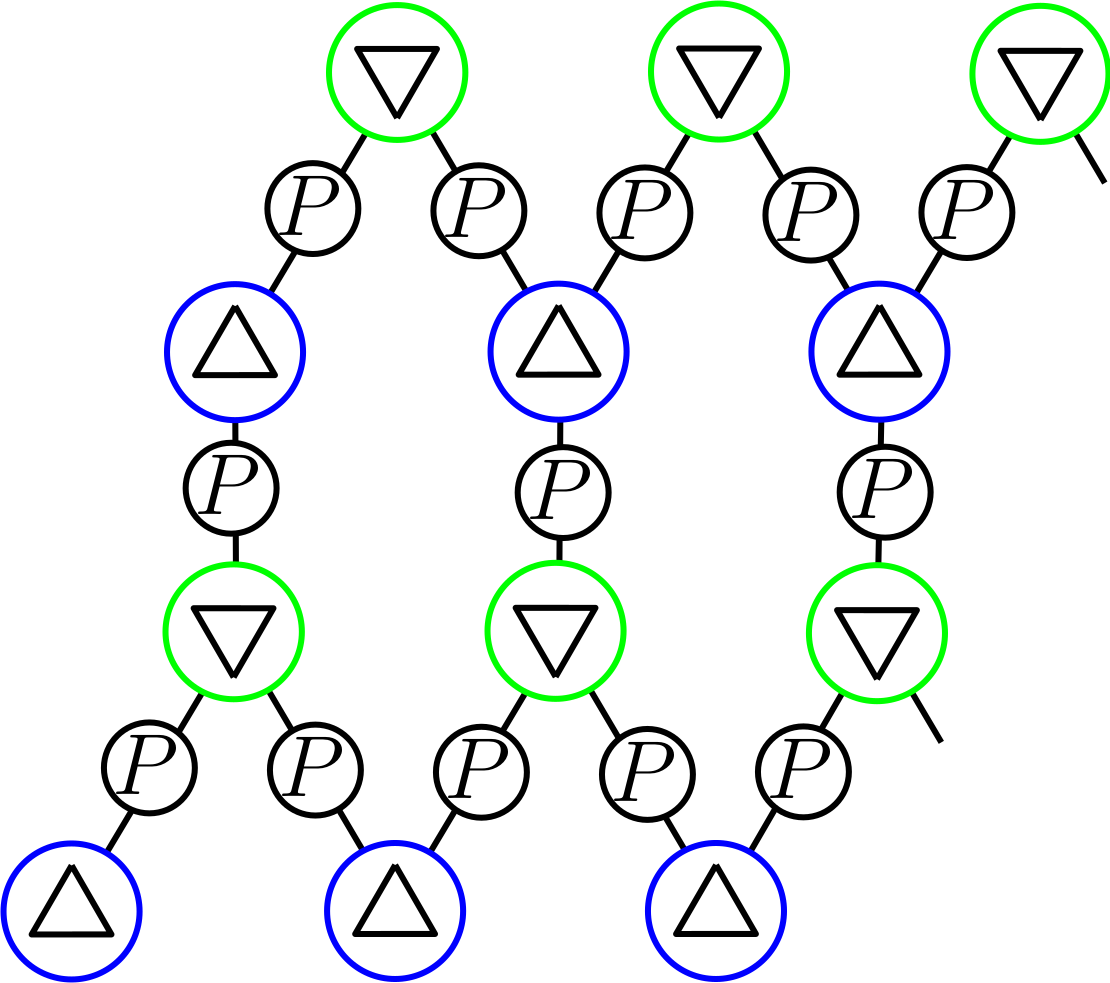
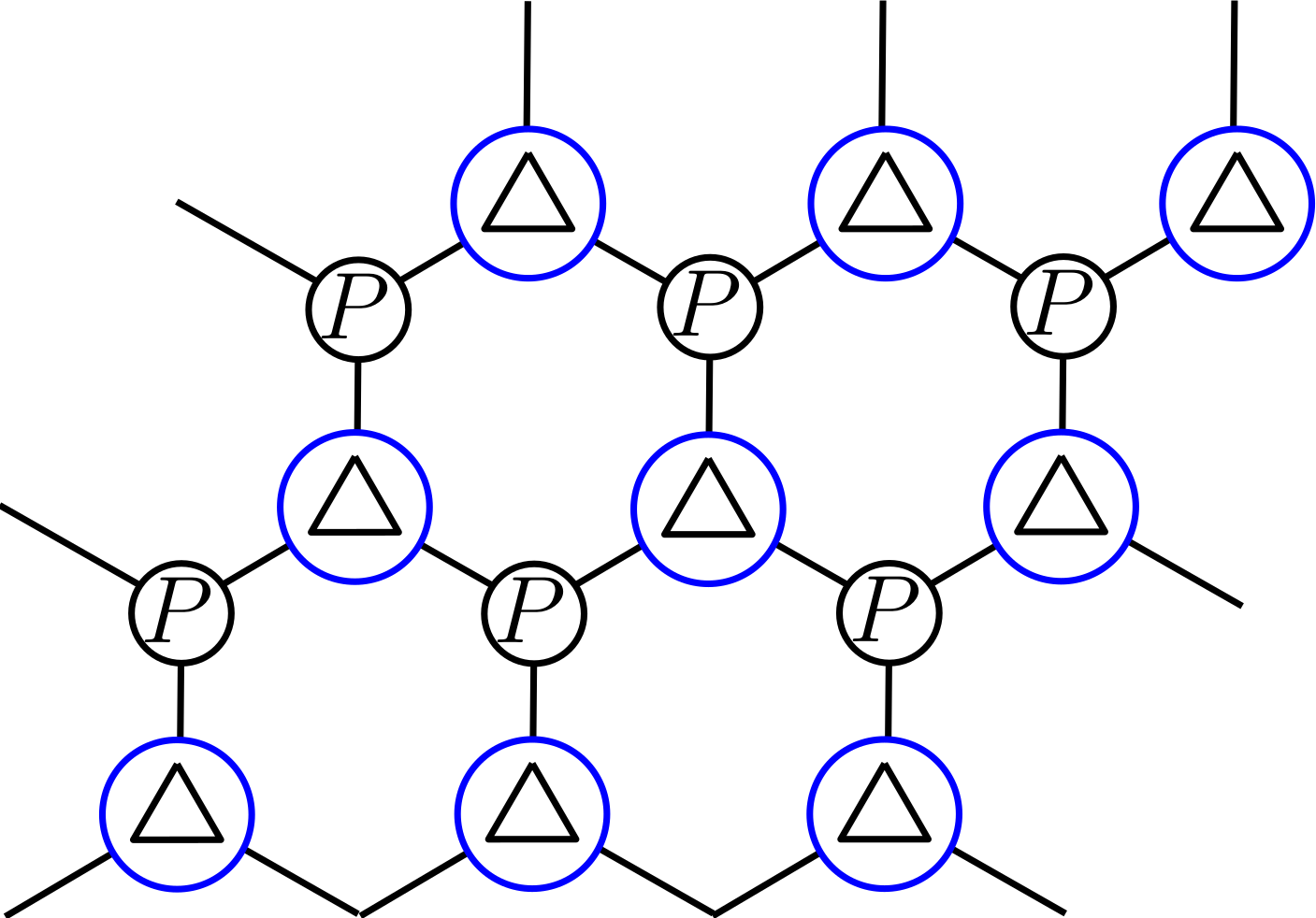
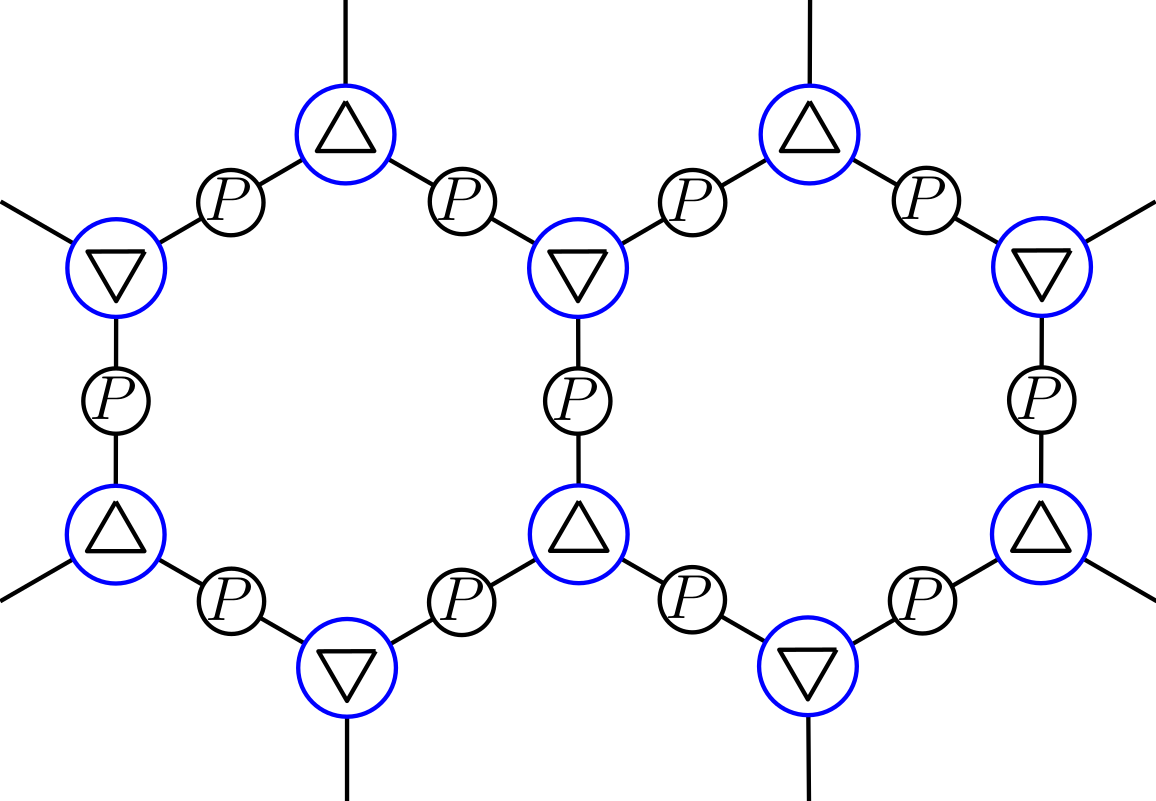
G.S. configurations

Delta tensor with bond dimension 6
16
Splitting the Hamiltonian
... on the triangular lattice
MPQ Theory seminar - 27.01.2021
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021



Spins must match

G.S. configurations
16
Splitting the Hamiltonian
... on the triangular lattice
MPQ Theory seminar - 27.01.2021
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
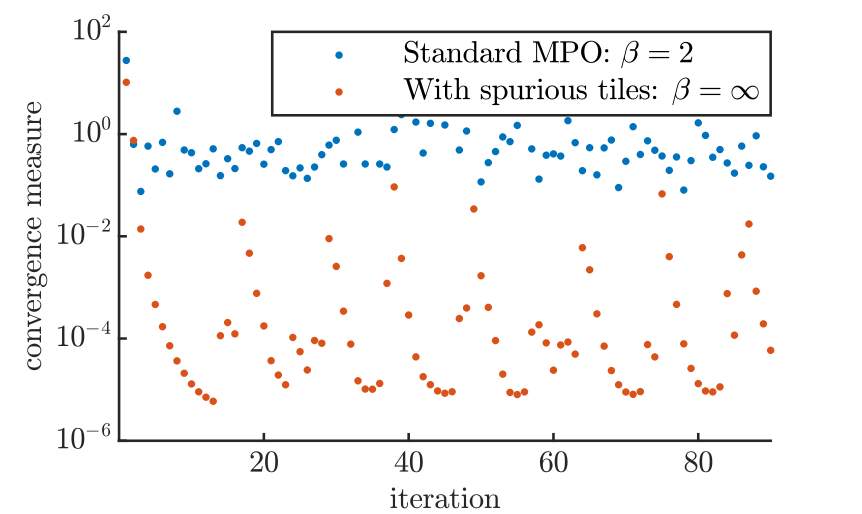
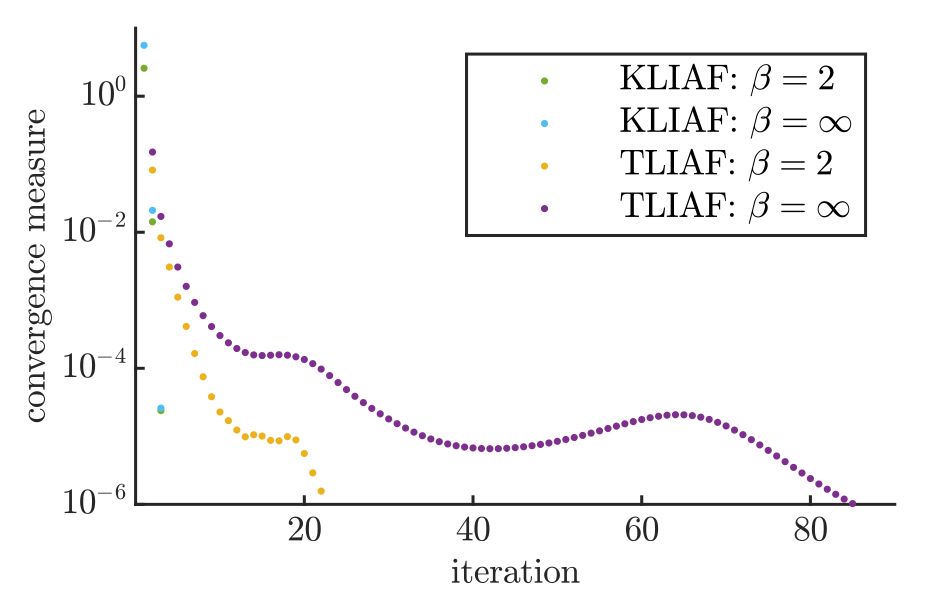
17
How come?
MPQ Theory seminar - 27.01.2021
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
What happens to configurations where a down triangle is ferromagnetic?
18
How come?
MPQ Theory seminar - 27.01.2021
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
What happens to configurations where a down triangle is ferromagnetic?

The local rule is imposed locally
18
How come?


MPQ Theory seminar - 27.01.2021
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
What happens to configurations where a down triangle is ferromagnetic?
The local rule is imposed locally
The local rule has to be computed
18
MPQ Theory seminar - 27.01.2021
Can we perform this splitting in a systematic way?
Huang, et al., Phys. Rev. B 94, 2016
Proving the ground state energies of generalized Ising models
MPQ Theory seminar - 27.01.2021
Side question: can we detect problematic cases without prior knowledge of the model?
Can we perform this splitting in a systematic way?
Huang, et al., Phys. Rev. B 94, 2016
Proving the ground state energies of generalized Ising models
Splitting the Hamiltonian
MPQ Theory seminar - 27.01.2021


19
Splitting the Hamiltonian
MPQ Theory seminar - 27.01.2021

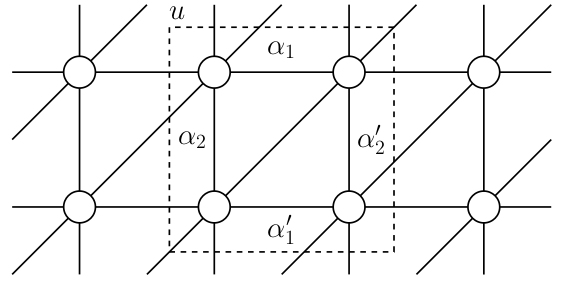
Select a cluster, with which one can tile the lattice with overlaps
19
Splitting the Hamiltonian
MPQ Theory seminar - 27.01.2021


For each bond, a set of weight describes how to split it among the clusters
19
Splitting the Hamiltonian
MPQ Theory seminar - 27.01.2021


For each bond, a set of weight describes how to split it among the clusters
19
Splitting the Hamiltonian
MPQ Theory seminar - 27.01.2021


20
Splitting the Hamiltonian
MPQ Theory seminar - 27.01.2021


20
Ground state lower bounds
MPQ Theory seminar - 27.01.2021
21
Ground state lower bounds
MPQ Theory seminar - 27.01.2021
For a given cluster and weights, the
local ground state energy imposes a
lower bound
on the global g.s. energy (per cluster)
21
Ground state lower bounds
MPQ Theory seminar - 27.01.2021
For a given cluster and weights, the
local ground state energy imposes a
lower bound
on the global g.s. energy (per cluster)
21
Restricting the weights
MPQ Theory seminar - 27.01.2021
22
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021



Getting the ground state entropy
We have a g.s. energy lower bound, what if it is saturated?
MPQ Theory seminar - 27.01.2021
23
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
Getting the ground state entropy
We have a g.s. energy lower bound, what if it is saturated?
MPQ Theory seminar - 27.01.2021
realize the g.s. energy
All the local cluster Hamiltonians can be minimised simultaneously
23
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
Getting the ground state entropy
We have a g.s. energy lower bound, what if it is saturated?
MPQ Theory seminar - 27.01.2021
The frustration is "relaxed"
realize the g.s. energy
All the local cluster Hamiltonians can be minimised simultaneously
23
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
Getting the ground state entropy
We have a g.s. energy lower bound, what if it is saturated?
ALL the ground states are described as tilings of the local g.s. configurations
MPQ Theory seminar - 27.01.2021
The frustration is "relaxed"
realize the g.s. energy
All the local cluster Hamiltonians can be minimised simultaneously
(Local rule; vertex model)

23
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
What happened in the triangular case?

MPQ Theory seminar - 27.01.2021
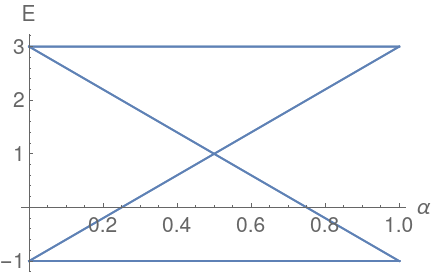
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
24
What happened in the triangular case?

MPQ Theory seminar - 27.01.2021


Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
24
What happened in the triangular case?

MPQ Theory seminar - 27.01.2021



Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
24
What happened in the triangular case?

MPQ Theory seminar - 27.01.2021




Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
24
What happened in the triangular case?

MPQ Theory seminar - 27.01.2021



On the boundary : additional "spurious" tiles. Always select weights in the interior.
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
24
Selecting the weights
- We are trying to maximize a function under linear constraints
- Linear programming
- With this we can find weights in the interior of the set of weights which maximise the g.s. energy lower bound.
- Systematically try clusters

MPQ Theory seminar - 27.01.2021
(Credit goes fully to Bram Vanhecke)
25
Once you have the tiles...
- Tensor network based on the g.s. local rule
- bond tensors which impose overlapping spins to match
MPQ Theory seminar - 27.01.2021

Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
26
Once you have the tiles...
- Tensor network based on the g.s. local rule
- bond tensors which impose overlapping spins to match
Bond dimension?
- # local g.s.?
- Actually, P matrices are rank-deficient : SVD and group, much lower bond dimension
- Note that Ps are typically not symmetric

MPQ Theory seminar - 27.01.2021

Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
26
Proving the g.s. energy
Rigorously:
1. Find an upper bound, or
2. Find a state with the lower bound energy, or
3. Show that the tiles in can tile the lattice
Z. Wang, M. Navascues, Proc. Roy. Soc. A 474, (2018)
W. Huang, D. A. Kitchaev, S. T. Dacek et. al. , Phys. Rev. B 94, (2016)
MPQ Theory seminar - 27.01.2021
27
An example
Further neighbour model on the kagome lattice
MPQ Theory seminar - 27.01.2021
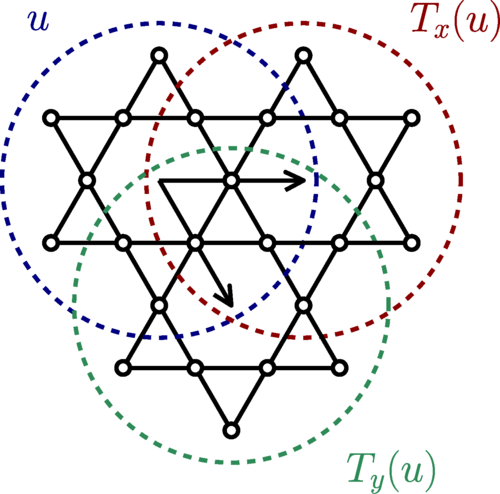
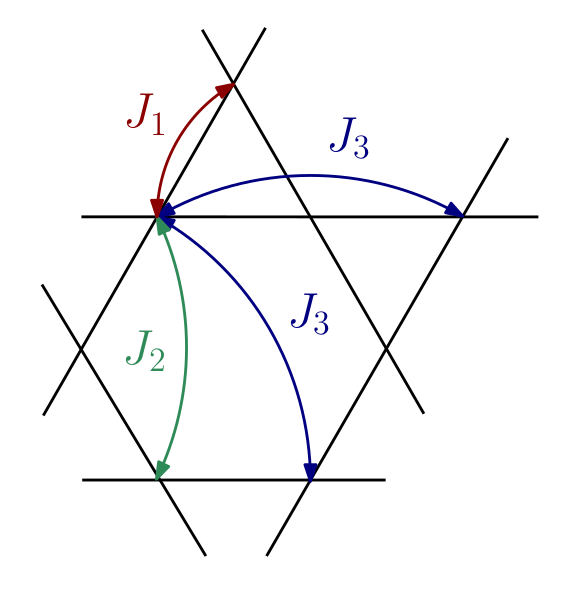
A further neighbour model on the kagome lattice
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
MPQ Theory seminar - 27.01.2021

28
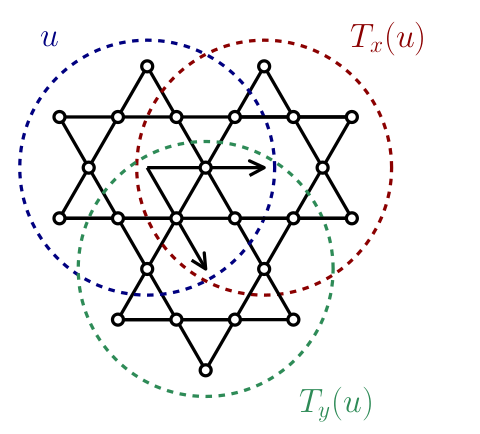
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
A further neighbour model on the kagome lattice
MPQ Theory seminar - 27.01.2021
28
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
A further neighbour model on the kagome lattice
MPQ Theory seminar - 27.01.2021

132 G.S. tiles
Bond dimension 18
28
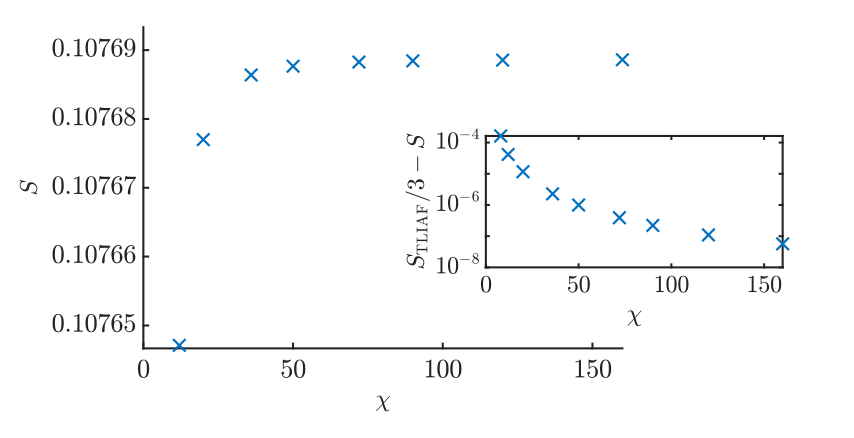
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
A further neighbour model on the kagome lattice
MPQ Theory seminar - 27.01.2021
29
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
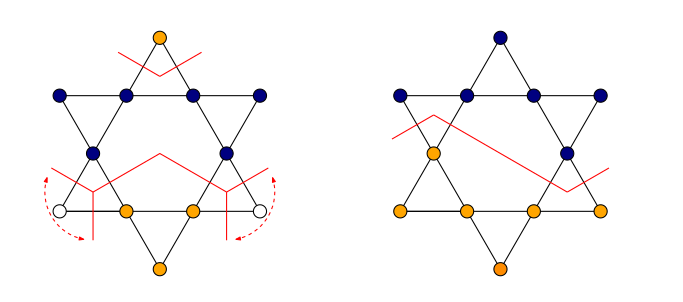
A further neighbour model on the kagome lattice
MPQ Theory seminar - 27.01.2021
30
Type I
Type II

Type I
Type II
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
A further neighbour model on the kagome lattice
MPQ Theory seminar - 27.01.2021
30

Only type I tiles
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
A further neighbour model on the kagome lattice
MPQ Theory seminar - 27.01.2021
31
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
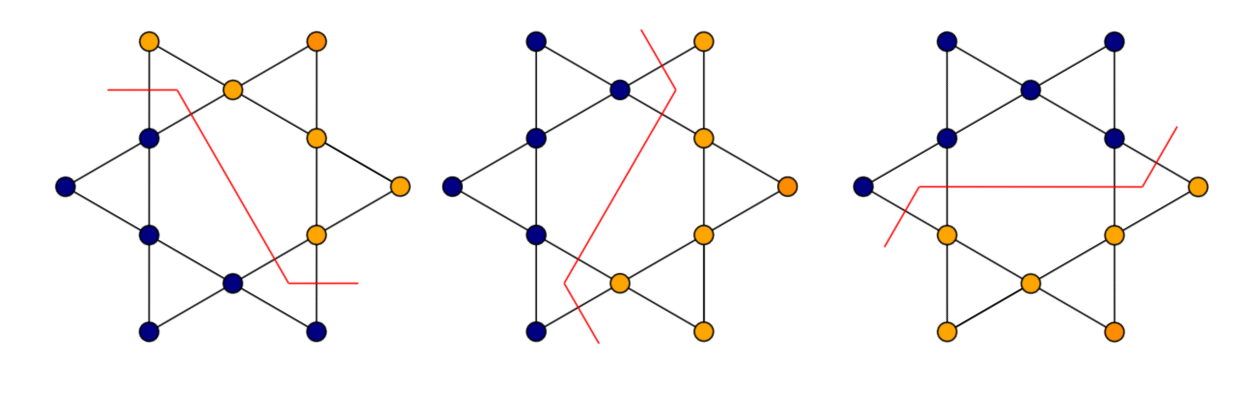
A further neighbour model on the kagome lattice
MPQ Theory seminar - 27.01.2021
32
Type I
Type II
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
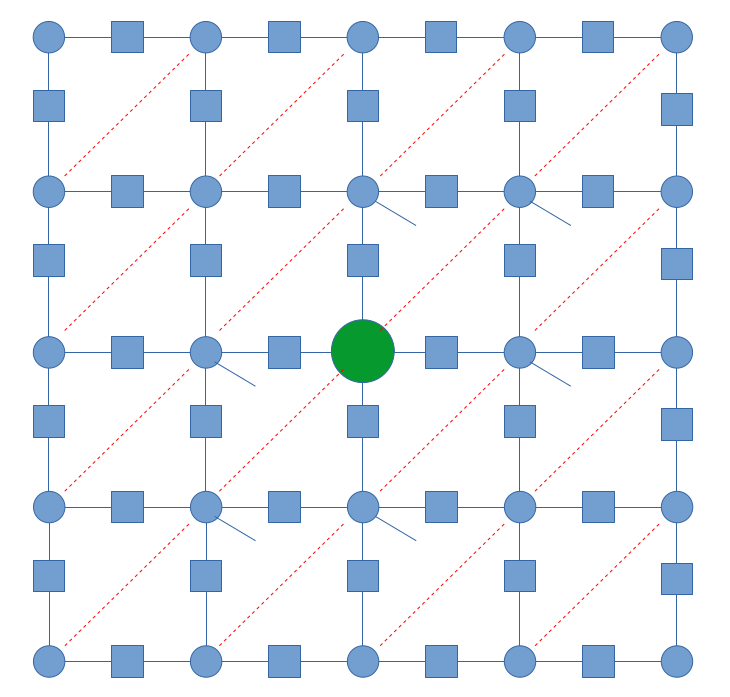
A further neighbour model on the kagome lattice
MPQ Theory seminar - 27.01.2021
33
Type I
Type II
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
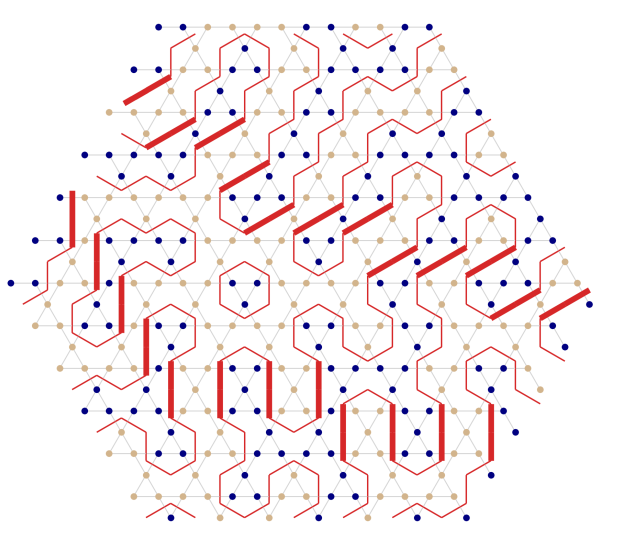
A further neighbour model on the kagome lattice
MPQ Theory seminar - 27.01.2021
34
Conclusion
Facilitates a quick exploration of ground state phases (on top of the ground state energy).
1. Allows extremely precise extraction of the residual entropy with very limited computational effort
2. Tiles and exact contractions allow for some understanding
MPQ Theory seminar - 27.01.2021
35
Conclusion
Facilitates a quick exploration of ground state phases (on top of the ground state energy).
1. Allows extremely precise extraction of the residual entropy with very limited computational effort
2. Tiles and exact contractions allow for some understanding
Maps frustrated problems onto tiling problems
1. Question of the existence of the scale at which frustration is relaxed
2. Still have to explore how this mapping could help through well-studied questions on tilings.
MPQ Theory seminar - 27.01.2021
35
Conclusion
Facilitates a quick exploration of ground state phases (on top of the ground state energy).
1. Allows extremely precise extraction of the residual entropy with very limited computational effort
2. Tiles and exact contractions allow for some understanding
Maps frustrated problems onto tiling problems
1. Question of the existence of the scale at which frustration is relaxed
2. Still have to explore how this mapping could help through well-studied questions on tilings.
MPQ Theory seminar - 27.01.2021
Alternative approaches?
1. Tropical tensor networks: Jin-Guo Liu, Lei Wang, and Pan Zhang, arXiv:2008.06888
2. A systematic way of making the MPO hermitian?
35
Acknowledgments
MPQ Theory seminar - 27.01.2021
Bram Vanhecke
Laurens Vanderstraeten, Frank Verstraete,
Frédéric Mila
Thank you for your attention!
Manuel Stathis, Patrick Emonts, Mithilesh Nayak, Jonathan D'Emidio
(And the Centro de ciencias de Benasque Pedro Pascual)
Discussions:
Collaborators:
Finite temperature
MPQ Theory seminar - 27.01.2021
Linear programming ideas
- Linear program gives extreme points, i.e. get weights on the boundary
- So instead find an interior simplex of the same dimension as A
- Find a point in the interior of A
- Number of constraints exponential in number of sites
- Incoroporate only useful ones

MPQ Theory seminar - 27.01.2021
(Credit goes fully to Bram Vanhecke)
1. Type-II tiles can connect reflection-symmetry-broken sectors
2. Each type-II tile has to have exactly two neighbours of the same sub-type (can have of other sub-type)
3. No sharp angles (only straight or 120°)
4. No way to go back
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
More about the type-II tiles
MPQ Theory seminar - 27.01.2021
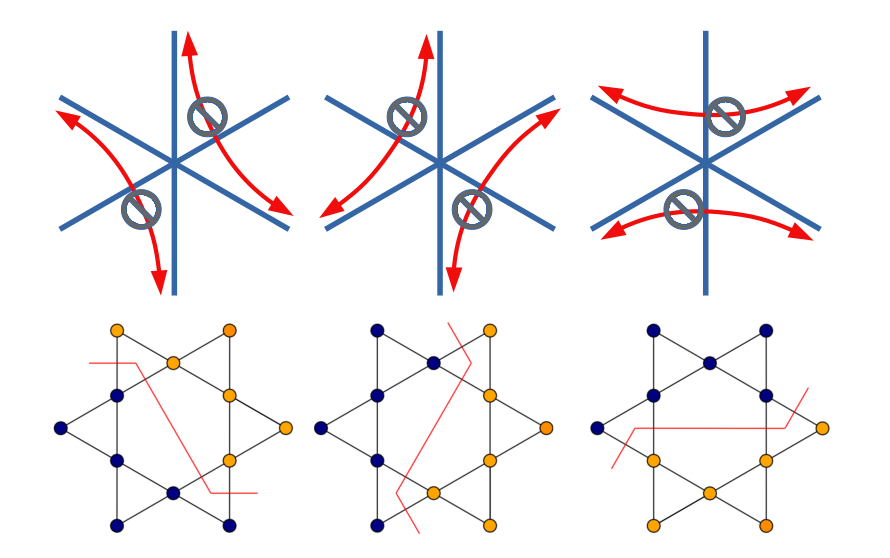
Unending strings separating symmetry-broken sectors
Idea used in the classical context:
Inequalities based on a systematic splitting of the Hamiltonian
M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , 1975
Finding ground states of generalised Ising models
W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, 2016
Exact results for square lattice Ising models
Z. Wang, M. Navascues, Proc. Roy. Soc. A 474, 2018
(and many more)
Splitting the Hamiltonian to learn about ground states
MPQ Theory seminar - 27.01.2021
Idea used in the quantum context:
Exact ground state in the J1-J2, spin-1/2 Heisenberg chain (Majumdar-Ghosh point)
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, 1969
Eigenstate in the Shastry-Sutherland model (for small J'/J)
B. Sriram Shastry and B. Sutherland, Physica 108 B+C, 1981
(and many more)
Splitting the Hamiltonian to learn about ground states
MPQ Theory seminar - 27.01.2021
Proving the g.s. energy
- Numerical evidence -
Consider the "partition function" at zero temperature
- If one cannot make a ground state, then the partition function is zero
- Reciprocally, if the exact leading eigenvalue is 1 or larger, then the tiles can be combined into a state
- Approximate contraction = numerical evidence of tiling
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
MPQ Theory seminar - 27.01.2021
Proving the g.s. energy
- Numerical evidence -
Cases
1. The approximate contraction converges consistently to a leading eigenvalue which is 1 or larger
2. The approximate contraction converges only for some bond dimensions
3. The approximate contraction does not converge
MPQ Theory seminar - 27.01.2021
Remark on tilings
Given a Hamiltonian and a cluster, we have a tiling rule (corresponding to the maximal lower bound).
1. Does it have a solution, i.e. does it admit a tiling?
2. Does it admit a periodic tiling, or only non-periodic ones?
The first problem is undecidable. It relates to the undecidability of the energy problem in 2D (Wang, Navascues 2017)

Fh, Fv associate an energy to the bonds.
They correspond to our bond P tensors here.
Z. Wang, M. Navscues, Proc. Roy. Soc. A 474, (2018)
MPQ Theory seminar - 27.01.2021
Remark on tilings
Given only the Hamiltonian
1. Does it admit a cluster which gives rise to a solvable tiling rule?
2. Does it admit a cluster whose tiling rule admits periodic tilings?
And for the approximate contractions:
How do the algorithms react if given a rule for aperiodic tilings? What if only some of the tilings corresponding to the rule are periodic?
MPQ Theory seminar - 27.01.2021

Experimental motivations
MPQ Theory seminar - 27.01.2021

Chioar,et. al. PRB 90, 2014
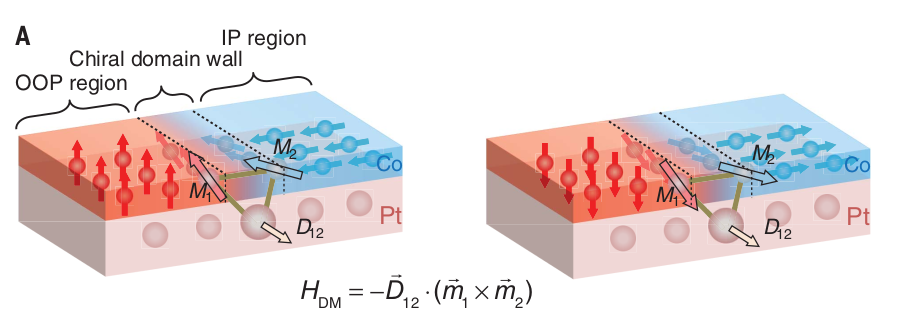
Luo et. al. , Science 363, 2019
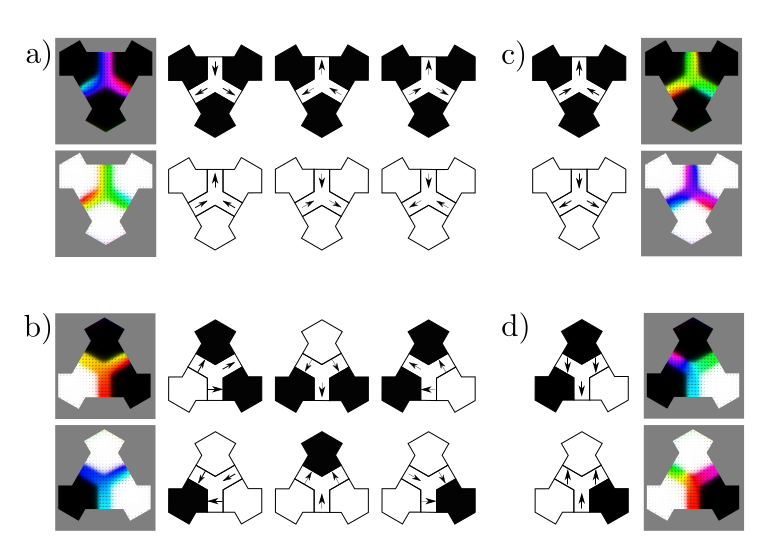
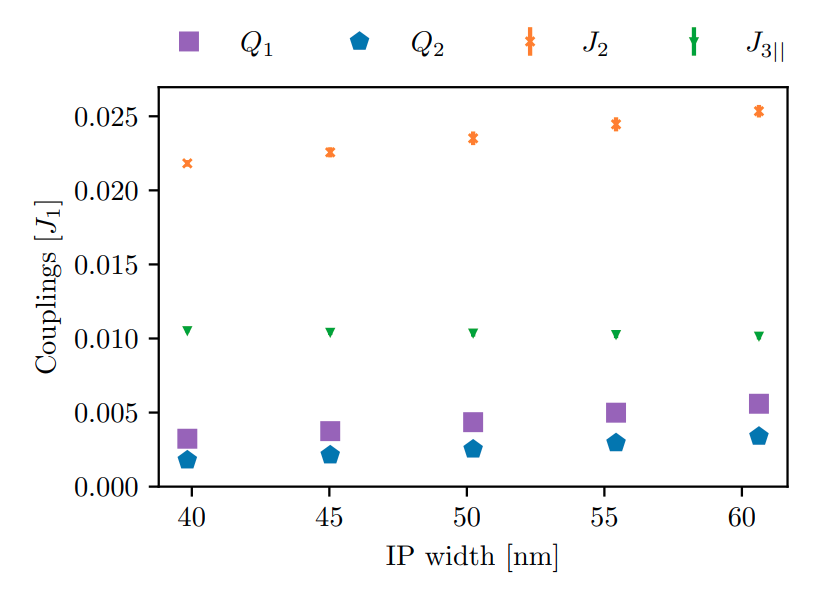
JC et. al. , In preparation
MPQ Theory seminar - 27.01.2021
Why was that not a problem?
... on the kagome lattice
MPQ Theory seminar - 27.01.2021
Kano, Naya, Prog. Theor. Phys. 10 , 1953
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
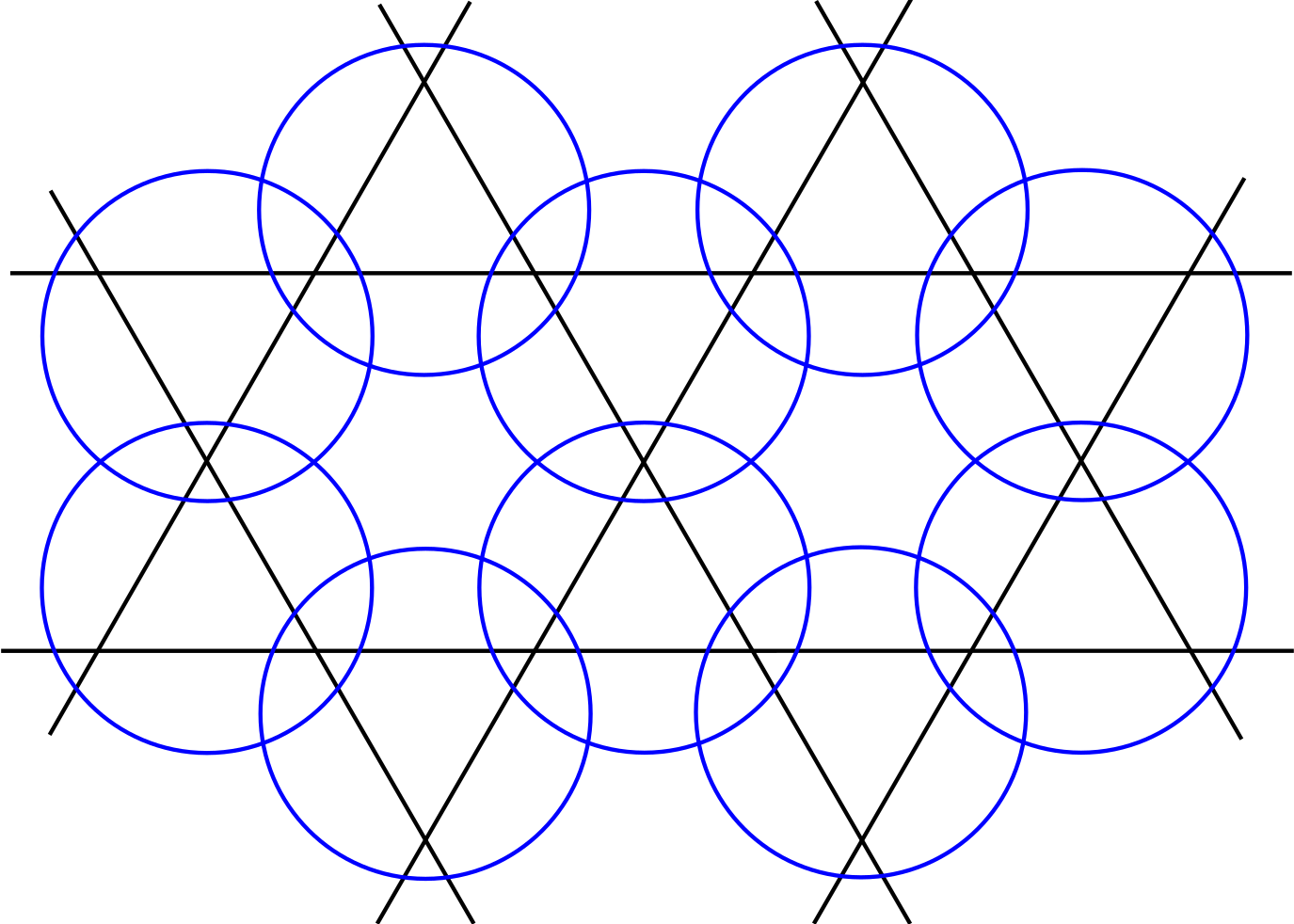
Why was that not a problem?
... on the kagome lattice
MPQ Theory seminar - 27.01.2021
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021



G.S. configurations
Spins must match
Why was that not a problem?
... on the kagome lattice
MPQ Theory seminar - 27.01.2021


G.S. configurations
Spins must match
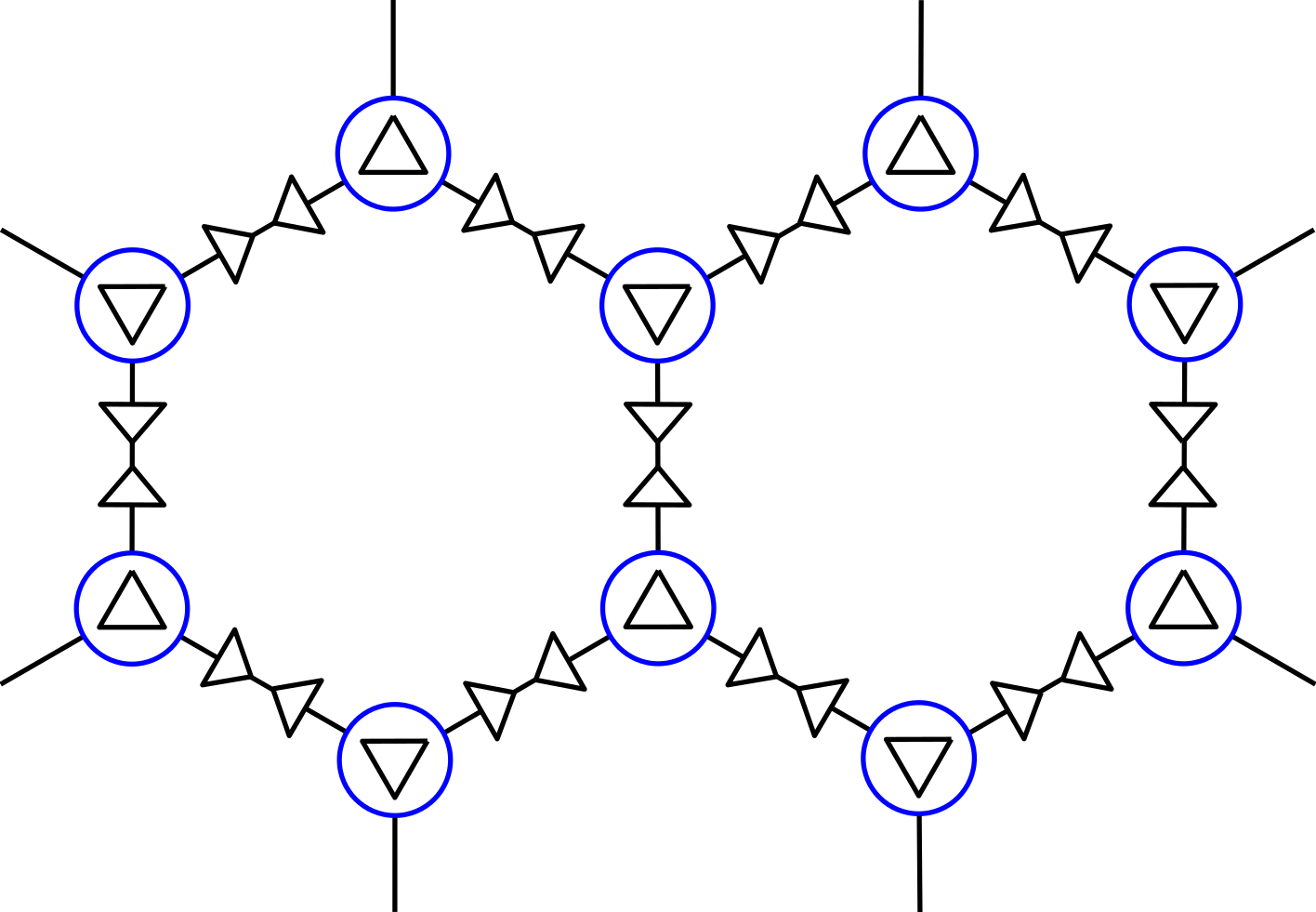
Vanhecke, JC, Vanderstraeten, Verstraete, Mila, PRR 3, 2021
MPQ Theory seminar - 27.01.2021
1D Ising model, transfer matrix and TN

Your statistical physics lecture, or Baxter's Exactly solved models in statistical mechanics
MPQ Theory seminar - 27.01.2021
1D Ising model, transfer matrix and TN

Your statistical physics lecture, or Baxter's Exactly solved models in statistical mechanics
MPQ Theory seminar - 27.01.2021
1D Ising model, transfer matrix and TN

Your statistical physics lecture, or Baxter's Exactly solved models in statistical mechanics
1D Ising model, transfer matrix and TN
Your statistical physics lecture, or Baxter's Exactly solved models in statistical mechanics

MPQ Theory seminar - 27.01.2021
MPQ Theory seminar - 27.01.2021
"Standard" construction
Partition functions of classical spin systems as a tensor network

MPQ Theory seminar - 27.01.2021
"Standard" construction
Partition functions of classical spin systems as a tensor network


MPQ Theory seminar - 27.01.2021
"Standard" construction
Partition functions of classical spin systems as a tensor network


MPQ Theory seminar - 27.01.2021
"Standard" construction
Partition functions of classical spin systems as a tensor network


MPQ Theory seminar - 27.01.2021
"Standard" construction
Partition functions of classical spin systems as a tensor network

Discussion on VUMPS
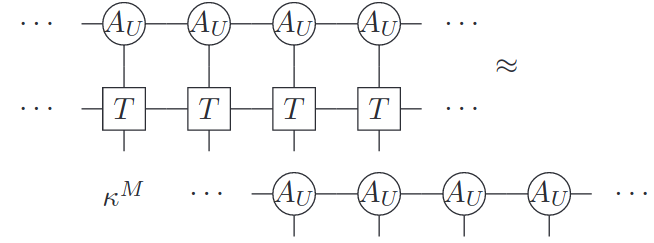
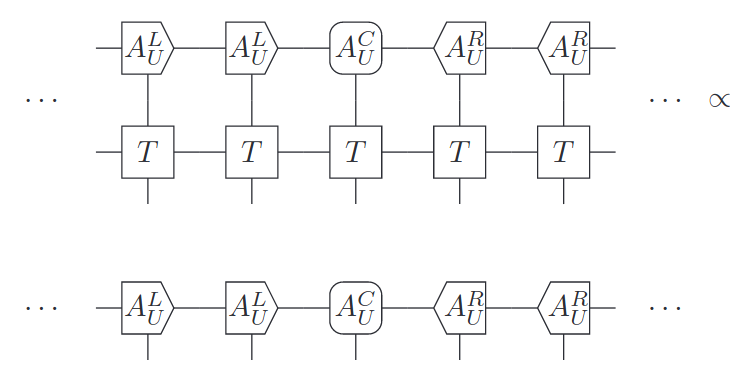
MPQ Theory seminar - 27.01.2021
Discussion on VUMPS


MPQ Theory seminar - 27.01.2021
Discussion on VUMPS

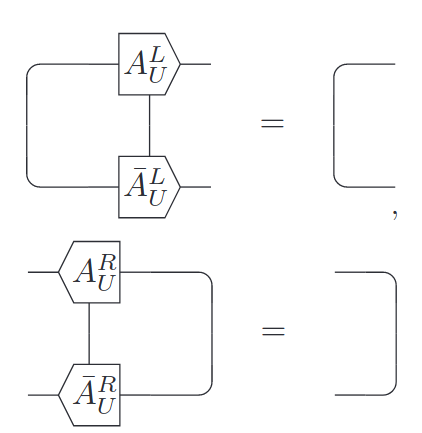
MPQ Theory seminar - 27.01.2021
Discussion on VUMPS
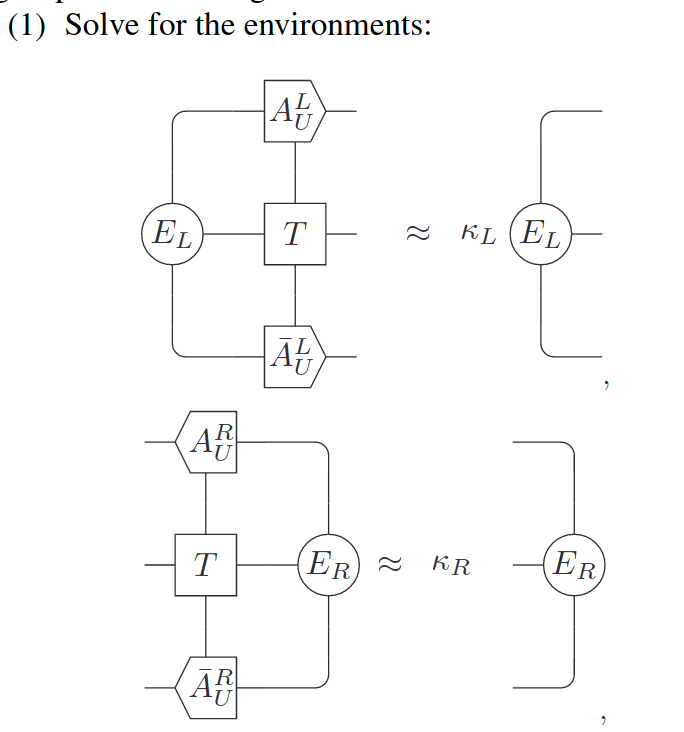
MPQ Theory seminar - 27.01.2021
Discussion on VUMPS
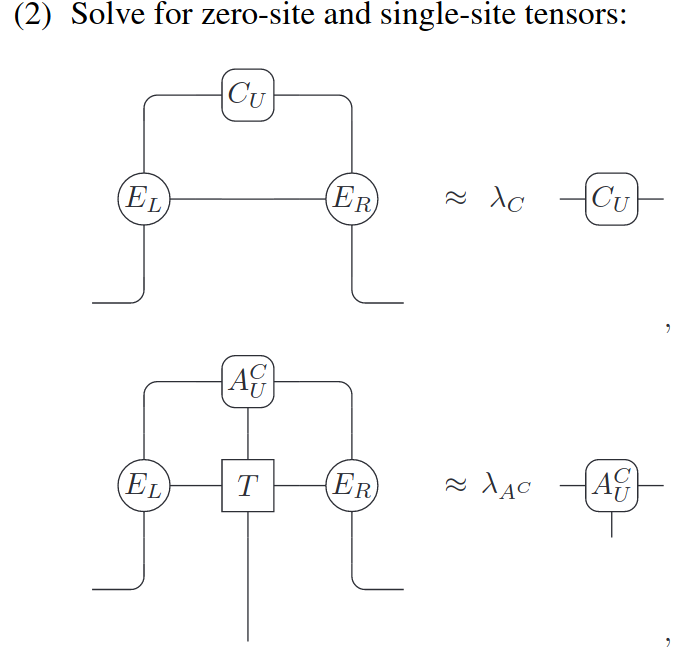
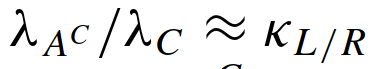
MPQ Theory seminar - 27.01.2021
Discussion on VUMPS


MPQ Theory seminar - 27.01.2021
MPQ Theory seminar - 27.01.2021