Jeanne Colbois | Institut Néel CNRS | Grenoble, France

Tensor networks
Statistical mechanics
Tensor networks
Frustrated magnetism
What can classical frustrated models
teLL us about tensor networks ?
Fixnet | UZH | 14-16 January 2026, Zurich, Switzerland
What can classical frustrated models
teLL us about tensor networks ?


Jeanne Colbois | Institut Néel CNRS | Grenoble, France

Contracting the TN
partition function
of a
frustrated model
Fixnet | UZH | 14-16 January 2026, Zurich, Switzerland
What can classical frustrated models
teLL us about tensor networks ?


Jeanne Colbois | Institut Néel CNRS | Grenoble, France

Contracting the TN
partition function
of a
frustrated model
Numerical problem
MPO properties
Emergent d.o.fs
Fixnet | UZH | 14-16 January 2026, Zurich, Switzerland
COLBOIS | FRUSTRATED TNS | 01.2026
sCOPE
1
1. Motivation
2. The case of frustrated spin systems
3. Range of constraints
4. Conclusions
COLBOIS | FRUSTRATED TNS | 01.2026
Acknowledgments
2

Samuel Nyckees

Afonso Rufino

Andrew Smerald
Frédéric Mila

Frank Verstraete

Laurens Vanderstraeten

Bram Vanhecke

TN contraction problem instances:
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Vanderstraeten et al., PRE 98 (2018)
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721, (2019)
J. G. Liu, L. Wang, P. Zhang, PRL 126, (2021)
B. Vanhecke, JC, et al. PRR 3, (2021)
FF Song, GM Zhang, PRB 105, (2022)
G. Giudice, F. Surace, H. Pichler, G. Giudici, PRB 106, (2022)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, (2023)
F.F. Song, H. Numoin, N. Kawashima, PRB 111, (2025)
W. Tang, F. Verstraete, J. Haegeman, PRB 111, (2025)
Homma et al., PRB 111, (2025)
Our applications:
JC, B. Vanhecke, et al, PRB 106, (2022)
Nyckees et al, PRE 108, (2023)
A. Rufino, et al., arXiv:2505.05889 (to appear in PRL)
A. Rufino et al., in prep

Nathan Perruchoud
Motivation
Frustrated magnetism and constrained models: why?
How? (a priori?)
Frustrated Spin systems
3
COLBOIS | FRUSTRATED TNS | 01.2026
Frustrated Spin systems
3
Incompatible constraints
COLBOIS | FRUSTRATED TNS | 01.2026

Cannot simultaneously minimize all terms
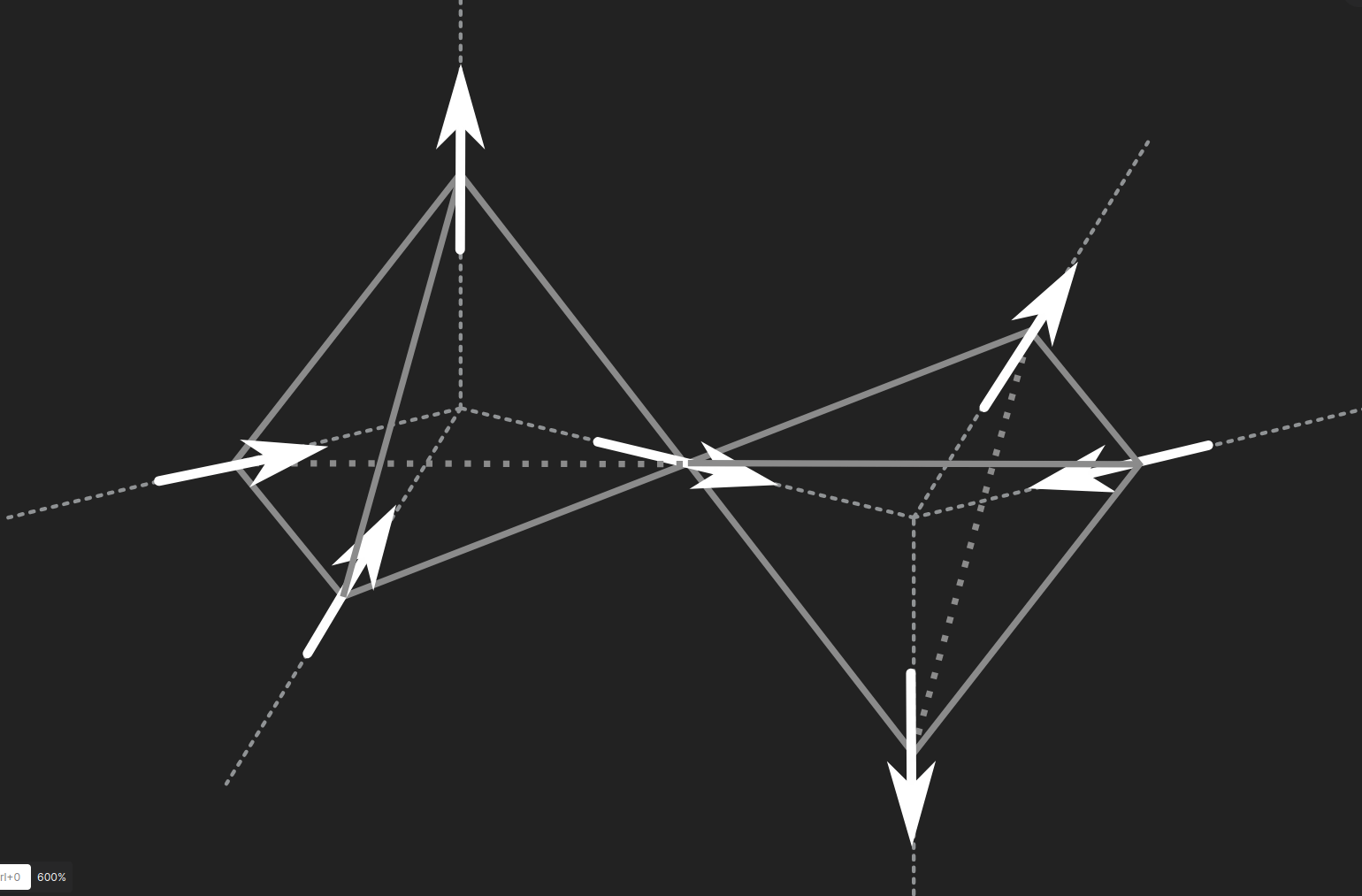
Frustrated Spin systems
3
Incompatible constraints
Macroscopic ground-state degeneracy
COLBOIS | FRUSTRATED TNS | 01.2026

Cannot simultaneously minimize all terms

Frustrated Spin systems
3
Incompatible constraints
Macroscopic ground-state degeneracy
Spin liquid with algebraic or exponential correlations; Partial order
COLBOIS | FRUSTRATED TNS | 01.2026

Cannot simultaneously minimize all terms

Frustrated Spin systems
3
Incompatible constraints
Macroscopic ground-state degeneracy
Spin liquid with algebraic or exponential correlations; Partial order
Emergent degrees-of-freedom
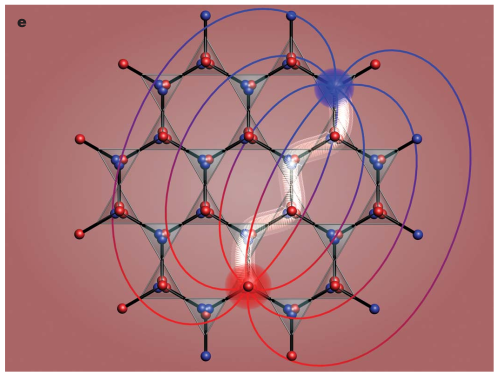
C. Castlenovo, R. Moessner, S. L. Sondhi, Nature 451 (2008)
COLBOIS | FRUSTRATED TNS | 01.2026


Cannot simultaneously minimize all terms

Classical constrained / Frustrated stat Mech models: why?
4
COLBOIS | FRUSTRATED TNS | 01.2026
Classical constrained / Frustrated stat Mech models: why?
4
COLBOIS | FRUSTRATED TNS | 01.2026
Exotic classical phenomena / directly relevant for classical degrees-of-freedom
Classical constrained / Frustrated stat Mech models: why?
4
COLBOIS | FRUSTRATED TNS | 01.2026
Exotic classical phenomena / directly relevant for classical degrees-of-freedom
"Simple" limits of quantum many-body systems
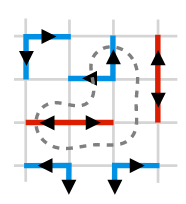
Fig. from Giudice etal.
PRB 106, (2022)
(Generalized-)RK type wavefunctions
Classical limit of the dof.
Effective models
...
Classical constrained / Frustrated stat Mech models: why?
4
COLBOIS | FRUSTRATED TNS | 01.2026
Partition functions as exact* tensor networks
- particularly hard to contract?
* when the dofs are discrete
Exotic classical phenomena / directly relevant for classical degrees-of-freedom
"Simple" limits of quantum many-body systems

Fig. from Giudice etal.
PRB 106, (2022)
(Generalized-)RK type wavefunctions
Classical limit of the dof.
Effective models
...
Classical constrained / Frustrated stat Mech models: why?
4
COLBOIS | FRUSTRATED TNS | 01.2026
* when the dofs are discrete
Partition functions as exact* tensor networks
- particularly hard to contract?
Exotic classical phenomena / directly relevant for classical degrees-of-freedom
"Simple" limits of quantum many-body systems

Fig. from Giudice etal.
PRB 106, (2022)
(Generalized-)RK type wavefunctions
Classical limit of the dof.
Effective models
...
Why TNS for (not exactly solvable) constrained models?
5
COLBOIS | FRUSTRATED TNS | 01.2026
Why TNS for (not exactly solvable) constrained models?
5
COLBOIS | FRUSTRATED TNS | 01.2026
No sign problem!
Monte Carlo:
Why TNS for (not exactly solvable) constrained models?
5
COLBOIS | FRUSTRATED TNS | 01.2026
No sign problem!
Monte Carlo:
Finite-size scaling
Why TNS for (not exactly solvable) constrained models?
5
COLBOIS | FRUSTRATED TNS | 01.2026
No sign problem!
Monte Carlo:
Finite-size scaling
Ergodicity issues
Why TNS for (not exactly solvable) constrained models?
5
COLBOIS | FRUSTRATED TNS | 01.2026
No sign problem!
Monte Carlo:
Finite-size scaling
Tensor networks:
Finite-entanglement scaling / RG
Ergodicity issues
Why TNS for (not exactly solvable) constrained models?
5
COLBOIS | FRUSTRATED TNS | 01.2026
No sign problem!
Monte Carlo:
Finite-size scaling
Tensor networks:
Finite-entanglement scaling / RG
Entropy as the first outcome (free energy per site)
Ergodicity issues
Why TNS for (not exactly solvable) constrained models?
5
COLBOIS | FRUSTRATED TNS | 01.2026
No sign problem!
Monte Carlo:
Finite-size scaling
Tensor networks:
Finite-entanglement scaling / RG
A priori:
Entropy as the first outcome (free energy per site)
Ergodicity issues


Why TNS for (not exactly solvable) constrained models?
5
COLBOIS | FRUSTRATED TNS | 01.2026
No sign problem!
Monte Carlo:
Finite-size scaling
Tensor networks:
Finite-entanglement scaling / RG
A priori:


Entropy as the first outcome (free energy per site)
Ergodicity issues
1. Associate a Boltzmann weight with each interaction
Why TNS for (not exactly solvable) constrained models?
5
COLBOIS | FRUSTRATED TNS | 01.2026
No sign problem!
Monte Carlo:
Finite-size scaling
Tensor networks:
Finite-entanglement scaling / RG
A priori:


Entropy as the first outcome (free energy per site)
Ergodicity issues
1. Associate a Boltzmann weight with each interaction
2. split
Why TNS for (not exactly solvable) constrained models?
5
COLBOIS | FRUSTRATED TNS | 01.2026
No sign problem!
Monte Carlo:
Finite-size scaling
Tensor networks:
Finite-entanglement scaling / RG
A priori:


1. Associate a Boltzmann weight with each interaction
2. split
3. group and reshape
Entropy as the first outcome (free energy per site)
Ergodicity issues
Why TNS for (not exactly solvable) constrained models?
5
COLBOIS | FRUSTRATED TNS | 01.2026
No sign problem!
Monte Carlo:
Finite-size scaling
Tensor networks:
Finite-entanglement scaling / RG
A priori:


1. Associate a Boltzmann weight with each interaction
2. split
3. group and reshape
4. contract the 2D TN with your favourite tool
Entropy as the first outcome (free energy per site)
Ergodicity issues
The case of frustrated spin systems
Understanding the triangular lattice Ising antiferromagnet
How to go beyond
Current limitations
An exactly solvable example : the TIAFM

Ground state:
6
COLBOIS | FRUSTRATED TNS | 01.2026
An exactly solvable example : the TIAFM


Ground state:
6
COLBOIS | FRUSTRATED TNS | 01.2026
An exactly solvable example : the TIAFM


Ground state:
G.H. Wannier, PR 79, (1950, 1973)
6
COLBOIS | FRUSTRATED TNS | 01.2026
An exactly solvable example : the TIAFM



Ground state:
G.H. Wannier, PR 79, (1950, 1973)
6
COLBOIS | FRUSTRATED TNS | 01.2026
An exactly solvable example : the TIAFM



Ground state:
G.H. Wannier, PR 79, (1950, 1973)
Boltzmann Weight
6
COLBOIS | FRUSTRATED TNS | 01.2026
An exactly solvable example : the TIAFM



Ground state:
G.H. Wannier, PR 79, (1950, 1973)
Boltzmann Weight
6
COLBOIS | FRUSTRATED TNS | 01.2026
6
An exactly solvable example : the TIAFM



Ground state:
G.H. Wannier, PR 79, (1950, 1973)
Boltzmann Weight
COLBOIS | FRUSTRATED TNS | 01.2026
7
An exactly solvable example : the TIAFM
Vanhecke, JC et al (2021)

COLBOIS | FRUSTRATED TNS | 01.2026
7
An exactly solvable example : the TIAFM
Vanhecke, JC et al (2021)

COLBOIS | FRUSTRATED TNS | 01.2026
7
An exactly solvable example : the TIAFM
Vanhecke, JC et al (2021)


1. Cancellation of big / small factors
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
\(\rightarrow\) precision?
COLBOIS | FRUSTRATED TNS | 01.2026
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
\(\rightarrow\) log / tropical algebra
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Rams et al, PRE 104, (2021)
Note: no approximate contraction scheme
7
An exactly solvable example : the TIAFM
Vanhecke, JC et al (2021)


COLBOIS | FRUSTRATED TNS | 01.2026
Local tensor:
1. Cancellation of big / small factors
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
\(\rightarrow\) precision?
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
\(\rightarrow\) log / tropical algebra
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Rams et al, PRE 104, (2021)
7
An exactly solvable example : the TIAFM
Vanhecke, JC et al (2021)


COLBOIS | FRUSTRATED TNS | 01.2026
2. Low-temperature limit / emergent dofs
Vanderstraeten et al., PRE 98 (2018)
B. Vanhecke, JC, et al. PRR 3, (2021)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, (2023)
1. Cancellation of big / small factors
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
\(\rightarrow\) precision?
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
\(\rightarrow\) log / tropical algebra
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Rams et al, PRE 104, (2021)
7
An exactly solvable example : the TIAFM
Vanhecke, JC et al (2021)


3. MPO properties
W. Tang, F. Verstraete, J. Haegeman, PRB 111, (2025)
COLBOIS | FRUSTRATED TNS | 01.2026
Vanderstraeten et al., PRE 98 (2018)
B. Vanhecke, JC, et al. PRR 3, (2021)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, (2023)
2. Low-temperature limit / emergent dofs
1. Cancellation of big / small factors
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
\(\rightarrow\) precision?
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
\(\rightarrow\) log / tropical algebra
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Rams et al, PRE 104, (2021)
7
An exactly solvable example : the TIAFM
Vanhecke, JC et al (2021)


3. MPO properties
2. Low-temperature limit / emergent dofs
Vanderstraeten et al., PRE 98 (2018)
B. Vanhecke, JC, et al. PRR 3, (2021)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, (2023)
W. Tang, F. Verstraete, J. Haegeman, PRB 111, (2025)
COLBOIS | FRUSTRATED TNS | 01.2026
1. Cancellation of big / small factors
Z. Zhu, H. G. Katzgraber, arXiv:1903.07721 (2019)
\(\rightarrow\) precision?
J. G. Liu, L. Wang, P. Zhan, PRL 126, (2021)
\(\rightarrow\) log / tropical algebra
C. Wang, S.-M. Qin, H.-J. Zhou, PRB 90, (2014)
Rams et al, PRE 104, (2021)
9
The ground-state local rule / emergent DOF
COLBOIS | FRUSTRATED TNS | 01.2026
with all entries smaller or equal to 1?
9
The ground-state local rule / emergent DOF
COLBOIS | FRUSTRATED TNS | 01.2026


with all entries smaller or equal to 1?
Dimer counting problem on a honeycomb lattice!
see e.g. Vanderstraeten et al, PRE 98 (2018)
9
The ground-state local rule / emergent DOF
COLBOIS | FRUSTRATED TNS | 01.2026


Dimer counting problem on a honeycomb lattice!
Wannier, PR 79 1950;
Kasteleyn, 1960;
Levin, Nave, PRL 99, 2007
with all entries smaller or equal to 1?
see e.g. Vanderstraeten et al, PRE 98 (2018)
9
The ground-state local rule / emergent DOF
COLBOIS | FRUSTRATED TNS | 01.2026

Dimer counting problem on a honeycomb lattice!
with all entries smaller or equal to 1?


see e.g. Vanderstraeten et al, PRE 98 (2018)
Wannier, PR 79 1950;
Kasteleyn, 1960;
Levin, Nave, PRL 99, 2007
Xie et al, Phys. Rev. X 4 (2014)
10
Hamiltonian splitting
COLBOIS | FRUSTRATED TNS | 01.2026
Text
\(\omega\) on all triangles
Vanhecke, JC et al (2021)
\(E_{\mathrm{GS}}/N_{\triangle}\) = \(\min_{\vec{\sigma }}H_{\triangle}(\vec{\sigma})\)
Hamiltonian splitting
COLBOIS | FRUSTRATED TNS | 01.2026
Text


Vanhecke, JC et al (2021)
10
\(\omega\) on all triangles
\(E_{\mathrm{GS}}/N_{\triangle}\) = \(\min_{\vec{\sigma }}H_{\triangle}(\vec{\sigma})\)
all entries smaller or equal to 1
Hamiltonian splitting
COLBOIS | FRUSTRATED TNS | 01.2026
Text

Vanhecke, JC et al (2021)
10
\(\omega\) on all triangles
\(E_{\mathrm{GS}}/N_{\triangle}\) = \(\min_{\vec{\sigma }}H_{\triangle}(\vec{\sigma})\)

all entries smaller or equal to 1
Hamiltonian splitting
COLBOIS | FRUSTRATED TNS | 01.2026
Text


Vanhecke, JC et al (2021)
10
\(\omega\) on all triangles
\(E_{\mathrm{GS}}/N_{\triangle}\) = \(\min_{\vec{\sigma }}H_{\triangle}(\vec{\sigma})\)

all entries smaller or equal to 1
Hamiltonian splitting
COLBOIS | FRUSTRATED TNS | 01.2026
Text


Vanhecke, JC et al (2021)
JC, PhD Thesis
10
\(\omega\) on all triangles
\(E_{\mathrm{GS}}/N_{\triangle}\) = \(\min_{\vec{\sigma }}H_{\triangle}(\vec{\sigma})\)

all entries smaller or equal to 1
11
COLBOIS | FRUSTRATED TNS | 01.2026
Text
Vanhecke, JC et al (2021)
Does the way of splitting matter?
11
COLBOIS | FRUSTRATED TNS | 01.2026
Text
Same Hamiltonian in PBC
Vanhecke, JC et al (2021)
Does the way of splitting matter?
11
COLBOIS | FRUSTRATED TNS | 01.2026
Text


Boltzmann weight
(half for each bond)
Boltzmann weight
(half for each bond)
Kronecker Delta
Boltzmann weight
Does the way of splitting matter?
Vanhecke, JC et al (2021)
Same Hamiltonian in PBC
COLBOIS | FRUSTRATED TNS | 01.2026
Text


11
Vanhecke, JC et al (2021)
Does the way of splitting matter?
Same Hamiltonian in PBC
A non-local Gauge transformation
COLBOIS | FRUSTRATED TNS | 01.2026
See e.g. Kasteleyn 1960
12

\(U(1)\)
COLBOIS | FRUSTRATED TNS | 01.2026
See e.g. Kasteleyn 1960

A non-local Gauge transformation
12
\(U(1)\)
COLBOIS | FRUSTRATED TNS | 01.2026
See e.g. Kasteleyn 1960

A non-local Gauge transformation
12
\(U(1)\)
COLBOIS | FRUSTRATED TNS | 01.2026
See e.g. Kasteleyn 1960

A non-local Gauge transformation
12
\(U(1)\)
COLBOIS | FRUSTRATED TNS | 01.2026
See e.g. Kasteleyn 1960
A non-local Gauge transformation
12
\(U(1)\)

COLBOIS | FRUSTRATED TNS | 01.2026
See e.g. Kasteleyn 1960
A non-local Gauge transformation
12
\(U(1)\)

COLBOIS | FRUSTRATED TNS | 01.2026
See e.g. Kasteleyn 1960

A non-local Gauge transformation
12
\(U(1)\)
COLBOIS | FRUSTRATED TNS | 01.2026
See e.g. Kasteleyn 1960
See also, Nourhani et al, PRE 98 (2018)


Tang, Vestraete, Haegeman, PRB 111, (2025)
A non-local Gauge transformation
12
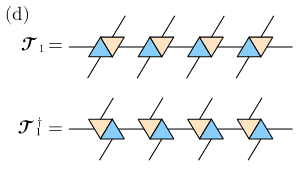
1. Transfer matrix \(\mathcal{T}_1\)
\(U(1)\)
COLBOIS | FRUSTRATED TNS | 01.2026
See e.g. Kasteleyn 1960
See also, Nourhani et al, PRE 98 (2018)



Tang, Vestraete, Haegeman, PRB 111, (2025)
A non-local Gauge transformation
12
1. Transfer matrix \(\mathcal{T}_1\)
- is normal : \(\mathcal{T}_1^{\dagger} \mathcal{T}_1 = \mathcal{T}_1 \mathcal{T}_1^{\dagger}\)
- conserves U(1) (conserves the sector)
\(U(1)\)
COLBOIS | FRUSTRATED TNS | 01.2026
See e.g. Kasteleyn 1960
1. Transfer matrix \(\mathcal{T}_1\)
- is normal : \(\mathcal{T}_1^{\dagger} \mathcal{T}_1 = \mathcal{T}_1 \mathcal{T}_1^{\dagger}\)
- conserves U(1) (conserves the sector)
See also, Nourhani et al, PRE 98 (2018)
1. Transfer matrix \(\mathcal{T}_2 = \mathcal{T}_1 + \Delta \mathcal{T}\)
- non-normal
- related to \(\mathcal{T}_1\) by a bond-dimension 2 MPO \(\mathcal{P}\) that allows to interpolate between them
- affects scaling of the entanglement entropy




Tang, Vestraete, Haegeman, PRB 111, (2025)
A non-local Gauge transformation
12
\(U(1)\)
13
What is needed to go beyond the tiafm
COLBOIS | FRUSTRATED TNS | 01.2026
What is needed to go beyond the tiafm
Numerical problem
Tropical algebra: approximate contraction?
COLBOIS | FRUSTRATED TNS | 01.2026
13
What is needed to go beyond the tiafm
Numerical problem
MPO properties
Tropical algebra: approximate contraction?
COLBOIS | FRUSTRATED TNS | 01.2026
Given the (badly conditioned) MPO \(\rightarrow\) how to find the (non-local) gauge?
13
What is needed to go beyond the tiafm
Numerical problem
MPO properties
Tropical algebra: approximate contraction?
Finding the ground-state local rule / emergent dof?
Given the (badly conditioned) MPO \(\rightarrow\) how to find the (non-local) gauge?
COLBOIS | FRUSTRATED TNS | 01.2026
13
Emergent d.o.fs: dual construction?
What is needed to go beyond the tiafm
Numerical problem
MPO properties
Tropical algebra: approximate contraction?
Finding the ground-state local rule / emergent dof?
1. Beyond nearest-neighbor couplings
Given the (badly conditioned) MPO \(\rightarrow\) how to find the (non-local) gauge?
COLBOIS | FRUSTRATED TNS | 01.2026


13
Emergent d.o.fs: dual construction?
What is needed to go beyond the tiafm
Numerical problem
MPO properties
Tropical algebra: approximate contraction?
Finding the ground-state local rule / emergent dof?
1. Beyond nearest-neighbor couplings
2. Beyond discrete spins: XY models
Given the (badly conditioned) MPO \(\rightarrow\) how to find the (non-local) gauge?
COLBOIS | FRUSTRATED TNS | 01.2026


13
Emergent d.o.fs: dual construction?
What is needed to go beyond the tiafm
Numerical problem
MPO properties
Emergent d.o.fs: dual construction?
Tropical algebra: approximate contraction?
Finding the ground-state local rule / emergent dof?
1. Beyond nearest-neighbor couplings
2. Beyond discrete spins: XY models
Given the (badly conditioned) MPO \(\rightarrow\) how to find the (non-local) gauge?
COLBOIS | FRUSTRATED TNS | 01.2026


13
What is needed to go beyond the tiafm
Numerical problem
MPO properties
Tropical algebra: approximate contraction?
Finding the ground-state local rule / emergent dof?
1. Beyond nearest-neighbor couplings
2. Beyond discrete spins: XY models
Given the (badly conditioned) MPO \(\rightarrow\) how to find the (non-local) gauge?
COLBOIS | FRUSTRATED TNS | 01.2026


13
Emergent d.o.fs: dual construction?
Farther-neighbor couplings:
Ising models as weighted counting problems
COLBOIS | FRUSTRATED TNS | 01.2026
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969); M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975); B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981); W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016);
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021); Nagy et al; PRE 109 (2024)
Essential idea : Anderson bounds
14
Farther-neighbor couplings:
Ising models as weighted counting problems
COLBOIS | FRUSTRATED TNS | 01.2026
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969); M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975); B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981); W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016);
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021); Nagy et al; PRE 109 (2024)
Essential idea : Anderson bounds
14
LINEAR PROGRAM:

Farther-neighbor couplings:
Ising models as weighted counting problems
COLBOIS | FRUSTRATED TNS | 01.2026
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969); M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975); B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981); W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016);
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021); Nagy et al; PRE 109 (2024)
Essential idea : Anderson bounds
LINEAR PROGRAM:

1. Split with clusters that overlap
14
Farther-neighbor couplings:
Ising models as weighted counting problems
COLBOIS | FRUSTRATED TNS | 01.2026
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969); M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975); B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981); W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016);
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021); Nagy et al; PRE 109 (2024)
Essential idea : Anderson bounds
LINEAR PROGRAM:

1. Split with clusters that overlap
2. Minimize : G.S. lower-bound
14
Farther-neighbor couplings:
Ising models as weighted counting problems
COLBOIS | FRUSTRATED TNS | 01.2026
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969); M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975); B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981); W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016);
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021); Nagy et al; PRE 109 (2024)
Essential idea : Anderson bounds
LINEAR PROGRAM:

3. Maximize w.r.t the weights:
1. Split with clusters that overlap
2. Minimize : G.S. lower-bound
14
Farther-neighbor couplings:
Ising models as weighted counting problems
COLBOIS | FRUSTRATED TNS | 01.2026
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969); M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975); B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981); W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016);
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021); Nagy et al; PRE 109 (2024)
Essential idea : Anderson bounds
LINEAR PROGRAM:

3. Maximize w.r.t the weights:
1. Split with clusters that overlap
2. Minimize : G.S. lower-bound
Obtain the ground states by tiling!
14
Farther-neighbor couplings:
Ising models as weighted counting problems
COLBOIS | FRUSTRATED TNS | 01.2026
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969); M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975); B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981); W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016);
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021); Nagy et al; PRE 109 (2024)
Essential idea : Anderson bounds
LINEAR PROGRAM:

3. Maximize w.r.t the weights:
1. Split with clusters that overlap
2. Minimize : G.S. lower-bound
Obtain the ground states by tiling!
And more generally :
14
Farther-neighbor couplings:
Ising models as weighted counting problems
COLBOIS | FRUSTRATED TNS | 01.2026
C. K. Majumdar and D. K. Ghosh, J. Math. Phys. 10, (1969); M. Kaburagi, J. Kanamori, Prog. Theor. Phys. 54 , (1975); B. Sriram Shastry and B. Sutherland, Physica 108 B+C, (1981); W. Huang, D. A. Kitchaev, et. al. , Phys. Rev. B 94, (2016);
B. Vanhecke, JC, L. Vanderstraeten, F. Verstraete, F. Mila, PRR 3, (2021); Nagy et al; PRE 109 (2024)
Essential idea : Anderson bounds
LINEAR PROGRAM:

3. Maximize w.r.t the weights:
1. Split with clusters that overlap
2. Minimize : G.S. lower-bound
Obtain the ground states by tiling!
And more generally :
"Interactions round a face"
14
R. J. Baxter, J. Stat. Phys. 19, (1978), T. Nishino, J. Phys. Soc. Jpn. 64, (1995), T. Nishino and K. Okunishi, J. Phys. Soc. Jpn. 66, (1997)
Xie et al, Phys. Rev. X 4 (2014)
15
Remarks on The linear program and symMetries
COLBOIS | FRUSTRATED TNS | 01.2026
The linear program is invariant under the cluster symmetry group \(G\)
15
Remarks on The linear program and symMetries
COLBOIS | FRUSTRATED TNS | 01.2026
The linear program is invariant under the cluster symmetry group \(G\)
1. We can look for optimal solutions in the subspace of \(G\)-invariant solutions.
2. We can keep only one configuration per orbit when solving the linear program
Beyond discrete spins: frustrated XY Models
COLBOIS | FRUSTRATED TNS | 01.2026
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, 224404 (2023)
(see also FF Song, H Nuomin, N Kawashima PRB 111 (2025))
16
Beyond discrete spins: frustrated XY Models
COLBOIS | FRUSTRATED TNS | 01.2026
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, 224404 (2023)
(see also FF Song, H Nuomin, N Kawashima PRB 111 (2025))
16
Beyond discrete spins: frustrated XY Models
COLBOIS | FRUSTRATED TNS | 01.2026
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, 224404 (2023)
(see also FF Song, H Nuomin, N Kawashima PRB 111 (2025))
What happens when your partition function cannot be exactly expressed as a TN?
16
Beyond discrete spins: frustrated XY Models
COLBOIS | FRUSTRATED TNS | 01.2026
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, 224404 (2023)
(see also FF Song, H Nuomin, N Kawashima PRB 111 (2025))
What happens when your partition function cannot be exactly expressed as a TN?
1. Similar issue as TIAFM (on square XY)
16
Beyond discrete spins: frustrated XY Models
COLBOIS | FRUSTRATED TNS | 01.2026
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, 224404 (2023)
(see also FF Song, H Nuomin, N Kawashima PRB 111 (2025))
What happens when your partition function cannot be exactly expressed as a TN?
1. Similar issue as TIAFM (on square XY)
2. A slightly different issue on the kagome: truncation leads to wrong results
16
COLBOIS | FRUSTRATED TNS | 01.2026
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, 224404 (2023)
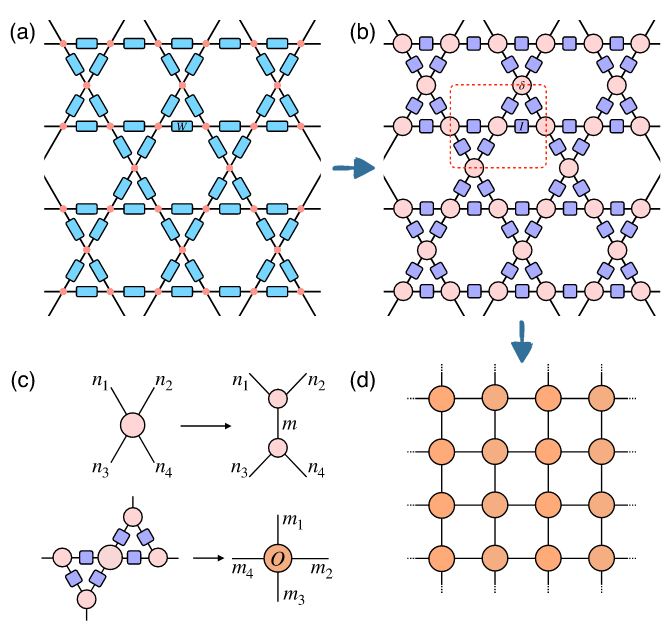
(1) decomposition onto cylindrical harmonics
(2) split and group
Comparing two constructions for frustrated XY Models
\(t = \exp(-\beta J \cos(\theta_i - \theta_j)\)
17
COLBOIS | FRUSTRATED TNS | 01.2026
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, 224404 (2023)
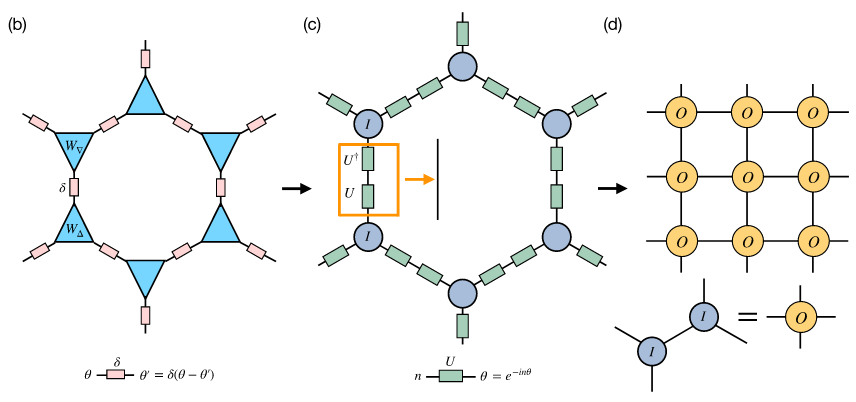

(2) split and group
Comparing two constructions for frustrated XY Models
\(t = \exp(-\beta J \cos(\theta_i - \theta_j)\)
(1) Fourier transform or decomposition onto Bessel functions
(2) split and group
17
(1) decomposition onto cylindrical harmonics
COLBOIS | FRUSTRATED TNS | 01.2026
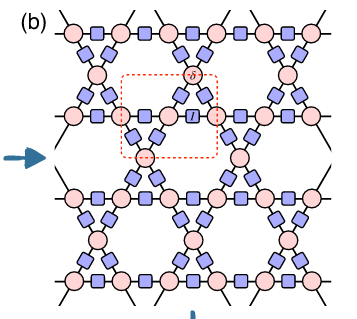
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
see also FF. Song; GM Zhang, Ch. Phys. Letters (2025)
Comparing two constructions for frustrated XY Models
18
COLBOIS | FRUSTRATED TNS | 01.2026
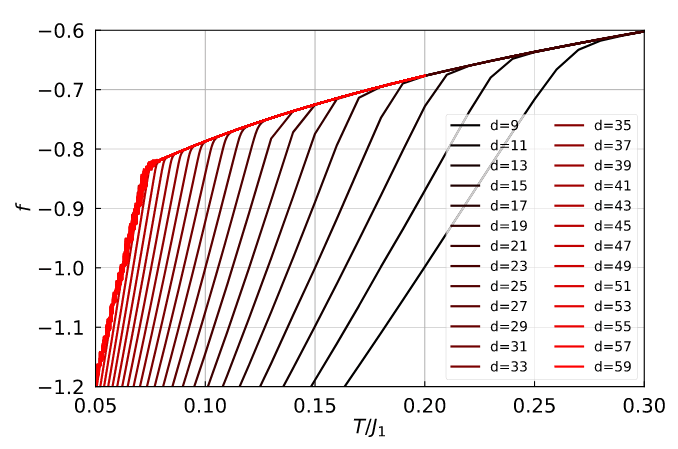

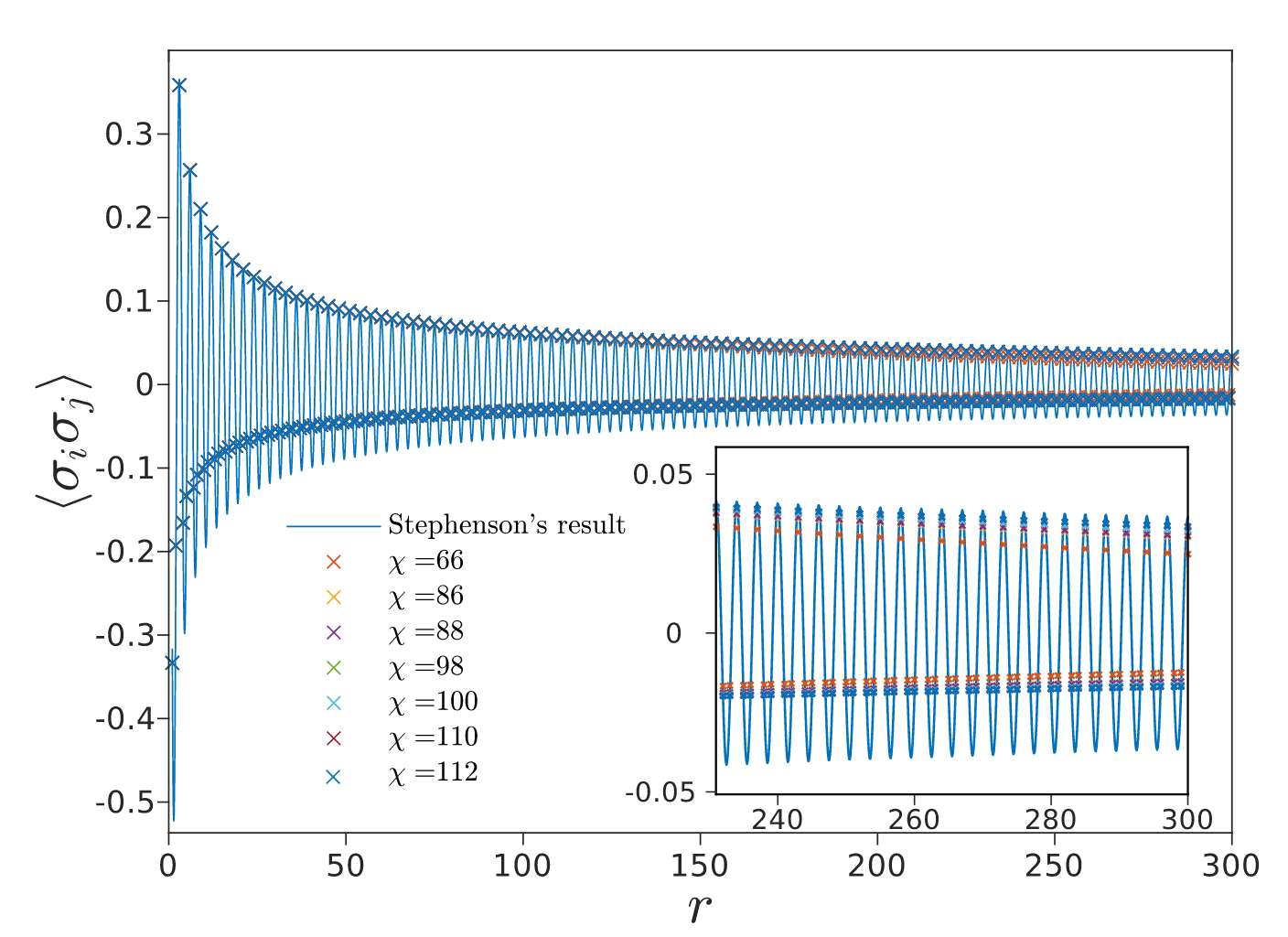
First-order phase transition?
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
see also FF. Song; GM Zhang, Ch. Phys. Letters (2025)
Comparing two constructions for frustrated XY Models
18
COLBOIS | FRUSTRATED TNS | 01.2026


First-order phase transition?
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
see also FF. Song; GM Zhang, Ch. Phys. Letters (2025)
Comparing two constructions for frustrated XY Models
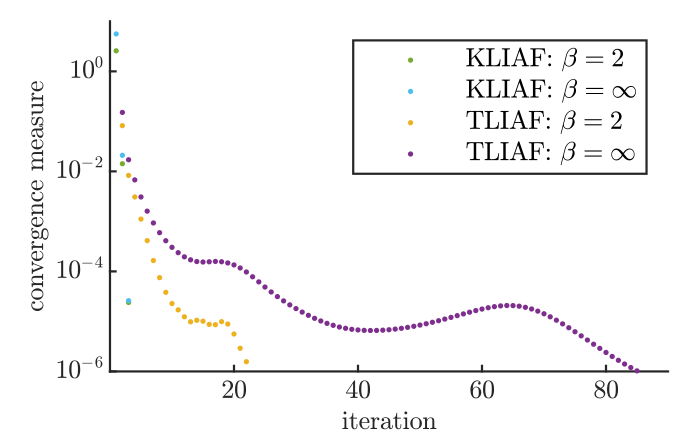
Converges
but not reliably
18
COLBOIS | FRUSTRATED TNS | 01.2026


First-order phase transition?
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
see also FF. Song; GM Zhang, Ch. Phys. Letters (2025)
Comparing two constructions for frustrated XY Models
Converges
but not reliably

18
COLBOIS | FRUSTRATED TNS | 01.2026


First-order phase transition?
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
see also FF. Song; GM Zhang, Ch. Phys. Letters (2025)
Comparing two constructions for frustrated XY Models
Converges
but not reliably

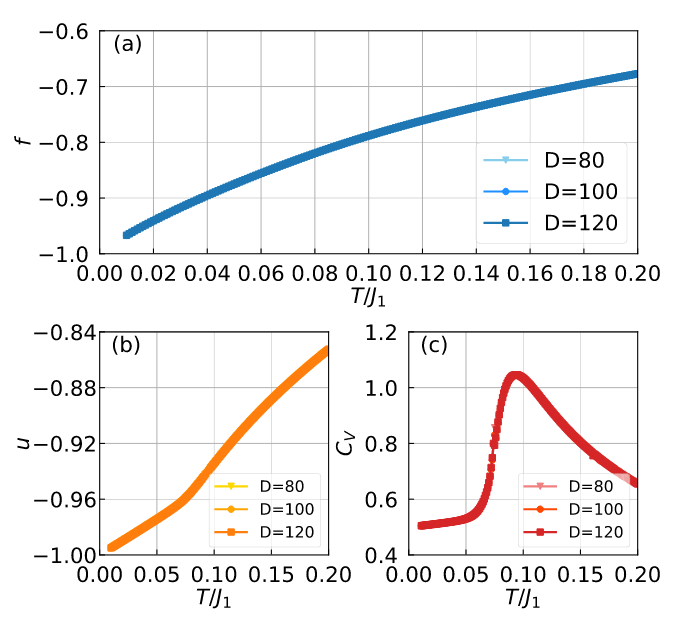
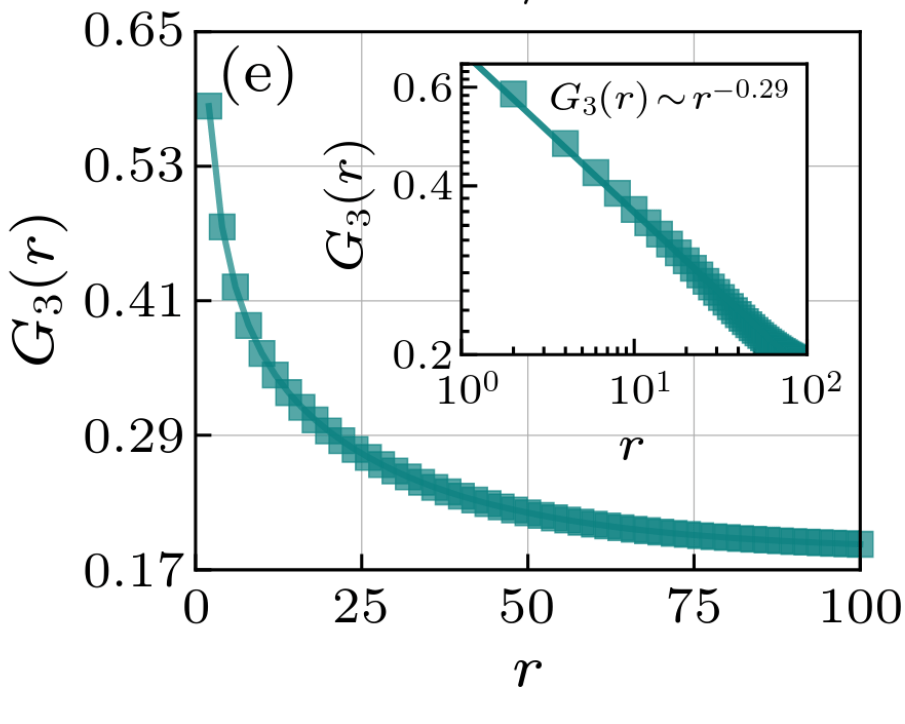
BKT
18
19
Do we have a systematic solution?
COLBOIS | FRUSTRATED TNS | 01.2026
19
Do we have a systematic solution?
COLBOIS | FRUSTRATED TNS | 01.2026
1. Finding the ground state rule / emergent dof: range of frustration?
Ronceray & Le Floch (2020)
19
Do we have a systematic solution?
COLBOIS | FRUSTRATED TNS | 01.2026
1. Finding the ground state rule / emergent dof: range of frustration?
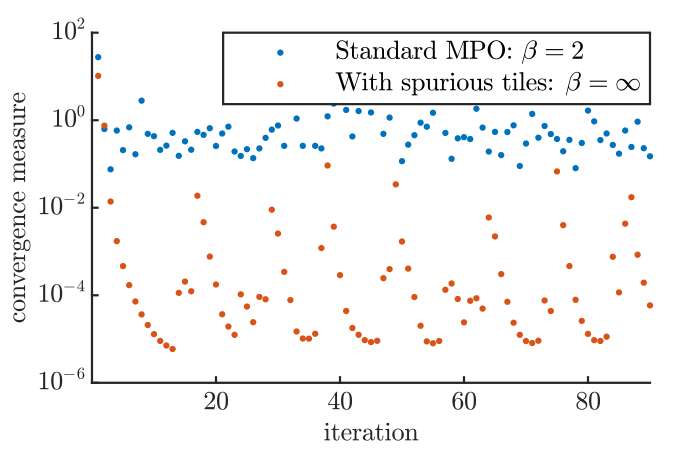
2. Making sure that no "spurious tile" spoils the convergence?
Ronceray & Le Floch (2020)
19
Do we have a systematic solution?
COLBOIS | FRUSTRATED TNS | 01.2026
1. Finding the ground state rule / emergent dof: range of frustration?
Ronceray & Le Floch (2020)
3. More fundamentally: tiling problems
2. Making sure that no "spurious tile" spoils the convergence?
19
Do we have a systematic solution?
COLBOIS | FRUSTRATED TNS | 01.2026
1. Finding the ground state rule / emergent dof: range of frustration?
3. More fundamentally: tiling problems
\(\rightarrow\) undecidability in general

Ronceray & Le Floch (2020)


2. Making sure that no "spurious tile" spoils the convergence?
19
Do we have a systematic solution?
COLBOIS | FRUSTRATED TNS | 01.2026
1. Finding the ground state rule / emergent dof: range of frustration?
3. More fundamentally: tiling problems
\(\rightarrow\) practical cases?
\(\rightarrow\) undecidability in general

Ronceray & Le Floch (2020)


2. Making sure that no "spurious tile" spoils the convergence?
Range of the constraint : Beyond dimers

Nathan Perruchoud

Afonso Rufino
Multimer modelS
20
COLBOIS | FRUSTRATED TNS | 01.2026
Fig. from N. Perruchoud's Master thesis
Given a lattice : packing polymers of length \(k\)
Multimer modelS
20
COLBOIS | FRUSTRATED TNS | 01.2026
Fig. from N. Perruchoud's Master thesis
Given a lattice : packing polymers of length \(k\)
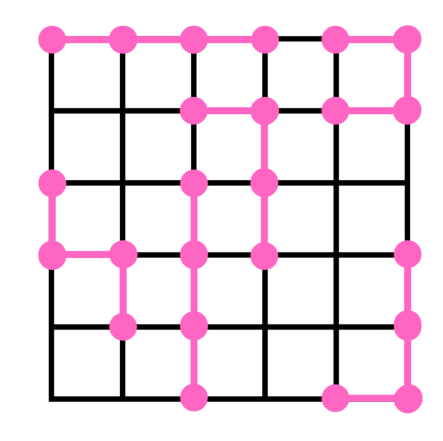
Multimer modelS
20
COLBOIS | FRUSTRATED TNS | 01.2026
Fig. from N. Perruchoud's Master thesis
RVB state properties?
Given a lattice : packing polymers of length \(k\)

See eg. Giudice et al, PRB 106 (2022),
Zhang et al, Commun. Mat. 6 (2025)
Multimer modelS
20
COLBOIS | FRUSTRATED TNS | 01.2026
Fig. from N. Perruchoud's Master thesis
RVB state properties?
Statistical mechanics ?
Given a lattice : packing polymers of length \(k\)

See eg. Giudice et al, PRB 106 (2022),
Zhang et al, Commun. Mat. 6 (2025)
See next slide
Focusing on straight rods
21
COLBOIS | FRUSTRATED TNS | 01.2026
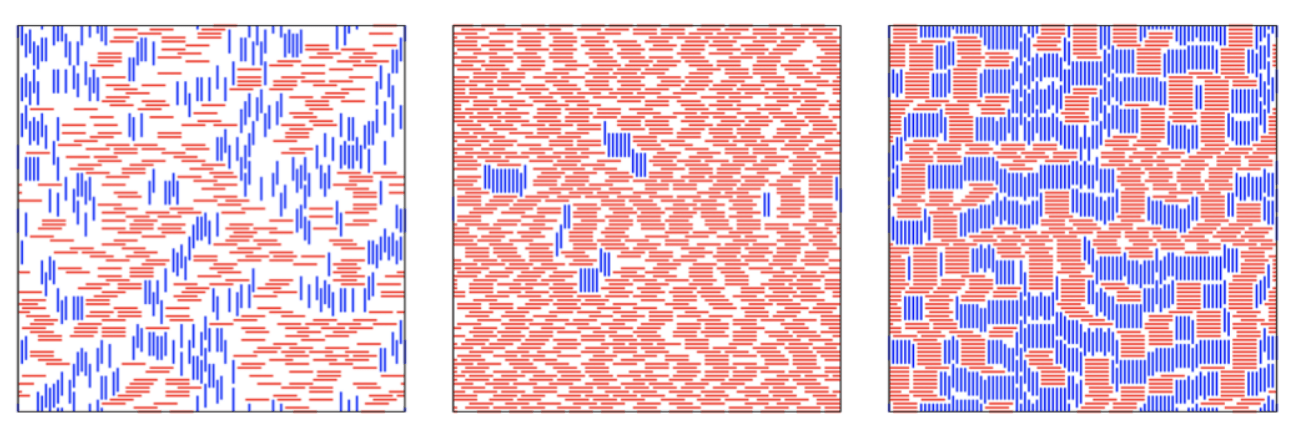
Fig: Shah et al, PRE 105 (2022)
Nice review: Shah et al, PRE 105 (2022)
Focusing on straight rods
COLBOIS | FRUSTRATED TNS | 01.2026

Fig: Shah et al, PRE 105 (2022)
Nice review: Shah et al, PRE 105 (2022)
Low-density disordered
21
Focusing on straight rods
COLBOIS | FRUSTRATED TNS | 01.2026

Fig: Shah et al, PRE 105 (2022)
Nice review: Shah et al, PRE 105 (2022)
Low-density disordered
Intermediate density nematic
21
Focusing on straight rods
COLBOIS | FRUSTRATED TNS | 01.2026

Fig: Shah et al, PRE 105 (2022)
Nice review: Shah et al, PRE 105 (2022)
Low-density disordered
Intermediate density nematic
High density disordered
21
Focusing on straight rods
COLBOIS | FRUSTRATED TNS | 01.2026

Low-density disordered
Intermediate density nematic
High density disordered
Fig: Shah et al, PRE 105 (2022)
Nice review: Shah et al, PRE 105 (2022)
A. Ghosh and D. Dhar. Euro. Letters, 78 (2007).
- strong evidence of nematic phase for \(k \geq 7\)
21
Focusing on straight rods
COLBOIS | FRUSTRATED TNS | 01.2026

Low-density disordered
Intermediate density nematic
High density disordered
- strong evidence of nematic phase for \(k \geq 7\)
- proof of the existence of the nematic phase for \(k \rightarrow \infty\)
Fig: Shah et al, PRE 105 (2022)
Nice review: Shah et al, PRE 105 (2022)
Disertori and Giuliani.,Comm. Math.Phys, 323, (2013).
A. Ghosh and D. Dhar. Euro. Letters, 78 (2007).
21
Focusing on straight rods
COLBOIS | FRUSTRATED TNS | 01.2026

Low-density disordered
Intermediate density nematic
High density disordered
- strong evidence of nematic phase for \(k \geq 7\)
- proof of the existence of the nematic phase for \(k \rightarrow \infty\)
- first phase transition in the Ising universality class
Fig: Shah et al, PRE 105 (2022)
Nice review: Shah et al, PRE 105 (2022)
Disertori and Giuliani.,Comm. Math.Phys, 323, (2013).
A. Ghosh and D. Dhar. Euro. Letters, 78 (2007).
Matoz-Fernandez, et al, Europhys. Letters, 82 (2008).
21
Focusing on straight rods
COLBOIS | FRUSTRATED TNS | 01.2026

Low-density disordered
Intermediate density nematic
High density disordered
- strong evidence of nematic phase for \(k \geq 7\)
- proof of the existence of the nematic phase for \(k \rightarrow \infty\)
- first phase transition in the Ising universality class
- nature of the second phase transition?
Fig: Shah et al, PRE 105 (2022)
Nice review: Shah et al, PRE 105 (2022)
Disertori and Giuliani.,Comm. Math.Phys, 323, (2013).
A. Ghosh and D. Dhar. Euro. Letters, 78 (2007).
Matoz-Fernandez, et al, Europhys. Letters, 82 (2008).
21
Grand-canonical partition function
COLBOIS | FRUSTRATED TNS | 01.2026
22
Grand-canonical partition function
COLBOIS | FRUSTRATED TNS | 01.2026
22
Contraction with CTMRG :
- issues (see e.g. Chatelain & Gendiar, (2020))
- group at least 2x2
N. Perruchoud Master's thesis
Giudice etal. PRB 106, (2022)
- trimers: \(U(1) \times U(1)\) symmetry
- translation-invariant representation requires a 3x3 block
Grand-canonical partition function
22
COLBOIS | FRUSTRATED TNS | 01.2026
Contraction with CTMRG :
- issues (see e.g. Chatelain & Gendiar, (2020))
- group at least 2x2
N. Perruchoud Master's thesis
Giudice etal. PRB 106, (2022)
- trimers: \(U(1) \times U(1)\) symmetry
- translation-invariant representation requires a 3x3 block
CTMRG (extraplation): 0.158496(14)
TM with extapolation: 0.158539(37); 0.158520(15)
Serra et al, (2023)
Ghosh et al, (2023)
23
COLBOIS | FRUSTRATED TNS | 01.2026
Remark on Emergent non-local dofs

Afonso Rufino


A. Rufino, et al., arXiv:2505.05889 (to appear in PRL)
COLBOIS | FRUSTRATED TNS | 01.2026
Remark on Emergent non-local dofs

Afonso Rufino


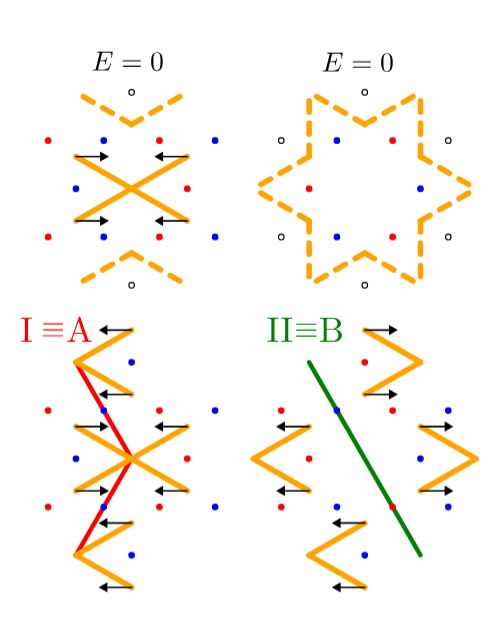
\(J_1, J_3 \rightarrow \infty\)
some of the constraints
A. Rufino, et al., arXiv:2505.05889 (to appear in PRL)
23
COLBOIS | FRUSTRATED TNS | 01.2026
Remark on Emergent non-local dofs

Afonso Rufino




\(J_1, J_3 \rightarrow \infty\)
some of the constraints
emergent string degrees of freedom
leading to a topological staircase
A. Rufino, et al., arXiv:2505.05889 (to appear in PRL)
23
Conclusions
Take-home messages
24
COLBOIS | FRUSTRATED TNS | 01.2026
Take-home messages
COLBOIS | FRUSTRATED TNS | 01.2026
1. Simple stat mech models written as exact TNs can lead to contraction failure
24
Take-home messages
COLBOIS | FRUSTRATED TNS | 01.2026
1. Simple stat mech models written as exact TNs can lead to contraction failure
2. Strategies: tropical algebra; gauging; finding the frustration-free cluster
Rules-of-thumb:
- normal MPO
- lattice symmetries
- emergent dofs : interactions-round-a-face
24
Take-home messages
COLBOIS | FRUSTRATED TNS | 01.2026
1. Simple stat mech models written as exact TNs can lead to contraction failure
3. Families of frustrated spin systems where we have a well-behaved formulation
Learn strategies to fix the gauge?
Topological devil's staircase:
non-local emergent dofs.
2. Strategies: tropical algebra; gauging; finding the frustration-free cluster
Rules-of-thumb:
- normal MPO
- lattice symmetries
- emergent dofs : interactions-round-a-face
24
Take-home messages
COLBOIS | FRUSTRATED TNS | 01.2026
1. Simple stat mech models written as exact TNs can lead to contraction failure
3. Families of frustrated spin systems where we have a well-behaved formulation
Learn strategies to fix the gauge?
Thank you!
Topological devil's staircase:
non-local emergent dofs.
2. Strategies: tropical algebra; gauging; finding the frustration-free cluster
Rules-of-thumb:
- normal MPO
- lattice symmetries
- emergent dofs : interactions-round-a-face
24
Bonus slides
Remark on U(1) symmetries and Back to dimers
COLBOIS | FRUSTRATED TNS | 01.2026
Giudice etal. PRB 106, (2022)
- trimers: \(U(1) \times U(1)\) symmetry
- translation-invariant representation requires a 3x3 block
Remark by Juraj Hasik:
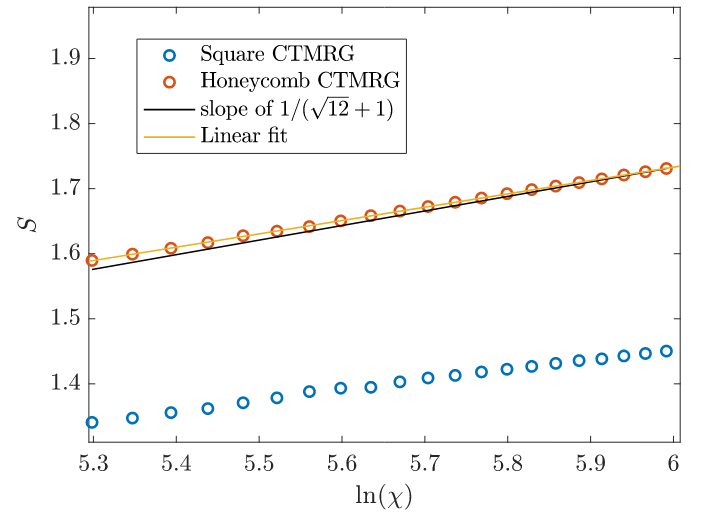
- enforcing U(1) symmetry for dimers on the honeycomb lattice \(\rightarrow\) /!\ boundary conditions
- could explain missing scaling of the entanglement entropy?
F. Pollmann, et al. PRL 102 (2009)
L. Tagliacozzoet al. PRB 78 (2008)
S. Nyckees et al. PRE 108 (2023)
F. Pollmann, et al. PRL 102 (2009)
L. Tagliacozzoet al. PRB 78 (2008)
Multi-site CTMRG failure
COLBOIS | FRUSTRATED TNS | 01.2026
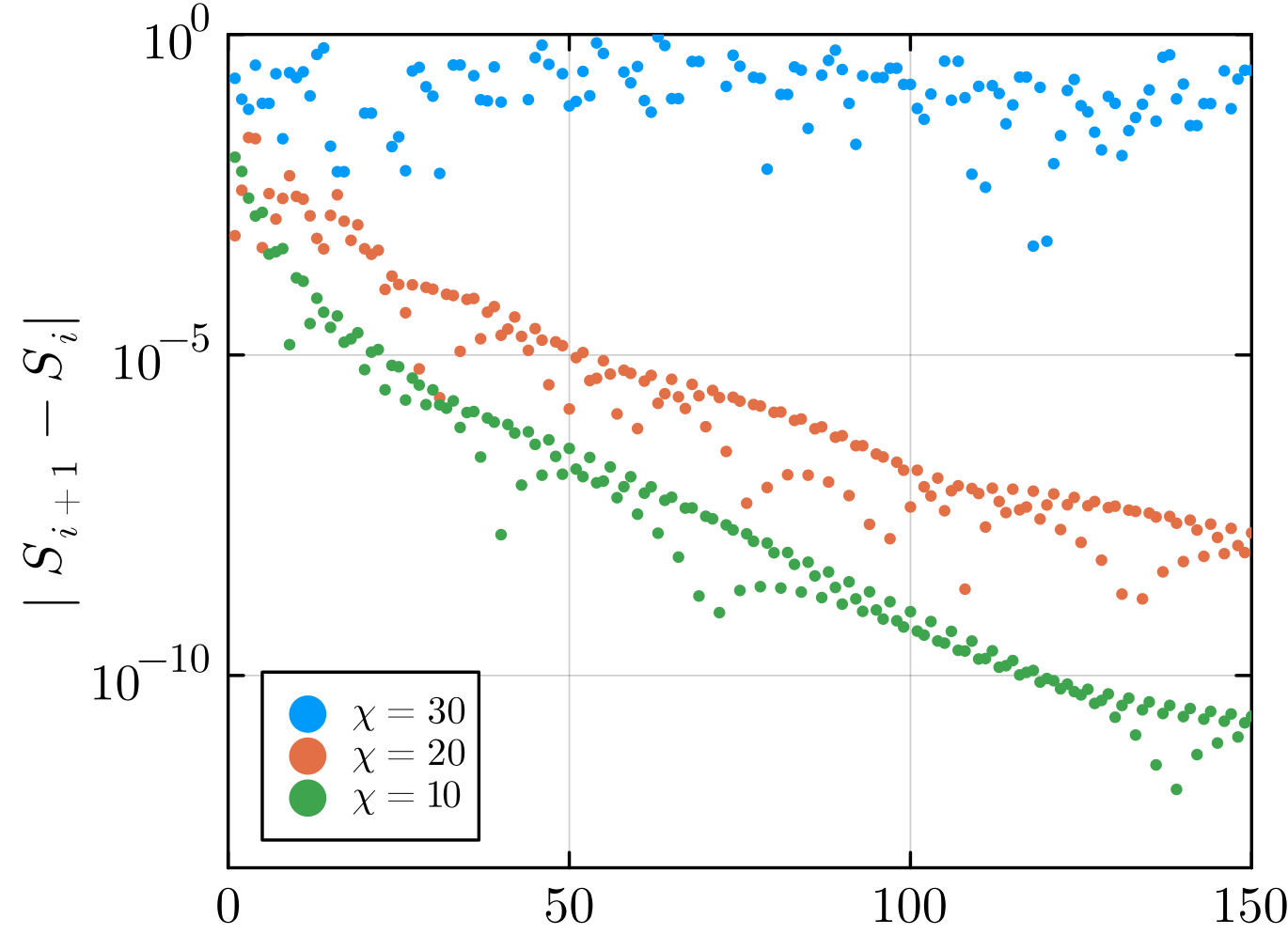
3x3

Afonso Rufino
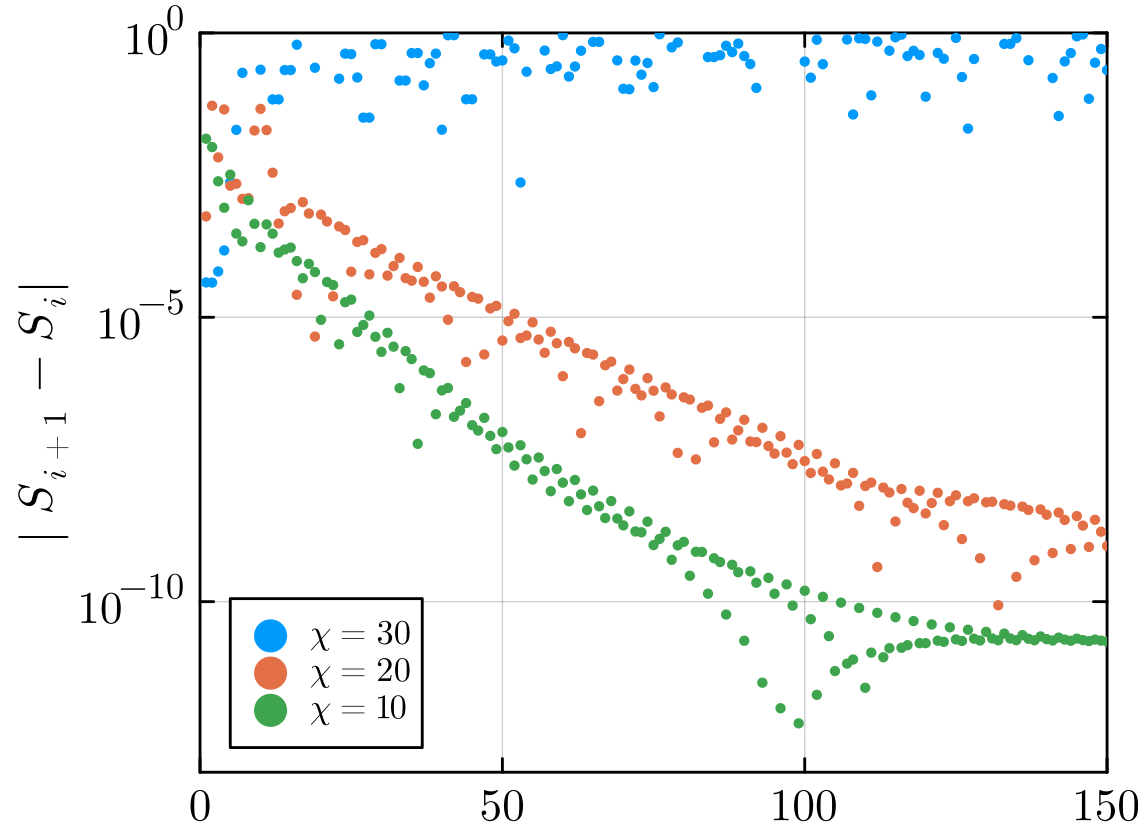
3x3
2x2
Remark on non-local emergent dofs
COLBOIS | FRUSTRATED TNS | 01.2026
\(E \propto L \)

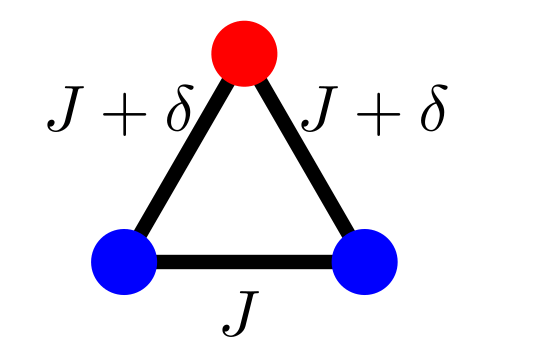
Nearest-neighbor anisotropic
Smerald & Mila, Scipost (2019)
Constrained limit \(J \gg T, \delta \)

Beyond discrete spins: frustrated XY Models
COLBOIS | FRUSTRATED TNS | 01.2026
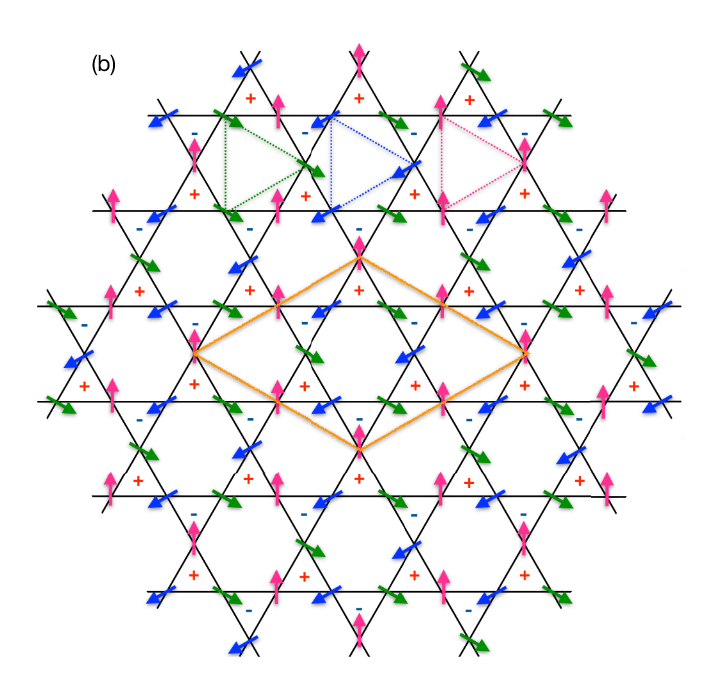
Ground-states: U(1) + 3-states clock
Huse, Rosenfeld, PRB 45, (1992)
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, 224404 (2023)
(see also FF Song, H Nuomin, N Kawashima PRB 111 (2025))
Beyond discrete spins: frustrated XY Models
COLBOIS | FRUSTRATED TNS | 01.2026

Ground-states: U(1) + 3-states clock
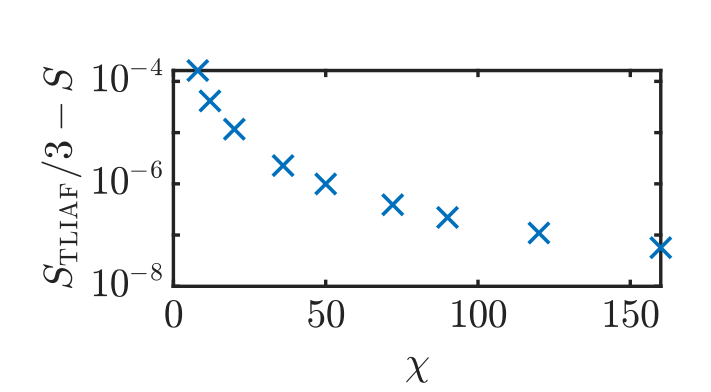
Residual entropy due to 3-states: \(S = 0.126...\)
Huse, Rosenfeld, PRB 45, (1992)
R. J. Baxter, J. Math. Phys. 11, (1970)
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, 224404 (2023)
(see also FF Song, H Nuomin, N Kawashima PRB 111 (2025))
Beyond discrete spins: frustrated XY Models
COLBOIS | FRUSTRATED TNS | 01.2026

Ground-states: U(1) + 3-states clock
Residual entropy due to 3-states: \(S = 0.126...\)
Huse, Rosenfeld, PRB 45, (1992)
R. J. Baxter, J. Math. Phys. 11, (1970)
F.F. Song, G. M. Zhang, PRB 108, 014424 (2023)
F.F. Song, T.-Y. Lin, G. M. Zhang, PRB 108, 224404 (2023)
(see also FF Song, H Nuomin, N Kawashima PRB 111 (2025))
Question:
- BKT transition, or
- pre-empted by a first-order or 2nd order transition in the chiralities?
R. J. Baxter, J. Math. Phys. 11, (1970)
COLBOIS | FRUSTRATED TNS | 01.2026
\(10^{-8}\) precision on the partition function per site
CTMRG (extraplation): 0.158496(14)
TM with extapolation: 0.158539(37); 0.158520(15)
Serra et al, (2023)
N. Perruchoud Master's thesis
Ghosh et al, (2023)

High-density limit
Tropical algebra