Svängningar
Vågor
Mekaniska vågor
Ljusvågor
Svängningar
Mekaniska Vågor
Del 1: Svängningar
Minns ni Hooke's lag?
\( F= k\cdot\Delta l\)
kraft = fjäderkonstant \(\cdot\) förlängning
Minns ni Hooke's lag?
Skriv ner en så tydlig definition som möjligt för begreppen:
* Amplitud
* Ytterlägen
* Jämviktsläge
* Periodtid
* Frekvens
Hitta ett översiktligt samband för hur periodtiden beror på fjäderkonstanten \(k\), viktens massa \(m\) och amplituden \(A\) i stil med:
"När x ökar så ökar/minskar periodtiden (\(T\))"
Testa om följande samband stämmer:
\(\displaystyle T= 2\pi\sqrt{\frac{m}{k}}\)
\(\displaystyle f = \frac{1}{T}\)
Använd sambanden för att bestämma fjäderkonstanten i fjädern bredvid.
Sammanfattning
- De flesta periodiska system har en så kallad egenfrekvens (och egenperiodtid) som bestäms av systemets egenskaper.
- Frekvens och periodtid är relaterade genom \( f=1/T\).
Periodtid mäts i enheten sekund (s).
Frekvens mäts i enheten Hertz (Hz = 1/s).
- Amplituden påverkar inte periodtiden eller frekvensen.
Bonusuppgift:
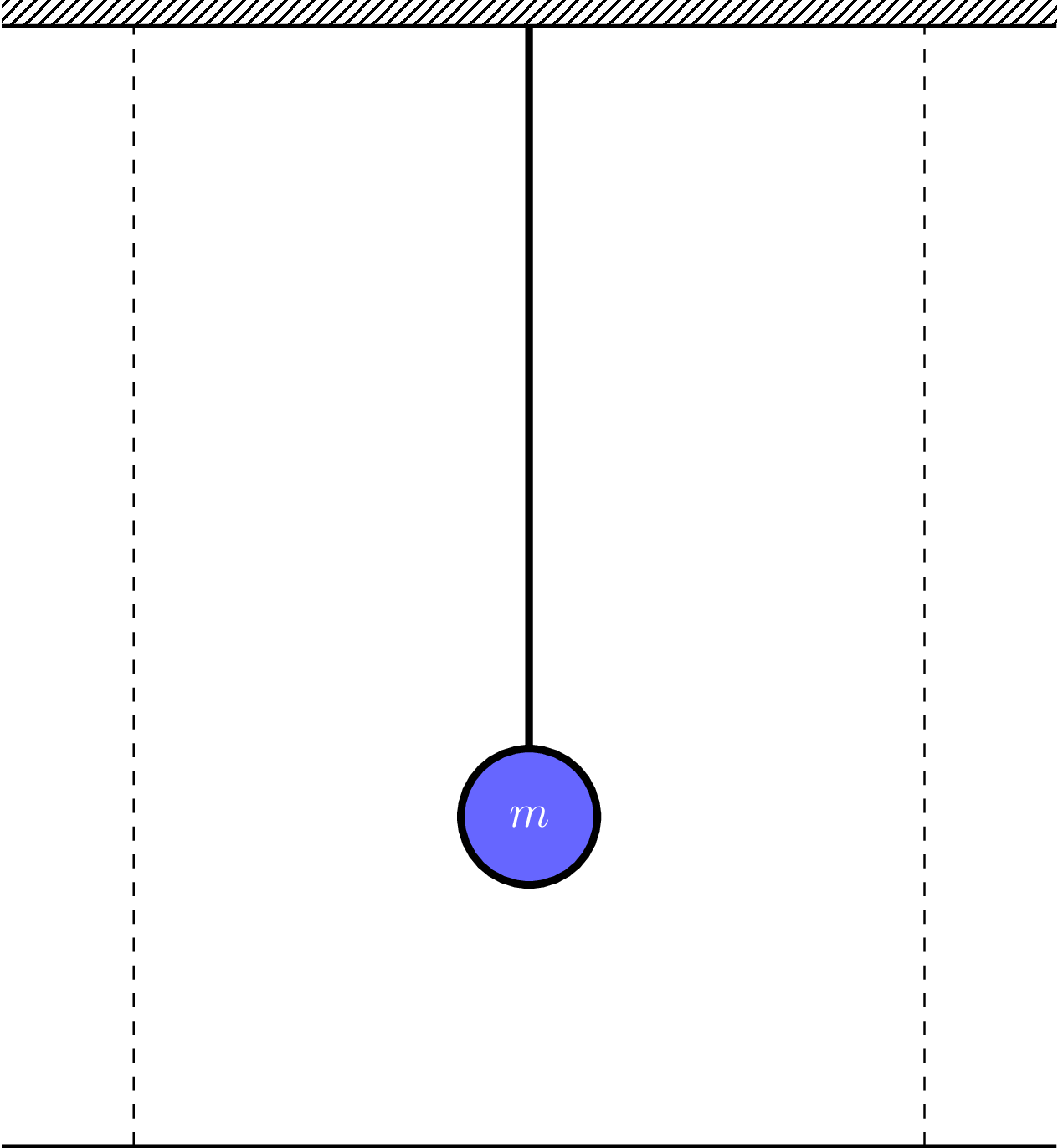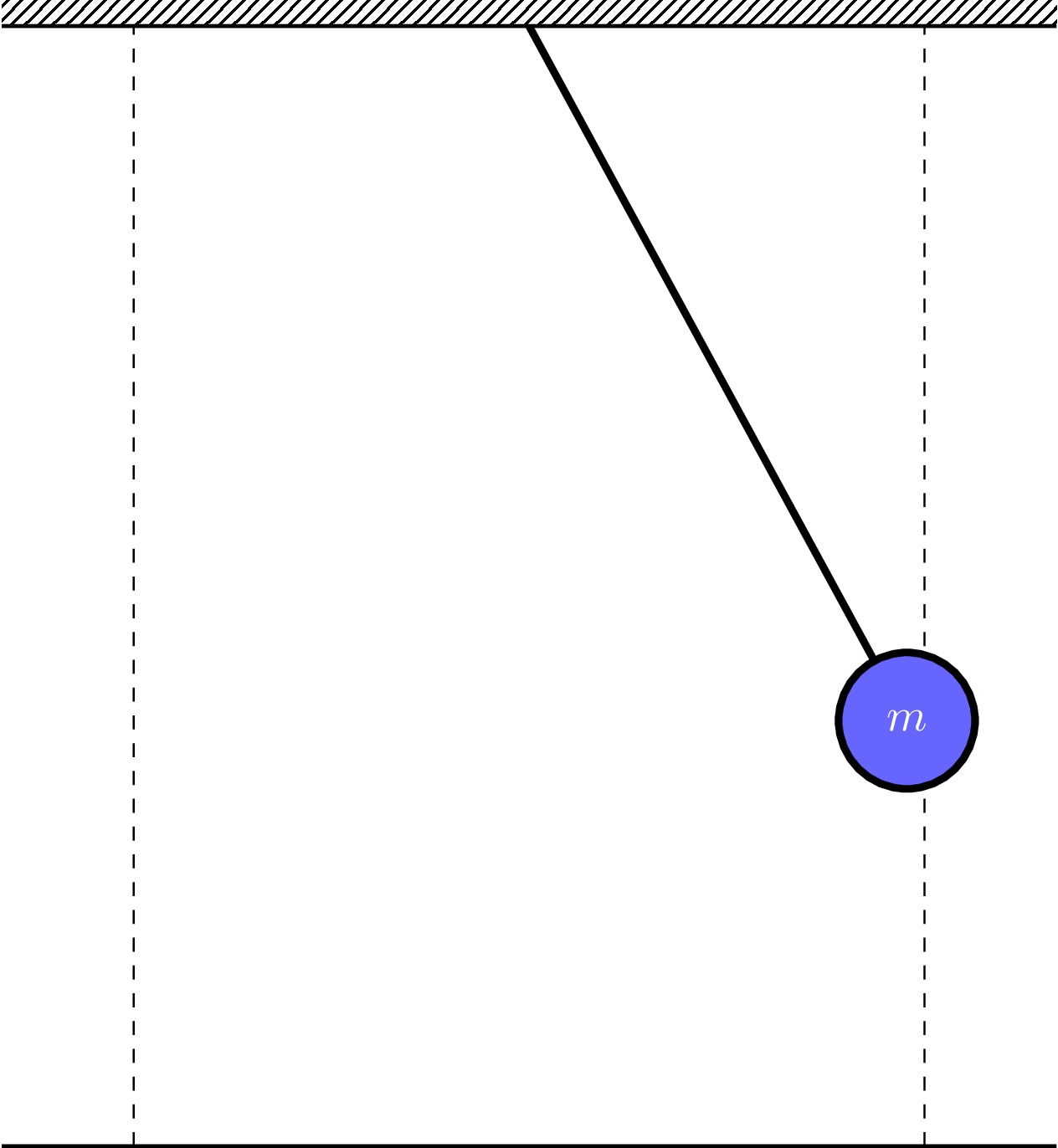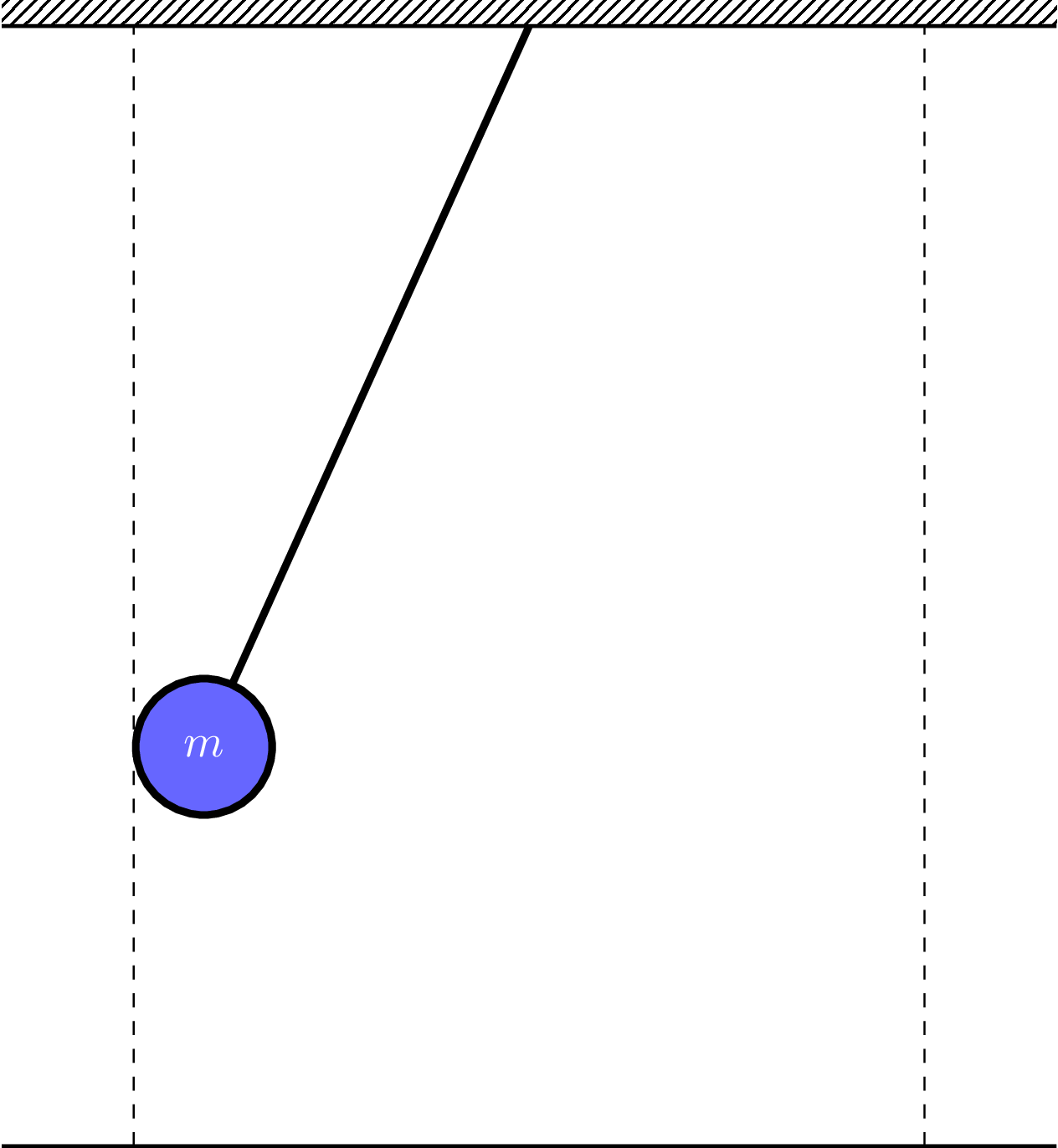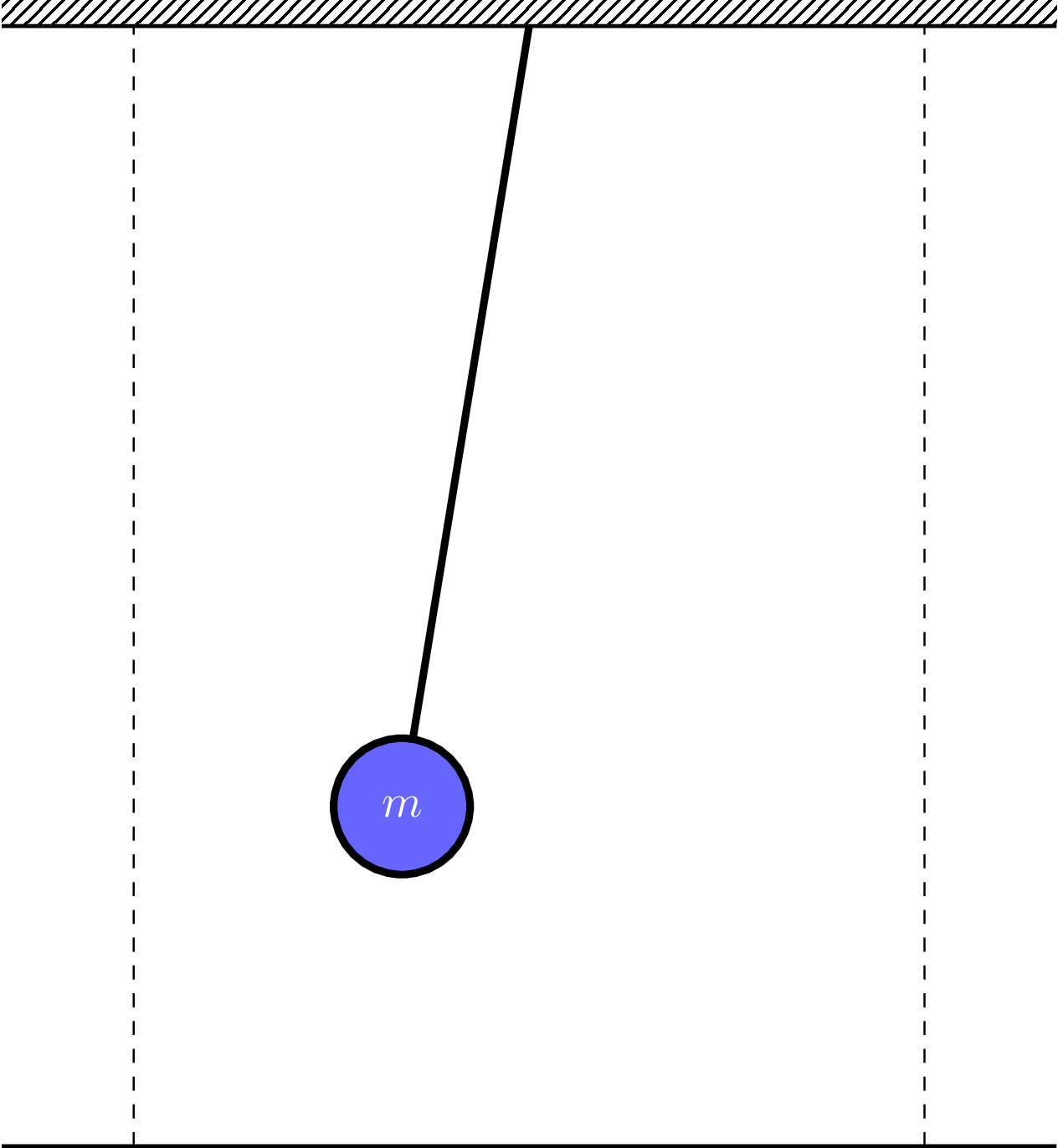
En pendel är ett periodiskt system och har alltså en egenfrekvens och en egenperiodtid.
Funder på hur ni skulle planera en laboration för att få ut formeln för en pendels periodtid. Vilka variabler kan ingå i formeln?
Resonans
Resonans kan uppstå när ett system påverkas av en periodisk kraft där kraftens frekvens matchar systemets egenfrekvens.
Exempel: När man puttar på en gunga i precis rätt takt så kommer gungan att komma högre och högre (svängningen får högre amplitud). Puttar man däremot i otakt kan man minska gungans amplitud, och till slut få den att stanna helt.
Uppgift: Gå in på
https://phet.colorado.edu/sims/resonance/resonance_en.html
och undersök hur fjädersvängningarnas amplitud beror på kraftens frekvens, ändra sedan fjäderkonstant och massa och upprepa. Ställ upp en hypotes.