Derivata

Begreppet derivata

Hastighet

Grafens lutning ger bilens hastighet

Förändringshastighet

Grafens lutning - förändringshastighet

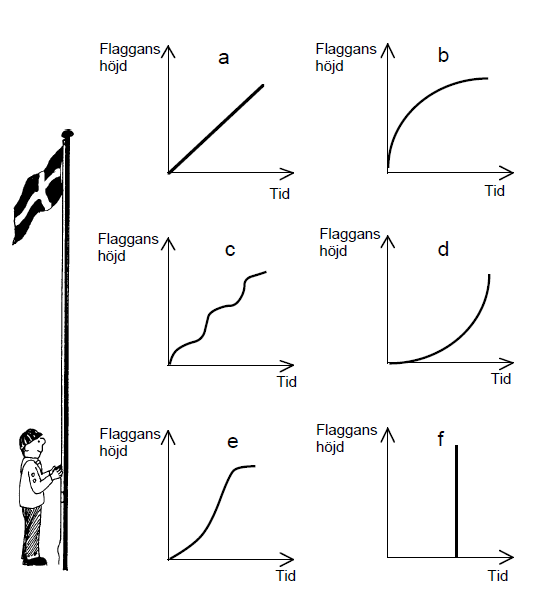
Vilken av graferna passar bäst?

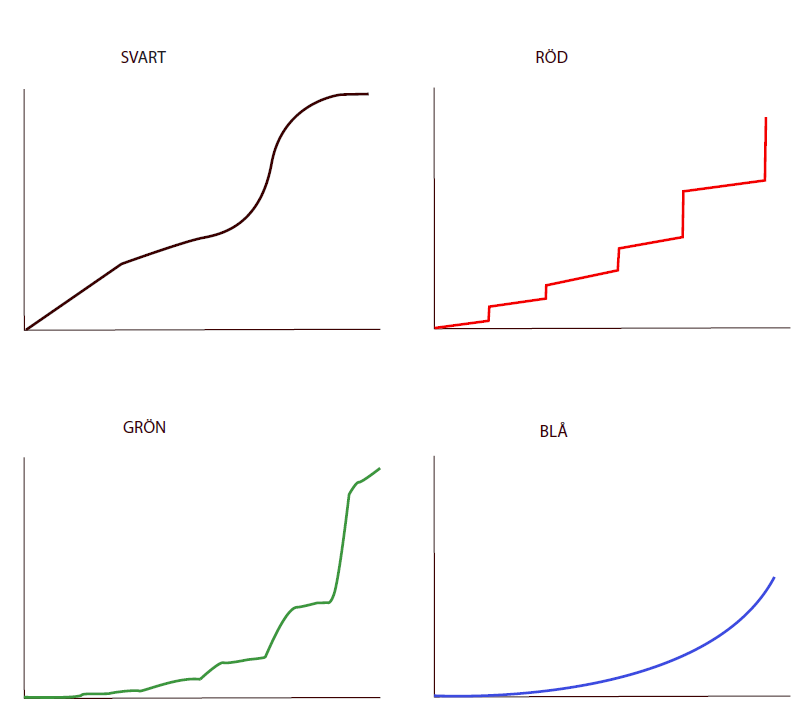
Bilden i nedre hörnet har fyra grafer.

Para ihop dem med alternativen.

Från sekant till tangent

http://ggbtu.be/m294935

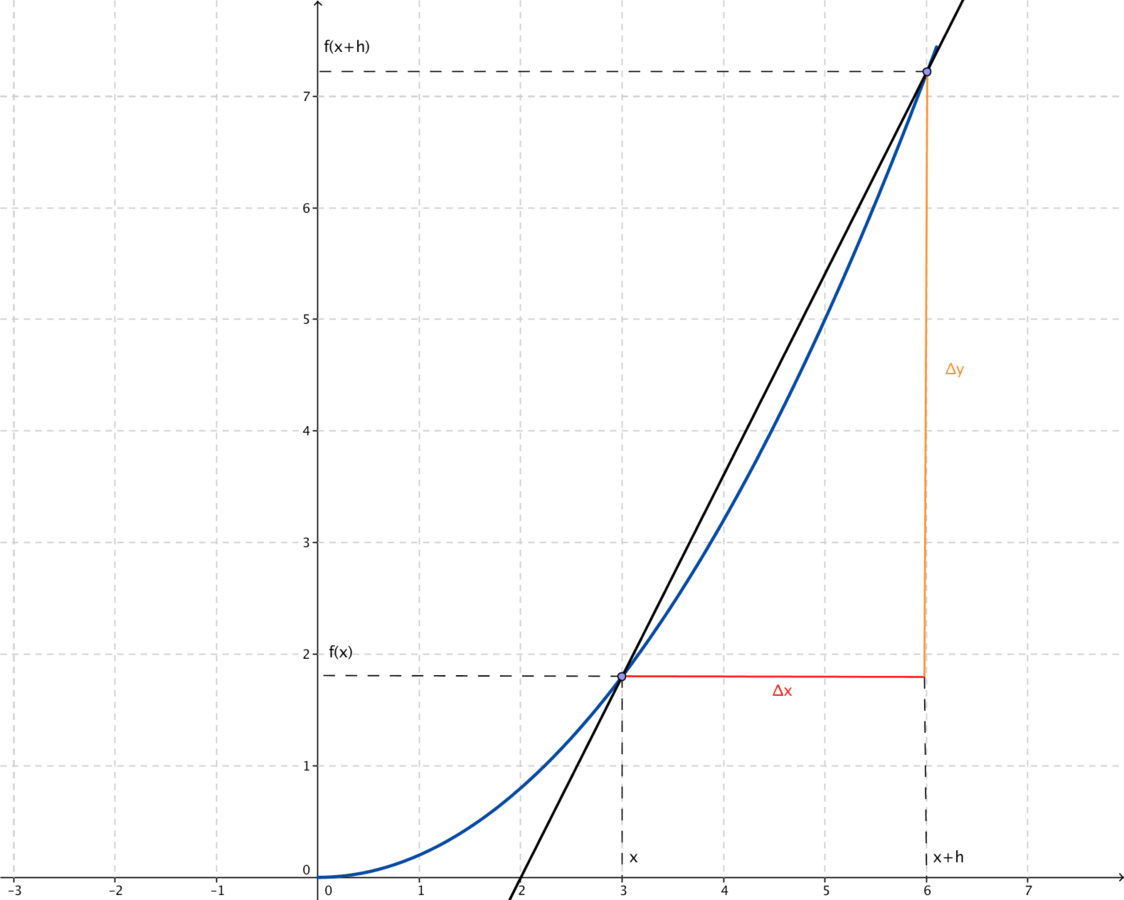
\text{Lutning}=\frac{\Delta y}{\Delta x}=\frac{f(x+h)-f(x)}{h}

L u t n i n g = \frac{​ Δ y ​ ​}{​ Δ x ​} = \frac{​ f ( x + h ) - f ( x ) ​ ​}{​ h ​}

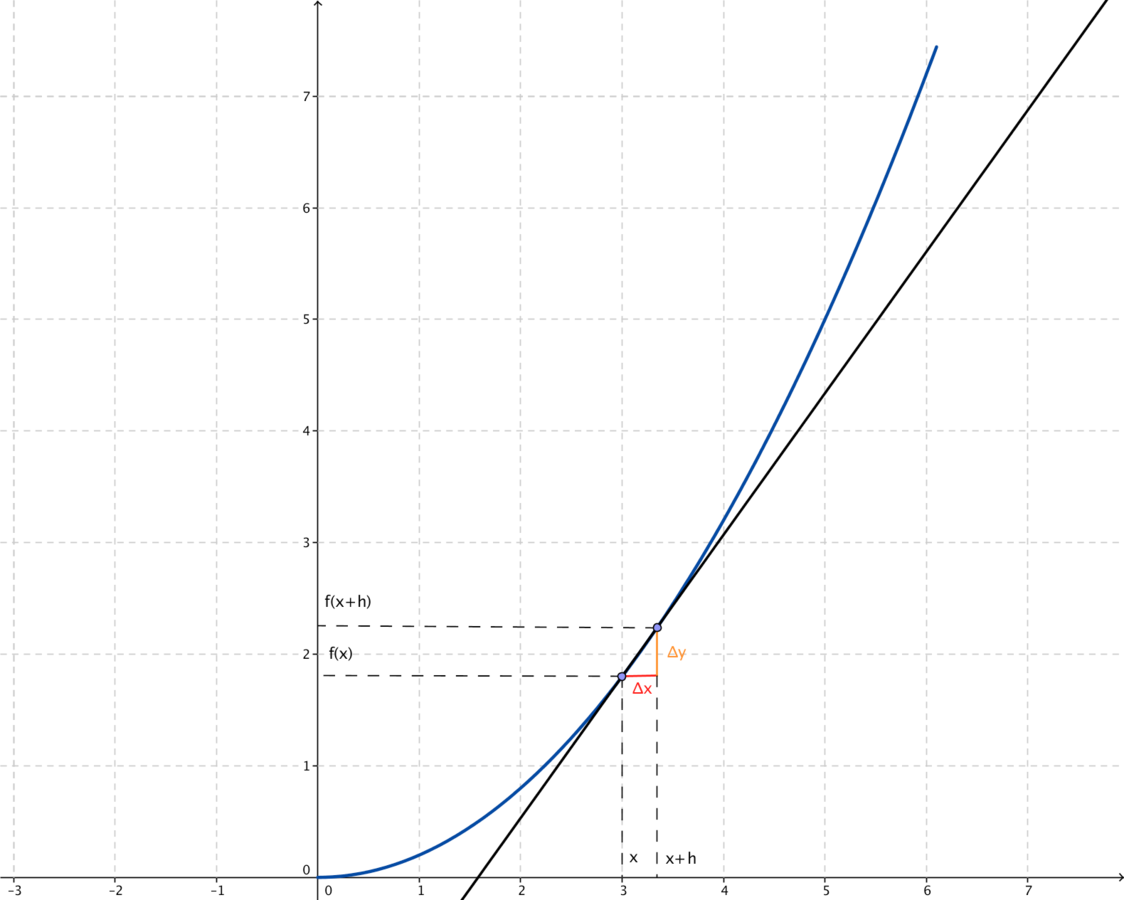
\text{Lutning}=\frac{\Delta y}{\Delta x}=\frac{f(x+h)-f(x)}{h}

L u t n i n g = \frac{​ Δ y ​ ​}{​ Δ x ​} = \frac{​ f ( x + h ) - f ( x ) ​ ​}{​ h ​}

\displaystyle\text{Derivata}=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}

D e r i v a t a = ​ h \to 0 ​ lim ​ ​ \frac{​ f ( x + h ) - f ( x ) ​ ​}{​ h ​}