Gränsvärde och derivatans definition

Först lite om modellering med derivata

Fråga 1:

 

Temperaturen (°C) i en termos med kaffe beskrivs av funktionen \(f(t)\), där \(t\) är tiden i timmar efter kl 08:00.

 

Vad betyder det att:

a) \(f(2)=75\)

b) \(f'(2)=-5\)

 

Först lite om modellering med derivata

Fråga 2:

 

Pelle är \(f(x)\) cm lång när han är \( x\) år.

När han är 14 år är han 162 cm lång och växer 8 cm/år.

 

Formulera detta påsteånde med en eller flera matematiska uttryck som involverar funktionen \( f(x)\).

 

Först lite om modellering med derivata

Fråga 3:

 

En bil har efter tiden \(t \) sekunder kört sträckan \(s(t)\) meter.

Efter 5 sekunder är hastigheten 20 m/s.

 

Formulera detta påsteånde med en eller flera matematiska uttryck som involverar funktionen \( s(t)\).

 

Först lite om modellering med derivata

Fråga 4:

 

I ett skyddat område bor det kaniner, men rovdjur saknas.

Antalet kaniner det första halvåret ges av funktionen

\[N(t)=2 e^{\frac{t}{30}}\]

 

a) Hur många kaniner finns det från början?

b) Hur många finns det efter 60 dagar?

c) Beräkna och tolka \(N'(30)\).

 

Sen lite om begreppet derivata

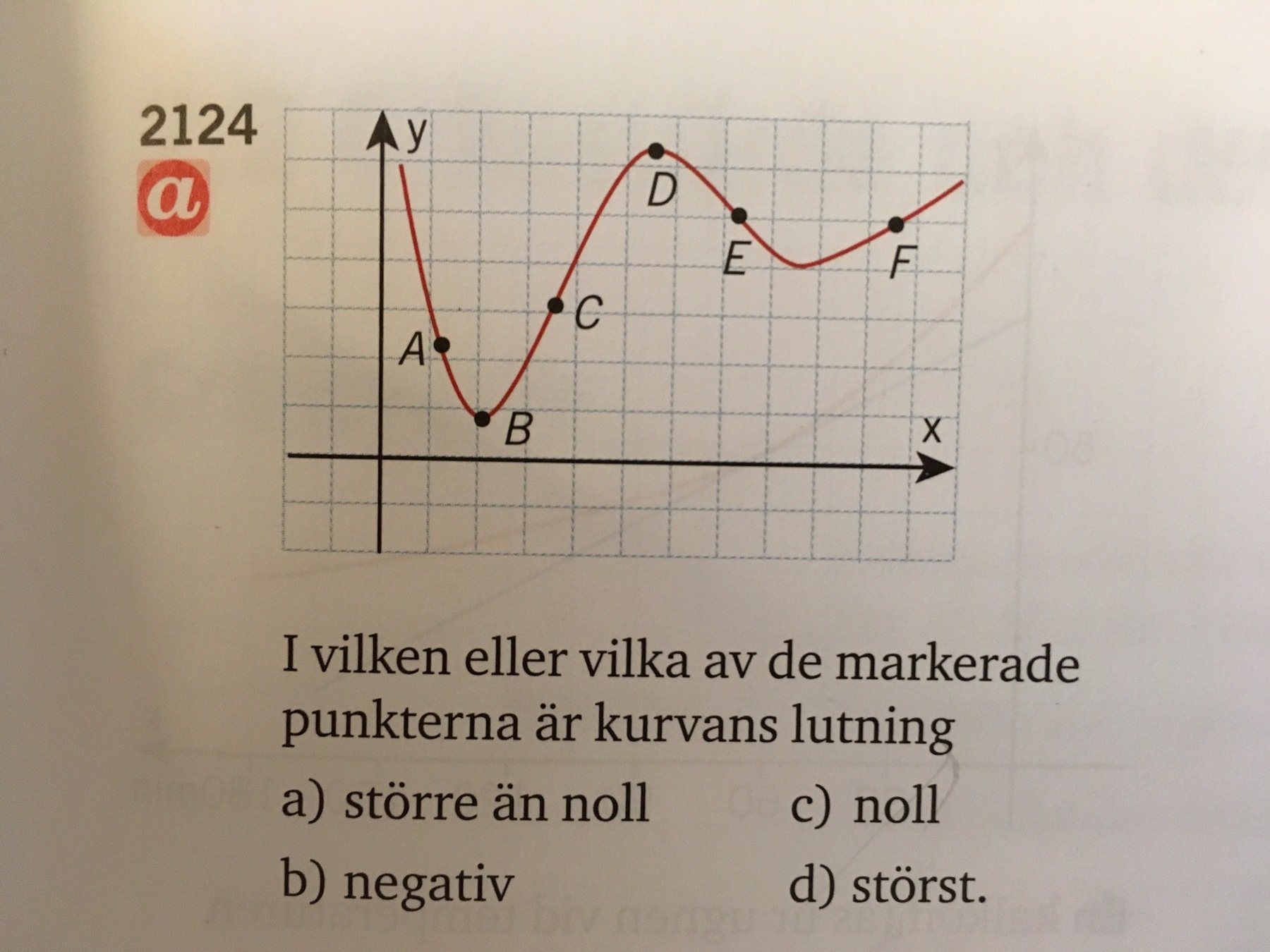
Sen lite om begreppet derivata

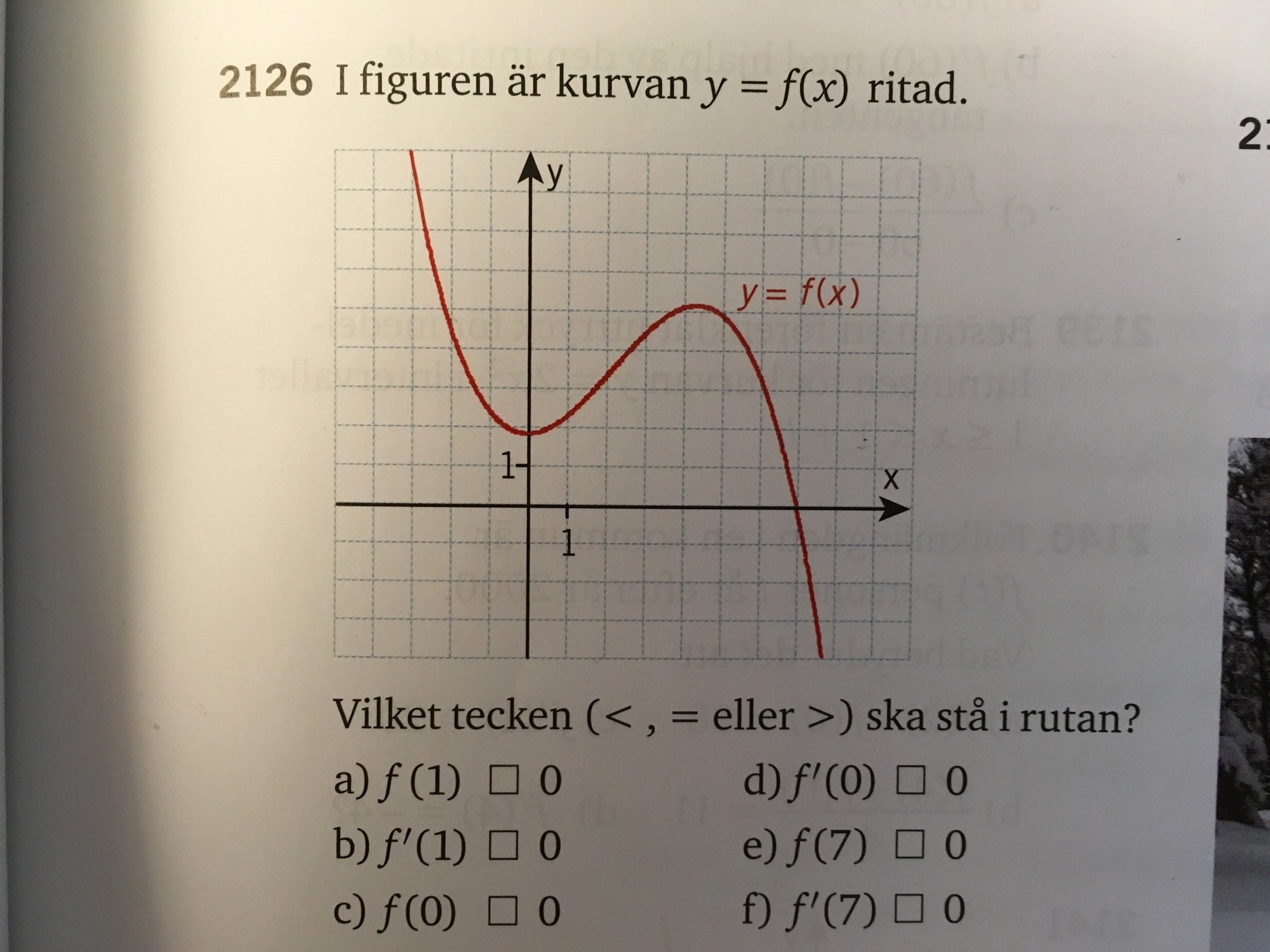
Sen lite om begreppet derivata

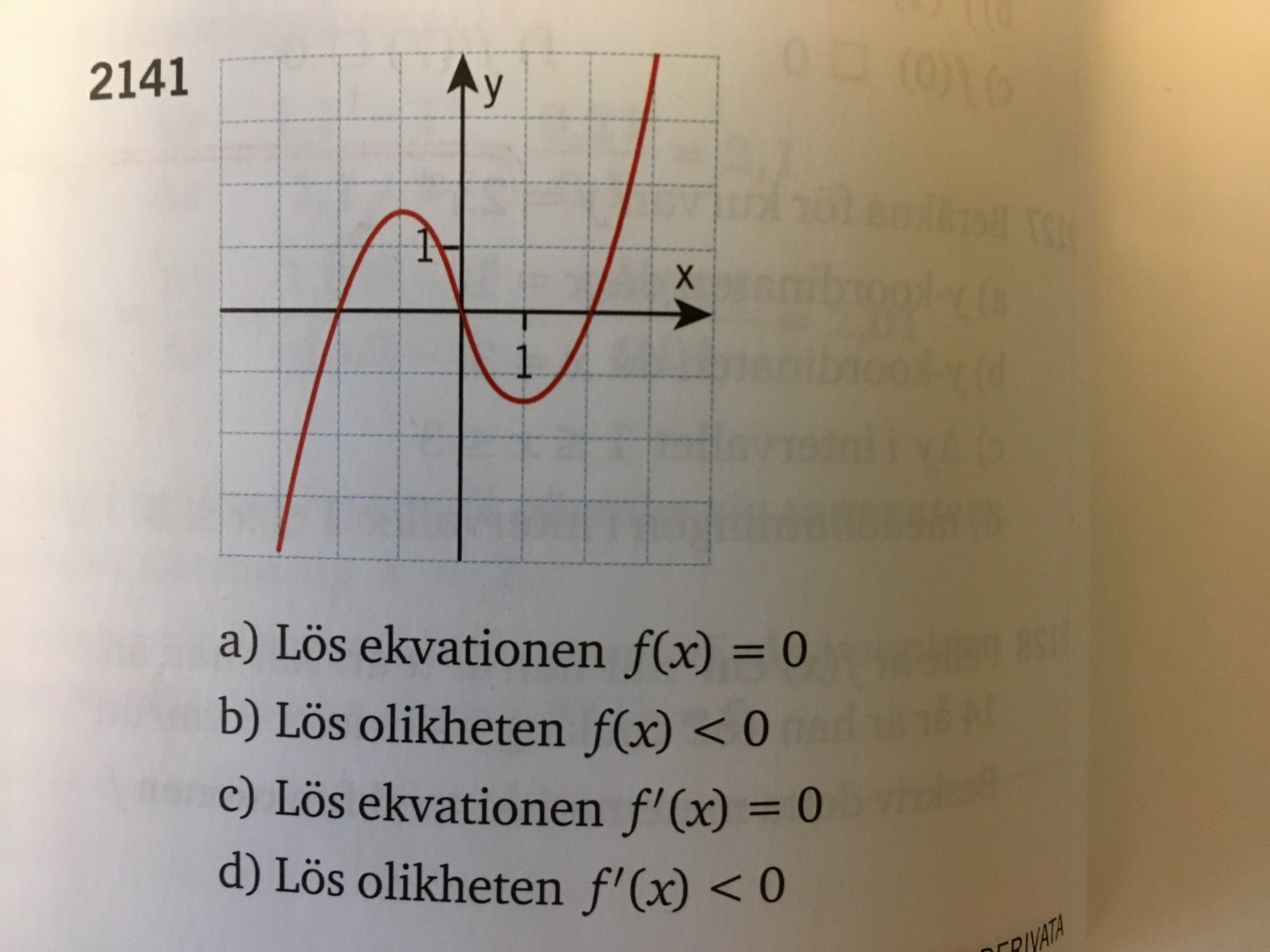
Hur beräknas derivatan (lutningen i en punkt) då?

Sekanten närmar sig tangenten då de två punkterna närmar sig varandra

Ändringskvoten närmar sig derivatan då de två punkterna närmar sig varandra

Exempel: \(f(x)=x^2\)

Ändringskvot

\[\begin{aligned} \frac{\color{purple}\Delta y}{\color{orange}\Delta x}&=\frac{\color{purple}f(a+h)-f(a)}{\color{orange}(a+h)-a}\end{aligned}\]

Uppskatta \(f'(1)\) genom att bestämma ändringskvoten då \(a=1\) och \(h=0{,}1\).

Dvs bestäm \[ f'(1)\approx \frac{\color{purple}f(1{,}1)-f(1)}{\color{orange}1{,}1-1}\]

Ändringskvoten närmar sig derivatan då de två punkterna närmar sig varandra

Exempel: \(f(x)=x^2\)

Ändringskvot

\[\begin{aligned} \frac{\color{purple}\Delta y}{\color{orange}\Delta x}&=\frac{\color{purple}f(a+h)-f(a)}{\color{orange}(a+h)-a}\\ &=\frac{\color{purple}(a+h)^2-a^2}{\color{orange}(a+h)-a}\end{aligned}\]

a) Förenkla uttrycket.

b) Använd det förenklade uttrycket för att uppskatta \(f'(1)\).

Ändringskvoten närmar sig derivatan då de två punkterna närmar sig varandra

Exempel: \(f(x)=x^2\)

Ändringskvot

\[\begin{aligned} \frac{\color{purple}\Delta y}{\color{orange}\Delta x}&=\frac{\color{purple}f(a+h)-f(a)}{\color{orange}(a+h)-a}\\ &=\frac{\color{purple}(a+h)^2-a^2}{\color{orange}(a+h)-a}\\ &=\frac{\color{purple}a^2+2ah+h^2-a^2}{\color{orange}h}\\ &=\frac{\color{purple}2ah+h^2}{\color{orange}h}\\ &=\frac{\color{purple}(2a+h)h}{\color{orange}h}=2a+h\end{aligned}\]

Med \(a=1\) och \(h=0{,}1\):

\[ f'(1)\approx 2\cdot 1+0{,}1=2{,}1\]

Med \(a=1\) och \(h=0{,}01\):

\[f'(1)\approx 2\cdot 1+0{,}01=2{,}01\]

Introducerar begreppet gränsvärde

Gränsvärde

Vi skriver

\(\displaystyle \lim_{x\rightarrow a}f(x)=L\) 

om \(f\) utav \(x\) går mot \(L\) då \(x\) går mot \(a\) (men aldrig blir \(a\)). 

 

Exempel:

\(\displaystyle \lim_{x\rightarrow 1}\left(2x^2+3x\right)=5\)

\(\displaystyle \lim_{x\rightarrow 0}\left(3x+2\right)=2\)

\(\displaystyle \lim_{x\rightarrow 0} \left(\frac{1}{x}\right)=\infty\)

\( \displaystyle \lim_{x\rightarrow 0} \left(\frac{2x^2+3x}{x}\right) = \lim_{x\rightarrow 0}\left(2x+3\right)=3\)

 

Derivatans definition

Derivatan i en punkt \(x=a\) ges av gränsvärdet:

 

\(\displaystyle f'(a)=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}\)

 

Exempel:

\(f(x)=2x^2\)

 

\(\displaystyle f'(a)=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h} =\lim_{h\rightarrow 0}\frac{h(4a+2h)}{h}=\lim_{h\rightarrow 0}\left(4a+2h\right)=4a\)

 

Så \(f'(1)=4\cdot 1=4\), \(f'(2)=4\cdot 2=8\) osv.