Four questions

Jeremias Sulam

On learned proximals and conformal risk control

Inverse Problems

y = A x^* + v

measurements

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)

reconstruction

Inverse Problems

y = A x^* + v

measurements

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)

reconstruction

= \arg\min_x ~-\log p(y|x) - \log p(x)

= \arg\max_x~ p(x|y)

\text{MAP estimate when }R(x) \propto -~p_x(x):\text{ prior}

Mathematical tractability vs Complexity

in a box

simpler models

more assumptions

any model

no assumptions

Denoiser

Linear models

Linear networks

Shallow

ReLU Networks

PnP

Just ask GPT

Learned Proximals

Conformal guarantees for diffusion models

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)

Proximal Gradient Descent: \( x^{t+1} = \text{prox}_R \left(x^t - \eta A^T(Ax^t-y)\right) \)

\text{prox}_R \left( u \right) = \arg\min_x \frac 12 \|u - x\|_2^2 + R(x)

= \texttt{MAP}(x|u), \qquad u = x + v

... a denoiser

\({\color{red}f_\theta}\)

[Venkatakrishnan et al., 2013; Zhang et al., 2017b; Meinhardt et al., 2017; Zhang et al., 2021; Gilton, Ongie, Willett, 2019; Kamilov et al., 2023b; Terris et al., 2023; S Hurault et al. 2021, Ongie et al, 2020; ...]

Learned Proximals

: revisiting PnP

Question 1)

When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\), and for what \(R(x)\)?

Question 2)

How do we find \(f(x) = \text{prox}_R(x)\) for the "correct"

\(R(x) \propto -\log p_x(x)\)?

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)

Proximal Gradient Descent: \( x^{t+1} = \text{prox}_R \left(x^t - \eta A^T(Ax^t-y)\right) \)

\text{prox}_R \left( u \right) = \arg\min_x \frac 12 \|u - x\|_2^2 + R(x)

= \texttt{MAP}(x|u), \qquad u = x + v

... a denoiser

\({\color{red}f_\theta}\)

[Venkatakrishnan et al., 2013; Zhang et al., 2017b; Meinhardt et al., 2017; Zhang et al., 2021; Gilton, Ongie, Willett, 2019; Kamilov et al., 2023b; Terris et al., 2023; S Hurault et al. 2021, Ongie et al, 2020; ...]

Learned Proximals

: revisiting PnP

Theorem [Fang, Buchanan, S.]

Question 1)

When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\), and for what \(R(x)\)?

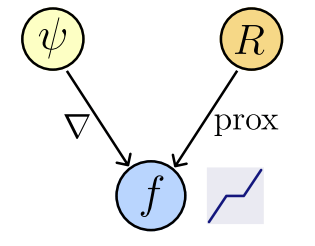
Let \(f_\theta : \mathbb R^n\to\mathbb R^n\) be a network : \(f_\theta (x) = \nabla_\theta \psi (x)\),

where \(\psi_\theta : \mathbb R^n \to \mathbb R,\) convex and differentiable (ICNN).

Then,

1. \(\exists ~R_\theta : \mathbb R^n \to \mathbb R\) not necessarily convex : \(f_\theta(x) \in \text{prox}_{R_\theta}(x),\)

(1. Follows from [Gribonval & Nikolova, 2020, Corollary 1])

2. We can compute \(R_{\theta}(x)\) by solving a convex problem

Learned Proximals

: revisiting PnP

\text{Let } y = x+v , \quad ~ x\sim p_x, ~~v \sim \mathcal N(0,\sigma^2I)

f_\theta = \arg\min_{f_\theta:\text{prox}} \mathbb E_{x,y} \left[ {\ell (f_\theta(y),x)} \right]

Question 2)

How do we find \(f(x) = \text{prox}_R(x)\) for the "correct" \(R(x) \propto -\log p_x(x)\)?

Learned Proximals

: revisiting PnP

Theorem [Fang, Buchanan, S.] (informal)

\hat{f}^* = \arg\min_{f} \lim_{\gamma \searrow 0}~ \mathbb E_{x,y} \left[ \ell^\gamma_\text{PM}(f_\theta(y),x)\right]

\hat{f}^*(y) = \arg\max_c p_{x|y}(c) = \text{prox}_{-\sigma^2\log p_x}(y)

\ell^\gamma_\text{PM} (f_\theta(y),x) = 1- \frac{c}{\gamma^{2n}} \exp\left( -\frac{\|f(y)-x\|_2^2}{\gamma} \right)

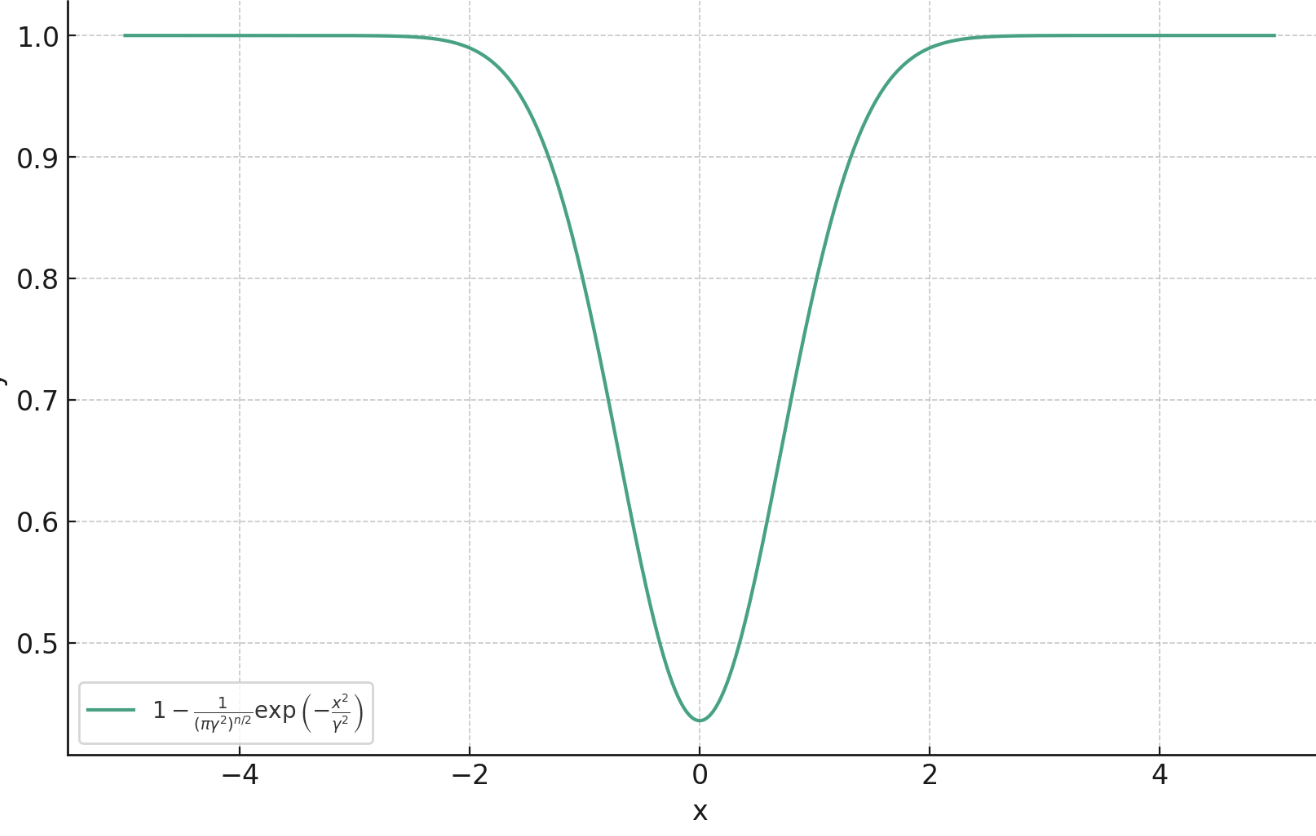
Proximal Matching Loss:

\(\gamma\)

Learned Proximal Networks

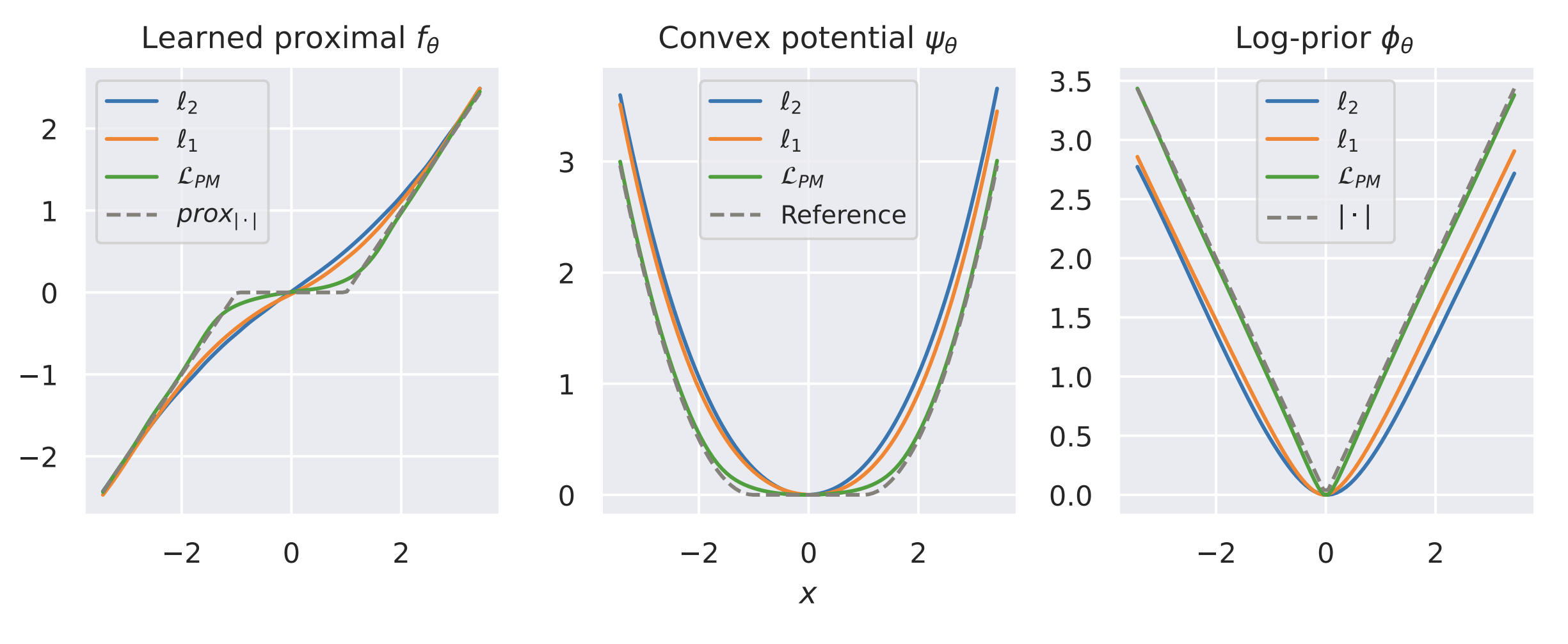
\text{Sample } y = x+v,~ \text{ with } x \sim \text{Laplace}(0,1) \text{ and } v \sim \mathcal N(0,\sigma^2)

Example 1: recovering a prior

Fang, Buchanan & S. What's in a Prior? Learned Proximal Networks for Inverse Problems, ICLR 2024.

Learned Proximal Networks

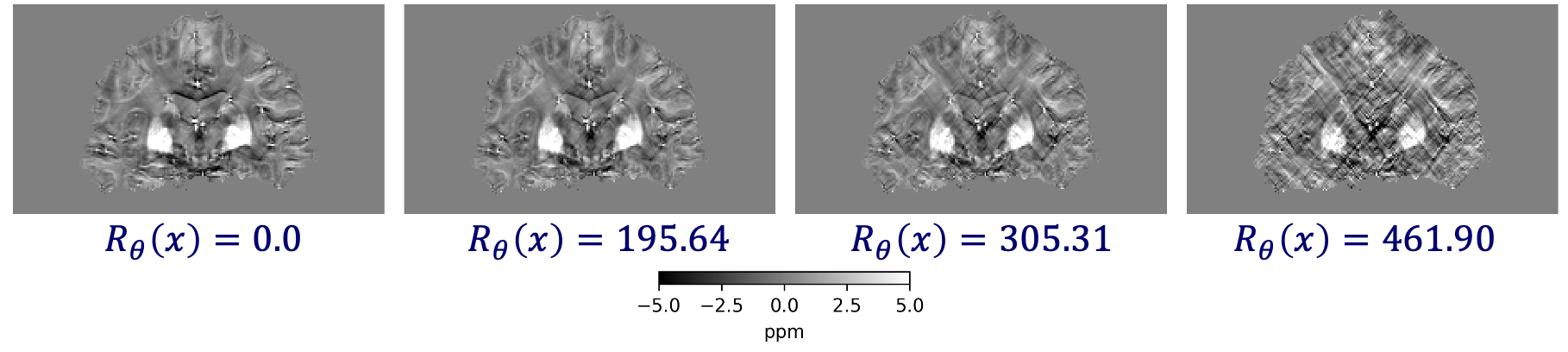
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \hat{R}_\theta(x)

\(R_\theta(x) = 0.0\)

\(R_\theta(x) = 127.37\)

\(R_\theta(x) = 274.13\)

\(R_\theta(x) = 290.45\)

Convergence guarantees

Mathematical tractability vs Complexity

in a box

simpler models

more assumptions

any model

no assumptions

Denoiser

Linear models

Linear networks

Shallow

ReLU Networks

PnP

Just ask GPT

Learned Proximals

Conformal guarantees for diffusion models

in a box

Denoiser

diffusion

Measurements

\[y = Ax + \epsilon,~\epsilon \sim \mathcal{N}(0, \sigma^2\mathbb{I})\]

\[\hat{x} = F(y) \sim \mathcal{P}_y\]

Hopefully \(\mathcal{P}_y \approx p(x \mid y)\), but not needed!

Reconstruction

Question 3)

How much uncertainty is there in the samples \(\hat x \sim \mathcal P_y?\)

Question 4)

How far will the samples \(\hat x \sim \mathcal P_y\) be from the true \(x\)?

Conformal guarantees for diffusion models

Lemma

Given \(m\) samples from \(\mathcal P_y\), let

\[\mathcal{I}(y)_j = \left[ Q_{y_j}\left(\frac{\lfloor(m+1)\alpha/2\rfloor}{m}\right), Q_{y_j}\left(\frac{\lceil(m+1)(1-\alpha/2)\rceil}{m}\right)\right]\]

Then \(\mathcal I(y)\) provides entriwise coverage for a new sample \(\hat x \sim \mathcal P_y\), i.e.

\[\mathbb{P}\left[\hat{x}_j \in \mathcal{I}(y)_j\right] \geq 1 - \alpha\]

\(0\)

\(1\)

low: \( l(y) \)

\(\mathcal{I}(y)\)

up: \( u(y) \)

Question 3)

How much uncertainty is there in the samples \(\hat x \sim \mathcal P_y?\)

(distribution free)

 cf [Feldman, Bates, Romano, 2023]

\(y\)

lower

upper

intervals
\(|\mathcal I(y)_j|\)

Conformal guarantees for diffusion models

\(0\)

\(1\)

ground-truth is

contained

\(\mathcal{I}(y_j)\)

\(x_j\)

Conformal guarantees for diffusion models

Question 4)

How far will the samples \(\hat x \sim \mathcal P_y\) be from the true \(x\)?

Conformal guarantees for diffusion models

[Angelopoulos et al, 2022]

Risk Controlling Prediction Set

For risk level \(\epsilon\), failure probability \(\delta\), \(\mathcal{I}(y_j) \) is a RCPS if

\[\mathbb{P}\left[\mathbb{E}\left[\text{fraction of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]

[Angelopoulos et al, 2022]

Question 4)

How far will the samples \(\hat x \sim \mathcal P_y\) be from the true \(x\)?

\(0\)

\(1\)

ground-truth is

contained

\(\mathcal{I}(y_j)\)

\(x_j\)

Conformal guarantees for diffusion models

[Angelopoulos et al, 2022]

ground-truth is

contained

\(0\)

\(1\)

\(\mathcal{I}(y_j)\)

\(\lambda\)

\(x_j\)

Procedure:

\[\hat{\lambda} = \inf\{\lambda \in \mathbb{R}:~ \hat{\text{risk}}_{(\mathcal S_{cal})} \leq \epsilon,~\forall \lambda' \geq \lambda \}\]

[Angelopoulos et al, 2022]

single \(\lambda\) for all \(\mathcal I(y_j)\)!

Risk Controlling Prediction Set

For risk level \(\epsilon\), failure probability \(\delta\), \(\mathcal{I}(y_j) \) is a RCPS if

\[\mathbb{P}\left[\mathbb{E}\left[\text{fraction of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]

[Angelopoulos et al, 2022]

Question 4)

How far will the samples \(\hat x \sim \mathcal P_y\) be from the true \(x\)?

\(\mathcal{I}_{\bm{\lambda}}(y)_j = [l_\text{low,j} - \lambda, l_\text{up,j} + \lambda]\)

Conformal guarantees for diffusion models

\(K\)-RCPS: High-dimensional Risk Control

\[\tilde{{\lambda}}_K = \underset{\lambda \in \mathbb R^K}{\arg\min}~\sum_{k \in [K]}\lambda_k~\quad \text{s.t. }\quad \mathcal I_{\lambda_j}(y) : \text{RCPS}\]

scalar \(\lambda \in \mathbb{R}\)

vector \(\bm{\lambda} \in \mathbb{R}^d\)

\(\mathcal{I}_{\lambda}(y)_j = [\text{low}_j - \lambda, \text{up}_j + \lambda]\)

\(\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{low}_j - \lambda_j, \text{up}_j + \lambda_j]\)

\(\rightarrow\)

Procedure:

1. Find anchor point

\[\tilde{\bm{\lambda}}_K = \underset{\bm{\lambda}}{\arg\min}~\sum_{k \in [K]}\lambda_k~\quad\text{s.t.}~~~\hat{\text{risk}}^+(\bm{\lambda})_{(S_{opt})} \leq \epsilon\]

2. Choose

\[\hat{\beta} = \inf\{\beta \in \mathbb{R}:~\hat{\text{risk}}_{S_{cal}}^+(\tilde{\bm{\lambda}}_K + \beta'\bf{1}) \leq \epsilon,~\forall~ \beta' \geq \beta\}\]

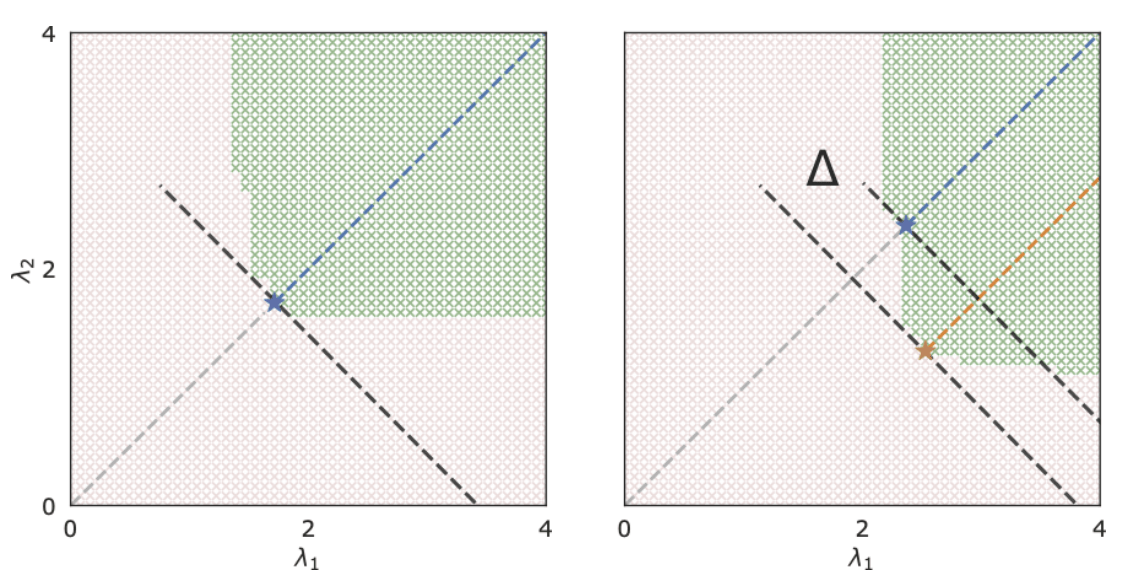
\(\tilde{\bm{\lambda}}_K\)

Conformal guarantees for diffusion models

\(K\)-RCPS: High-dimensional Risk Control

\[\tilde{{\lambda}}_K = \underset{\lambda \in \mathbb R^K}{\arg\min}~\sum_{k \in [K]}\lambda_k~\quad \text{s.t. }\quad \mathcal I_{\lambda_j}(y) : \text{RCPS}\]

scalar \(\lambda \in \mathbb{R}\)

vector \(\bm{\lambda} \in \mathbb{R}^d\)

\(\rightarrow\)

Procedure:

1. Find anchor point

\[\tilde{\bm{\lambda}}_K = \underset{\bm{\lambda}}{\arg\min}~\sum_{k \in [K]}\lambda_k~\quad\text{s.t.}~~~\hat{\text{risk}}^+(\bm{\lambda})_{(S_{opt})} \leq \epsilon\]

2. Choose

\[\hat{\beta} = \inf\{\beta \in \mathbb{R}:~\hat{\text{risk}}_{S_{cal}}^+(\tilde{\bm{\lambda}}_K + \beta'\bf{1}) \leq \epsilon,~\forall~ \beta' \geq \beta\}\]

\(\hat{R}^{\gamma}(\bm{\lambda}_{S_{opt}})\leq \epsilon\)

Guarantee: \(\mathcal{I}_{\bm{\lambda}_K,\hat{\beta}}(y)_j \) are \((\epsilon,\delta)\)-RCPS

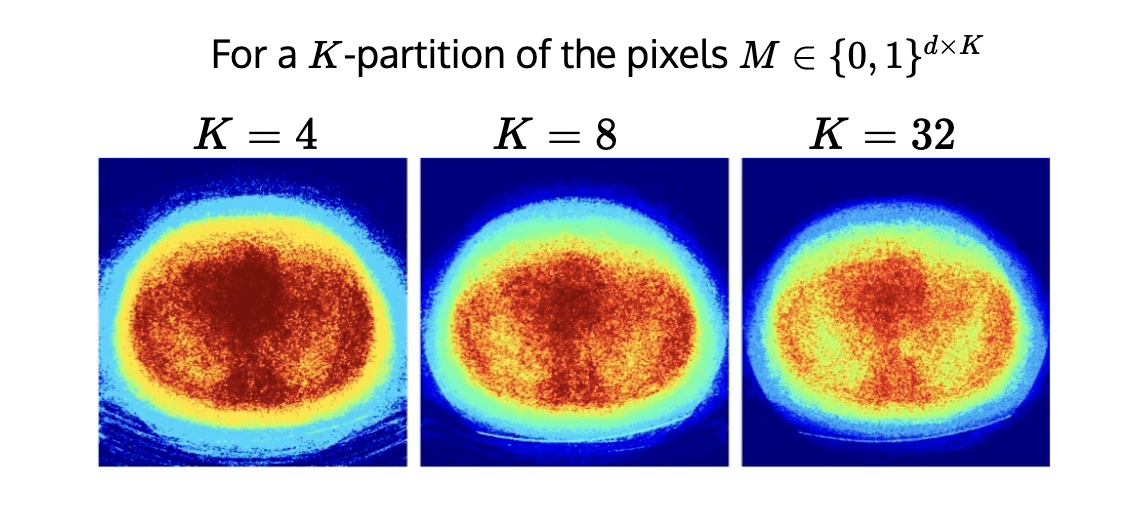
\(\tilde{\bm{\lambda}}_K\)

\(\mathcal{I}_{\lambda}(y)_j = [\text{low}_j - \lambda, \text{up}_j + \lambda]\)

\(\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{low}_j - \lambda_j, \text{up}_j + \lambda_j]\)

\(\hat{\lambda}_K\)

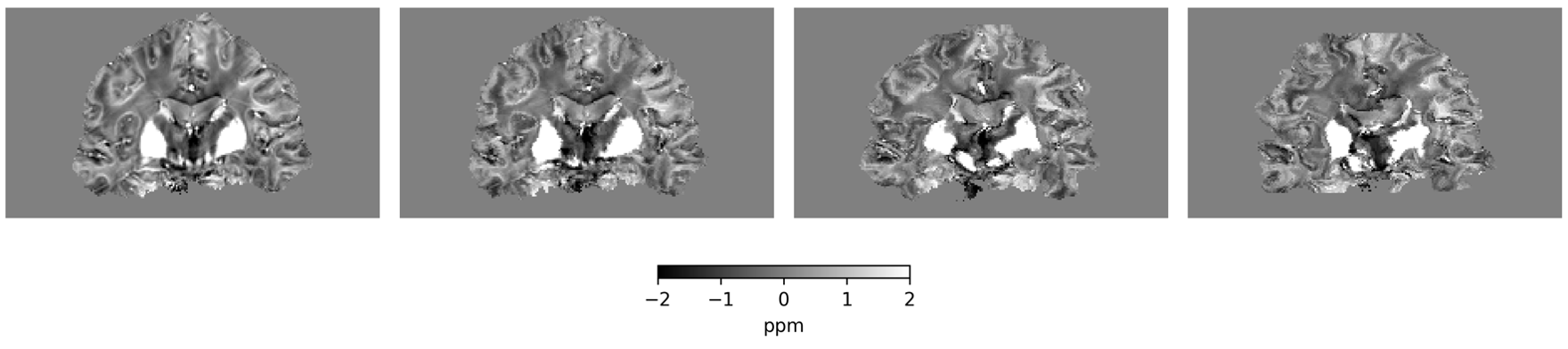
conformalized uncertainty maps

\(K=4\)

\(K=8\)

\[\mathbb{P}\left[\mathbb{E}\left[\text{fraction of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]

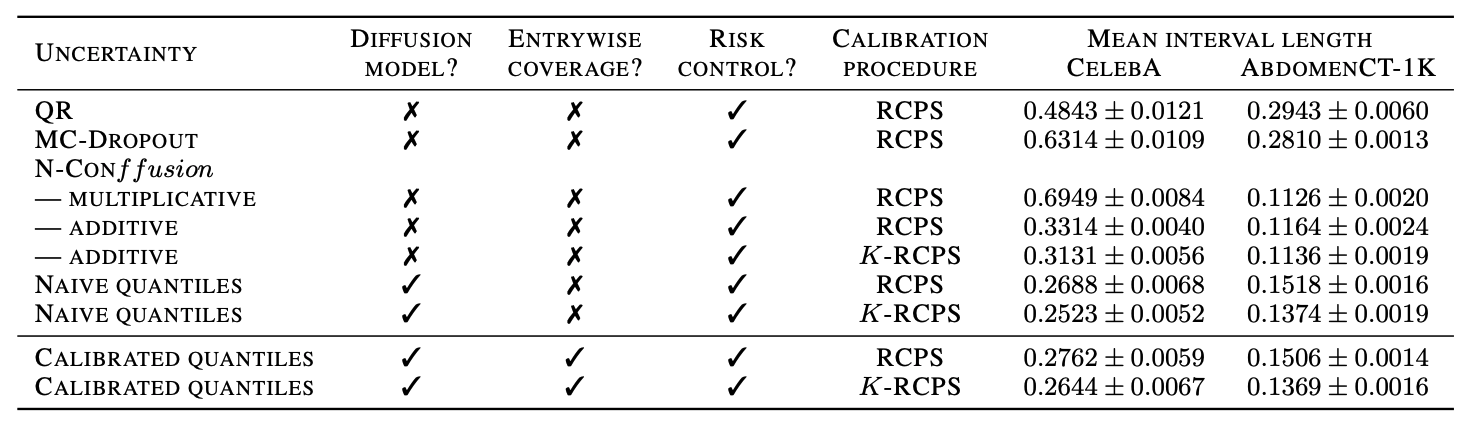
Conformal guarantees for diffusion models

c.f. [Kiyani et al, 2024]

Teneggi, Tivnan, Stayman, S. How to trust your diffusion model: A convex optimization approach to conformal risk control. ICML 2023

Question 1)

When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\), and for what \(R(x)\)?

Gradients of ICNN, and computable \(R(x)\)

Question 2)

How do we find \(f(x) = \text{prox}_R(x)\) for the "correct"

\(R(x) \propto -\log p_x(x)\)?

Use proximal matching loss

Calibrated quantiles

Question 3)

How much uncertainty is there in the samples \(\hat x \sim \mathcal P_y?\)

Use K-RCPS to conformalize

Question 4)

How far will the samples \(\hat x \sim \mathcal P_y\) be from the true \(x\)?

Question 1)

When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\), and for what \(R(x)\)?

Gradients of ICNN, and computable \(R(x)\)

Question 2)

How do we find \(f(x) = \text{prox}_R(x)\) for the "correct"

\(R(x) \propto -\log p_x(x)\)?

Use proximal matching loss

Calibrated quantiles

Question 3)

How much uncertainty is there in the samples \(\hat x \sim \mathcal P_y?\)

Use K-RCPS to conformalize

Question 4)

How far will the samples \(\hat x \sim \mathcal P_y\) be from the true \(x\)?

...that's it!

Zhenghan Fang
JHU

Jacopo Teneggi
JHU

Sam Buchanan
TTIC

Learned Proximal Networks

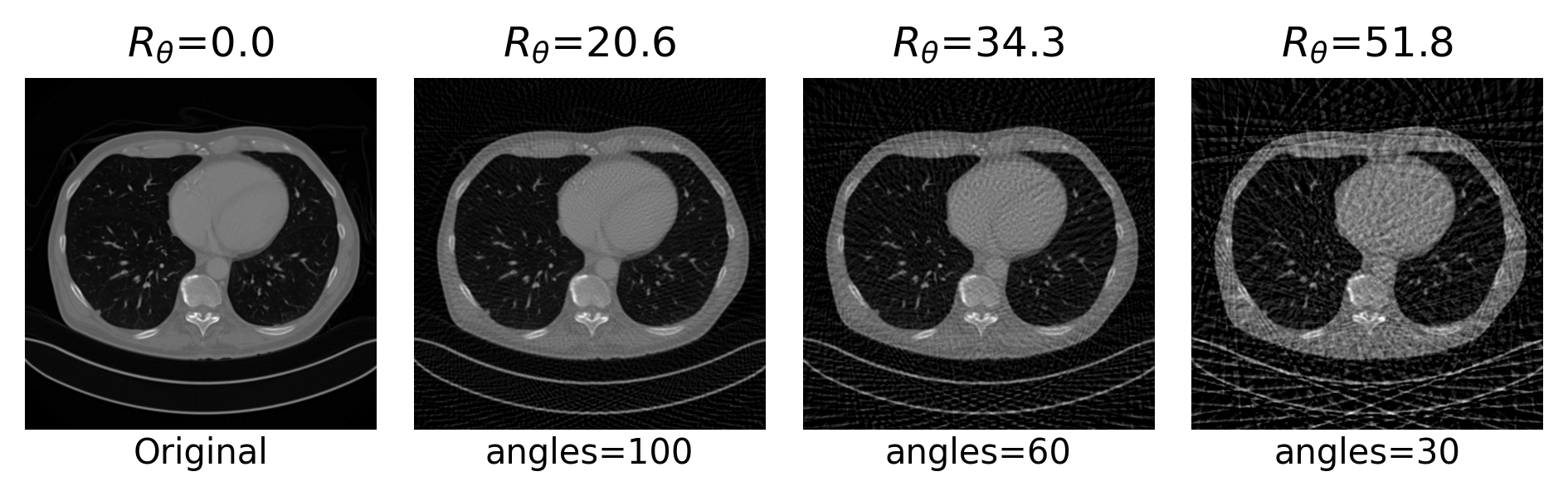
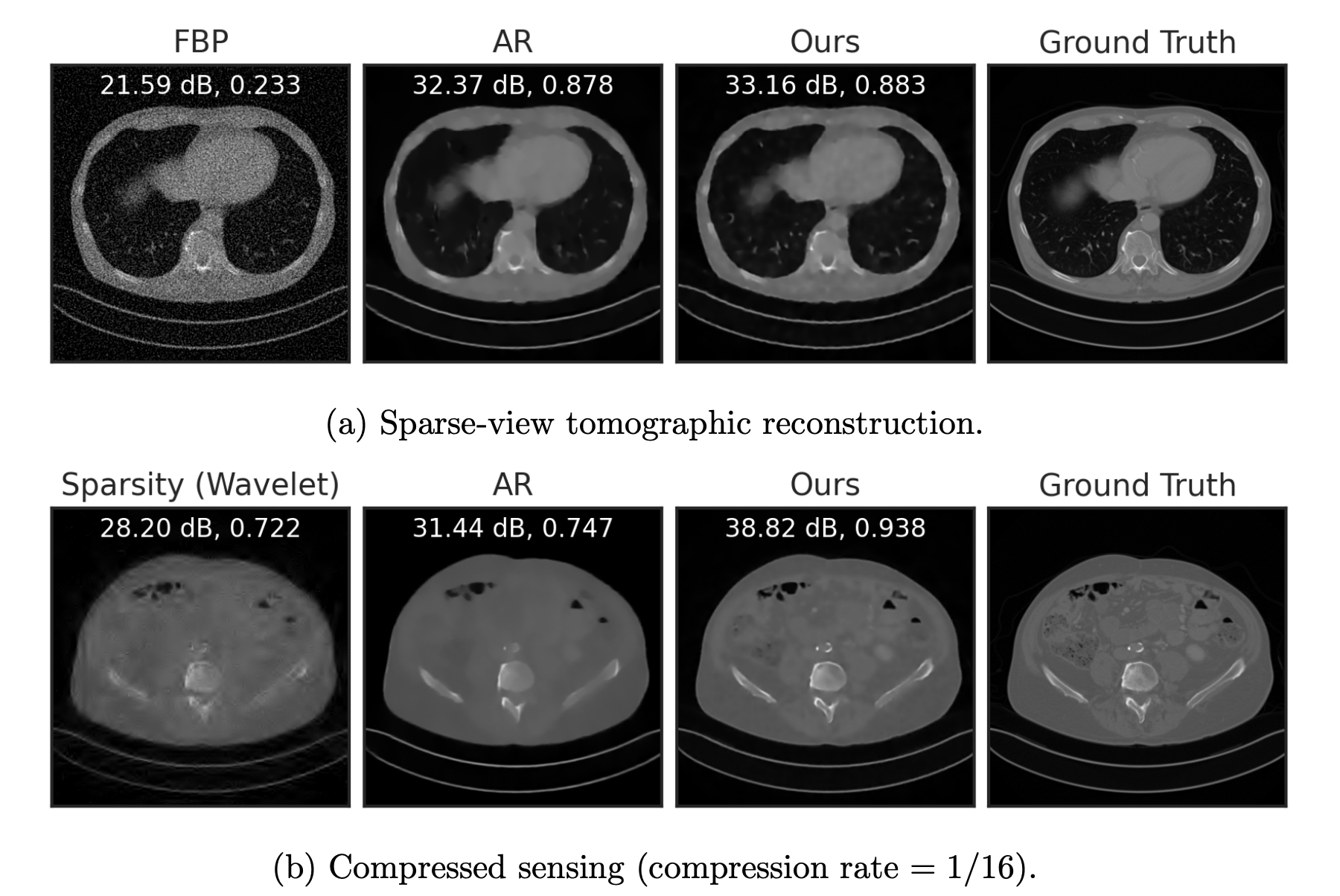
Example 2: a prior for CT

Learned Proximal Networks

Example 2: a prior for CT

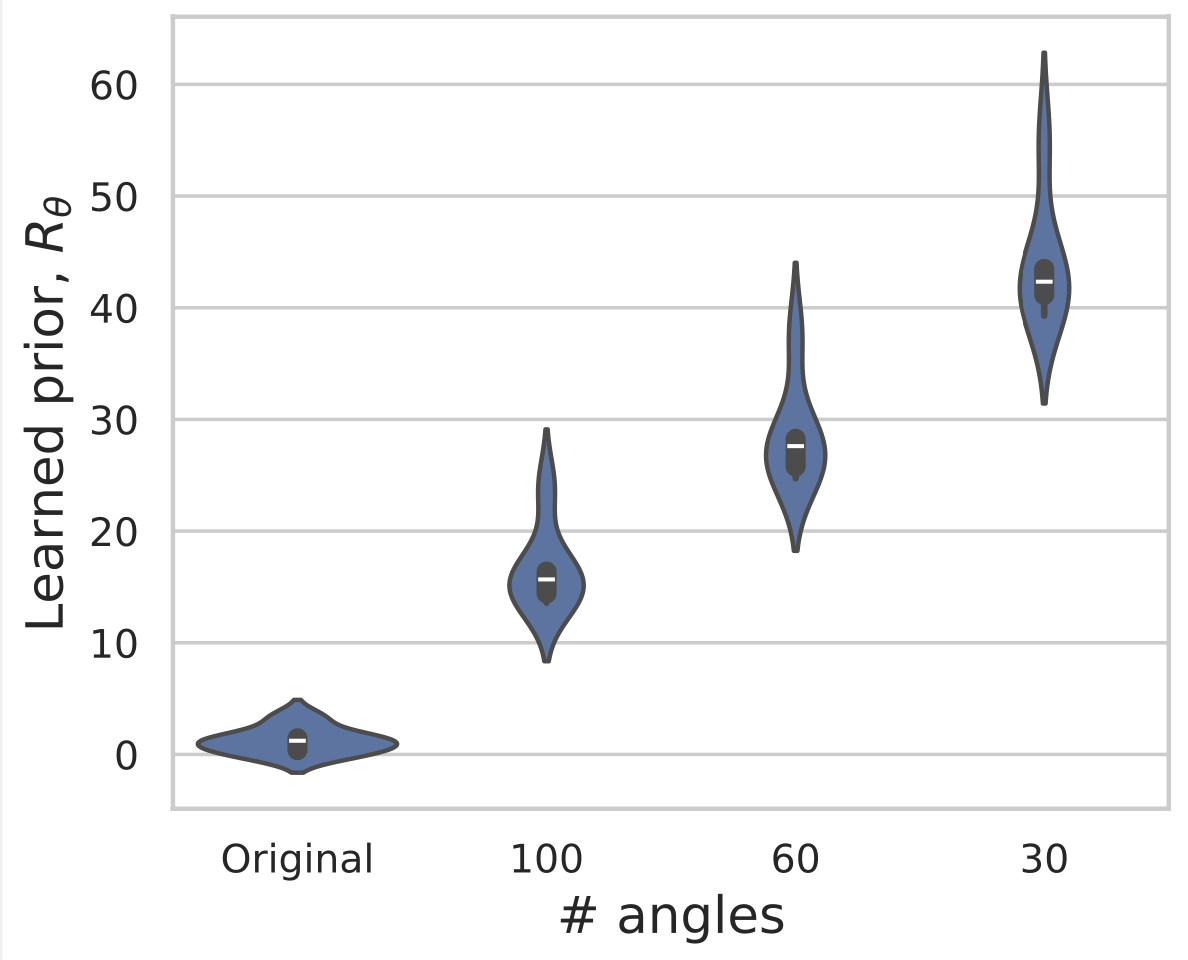
Learned Proximal Networks

Example 2: a prior for CT

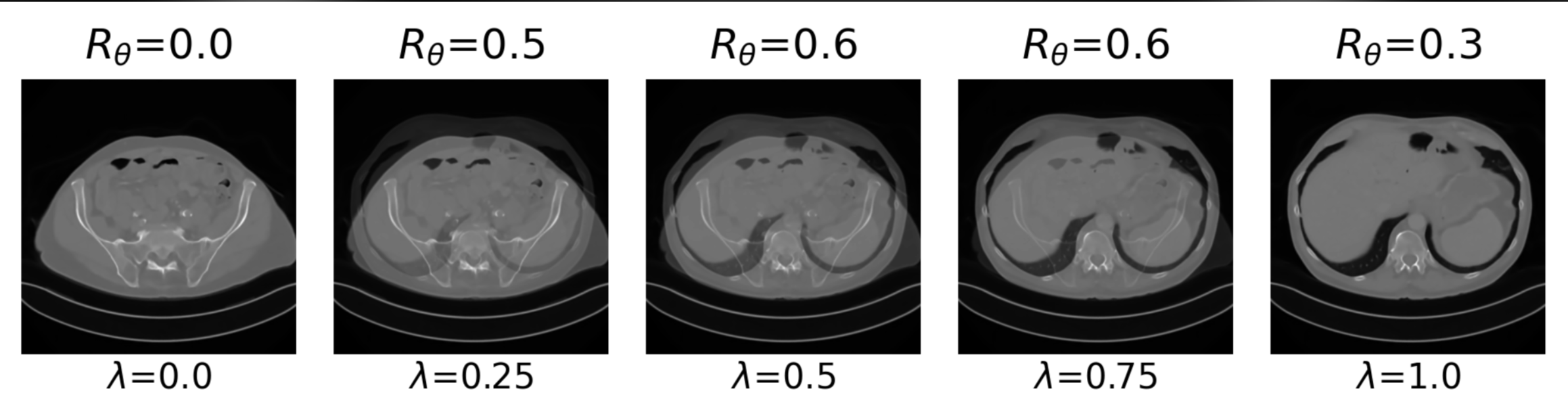
Learned Proximal Networks

Example 2: a prior for CT

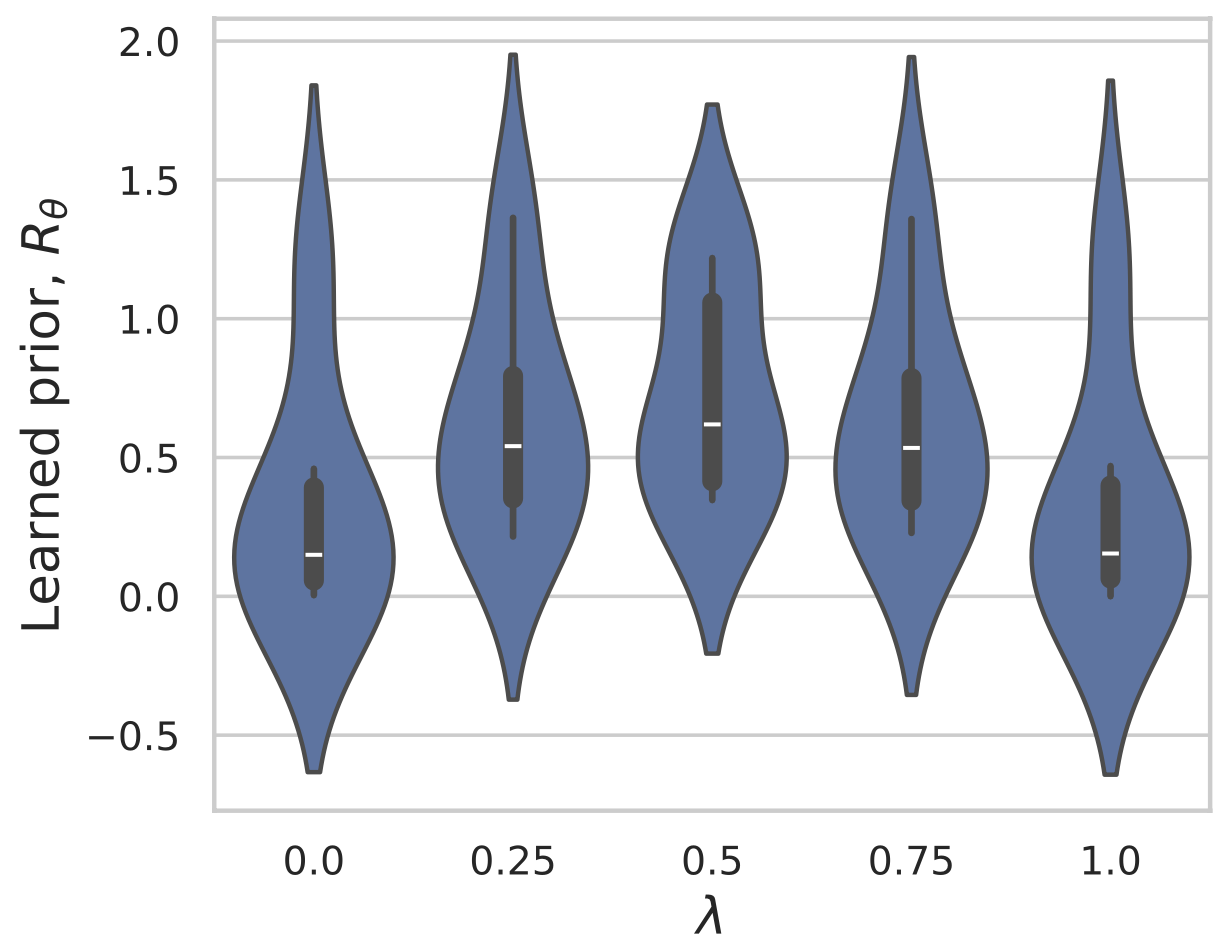
Learned Proximal Networks

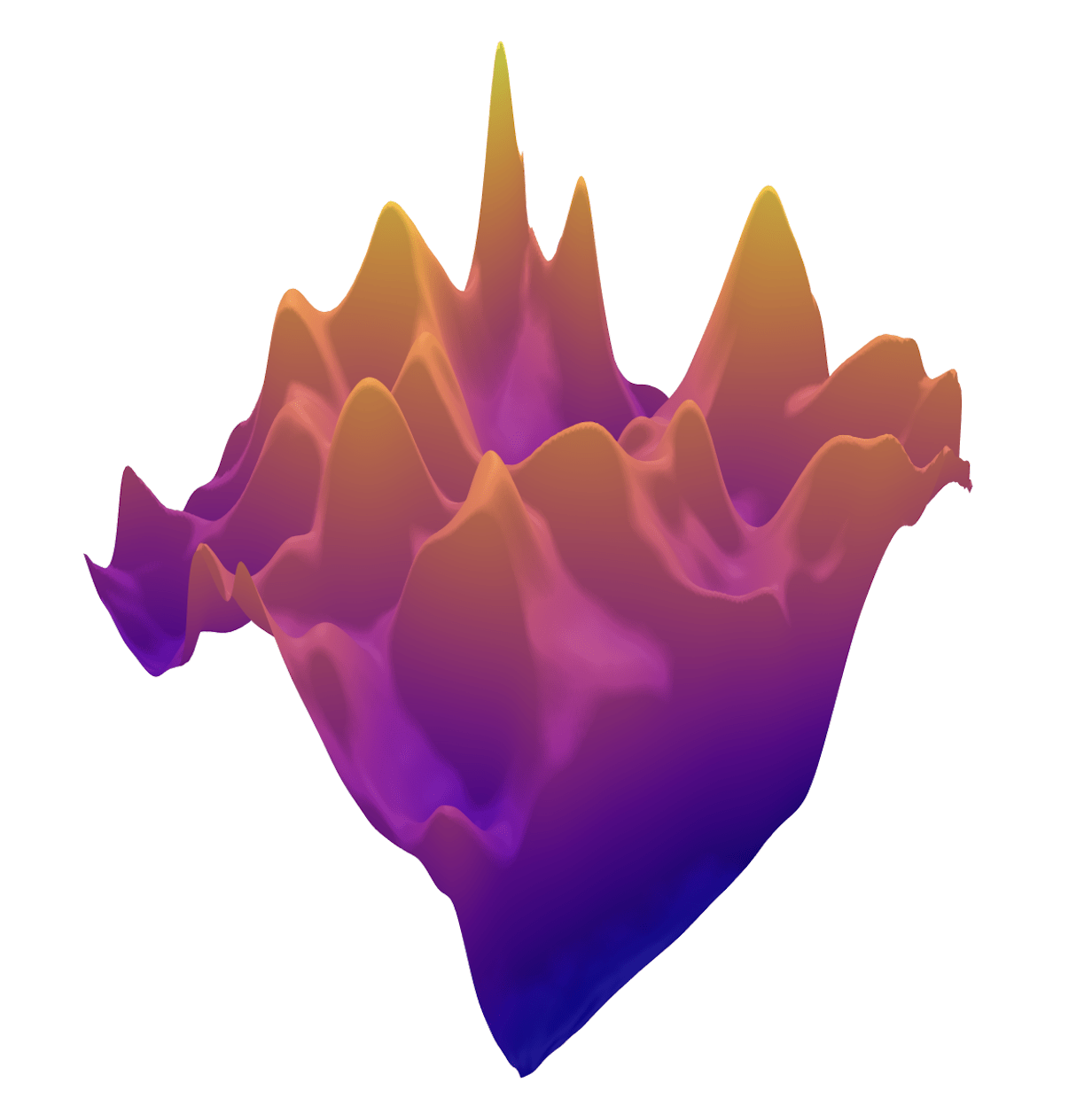
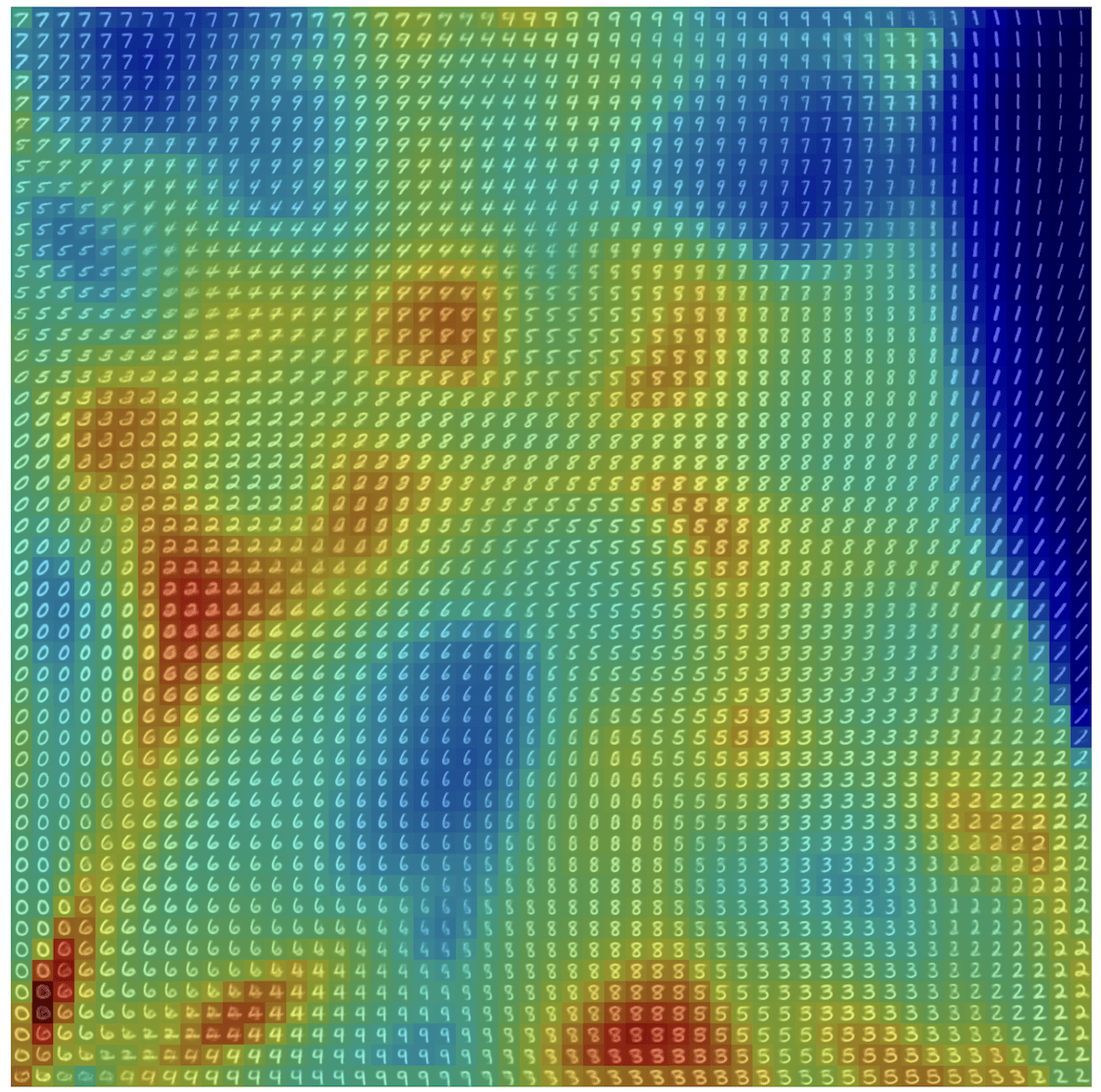
\(R(\tilde{x})\)

Example 2: priors for images

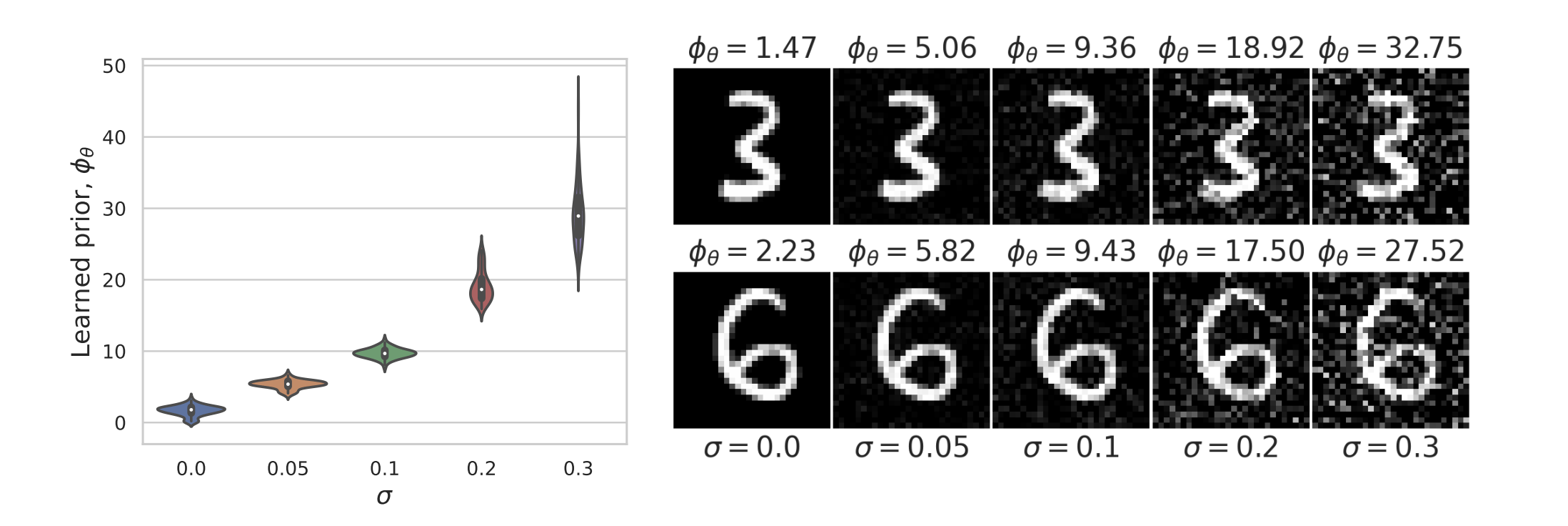
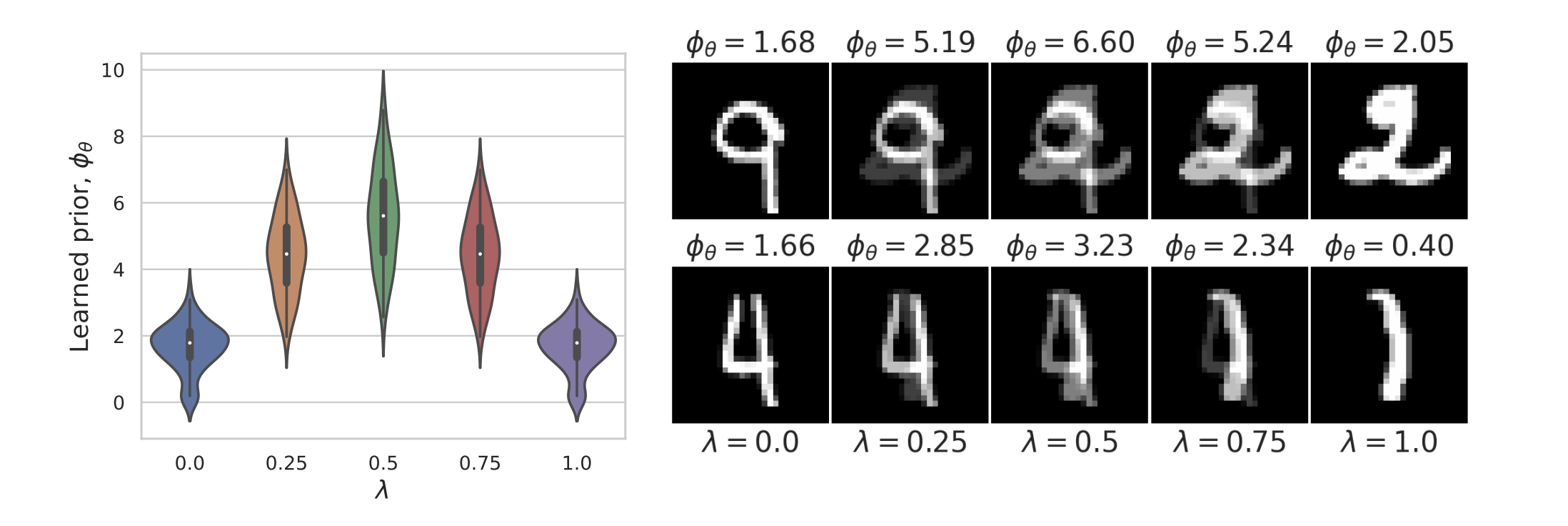
Learned Proximal Networks

Example 2: priors for images

x^{t+1} = \text{prox}_{\hat R} \left(x^t - \eta A^T(Ax^t - y)\right)

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \hat{R}(x)

Learned Proximal Networks

via

Convergence Guarantees

Theorem (PGD with Learned Proximal Networks)

x^{t+1} = \text{prox}_{\hat R} \left(x^t - \eta A^T(Ax^t - y)\right)

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \hat{R}(x)

Let \(f_\theta = \text{prox}_{\hat{R}} {\color{grey}\text{ with } \alpha>0}, \text{ and } 0<\eta<1/\sigma_{\max}(A) \) with smooth activations

\text{Then } \exists x^* : \lim_{k\to\infty} x^t = x^* \text{ and }

f_\theta(x^* - \eta A^T(Ax^*-y)) = x^*

(Analogous results hold for ADMM)

Learned Proximal Networks

Convergence guarantees for PnP