Computational Inverse Problems

From Foundations to Modern Approaches

J. Sulam

Bogotá, Colombia

Octubre 2025

Inverse Problems

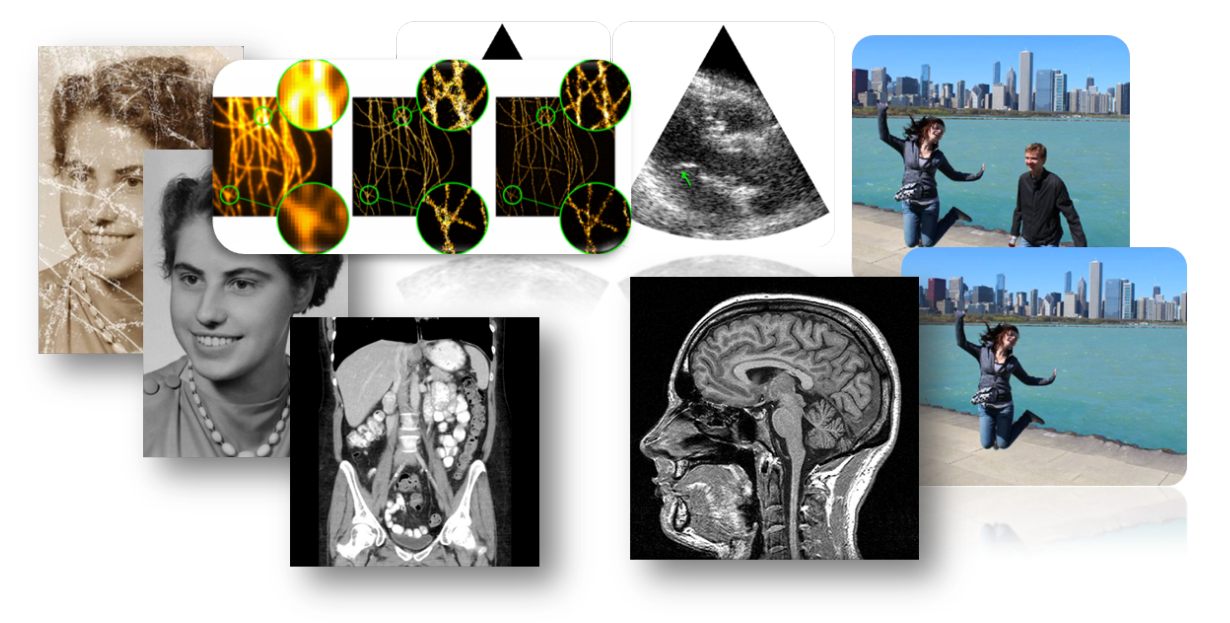
\(x:\) phenomenon of interest

\(y = A(x):\) measurements

How do we estimate \(x\) from \(y\)?

Inverse Problems

\(\mathbb{R}^n\)

\(A :  \mathbb{R}^n \to \mathbb{R}^m\)

\(x\)

\(y\)

\(\mathbb{R}^m\)

inversion

Inverse Problems

\(A :  \mathbb{R}^n \to \mathbb{R}^m\)

\(\mathbb{R}^n\)

\(x\)

\(y\)

\(\mathbb{R}^m\)

  • Computed Tomography

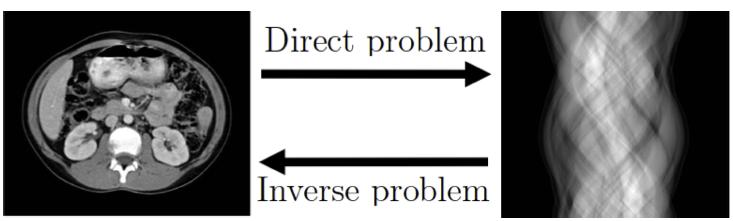
inversion

inversion

Inverse Problems

\(A :  \mathbb{R}^n \to \mathbb{R}^m\)

\(\mathbb{R}^n\)

\(x\)

\(y\)

\(\mathbb{R}^m\)

  • Computed Tomography

inversion

  • Imaging

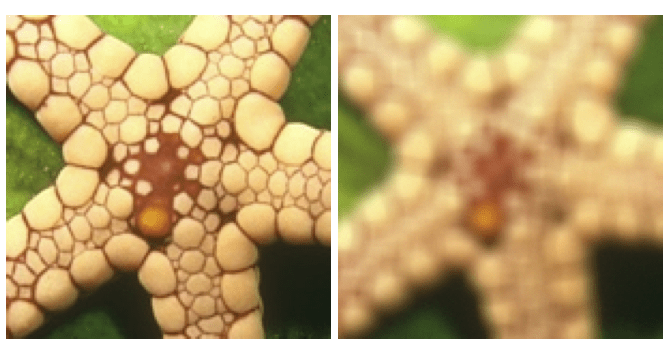
inversion

[Xiang et al, 2024]

Inverse Problems

\(A :  \mathbb{R}^n \to \mathbb{R}^m\)

\(\mathbb{R}^n\)

\(x\)

\(y\)

\(\mathbb{R}^m\)

  • Computed Tomography

inversion

  • Imaging
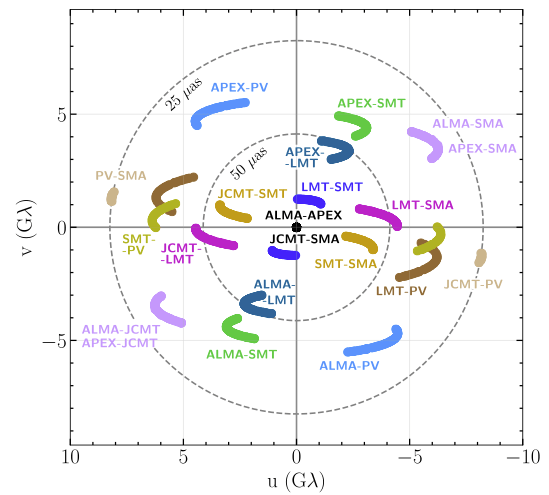
  • Astronomy

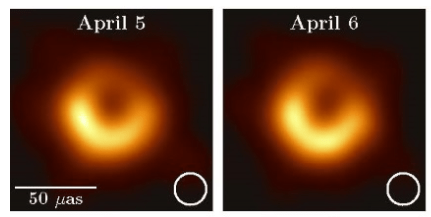
inversion

[Event Horizon Telescope Collaboration, Astrophys. J. Lett. 875 (2019).]

Agenda

PART I:  Foundations

PART II:  Regularization and Priors

PART III:  Data-driven Models

PART I:  Foundations

PART I:  Foundations

A problem is a well-posed problem if
 

1. (Existence) There exist at least one solution

2. (Uniqueness) There is at most one solution

3. (Stability) The solution depends continuously on the data

Forward problem   (well-posed)

\[y = A x + z\]

forward operator
phenomenon of interest
measurements
noise

A problem is a well-posed problem if
 

1. (Existence) There exist at least one solution

2. (Uniqueness) There is at most one solution

3. (Stability) The solution depends continuously on the data

Inverse problem

\[\text{find }x \text{ so that }y = A x + z\]

Can we invert the operator \(A\)? 

PART I:  Foundations


\[\text{find }x \text{ so that }y = A x + z\]

(unstable)

 

Error \(\|x - \hat x\|_2 \leq \|A^{-1}\|_2\|z\|_2 \propto \frac{1}{\lambda_n} \|z\|_2\)

 

\[\hat x = A^{-1}y = x + A^{-1}z\]

 

\(1~ \bullet~\) If \(n=m\) and \(A:\) non-singular:

 

 

\(=\)

\(+\)

Inverse Problem

\(2~ \bullet~\) If \(n<m\), then \(A\) cannot span \(\mathbb R^m\).

Thus, \(y \notin \text{span}(A)\), and thus \(\nexists ~ x :  y = Ax\).

(non-existence)

\(=\)

\(+\)

 

\[\hat x = A^{-1}y = x + A^{-1}z\]

 

\(1~ \bullet~\) If \(n=m\) and \(A:\) non-singular:

 

 


\[\text{find }x \text{ so that }y = A x + z\]

Inverse Problem

(non-uniqueness)

\(3~ \bullet~\) If \(n>m\), and \(A:\) full-rank. 

\(=\)

\(+\)

\(2~ \bullet~\) If \(n<m\), then \(A\) cannot span \(\mathbb R^m\).

Thus, \(y \notin \text{span}(A)\), and thus \(\nexists ~ x :  y = Ax\).

 

\[\hat x = A^{-1}y = x + A^{-1}z\]

 

\(1~ \bullet~\) If \(n=m\) and \(A:\) non-singular:

 

 


\[\text{find }x \text{ so that }y = A x + z\]

Inverse Problem

(non-uniqueness)

\(3~ \bullet~\) If \(n>m\), and \(A:\) full-rank. 

\(=\)

\(+\)

\[\min_x ~R(x) ~~ \text{s.t.}~~ y = Ax\]

Strategy: define a new criteria, \(R(x): \mathbb R^n \to \mathbb R\)

Analytical Example ->


\[\text{find }x \text{ so that }y = A x + z\]

Inverse Problem

PART I:  Foundations

PART II:  

Regularization and Priors

PART II:  Regularization and Priors

A Bayesian Perspective on Inverse Problems

Forward Model:

\(y = A x + z\)

where \(x \sim p, Z\sim\mathcal N(0,\sigma^2 I_n)\)

problem modeled by a joint density \(p(x,y,z)\)

What is the posterior distribution for the unknown, \(p(x|y)\)?

Inversion: (inference)

What is the most likely unknown, \(\arg\max_x p(x|y)\)?

Maximum a Posteriori (MAP)

\(x_\text{MAP}\)

\[\arg\max_x~ p(x|y)\]

Maximum a Posteriori (MAP)

\[= \arg\max_x~\frac{p(y|x)~p(x)}{p(y)}\]

\[= \arg\max_x~ p(y|x)p(x)\]

\[= \arg\min_x~ -\log p(y|x) - \log p(x)\]

 \(y = Ax + z\), with Gaussian \(z ~~\Rightarrow ~~ p(y|x) =\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}{\|Ax-y\|^2_2}}\) 

\[= \arg\min_x~ \frac{1}{2\sigma^2} \|Ax-y\|^2_2 - \log p(x)\]

\[= \arg\min_x~ \frac{1}{2} \|Ax-y\|^2_2 + \lambda R(x)\]

PART II:  Regularization and Priors

likelihood
prior distribution

What priors should we choose?

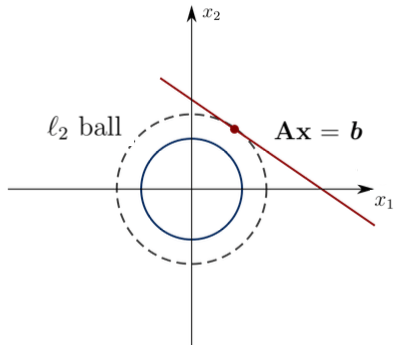
\(1~ \bullet~\) \(R(x) =\|x\|^2_2\): low Euclidean norm

does not allow for recovery

\(A^\dagger y = A^\dagger (Ax_0)=A^\top (AA^\top)^{-1}A x_0 \neq x_0\)

\[\min_x~ \frac{1}{2} \|Ax-y\|^2_2 + \lambda R(x)\]

What priors should we choose?

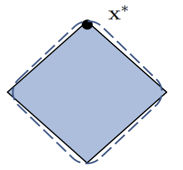
\(2~ \bullet~\) \(R(x) =\|x\|_0 = |\{x_i : x_i\neq 0\}|\): promoting sparsity

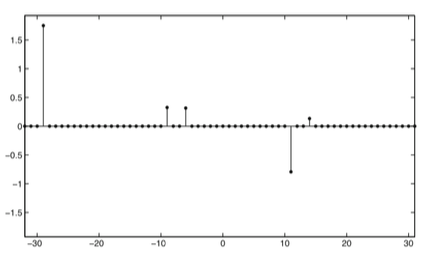
\[\min_x~ \frac{1}{2} \|Ax-y\|^2_2 + \lambda R(x)\]

What priors should we choose?

\(2~ \bullet~\) \(R(x) = \|x\|_0 = |\{x_i : x_i\neq 0\}|\): promoting sparsity

\(2'~ \bullet~\) \(R(x) =\|x\|_1 = \sum_{i=1}^n |x_i|\),   closest norm to \(\|x\|_0\), and promoting sparsity

\[\min_x~ \frac{1}{2} \|Ax-y\|^2_2 + \lambda R(x)\]

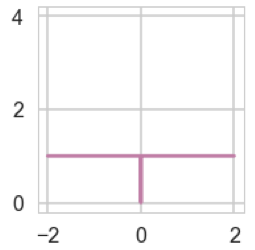
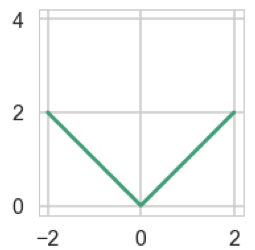
\(\|x\|_0\)

\(\|x\|_1\)

What priors should we choose?

Sometimes, yes

[Xu et al, 2023]

\(2'~ \bullet~\) \(R(x) = \|x\|_1 = \sum_{i=1}^n |x_i|\),   closest norm to \(\|x\|_0\), and promoting sparsity

\[\min_x~ \frac{1}{2} \|Ax-y\|^2_2 + \lambda R(x)\]

Is real data sparse?

What priors should we choose?

Sometimes, kind of...

\(2'~ \bullet~\) \(R(x) =\|x\|_1 = \sum_{i=1}^n |x_i|\),   closest norm to \(\|x\|_0\), and promoting sparsity

\[\min_x~ \frac{1}{2} \|Ax-y\|^2_2 + \lambda R(x)\]

Is real data sparse?

What priors should we choose?

\(2'~ \bullet~\) \(R(x) =\|x\|_1 = \sum_{i=1}^n |x_i|\),   closest norm to \(\|x\|_0\), and promoting sparsity

\[\min_x~ \frac{1}{2} \|Ax-y\|^2_2 + \lambda R(x)\]

Is real data sparse?

Mostly, not

\(x\)

... unless in an appropriate basis

\(z=Wx\)

\[\min_x~ \frac{1}{2} \|AWx-y\|^2_2 + \lambda \|x\|_1\]

Thus, if \(y = Ax + z\) and \(x\) is sparse under \(W\), 

Sparsity-based Priors

\[\arg\min_x~ \frac{1}{2} \|x-y\|^2_2 + \lambda \|x\|_1\]

Consider the simple setting \(y = x + z\) and \(x\) sparse 

 \(=\arg\max_x p(x|y)\)

\[\text{prox}_{\lambda\|\cdot\|_1}(y) \vcentcolon=\]

Proximal Operators:

\[\text{prox}_{\lambda f}(y) = \arg\min_x \frac12\|y-x\|^2_2 + \lambda f(x)\]

Why?

\[\left[\text{prox}_{\lambda\|\cdot\|_1}(y) \right]_i= \begin{cases} y_i-\lambda, & y_i>\lambda, \\ 0, & |y_i| \leq \lambda, \\ y_i+\lambda, & y_i< -\lambda. \end{cases}\]

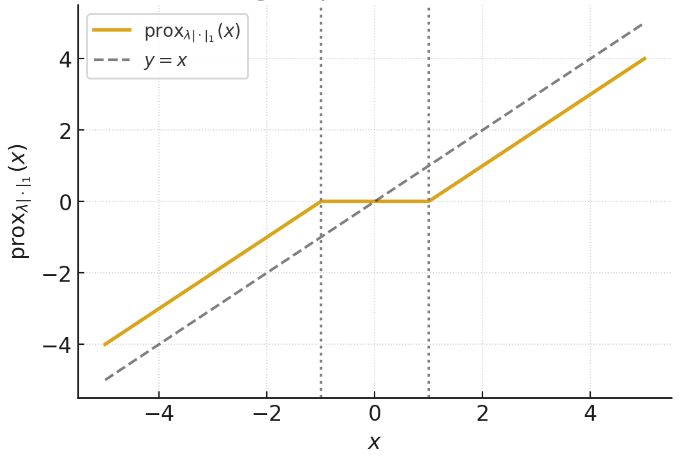
Sparsity-based Priors

\[\arg\min_x~ \frac{1}{2} \|Ax-y\|^2_2 + \lambda \|x\|_1\]

Consider the setting \(y = Ax + z\) and \(x\) sparse 

 \(=\arg\max_x p(x|y)\)

\(\nabla_x h(x)\)

\(h(x)\)

Proximal Gradient Descent:

\[x^{k+1}= \text{prox}_{\lambda \|\cdot\|_1}(x^k - \eta A^\top( A x^k - y))\]

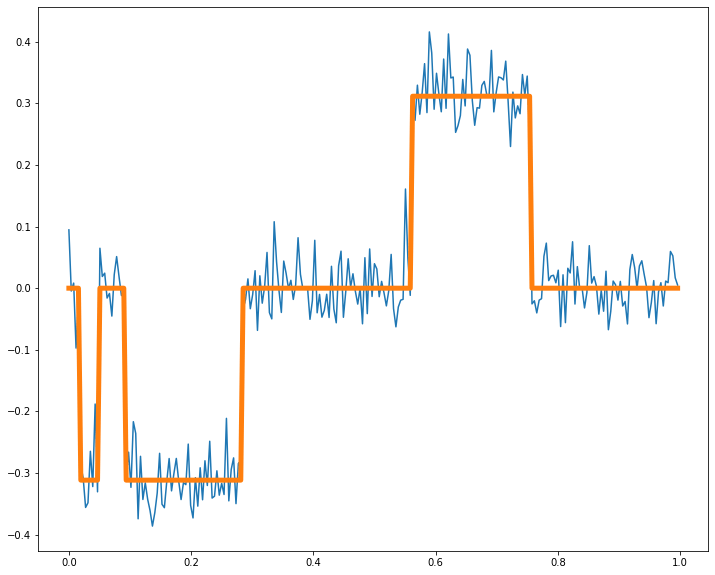
Sparsity-based Priors: Examples

Consider the setting \(y = x + z\) , \(z\sim\mathcal N(0,\sigma^2I)\)

P1)     \(\arg\min_x~ \frac{1}{2} \|x-y\|^2_2 + \lambda \|x\|^2_2\)

P2)     \(\arg\min_x~ \frac{1}{2} \|x-y\|^2_2 + \lambda \|x\|_1\)

P3)     \(\arg\min_x~ \frac{1}{2} \|W_{wavelet}~x-y\|^2_2 + \lambda \|x\|_1\)

PART II:  

Regularization and Priors

PART III: 

Data-driven Models

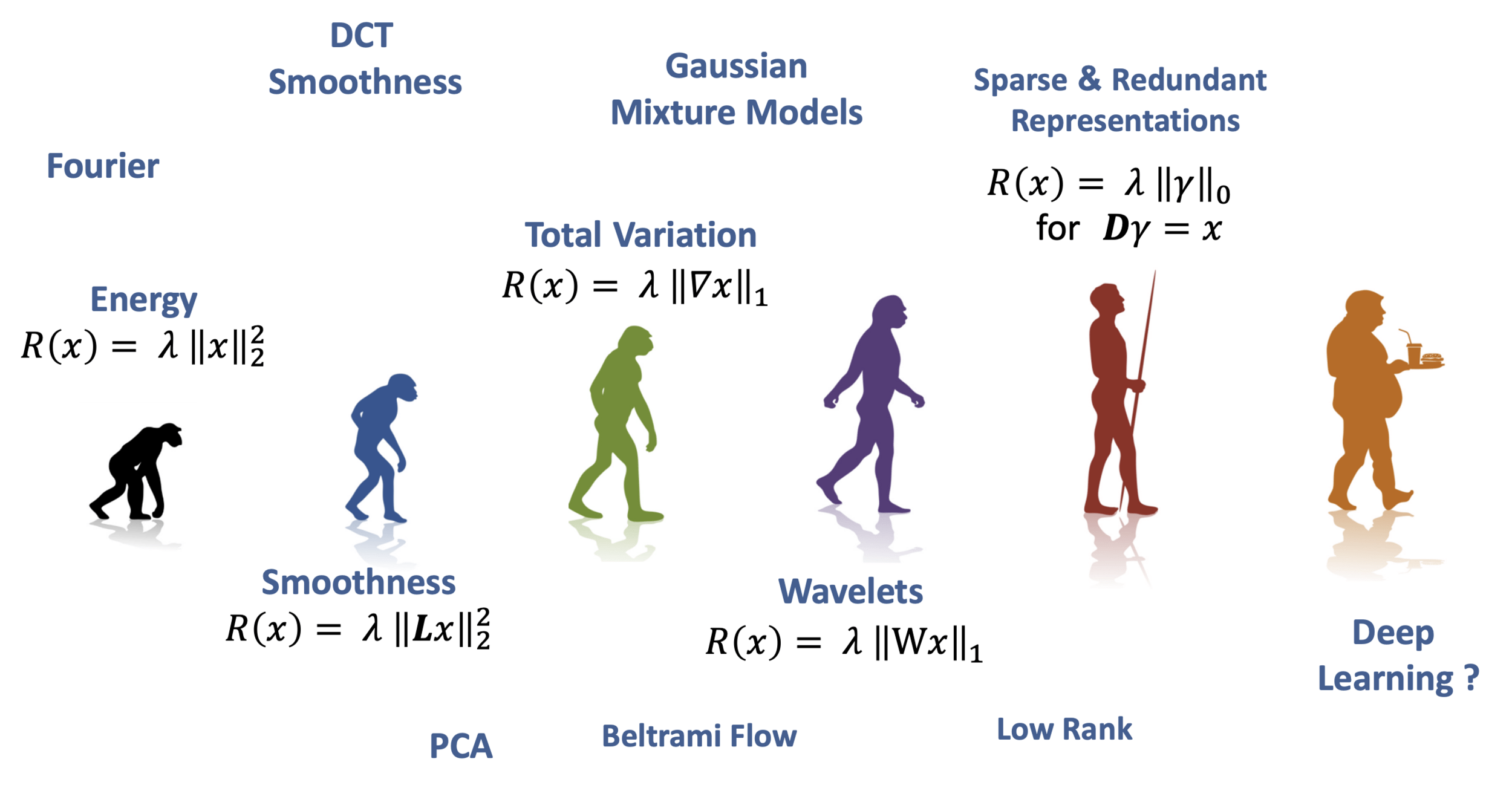
PART III:  Data-driven Models

Deep Learning in Inverse Problems

2) choose loss function \(\ell: \mathbb R^n \times \mathbb R^n \to \mathbb R\) (and other hyper parameters)

Option A: agnostic methods train a network \(f_\theta \in \mathcal F_\theta = \{f_\theta: \mathbb R^n \to \mathbb R^n\}\)

1) choose architecture \(\mathcal F_\theta\)

So that hopefully \(f_\theta(y) \approx x\) in expectation

\[\min_\theta \frac1N \sum_{i=1}^N \ell(f_\theta(y_i),x_i) \]

3) collect training data \( \{(x_i,y_i)\}_{i=1}^N \) and train by minimizing the empirical risk

Deep Learning in Inverse Problems

So that hopefully \(f_\theta(y) \approx x\) in expectation

\[\min_\theta \frac1N \sum_{i=1}^N \ell(f_\theta(y_i),x_i) \]

1) choose architecture \(\mathcal F_\theta\)

2) choose loss function \(\ell: \mathbb R^n \times \mathbb R^n \to \mathbb R\) (and other hyper parameters)

3) collect training data \( \{(x_i,y_i\}_{i=1}^N \) and train by minimizing the empirical risk

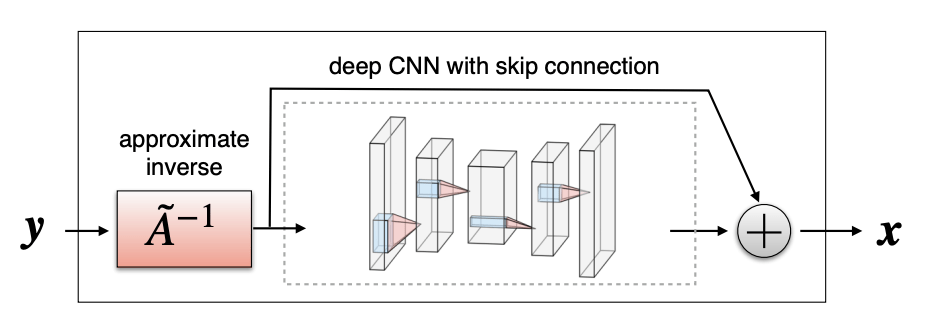
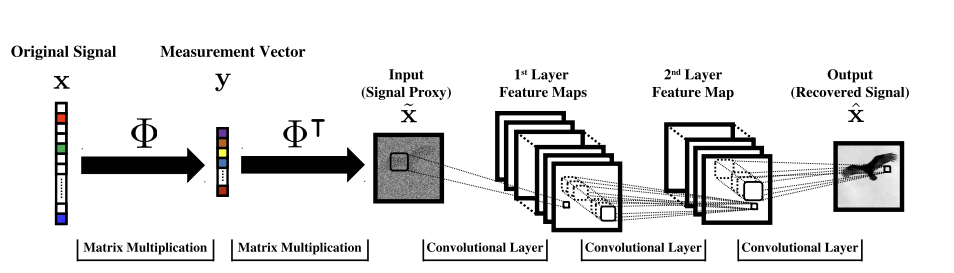
[Mousavi & Baraniuk, 2017]
[Ongie, Willet, et al, 2020] 
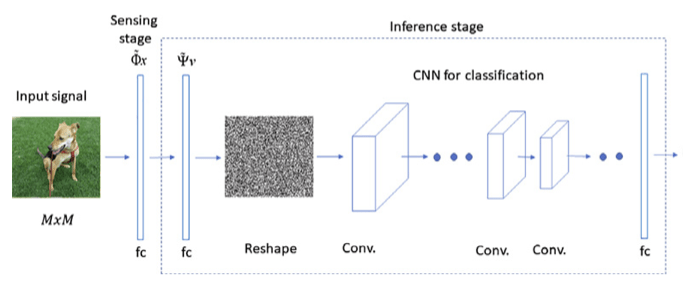
[Adler et al, 2016]
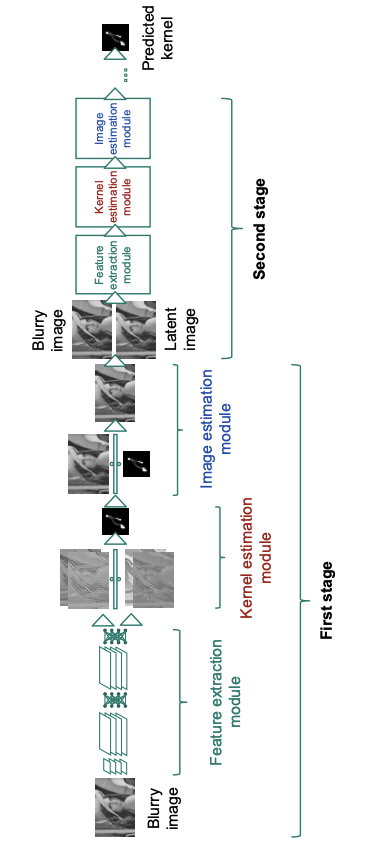
[Schuler et al, 2015]

Option A: agnostic methods train a network \(f_\theta \in \mathcal F_\theta = \{f_\theta: \mathbb R^n \to \mathbb R^n\}\)

Option B: data-driven regularizer \(R_\theta \in \mathcal R_\theta = \{R_\theta: \mathbb R^n \to \mathbb R\}\)

  • Priors as critics   
    [Lunz, Öktem, Schönlieb, 2020] and others ..
\displaystyle \hat R_\theta(x) = \arg\min_{R_\theta\in \mathcal R} ~ \mathbb E_{x\sim p_x}[R(x)] - \mathbb E_{x\sim q }[R(x)]
  • via MLE 
    [Ye Tan, ..., Schönlieb, 2024], ...
  • RED 
    [Romano et al, 2017] ...
  • Generative Models 
    [Bora et al, 2017] ...
\displaystyle \hat R_\theta(x) = \mathbb 1_{[\exist z : G(z)=x]}

\[\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \]

\[\hat R_\theta(x)\]

Deep Learning in Inverse Problems

Option C: Implicit Priors (via Plug&Play)

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)

Proximal Gradient Descent:       \( x^{t+1} = \text{prox}_R \left(x^t - \eta  A^T(Ax^t-y)\right) \)

\text{prox}_R \left( u \right) = \arg\min_x \frac 12 \|u - x\|_2^2 + R(x)
\text{prox}_R \left( u \right) = \arg\max_x p(x|y), \qquad \text{when } u = x + v, ~ v\sim\mathcal N(0,I\sigma^2)

... a denoiser

Deep Learning in Inverse Problems

 \(=\arg\max_x p(x|y)\)

Option C: Implicit Priors (via Plug&Play)

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)

Proximal Gradient Descent:       \( x^{t+1} = {\color{red}f_\theta} \left(x^t - \eta  A^T(A(x^t)-y)\right) \)

Deep Learning in Inverse Problems

any denoiser

[Venkatakrishnan et al., 2013; Zhang et al., 2017b; Meinhardt et al., 2017; Zhang et al., 2021; Kamilov et al., 2023b; Terris et al., 2023]
[Gilton, Ongie, Willett, 2019]

Learned Proximals for Inverse Problems

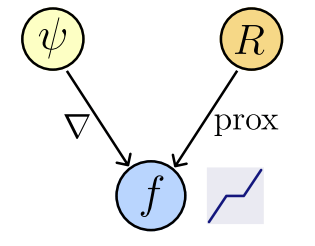
Theorem [Fang, Buchanan, S.]

When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\), and for what \(R(x)\)?

Let \(f_\theta : \mathbb R^n\to\mathbb R^n\) be a network : \(f_\theta (x) = \nabla \psi_\theta (x)\),

where \(\psi_\theta : \mathbb R^n \to \mathbb R,\) convex and differentiable (ICNN).

 

Then,

1. Existence of regularizer
\(\exists ~R_\theta : \mathbb R^n \to \mathbb R\) not necessarily convex : \(f_\theta(x) \in \text{prox}_{R_\theta}(x),\)

2. Computability
We can compute \(R_{\theta}(x)\) by solving a convex problem

Learned Proximals for Inverse Problems

\text{Let } y = x+v , \quad ~ x\sim p_x, ~~v \sim \mathcal N(0,\sigma^2I)

How do we find \(f(x) = \text{prox}_R(x)\) for the "correct" \(R(x) \propto -\log p_x(x)\)?

Goal: train a denoiser \(f(y)\approx x\)

f_\theta = \arg\min_{f_\theta:\text{prox}} \mathbb E_{x,y} \left[ {\ell (f_\theta(y),x)} \right]
\bullet ~~ {\ell (f_\theta(y),x)} = \|f_\theta(y) - x\|^2_2 ~~\implies~~ \mathbb E[x|y] \text{ (MMSE)}
\bullet ~~ {\ell (f_\theta(y),x)} = \|f_\theta(y) - x\|_1 ~~\implies~~ \texttt{median}(p_{x|y})

Which loss function?

Learned Proximals for Inverse Problems

\text{Let } y = x+v , \quad ~ x\sim p_x, ~~v \sim \mathcal N(0,\sigma^2I)

How do we find \(f(x) = \text{prox}_R(x)\) for the "correct" \(R(x) \propto -\log p_x(x)\)?

Theorem [Fang, Buchanan, S.]

f^* = \arg\min_{f} \lim_{\gamma \searrow 0}~ \mathbb E_{x,y} \left[ \ell^\gamma_\text{PM}(f_\theta(y),x)\right]
f^*(y) = \arg\max_c p_{x|y}(c) \triangleq \text{prox}_{-\sigma^2\log p_x}(y)
\ell^\gamma_\text{PM} (f_\theta(y),x) = 1- \frac{c}{\gamma^{2n}} \exp\left( -\frac{\|f(y)-x\|_2^2}{\gamma} \right) 
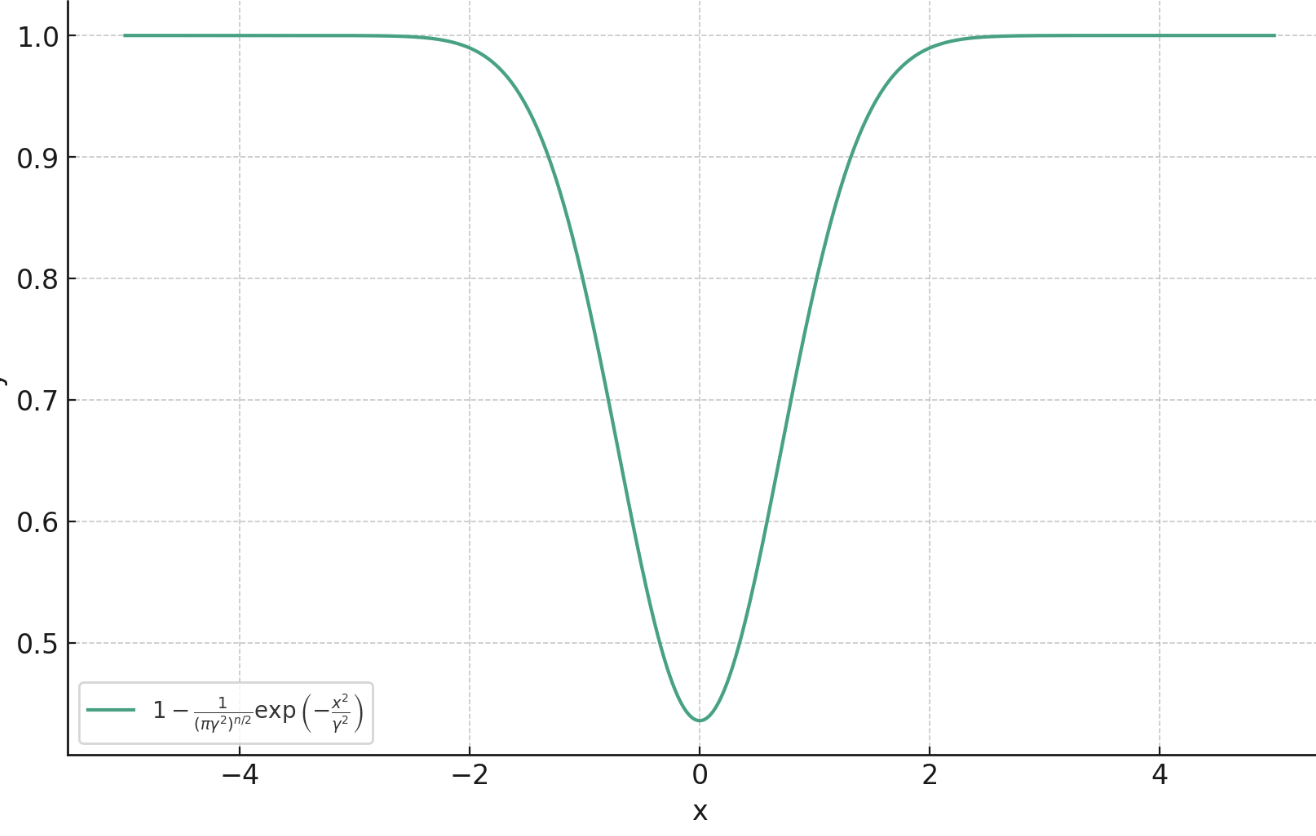
Proximal Matching Loss:

\(\gamma\)

Goal: train a denoiser \(f(y)\approx x\)

Let

Then,

a.s.

Learned Proximals for Inverse Problems

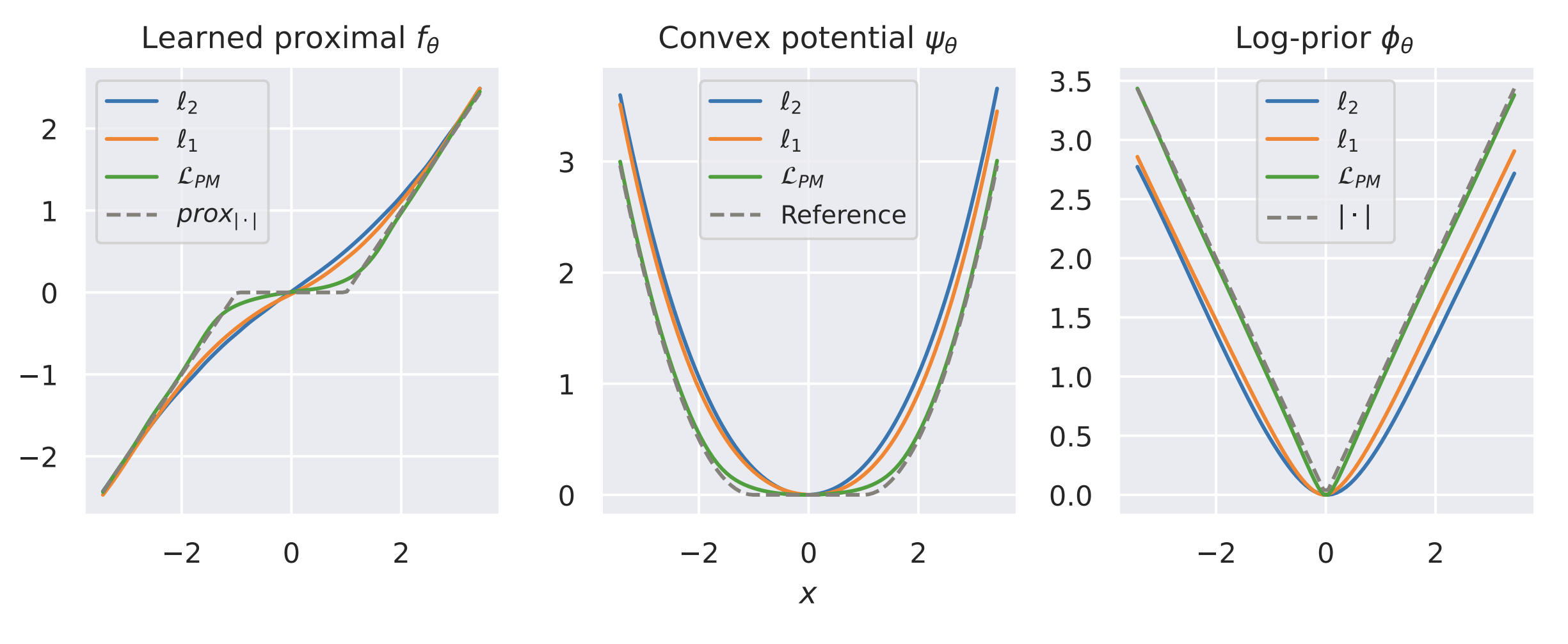
\text{Sample } y = x+v,~ \text{ with } x \sim \text{Laplace}(0,1) \text{ and } v \sim \mathcal N(0,\sigma^2)

Example: recovering a prior

\(p(x) = \frac{1}{2}e^{-|x|} ~~ \Rightarrow ~~ -\log p(x) = |x| ~~ \Rightarrow ~~ \text{prox}_{|\cdot|}(x) = \operatorname{sign}(x)\,\max(|x| - \lambda, 0)\)

Learned Proximals for Inverse Problems

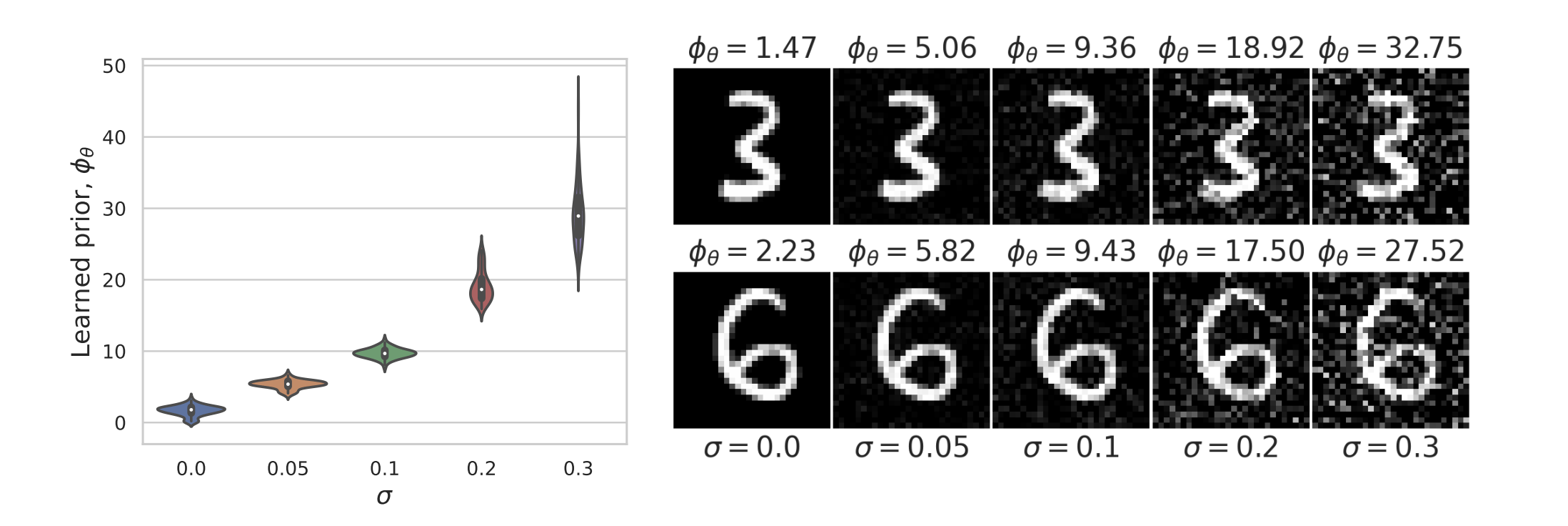
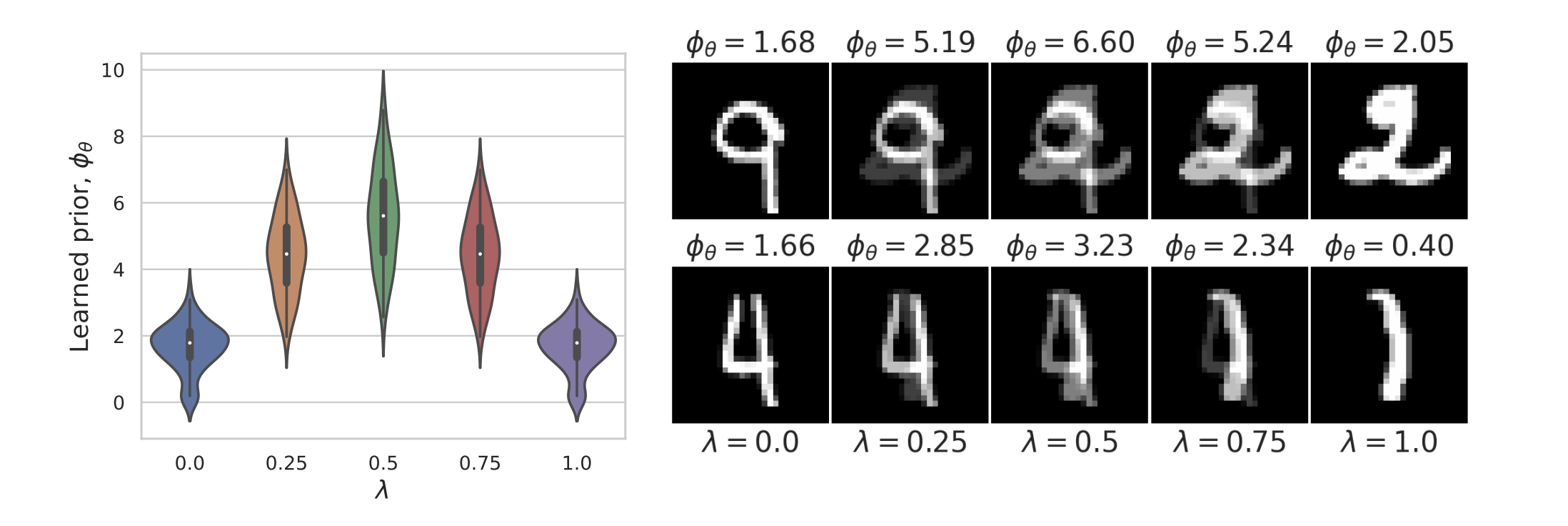
Learned Proximals for Inverse Problems

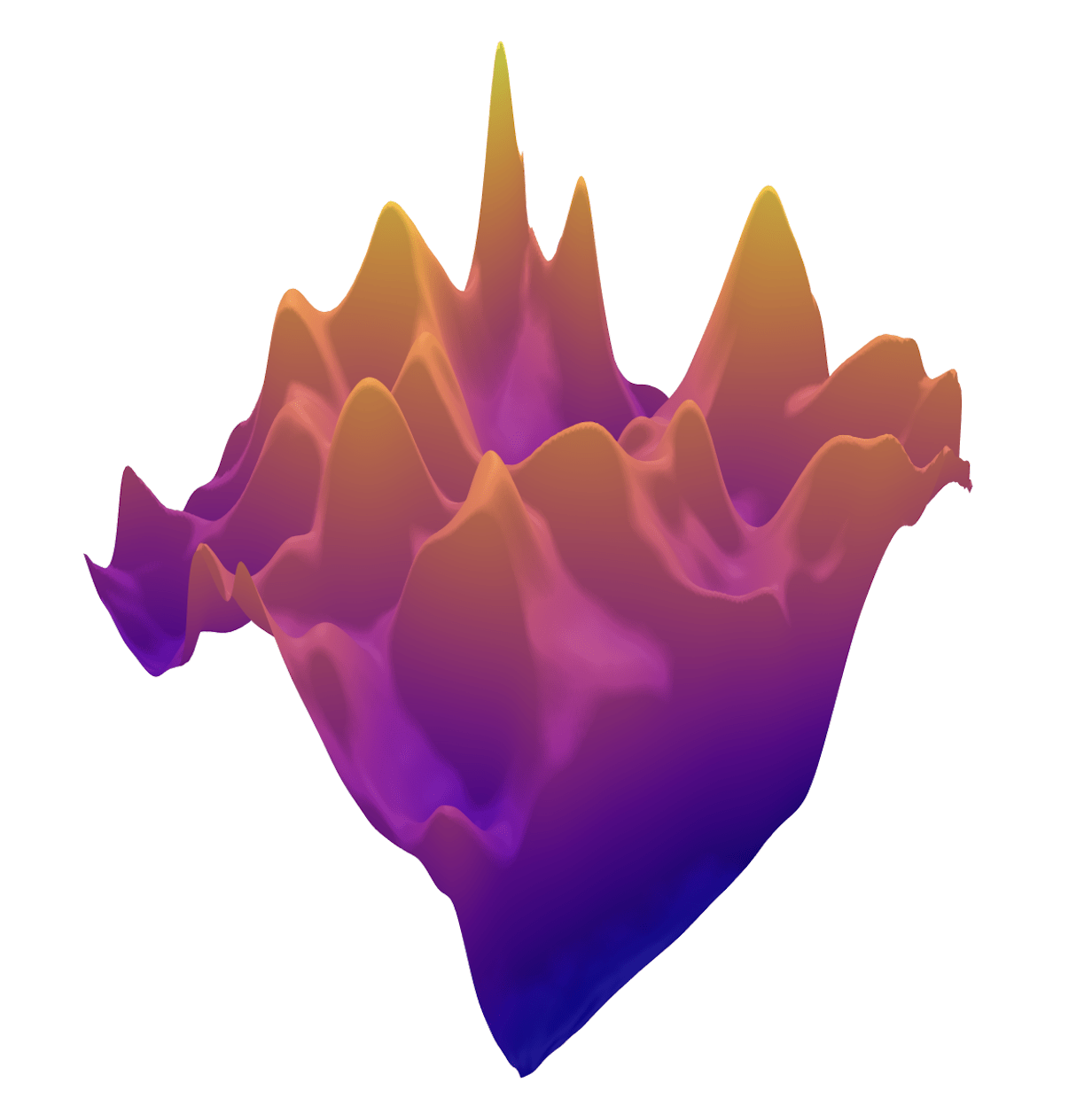
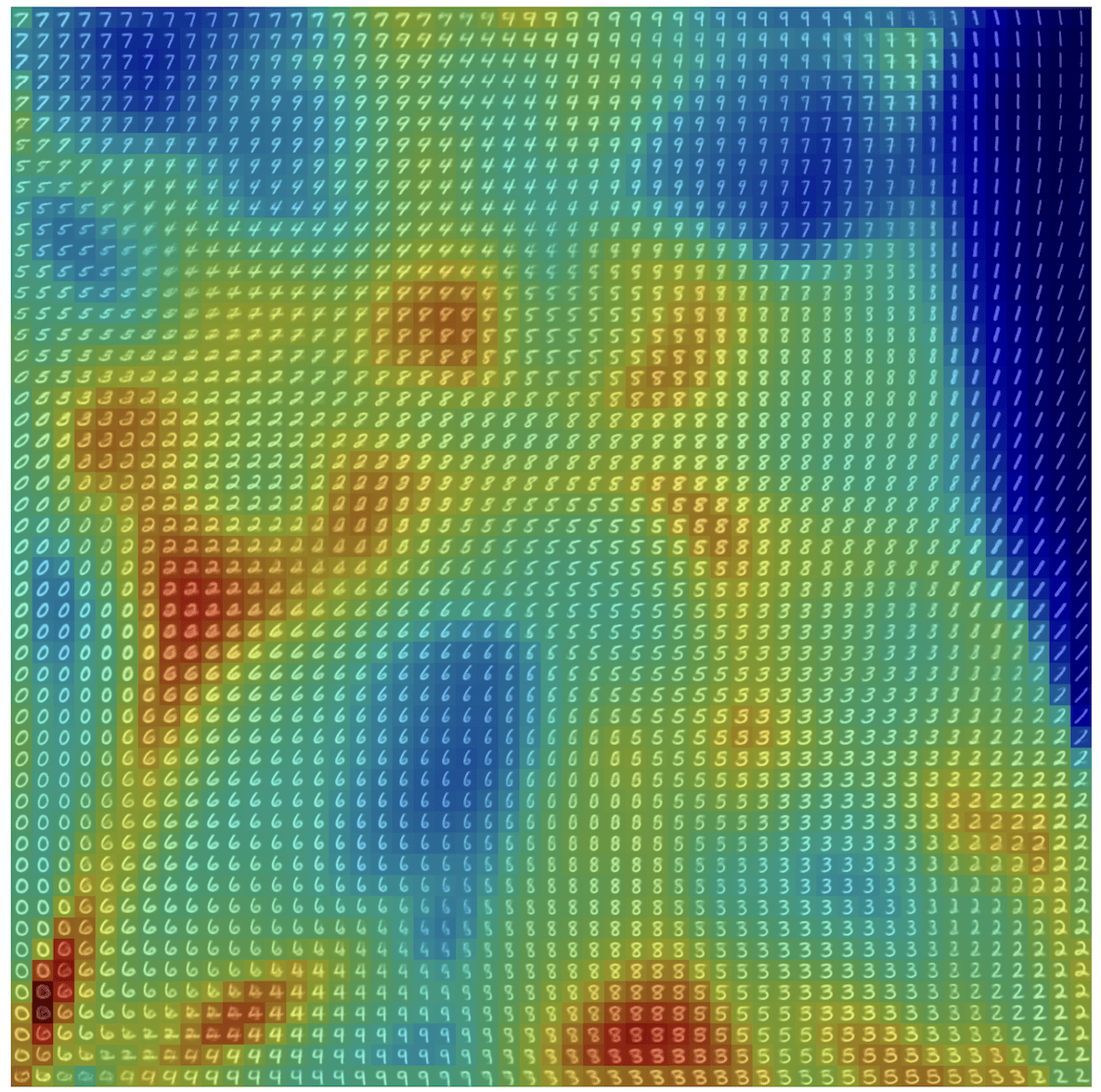
\(R(\tilde{x})\)

Learned Proximals for Inverse Problems

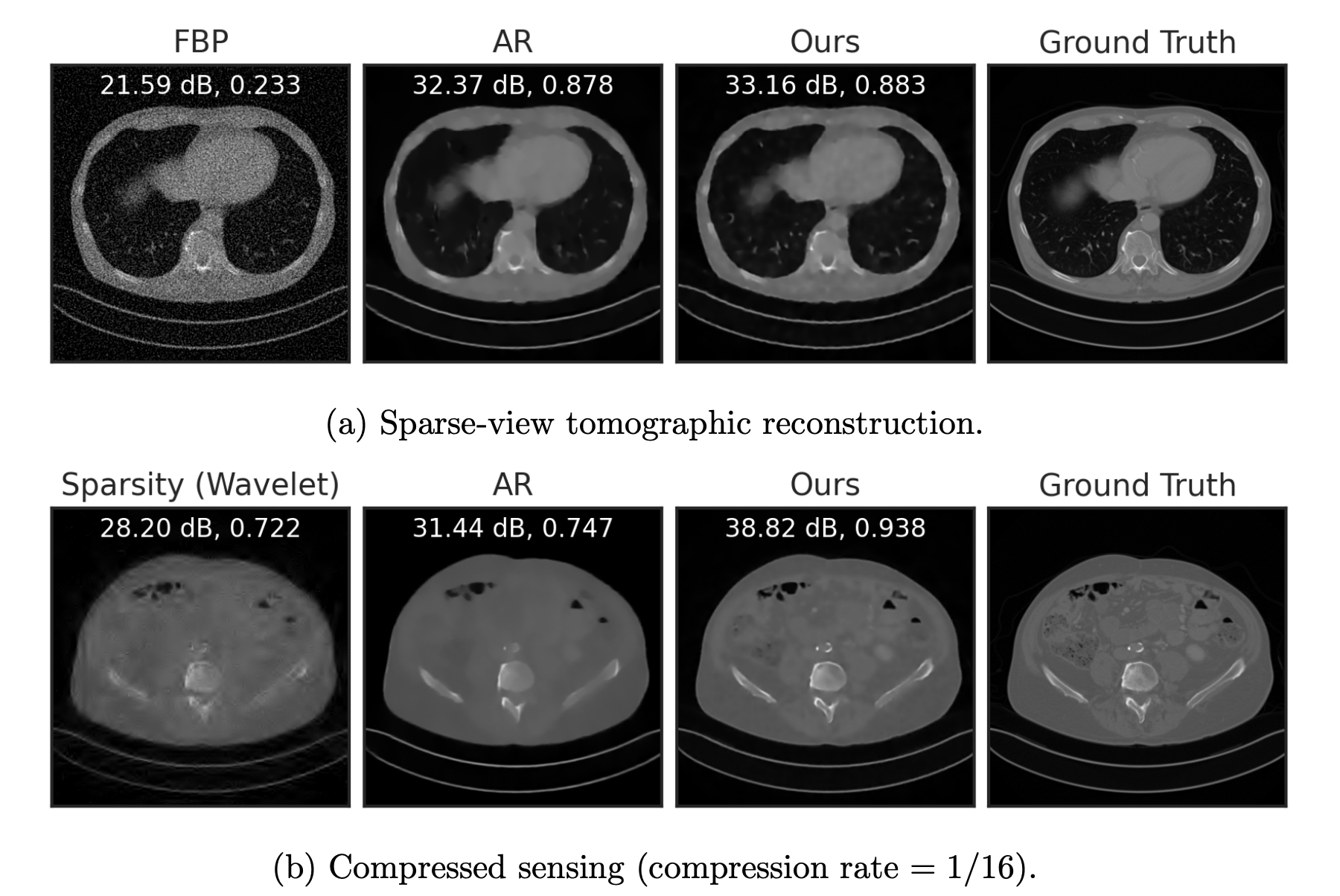
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \hat{R}_\theta(x)
[Fang, Buchanan & S. What's in a Prior? Learned Proximal Networks for Inverse Problems, ICLR 2024]

Convergence guarantees!

Inverse Problems with data-driven denoisers: Examples

Consider the setting \(y = Ax + z\) , \(z\sim\mathcal N(0,\sigma^2I)\)

\( x^{t+1} = {\color{red}f_\theta} \left(x^t - \eta  A^T(A(x^t)-y)\right) \)

a) \(f_\theta = \text{BM3D}\) [Dabov et al, 2007]

b) \(f_\theta = \text{DnCNN}\) [Zhang et al., 2017]

c) \(f_\theta = \text{LPN}\) [Fang et al, 2024]

i) \(A: \text{deblurring}\)

ii) \(A : \text{subsampling}\)

That is all, folks!

http://jsulam.github.io
jsulam1@jhu.edu

Questions?