Imaging, Data, and Learning:

Jeremias Sulam

Modern challenges in biomedical data science

microstrategy - 2024

Part I: Embracing AI 

Three vignettes on medical imaging

Macro
 

Meso

Micro

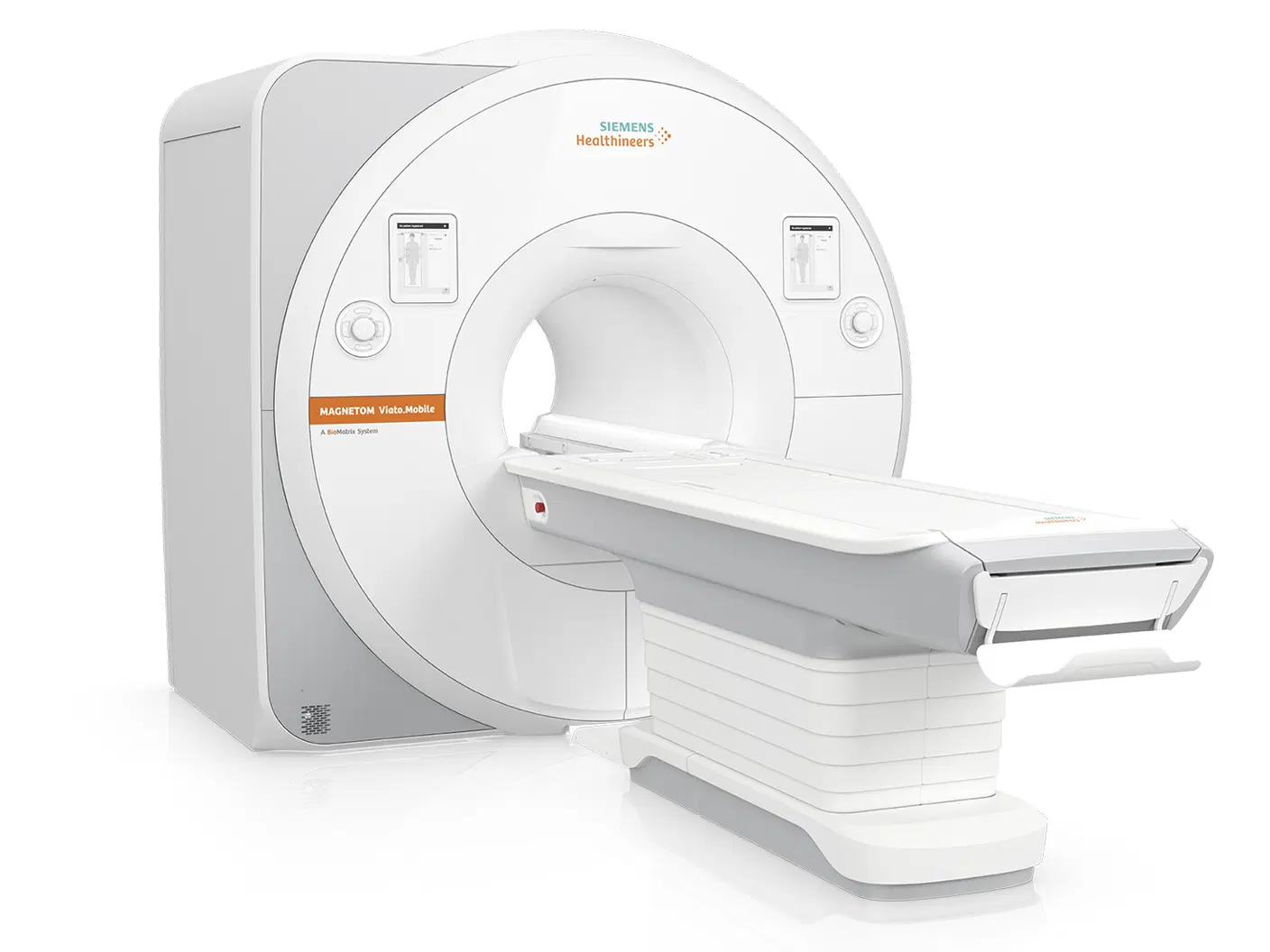
Learning to image the human brain

Magnetic Susceptibility

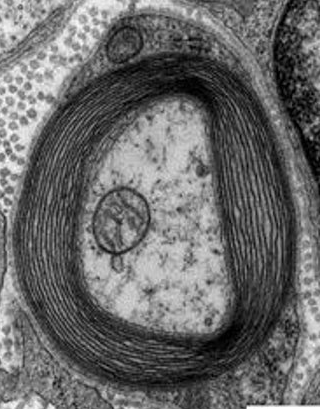
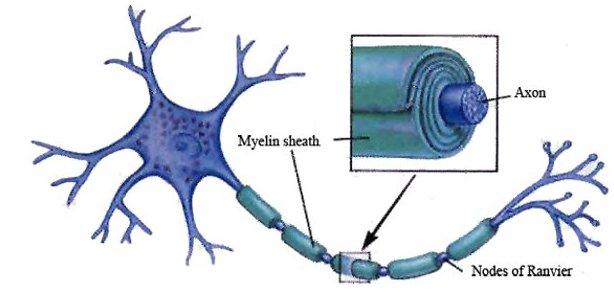
  • degree to which a material is magnetized when placed in a magnetic field


     
  • Heme Iron (RBCs)
     
  • Myelin (diamagnetic)
\underset{x}{\min} ~ \frac{1}{2} \| y - \Phi_\text{\tiny STI} x \|^2_2 + g_{\theta}(x)

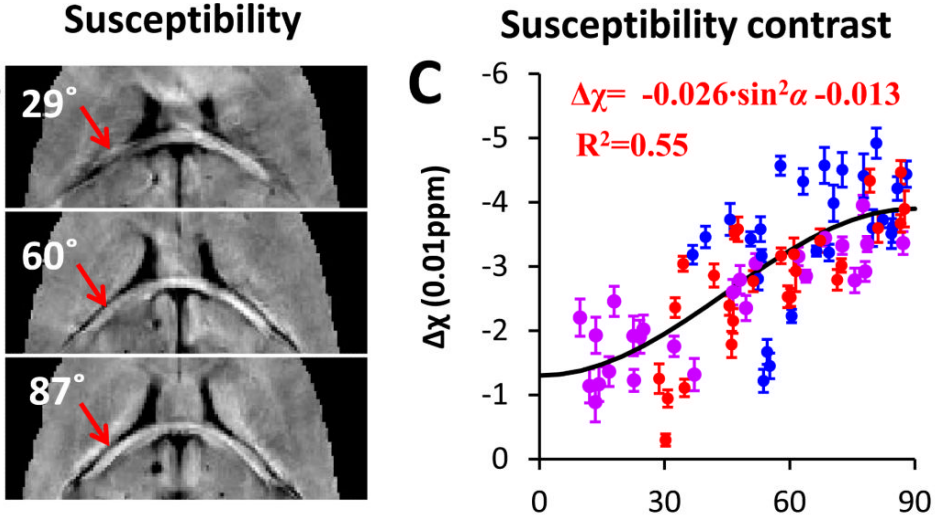
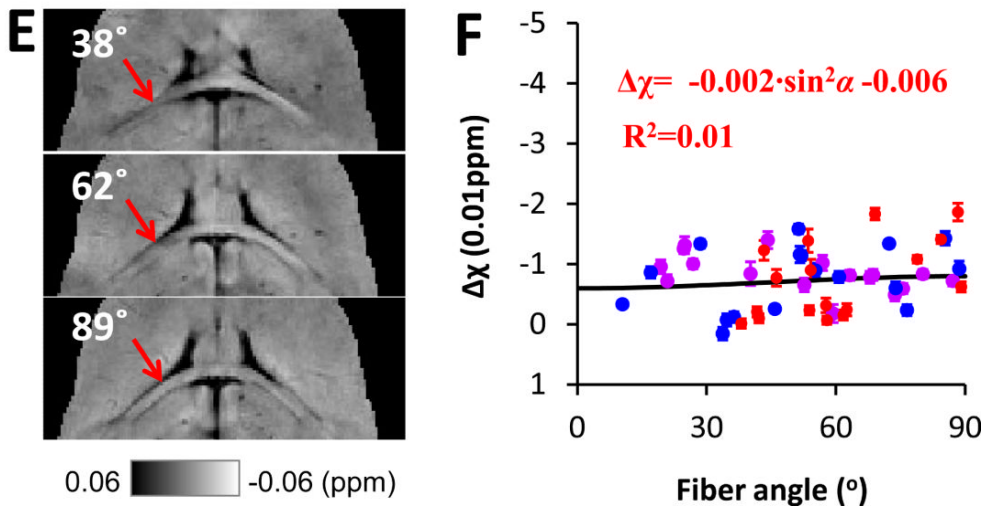
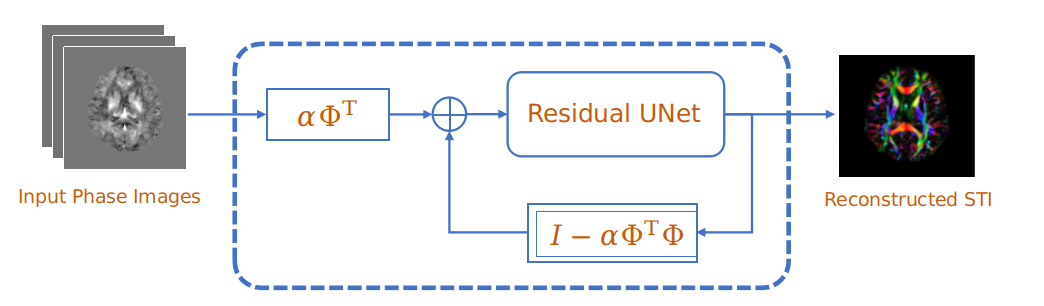
learned, data-driven regularizer

Learning to image the human brain

Magnetic Susceptibility

  • degree to which a material is magnetized when placed in a magnetic field


     
  • Heme Iron (RBCs)
     
  • Myelin (diamagnetic)

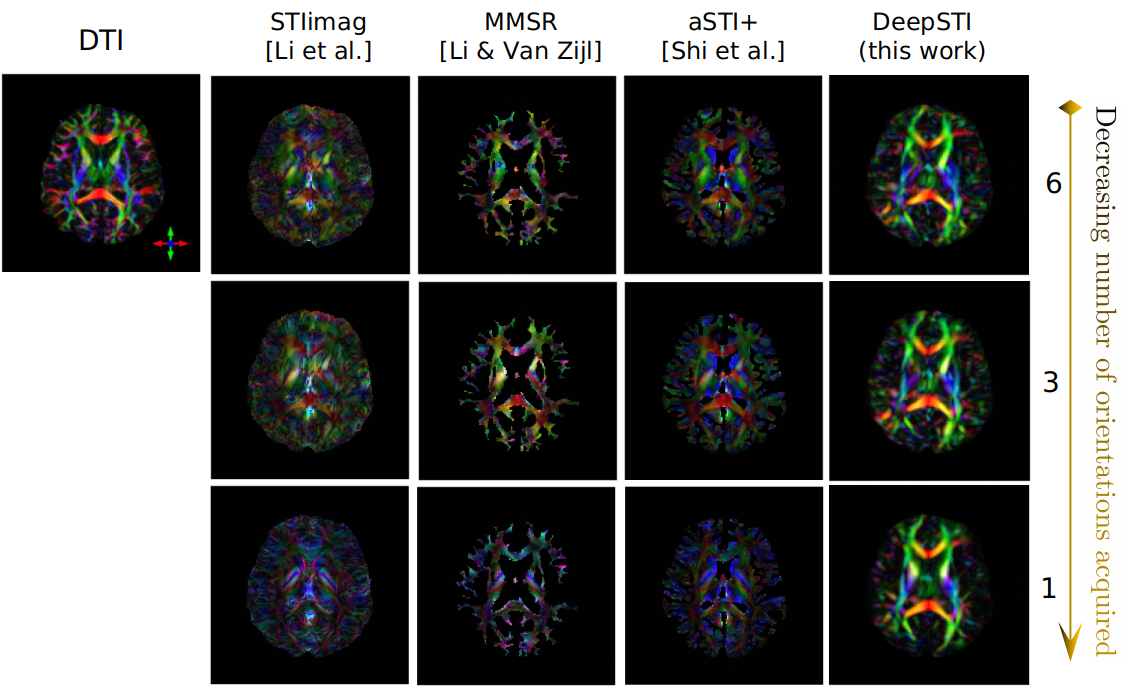
Learning to image the human brain

Part I: Embracing AI 

Three vignettes on medical imaging

Macro
 

Meso

Micro

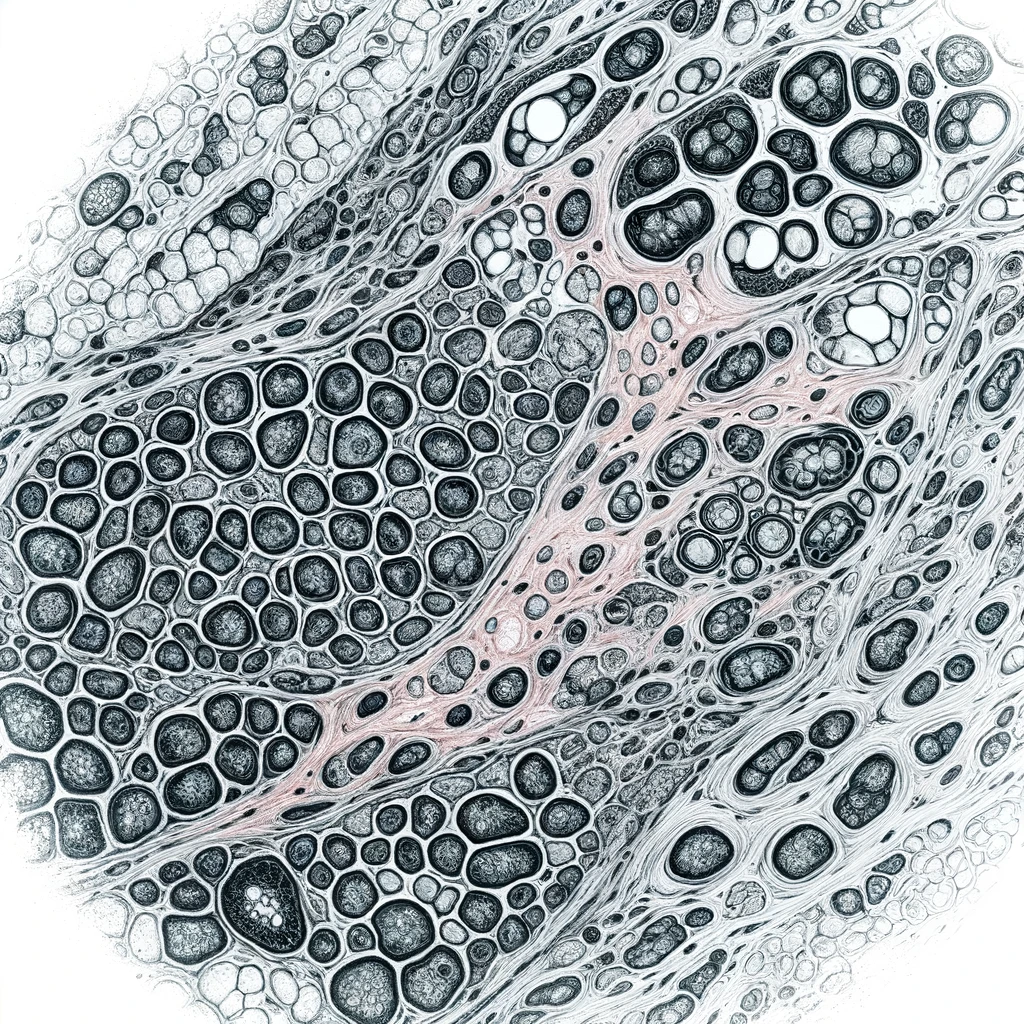
Tools in Digital Pathology

Tools in Digital Pathology

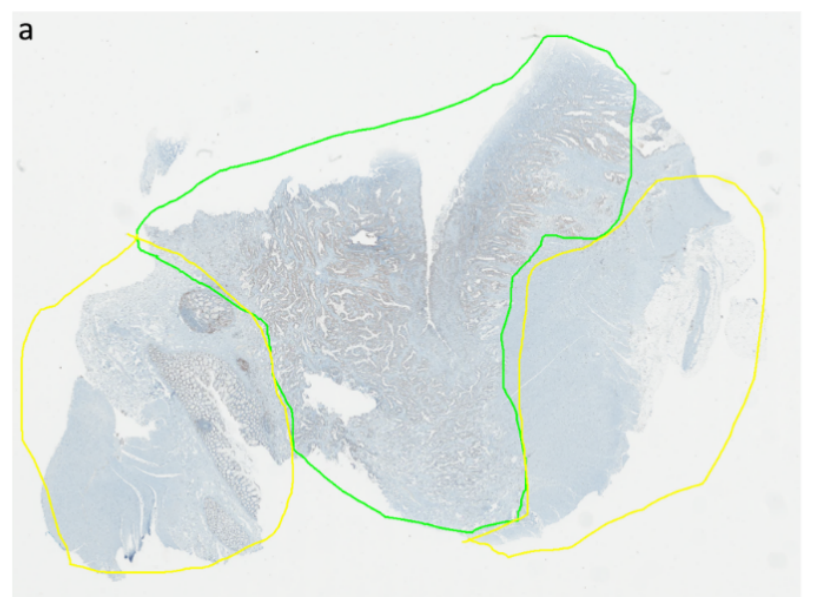
tumor

non tumor

Can we refine these automatically?

false positives

false negatives

Tools in Digital Pathology

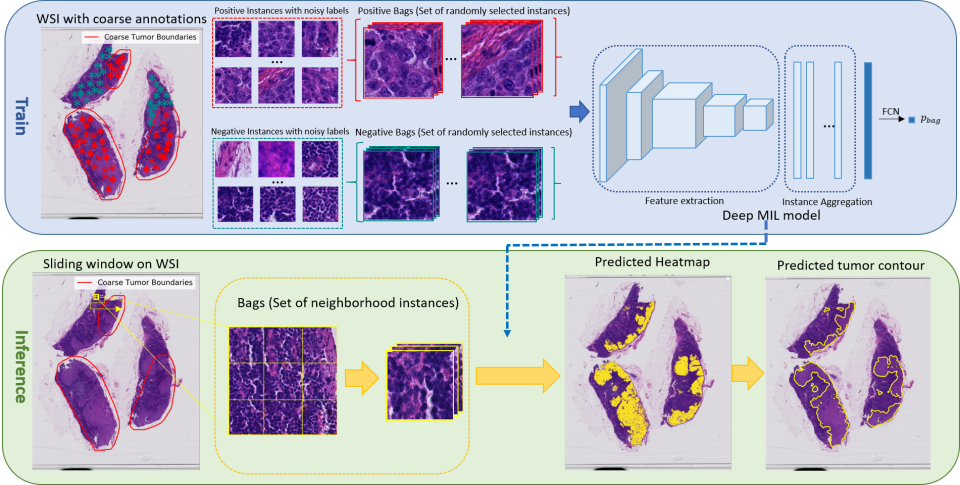
  • Training on a single slide

Tools in Digital Pathology

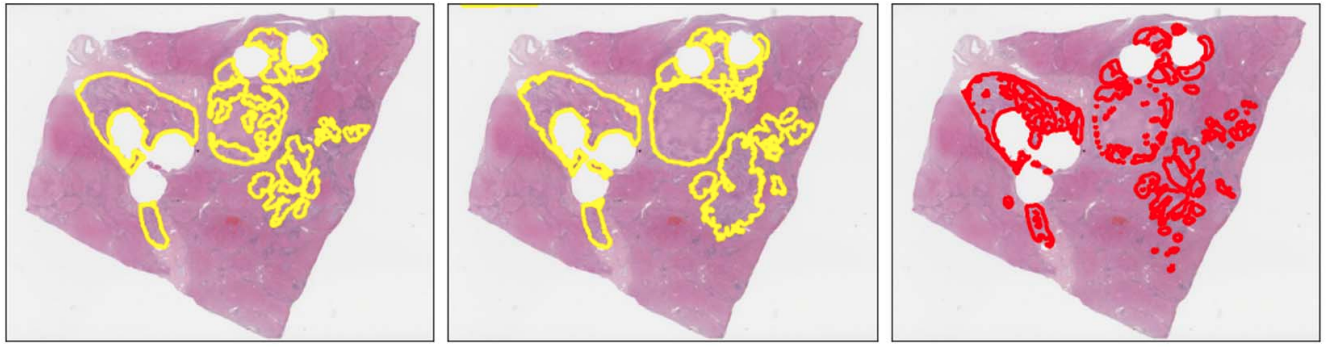
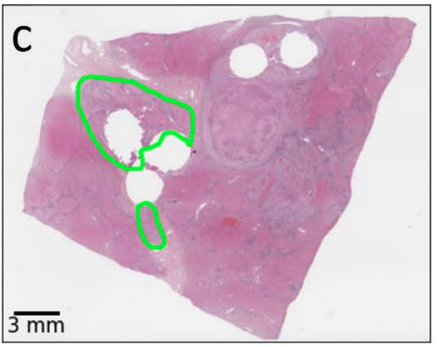
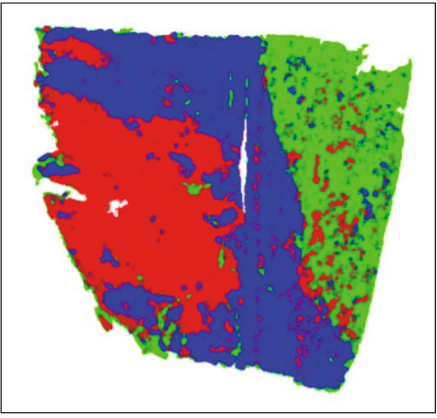
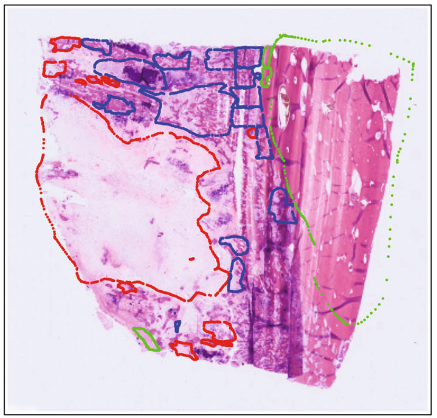
necrotic tumor

viable tumor

non-tumor

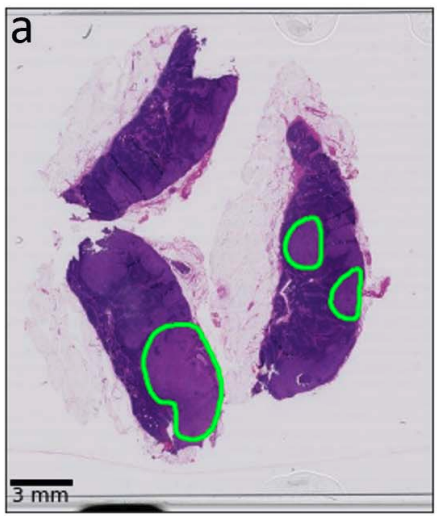
Manual coarse annotation

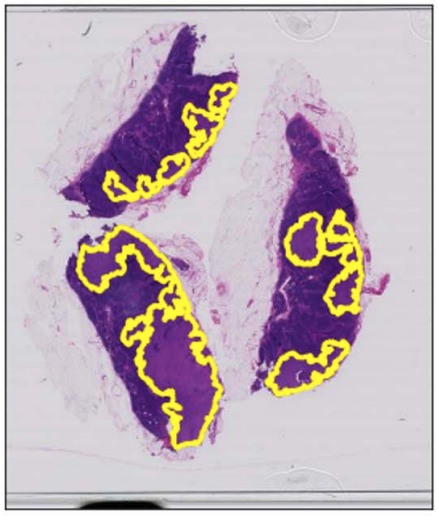
Computational refinement

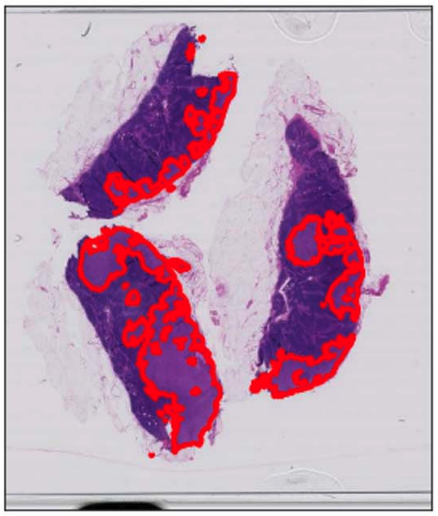
Ground truth

Part I: Embracing AI 

Three vignettes on medical imaging

Part I: Embracing AI 

Three vignettes on medical imaging

Macro
 

Meso

Micro

Imaging thousands of synapses in vivo

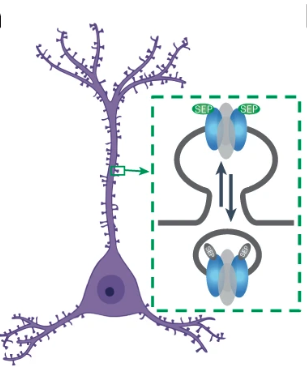
GluA2 AMPAR receptor subunit with a pH-dependent fluorescent tag (SEP) enables in vivo visualization of endogenous GluA2-containing synapses.

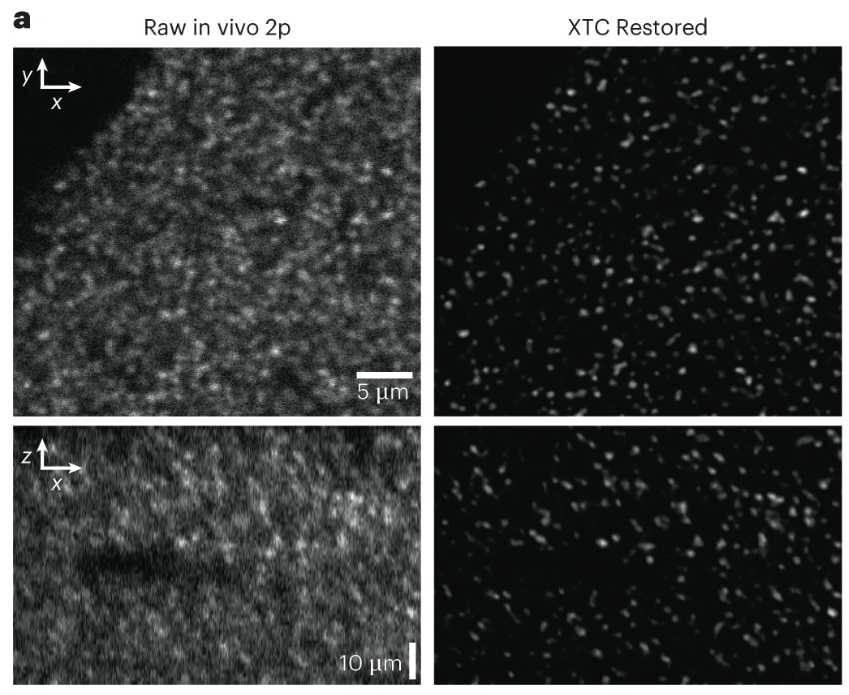
Imaging thousands of synapses in vivo

GluA2 AMPAR receptor subunit with a pH-dependent fluorescent tag (SEP) enables in vivo visualization of endogenous GluA2-containing synapses.

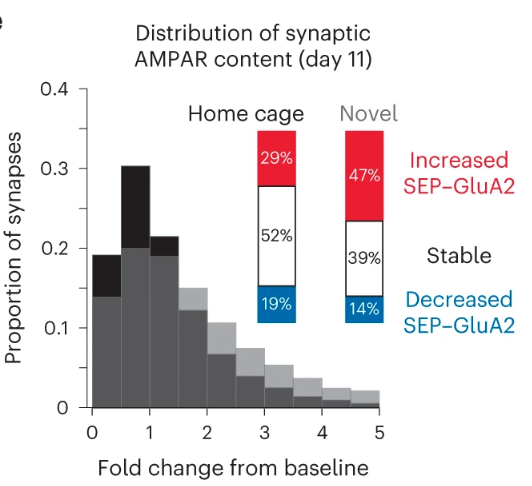
Imaging thousands of synapses in vivo

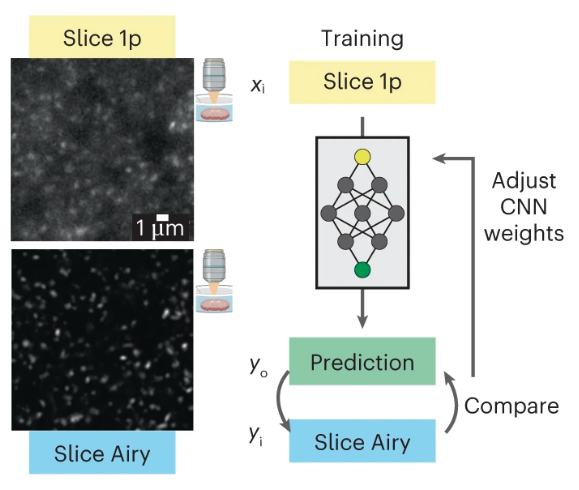
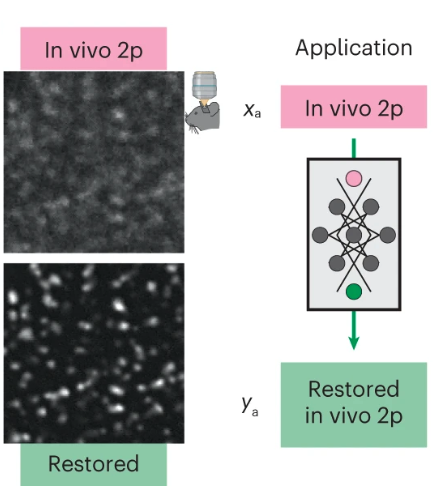
Imaging thousands of synapses in vivo

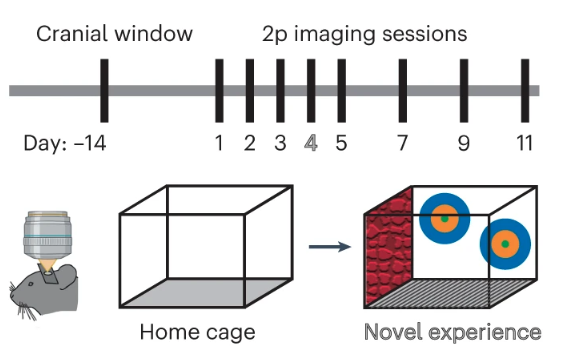
Part II: Embracing AI (carefully)

Interpretability

Fairness

Uncertainty Quantification

Uncertainty Quantification

How to quantify and report uncertainty?

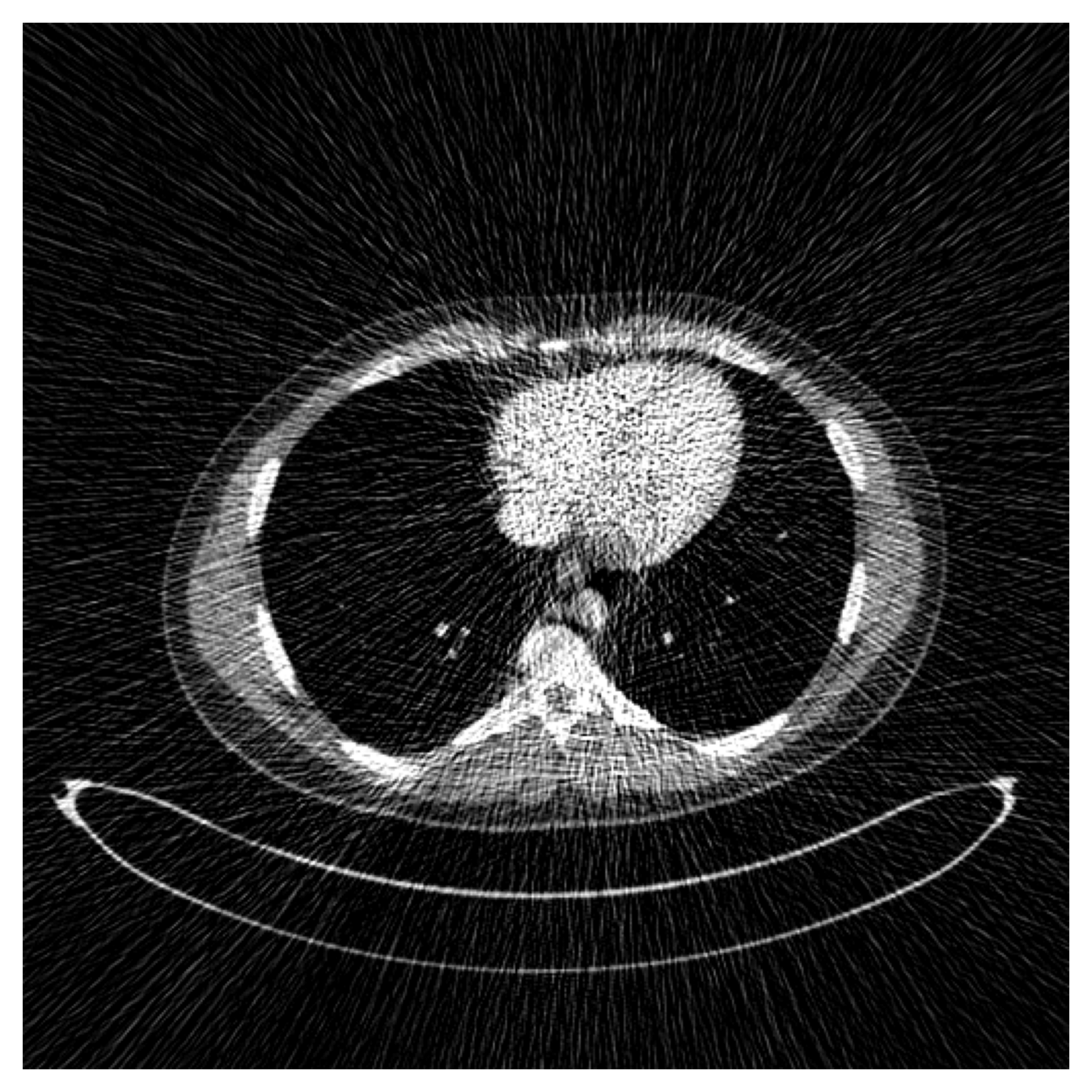
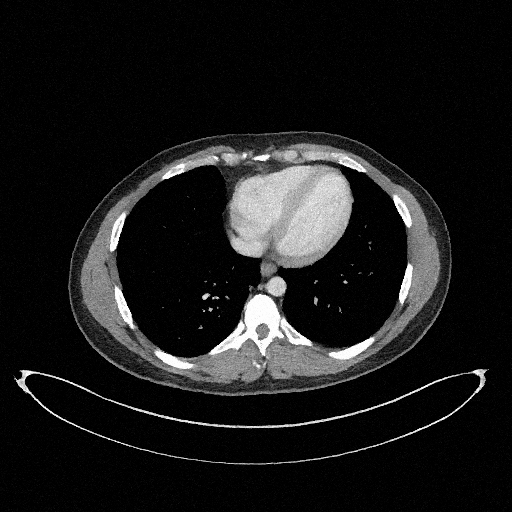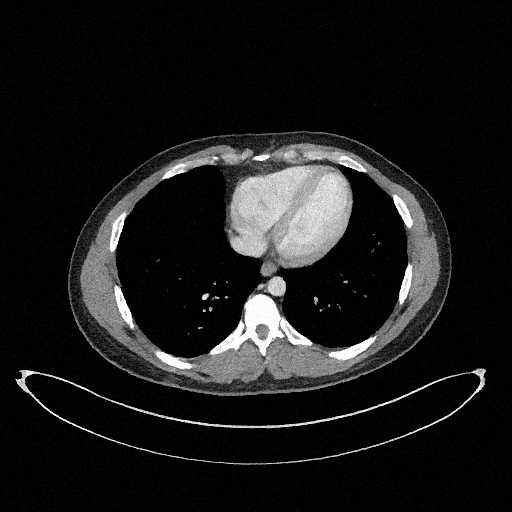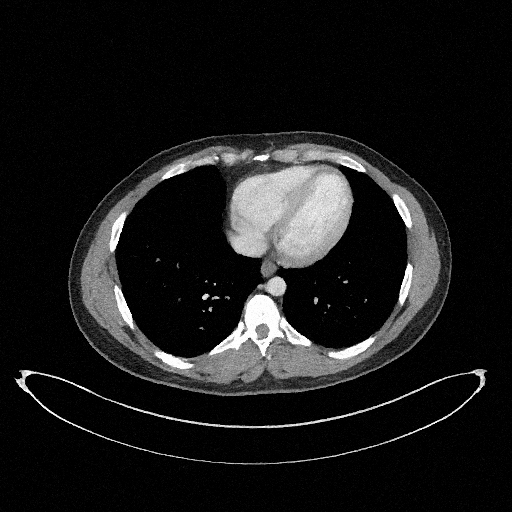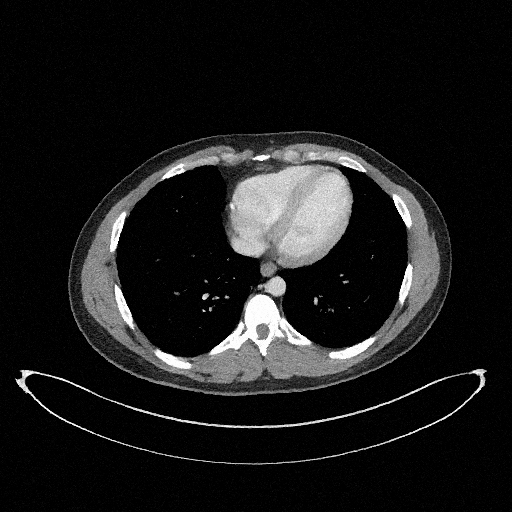
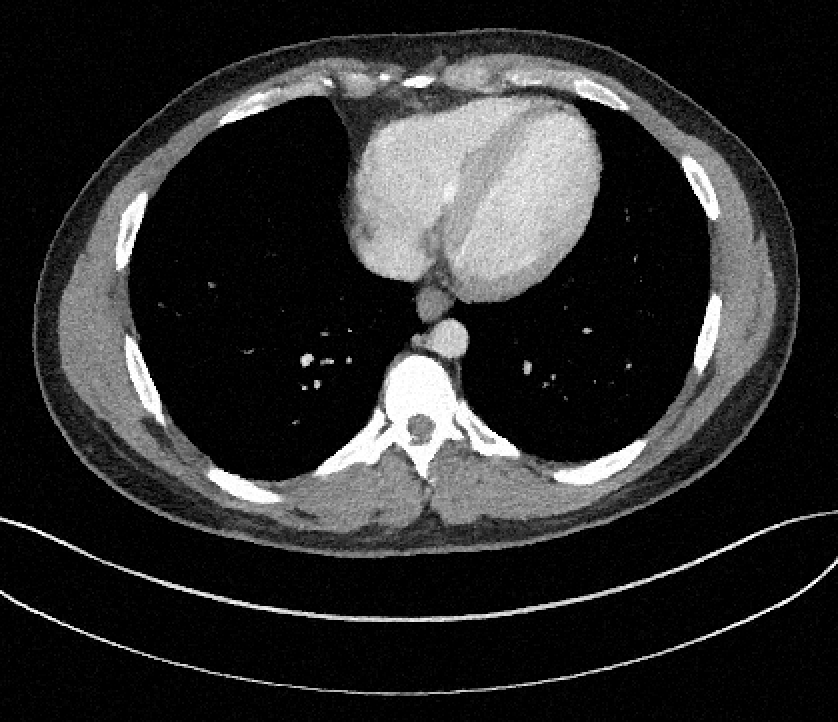
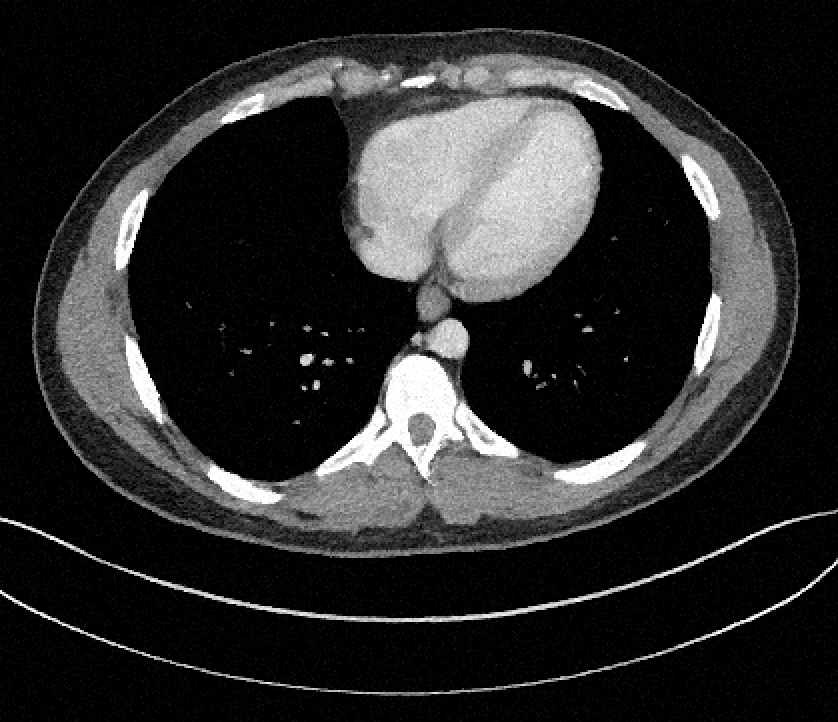
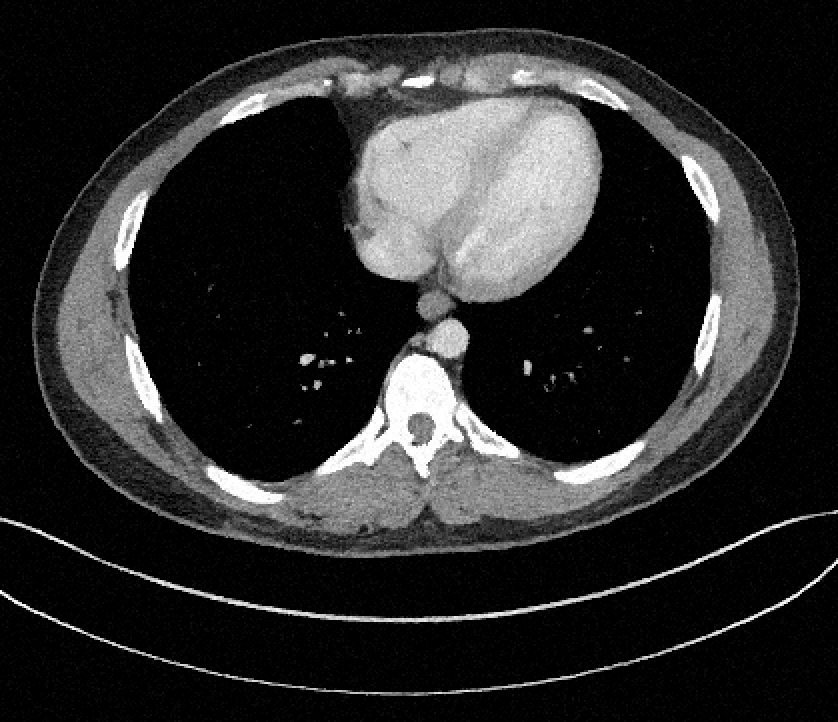
Filtered Back Projection

Diffusion Model

Uncertainty Quantification

For an observation \(y\)

\[y = x + \epsilon,~\epsilon \sim \mathcal{N}(0, \sigma^2\mathbb{I})\]

reconstruct \(x\) with

\[\hat{x} = F(y) \sim \mathcal{Q}_y \approx p(x \mid y)\]

Uncertainty Quantification

\(x\)

\(y\)

\(F(y)\)

Lemma

\(\mathcal I(y)\) provides entrywise coverage for pixel \(j\), i.e.

\[\mathbb{P}\left[\text{next sample}_j \in \mathcal{I}(y)_j\right] \geq 1 - \alpha\]
If \[\mathcal{I}(y)_j = \left[ \frac{\lfloor(m+1)Q_{\alpha/2}(y_j)\rfloor}{m} , \frac{\lceil(m+1)Q_{1-\alpha/2}(y_j)\rceil}{m}\right]\]

Uncertainty Quantification

\(0\)

\(1\)

low: \( l(y) \)

\(\mathcal{I}(y)\)

up: \( u(y) \)

(distribution free)

\(x\)

\(y\)

lower

upper

intervals
\(|\mathcal I(y)_j|\)

Uncertainty Quantification

\(0\)

\(1\)

Risk Controlling Prediction Sets

ground-truth is

contained

\(\mathcal{I}(y_j)\)

\(x_j\)

Procedure     For pixel \(j\)

\[\mathcal{I}_{\lambda}(y)_j = [\text{lower} - \lambda, \text{upper} + \lambda]\]

choose

\[\hat{\lambda} = \inf\{\lambda \in \mathbb{R}:~\forall \lambda' \geq \lambda,~\text{risk}(\lambda') \leq \epsilon\}\]

ground-truth is

contained

\(0\)

\(1\)

\(\mathcal{I}(y_j)\)

\(\lambda\)

\(x_j\)

Risk Controlling Prediction Sets

Definition      For risk level \(\epsilon\), failure probability \(\delta\), \(\mathcal{I}(y_j) \) is a RCPS if

\[\mathbb{P}\left[\mathbb{E}\left[\text{fraction of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]

\(K\)-RCPS: High-dimensional Risk Control

scalar \(\lambda \in \mathbb{R}\)

\(\mathcal{I}_{\lambda}(y)_j = [\text{low} - \lambda, \text{up} + \lambda]\)

\(\rightarrow\)

vector \(\bm{\lambda} \in \mathbb{R}^d\)

\(\rightarrow\)

\(\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{low} - \lambda_j, \text{up} + \lambda_j]\)

Guarantee:    \(\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{low} - \lambda_j, \text{up} + \lambda_j]\)   are RCPS 

For a \(K\)-partition of the pixels \(M \in \{0, 1\}^{d \times K}\)

\(K=4\)

\(K=8\)

\(K=32\)

\(\hat{\lambda}_K\)

conformalized uncertainty maps

\(K=4\)

\(K=8\)

Teneggi, J., Tivnan, M., Stayman, W., & Sulam, J. (2023, July). How to trust your diffusion model: A convex optimization approach to conformal risk control. In International Conference on Machine Learning. PMLR.

\(K\)-RCPS: High-dimensional Risk Control

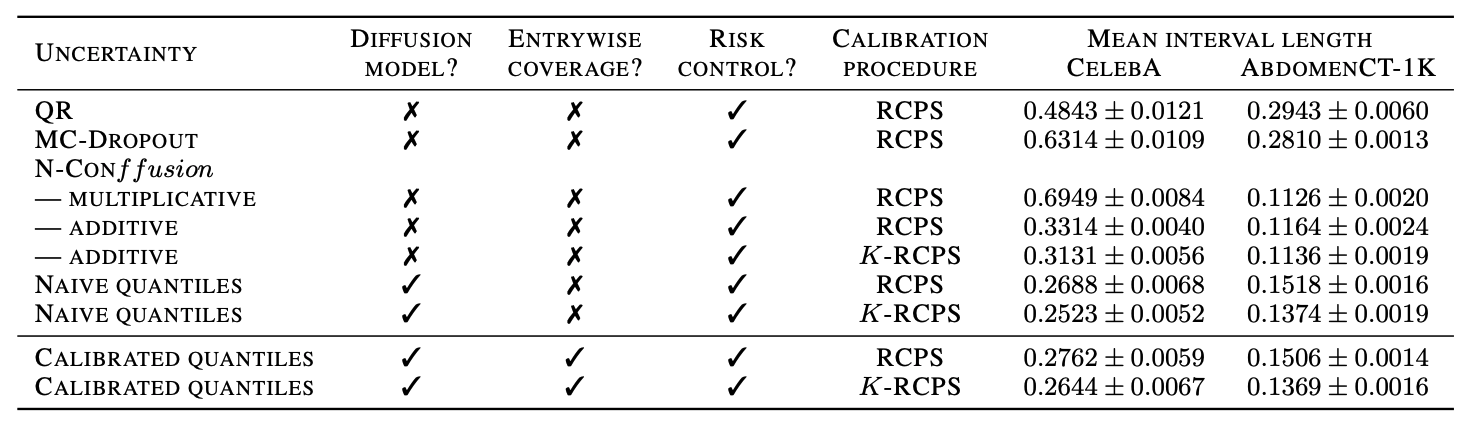
\[\mathbb{P}\left[\mathbb{E}\left[\text{fraction of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]

Interpretability

\bullet \quad \mathbb P\left[ \hat x_i \in \tau_i \right] > 1-\alpha \qquad \text{(say, $\alpha=5\%$)}
\hat{x}
\bullet \quad \mathbb P\left[ \text{``less than $\epsilon$ of $x_i$ pixels are not in $\tau_i$''} \right] > 1-\delta

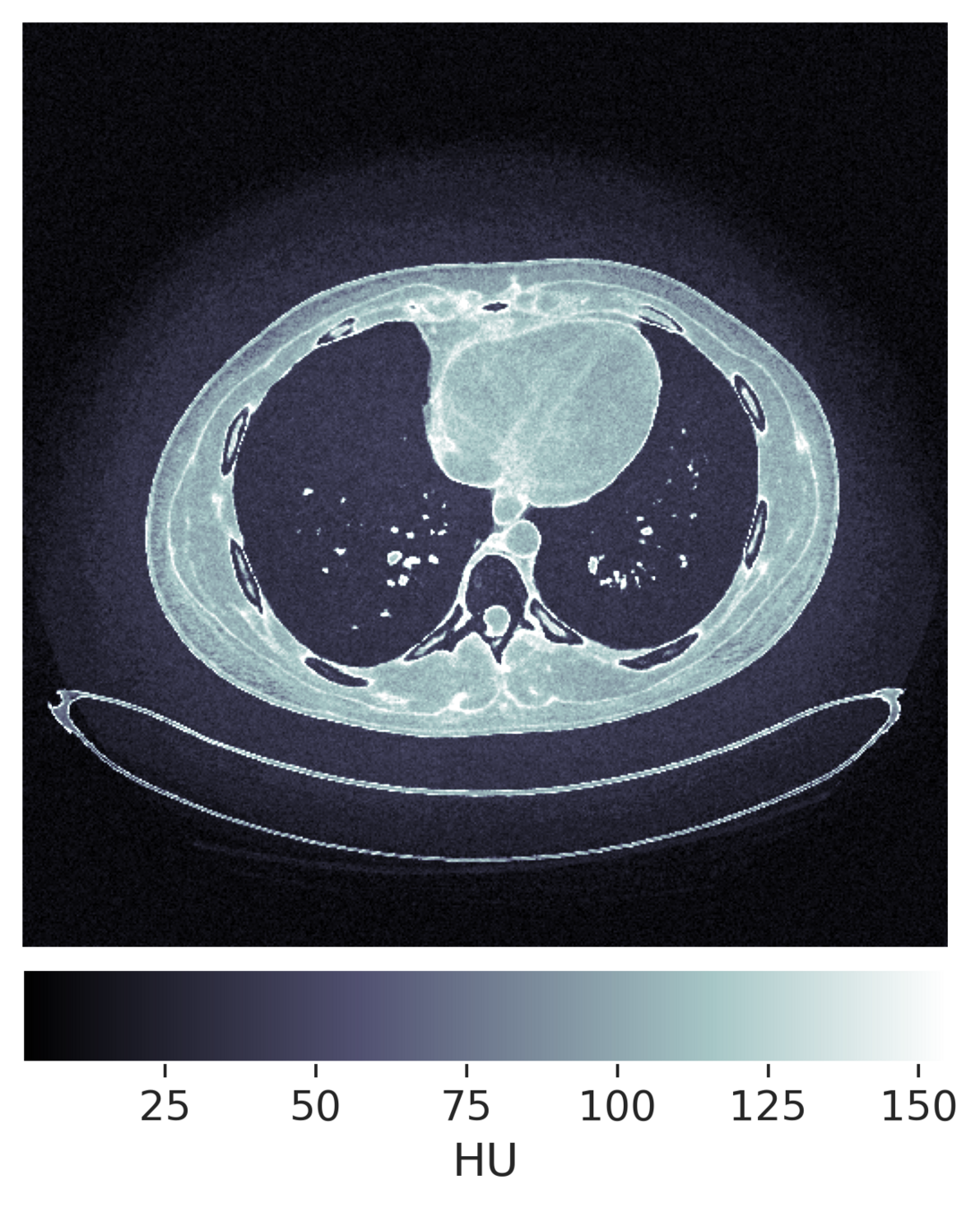
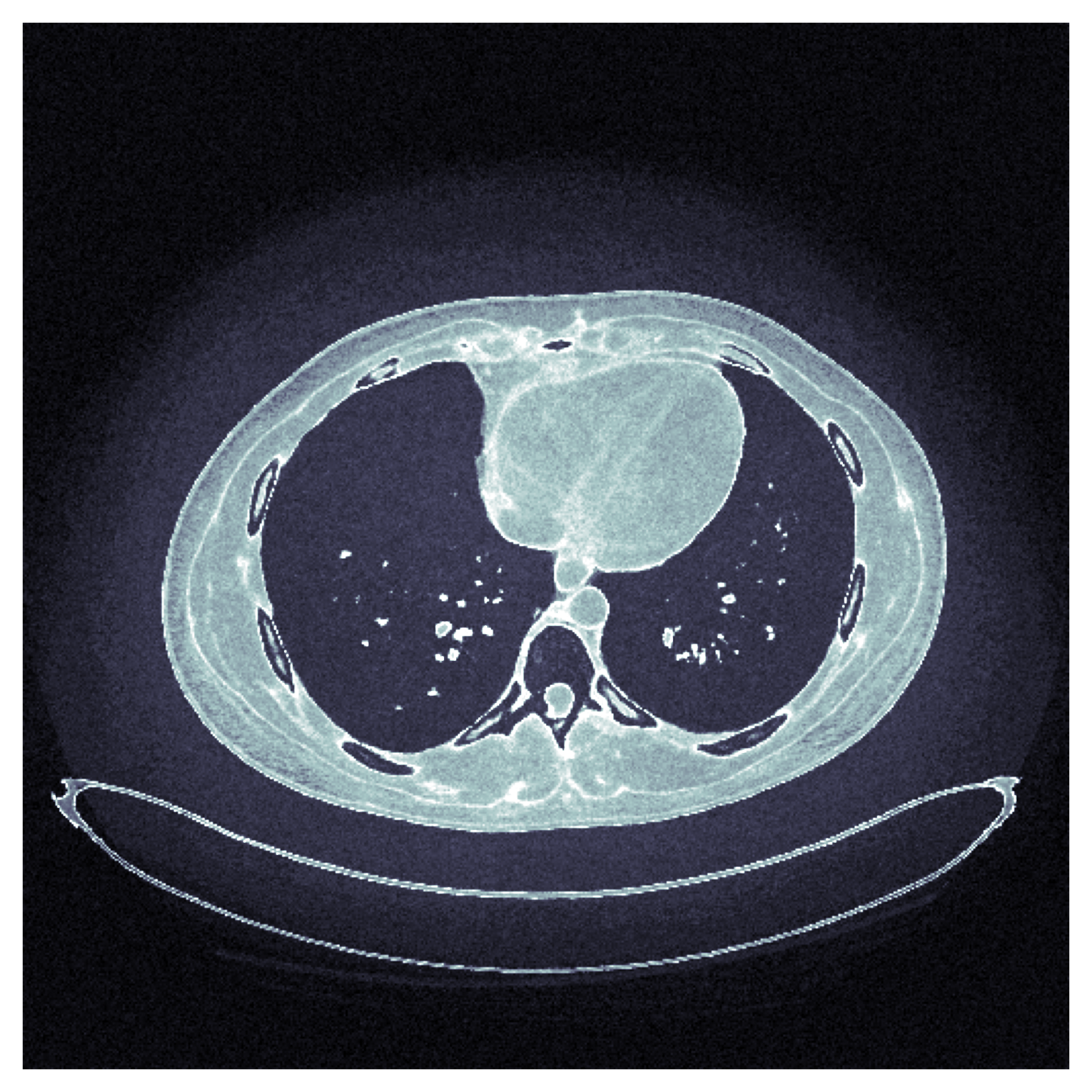
ground truth pixels!

true whatever your model, whatever your training data,
distribution free

\tau_i
\hat{x}_i
\left[ \qquad \right]

uncertainty intervals:

K-RCPS: High dimensional conformal risk control

Part II: Embracing AI (carefully)

Interpretability

Fairness

Uncertainty Quantification

Interpretability

{f}\huge(
{\huge)} = \text{\texttt{sick}}

  • What parts of the image are important for this prediction?

  • What are the subsets of the input                so that 

{f}(x_C) \approx {f}(x) ?
C \subseteq [d]

Hierarchical Shapley

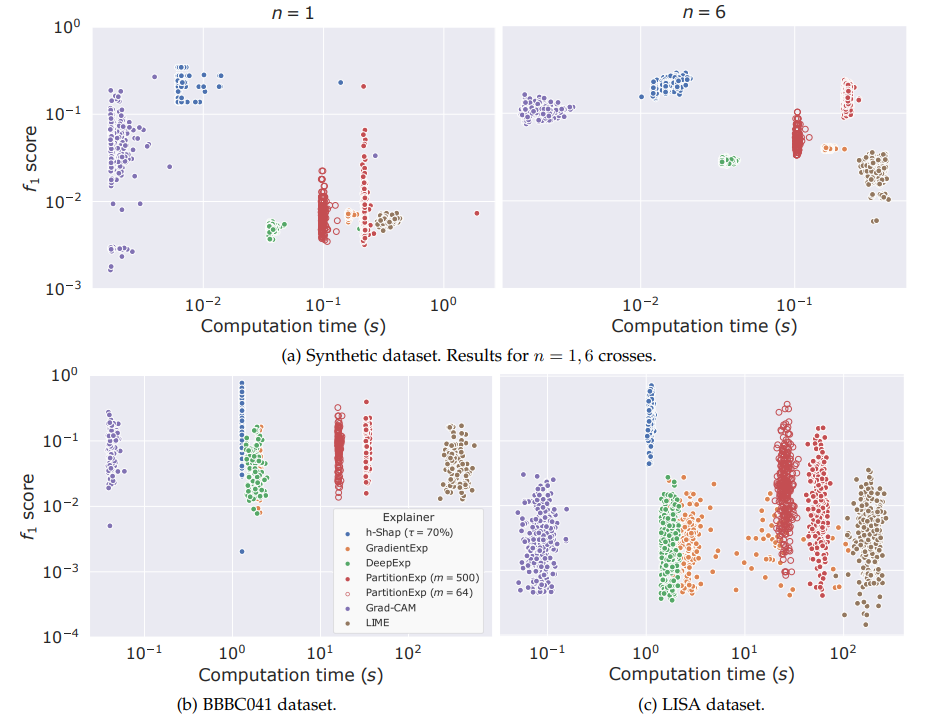
Fast hierarchical games for image explanations, Teneggi, Luster & Sulam,
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022

Hierarchical Shapley

\text{reject} ~\Rightarrow~ j=2 \text{: important}
\text{For any } S \subseteq [n]\setminus \{j\}, \text{ and a sample } x\sim \mathcal D_X
H^0_{j,S}: \quad f(\tilde X_{S\cup \{j\}}) \overset{d}{=} f(\tilde X_{S})
H^0_{j=2,S=\{1,3,4\}}
Teneggi, J., Bharti, B., Romano, Y., & Sulam, J. (2023). SHAP-XRT: The Shapley Value Meets Conditional Independence Testing. Transactions on Machine Learning Research.

Precise Notions of Importance

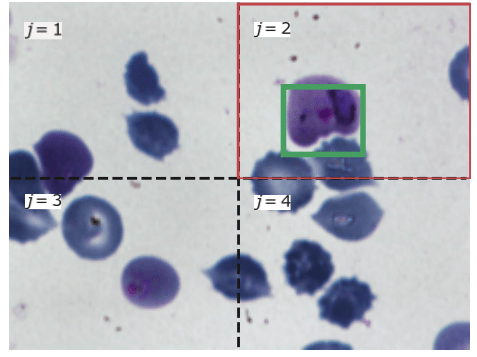
(Interpretability as Hypothesis Testing)

Text

\(H_0:\) "The distribution of \(f(x)\) w.r.t. a feature set \(S\) remains unchanged when the  \(i^{th}\) feature is introduced"

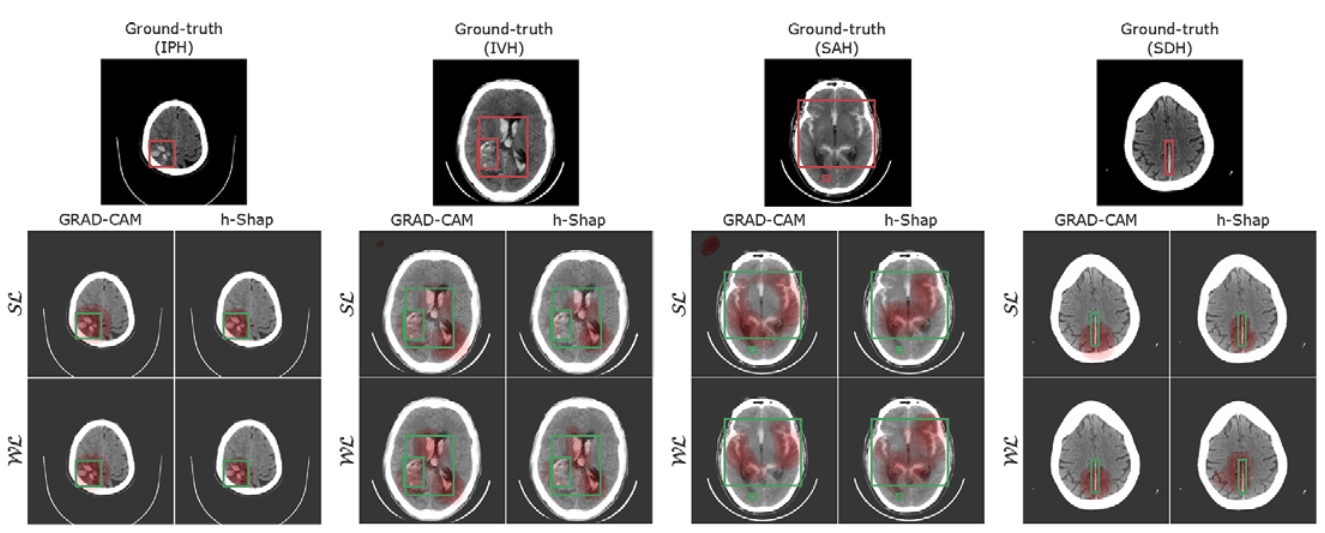
Teneggi, J., Yi, P. H., & Sulam, J. (2023). Examination-level supervision for deep learning–based intracranial hemorrhage detection at head CT. Radiology: Artificial Intelligence, e230159.

Precise Notions of Importance

Part II: Embracing AI (carefully)

Interpretability

Fairness

Uncertainty Quantification

Fairness

Is the model fair?

\text{TPR}_{A} = \mathbb P [\hat Y = 1 | Y = 1, {A}]

Pneumonia

Clear

95% accurate

\Delta_{\text{TPR}} = {\Large|} \mathbb P [\hat Y = 1 | Y = 1, {\color{blue}A=0}] - \mathbb P [\hat Y = 1 | Y = 1, {\color{blue}A=1}] {\Large|}

Fairness

Pneumonia

Clear

Does your model achieve a \(\Delta_{\text{TPR}}\) of at most (say) 6% ?

95% accurate

Fairness

Pneumonia

Clear

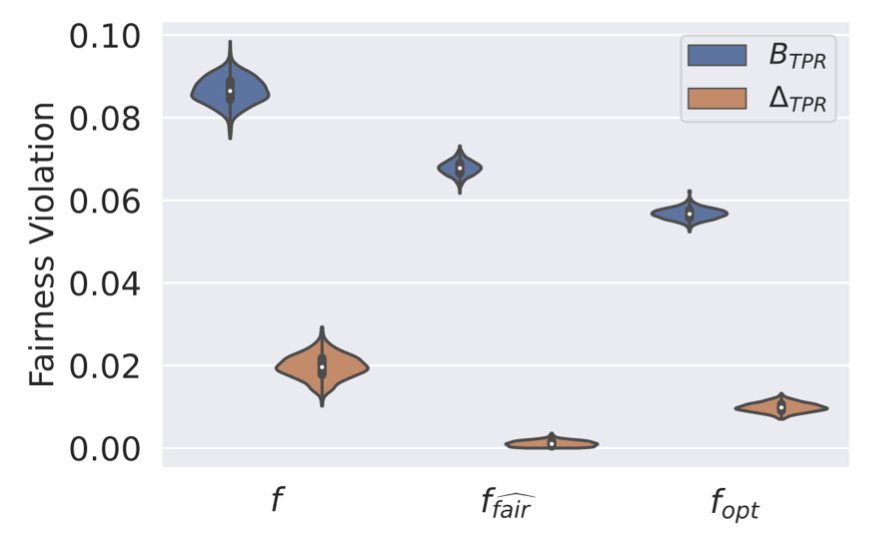
  • Tight upper bounds to fairness violations
     

  • (optimally) Actionable
     

Maximum TPR
discrepancy

True TPR
discrepancy

Bharti, B., Yi, P., & Sulam, J. (2023). Estimating and Controlling for Equalized Odds via Sensitive Attribute Predictors. Neurips.

Fairness

95% accurate

Collaborators

Adam Charles (BME)

Peter van Zijl (Radiology)

Xu Li (Radiology)

Paul H. Yi (UMB, Radiology)

Web Stayman (BME)

Mat Tivnan (BME)

Sasha Popel (BME)

Tiger Xu (Neuro)

Dwight Bergles (Neuro)
Rick Huganir (Neuro)

Agustin Graves (Neuro, BME)

Gabrielle Coste (Neuro)

Aaron W. James (Pathology)

Carla Saoud (Pathology)

Sintawat Wangsiricharoen (Patho)

Christa L LiBrizzi (Patho)

Carol D Morris (Patho)

Adam S Levin (Patho)

Thank you

Game Changers: Artificial Intelligence Part I, 2028