Model Interpretability with

Shapley Coefficients

Jeremias Sulam (JHU)

 

Foundations of Interpretable AI

Conference on Parsimony and Learning 2025

Aditya Chattopadhyay (Amazon)

René Vidal (UPenn)

Foundations of Interpretable AI

Jeremias Sulam (JHU)

 

CVPR 2025

Aditya Chattopadhyay (Amazon)

René Vidal (UPenn)

Part I: Motivations and Post-hoc (9-9:45)

Part II: Shapley values (9:45 - 10:30)

Part III: Interpretable by Design (11 - 11:45)

Shapley Values

Popularity on 

Popularity on 

Shapley Values

TODAY

What are they?

How are they computed?

(Shapley for local feature importance)

  • Not an exhaustive literature review
  • Not a code & repos review
  • Not a demonstration on practical problems
  • Review of general approaches and methodology
  • Pointers to where to start looking in different problem domains

Shapley Values

Lloyd S Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.

Let                       be an    -person cooperative game with characteristic function 

G = ([n],f)
n
v : \mathcal P([n]) \mapsto \mathbb R

How important is each player for the outcome of the game?

Shapley Values

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]

marginal contribution of player i with coalition S 

Lloyd S Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]

Shapley Values

  • Efficiency

\displaystyle v([n]) = v(\empty) + \sum_{i=1}^n \phi_i(v)

  • Linearity

\displaystyle \phi_i( \alpha_1 v_1 + \alpha_2 v_2) = \alpha_1 \phi_i(v_1) + \alpha_2 \phi_i(v_2) \newline \text{ for characteristic functions }v_1,v_2

  • Symmetry

\text{If}~~ v(S\cup i) = v(S\cup j) ~~ \forall S\subseteq [n]\setminus \{i,j\} \newline \text{Then}~~ \phi_i(v) = \phi_j(v)
\text{If}~~ v(S\cup i) = v(S) ~~ \forall S\subseteq [n]\setminus \{i\} \newline \text{Then}~~ \phi_i(v)=0

  • Nullity

Shapley Explanations for ML

lung opacity
cardiomegaly
fracture
no findding
X \in \mathcal X \subset \mathbb R^n

inputs

responses

f:\mathcal X \to \mathcal Y

predictor

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]
f(X) = \hat{Y} \approx Y
Y\in \mathcal Y = [C]

Shapley Explanations for ML

Question 2:

           How can we (when) compute \(\phi_i(v)\)?

Question 3:

           What do \(\phi_i(v)\) say (and don't) about the problem?

X \in \mathcal X \subset \mathbb R^n

inputs

responses

f:\mathcal X \to \mathcal Y

predictor

Question 1:

           How should (can) we choose the function \(v\)?

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]
f(X) = \hat{Y} \approx Y
Y\in \mathcal Y = [C]

Shapley Explanations for ML

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
Question 2:

           How can we (when) compute \(\phi_i(v)\)?

Question 3:

           What do \(\phi_i(v)\) say (and don't) about the problem?

f(X) = \hat{Y} \approx Y
X \in \mathcal X \subset \mathbb R^n
Y\in \mathcal Y = [C]

inputs

responses

f:\mathcal X \to \mathcal Y

predictor

Question 1:

           How should (can) we choose the function \(v\)?

Question 1:

           How should (can) we choose the function \(v\)?

For any \(S \subseteq [n]\), and a sample \(x\sim p_X\), we need

\(v_f(S,x) : \mathcal P([n])\times \mathcal X \to \mathbb R\)

[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]


[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]
Question 1:

           How should (can) we choose the function \(v\)?

  • Fixed reference value
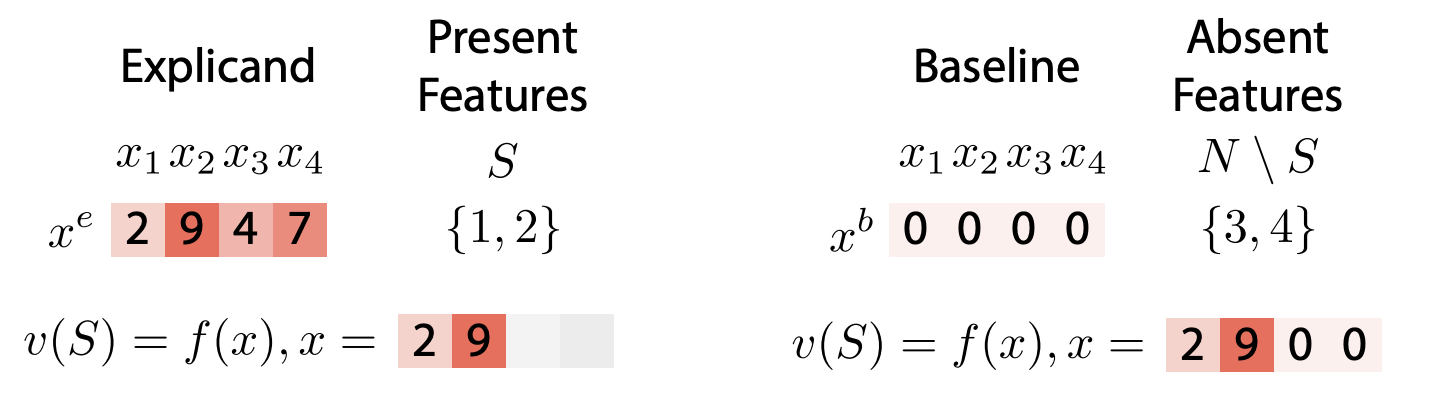
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]


[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]

\(v_f(S,x) = f(x_S,\mathbb x^{b}_{\bar{S}})\)

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ f(x_{S\cup i},x^b_{\overline{S\cup i}}) - f(x_{S},x^b_{\overline{S}}) \right]
Question 1:

           How should (can) we choose the function \(v\)?

  • Fixed reference value
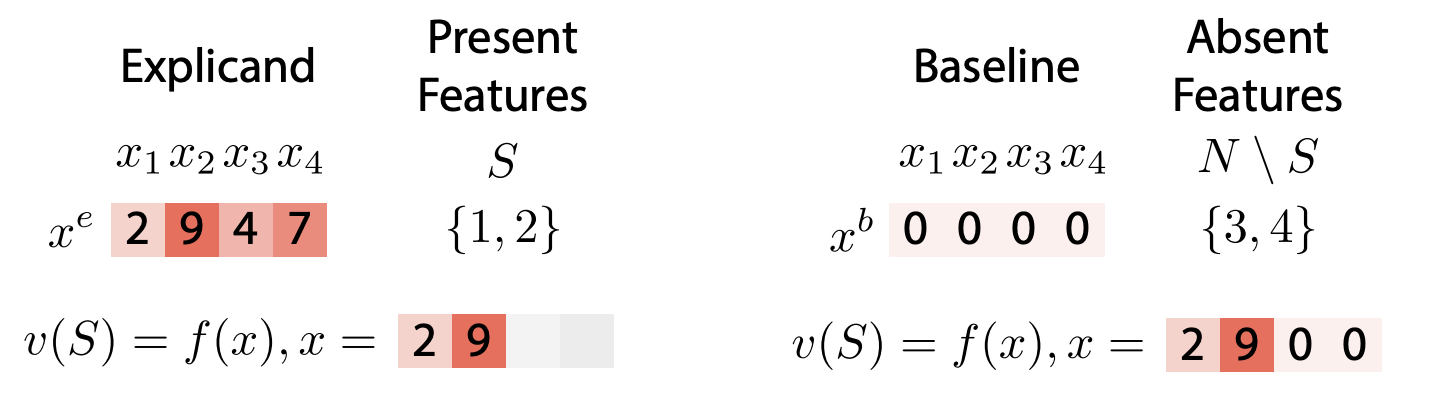
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]


[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]

\(v_f(S,x) = f(x_S,\mathbb x^{b}_{\bar{S}})\)

Easy, cheap

\( (x_S,x^b_{\bar{S}})\not\sim p_X\)

(x_S,x^b_{\bar{S}})
x
Question 1:

           How should (can) we choose the function \(v\)?

  • Conditional Data Distribution

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)

[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]
Question 1:

           How should (can) we choose the function \(v\)?

  • Conditional Data Distribution

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)

\((x_S,\tilde{X}_{\bar{S}})\)

  • Difficult/expensive

\( (x_S,\tilde{X}_{\bar{S}})\sim p_X\)

  • Breaks the Null axiom
    unimportant \(i \not\Rightarrow \phi_i(f) \neq 0\)

"True to the data"

[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]
Question 1:

           How should (can) we choose the function \(v\)?

  • Conditional Data Distribution

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)

\( (x_S,\tilde{X}_{\bar{S}})\sim p_X\)

(x_S,\tilde{X}_{\bar{S}})
x_S
x

"True to the data"

  • Difficult/expensive
  • Breaks the Null axiom
    unimportant \(i \not\Rightarrow \phi_i(f) \neq 0\)
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]
Question 1:

           How should (can) we choose the function \(v\)?

  • Conditional Data Distribution

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)

\( (x_S,\tilde{X}_{\bar{S}})\sim p_X\)

(x_S,\tilde{X}_{\bar{S}})
x_S
x

"True to the data"

  • Difficult/expensive
  • Breaks the Null axiom
    unimportant \(i \not\Rightarrow \phi_i(f) \neq 0\)

Alternative: learn a model \(g_\theta\) for the conditional expectation

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S] \approx g_\theta (x,S)\)

[Frye et al, 2021]
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]
Question 1:

           How should (can) we choose the function \(v\)?

  • Marginal Data Distribution

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})]\)

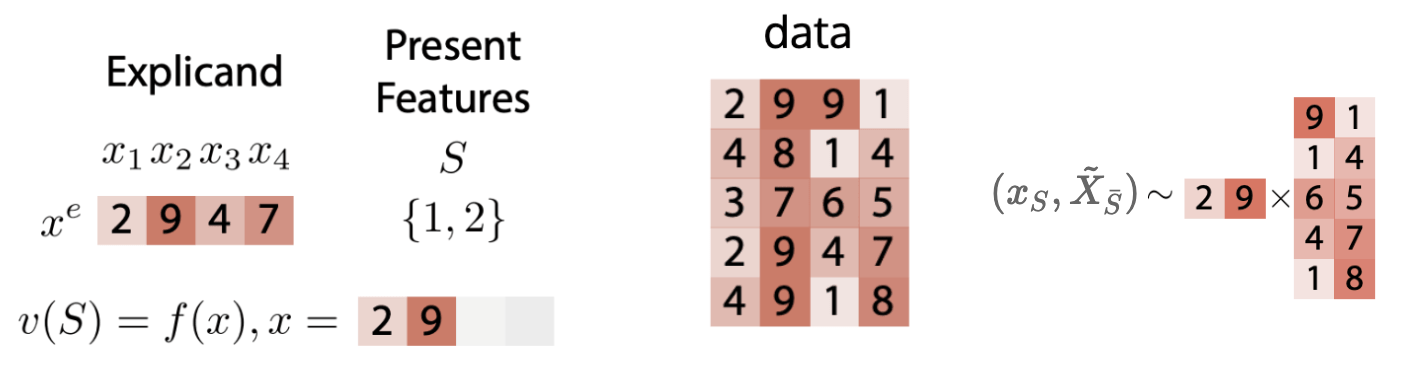
\( (x_S,\tilde{X}_{\bar{S}})\not\sim p_X\)
except if features independent

  • Easier than conditional
  • ``true to the model''
    maintains Null axiom     
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Lundberg & Lee, 2017][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]
Question 1:

           How should (can) we choose the function \(v\)?

  • Linear model (approximation)

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})] \approx f(x_S,\mathbb{E}[\tilde{X}_{\bar{S}}])\) 

\( (x_S,\tilde{X}_{\bar{S}})\not\sim p_X\)
except in linear models
(and feature independence)

  • Easiest, popular in practice

[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]

 

[Aas et al, 2019] [Lundberg & Lee, 2017][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]

 

Shapley Explanations for ML

X \in \mathcal X \subset \mathbb R^n

inputs

responses

f:\mathcal X \to \mathcal Y

predictor

Question 1:

           How should (can) we choose the function \(v\)?

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
Y\in \mathcal Y = [C]
f(X) = \hat{Y} \approx Y
Question 2:

           How can we (when) compute \(\phi_i(v)\)?

Question 3:

           What do \(\phi_i(v)\) say (and don't) about the problem?

Question 2:

           How can we (when) compute \(\phi_i(v)\)?

intractable.. \(\mathcal O (2^n)\)

\displaystyle \phi_i(v) = \frac{1}{n!} \sum_{\pi \subseteq \Pi(n)} \left[ v(\text{Pre}^i(\pi)\cup \{i\}) - v(\text{Pre}^i(\pi)) \right]
 
[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]

  • Weighted Least Squares (kernelSHAP )

\displaystyle \phi_i(v) = \argmin_{\color{red}\beta} \sum_{S \subseteq [n]} \omega(|S|,n) (v(S) - {\color{red}\beta_0} - \sum_{j\in S}{\color{red}\beta_j})^2

  • Monte Carlo Sampling

\displaystyle \phi_i(v) = \sum_{S \sim w(S)} \left[ v(S\cup \{i\}) - v(S) \right]
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
 
[Jethani et al, 2021]

  • Weighted Least Squares (kernelSHAP )

  • Weighted Least Squares, amortized ( FastSHAP )

\displaystyle \Phi_\text{fastShap} = \argmin_{\color{red}\phi_\theta:\mathcal X\to \mathbb R^n}~~ \underset{X}{\mathbb E} ~\sum_{y\in[k]} ~~ \sum_{S \subseteq [n]} \omega(|S|,n) (v(S,y) - \sum_{j\in S}{\color{red}\phi_\theta(X,y)_j})^2

... and stochastic versions [Covert et al, 2024]

Question 2:

           How can we (when) compute \(\phi_i(v)\)?

\displaystyle \phi_i(v) = \argmin_{\color{red}\beta} \sum_{S \subseteq [n]} \omega(|S|,n) (v(S) - {\color{red}\beta_0} - \sum_{j\in S}{\color{red}\beta_j})^2
Question 2:

           How can we (when) compute \(\phi_i(v)\) if we know more?

(about the model)

 
[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014][Chen et al, 2020]

  • Linear models \(f(x) = \beta^\top x \)

Closed-form expressions  (for marginal distributions and baselines)

\( \phi_i(f,x) = \beta_i (x_i-\mu_i ) \)

 (also for conditional if assuming Gaussian features)

  • Tree models

 
[Lundberg et al, 2020]

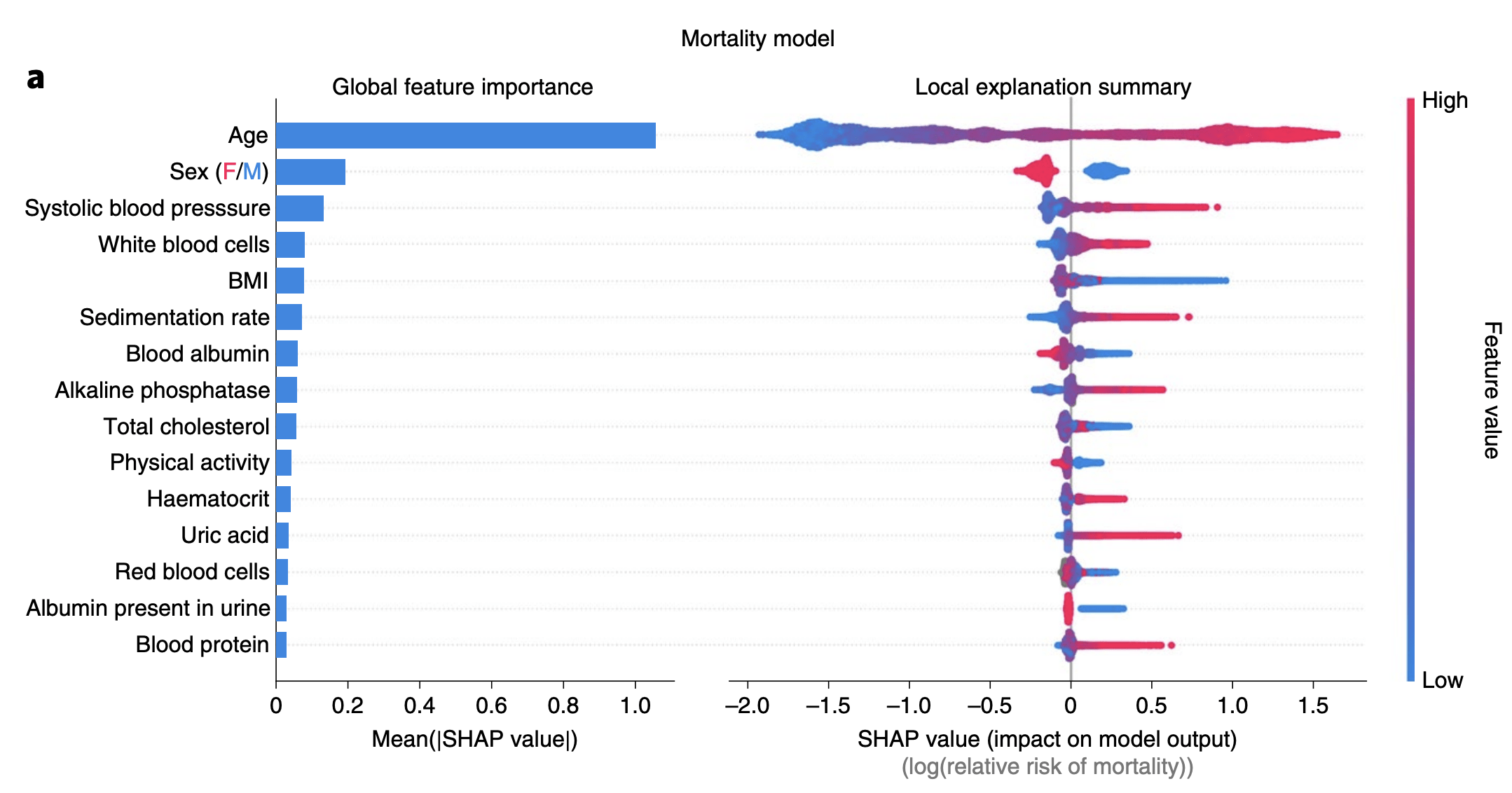
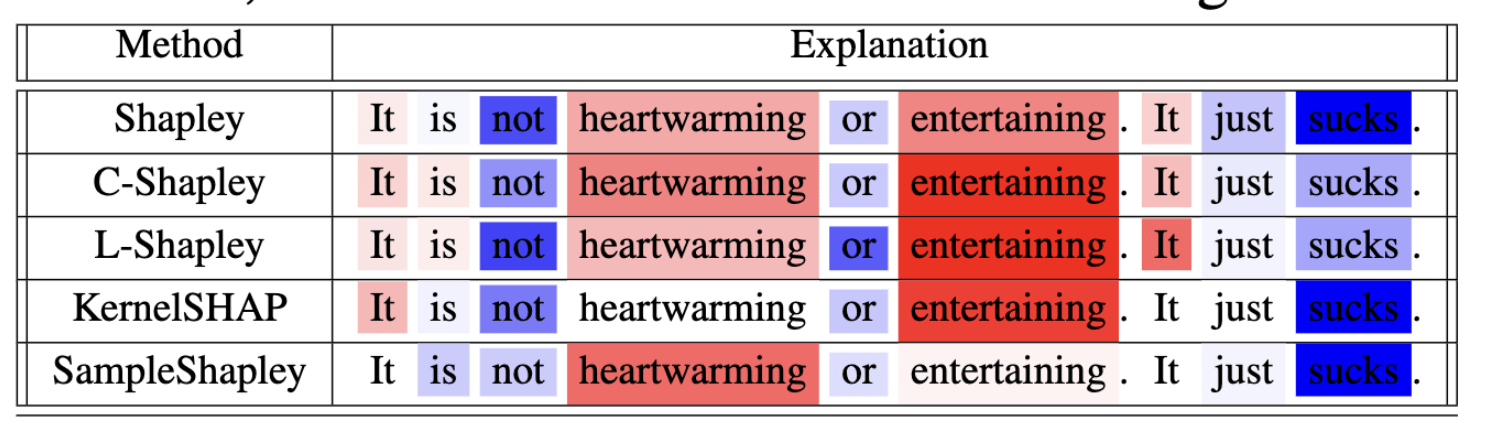
Polynomial time algorithm (exact) (TreeSHAP) for \(\phi_i(f)\)

\(\mathcal O(N_\text{trees}N_\text{leaves} \text{Depth}^2)\)

Question 2:

           How can we (when) compute \(\phi_i(v)\) if we know more?

  • Local models 

(about the model)

 
[Chen et al, 2019]

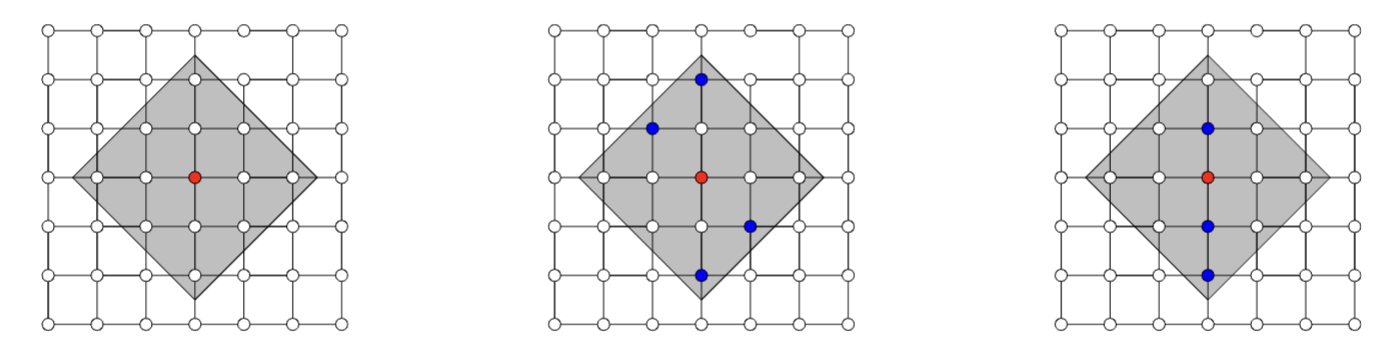
Observation: Restrict computation of \(\phi_i(f)\) to local areas of influence given by a graph structure

L-Shap
C-Shap
\displaystyle \hat{\phi}^k_i(v) = \frac{1}{|\mathcal N_k(i)|} \sum_{S\subseteq\mathcal N_k(i)\setminus i } w(S) \left[ v(S\cup \{i\}) - v(S) \right]

\(\Rightarrow\) complexity \(\mathcal O(2^k n)\)

Question 2:

           How can we (when) compute \(\phi_i(v)\) if we know more?

  • Local models 

(about the model)

 
[Chen et al, 2019]

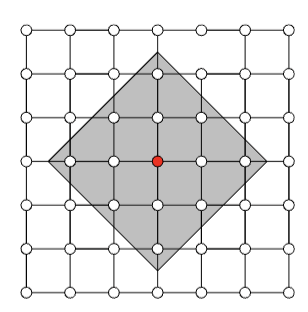
Observation: Restrict computation of \(\phi_i(f)\) to local areas of influence given by a graph structure

\(\Rightarrow\) complexity \(\mathcal O(2^k n)\)

Correct approximations (informal statement)

Let \(S\subset \mathcal N_k(i)\). If \((X_i \perp\!\!\!\perp X_{[n]\setminus S} | X_T) \) and \((X_i \perp\!\!\!\perp X_{[n]\setminus S} | X_T,Y) \) for any \(T\subset S\setminus i\).

Then \(\hat{\phi}^k_i(v) = \phi_i(v)\)

(and approximately bounded otherwise, controlled)

\displaystyle \hat{\phi}^k_i(v) = \frac{1}{|\mathcal N_k(i)|} \sum_{S\subseteq\mathcal N_k(i)\setminus i } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
Question 2:

           How can we (when) compute \(\phi_i(v)\) if we know more?

  • Local models 

(about the model)

 
[Chen et al, 2019]

Observation: Restrict computation of \(\phi_i(f)\) to local areas of influence given by a graph structure

\(\Rightarrow\) complexity \(\mathcal O(2^k n)\)

\displaystyle \hat{\phi}^k_i(v) = \frac{1}{|\mathcal N_k(i)|} \sum_{S\subseteq\mathcal N_k(i)\setminus i } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
Question 2:

           How can we (when) compute \(\phi_i(v)\) if we know more?

  • Hierarchical Shapley (h-Shap) 

(about the model)

 
[Teneggi et al, 2022]

Observation:   \(f(x) = 1 \Leftrightarrow \exist~ i: f(x_i,\tilde{X}_{-i}) = 1\)        (A1)  

{\huge)} = 0
{f}\huge(
{\huge)} = 1
{f}\huge(

Example:

f(x) = 1

if     contains a sick cell

x
{f}\huge(
{\huge)} = 0
Question 2:

           How can we (when) compute \(\phi_i(v)\) if we know more?

(about the model)

\gamma = 2

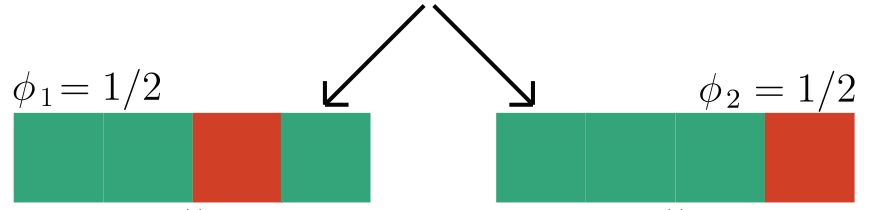
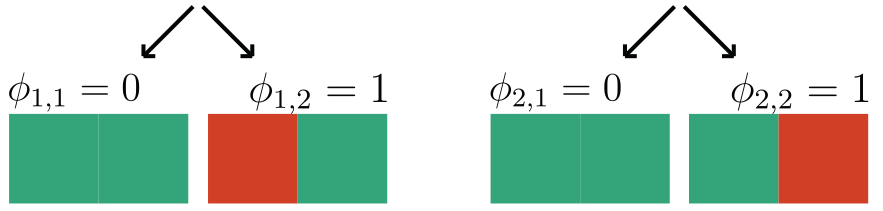
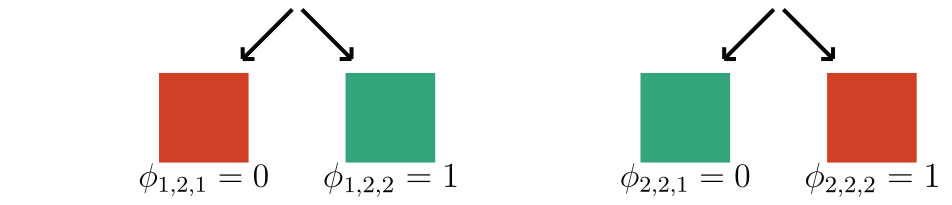
Observation:   \(f(x) = 1 \Leftrightarrow \exist~ i: f(x_i,\tilde{X}_{-i}) = 1\)        (A1)  

  • Hierarchical Shapley (h-Shap) 

 
[Teneggi et al, 2022]

  • Under A1, \(\phi^\text{h-Shap}_i(f) = \phi_i(f)\)

  • Bounded approximation as deviating from A1

2. Correct approximation (informal)

1. Complexity \(\mathcal O(2^\gamma k \log n)\)

Question 2:

           How can we (when) compute \(\phi_i(v)\) if we know more?

(about the model)

1. Complexity \(\mathcal O(2^\gamma k \log n)\)

  • Under A1, \(\phi^\text{h-Shap}_i(f) = \phi_i(f)\)

  • Bounded approximation as deviating from A1

Observation:   \(f(x) = 1 \Leftrightarrow \exist~ i: f(x_i,\tilde{X}_{-i}) = 1\)        (A1)  

2. Correct approximation (informal)

  • Hierarchical Shapley (h-Shap) 

 
[Teneggi et al, 2022]
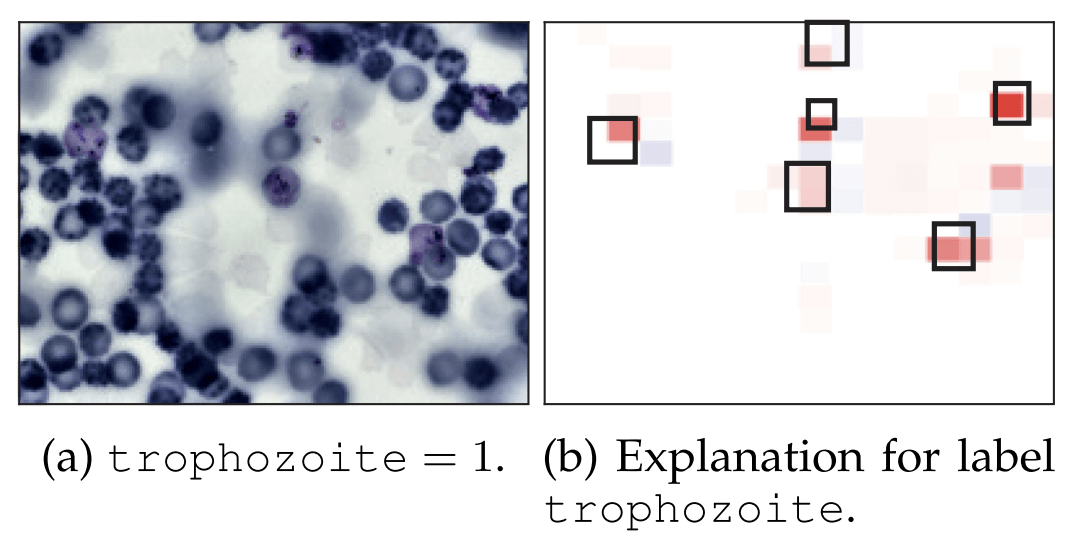
Question 2:

           How can we (when) compute \(\phi_i(v)\) if we know more?

  • Shapley Approximations for Deep Models

(about the model)

DeepLift (Shrikumar et al, 2017): biased estimation of baseline Shap

DeepShap (Chen et al, 2021): biased estimation of marginal Shap

DASP (Ancona et al, 2019) Uncertainty propagation for baseline (zero) Shap
                assuming Gaussianity and independence of features

Shapnets [Wang et al, 2020]: Computation for small-width networks

... not an exhaustive list!

Transformers (ViTs) [Covert et al, 2023]: leveraging attention to fine-tune a surrogate model for Shap estimation

Shapley Explanations for ML

Question 2:

           How can we (when) compute \(\phi_i(v)\)?

Question 3:

           What do \(\phi_i(v)\) say (and don't) about the problem?

X \in \mathcal X \subset \mathbb R^n

inputs

responses

f:\mathcal X \to \mathcal Y

predictor

Question 1:

           How should (can) we choose the function \(v\)?

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
Y\in \mathcal Y = [C]
f(X) = \hat{Y} \approx Y
Question 3:

           What do \(\phi_i(v)\) say (and don't) about the problem?

Interpretability as Conditional Independence

  • Explaining uncertainty via Shapley Values [Watson et al, 2023]

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v_\text{KL}(S\cup \{i\}) - v_\text{KL}(S) \right]

with   \(v_\text{KL}(S,x) = -D_\text{KL}(~p_{Y|x} ~||~ p_{Y|x_s}~)\)

Theorem (informal)

\(Y \perp\!\!\!\perp X_j  | X_s = x_s ~~\Rightarrow~~ v_\text{KL}(S\cup\{i\},x) - v_\text{KL}(S,x) = 0\)

Question 3:

           What do \(\phi_i(v)\) say (and don't) about the problem?

Interpretability as Conditional Independence

  • SHAP-XRT: Shapley meets Hypothesis Testing [Teneggi et al, 2023]

H^0_{{i},S}:~ (f(x_{S\cup \{{i}\}},\tilde{X}_{\overline{S\cup \{{i}\}}}) ) \overset{d}{=} (f(x_S,\tilde X_{\overline S}) )

\(\hat{p}_{i,S} \leftarrow \texttt{XRT}: \text{eXplanation Randomization Test}\), via access to \({X}_{\bar{S}} \sim p_{X_{\bar{S}}|x_s}\)

Theorem (informal)

For \(f:\mathcal X \to [0,1], ~~ \mathbb E [\hat{p}_{i,S}]\leq 1- \mathbb E [v(S\cup i) - v(S)] \)

 large   \(\mathbb E [v(S\cup i) - v(S)] ~ \Rightarrow \) reject \(H^0_{i,S}\)

Conclusions

  • Shapley Values are one of the most popular wrapper-explanation methods
  • Requires care when choosing what distributions to sample from, dependent on the setting
     "true to the model"  vs "true to the data"
  • While proposed in a different context, they can be used to test for specific statistical claims
Foundations of Interpretable AI

Conference on Parsimony and Learning 2025

Is the piano important for \(\hat Y = \text{cat}\)?

How can we explain black-box predictors with semantic features?

Is the piano important for \(\hat Y = \text{cat}\), given that there is a cute mammal in the image?

Semantic Interpretability of classifiers

Is the presence of \(\color{Blue}\texttt{edema}\) important for \(\hat Y = \text{lung opacity}\)?

How can we explain black-box predictors with semantic features?

Is the presence of \(\color{magenta}\texttt{devices}\) important for \(\hat Y = \texttt{lung opacity}\), given that there is \(\color{blue}\texttt{edema}\) in the image?

model-agnostic interpretability

lung opacity
cardiomegaly
fracture
no findding

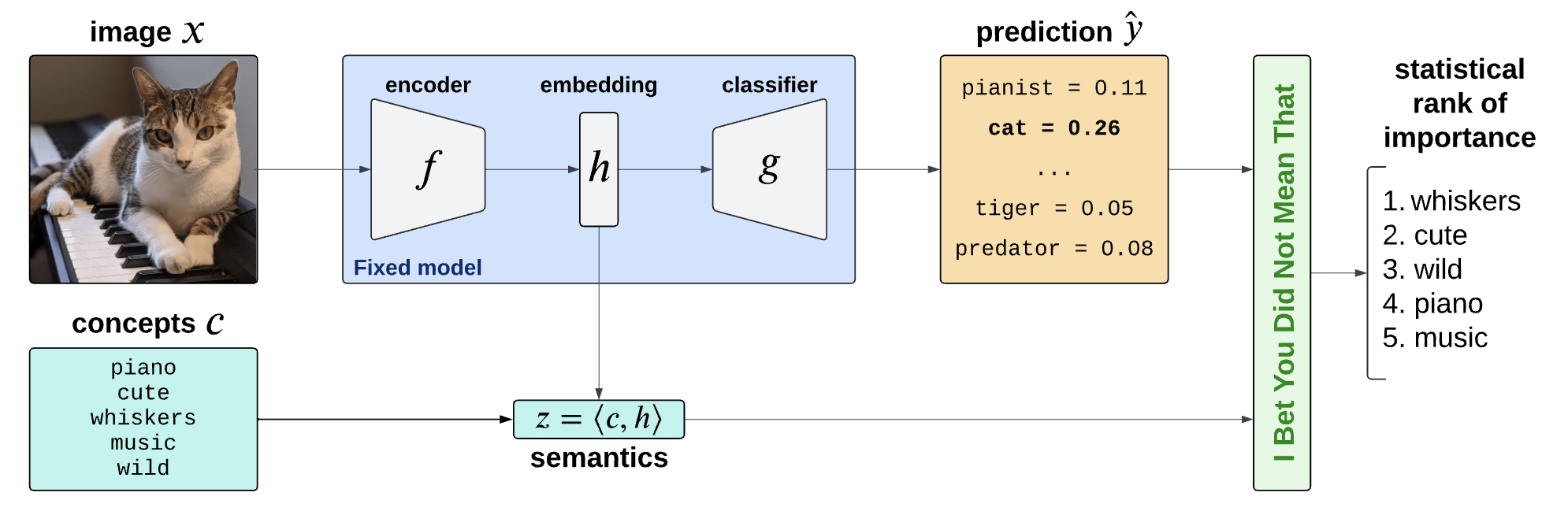
Semantic Interpretability of classifiers

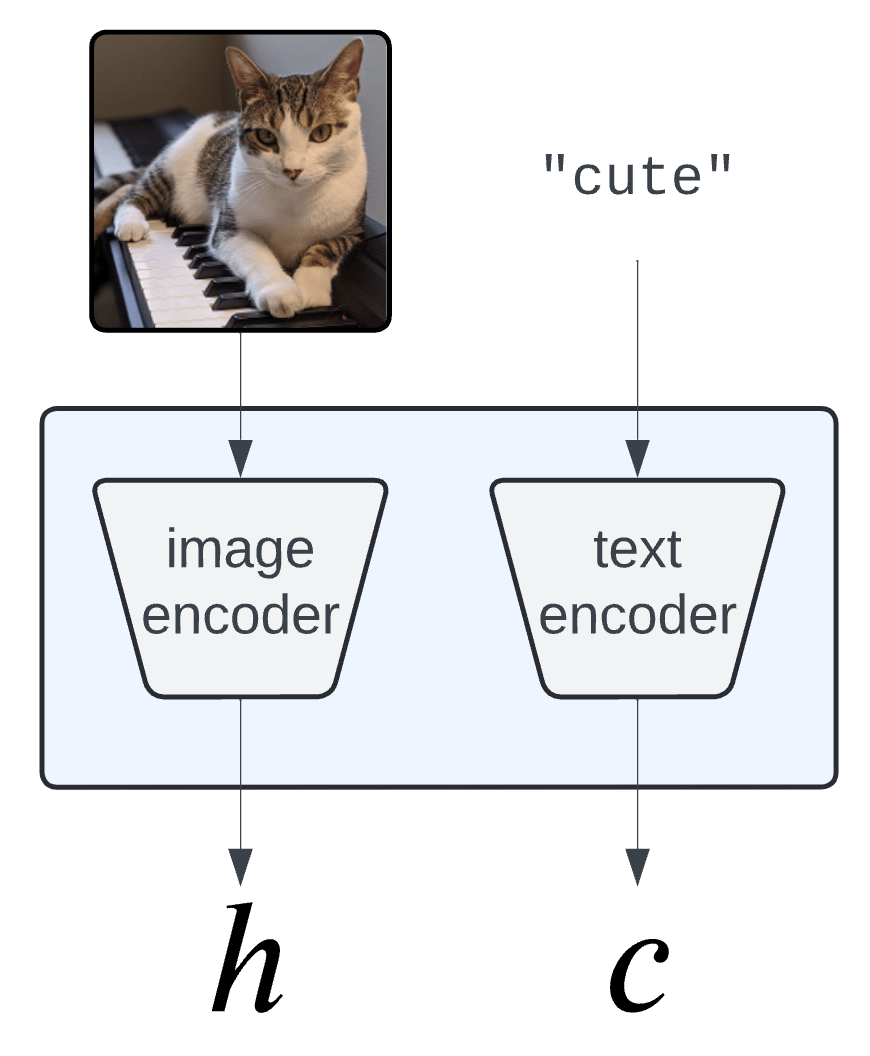
Concept Bank:     \(C = [c_1, c_2, \dots, c_m] \in \mathbb R^{d\times m}\)

Embeddings:     \(H = f(X) \in \mathbb R^d\)

Semantics:     \(Z = C^\top H \in \mathbb R^m\)

Concept Bank:     \(C = [c_1, c_2, \dots, c_m] \in \mathbb R^{d\times m}\)

Concept Activation Vectors

(Kim et al, 2018)

\(c_\text{cute}\)

Semantic Interpretability of classifiers

Vision-language models

(CLIP, BLIP, etc... )

Semantic Interpretability of classifiers

[Bhalla et al, "Splice", 2024]

Concept Bottleneck Models (CMBs)

[Koh et al '20, Yang et al '23, Yuan et al '22 ]

  • Need to engineer a (large) concept bank

  • Performance hit w.r.t. original predictor

\(\tilde{Y} = \hat w^\top Z\)

\(\hat w_j\) is the importance of the \(j^{th}\) concept

Desiderata

  • Fixed original predictor (post-hoc)

  • Global and local importance notions

  • Testing for any concepts (no need for large concept banks)

  • Precise testing with guarantees (Type 1 error/FDR control)

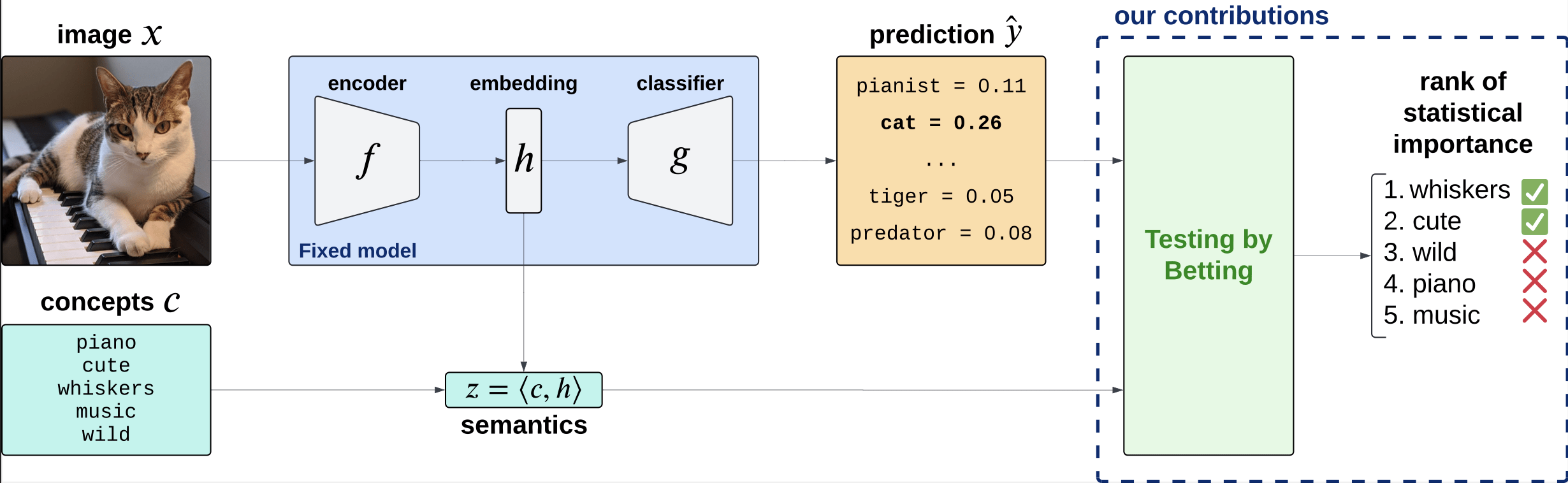
Precise notions of semantic importance

\(C = \{\text{``cute''}, \text{``whiskers''}, \dots \}\)

Global Importance

\(H^G_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j \)

Global Conditional Importance

\(H^{GC}_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j | Z_{-j}\)

Precise notions of semantic importance

Global Importance

\(C = \{\text{``cute''}, \text{``whiskers''}, \dots \}\)

\(H^G_{0,j} : g(f(X)) \perp\!\!\!\perp c_j^\top f(X) \)

Global Conditional Importance

\(H^{GC}_{0,j} : g(f(X)) \perp\!\!\!\perp c_j^\top f(X) | C_{-j}^\top f(X)\)

\(H^G_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j \)

\(H^{GC}_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j | Z_{-j}\)

Precise notions of semantic importance

"The classifier (its distribution) does not change if we condition

on concepts \(S\) vs on concepts \(S\cup\{j\} \)"

\(C = \{\text{``cute''}, \text{``whiskers''}, \dots \}\)

Local Conditional Importance

\[H^{j,S}_0:~ g({\tilde H_{S \cup \{j\}}}) \overset{d}{=} g(\tilde H_S), \qquad \tilde H_S \sim P_{H|Z_S = C_S^\top f(x)} \]

Precise notions of semantic importance

"The classifier (its distribution) does not change if we condition

on concepts \(S\) vs on concepts \(S\cup\{j\} \)"

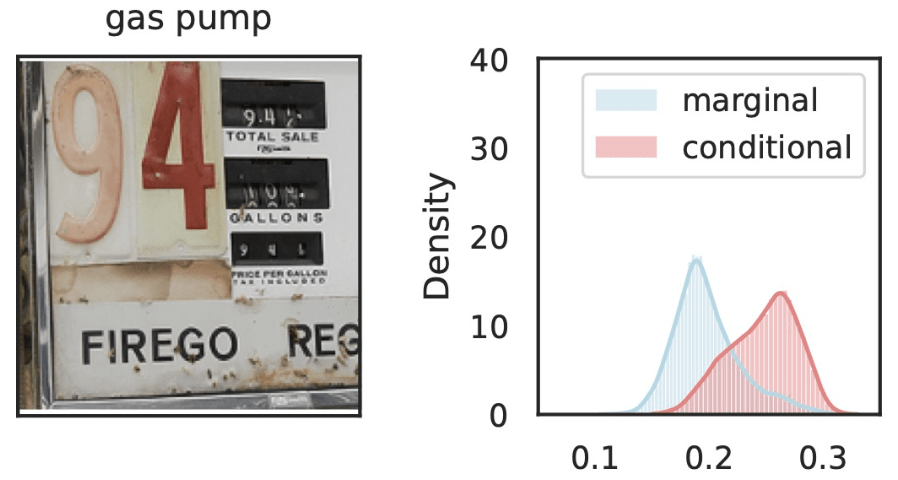
\(\hat{Y}_\text{gas pump}\)

\(Z_S\cup Z_{j}\)

\(Z_{S}\)

\(Z_j=\)

Local Conditional Importance

\[H^{j,S}_0:~ g({\tilde H_{S \cup \{j\}}}) \overset{d}{=} g(\tilde H_S), \qquad \tilde H_S \sim P_{H|Z_S = C_S^\top f(x)} \]

Precise notions of semantic importance

"The classifier (its distribution) does not change if we condition

on concepts \(S\) vs on concepts \(S\cup\{j\} \)"

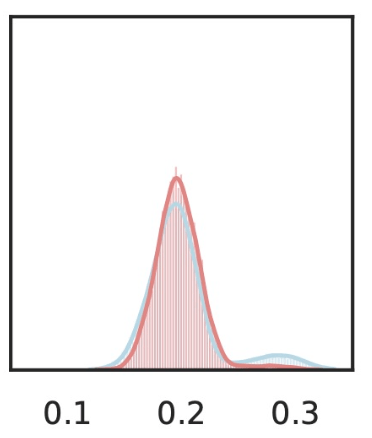
\(\hat{Y}_\text{gas pump}\)

\(\hat{Y}_\text{gas pump}\)

\(Z_S\cup Z_{j}\)

\(Z_{S}\)

\(Z_S\cup Z_{j}\)

\(Z_{S}\)

Local Conditional Importance

\(Z_j=\)

\(Z_j=\)

\[H^{j,S}_0:~ g({\tilde H_{S \cup \{j\}}}) \overset{d}{=} g(\tilde H_S), \qquad \tilde H_S \sim P_{H|Z_S = C_S^\top f(x)} \]

Testing by betting 

\(H^G_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j     \iff      P_{\hat{Y},Z_j} = P_{\hat{Y}} \times P_{Z_j}\)

Testing importance via two-sample tests

\(H^{GC}_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j | Z_{-j}     \iff      P_{\hat{Y}Z_jZ_{-j}} = P_{\hat{Y}\tilde{Z}_j{Z_{-j}}}\)

\(\tilde{Z_j} \sim P_{Z_j|Z_{-j}}\)

[Shaer et al, 2023]

[Teneggi et al, 2023]

\[H^{j,S}_0:~ g({\tilde H_{S \cup \{j\}}}) \overset{d}{=} g(\tilde H_S), \qquad \tilde H_S \sim P_{H|Z_S = C_S^\top f(x)} \]

Testing by betting

Goal: Test a null hypothesis \(H_0\) at significance level \(\alpha\)

Standard testing by p-values

Collect data, then test, and reject if \(p \leq \alpha\)

Online testing by e-values

Any-time valid inference, monitor online and reject when \(e\geq 1/\alpha\)

[Shaer et al. 2023, Shekhar and Ramdas 2023, Podkopaev et al 2023]

  • Consider a wealth process
    \(K_0 = 1;\)
    \(\text{for}~ t = 1, \dots \\ \)

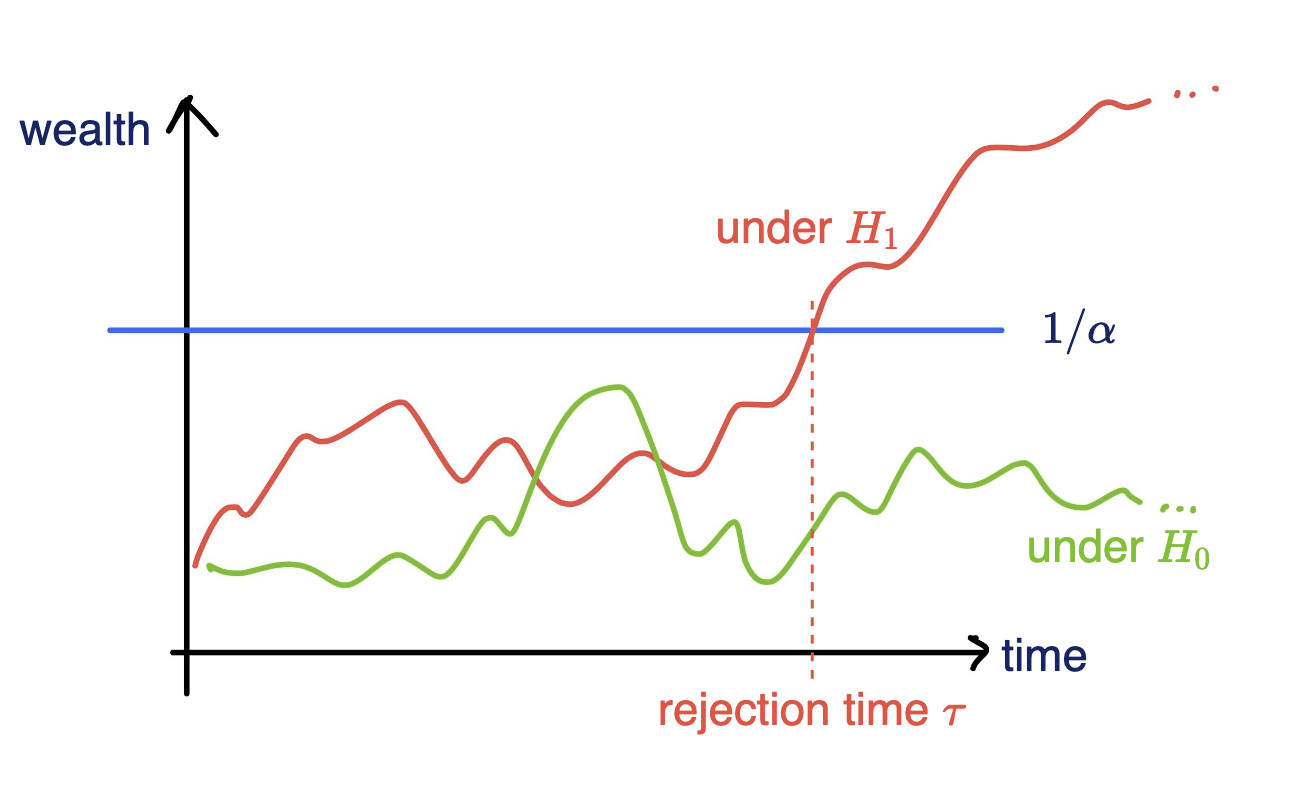
Online testing by e-values

Fair game: \(~~\mathbb E_{H_0}[\kappa_t | \text{Everything seen}_{t-1}] = 0\)

\(v_t \in (0,1):\) betting fraction

\(\kappa_t \in [-1,1]\) payoff

\( K_t = K_{t-1}(1+\kappa_t v_t)\)

Testing by betting via SKIT (Podkopaev et al., 2023)

[Shaer et al. 2023, Shekhar and Ramdas 2023, Podkopaev et al 2023]

Lemma: For a fair game, \(\mathbb P_{H_0}[\exists t \in \mathbb N : K_t \geq 1/\alpha ]\leq\alpha\)

Online testing by e-values

\(v_t \in (0,1):\) betting fraction

\(H_0: ~ P = Q\)

\(\kappa_t = \text{tahn}({\color{teal}\rho(X_t)} - {\color{teal}\rho(Y_t)})\)

Payoff function

\({\color{black}\text{MMD}(P,Q)} : \text{ Maximum Mean Discrepancy}\)

\({\color{teal}\rho} = \underset{\rho\in \mathcal R:\|\rho\|_\mathcal R\leq 1}{\arg\sup} ~\mathbb E_P [\rho(X)] - \mathbb E_Q[\rho(Y)]\)

\( K_t = K_{t-1}(1+\kappa_t v_t)\)

     Data efficient 

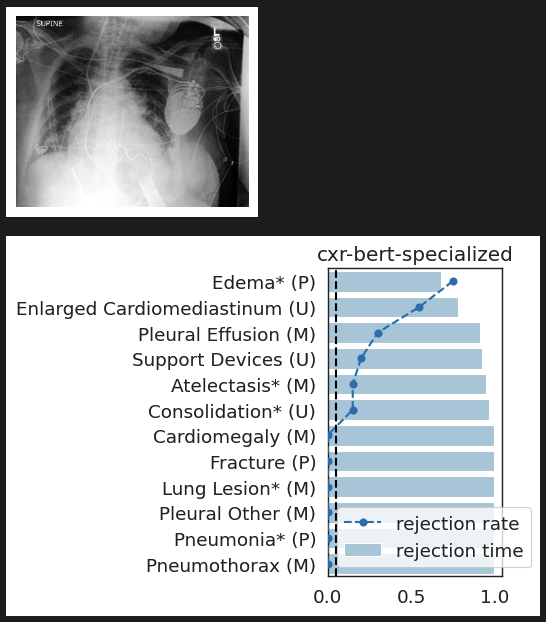
     Rank induced by rejection time

Testing by betting via SKIT (Podkopaev et al., 2023)

[Shaer et al. 2023, Shekhar and Ramdas 2023, Podkopaev et al 2023]

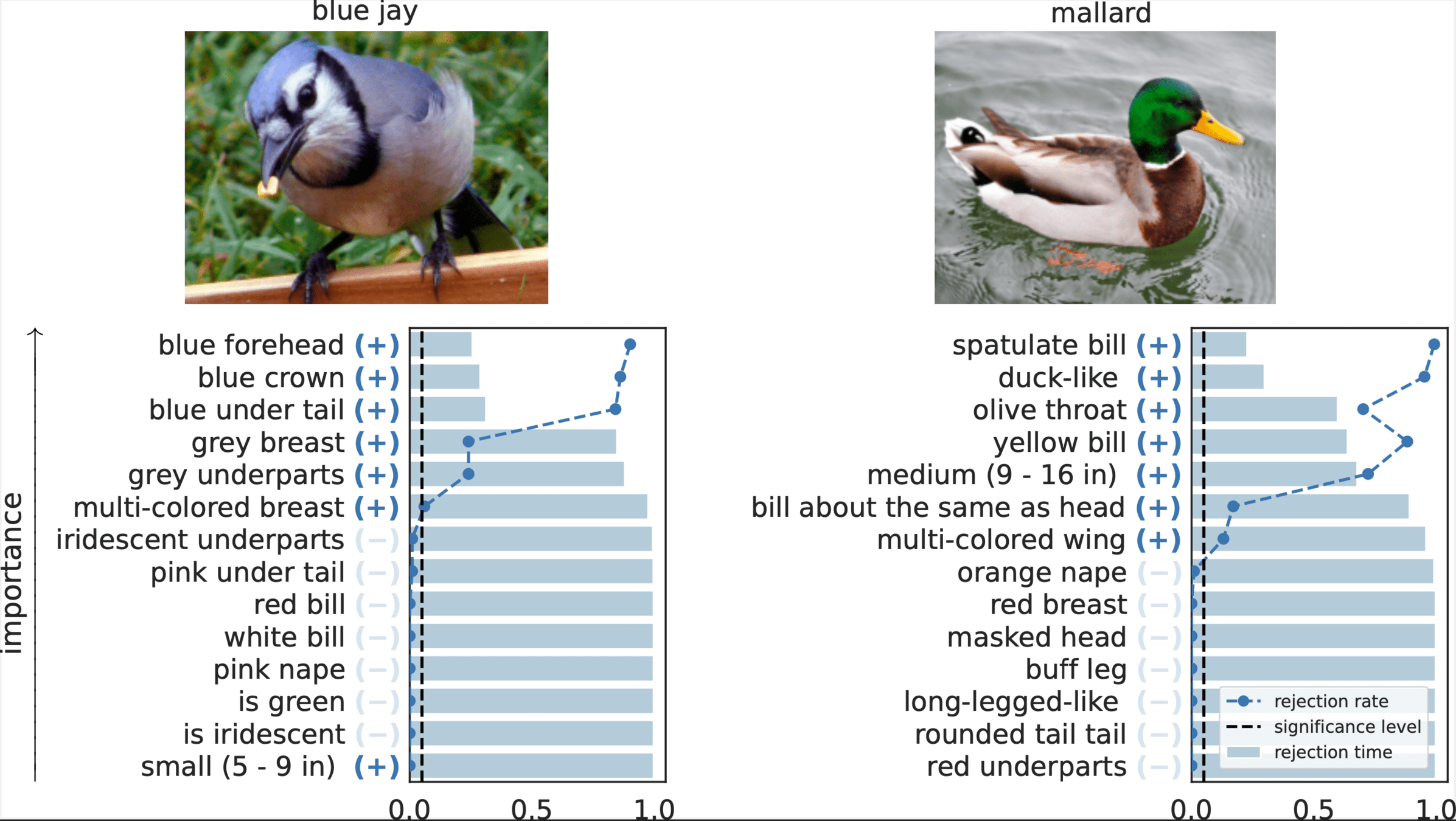
rejection time

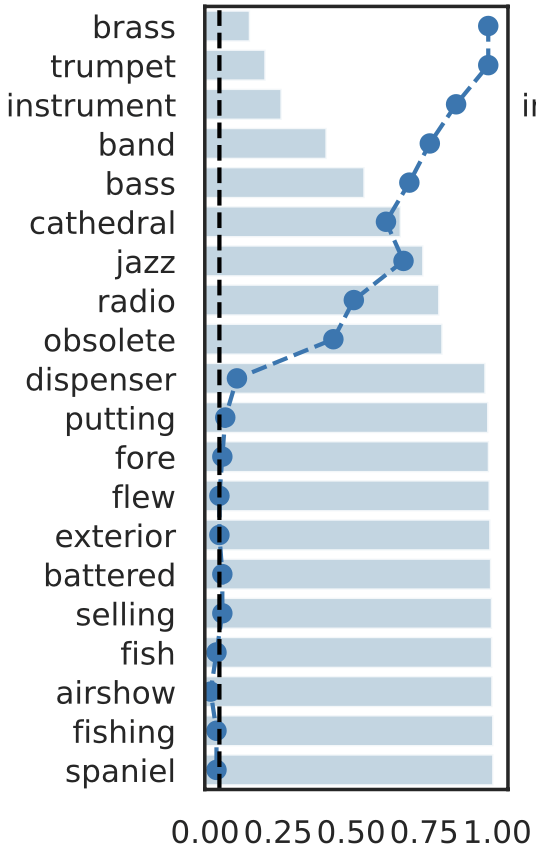
rejection rate

Important Semantic Concepts
(Reject \(H_0\))

Unimportant Semantic Concepts

(fail to reject \(H_0\))

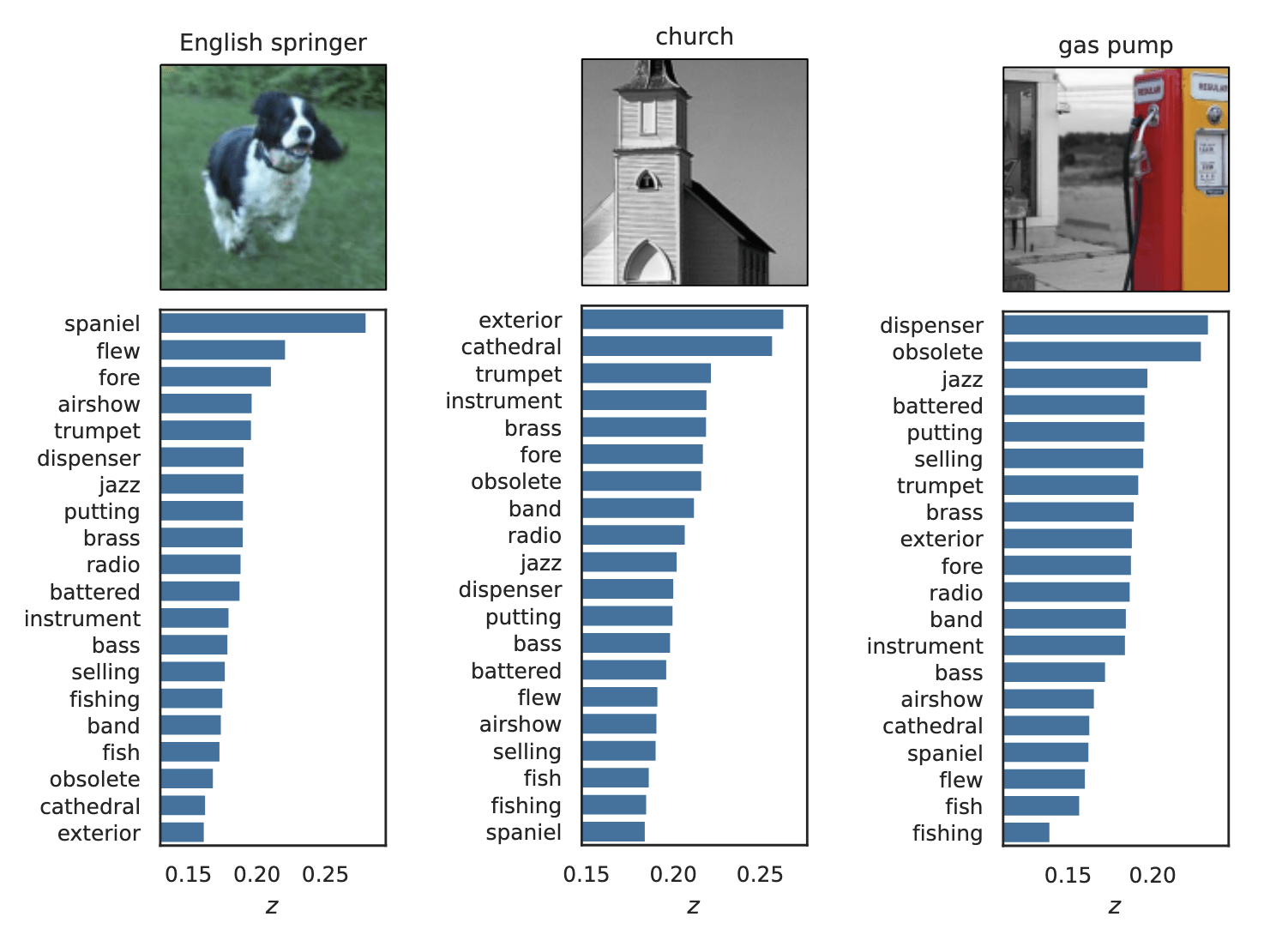
Results:     Imagenette

Type 1 error control

   False discovery rate control

Results:     Imagenette

Results:     CUB dataset

CheXpert: validating BiomedVLP 

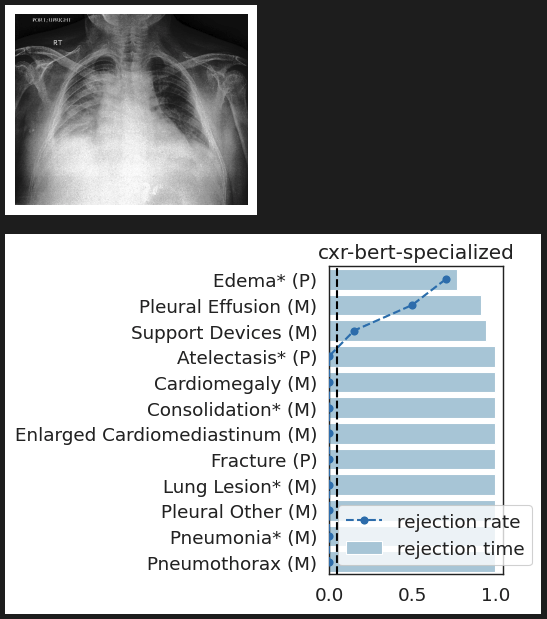
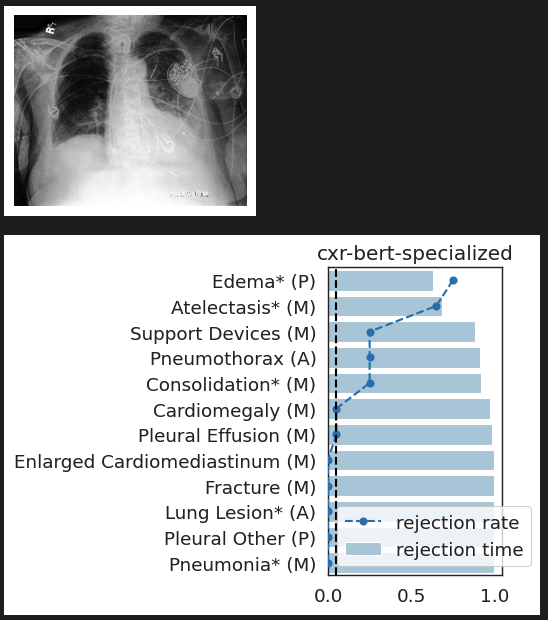
What concepts does BiomedVLP find important to predict                                 ? 

lung opacity

Results: RSNA Brain CT Hemorrhage Challenge

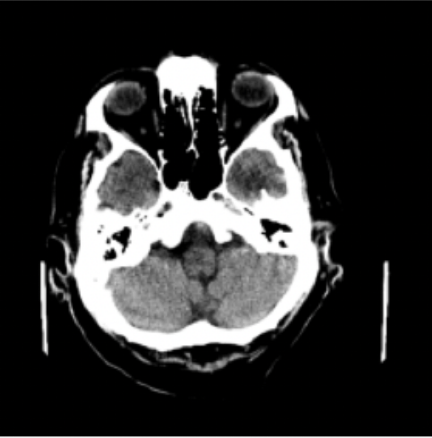
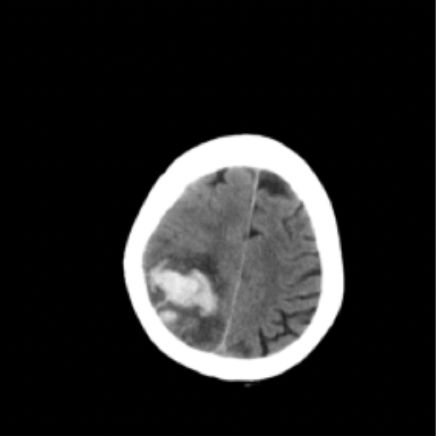
Hemorrhage
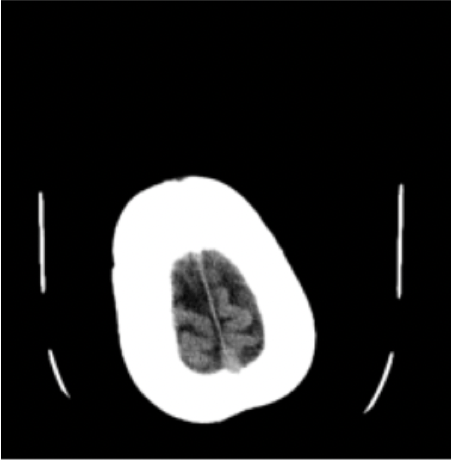
No Hemorrhage
Hemorrhage
Hemorrhage
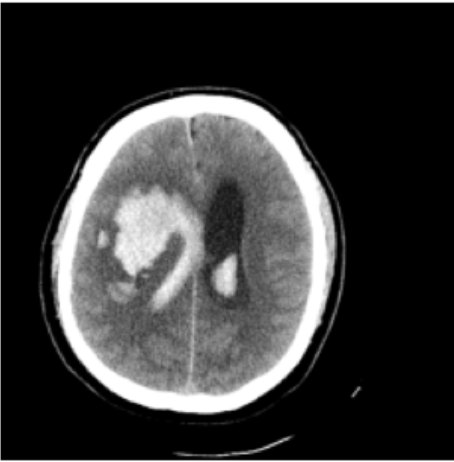
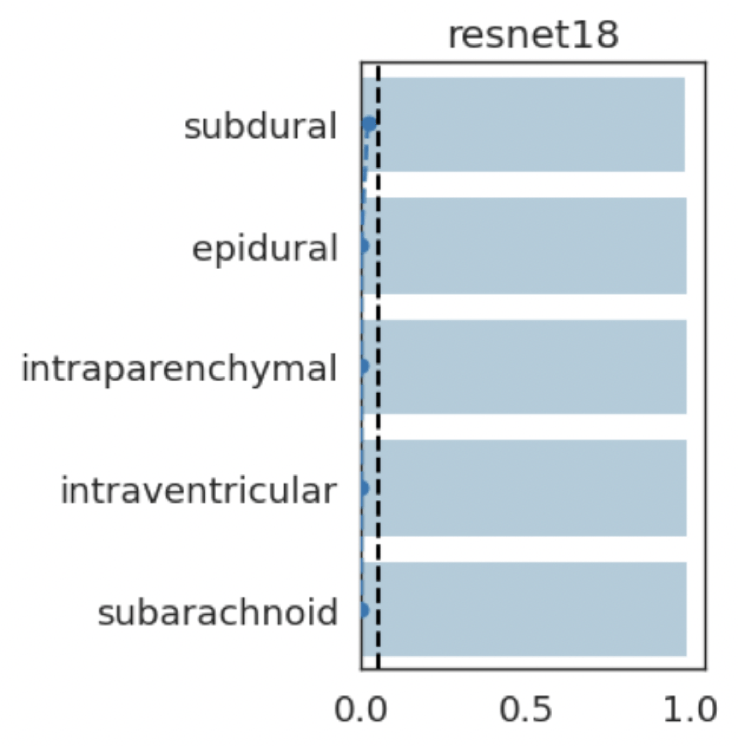
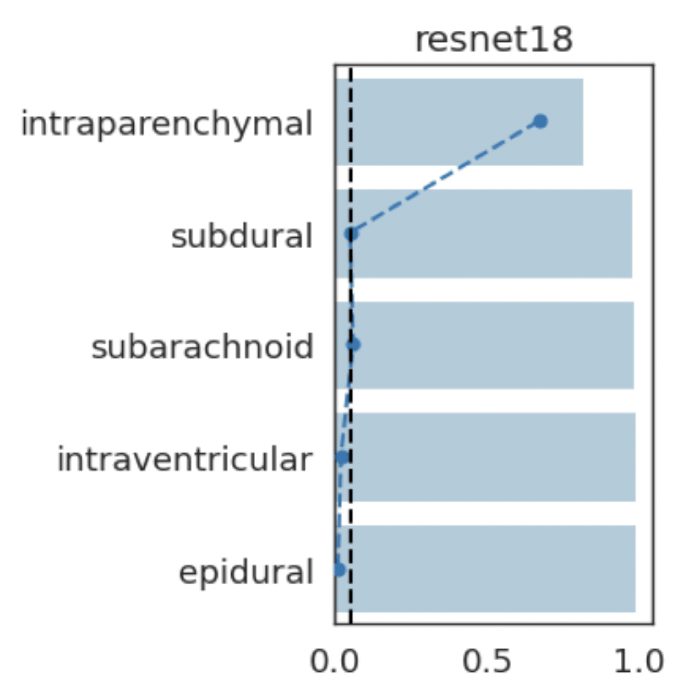
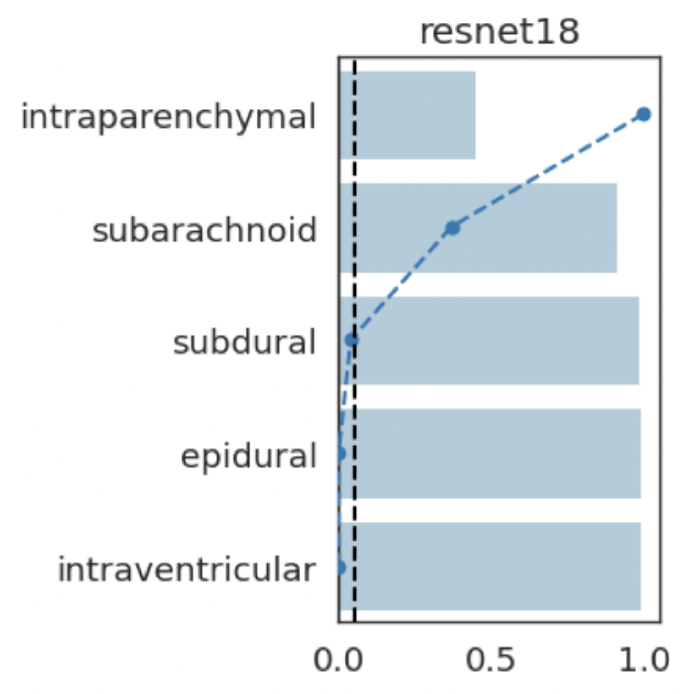
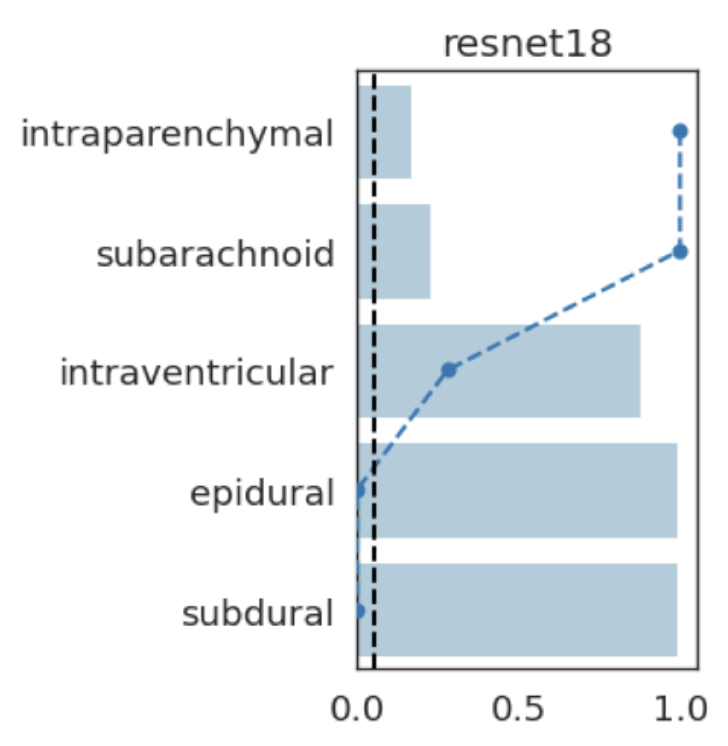
intraparenchymal
subdural
subarachnoid
intraventricular
epidural
intraparenchymal
subarachnoid
intraventricular
epidural
subdural
intraparenchymal
subarachnoid
subdural
epidural
intraventricular
intraparenchymal
subarachnoid
intraventricular
epidural
subdural
(+)
(-)
(-)
(-)
(-)
(+)
(-)
(+)
(-)
(-)
(+)
(+)
(-)
(-)
(-)
(-)
(-)
(-)
(-)
(-)

Results:     Imagenette

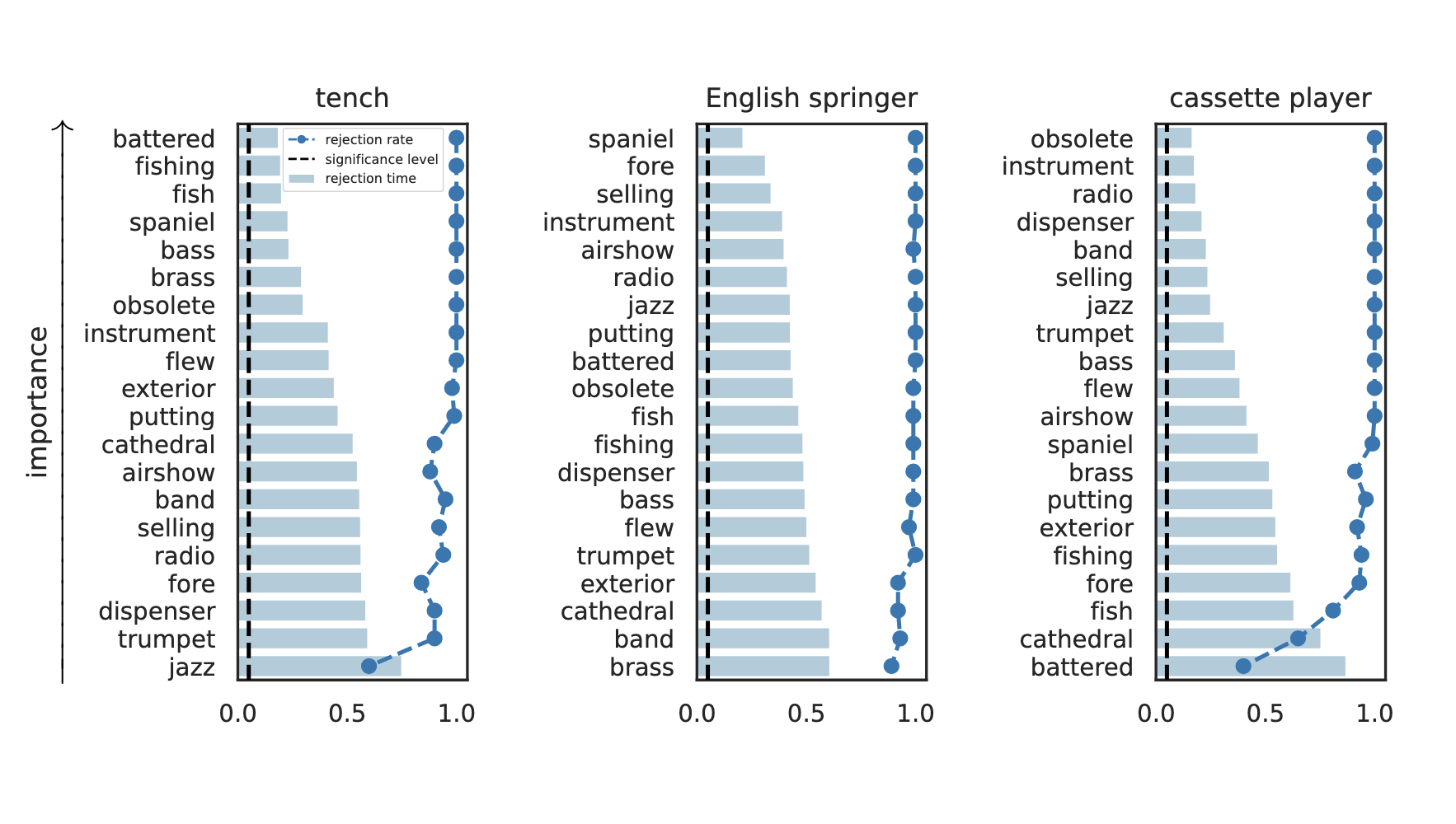
Global Importance

Results:     Imagenette

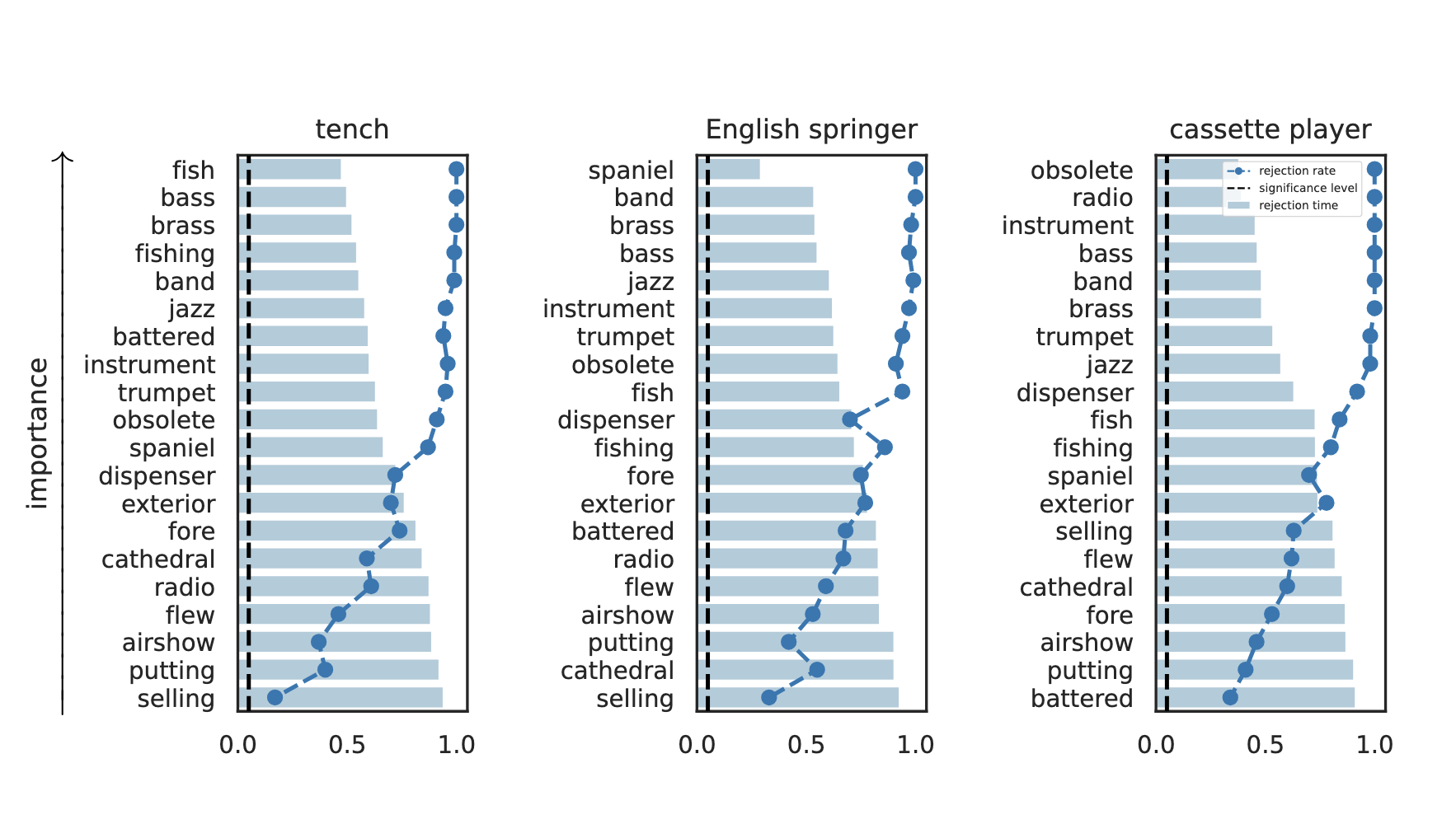
Global Conditional Importance

Results:     Imagenette

Results:     Imagenette

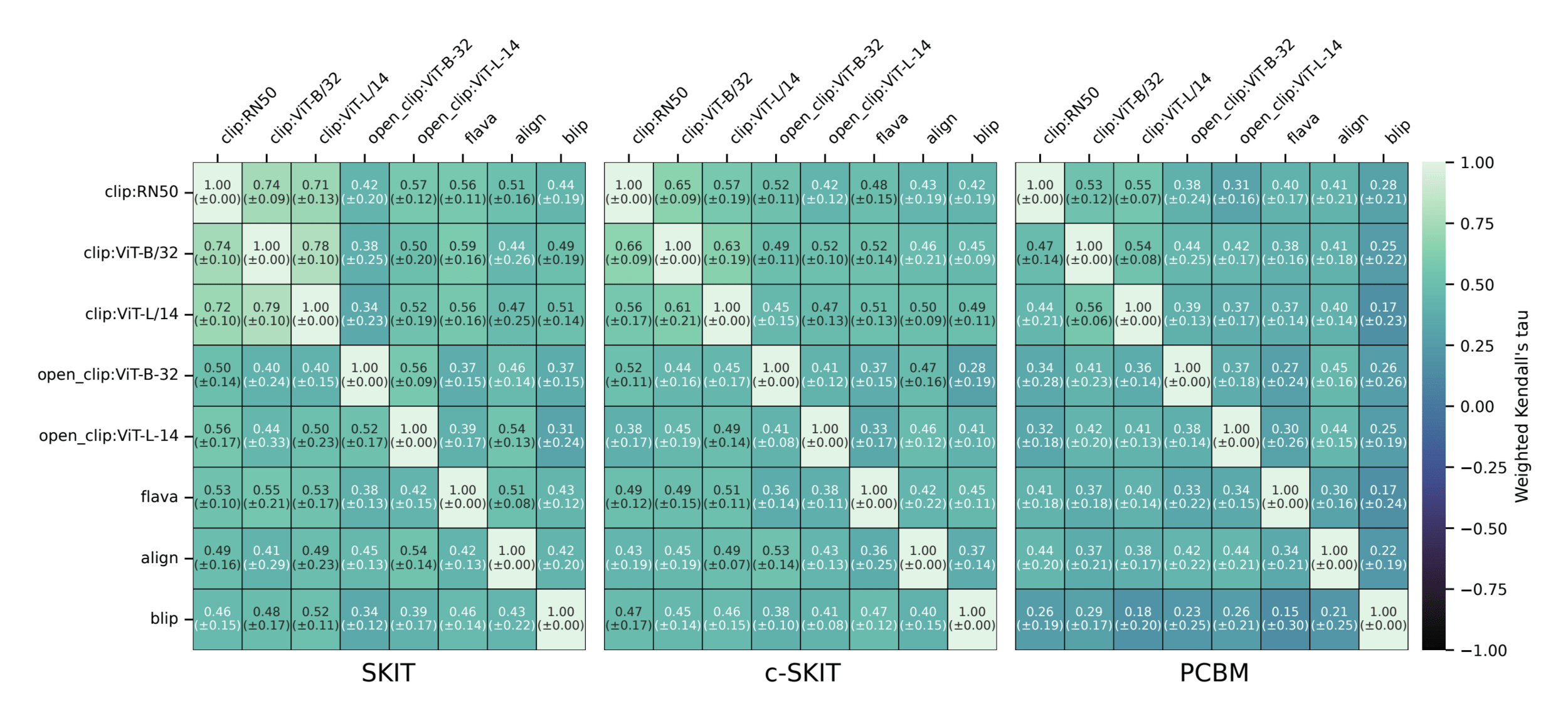
Semantic comparison of vision-language models

Question 1)

Can we resolve the computational bottleneck (and when)?

Question 2)

What do these coefficients mean statistically?

Question 3)

How to go beyond input-features explanations?

Concluding

Distributional assumptions + hierarchical extensions

Allow us to conclude on differences in distributions

Use online testing by betting for semantic concepts

Jacopo Teneggi
JHU

Beepul Bharti
JHU

Teneggi et al, SHAP-XRT: The Shapley Value Meets Conditional Independence Testing, TMLR (2023).
Teneggi et al, Fast hierarchical games for image explanations, Teneggi, Luster & S., IEEE TPAMI (2022)
Teneggi & S., Testing Semantic Importance via Betting, Neurips (2024).
Yaniv Romano Technion

Appendix