Foundations of Interpretable AI

Tutorial @

PART I: Motivation and Post-hoc Methods

(9:00 - 9:45 am)

Aditya Chattopadhyay (Amazon)

PART II: Shapley Value based Methods

(9:45 - 10:30 am)

Jeremias Sulam (Johns Hopkins)

PART III: Interpretable by Design Methods

(11:00 - 11:45 am)

René Vidal (Penn)

Coffee break

(10:30 - 11:00 am)

Shapley Values

Popularity on

Shapley Values

TODAY

What are they?

How are they computed?

(Shapley for local feature importance)

Not an exhaustive literature review
Not a code & repos review
Not a demonstration on practical problems

Review of general approaches and methodology
Pointers to where to start looking in different problem domains

Shapley Values

Lloyd S Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.

Let be an -person cooperative game with characteristic function

G = ([n],f)

v : \mathcal P([n]) \mapsto \mathbb R

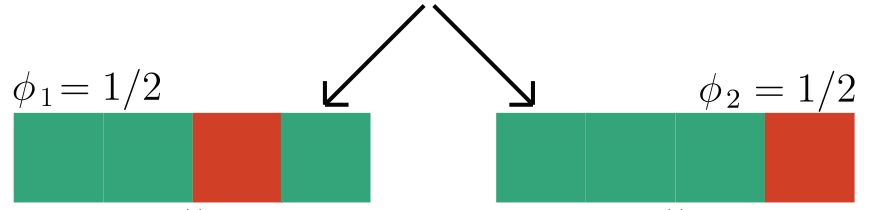
How important is each player for the outcome of the game?

Shapley Values

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]

marginal contribution of player i with coalition S

Lloyd S Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]

Shapley Values

Efficiency

\displaystyle v([n]) = v(\empty) + \sum_{i=1}^n \phi_i(v)

Linearity

\displaystyle \phi_i( \alpha_1 v_1 + \alpha_2 v_2) = \alpha_1 \phi_i(v_1) + \alpha_2 \phi_i(v_2) \newline \text{ for characteristic functions }v_1,v_2

Symmetry

\text{If}~~ v(S\cup i) = v(S\cup j) ~~ \forall S\subseteq [n]\setminus \{i,j\} \newline \text{Then}~~ \phi_i(v) = \phi_j(v)

\text{If}~~ v(S\cup i) = v(S) ~~ \forall S\subseteq [n]\setminus \{i\} \newline \text{Then}~~ \phi_i(v)=0

Nullity

Shapley Explanations for ML

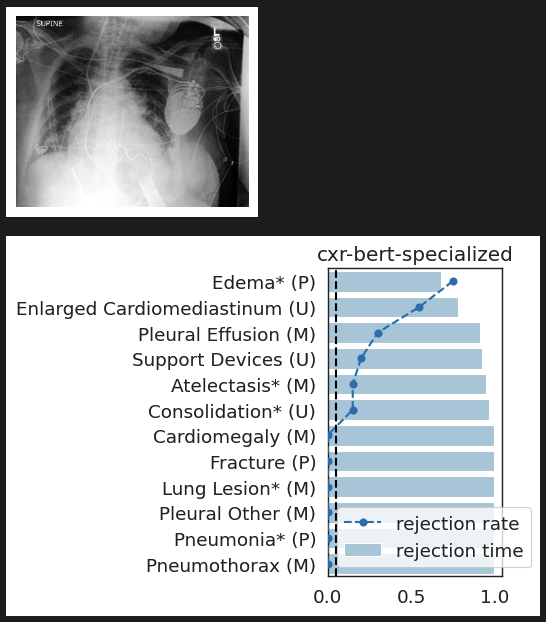
lung opacity

cardiomegaly

fracture

no findding

X \in \mathcal X \subset \mathbb R^n

inputs

responses

f:\mathcal X \to \mathcal Y

predictor

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]

f(X) = \hat{Y} \approx Y

Y\in \mathcal Y = [C]

Shapley Explanations for ML

Question 2:

How can we (when) compute \(\phi_i(v)\)?

Question 3:

What do \(\phi_i(v)\) say (and don't) about the problem?

X \in \mathcal X \subset \mathbb R^n

inputs

responses

f:\mathcal X \to \mathcal Y

predictor

Question 1:

How should (can) we choose the function \(v\)?

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]

f(X) = \hat{Y} \approx Y

Y\in \mathcal Y = [C]

Shapley Explanations for ML

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]

Question 2:

How can we (when) compute \(\phi_i(v)\)?

Question 3:

What do \(\phi_i(v)\) say (and don't) about the problem?

f(X) = \hat{Y} \approx Y

X \in \mathcal X \subset \mathbb R^n

Y\in \mathcal Y = [C]

inputs

responses

f:\mathcal X \to \mathcal Y

predictor

Question 1:

How should (can) we choose the function \(v\)?

Question 1:

How should (can) we choose the function \(v\)?

For any \(S \subseteq [n]\), and a sample \(x\sim p_X\), we need

\(v_f(S,x) : \mathcal P([n])\times \mathcal X \to \mathbb R\)

[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]

[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]

Question 1:

How should (can) we choose the function \(v\)?

Fixed reference value

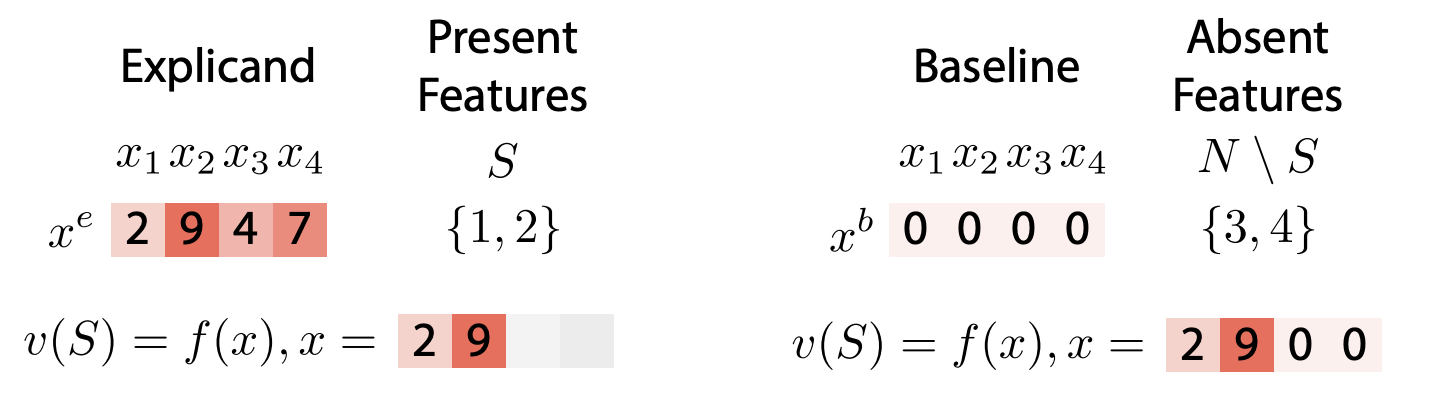
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]

[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]

\(v_f(S,x) = f(x_S,\mathbb x^{b}_{\bar{S}})\)

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ f(x_{S\cup i},x^b_{\overline{S\cup i}}) - f(x_{S},x^b_{\overline{S}}) \right]

Question 1:

How should (can) we choose the function \(v\)?

Fixed reference value

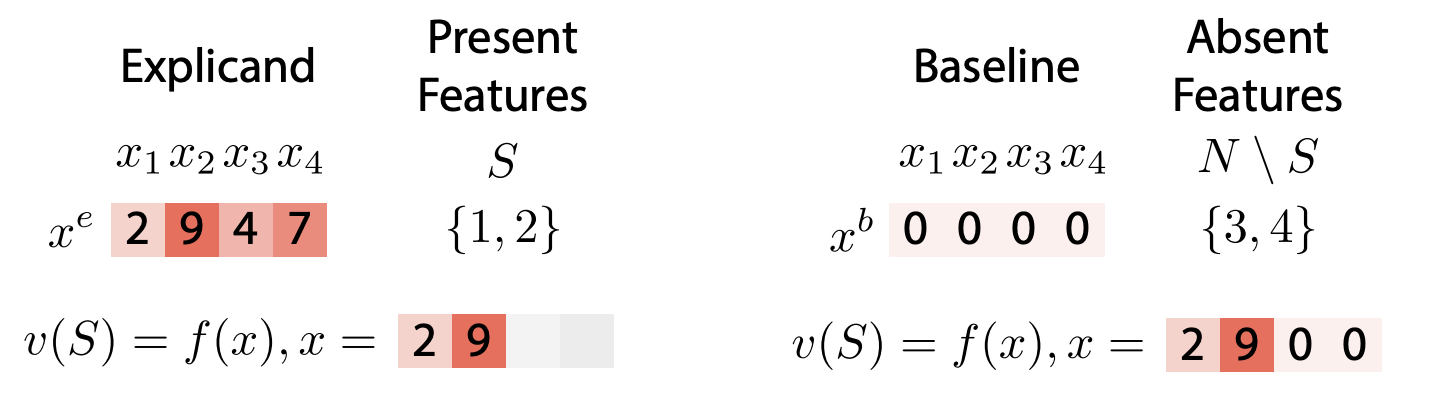
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]

[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]

\(v_f(S,x) = f(x_S,\mathbb x^{b}_{\bar{S}})\)

Easy, cheap

\( (x_S,x^b_{\bar{S}})\not\sim p_X\)

(x_S,x^b_{\bar{S}})

Question 1:

How should (can) we choose the function \(v\)?

Conditional Data Distribution

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)

[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]

Question 1:

How should (can) we choose the function \(v\)?

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)

\((x_S,\tilde{X}_{\bar{S}})\)

Difficult/expensive

\( (x_S,\tilde{X}_{\bar{S}})\sim p_X\)

"Breaks" the Null axiom:

"True to the data"

[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]

Conditional Data Distribution

if \(f(x_i,x_{i^C}) = f(x'_i,x_{i^C}) ~\forall x_{i^C}~\not\Rightarrow \phi_i(f) \neq 0\)

Question 1:

How should (can) we choose the function \(v\)?

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)

\( (x_S,\tilde{X}_{\bar{S}})\sim p_X\)

(x_S,\tilde{X}_{\bar{S}})

x_S

"True to the data"

Difficult/expensive

[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]

Conditional Data Distribution

"Breaks" the Null axiom:

if \(f(x_i,x_{i^C}) = f(x'_i,x_{i^C}) ~\forall x_{i^C}~\not\Rightarrow \phi_i(f) \neq 0\)

Question 1:

How should (can) we choose the function \(v\)?

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)

\( (x_S,\tilde{X}_{\bar{S}})\sim p_X\)

(x_S,\tilde{X}_{\bar{S}})

x_S

"True to the data"

Difficult/expensive

Alternative: learn a model \(g_\theta\) for the conditional expectation

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S] \approx g_\theta (x,S)\)

[Frye et al, 2021]

[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]

Conditional Data Distribution

"Breaks" the Null axiom:

if \(f(x_i,x_{i^C}) = f(x'_i,x_{i^C}) ~\forall x_{i^C}~\not\Rightarrow \phi_i(f) \neq 0\)

Question 1:

How should (can) we choose the function \(v\)?

Marginal Data Distribution

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})]\)

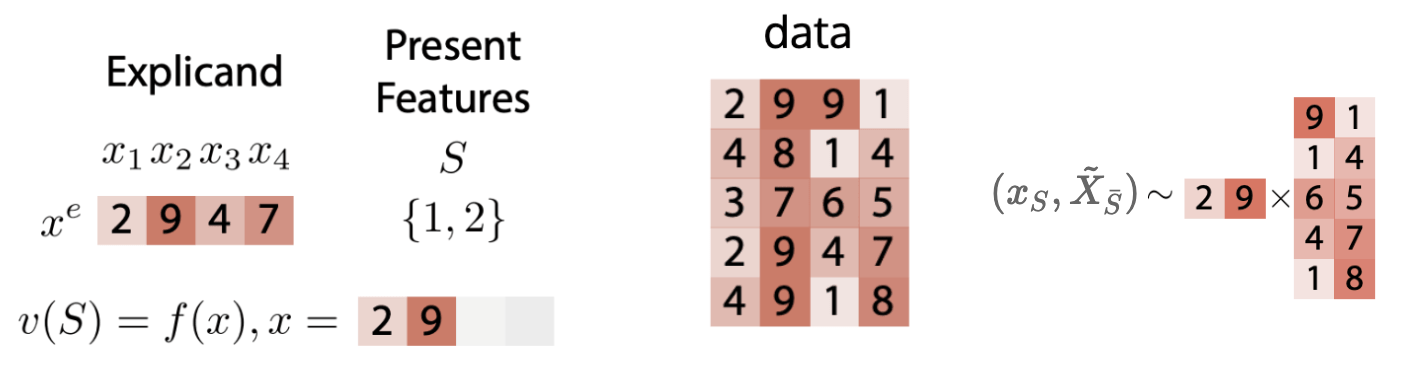
\( (x_S,\tilde{X}_{\bar{S}})\not\sim p_X\)

Easier than conditional

``true to the model''
maintains Null axiom

can hide correlations in the data

[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Lundberg & Lee, 2017][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]

\(=~~ \mathbb{E}[f(X)|do(S)]\)

(interventional expectation)

Question 1:

How should (can) we choose the function \(v\)?

National Health and Nutrition Examination Survey (NHANES)

[Chen et al, True to the model or true to the data? 2020]

(mortality prediction)

Example

X = (Age,IR,WaistC,BP,BMI)

\(f(x) = \beta^\top x\), with \(\beta_5 = 0\)

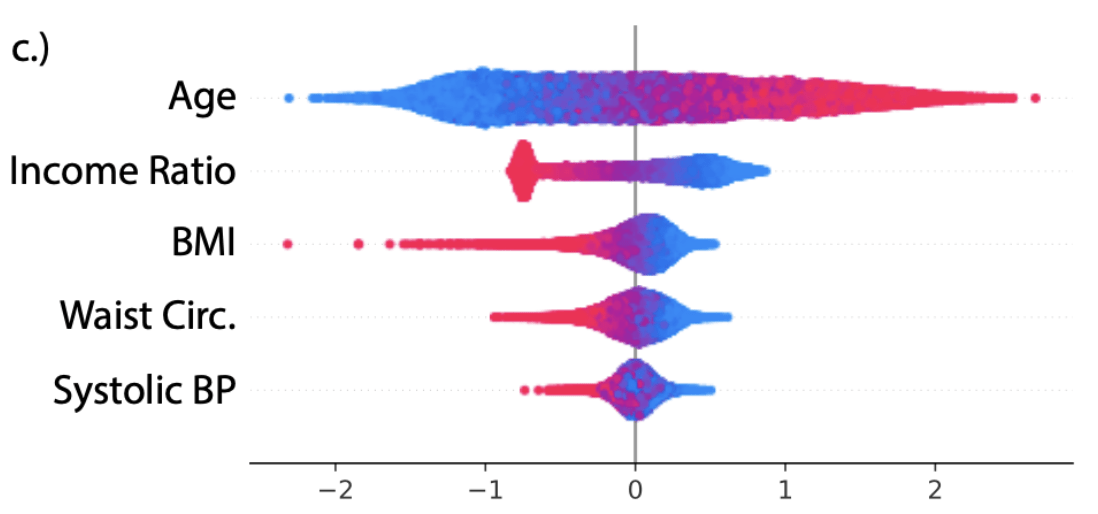
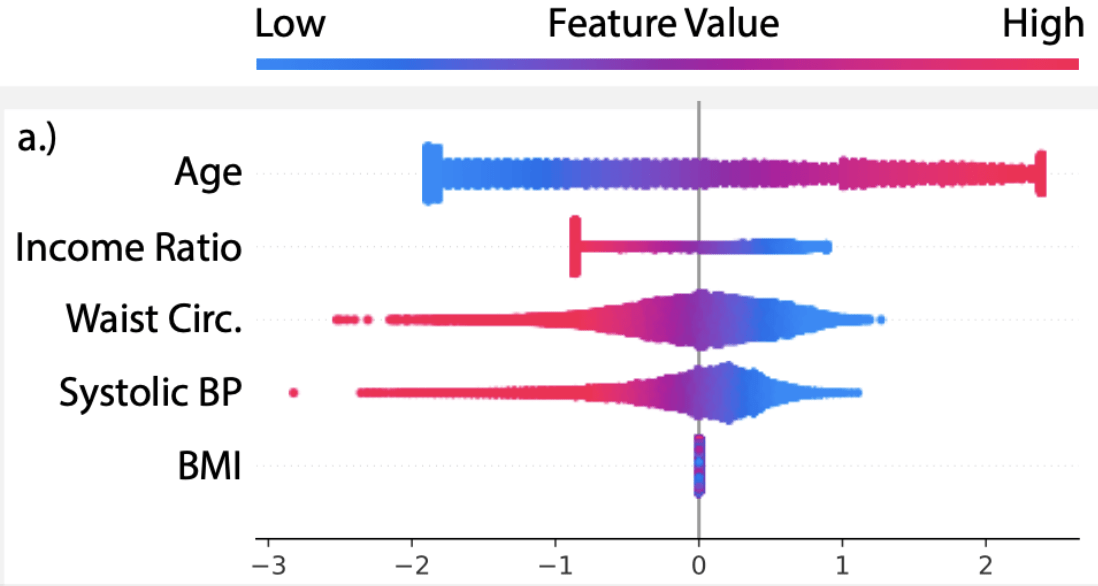
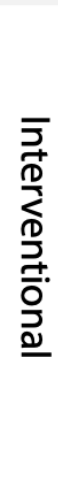
Auditing a predictor?
(e.g. loan recommendations?)
Feature discovery/bias analysis?

Question 1:

How should (can) we choose the function \(v\)?

Linear model (approximation)

\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})] \approx f(x_S,\mathbb{E}[\tilde{X}_{\bar{S}}])\)

\( (x_S,\tilde{X}_{\bar{S}})\not\sim p_X\)
except in linear models
(and feature independence)

Easiest, popular in practice

[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]

[Aas et al, 2019] [Lundberg & Lee, 2017][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]

Shapley Explanations for ML

X \in \mathcal X \subset \mathbb R^n

inputs

responses

f:\mathcal X \to \mathcal Y

predictor

Question 1:

How should (can) we choose the function \(v\)?

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]

Y\in \mathcal Y = [C]

f(X) = \hat{Y} \approx Y

Question 2:

How can we (when) compute \(\phi_i(v)\)?

Question 3:

What do \(\phi_i(v)\) say (and don't) about the problem?

Question 2:

How can we (when) compute \(\phi_i(v)\)?

intractable.. \(\mathcal O (2^n)\)

\displaystyle \phi_i(v) = \frac{1}{n!} \sum_{\pi \subseteq \Pi(n)} \left[ v(\text{Pre}^i(\pi)\cup \{i\}) - v(\text{Pre}^i(\pi)) \right]

[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]

Weighted Least Squares (kernelSHAP )

\displaystyle \phi_i(v) = \argmin_{\color{red}\beta\in\mathbb R^{n+1}} \sum_{S \subseteq [n]} \omega(S) (v(S) - {\color{red}\beta_0} - \sum_{j\in S}{\color{red}\beta_j})^2

Monte Carlo Sampling

\displaystyle \phi_i(v) = \sum_{S' \sim w(S)} \left[ v(S'\cup \{i\}) - v(S') \right]

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]

[Jethani et al, 2021]

Weighted Least Squares (kernelSHAP )

Weighted Least Squares, amortized ( FastSHAP )

\displaystyle \Phi_\text{fastShap} = \argmin_{\color{red}\phi_\theta:\mathcal X\to \mathbb R^n}~~ \underset{X}{\mathbb E} ~\sum_{y\in[k]} ~~ \sum_{S \subseteq [n]} \omega(S) (v(S,y) - \sum_{j\in S}{\color{red}\phi_\theta(X,y)_j})^2

... and stochastic versions [Covert et al, 2024]

Question 2:

How can we (when) compute \(\phi_i(v)\)?

\displaystyle \phi_i(v) = \argmin_{\color{red}\beta\in\mathbb R^{n+1}} \sum_{S \subseteq [n]} \omega(S) (v(S) - {\color{red}\beta_0} - \sum_{j\in S}{\color{red}\beta_j})^2

Question 2:

How can we (when) compute \(\phi_i(v)\) if we know more?

(about the model)

[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014][Chen et al, 2020]

Linear models \(f(x) = \beta^\top x \)

Closed-form expressions (for marginal distributions and baselines)

\( \phi_i(f,x) = \beta_i (x_i-\mu_i ) \)

(also for conditional if assuming Gaussian features)

Tree models

[Lundberg et al, 2020]

Polynomial time algorithm (exact) (TreeSHAP) for \(\phi_i(f)\)

\(\mathcal O(N_\text{trees}N_\text{leaves} \text{Depth}^2)\)

Question 2:

How can we (when) compute \(\phi_i(v)\) if we know more?

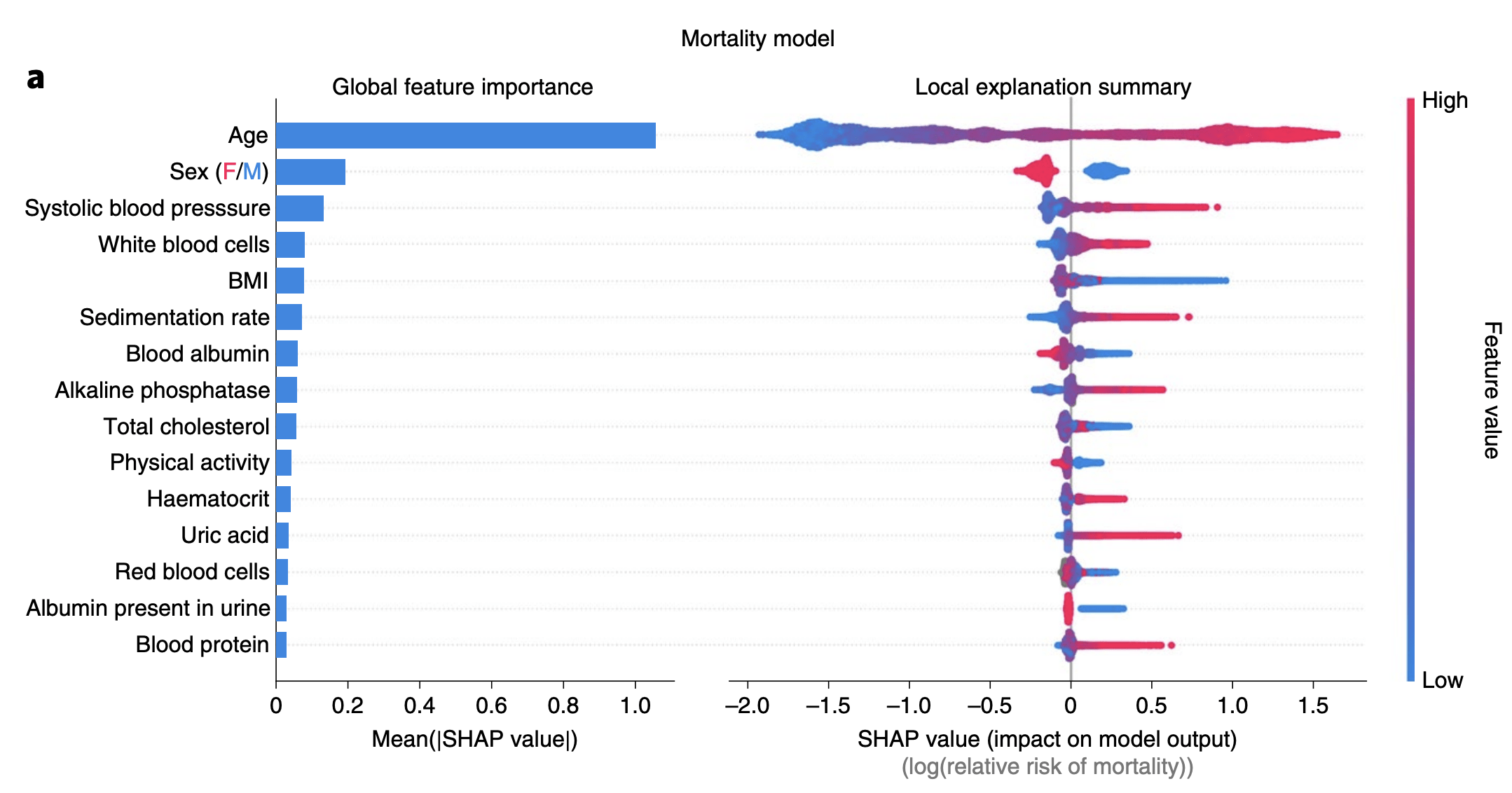
Local models

(about the model)

[Chen et al, 2019]

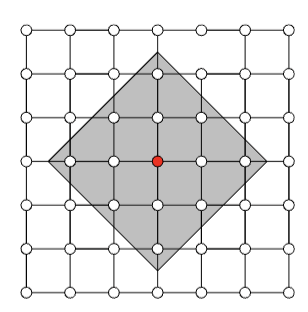
Observation: Restrict computation of \(\phi_i(f)\) to local areas of influence given by a graph structure

L-Shap

C-Shap

\displaystyle \hat{\phi}^k_i(v) = \frac{1}{|\mathcal N_k(i)|} \sum_{S\subseteq\mathcal N_k(i)\setminus i } w(S) \left[ v(S\cup \{i\}) - v(S) \right]

\(\Rightarrow\) complexity \(\mathcal O(2^k n)\)

Question 2:

How can we (when) compute \(\phi_i(v)\) if we know more?

Local models

(about the model)

[Chen et al, 2019]

Observation: Restrict computation of \(\phi_i(f)\) to local areas of influence given by a graph structure

\(\Rightarrow\) complexity \(\mathcal O(2^k n)\)

Correct approximations (informal statement)

Let \(S\subset \mathcal N_k(i)\). If, for any \(T\subseteq S\setminus \{i\}\), \((X_i \perp\!\!\!\perp X_{[n]\setminus S} | X_T) \) and \((X_i \perp\!\!\!\perp X_{[n]\setminus S} | X_T,Y) \)

Then \(\hat{\phi}^k_i(v) = \phi_i(v)\)

(and approximately bounded otherwise, controlled)

\displaystyle \hat{\phi}^k_i(v) = \frac{1}{|\mathcal N_k(i)|} \sum_{S\subseteq\mathcal N_k(i)\setminus i } w(S) \left[ v(S\cup \{i\}) - v(S) \right]

Question 2:

How can we (when) compute \(\phi_i(v)\) if we know more?

Local models

(about the model)

[Chen et al, 2019]

Observation: Restrict computation of \(\phi_i(f)\) to local areas of influence given by a graph structure

\(\Rightarrow\) complexity \(\mathcal O(2^k n)\)

\displaystyle \hat{\phi}^k_i(v) = \frac{1}{|\mathcal N_k(i)|} \sum_{S\subseteq\mathcal N_k(i)\setminus i } w(S) \left[ v(S\cup \{i\}) - v(S) \right]

Question 2:

How can we (when) compute \(\phi_i(v)\) if we know more?

Hierarchical Shapley (h-Shap)

(about the model)

[Teneggi et al, 2022]

Observation: \(f(x) = 1 \Leftrightarrow \exist~ i: f(x_i,\tilde{X}_{-i}) = 1\) (A1)

{\huge)} = 0

{f}\huge(

{\huge)} = 1

{f}\huge(

Example:

f(x) = 1

if contains a sick cell

{f}\huge(

{\huge)} = 0

Question 2:

How can we (when) compute \(\phi_i(v)\) if we know more?

(about the model)

\gamma = 2

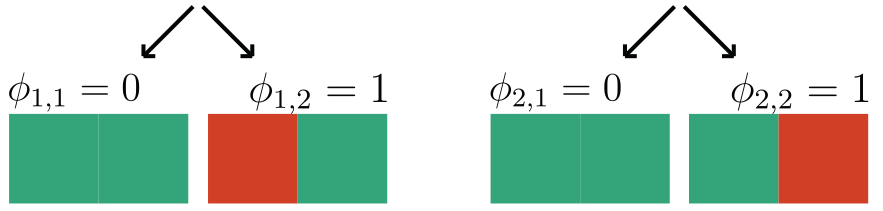
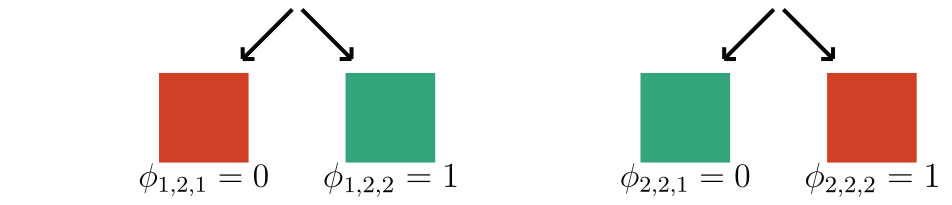
Observation: \(f(x) = 1 \Leftrightarrow \exist~ i: f(x_i,\tilde{X}_{-i}) = 1\) (A1)

Hierarchical Shapley (h-Shap)

[Teneggi et al, 2022]

Under A1, \(\phi^\text{h-Shap}_i(f) = \phi_i(f)\)

Bounded approximation as deviating from A1

2. Correct approximation (informal)

1. Complexity \(\mathcal O(2^\gamma k \log n)\)

Question 2:

How can we (when) compute \(\phi_i(v)\) if we know more?

(about the model)

Observation: \(f(x) = 1 \Leftrightarrow \exist~ i: f(x_i,\tilde{X}_{-i}) = 1\) (A1)

Hierarchical Shapley (h-Shap)

[Teneggi et al, 2022]

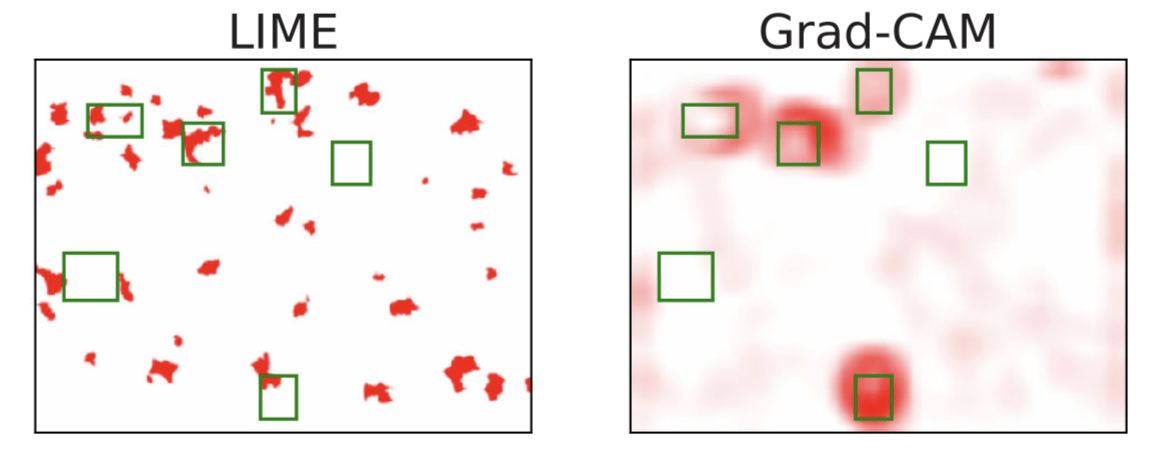
Question 2:

How can we (when) compute \(\phi_i(v)\) if we know more?

(about the model)

Observation: \(f(x) = 1 \Leftrightarrow \exist~ i: f(x_i,\tilde{X}_{-i}) = 1\) (A1)

Hierarchical Shapley (h-Shap)

[Teneggi et al, 2022]

Question 2:

How can we (when) compute \(\phi_i(v)\) if we know more?

Shapley Approximations for Deep Models

(about the model)

DeepLift (Shrikumar et al, 2017): biased estimation of baseline Shap

DeepShap (Chen et al, 2021): biased estimation of marginal Shap

DASP (Ancona et al, 2019) Uncertainty propagation for baseline (zero) Shap
assuming Gaussianity and independence of features

Shapnets [Wang et al, 2020]: Computation for small-width networks

... not an exhaustive list!

Transformers (ViTs) [Covert et al, 2023]: leveraging attention to fine-tune a surrogate model for Shap estimation

Shapley Explanations for ML

Question 2:

How can we (when) compute \(\phi_i(v)\)?

Question 3:

What do \(\phi_i(v)\) say (and don't) about the problem?

X \in \mathcal X \subset \mathbb R^n

inputs

responses

f:\mathcal X \to \mathcal Y

predictor

Question 1:

How should (can) we choose the function \(v\)?

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]

Y\in \mathcal Y = [C]

f(X) = \hat{Y} \approx Y

Question 3:

What do \(\phi_i(v)\) say (and don't) about the problem?

Interpretability as Conditional Independence

Explaining uncertainty via Shapley Values [Watson et al, 2023]

\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v_\text{KL}(S\cup \{i\}) - v_\text{KL}(S) \right]

with \(v_\text{KL}(S,x) = -D_\text{KL}(~p_{Y|x} ~||~ p_{Y|x_s}~)\)

Theorem (informal)

\(Y \perp\!\!\!\perp X_j | X_s = x_s ~~\Rightarrow~~ v_\text{KL}(S\cup\{i\},x) - v_\text{KL}(S,x) = 0\)

Question 3:

What do \(\phi_i(v)\) say (and don't) about the problem?

Interpretability as Conditional Independence

SHAP-XRT: Shapley meets Hypothesis Testing [Teneggi et al, 2023]

H^0_{{i},S}:~ (f(x_{S\cup \{{i}\}},\tilde{X}_{\overline{S\cup \{{i}\}}}) ) \overset{d}{=} (f(x_S,\tilde X_{\overline S}) )

\(\hat{p}_{i,S} \leftarrow \texttt{XRT}: \text{eXplanation Randomization Test}\), via access to \({X}_{\bar{S}} \sim p_{X_{\bar{S}}|x_s}\)

Theorem (informal)

For \(f:\mathcal X \to [0,1], ~~ \mathbb E [\hat{p}_{i,S}]\leq 1- \mathbb E [v(S\cup i) - v(S)] \)

Thus, large \(\mathbb E [v(S\cup i) - v(S)] ~ \Rightarrow \) reject \(H^0_{i,S}\)

Last Question 3': Should we just focus on CIT?

Is the piano important for \(\hat Y = \text{cat}\), given that there is a cute mammal in the image?

Local Conditional Importance

\[H^{j,S}_0:~ f({\tilde H_{S \cup \{j\}}}) \overset{d}{=} f(\tilde H_S) \]

features with concepts \(S\cup \{i\}\)

features with concepts \(S\)

[Teneggi et al, Testing semantic importance via betting, 2024]

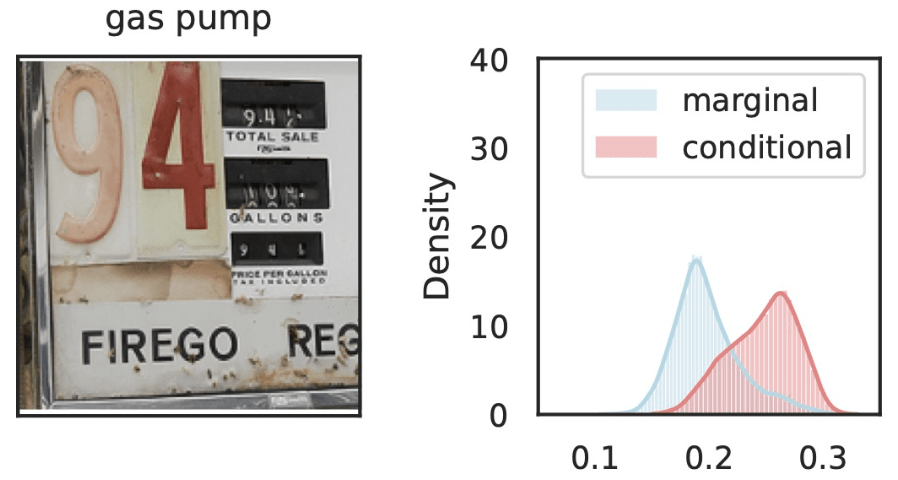
\(\hat{Y}_\text{gas pump}\)

\(Z_S\cup Z_{j}\)

\(Z_{S}\)

\(Z_j=\)

Local Conditional Importance

\(\tilde{Z}_S = [z_\text{text}, z_\text{old}, Z_\text{dispenser}, Z_\text{trumpet}, Z_\text{fire}, \dots ] \)

\(S\)

\(\tilde{Z}_{S\cup j} = [z_\text{text}, z_\text{old}, z_\text{dispenser}, Z_\text{trumpet}, Z_\text{Fire}, \dots ] \)

\(S\)

\(j\)

\[H^{j,S}_0:~ f({\tilde H_{S \cup \{j\}}}) \overset{d}{=} f(\tilde H_S) \]

Last Question 3': Should we just focus on CIT?

[Teneggi et al, Testing semantic importance via betting, 2024]

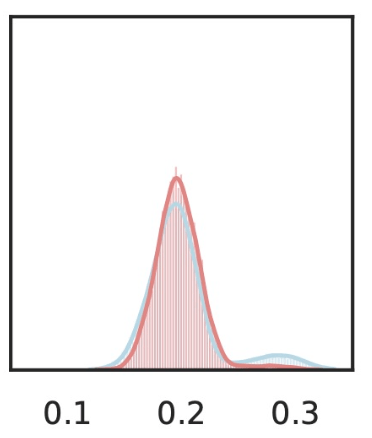
\(\hat{Y}_\text{gas pump}\)

\(Z_S\cup Z_{j}\)

\(Z_{S}\)

\(Z_S\cup Z_{j}\)

\(Z_{S}\)

Local Conditional Importance

\(Z_j=\)

\(\tilde{Z}_S = [z_\text{text}, z_\text{old}, Z_\text{dispenser}, Z_\text{trumpet}, Z_\text{fire}, \dots ] \)

\(\tilde{Z}_{S\cup j} = [z_\text{text}, z_\text{old}, Z_\text{dispenser}, z_\text{trumpet}, Z_\text{Fire}, \dots ] \)

\(S\)

\(j\)

\[H^{j,S}_0:~ f({\tilde H_{S \cup \{j\}}}) \overset{d}{=} f(\tilde H_S) \]

Last Question 3': Should we just focus on CIT?

[Teneggi et al, Testing semantic importance via betting, 2024]

Conclusions

Shapley Values are one of the most popular wrapper-explanation methods

Requires care when choosing what distributions to sample from, dependent on the setting
"true to the model" vs "true to the data"

While proposed in a different context, they can be used to test for specific statistical claims

Foundations of Interpretable AI

PART I: Motivation and Post-hoc Methods

(9:00 - 9:45 am)

Aditya Chattopadhyay (Amazon)

PART II: Shapley Values Based Methods

(9:45 - 10:30 am)

Jeremias Sulam (Johns Hopkins)

PART III: Interpretable by Design Methods

(11:00 - 11:45 am)

René Vidal (Penn)

Coffee break

(10:30 - 11:00 am)

Foundations of Interpretable AI

Shapley Values

Shapley Values

TODAY

Shapley Values

Shapley Values

marginal contribution of player i with coalition S

Shapley Values

Efficiency

Linearity

Symmetry

Nullity

Shapley Explanations for ML

Shapley Explanations for ML

Shapley Explanations for ML

Shapley Explanations for ML

intractable.. \(\mathcal O (2^n)\)

Shapley Explanations for ML

Conclusions