Responsible ML

Interpretable and fair machine

learning  models

Jeremias Sulam

Responsible ML

 

  • Reproducibility

  • Practical Accuracy

  • Explainability

  • Fairness

  • Privacy

  • Explainability

  • Fairness

[M. E. Kaminski, 2019]

E.U.: “right to an explanation” of decisions made

on individuals by algorithms

[FDA Guiding principles]

F.D.A.: “interpretability of the model outputs”

Explanations in ML

{f}\huge(
{\huge)} = \text{\texttt{sick}}
  • What parts of the image are important for this prediction?
  • What are the subsets of the input                so that 
{f}(x_C) \approx {f}(x) ?
C \subseteq [d]

  • Sensitivity or Gradient-based perturbations

  • Shapley coefficients

  • Variational formulations

LIME [Ribeiro et al, '16], CAM [Zhou et al, '16], Grad-CAM [Selvaraju et al, '17]

Shap [Lundberg & Lee, '17], ...

RDE [Macdonald et al, '19], ...

  • Adebayo et al, Sanity checks for saliency maps, 2018

  • Ghorbani et al, Interpretation of neural networks is fragile, 2019

  • Shah et al, Do input gradients highlight discriminative features? 2021

  • Sensitivity or Gradient-based perturbations

  • Shapley coefficients

  • Variational formulations

Explanations in ML

Shapley Value

  • efficiency
  • nullity
  • symmetry

Let                       be an    -person cooperative game with characteristic function 

G = ([n],f)
n
f : [n] \mapsto \mathbb R
  • exponential complexity

Lloyd S Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.

How important is each player for the outcome of the game?

\displaystyle \phi_i = \sum_{S_j\subseteq [n]\setminus \{i\} } w_{S_j} \left[ f(S_j\cup \{i\}) - f(S) \right]

marginal contribution of player i with coalition S

Shap-Explanations

\displaystyle \phi_i = \sum_{S_j\subseteq [n]\setminus \{i\}} w_j ~ \mathbb E \left[ f(\tilde X_{S\cup \{i\}}) - f(\tilde X_S) \right]
f \approx \mathbb E[Y|X=x]
X \in \mathcal X \subset \mathbb R^n
Y\in \mathcal Y = \{0,1\}

inputs

responses

f:\mathcal X \to \mathcal Y
\text{For any}~ S \subset [n],~ \text{and a sample } {\color{blue} x} \newline \text{ define }\tilde{X}_S = [{\color{blue}x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={\color{blue}x_S}}

Scott Lundberg and Su-In Lee. A Unified Approach to Interpreting Model Predictions, NeurIPS , 2017

Needs of approximations, largely ad-hoc

predictor

h-Shap: fast hierarchical games

We focus on data with certain structure:

\text{\textbf{Assumption 1:}}~ f^*(x) = 1 \Leftrightarrow \exist~ i: f^*(\tilde X_i) = 1
f\huge(
{\huge)} = 1
{f}\huge(
{\huge)} = 1
{f}\huge(
{\huge)} = 0

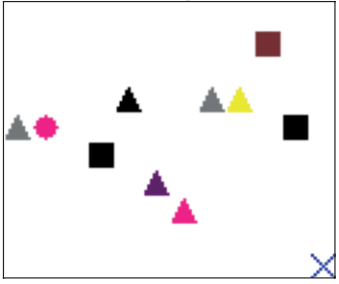
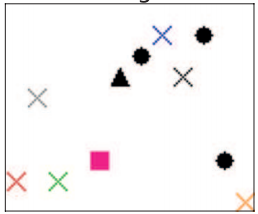
Example:

f(x) = 1

if     contains a cross

x

Theorem 1 (informal):

  • h-Shap runs in
  • Under A1, h-Shap -> Shapley
\mathcal O(2^\gamma k \log n)
\frac{\langle \Phi_{\text{Shap}} \Phi_{\text{h-Shap}}\rangle}{\|\Phi_{\text{Shap}}\| \|\Phi_{\text{h-Shap}}\|} \geq \max{ \left( 1/\sqrt{s}, \sqrt{k/n} \right)}
\gamma = 2

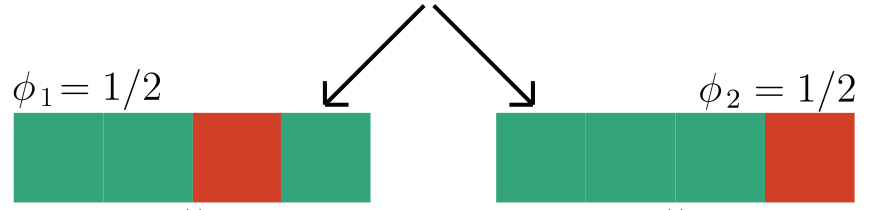
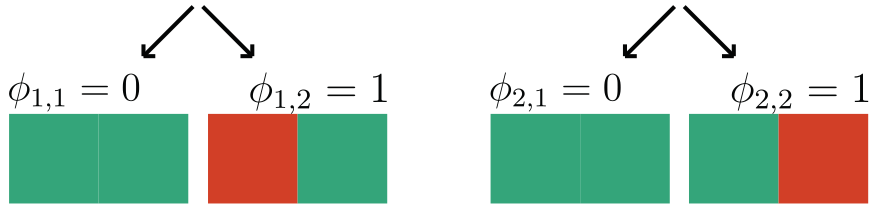
h-Shap: fast hierarchical games

h-Shap: fast hierarchical games

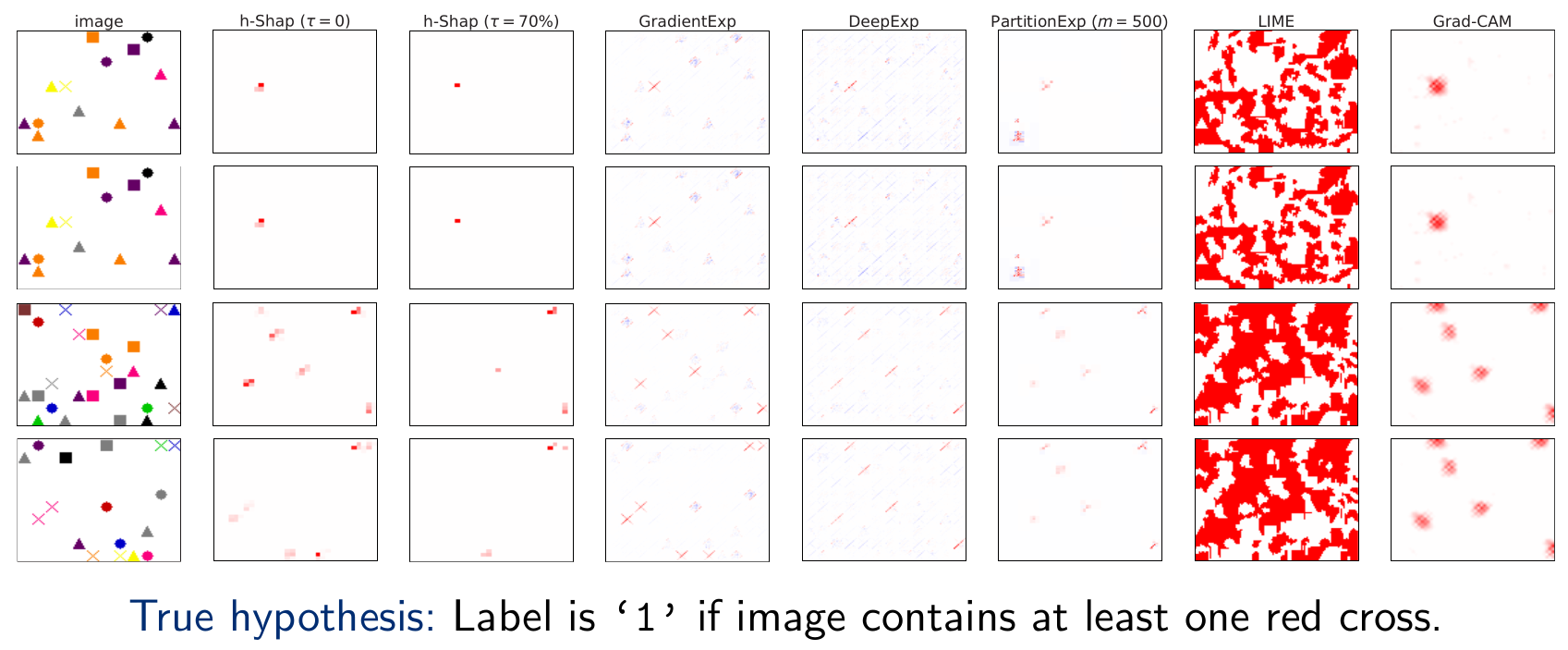
h-Shap: fast hierarchical games

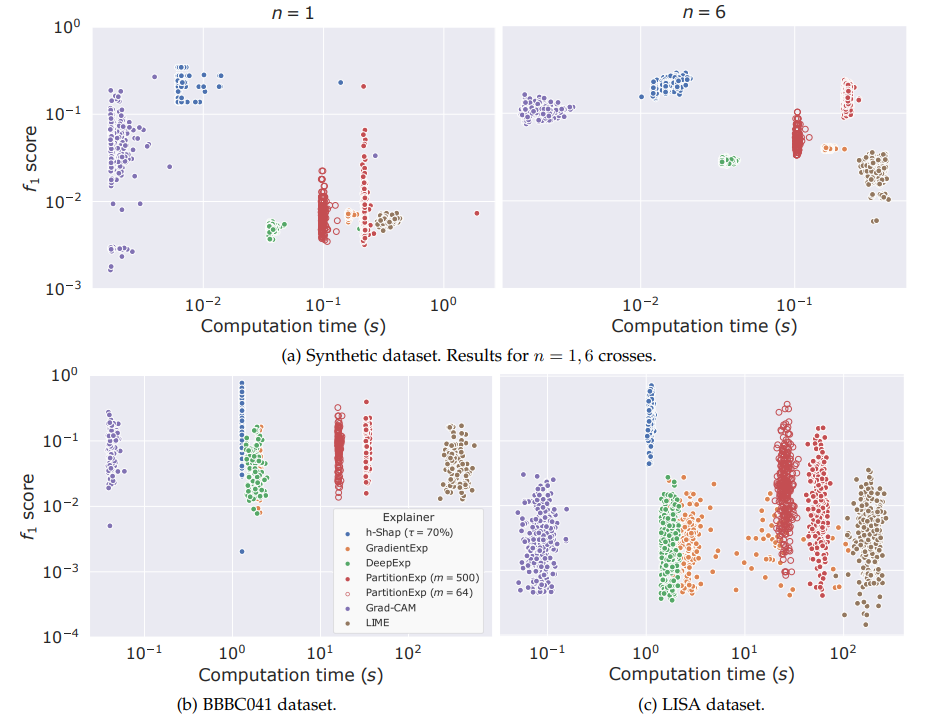
Fast hierarchical games for image explanations,
Teneggi, Luster & Sulam,
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022

Jacopo T.

JHU

Alex L.

EPFL

From Shapley back to Pearson

You are telling me that pixels play games?

Formal Feature Importance 

H_{0,i}:~ X_i \perp\!\!\!\perp Y | X_{[n]\setminus i}

[Candes et al, 2018]

(Y~|~ X_i = x_i, X_{i^c} = x_{i^c} ) \overset{d}{=} (Y ~|~ X_{i^c} = x_{i^c} )

There exists a procedure that tests for this null and returns a valid p-value,

p_{i,S}
\text{reject} ~\Rightarrow~ j=2 \text{: important}

Local Feature Importance 

\text{For any } S \subseteq [n]\setminus \{i\}, \text{ and a sample } x\sim \mathcal D_X
H^0_{i,S}:~ X_i \perp\!\!\!\perp f(\tilde X_{S\cup \{i\}}) | X_{S} = x_{S}
(f(\tilde X_{S\cup \{i\}}) ) \overset{d}{=} (f(\tilde X_{S}) )
H^0_{j=2,S=\{1,3,4\}}

Lemma:

From Shapley back to Pearson

\Gamma_{i,S}

Theorem 2 (informal): 

p_{i,S} \leq 1 - \Gamma_{i,S}.
i\in[n],
\Gamma_{i,S}

Large           values imply importance in a statistical sense:

(f(\tilde X_{S\cup \{i\}}) ) \overset{d}{\neq} (f(\tilde X_{S}) )
\displaystyle \phi_i = \sum_{S_j\subseteq [n]\setminus \{i\}} w_j ~ \mathbb E \left[ f(\tilde X_{S\cup \{i\}}) - f(\tilde X_S) \right]

Given the Shapley coefficient of any feature 

Then

p_{i,S}

and the p-value obtained for         , i.e.         ,

H^0_{i,S}

From Shapley back to Pearson: Hypothesis Testing via the Shapley Value
J Teneggi, B Bharti, Y Romano, J Sulam
arXiv preprint arXiv:2207.07038

Beepul B.
JHU

Yaniv R.
Technion

Jacopo T.
JHU

What does the Shap Value test for?

H^0_{i,S}: ~(f(\tilde X_{S\cup \{i\}}) ) \overset{d}{=} (f(\tilde X_{S}) )
\displaystyle H^0_\text{global} = \underset{{S\subseteq [n]\setminus \{i\}}}{\Large\cap} H^0_{i,S}
\displaystyle H^0_\text{global}

Theorem 3 (informal): 

Given the Shapley value for the i-th feature, and

\displaystyle p_\text{global} = \sum_{S_j\subseteq [n]\setminus i} w_j ~ p_{i,S}

Then, under              ,                is a valid p-value and

2 p_\text{global}
p_\text{global} \leq 1-\phi_i

From Shapley back to Pearson

Partial summary

  • Shapley values are popular among practitioners because of their "theoretical (game theoretic) foundations"

 

  • Despite their exponential computational advantage, one can often leverage structure in the data to compute or approximate these efficiently

 

  • Unbeknownst to users, these coefficients do convey statistical meaning with controlled Type I error 

Fairness in ML

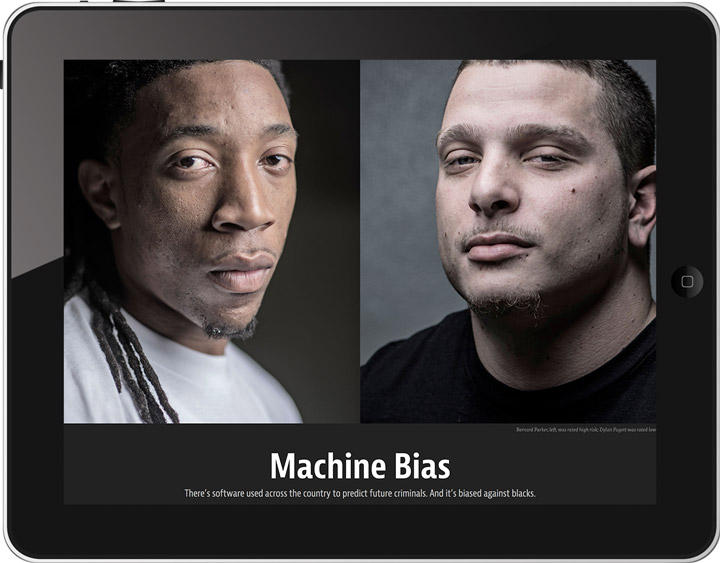
Formal Fairness in  ML

(Y,A,X) = (\text{label, sensitive attribute, features}),
\hat{Y} = f(X,A) \approx \mathbb E[Y|X]
A \in \{0,1\}

Demographic Parity

\mathbb P [ \hat{Y} = 1 | A = 0] = \mathbb P [ \hat{Y} = 1 | A=1]

prediction should not be correlated with the protected attribute

\mathbb P [ \hat{Y} = 1 | Y = 1, A=0 ] = \mathbb P [ \hat{Y} = 1 | Y = 1, A=1 ]

TPR should be equal for both groups

Equal Opportunity

\hat Y \perp \!\!\! \perp A | Y

Equalized Odds

TPR and FPR should be equal for both groups

\alpha_k = \mathbb P(\hat Y = 1 \mid Y = 1, A = k) \quad \text{for} \quad k \in \{0,1\}
\text{bias}(f) = |\alpha_0 - \alpha_1| = | \text{TPR}_{(A=0)} - \text{TPR}_{(A=1)} |

Estimating (and controlling) bias requires a dataset 

\mathcal D^m \sim (Y,X,A)

What if we only have                            ?!

\mathcal D_1^m \sim (Y,X)
\mathcal D_2^m \sim (X,A)
h : \mathcal X \to \mathcal A,~~ h\approx \mathbb E[A|X]
\hat \alpha_k = \mathbb P(\hat Y = 1 \mid Y = 1, {\color{Maroon}\hat A = k}) \quad \text{for} \quad k \in \{0,1\}
\widehat{\text{bias}}(f) = |\hat \alpha_0 - \hat\alpha_2|

(TPRs)

Formal Fairness in  ML

(estimated bias)

Solution?

  • Gupta et al., Proxy fairness, 2018

  • Prost et al., Measuring model fairness under noisy covariates, 2021.

  • Kallus et al., Assessing algorithmic fairness with unobserved protected class using data combination, 2022

  • Awasthi et al., Evaluating fairness of machine learning models under uncertain and incomplete information, 2021.

Fair Predictors with inaccurate sensitive attributes

Assumption 2:

\hat A \perp\!\!\!\perp \hat Y | A,Y

e.g. if h and f use features that are conditionally independent

* only needs the base rates 

Can I make

\hat Y \perp \!\!\! \perp \hat A | Y ?

Theorem 4:

Under Assumption 2,

|{\text{bias}}(f)| \leq k |\widehat{\text{bias}}(f)|
k = \left(1 + \frac{U}{2r^2s^2}\left(\frac{2s^4r + 2r^4s - Ur^4 - Us^4 + Ur^2s^2}{2rs -Ur - Us}\right)\right)

where k is an analytical function of the error of h and the base rates

r = \mathbb P(Y = 1, A = 1), ~~ s = \mathbb P(Y = 1, A = 0)

Controlling for Fairness with predicted attributes

Theorem 5:

|{\text{bias}}(f)| \leq |\widehat{\text{bias}}(f)| + U \left( \frac{\hat{\alpha}_1 s + \hat{\alpha}_0 r }{rs} \right)
\text{Assume } U = \mathbb P[h(X)\neq A] < \underset{(i,j)\in \{0,1\}^2}{\min} \mathbb P [A=i,Y=j].\text{ Then,}
r = \mathbb P(Y = 1, A = 1), ~~ s = \mathbb P(Y = 1, A = 0), ~~

Algorithm (informal)

\displaystyle \min_{f\in\mathcal H} ~\mathbb E[\ell(f(X)-Y)] ~~s.t.~~ f(X)\perp\!\!\!\perp \hat A | Y

Experiments

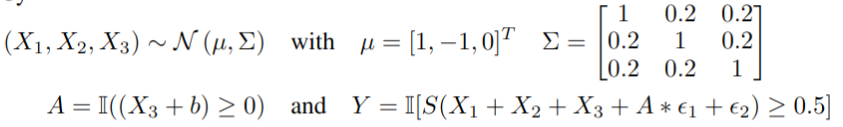
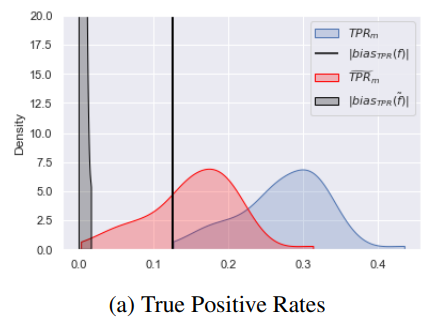
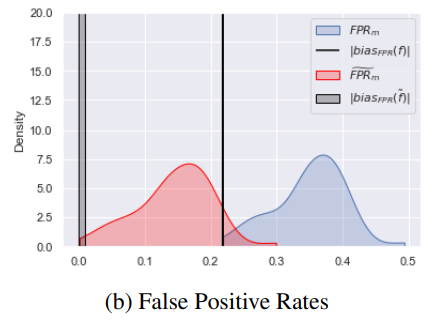
Experiments

FIFA 20 Data set

A : nationality = {Argentina,England}

Y : salary = {above of median, below of median}

X : player features = {quality score, name}

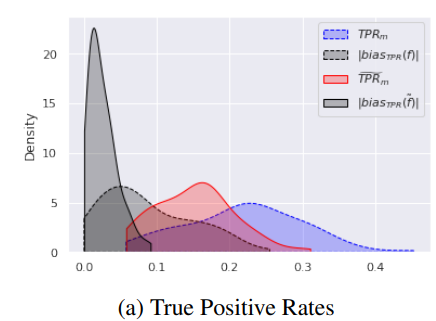
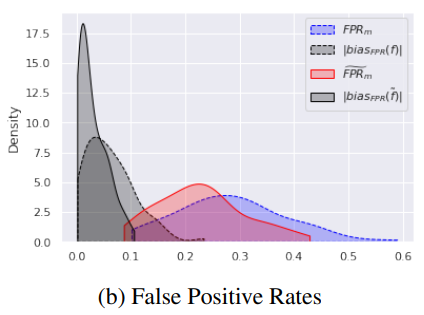
Experiments

Estimating and Controlling for Fairness via Sensitive Attribute Predictors
B Bharti, P Yi, J Sulam
arXiv preprint arXiv:2207.12497

Beepul B.
JHU

Paul Yi
UMD

Y = 1~ \text{ if pleural effusion}
Y = 1~ \text{ if any abnormal condition}

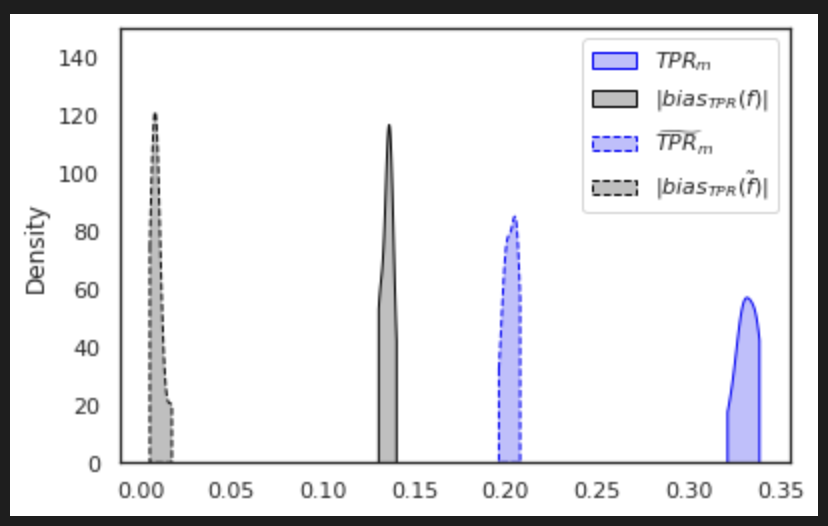
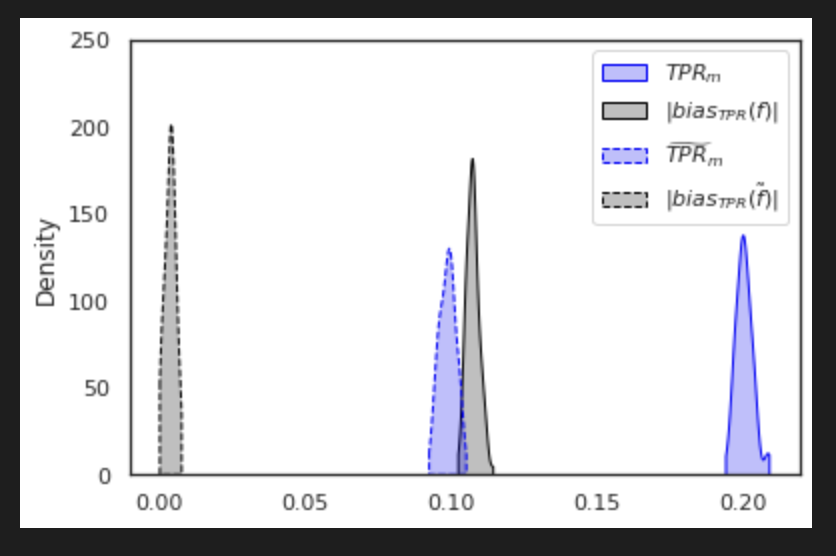
Final Thoughts

  • Fairness can be estimated and controlled for even when data is not fully observable​

  • Huge opportunity for development of methods to rigorously enforce Responsible Constraints in machine learning predictors