Formal Interpretability
Jeremias Sulam
for Machine Learning
Mathematics of Explainable AI with Applications to Finance and Medicine

SIAM 2024 Conference on Mathematics of Data Science

"The biggest lesson that can be read from 70 years of AI research is that general methods that leverage computation are ultimately the most effective, and by a large margin. [...] Seeking an improvement that makes a difference in the shorter term, researchers seek to leverage their human knowledge of the domain, but the only thing that matters in the long run is the leveraging of computation. [...]
We want AI agents that can discover like we can, not which contain what we have discovered."The Bitter Lesson, Rich Sutton 2019


Interpretability in Image Classification
\((X,Y) \in \mathcal X \times \mathcal Y\)
\((X,Y) \sim P_{X,Y}\)
\(\hat{Y} = f(X) : \mathcal X \to \mathcal Y\)
Setting:



-
What features are important for this prediction?
-
What does importance mean, exactly?
-
Sensitivity or Gradient-based perturbations
-
Shapley coefficients
-
Variational formulations
-
Counterfactual & causal explanations
LIME [Ribeiro et al, '16], CAM [Zhou et al, '16], Grad-CAM [Selvaraju et al, '17]
Shap [Lundberg & Lee, '17], ...
RDE [Macdonald et al, '19], ...
[Sani et al, 2020] [Singla et al '19],..

Post-hoc Interpretability in Image Classification
-
Adebayo et al, Sanity checks for saliency maps, 2018
-
Ghorbani et al, Interpretation of neural networks is fragile, 2019
-
Shah et al, Do input gradients highlight discriminative features? 2021



Is the piano important for \(\hat Y = \text{cat}\)?
Semantic Interpretability of classifiers
How can we explain black-box predictors with semantic features?
Is the piano important for \(\hat Y = \text{cat}\), given that there is a cute mammal in the image?



Is the piano important for \(\hat Y = \text{cat}\)?
Semantic Interpretability of classifiers
How can we explain black-box predictors with semantic features?
Is the piano important for \(\hat Y = \text{cat}\), given that there is a cute mammal in the image?
Post-hoc Interpretability Methods
Interpretable by
construction



Is the piano important for \(\hat Y = \text{cat}\)?
Semantic Interpretability of classifiers
How can we explain black-box predictors with semantic features?
Is the piano important for \(\hat Y = \text{cat}\), given that there is a cute mammal in the image?
Post-hoc Interpretability Methods
Interpretable by
construction
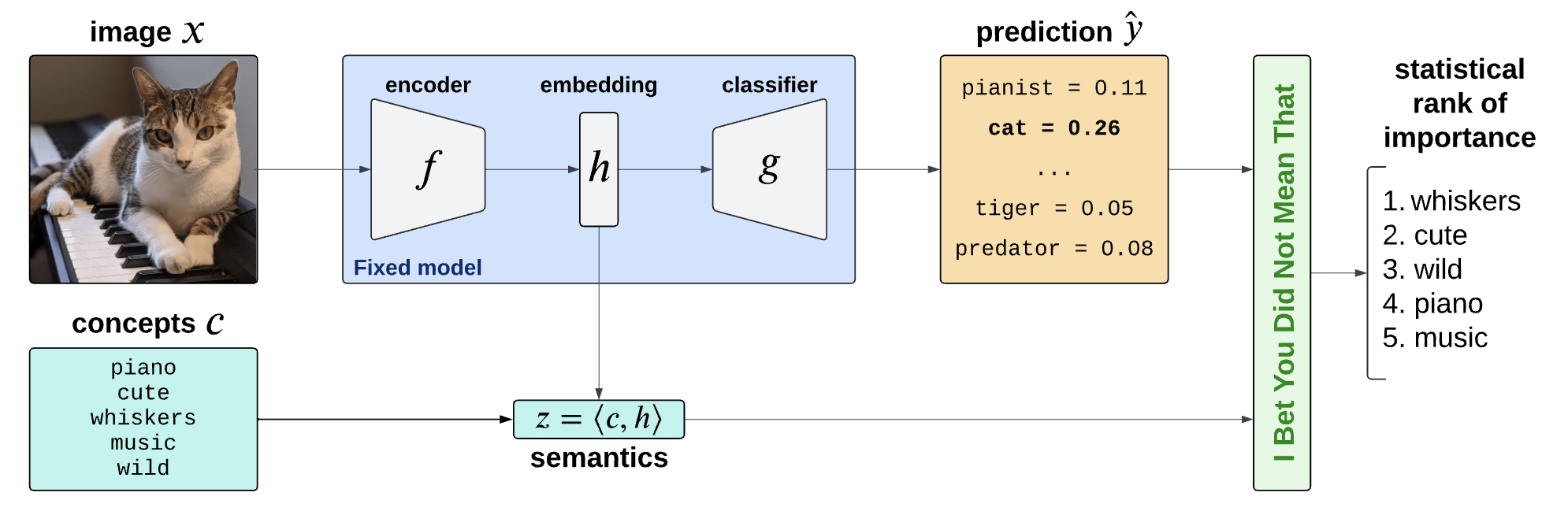

Semantic Interpretability of classifiers
Concept Bank: \(C = [c_1, c_2, \dots, c_m] \in \mathbb R^{d\times m}\)
Embeddings: \(H = f(X) \in \mathbb R^d\)
Semantics: \(Z = C^\top H \in R^m\)
Concept Bank: \(C = [c_1, c_2, \dots, c_m] \in \mathbb R^{d\times m}\)
Concept Activation Vectors
(Kim et al, 2018)
\(c_\text{cute}\)
Semantic Interpretability of classifiers
Vision-language models
(CLIP, BLIP, etc... )
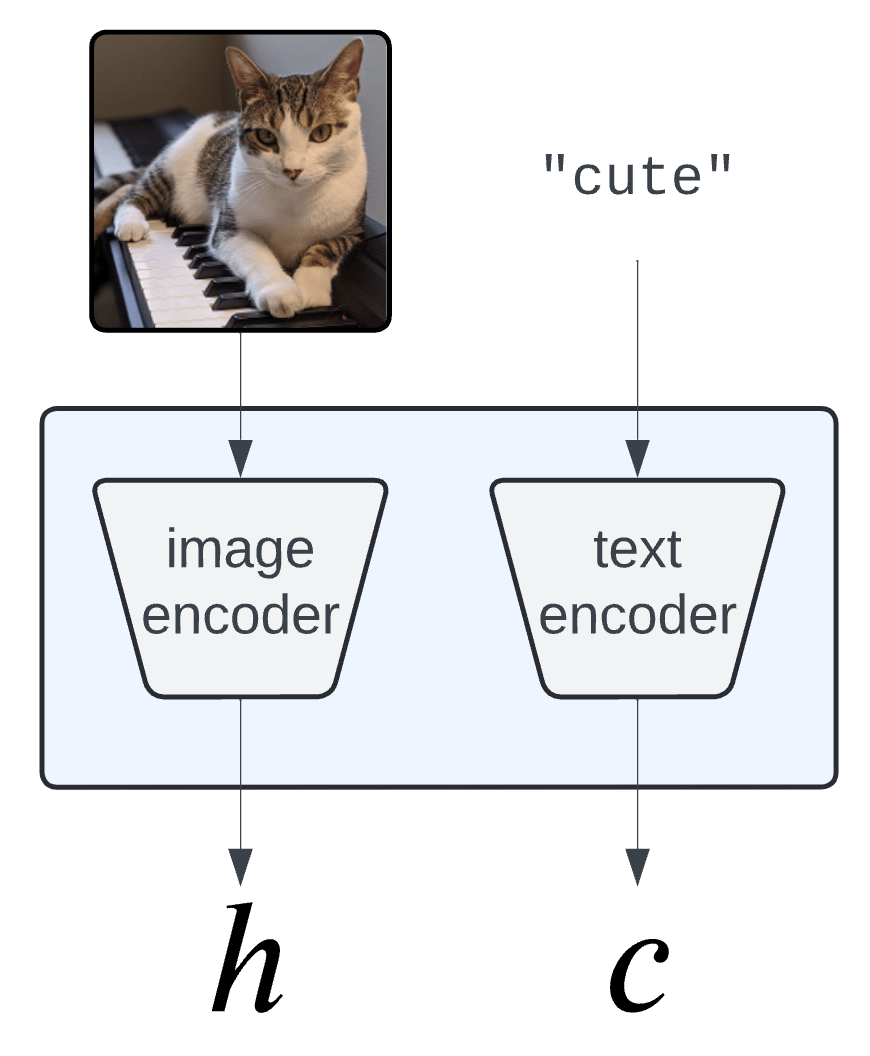
Semantic Interpretability of classifiers
[Bhalla et al, "Splice", 2024]
Concept Bottleneck Models (CMBs)

[Koh et al '20, Yang et al '23, Yuan et al '22 ]
- Need to engineer a (large) concept bank
- Performance hit w.r.t. original predictor
\(\tilde{Y} = \hat w^\top Z\)
\(\hat w_j\) is the importance of the \(j^{th}\) concept
Precise notions of semantic importance
Desiderata
- Rigorous testing with guarantees (Type 1 error/FDR control)
- Fixed original predictor (post-hoc)
- Global and local importance notions
- Testing for any concepts (no need for large concept banks)
Precise notions of semantic importance



\(C = \{\text{``cute''}, \text{``whiskers''}, \dots \}\)
Global Importance
\(H^G_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j \)
Global Conditional Importance
\(H^{GC}_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j | Z_{-j}\)
Precise notions of semantic importance



Global Importance
\(C = \{\text{``cute''}, \text{``whiskers''}, \dots \}\)
\(H^G_{0,j} : g(f(X)) \perp\!\!\!\perp c_j^\top f(X) \)
Global Conditional Importance
\(H^{GC}_{0,j} : g(f(X)) \perp\!\!\!\perp c_j^\top f(X) | C_{-j}^\top f(X)\)
\(H^G_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j \)
\(H^{GC}_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j | Z_{-j}\)
Precise notions of semantic importance
"The classifier (its distribution) does not change if we condition
on concepts \(S\) vs on concepts \(S\cup\{j\} \)"
\(C = \{\text{``cute''}, \text{``whiskers''}, \dots \}\)
Local Conditional Importance

Obiter dictum: tightly related to Shapley values!
\[H^{j,S}_0:~ g({\tilde H_{S \cup \{j\}}}) \overset{d}{=} g(\tilde H_S), \qquad \tilde H_S \sim P_{H|Z_S = C_S^\top H} \]
Precise notions of semantic importance
"The classifier (its distribution) does not change if we condition
on concepts \(S\) vs on concepts \(S\cup\{j\} \)"
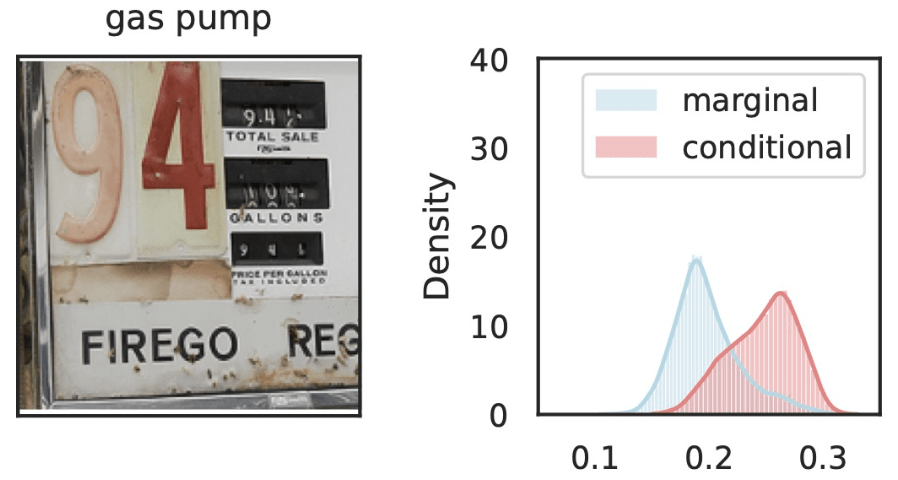

\(\hat{Y}_\text{gas pump}\)

\(Z_S\cup Z_{j}\)
\(Z_{S}\)
\(Z_j=\)
Local Conditional Importance
\[H^{j,S}_0:~ g({\tilde H_{S \cup \{j\}}}) \overset{d}{=} g(\tilde H_S), \qquad \tilde H_S \sim P_{H|Z_S = C_S^\top H} \]
Precise notions of semantic importance
"The classifier (its distribution) does not change if we condition
on concepts \(S\) vs on concepts \(S\cup\{j\} \)"

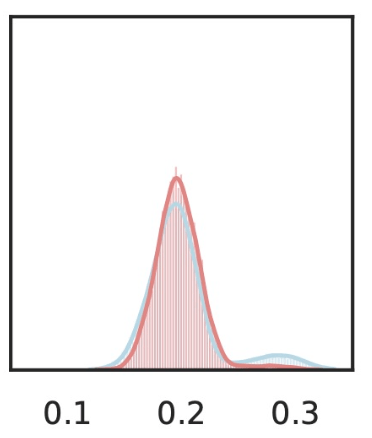

\(\hat{Y}_\text{gas pump}\)
\(\hat{Y}_\text{gas pump}\)

\(Z_S\cup Z_{j}\)
\(Z_{S}\)
\(Z_S\cup Z_{j}\)
\(Z_{S}\)
Local Conditional Importance

\(Z_j=\)
\(Z_j=\)
\[H^{j,S}_0:~ g({\tilde H_{S \cup \{j\}}}) \overset{d}{=} g(\tilde H_S), \qquad \tilde H_S \sim P_{H|Z_S = C_S^\top H} \]
Testing by betting
[Shaer et al. 2023, Shekhar and Ramdas 2023 ]
Goal: Test a null hypothesis \(H_0\) at significance level \(\alpha\)
Standard testing by p-values
Collect data, then test, and reject if \(p \leq \alpha\)
Online testing by e-values
Any-time valid inference, monitor online and reject when \(e\geq 1/\alpha\)
Testing by betting
- Consider a wealth process
\(K_0 = 1;\)
\(\text{for}~ t = 1, \dots \\ \quad K_t = K_{t-1}(1+\kappa_t v_t)\)
Reject \(H_0\) when \(K_t \geq 1/\alpha\)
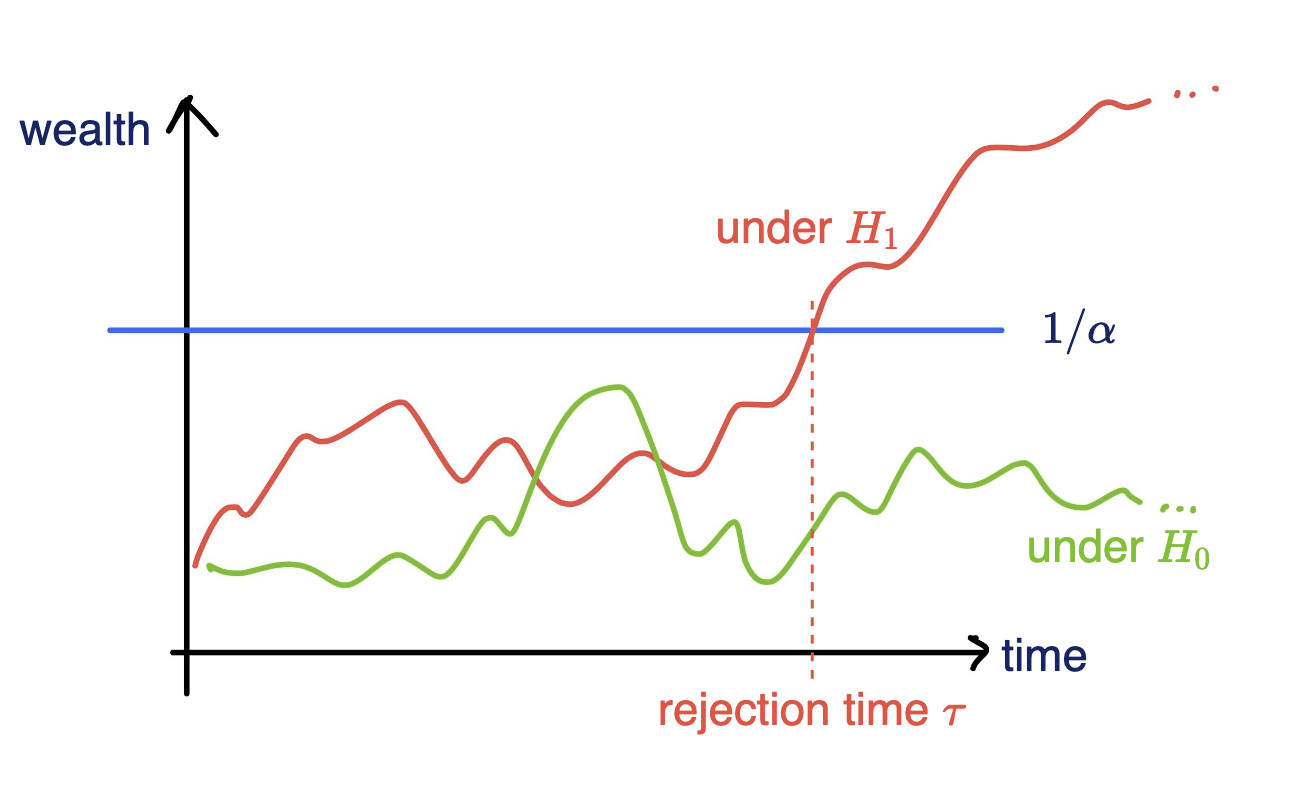
Online testing by e-values
[Shaer et al. 2023, Shekhar and Ramdas 2023 ]
Fair game: \(~~\mathbb E_{H_0}[\kappa_t | \text{Everything seen}_{t-1}] = 0\)
\(v_t \in (0,1):\) betting fraction
\(\kappa_t \in [-1,1]\) payoff
Testing by betting via SKIT (Podkopaev et al., 2023)
\(H^G_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j \iff P_{\hat{Y},Z_j} = P_{\hat{Y}} \times P_{Z_j}\)
Testing importance via two-sample tests
\(H^{GC}_{0,j} : \hat{Y} \perp\!\!\!\perp Z_j | Z_{-j} \iff P_{\hat{Y}Z_jZ_{-j}} = P_{\hat{Y}\tilde{Z}_j{Z_{-j}}}\)
\(\tilde{Z_j} \sim P_{Z_j|Z_{-j}}\)
\[H^{j,S}_0:~ g({\tilde H_{S \cup \{j\}}}) \overset{d}{=} g(\tilde H_S), \qquad \tilde H_S \sim P_{H|Z_S = C_S^\top H} \]
Test Statistic: Maximum Mean Discrepancy (MMD)
\(\text{MMD}(P,Q) = \underset{\rho \in R : \|\rho\|_\mathcal{R} \leq 1}{\sup} \mathbb E_P [g(X)] - \mathbb E_Q [g(X)]\)
[Shaer et al, 2023]
[Teneggi et al, 2023]
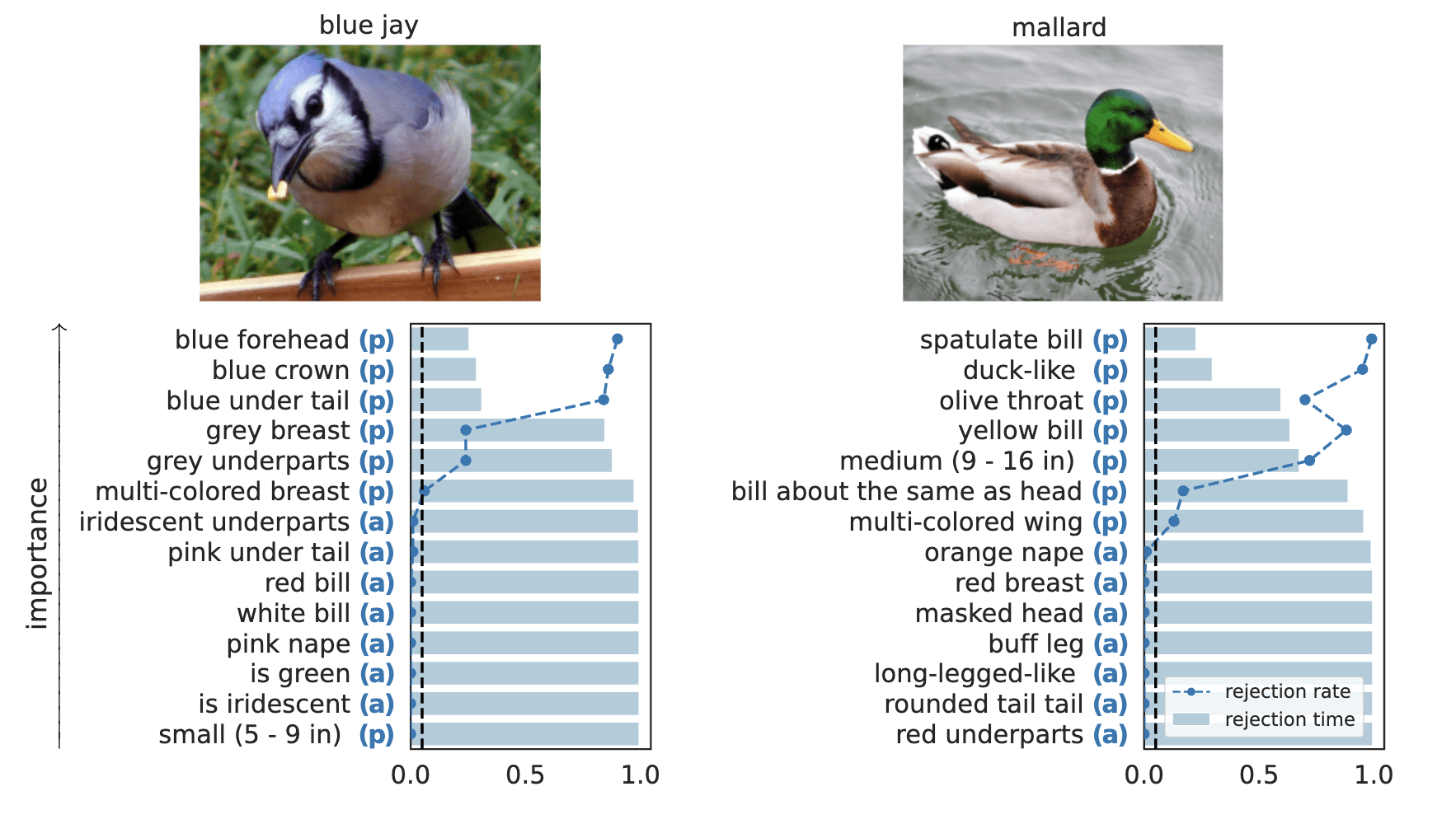
rejection time
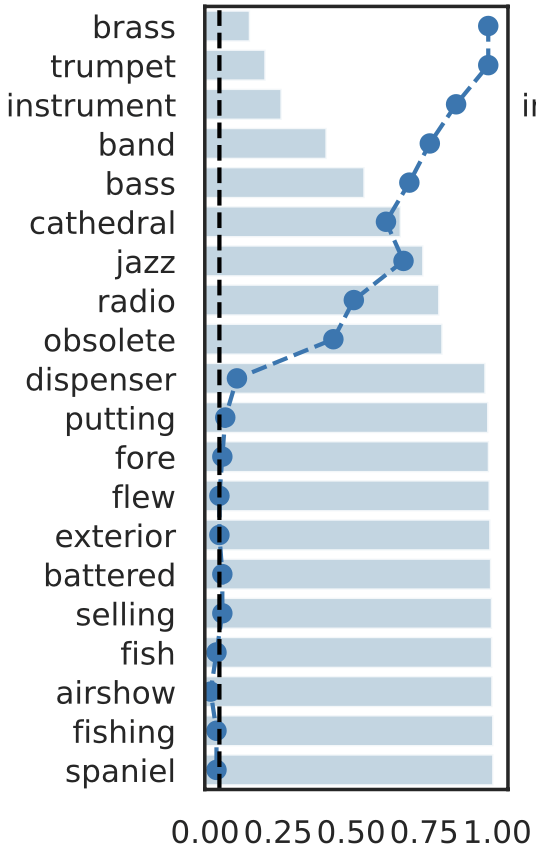

rejection rate
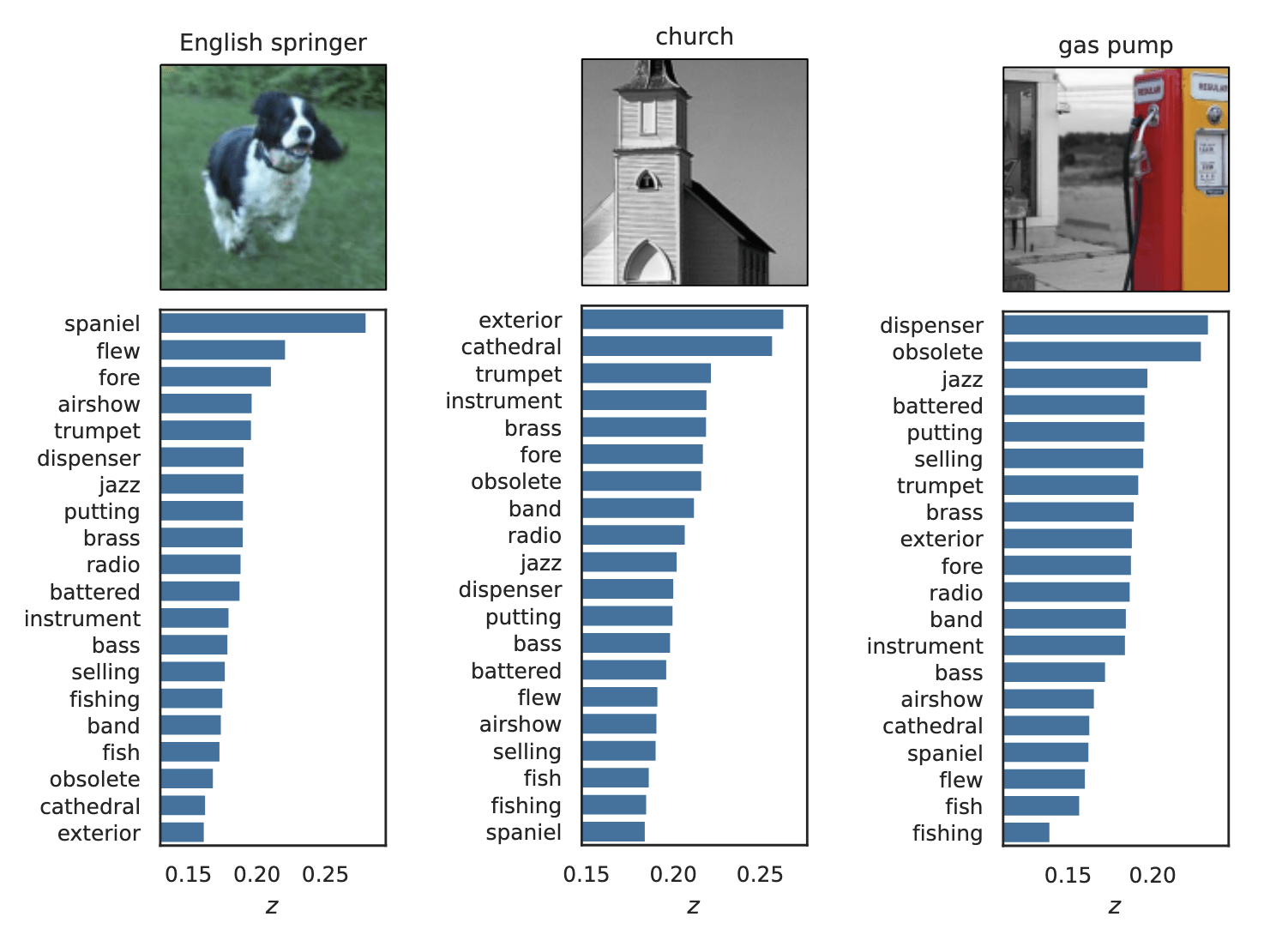
Important Semantic Concepts
(Reject \(H_0\))

Unimportant Semantic Concepts
(fail to reject \(H_0\))

Results
- Type 1 error control
- False discovery rate control
Results: CUB dataset
Results: Imagenette
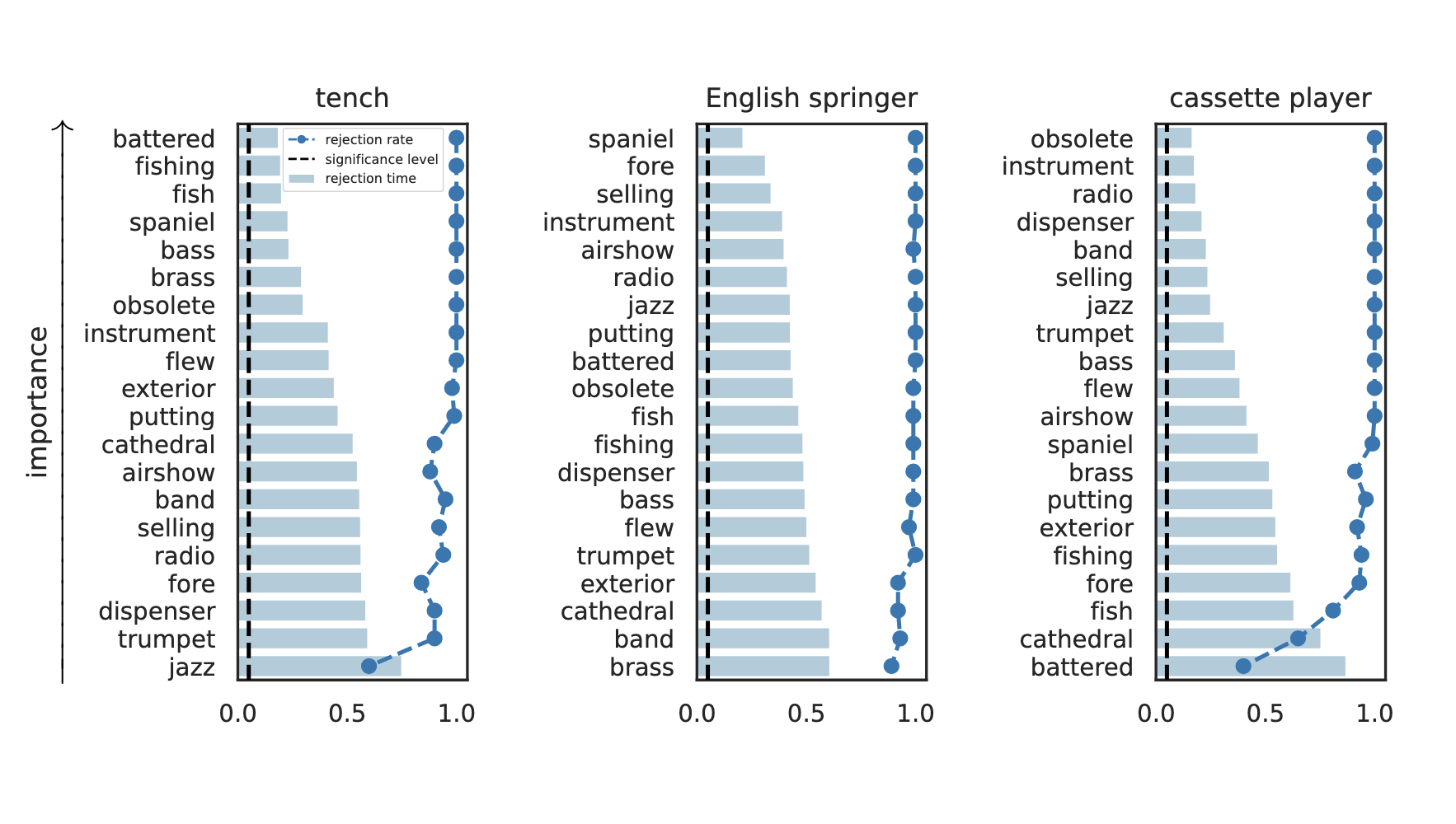
Global Importance
Results: Imagenette
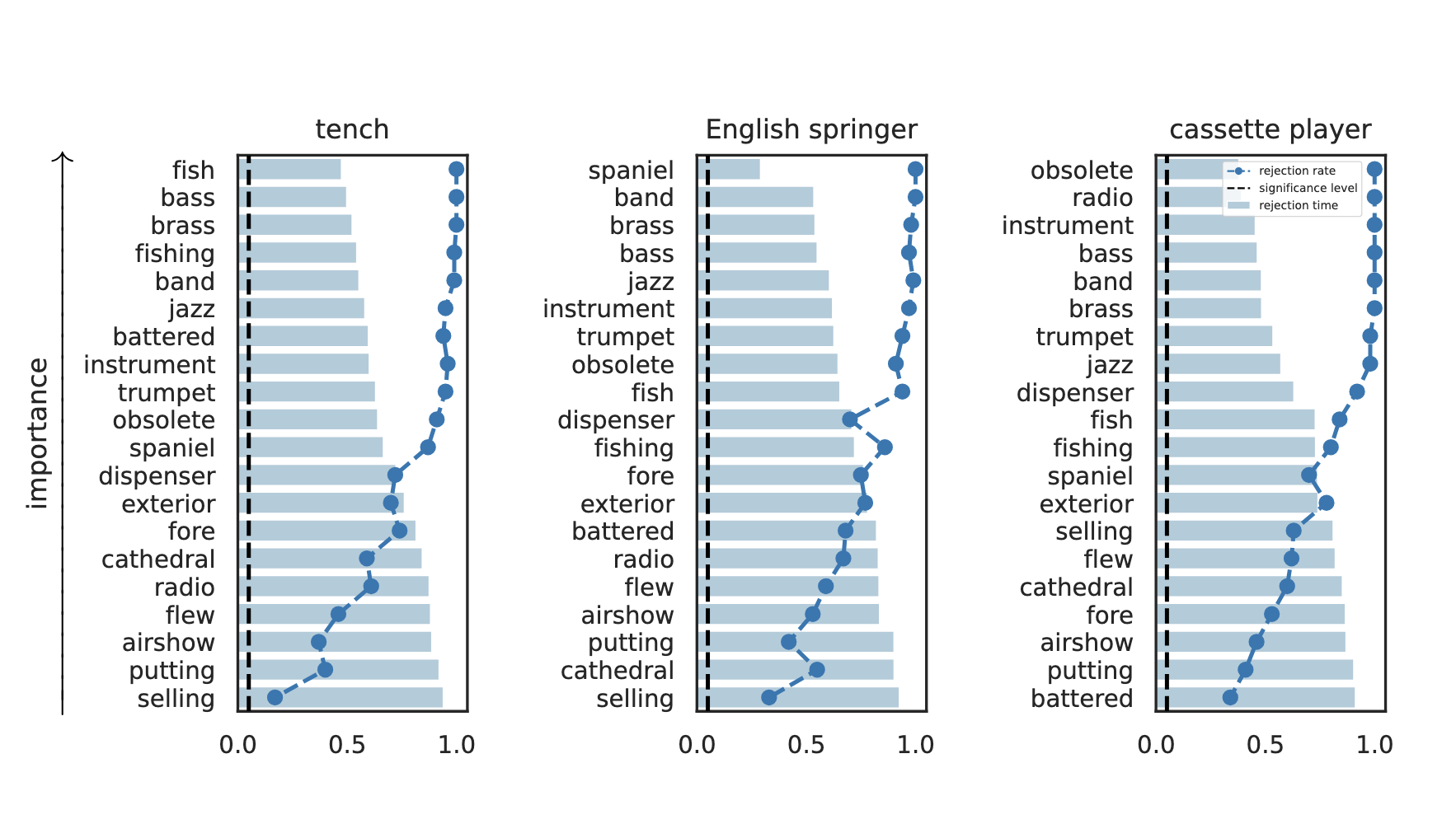
Global Conditional Importance

Results: Imagenette

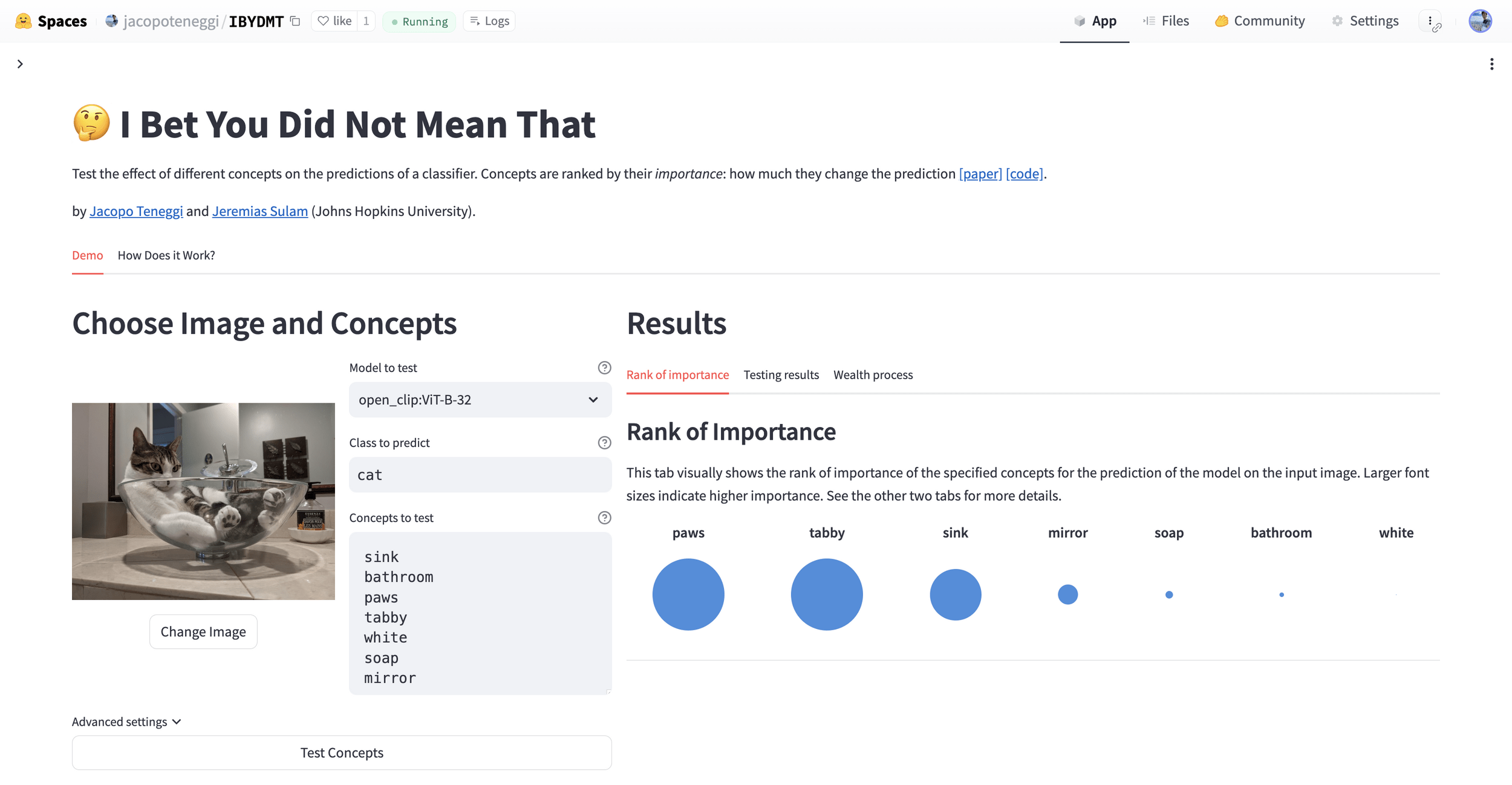
Results: Imagenette
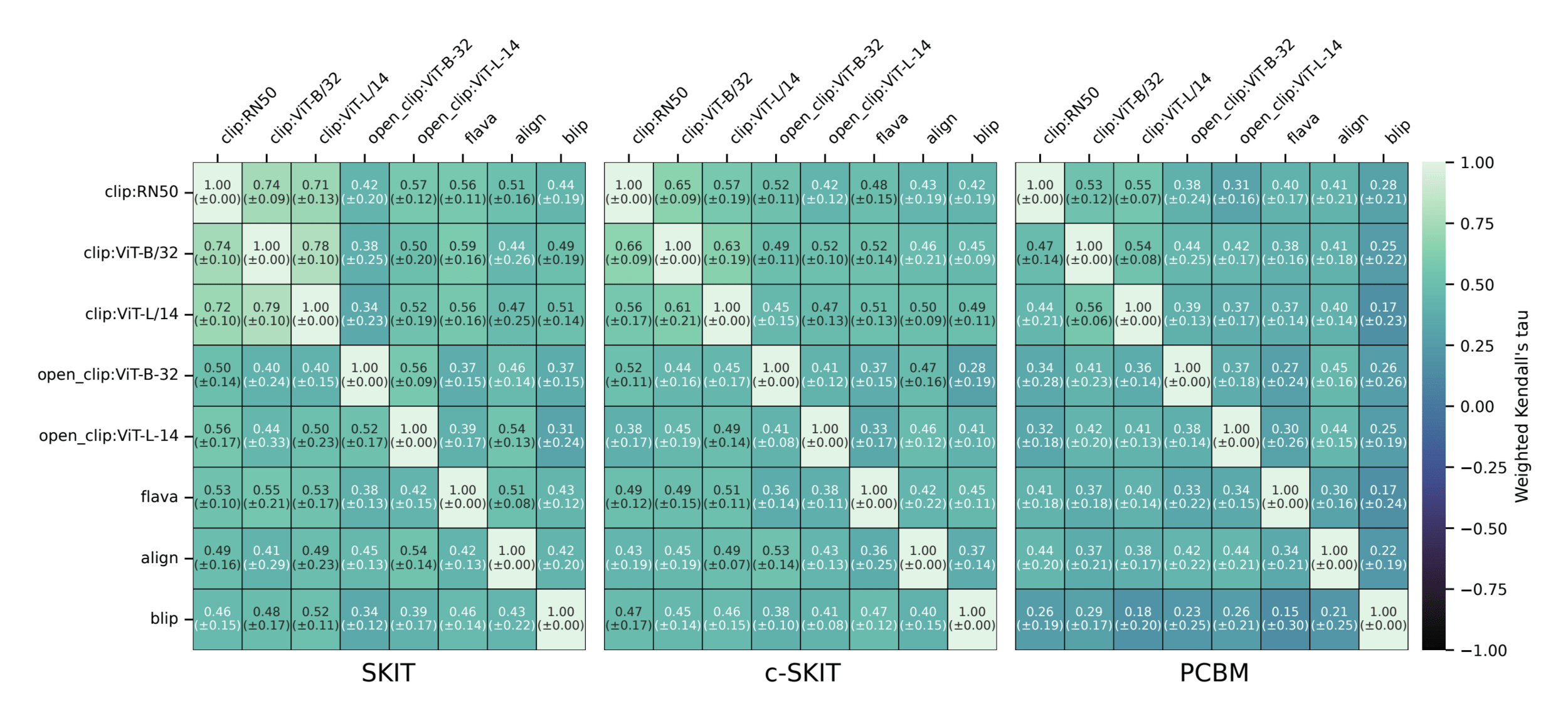
Results: Imagenette
Semantic comparison of vision-language models


...that's it!



Jacopo Teneggi
JHU



Appendix