Particle and wave:
Quantum information processing
with non-Gaussian light
Jonas Neergaard-Nielsen, bigQ - DTU Physics



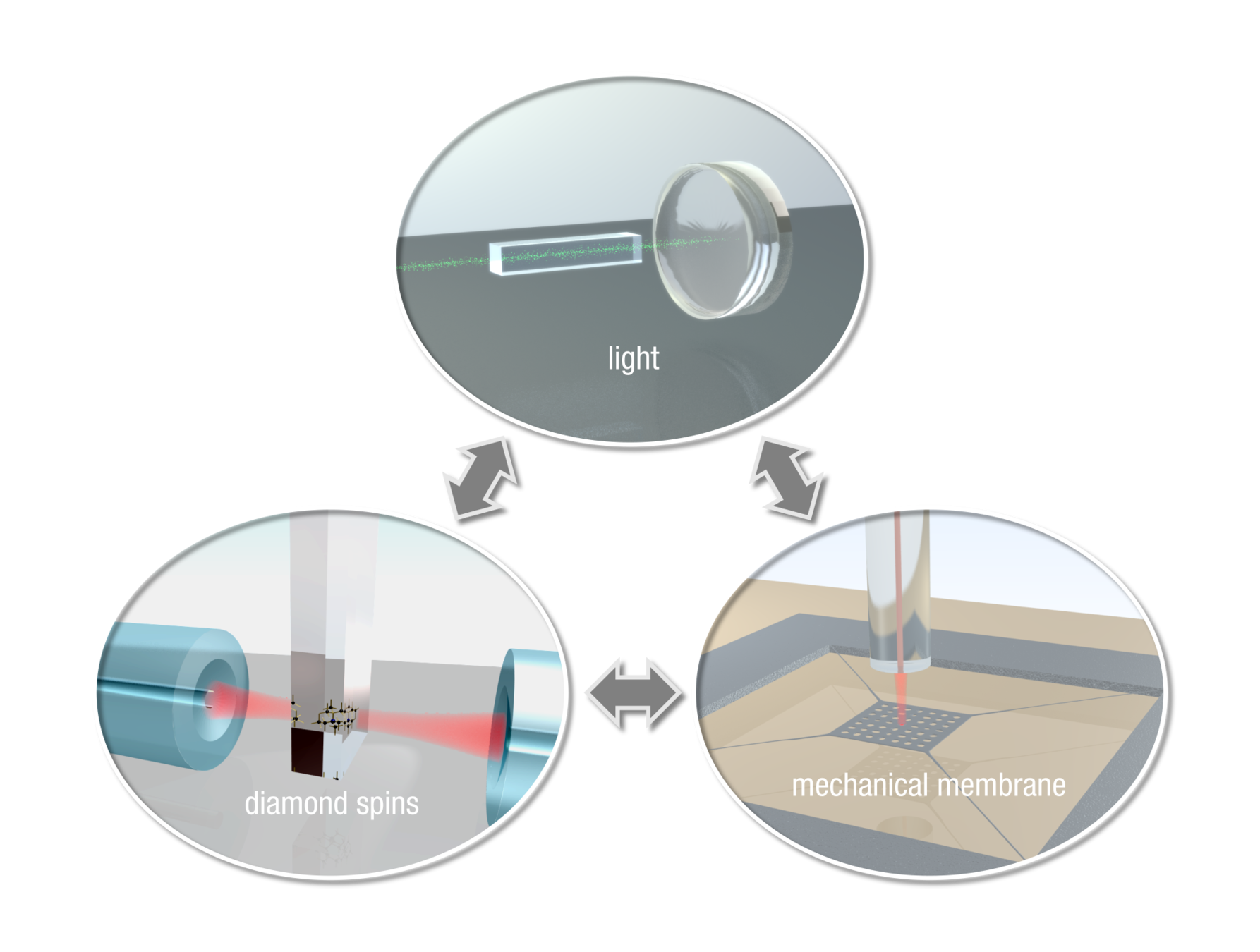
Vision:
...to advance our understanding of macroscopic quantum effects and to exploit these macroscopic effects for demonstrating quantum supremacy

DNRF Center for Macroscopic Quantum States
quadrature operators:
continuous variables for light
quadrature operators:
quadrature operators:
Gaussian states: Gaussian Wigner functions

squeezed
thermal
coherent

Gaussian operations: maintain Gaussianity
- most light is naturally Gaussian
- easy to do (experiment)
- easy to describe (theory)
- deterministic
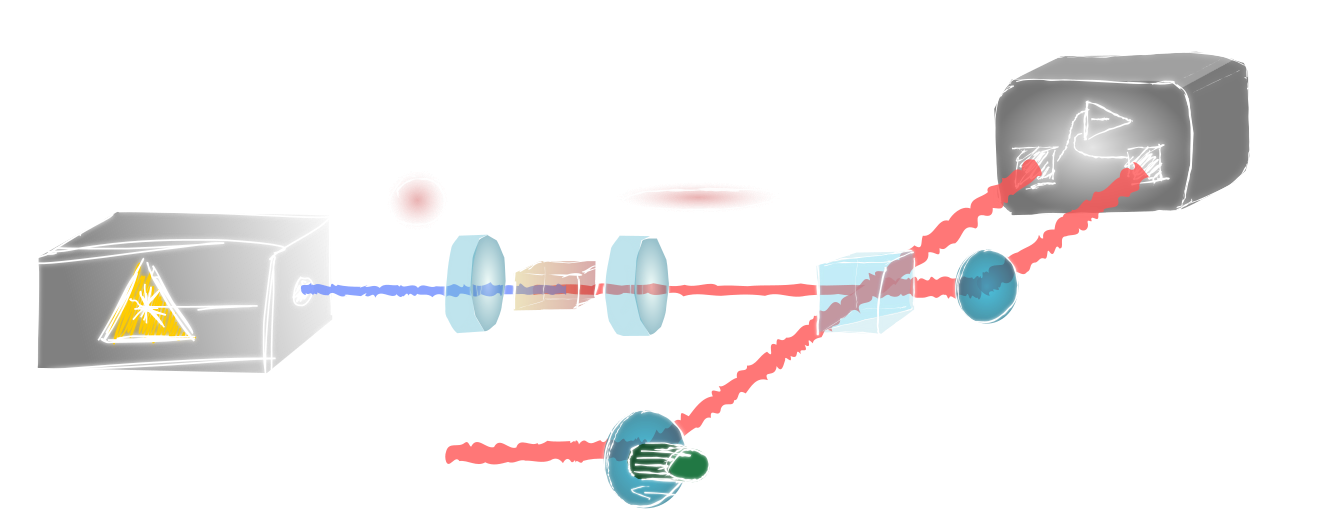
quadrature squeezing
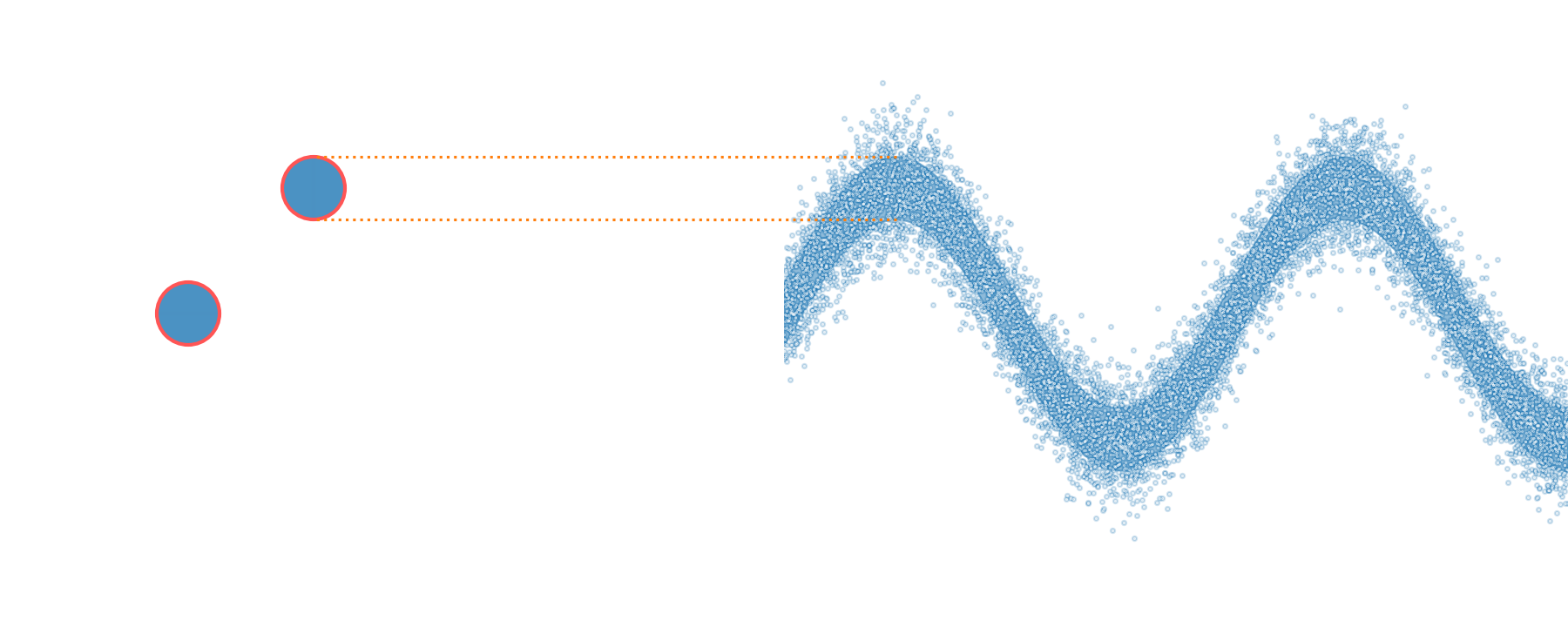
quadrature squeezing
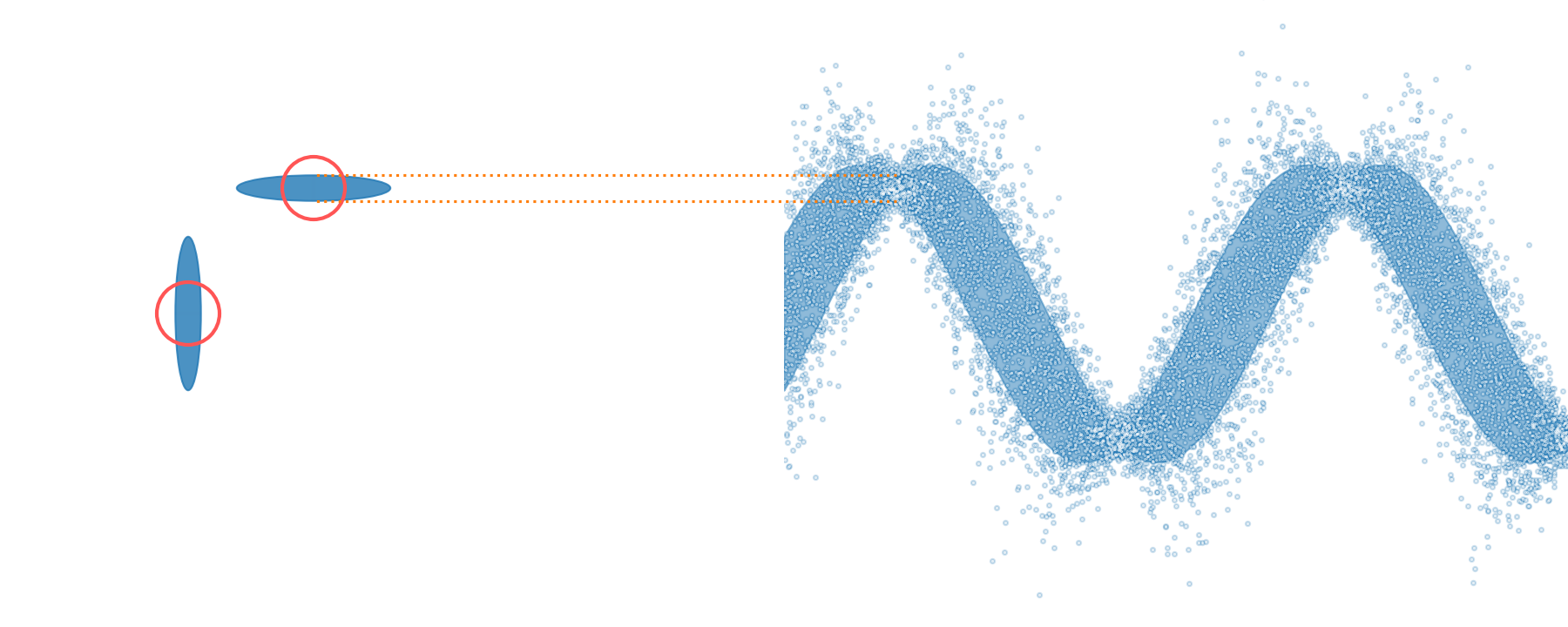
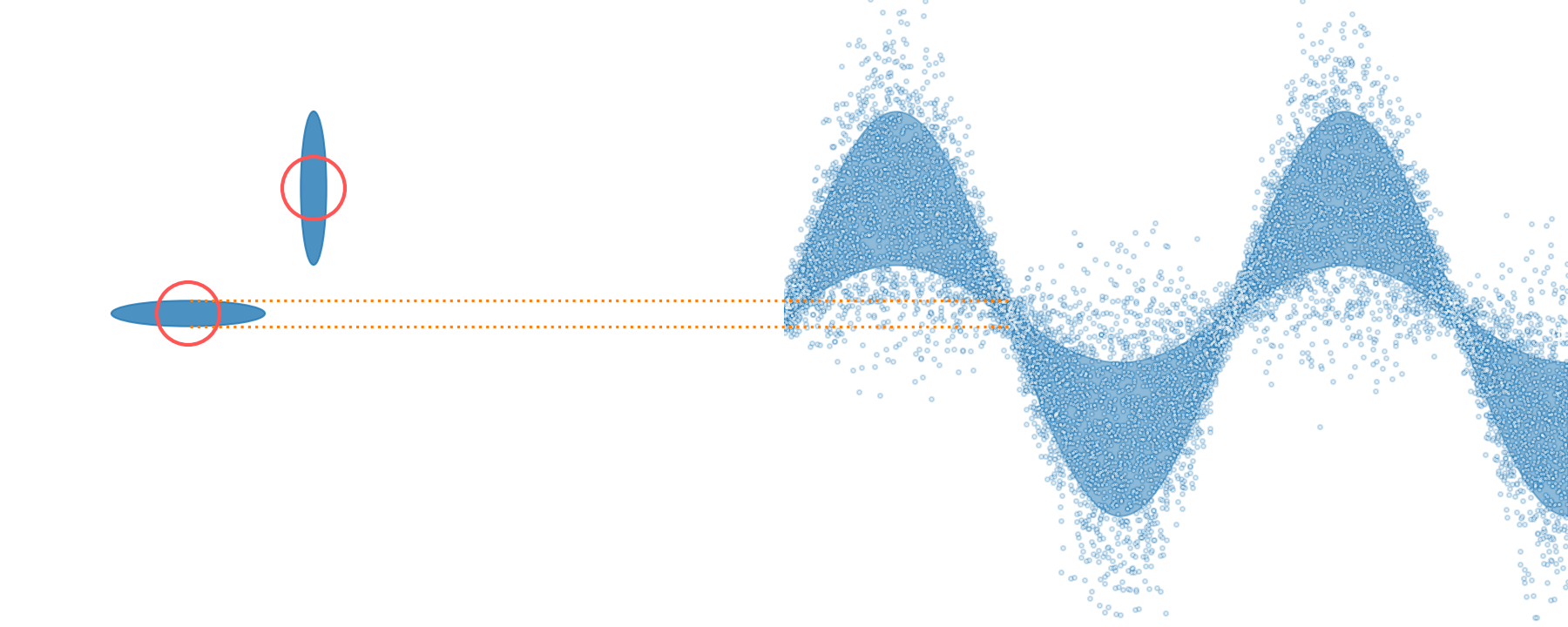
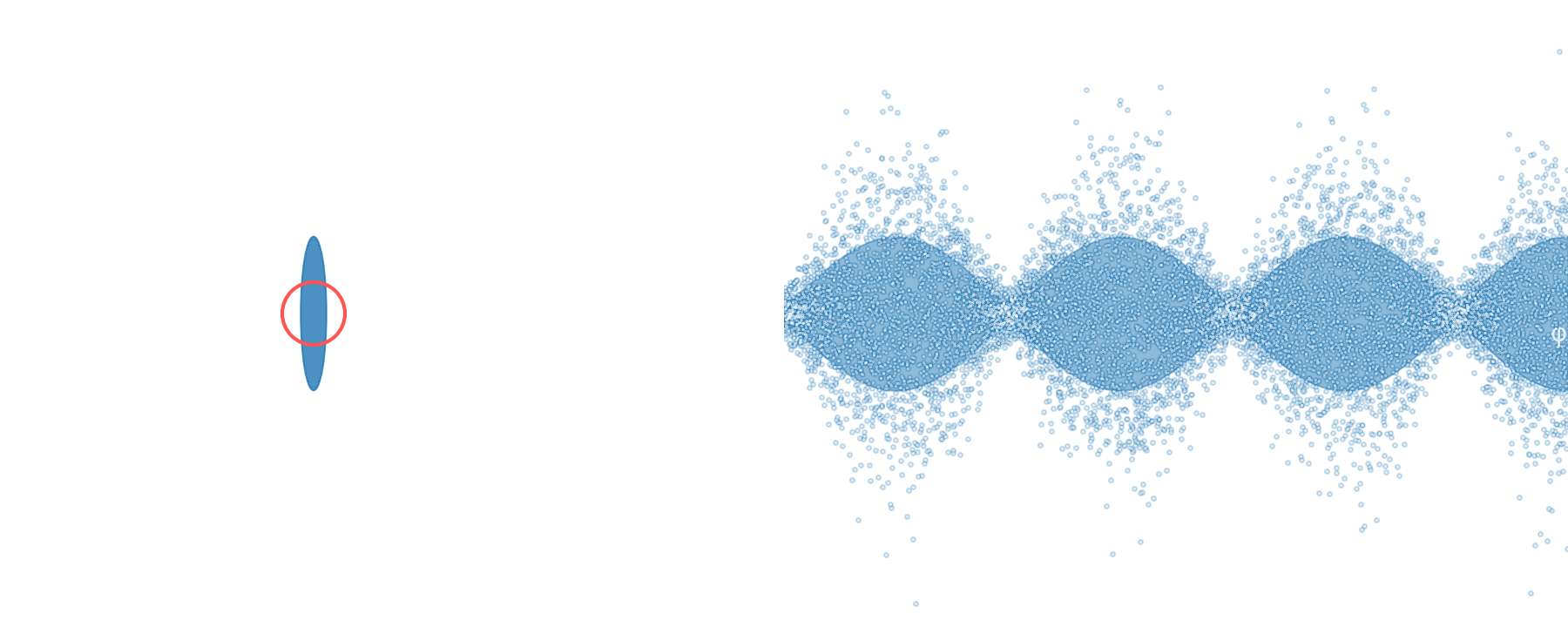



squeezer (OPO)
applications of squeezed light
sensing:
- enhanced sensitivity in quantum-limited measurements, e.g. LIGO
quantum information:
- quantum teleportation
- state encoding
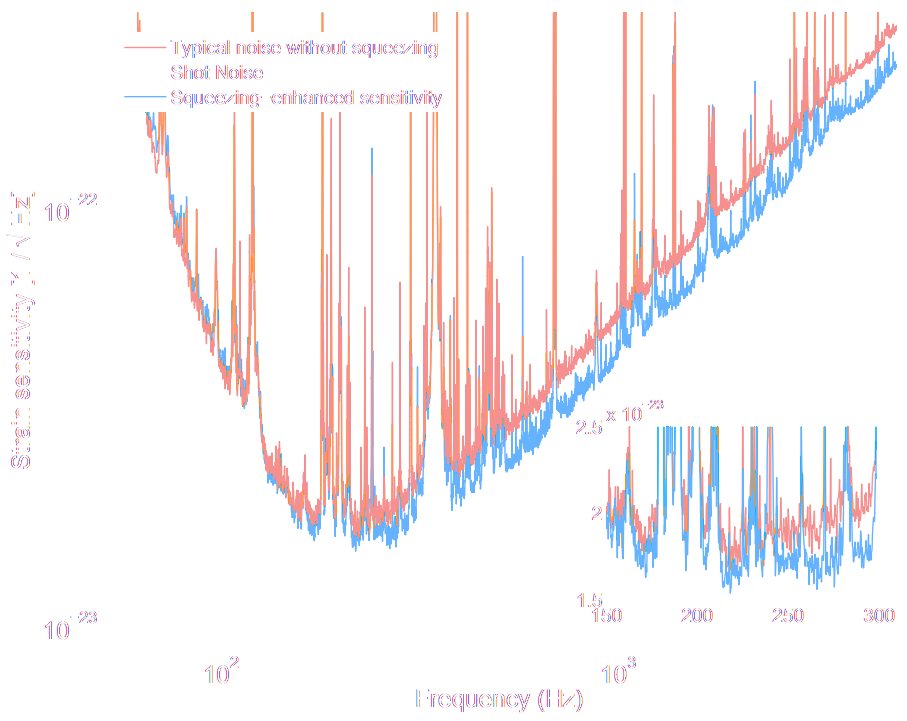
LIGO collaboration, Nature Photonics 7, 613 (2013)
squeezed posters - please enjoy tonight!
Casper Rubæk Breum
Distributed phase sensing
with 4-mode entanglement
Jens Arnbak
Extreme squeezing - towards 20 dB
Gaussian CV-QIP
- most light is naturally Gaussian
- easy to do (experiment)
- easy to describe (theory)
- deterministic
- NO universal quantum computation
- NO entanglement distillation
- NO error correction of Gaussian noise
Many experimental successes:
- quantum key distribution
- teleportation
- quantum memory
- various gates
- cluster state generation
- ...
non-Gaussian element needed to complete CV-QIP


+
the simplest: single photon detector


entanglement distillation by photon detection
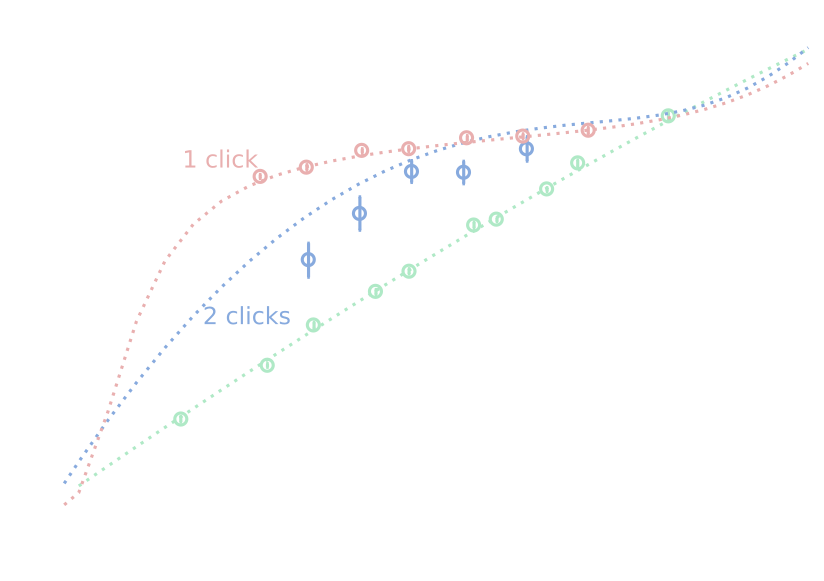
H Takahashi, JSNN, M Takeuchi, M Takeoka, K Hayasaka, A Furusawa & M Sasaki, Nature Photonics 4, 178 (2010)
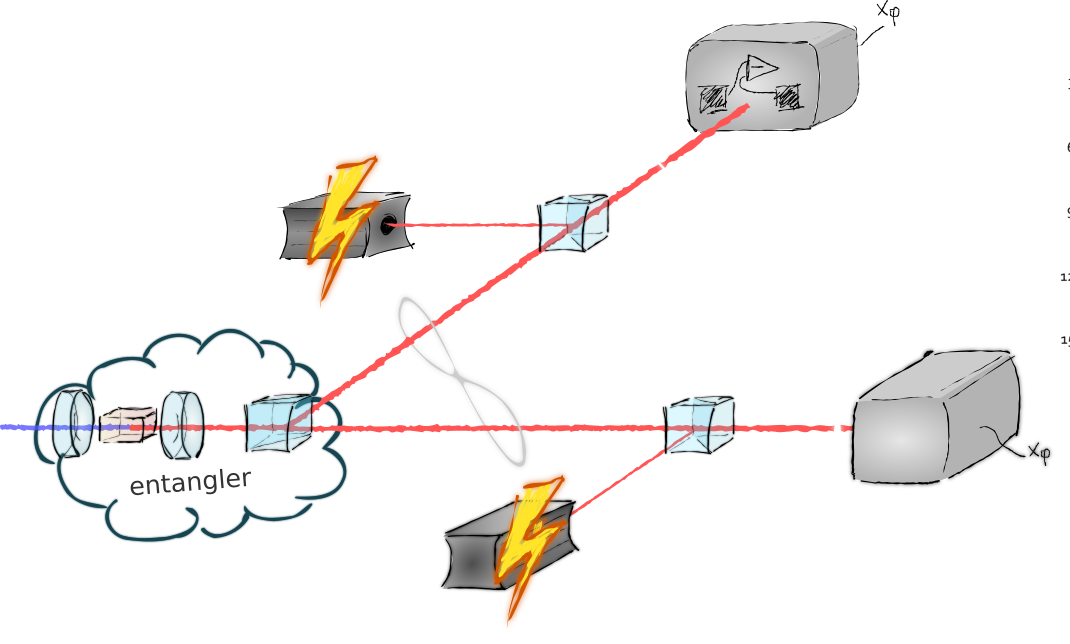
create non-Gaussian states by subtracting photons
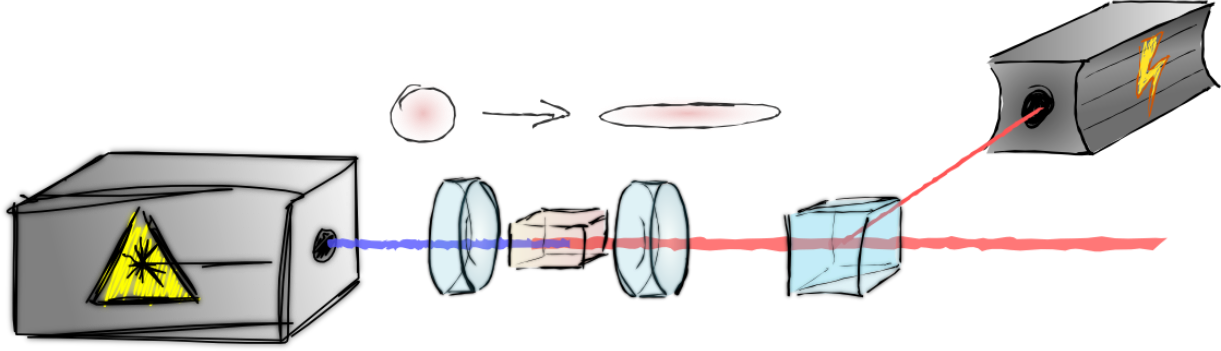
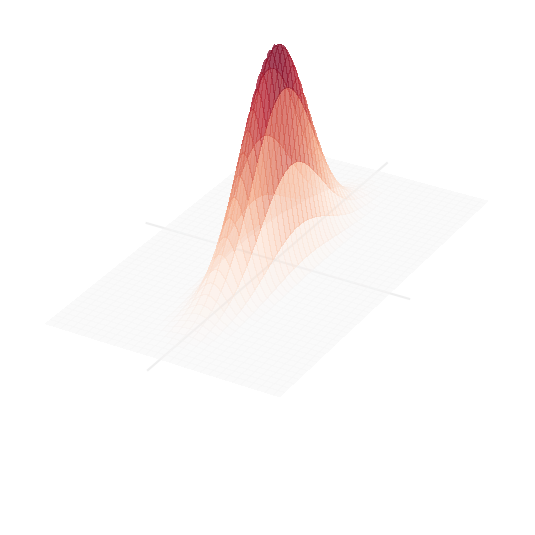

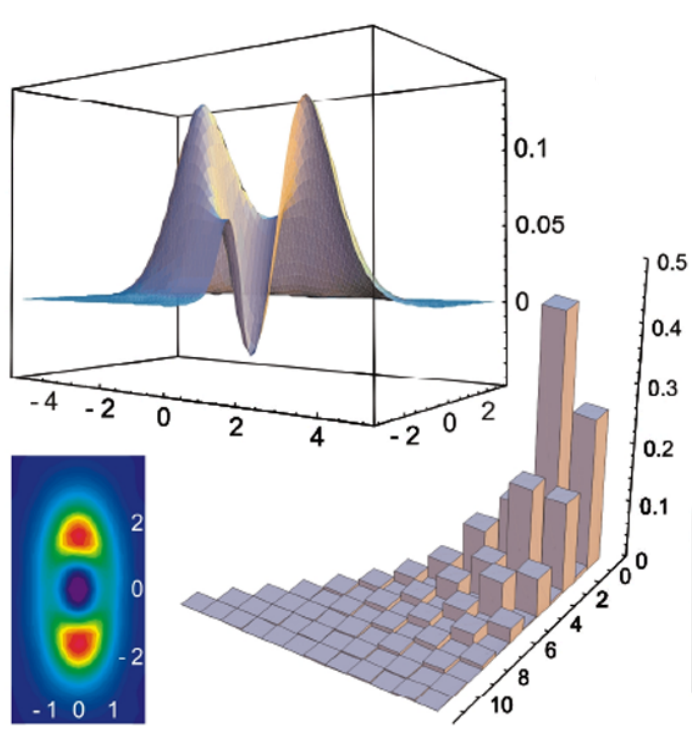
JSNN, BM Nielsen, C Hettich, K Mølmer & ES Polzik, PRL 97, 083604 (2006)
- and many others since then
squeezed qubits
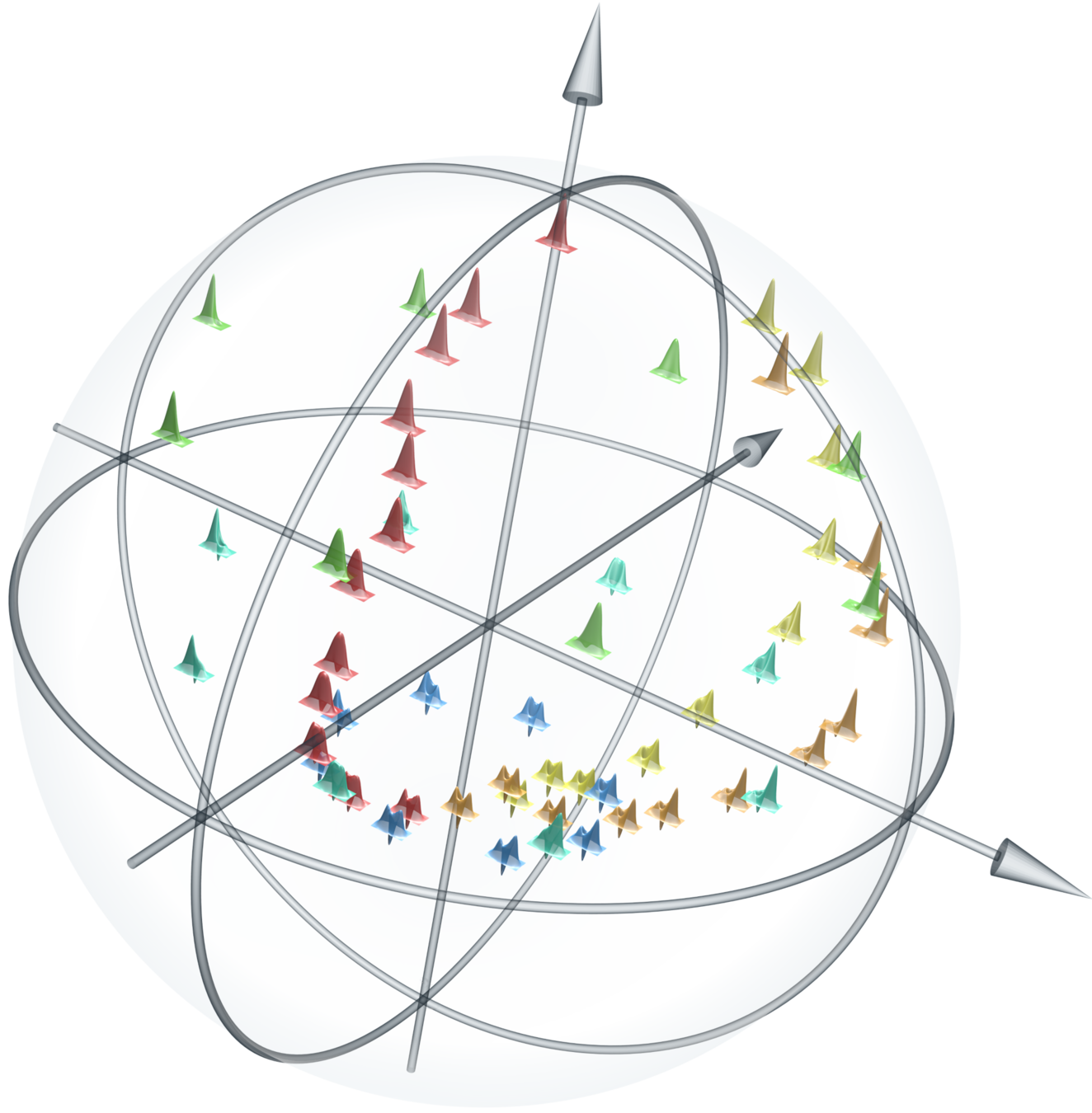
ambiguous photon subtraction (PS)
arbitrary superposition of PS and no-PS squeezed vacuum:
JSNN, M Takeuchi, K Wakui, H Takahashi, K Hayasaka,
M Takeoka & M Sasaki, PRL 105, 053602 (2010)
Schrödinger kittens
Squeezed photon is very similar to small-amplitude "Schrödinger cat" state, a superposition of clearly distinguishable coherent states
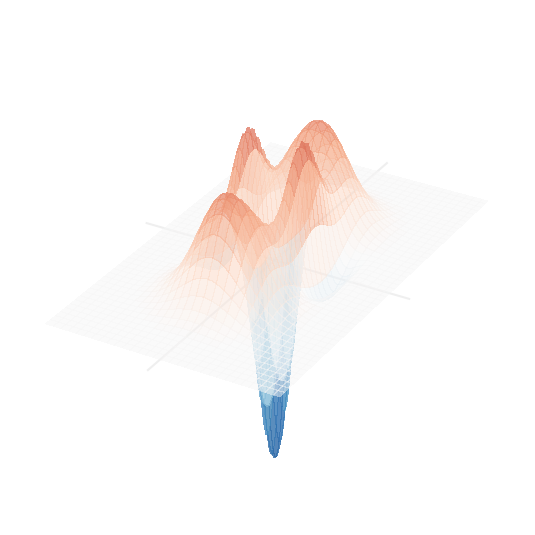

towards macroscopic quantum superpositions

larger states
more modes
massive physical systems
larger states
more modes
massive physical systems
micro-macro entangled states
micro-macro entangled states
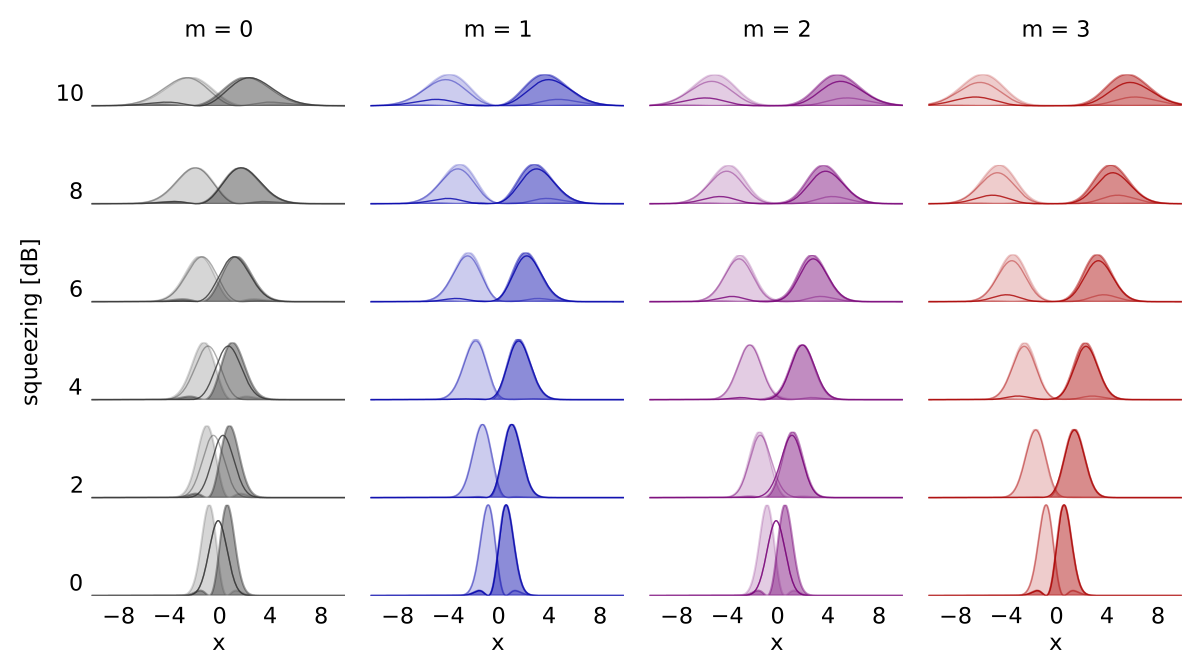
UL Andersen & JSNN, PRA 88, 022337 (2013)

larger states
more modes
massive physical systems
non-Gaussian cluster states
non-Gaussian cluster states
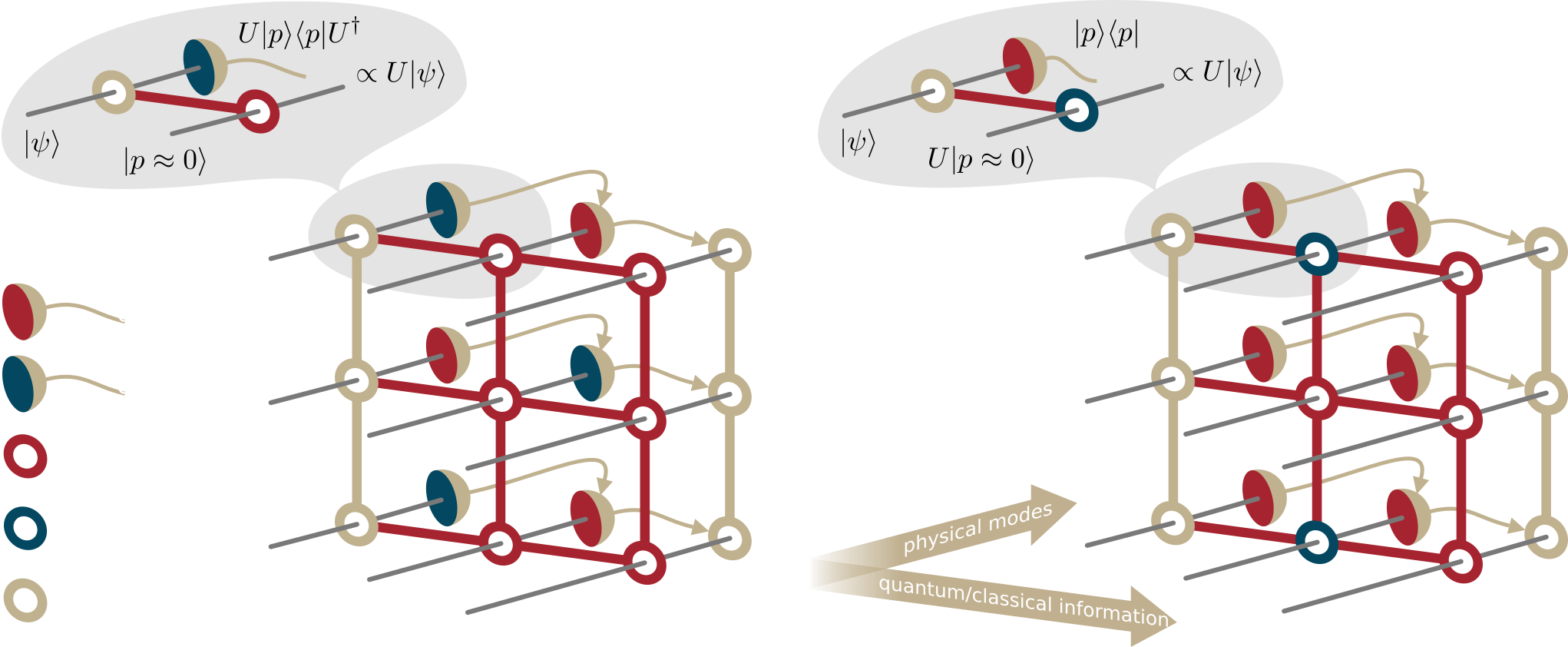
measurement-based quantum computation paradigm:
multimode-entanglement + measurement and feed-forward
Implement with temporal and spatial modes in fibres
- based on scheme by N. Menicucci, demonstrated in A. Furusawa lab:
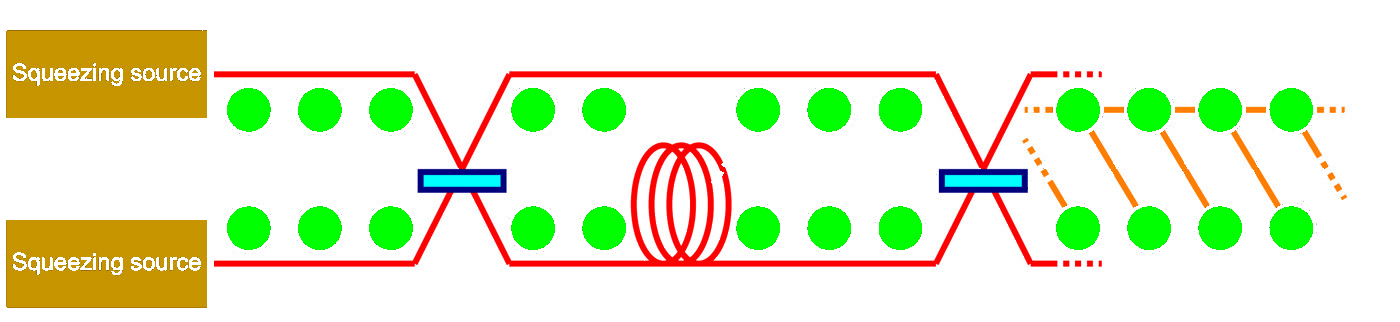
S Yokoyama et al., Nature Photonics 7, 982 (2013)
non-Gaussian cluster states
larger states
more modes
massive physical systems
"mechanical kittens"

"mechanical kittens"


grand goal: bring mechanical object in superposition of being "here" and "there"
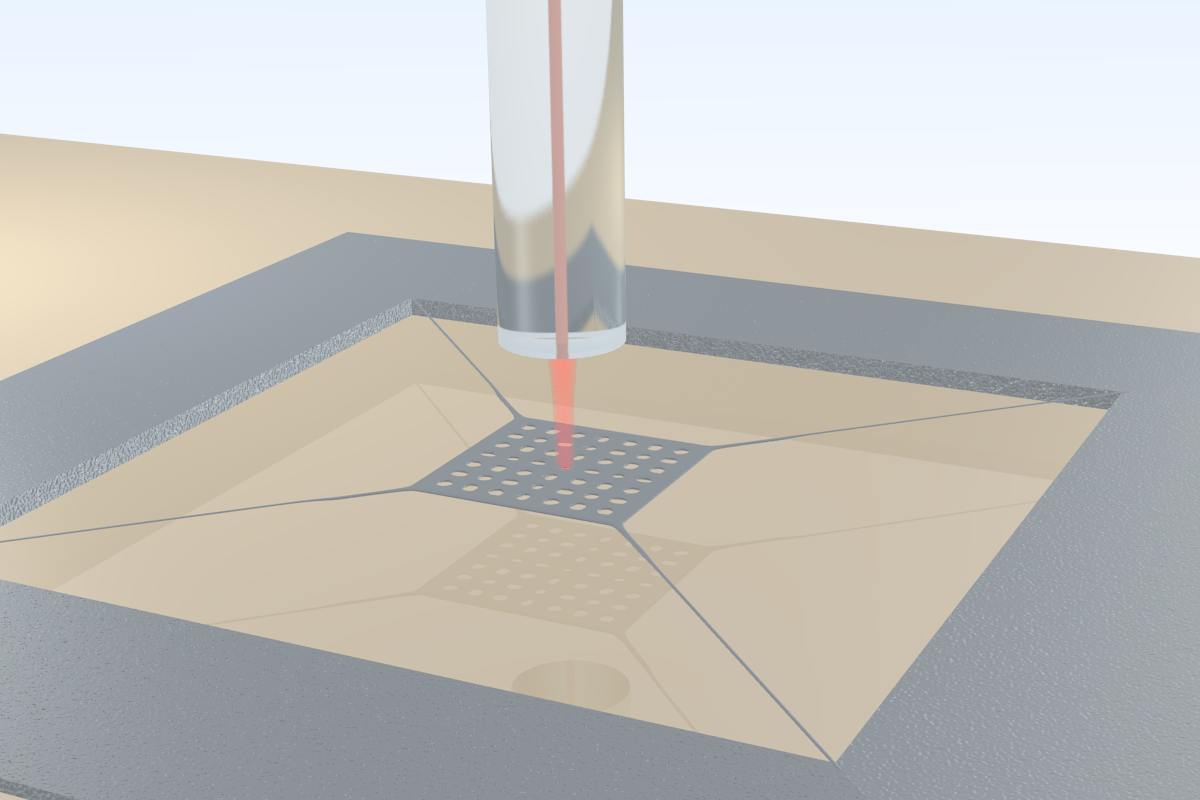
cavity opto-mechanical interaction: radiation pressure / phase shift
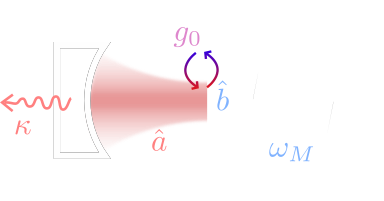
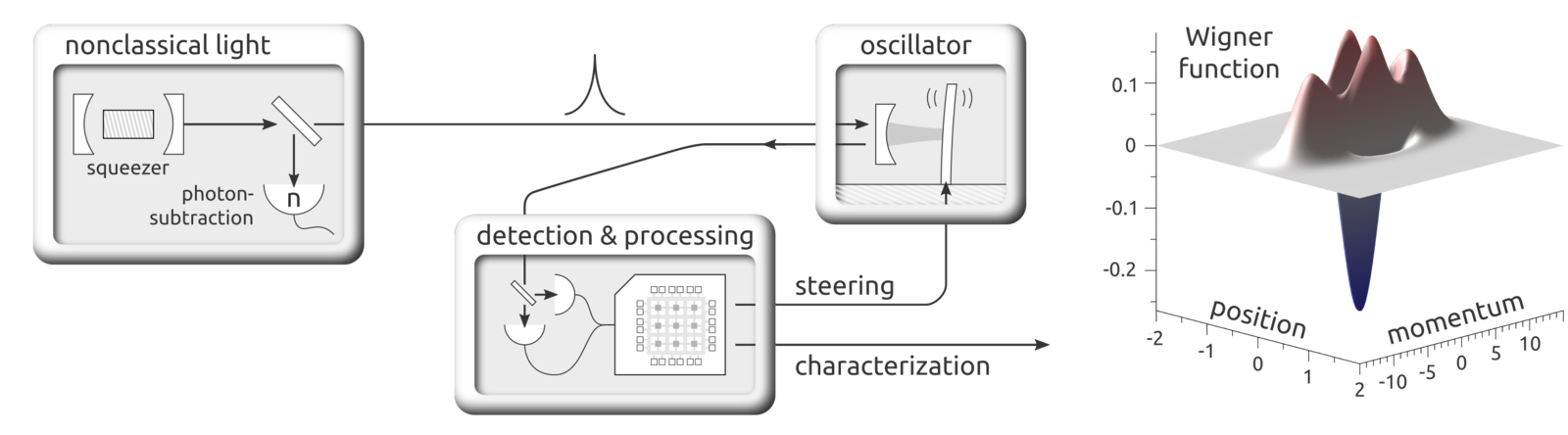
"mechanical kittens"
"mechanical kittens"
blessing and curse: large superpositions are extremely fragile and sensitive to e.g. phase noise - may be used for probing decoherence effects
UB Hoff, J Kollath-Bönig, JSNN, UL Andersen, PRL 117, 143601 (2016)
conclusion
non-Gaussian quantum optics have rich applications in
fundamental quantum mechanics
and quantum information processing
QPIT / bigQ

Xueshi Guo
Shuro Izumi
Dennis Høj
Kristian-Rasmussen
Jan Bilek
Casper Breum
Joost van der Heijden
Ulrik Andersen
Mikkel Larsen, Ulrich Hoff, Jens Arnbak
Thank you!


